A Framework for Analysis and Prediction of Operational Risk Stress
Abstract
:1. Introduction
“The main purpose of the stress-testing framework is to provide a forward-looking, quantitative assessment of the capital adequacy of the UK banking system as a whole, and individual institutions within it.”
1.1. Operational Risk: A Brief Overview
- The data used for this study (Section 4.1) did not include costs specific to the COVID-19 pandemic. Subsequently, £10 m was allocated to the costs of erecting protective perspex screens in UK bank branches.
- Repair costs following arson at the Wells Fargo Bank in Visalia, California, were estimated at $100,000. See https://eu.visaliatimesdelta.com/story/news/2020/04/22/arsonist-sets-fire-wells-fargo-causing-100-k-damage/3005549001/ (accessed on 6 January 2021).
- In October 2020, Goldman Sachs was fined £48,308,400 for breaches of conduct regulations (https://www.fca.org.uk/news/news-stories/2020-fines (accessed on 6 January 2021)).
- Monzo Bank reimbursed a customer £19,000 following an authorised push payment fraud (https://www.lovemoney.com/news/97578/authorised-push-payment-scam-compromised-account-direct-debits (accessed on 6 January 2021)).
- Smaller items included in the data set used for this study (see Section 4.1) include £9 (“compensation payment”), £10 (“reconciliation write-off”), and £68 (marked as “Simply thank you”).
1.2. Acronyms and Abbreviations
- OpRisk: Operational Risk
- VaR: Value-at-Risk
- CPBP: Clients, Products, and Business Practices, one of the seven categories discussed Section 1.3
- IF, EF, EPWS, DPA, BDSF, and EDPM: The remaining six risk categories. They are defined in Section 1.3
- Capital: Cash retained by banks annually for use as a buffer against unforeseen expenditure, details of which are specified by national regulatory bodies
- CCAR: Comprehensive Capital Analysis and Review (the US stress test regulations)
- FSF: Forward Stress Framework (the methodology presented in this paper)
- BoE: Bank of England
- ECB: European Central Bank
- Fed: Federal Reserve Bank
- GoF: Goodness-of-Fit (in the context of statistical distributions)
- TNA: The Transformed Normal ’A’ goodness-of-fit test, discussed in reference [5].
1.3. Operational Risk: Categorisation
1.4. Operational Risk: Measurement
2. Literature Review
2.1. Stress Testing Regulatory History
2.2. Financial Stress Testing Approaches
2.2.1. Forward Stress Testing
2.2.2. Reverse Stress Testing
2.2.3. Bayesian Stress Testing
2.3. Correlation of Operational Risk Losses with Economic Data
- There were increases in OpRisk losses during the 2008 crisis period, mostly for external fraud and process management.
- There was a decrease in internal fraud during the same period.
- In each risk category considered, there was a notable decline in OpRisk losses between 2002 and 2011, with an upwards jump in 2008.
- A conclusion that the effects of an economic shock on OpRisk losses is not persistent.
The US Federal Reserve Board’s Regression Model
- A loss distribution model incorporating sums of random variables (see [30])
- A predictor of future losses to account for potential significant and infrequent events
- A linear regression using a set of macroeconomic factors as explanatory variables. The regressand is industry-aggregated operational-risk losses.
- Projected losses allocated to firms based on their size
2.4. Operational Risk Stress Testing in Practice
- Many banks take the BoE guidance literally and base predictions on economic scenario correlations, with the addition of the ECB lower limit. That approach would not be adequate for severe stress.
- Others use the LDA method described in Section 1.4 and supplement historic OpRisk losses with additional “synthetic losses” that represent scenarios. That approach necessitates a reduction in the array of economic data (as supplied by a regulatory authority) to a short list of impacts that can be used in an LDA process. The idea is to consider specific events that could lead to a consequential total loss via all viable pathways. Fault Tree Analysis is a common technique used to trace and value those paths. The task is usually performed by specialist subject matter experts, and a discussion may be found in [31]. There is a brief description of the “Impact-Horizon” form of such scenarios in Section 3.3. The horizon would be set to 1 year, for which the interpretation is that at least one loss with the stated impact or more is expected in the next year.
- A common way to implement known but as yet unrealised OpRisk liabilities (such as anticipated provisions) is to regard the liability as a realised loss and to recalculate capital on that basis. The same often applies for “near miss” losses, which did not actually result in an OpRisk loss but could have done with high probability. An example is a serious software error that was identified just as new software was about to be installed and was then corrected just before installation.
3. Method: Forward Stress Framework
3.1. Forward Stress Framework: Operation
| Algorithm 1: Forward Stress Framework (FSF) process | |
| |
Parameter Prediction
3.2. Stress Factor Calculation
3.3. Theoretical Basis of the FSF
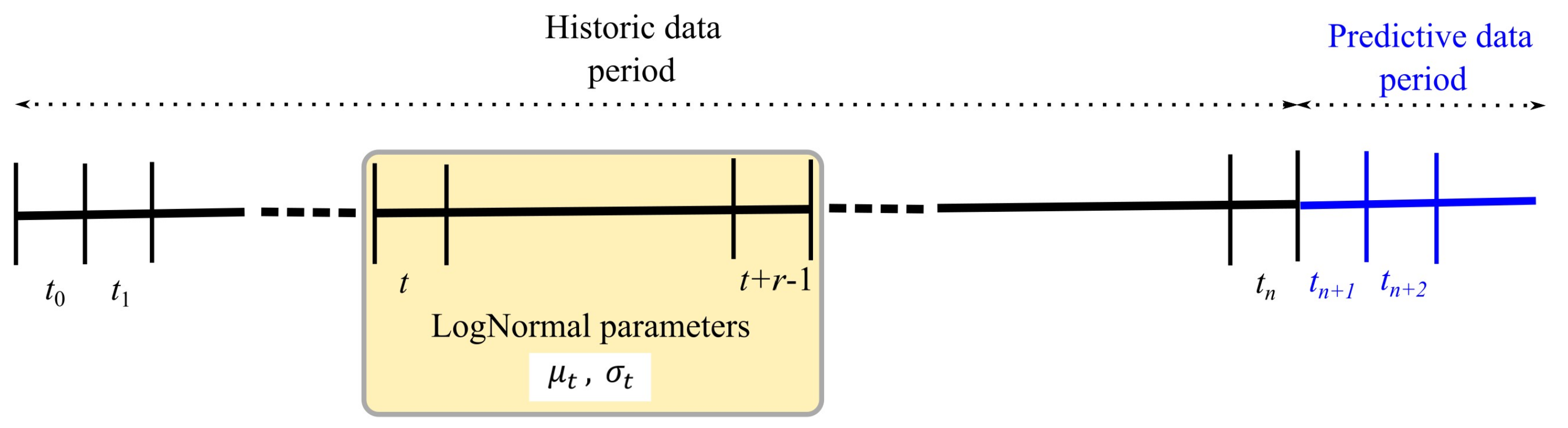
- A calculation of the estimated lognormal parameters and , the details of the discrete version of which are in Equation (5). Nominally, is one quarter.
- Generation of a random sample of size lognormal losses using and , where is the number of days in the period .
- Calculate the stress factor (Equation (6)) .
- Apply the stress in the form .
Stress Factor Types
3.4. Choice of Distribution
4. Results
4.1. Data and Implementation
- UK.Real.GDP; UK.CPI; UK.Unemployment.Rate;
- UK.Corporate.Profits; UK.Residential.Property; UK.Equity.Prices;
- Bank.Rate; Sterling.IG.Corp.Bond.Spread; Secured.Lending.Individuals;
- Consumer.Credit.Individuals; Oil.Price;
- Volatility.Index; GBPEUR; GBPUSD.
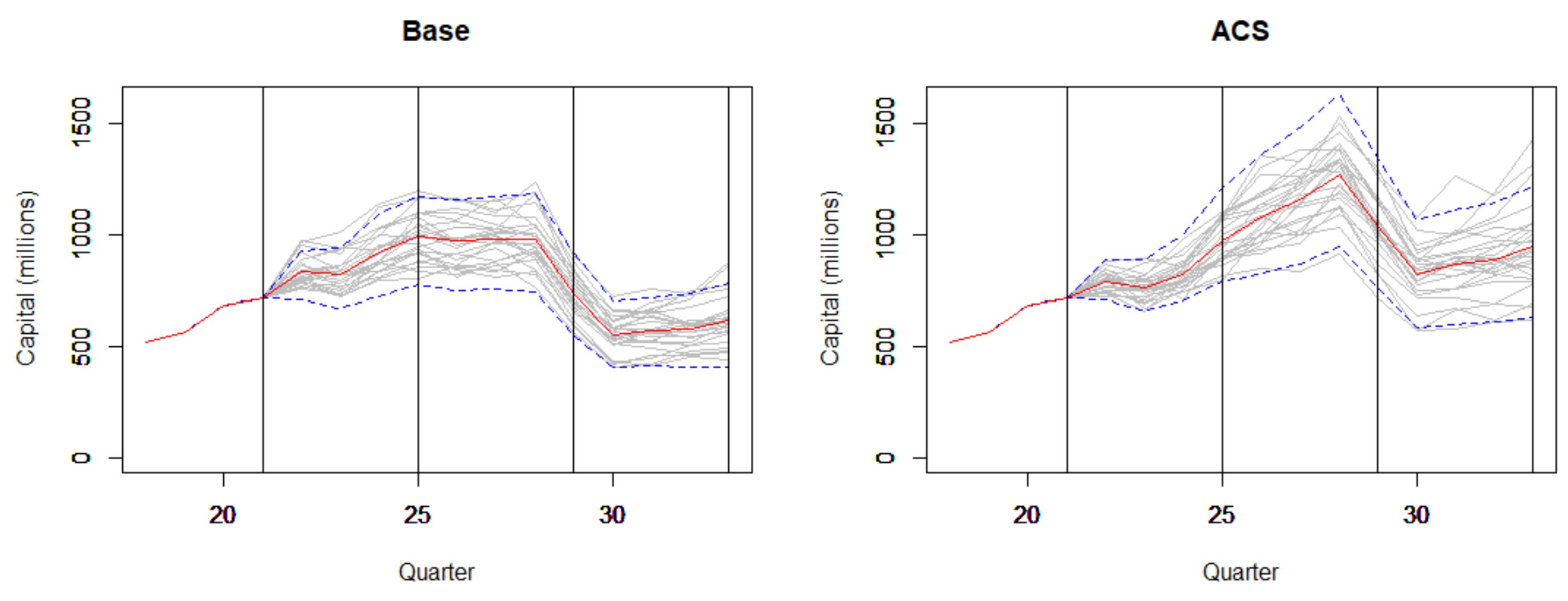
4.2. Forward Stress Framework Results
4.2.1. Forward Stress Framework Predictions
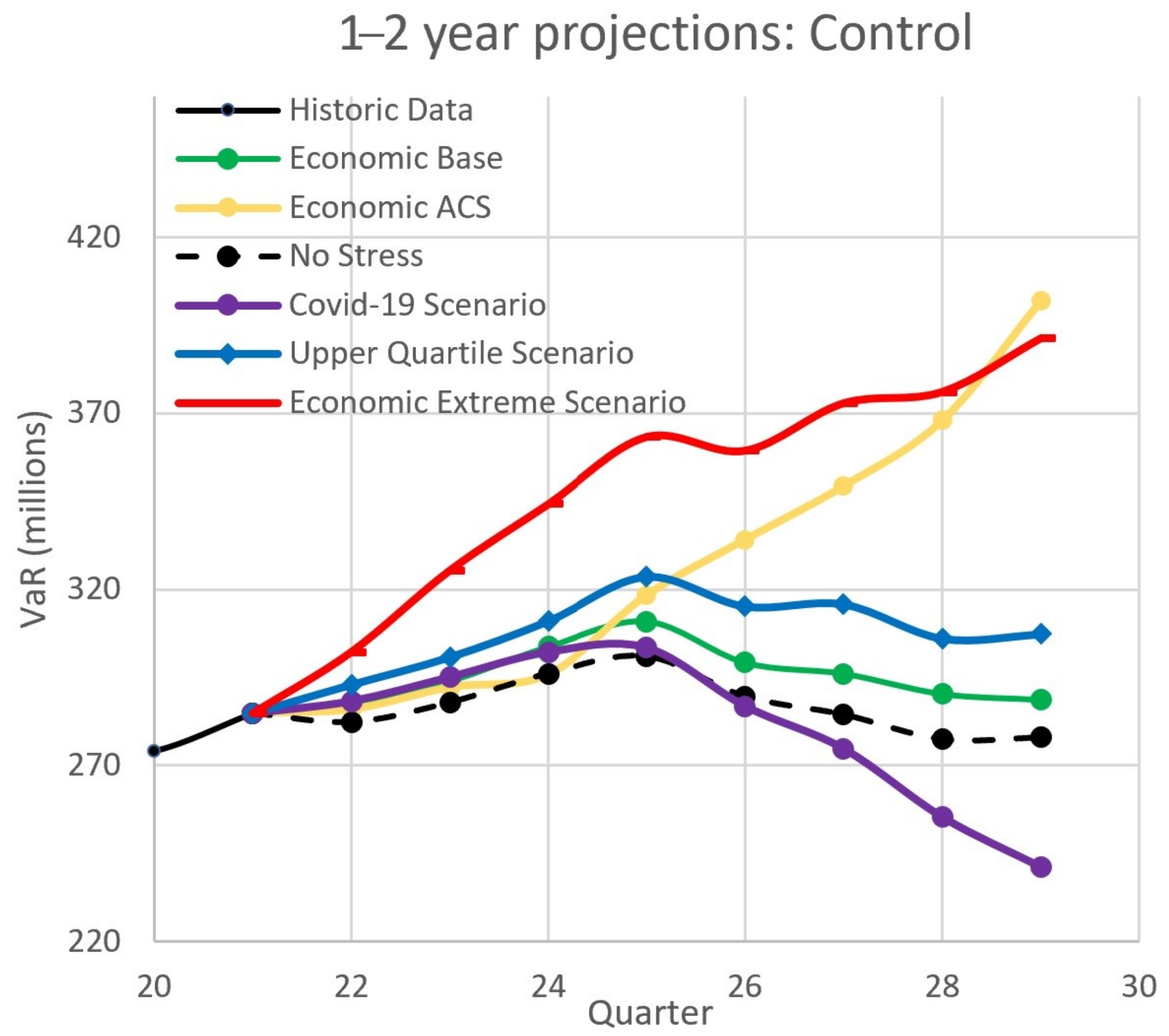
4.2.2. Projections: Economic and Scenario Stress
4.2.3. The Effect of Global Warming
4.3. Results Using Other Distributions
- Does the model predict a sufficient distinction between the “no stress” case and stresses due to the base and ACS scenarios in both 1 and 2 years?
- As many as possible data sets tested should pass an appropriate GoF test.
- Are predicted capitals consistent with the capital calculated using empirical losses only. We expect capitals predicted using a distribution to be greater than the capitals calculated using empirical losses only, since the empirical capital is limited by the maximum loss. Capitals calculated from distributions are theoretically not bounded above. However, they should not be “too high”. As our “rule of thumb”, 5 times the empirical capital would to “too high”.
4.4. Correlation Results
- There were 15 economic indicators.
- Only one (UK.CPI) was significantly correlated (at 95% significance) with nonCPBP loss severity.
- Only two (Bank.Rate and Volatility.Index) were not significantly correlated with nonCPBP loss frequency.
- Eleven significant frequency correlations were at a confidence level of 99% or more.
- Two significant frequency correlations were at a confidence level of between 95% and 99%.
Correlation Persistence
4.5. Inappropriate Correlations
5. Discussion
5.1. Economic Effects of Operational Risk: Intuitions
5.2. Overall Assessment of the FSF
- Advantages:
- (a)
- It is flexible: stress factors can be added or removed easily.
- (b)
- Correlation is not assumed.
- (c)
- Using projected losses eliminates idiosyncratic shocks since it assumes a “business as usual” environment.
- (d)
- Generating projected losses allows for modification of all or some of the projected losses, which is more flexible than modifying single capital values.
- (e)
- The degree of stress for any given stress type can be geared to achieve any (reasonable) required amount of retained capital. This is an objective way to calculate capital, based on factors that could affect capital.
- (f)
- The framework is able to detect the relative effects of the stress types considered. Some have little effect (e.g., global warming), whereas others have a significant effect (e.g., increasing the largest loss).
- Disadvantages:
- (a)
- It is not entirely straightforward to include stresses that act on parts of the projected data only. Specialised procedures must be used to generate the necessary stress factors.
- (b)
- Generating projected losses requires a loss frequency of approximately 250 per year. Accuracy is lost with fewer losses. For that reason, the aggregate risk class nonCPBP was used to obtain an overall view of the effect of stress.
- (c)
- Special treatment is needed for stresses that have a decreasing trend with time but are thought to increase capital. Decreasing stress values would result in stress factors that are less than 1. We suggest replacing a stress factor by in such cases. Stresses in this category have to be identified in advance of calculating stress factors.
- (d)
- There is no objective way to decide what stress types should be used.
5.3. Guidance for Practitioners, Modellers, and Regulation
5.3.1. Regulation
5.3.2. Modelling
5.3.3. Practice
6. Conclusions
- Predictions of OpRisk capital based on economic factor correlations is unsafe, as statistically significant correlations do not always exist. The proposed FSF provides a viable alternative to naive use of correlations in the context of OpRisk/Economic factor stress testing.
- The FSF works by calculating stress factors based on changes in economic factors (or any other stress type) and by applying them to projected OpRisk losses. As such, it acknowledges that OpRisk capital should increase in response to economic stress.
- The FSF is flexible and responsive. It allows for investigation using appropriate time series (not only the BoE economic data) as well as using user-defined scenarios.
- FSF has a disadvantage in that it requires a minimal volume of data to generate the necessary samples and predictions. Therefore, using individual Basel risk classes is not always feasible.
Further Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
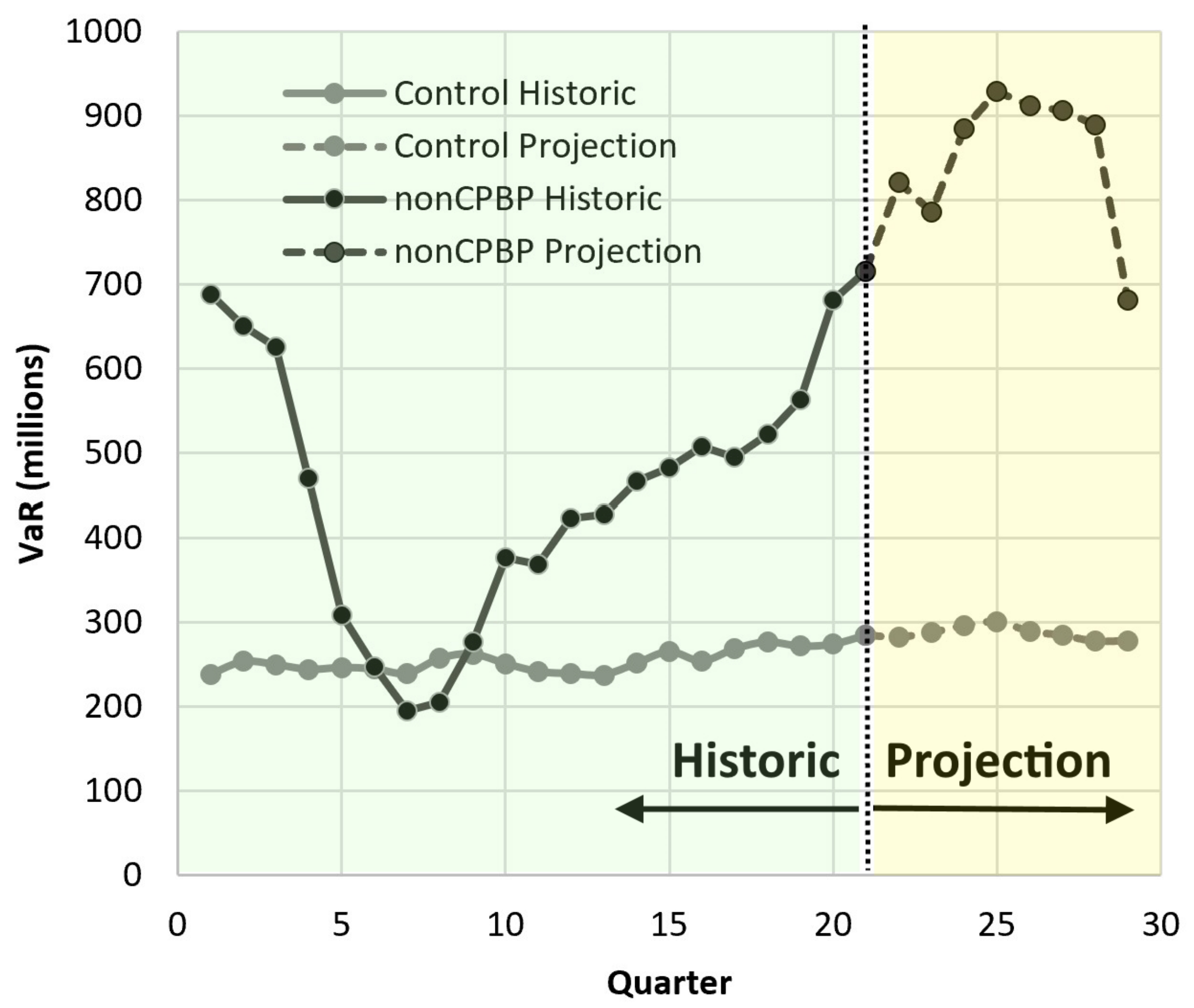
Appendix A. Upper and Lower Confidence Surfaces
- Very uneven surfaces due to data volatility.
- Increasing capital with increasing time, apart from quarters 27 and 28, when there were much reduced losses.
- Small overall increases in capital with increasing stress.
- Non-divergent upper and lower confidence surfaces, indicating a stable stochastic error component.

Appendix B. Stress Factor Produced by Using a Supplied Formula
- sf.1 <- replicate( floor(0.25∗length(DATA)), 1.5);
- sf.2 <- replicate(length(DATA) - floor(0.25∗length(DATA)), 1);
- STF <- c(sf.1,sf.2)
- txt <- "DATA <- sort(DATA, decreasing = T); " # sort DATA
- # Read formula
- txt <- paste(txt, Formula_Q4[Formula_Q4$Quarter==qtr,], sep="")
- # Evaluate formula and to output STF
- eval(parse(text = txt))
Appendix C. Scenario-Defined Stress Factors
Appendix D. Sensitivity of Capital with Respect to the Stress Factor
- R = Rao[m, s, lambda, r, u, n, p]
- CU = q + zc R
- dCU = dlambda D[CU, lambda]
- CL = q - zc R
- dCL = dlambda D[CL, lambda]
- Left-hand-most term
- Middle term
- Right-hand-most term
References
- Bank of England. Stress Testing. Available online: https://www.bankofengland.co.uk/stress-testing (accessed on 16 December 2020).
- European Central Bank. 2020 EU-Wide Stress Test—Methodological Note. Available online: https://eba.europa.eu/documents/10180/2841396/2020+EU-wide+stress+test+-+Draft+Methodological+Note.pdf (accessed on 16 December 2020).
- US Federal Reserve Bank. Dodd-Frank Act Stress Test 2019: Supervisory Stress Test Methodology. Available online: https://www.federalreserve.gov/publications/files/2019-march-supervisory-stress-test-methodology.pdf (accessed on 16 December 2020).
- Basel Committee on Banking Supervision. International Convergence of Capital Measurement and Capital Standards, Clause 644. Available online: https://www.bis.org/publ/bcbs128.pdf (accessed on 8 February 2021).
- Mitic, P. Improved Goodness-of-Fit Tests for Operational Risk. J. Oper. Risk 2015, 15, 77–126. [Google Scholar] [CrossRef]
- Jorion, P. Value at Risk: The New Benchmark for Managing Financial Risk, 3rd ed.; McGraw Hill: New York, NY, USA, 2007. [Google Scholar]
- Basel Committee on Banking Supervision. QIS 2: Summary of Results. Available online: https://www.bis.org/bcbs/qis/qisresult.htm (accessed on 16 December 2020).
- Mitic, P. Conduct Risk: Distribution Models with Very Thin Tails. In Proceedings of the 3rd International Conference on Numerical and Symbolic Computation Developments and Applications (SYMCOMP 2017), Guimarães, Portugal, 6–7 April 2017. [Google Scholar]
- Mitic, P.; Hu, J. Estimation of value-at-risk for conduct risk losses using pseudo-marginal Markov chain Monte Carlo. J. Oper. Risk 2019, 14, 1–42. [Google Scholar] [CrossRef]
- Frachot, A.; Georges, P.; Roncalli, T. Loss Distribution Approach for Operational Risk. Available online: http://ssrn.com/abstract=1032523 (accessed on 16 December 2020).
- Baudino, P.; Goetschmann, R.; Henry, J.; Taniguchi, K.; Zhu, W. FSI Insights on Policy Implementation No 12: Stress-Testing Banks—A Comparative Analysis. Available online: https://www.bis.org/fsi/publ/insights12.pdf (accessed on 16 December 2020).
- Blaschke, W.; Jones, M.; Majnoni, G.; Peria, S. Stress Testing of Financial Systems: An Overview of Issues, Methodologies, and FASP Experiences. Available online: https://www.imf.org/external/pubs/ft/wp/2001/wp0188.pdf (accessed on 16 December 2020).
- Basel Committee on Banking Supervision. Amendment to the Capital Accord to Incorporate Market Risks. Available online: www.bis.org/publ/bcbs24.pdf (accessed on 17 December 2020).
- Basel Committee on Banking Supervision. Stress Testing Principles. Available online: https://www.bis.org/bcbs/publ/d450.pdf (accessed on 17 December 2020).
- Axtria Inc. Portfolio Stress Testing Methodologies. Available online: https://insights.axtria.com/whitepaper-portfolio-stress-testing-methodologies (accessed on 3 October 2020).
- Drehmann, M. Macroeconomic stress-testing banks: A survey of methodologies. In Stress-Testing the Banking System: Methodologies and Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Grundke, P. Reverse stress tests with bottom-up approaches. J. Risk Model Valid. 2011, 5, 71–90. [Google Scholar] [CrossRef] [Green Version]
- Rebonato, R.; Denev, A. A Bayesian Approach to Stress Testing and Scenario Analysis. J. Investig. Manag. 2010, 8, 1–13. [Google Scholar]
- De Fontnouvelle, P.; DeJesus-Rueff, V.; Jordan, J.S.; Rosengren, E.S. Capital and Risk: New Evidence on Implications of Large Operational Losses. J. Money Credit Bank. 2006, 38, 1819–1846. [Google Scholar] [CrossRef] [Green Version]
- Allen, L.; Bali, T. Cyclicality in catastrophic and operational risk measurements. J. Bank. Financ. 2006, 31, 1191–1235. [Google Scholar] [CrossRef] [Green Version]
- Moosa, I. Operational risk as a function of the state of the economy. Econ. Model. 2011, 28, 2137–2142. [Google Scholar] [CrossRef]
- Cope, E.W.; Antonini, G. Observed correlations and dependencies among operational losses in the ORX consortium database. J. Oper. Risk 2008, 3, 47–74. [Google Scholar] [CrossRef]
- Cope, E.W.; Piche, M.T.; Walter, J.S. Macroenvironmental determinants of operational loss severity. J. Bank. Financ. 2012, 36, 1362–1380. [Google Scholar] [CrossRef]
- Cope, E.W.; Carrivick, L. Effects of the financial crisis on banking operational losses. J. Oper. Risk 2013, 8, 3–29. [Google Scholar] [CrossRef]
- Bank of England. Financial Stability Report June. Available online: www.bankofengland.co.uk/financial-stability-report/2018/june-2018 (accessed on 18 December 2020).
- Bank of England. Financial Stability Report, Financial Policy Committee Record and Stress Testing Results—December 2019. Available online: https://www.bankofengland.co.uk/financial-stability-report/2019/december-2019 (accessed on 18 December 2020).
- Bank of England. Interim Financial Stability Report May 2020. Available online: https://www.bankofengland.co.uk/-/media/boe/files/financial-stability-report/2020/may-2020.pdf (accessed on 18 December 2020).
- Curti, F.; Migueis, M.; Stewart, R. Benchmarking Operational Risk Stress Testing Models. Available online: https://doi.org/10.17016/FEDS.2019.038 (accessed on 18 December 2020).
- US Federal Reserve Bank. Stress Tests and Capital Planning: Comprehensive Capital Analysis and Review. Available online: https://www.federalreserve.gov/supervisionreg/ccar.htm (accessed on 18 December 2020).
- Klugman, S.A.; Panjer, H.H.; Willmot, G.E. Loss Models, 2nd ed.; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Hassani, B.K. Scenario Analysis in Risk Management; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Risk.net. Stress-Testing Special Report. Available online: https://www.risk.net/stress-testing-special-report-2020 (accessed on 15 February 2020).
- Mitic, P.; Bloxham, N. A Central Limit Theorem Formulation for Empirical Bootstrap Value-at-Risk. J. Model Risk Valid. 2018, 12, 1–34. [Google Scholar] [CrossRef]
- Pascual, A.; Marchini, K.; Miller, S. Identity Fraud: Fraud Enters a New Era of Complexity. Available online: https://www.javelinstrategy.com/coverage-area/2018-identity-fraud-fraud-enters-new-era-complexity (accessed on 20 December 2020).
- Tedder, K.; Buzzar, J. 2020 Identity Fraud Study: Genesis of the Identity Fraud Crisis. Available online: https://www.javelinstrategy.com/coverage-area/2020-identity-fraud-study-genesis-identity-fraud-crisis (accessed on 20 December 2020).
- UK Office for National Statistics. Crime in England and Wales: Appendix Tables (Table A4 Computer Fraud). Available online: https://www.ons.gov.uk/peoplepopulationandcommunity/crimeandjustice/datasets/crimeinenglandandwalesappendixtables (accessed on 20 December 2020).
- Haustein, K.; Allen, M.R.; Forster, P.M.; Otto, F.E.L.; Mitchell, D.M.; Matthews, H.D.; Frame, D.J. A Real-Time Global Warming Index. Sci. Rep. 2017, 7, 15417. [Google Scholar] [CrossRef] [Green Version]
- Risk.net. Op Risk Data: Losses Plummet During Lockdown (ORX News). Available online: https://www.risk.net/comment/7652866/op-risk-data-losses-plummet-during-lockdown (accessed on 20 December 2020).
- World Bank. Commodities Markets. ’Pink Sheet’ Data Monthly. Available online: https://www.worldbank.org/en/research/commodity-markets (accessed on 20 December 2020).
- Financial Stability Institute: Bank for International Settlements. Covid-19 and Operational Resilience: Addressing Financial Institutions’ Operational Challenges in a Pandemic. Available online: https://www.bis.org/fsi/fsibriefs2.pdf (accessed on 20 December 2020).
- Rao, C.R. Linear Statistical Inference and Its Applications, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2009. [Google Scholar]

| Year | Type | Mean | SD | Mean | SD |
|---|---|---|---|---|---|
| nonCPBP | Control | ||||
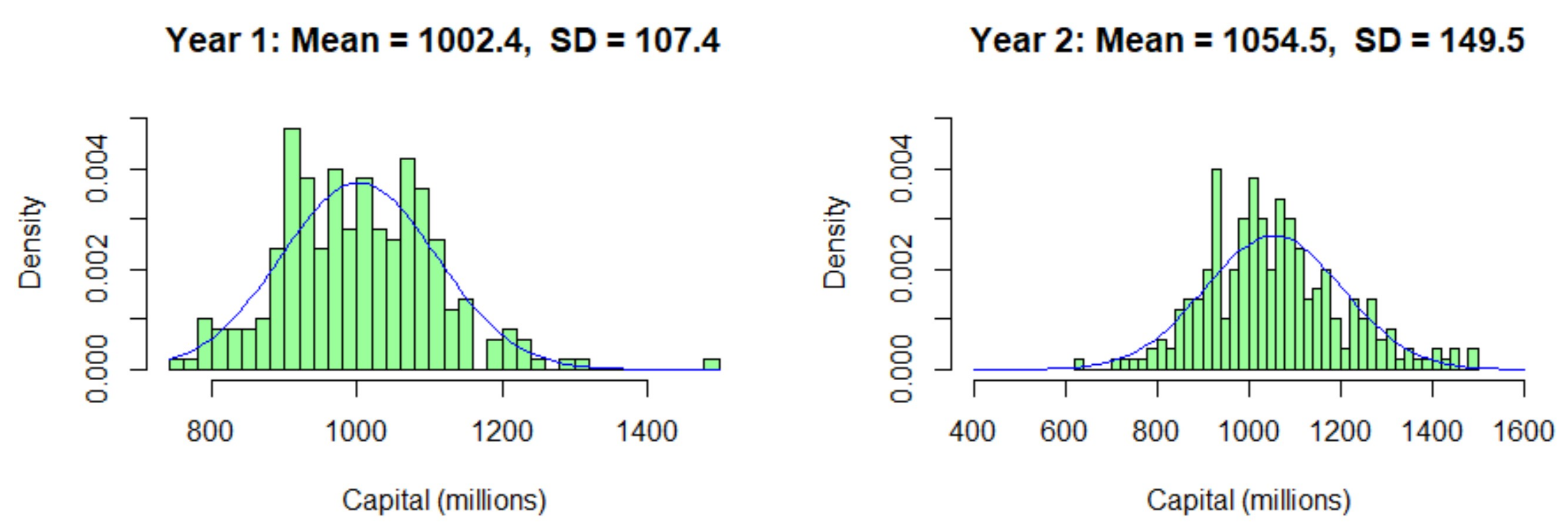
| 1 | Base | 987.48 | 112.05 | 310.86 | 25.47 |
| 2 | Base | 756.89 | 98.66 | 288.69 | 27.68 |
| 1 | ACS | 988.95 | 127.91 | 318.24 | 22.47 |
| 2 | ACS | 1012.45 | 146.94 | 402.02 | 41.73 |
| Stress Movement | Period | nonCPBP | Control |
|---|---|---|---|
| None to Base | 1 year | 5.42 | 3.31 |
| None to Base | 2 year | 7.15 | 3.85 |
| None to ACS | 1 year | 7.97 | 5.76 |
| None to ACS | 2 year | 52.91 | 44.61 |
| None to Extreme | 1 year | 32.25 | 20.72 |
| None to Extreme | 2 years | 65.41 | 40.77 |
| None to COVID-19 | 1 year | −9.07 | 0.84 |
| None to COVID-19 | 2 years | −33.08 |
| Data Set | Period | % Change |
|---|---|---|
| nonCPBP | 1 year | 1.9 |
| nonCPBP | 2 year | 2.2 |
| Control | 1 year | 1.7 |
| Control | 2 year | 1.6 |
| % Increase in Capital Relative to `No Stress’ | ||||
|---|---|---|---|---|
| Distribution | Base Year 1 | Base Year 2 | ACS Year 1 | ACS Year 2 |
| LogNormal | 5.42 | 7.15 | 7.97 | 52.91 |
| Weibull | 5.53 | 7.44 | 14.18 | 18.11 |
| LogGamma | 2.97 | 0.38 | 3.54 | 3.94 |
| Gamma | 0.16 | 3.55 | 2.69 | 7.42 |
| LogNormal Mixture | 1.63 | 3.57 | 26.21 | 13.76 |
| Pareto (Type II) | 1.43 | 2.64 | 15.67 | 9.08 |
| Burr (Type VII) | 1.30 | 2.87 | 16.82 | 17.25 |
| Tukey G&H | 16.61 | 5.21 | 18.87 | 2.42 |
| LogLogistic | 0.93 | 1.50 | 9.91 | 4.94 |
| Distribution | GoF Passes at 5% | Mean TNA Value | Consistency with Empirical VaR |
|---|---|---|---|
| LogNormal | 21 | 0.0262 | Y |
| Weibull | 14 | 0.0654 | N |
| LogNormal Mixture | 3 | 0.0873 | Y |
| Gamma | 21 | 0.0387 | N |
| LogGamma | 21 | 0.0159 | Y |
| Pareto (Type II) | 9 | 0.069 | N |
| Burr (Type VII) | 21 | 0.0569 | N |
| Tukey G&H | 3 | 0.083 | N |
| LogLogistic | 21 | 0.0174 | N |
| Economic Factor | nonCPBP | Control | ||
|---|---|---|---|---|
| 99% | 95% | 99% | 95% | |
| UK.Real.GDP | 1 | 1 | 17 | 0 |
| UK.CPI | 1 | 1 | 17 | 0 |
| UK.Unemployment.Rate | 0 | 0 | 17 | 1 |
| UK.Corporate.Profits | 1 | 1 | 17 | 0 |
| UK.Residential.Property | 0 | 0 | 20 | 1 |
| UK.Equity.Prices | 0 | 1 | 6 | 4 |
| Bank.Rate | 0 | 0 | 5 | 2 |
| Sterling.Corp.Bond.Spread | 0 | 0 | 0 | 2 |
| Secured.Lending.Individuals | 0 | 0 | 17 | 0 |
| Consumer.Credit.Individuals | 1 | 1 | 12 | 1 |
| Oil.Price | 0 | 0 | 9 | 4 |
| Volatility.Index | 0 | 3 | 0 | 0 |
| GBPEUR | 0 | 0 | 7 | 1 |
| GBPUSD | 0 | 0 | 9 | 2 |
| Severity | Frequency | |||
|---|---|---|---|---|
| Significance level | 99% | 95% | 99% | 95% |
| significant correlations | 1.4 | 2.7 | 52.0 | 6.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitic, P. A Framework for Analysis and Prediction of Operational Risk Stress. Math. Comput. Appl. 2021, 26, 19. https://doi.org/10.3390/mca26010019
Mitic P. A Framework for Analysis and Prediction of Operational Risk Stress. Mathematical and Computational Applications. 2021; 26(1):19. https://doi.org/10.3390/mca26010019
Chicago/Turabian StyleMitic, Peter. 2021. "A Framework for Analysis and Prediction of Operational Risk Stress" Mathematical and Computational Applications 26, no. 1: 19. https://doi.org/10.3390/mca26010019
APA StyleMitic, P. (2021). A Framework for Analysis and Prediction of Operational Risk Stress. Mathematical and Computational Applications, 26(1), 19. https://doi.org/10.3390/mca26010019





