Prediction of Maximum Pressure at the Roofs of Rectangular Water Tanks Subjected to Harmonic Base Excitation Using the Multi-Gene Genetic Programming Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Modelling
2.1.1. Computational Setup
2.1.2. CFD Details
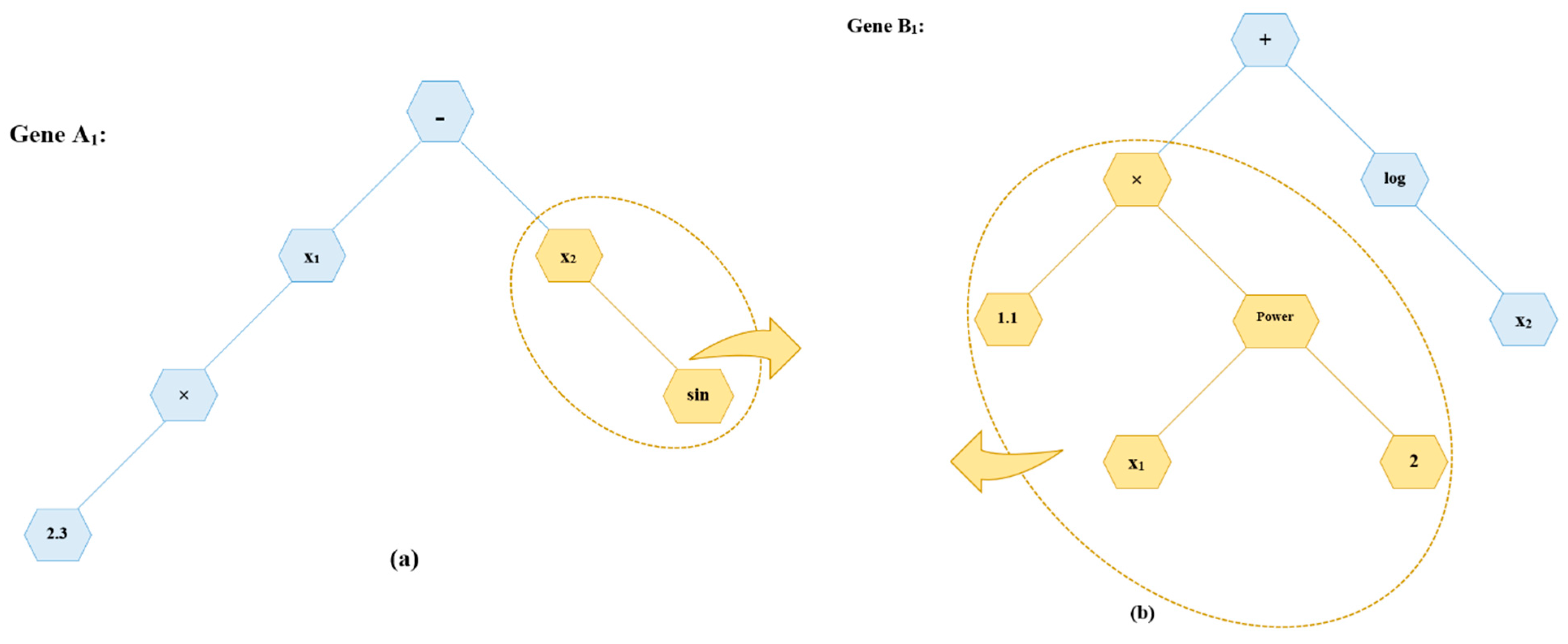
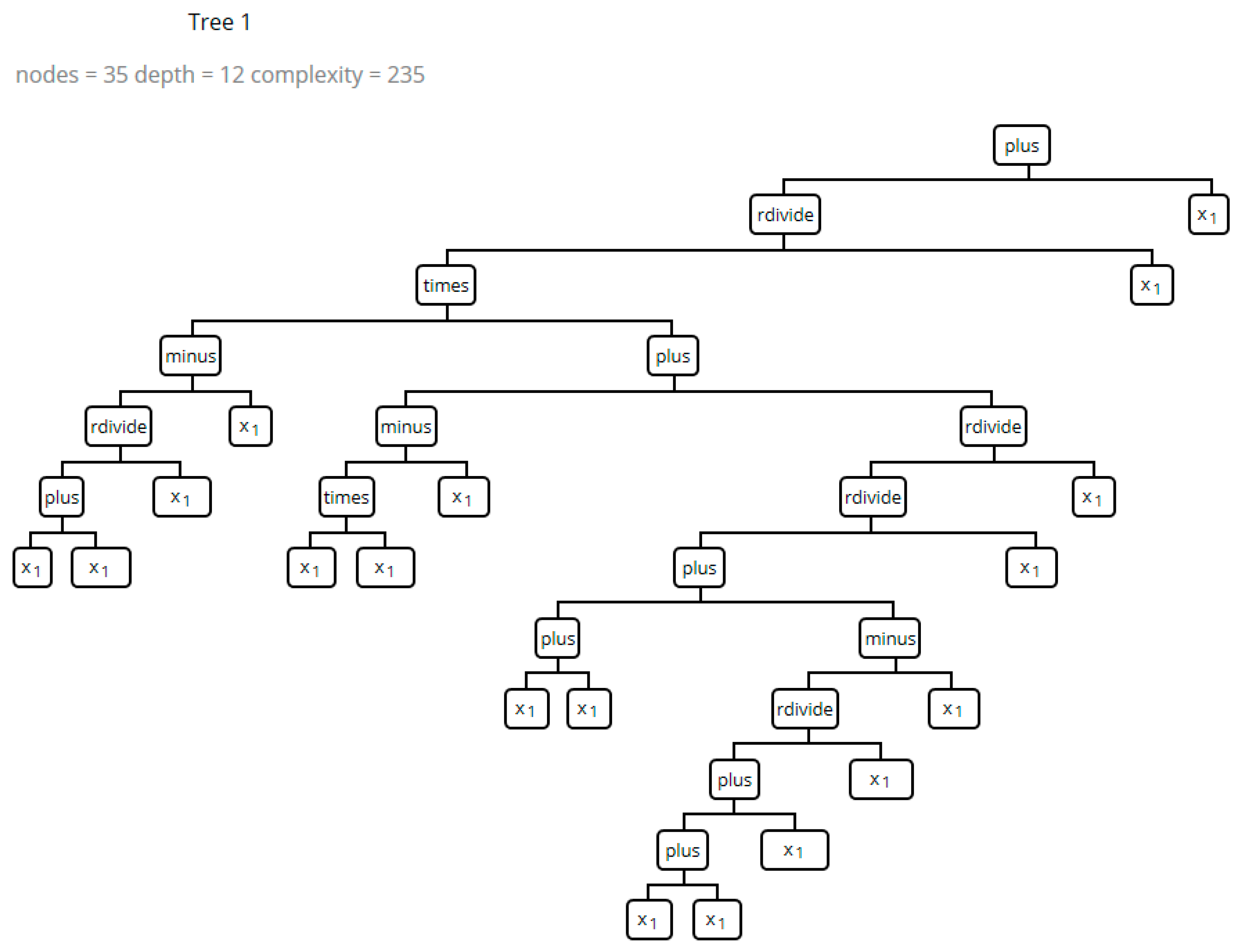
2.2. Genetic Programming
- A set of variables is initiated.
- The chromosomes’ architecture is defined.
- The chromosomes are randomly formulated.
3. Results and Discussion
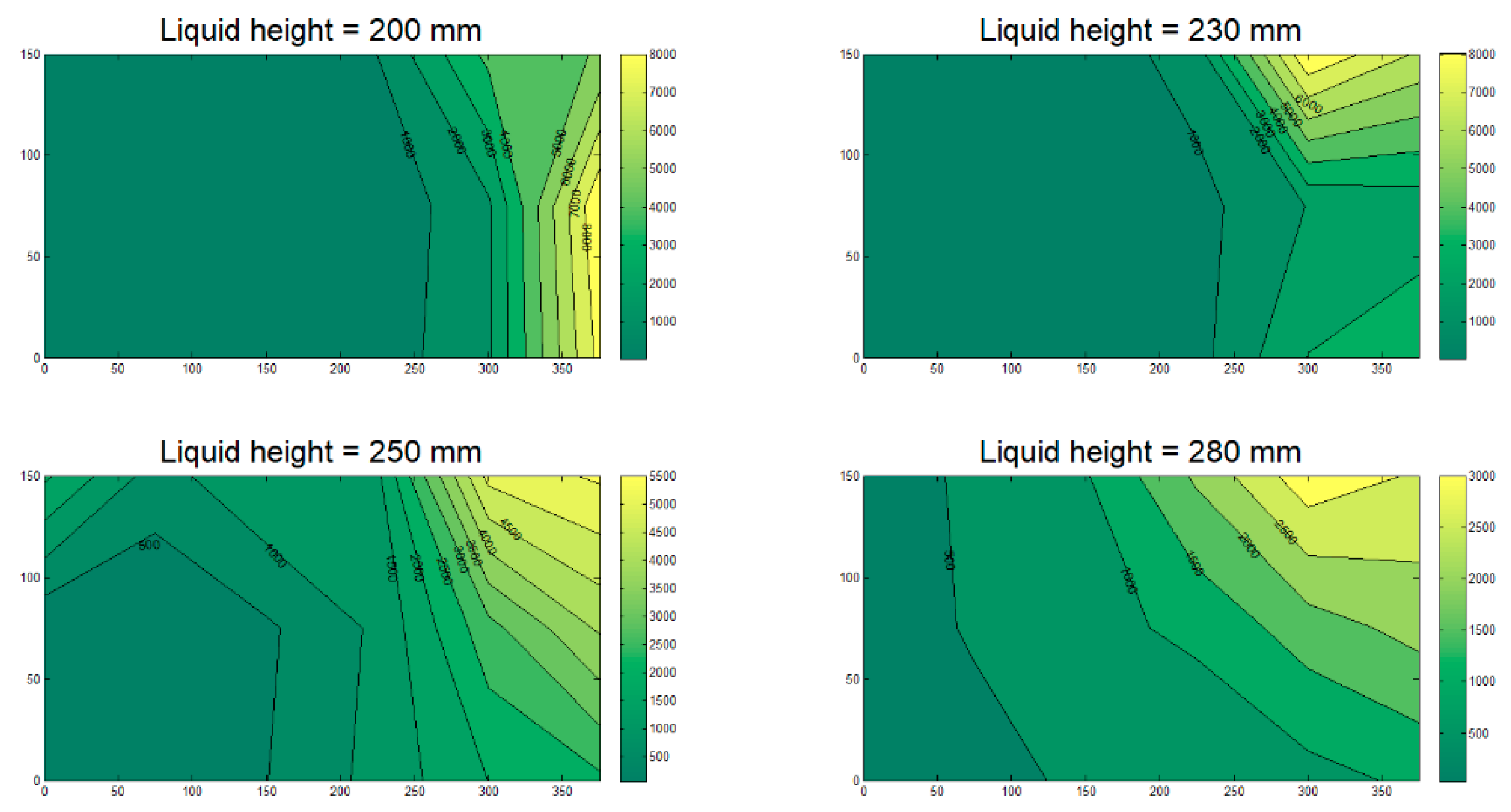
3.1. Numerical Modelling
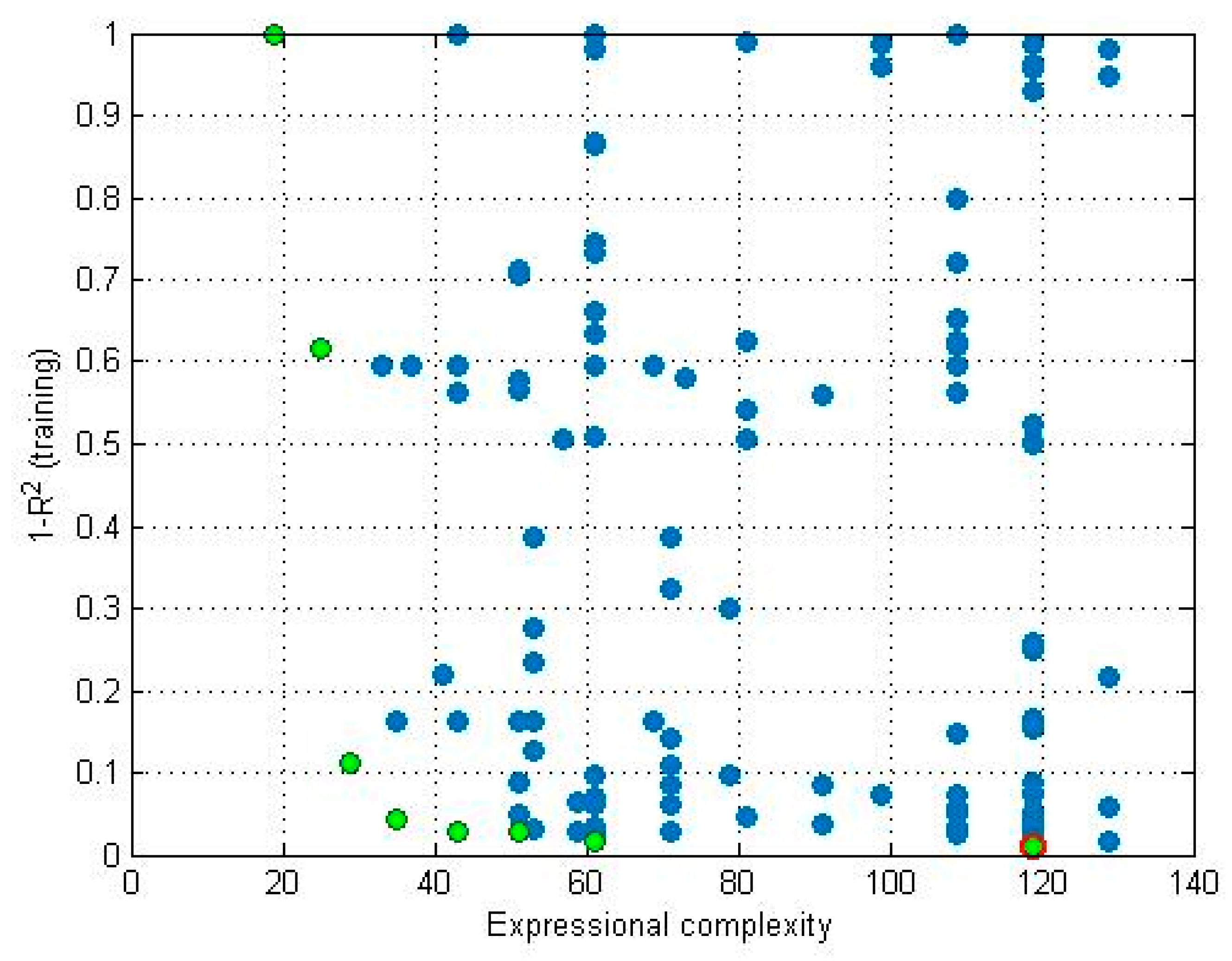
3.2. Genetic Programming
3.2.1. Single-Gene Solution
3.2.2. Multi-Gene Solution (MGGP)
3.2.3. Error Estimations
a. R-Squared (R2)
b. Root Mean Squared Error (RMSE)
c. Mean Absolute Deviation (MAD)
d. Mean Absolute Error (MAE)
e. Mean Absolute Percentage Error (MAPE)
f. Akaike Information Criterion (AIC):
g. Performance Index (PI):
3.3. Uncertainty Analysis and Confidence Bands
3.4. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Housner, W.G. The Dynamic Behavior of Water Tanks. Bull. Seismol. Soc. Am. 1963, 53, 381–387. [Google Scholar]
- ACI 350.3. Seismic Design of Liquid-Containing Concrete Structures and Commentary (ACI 350.3-6); American Concrete Institute: Farmington Hills, MI, USA, 2006. [Google Scholar]
- Isaacson, M. Earthquake-induced hydrodynamic forces on reservoir roofs. Can. J. Civ. Eng. 2010, 37, 1107–1115. [Google Scholar] [CrossRef] [Green Version]
- Cho, K.H.; Cho, S.Y. Seismic Response of Cylindrical Steel Tanks Considering Fluid-Structure Interaction. J. Steel Struct. 2007, 7, 147–152. [Google Scholar]
- Liu, D.; Lin, P. A numerical study of three-dimensional liquid sloshing in tanks. J. Comput. Phys. 2008, 227, 3921–3939. [Google Scholar] [CrossRef]
- Chen, Y.G.; Djidjeli, K.; Price, W.G. Numerical simulation of liquid sloshing phenomena in partially filled containers. J. Comput. Fluids 2009, 38, 830–842. [Google Scholar] [CrossRef]
- Kang, D.H.; Lee, Y.B. Summary Report of Sloshing Model Test for Rectangular Model; Daewoo Shipbuilding & Marine Engineering Co. Ltd.: Geoje, Korea, 2005; Volume 1. [Google Scholar]
- Afan, H.A.; El-shafie, A.; Mohtar, W.H.; Yaseen, Z.M. Past, present and prospect of an Artificial Intelligence (AI) based model for sediment transport prediction. J. Hydrol. 2016, 541, 902–913. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G.; Ivakhnenko, G.A. The review of problems solvable by algorithms of the group method of data handling (GMDH). Pattern Recognit. Image Anal. C/C Raspoznavaniye Obrazov I Anal. Izobrazhenii 1995, 5, 527–535. [Google Scholar]
- Mohammadpour, R.; Ghani, A.; Azamathulla, H.M. Estimating time to equilibrium scour at long abutment by using genetic programming. In Proceedings of the 3rd International Conference on Managing Rivers in the 21st Century (Rivers 2011), Penang, Malaysia, 6–9 December 2011. [Google Scholar]
- Lallahem, S.; Mania, J.; Hani, A.; Najjar, Y. On the use of neural networks to evaluate groundwater levels in fractured media. J. Hydrol. 2005, 307, 92–111. [Google Scholar] [CrossRef]
- Ghani, A.A.; Azamathulla, H.M. Development of GEP-based functional relationship for sediment transport in tropical rivers. Neural Comput. Appl. 2014, 24, 271–276. [Google Scholar] [CrossRef]
- He, Z.; Wen, X.; Liu, H.; Du, J. A comparative study of artificial neural network, adaptive neuro fuzzy inference system and support vector machine for forecasting river flow in the semiarid mountain region. J. Hydrol. 2014, 509, 379–386. [Google Scholar] [CrossRef]
- Daliakopoulos, I.N.; Coulibaly, P.; Tsanis, I.K. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Mirzavand, M.; Khoshnevisan, B.; Shamshirband, S.; Kisi, O.; Ahmad, R.; Akib, S. Evaluating groundwater level fluctuation by support vector regression and neuro-fuzzy methods: A comparative study. Nat. Hazards 2015, 1, 1–15. [Google Scholar] [CrossRef]
- Mohammadpour, R.; Shaharuddin, S.; Chang, C.K.; Zakaria, N.A.; Ghani, A.; Chan, N.W. Prediction of water quality index in constructed wetlands using support vector machine. Environ. Sci. Pollut. Res. 2015, 22, 6208–6219. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, N.; Londhe, S.; Kulkarni, S. Modeling compressive strength of recycled aggregate concrete by artificial neural network, model tree and non-linear regression. Int. J. Sustain. Built Environ. 2014, 3, 187–198. [Google Scholar] [CrossRef] [Green Version]
- Loh, W.Y. Classification and Regression Tree Methods; Statistics Reference Online; Wiley StatsRef: Hoboken, NJ, USA, 2014. [Google Scholar]
- Garg, A.; Garg, A.; Tai, K.J.C.G. A multi-gene genetic programming model for estimating stress-dependent soil water retention curves. Comput. Geosci. 2014, 18, 45–56. [Google Scholar] [CrossRef]
- Sattar, A.M.; Gharabaghi, B. Gene expression models for prediction of longitudinal dispersion coefficient in streams. J. Hydrol. 2015, 524, 587–596. [Google Scholar] [CrossRef]
- Sattar, A.M.A.; Gharabaghi, B.; McBean, E.A. Prediction of Timing of Watermain Failure Using Gene Expression Models. Water Resour. Manag. 2016, 30, 1635–1651. [Google Scholar] [CrossRef]
- Azamathulla, H.M. Gene expression programming for prediction of scour depth downstream of sills. J. Hydrol. 2012, 460, 156–159. [Google Scholar] [CrossRef]
- Chinnarasri, C.; Kositgittiwong, D. Laboratory study of maximum scour depth downstream of sills. In Proceedings of the Institution of Civil Engineers-Water Management. Vol. 161. No. 5; Thomas Telford Ltd.: London, UK, 2008. [Google Scholar]
- Najafzadeh, M.; Rezaie, M.; Rashedi, E. Prediction of maximum scour depth around piers with debris accumulation using EPR, MT, and GEP models. J. Hydroinform. 2016, 18, 867–884. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Zeynoddin, M.; Ebtehaj, I.; Gharabaghi, B.; Khodashenas, S.R. Reliable method of determining stable threshold channel shape using experimental and gene expression programming techniques. Neural Comput. 2019, 31, 5799–5817. [Google Scholar] [CrossRef]
- Khozani, Z.S.; Bonakdari, H.; Ebtehaj, I. An analysis of shear stress distribution in circular channels with sediment deposition based on Gene Expression Programming. Int. J. Sediment Res. 2017, 32, 575–584. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. A new multi-gene genetic programming approach to nonlinear system modeling. Part I: Materials and structural engineering problems. Neural Comput. Appl. 2012, 21, 171–187. [Google Scholar] [CrossRef]
- Kaydani, H.; Mohebbi, A.; Eftekhari, M. Permeability estimation in heterogeneous oil reservoirs by multi-gene genetic programming algorithm. J. Pet. Sci. Eng. 2014, 123, 201–206. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Mehr, A.D. Multi-gene genetic programming for sediment transport modeling in sewers for conditions of non-deposition with a bed deposit. Int. J. Sediment Res. 2018, 33, 262–270. [Google Scholar] [CrossRef]
- Mehr, A.D.; Nourani, V. Season algorithm-multigene genetic programming: A new approach for rainfall-runoff modelling. Water Resour. Manag. 2018, 32, 2665–2679. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yun, G.J.; Alavi, A.H. An evolutionary approach for modeling of shear strength of RC deep beams. Mater. Struct. 2013, 46, 2109–2119. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H.; Kazemi, S.; Gandomi, M. Formulation of shear strength of slender RC beams using gene expression programming, part I: Without shear reinforcement. Autom. Constr. 2014, 42, 112–121. [Google Scholar] [CrossRef]
- Zahiri, A.; Dehghani, A.A.; Azamathulla, H.M. Application of Gene-Expression Programming in Hydraulic Engineering. In Handbook of Genetic Programming Applications; Gandomi, A.H., Alavi, A.H., Ryan, C., Eds.; Springer: Cham, Switzerland, 2015; pp. 71–97. [Google Scholar]
- OpenFOAM version 2.3.1. Computer Software. Available online: https://openfoam.org/version/2-3-1/ (accessed on 31 December 2020).
- Bahreini Toussi, I.; Kianoush, R.; Mohammadian, A. Numerical and Experimental Investigation of Rectangular Liquid-Containing Structures under Seismic Excitation. Infrastructures 2021, 6, 1. [Google Scholar] [CrossRef]
- Jaiswal, O.R.; Kulkarni, S.; Pathak, P. A Study on Sloshing Frequencies of Fluid-Tank System. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Moslemi, M.; Kianoush, M.R. Parametric study on dynamic behavior of cylindrical ground-supported tanks. Eng. Struct. 2012, 42, 214–230. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Greenshields, C.J. OpenFOAM User Guide; The OpenFOAM Foundation: London, UK, 2018. [Google Scholar]
- Koza, J.R.; Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection (Vol. 1); MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Pandey, D.S.; Pan, I.; Das, S.; Leahy, J.J.; Kwapinski, W. Multi-gene genetic programming based predictive models for municipal solid waste gasification in a fluidized bed gasifier. Bioresour. Technol. 2015, 179, 524–533. [Google Scholar] [CrossRef] [Green Version]
- Searson, D.P.; Leahy, D.E.; Willis, M.J. GPTIPS: An open source genetic programming toolbox for multigene symbolic regression. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, 17–19 March 2010; Volume 1, pp. 77–80. [Google Scholar]
- Bonakdari, H.; Moeeni, H.; Ebtehaj, I.; Zeynoddin, M.; Mahoammadian, A.; Gharabaghi, B. New insights into soil temperature time series modeling: Linear or nonlinear? Theor. Appl. Climatol. 2019, 135, 1157–1177. [Google Scholar] [CrossRef]
- Azimi, H.; Bonakdari, H.; Ebtehaj, I.; Gharabaghi, B.; Khoshbin, F. Evolutionary design of generalized group method of data handling-type neural network for estimating the hydraulic jump roller length. Acta Mech. 2018, 229, 1197–1214. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Roke, D.A. Assessment of artificial neural network and genetic programming as predictive tools. Adv. Eng. Softw. 2015, 88, 63–72. [Google Scholar] [CrossRef]
- Dolan, K.D.; Yang, L.; Trampel, C.P. Nonlinear regression technique to estimate kinetic parameters and confidence intervals in unsteady-state conduction-heated foods. J. Food Eng. 2007, 80, 581–593. [Google Scholar] [CrossRef]









| Length (mm) | Width (mm) | Height (mm) | |
|---|---|---|---|
| Size 1 | 755 | 300 | 300 |
| Size 2 | 1978 | 779 | 1200 |
| Size 3 | 1283 | 327 | 1200 |
| Size 4 | 683 | 342 | 1200 |
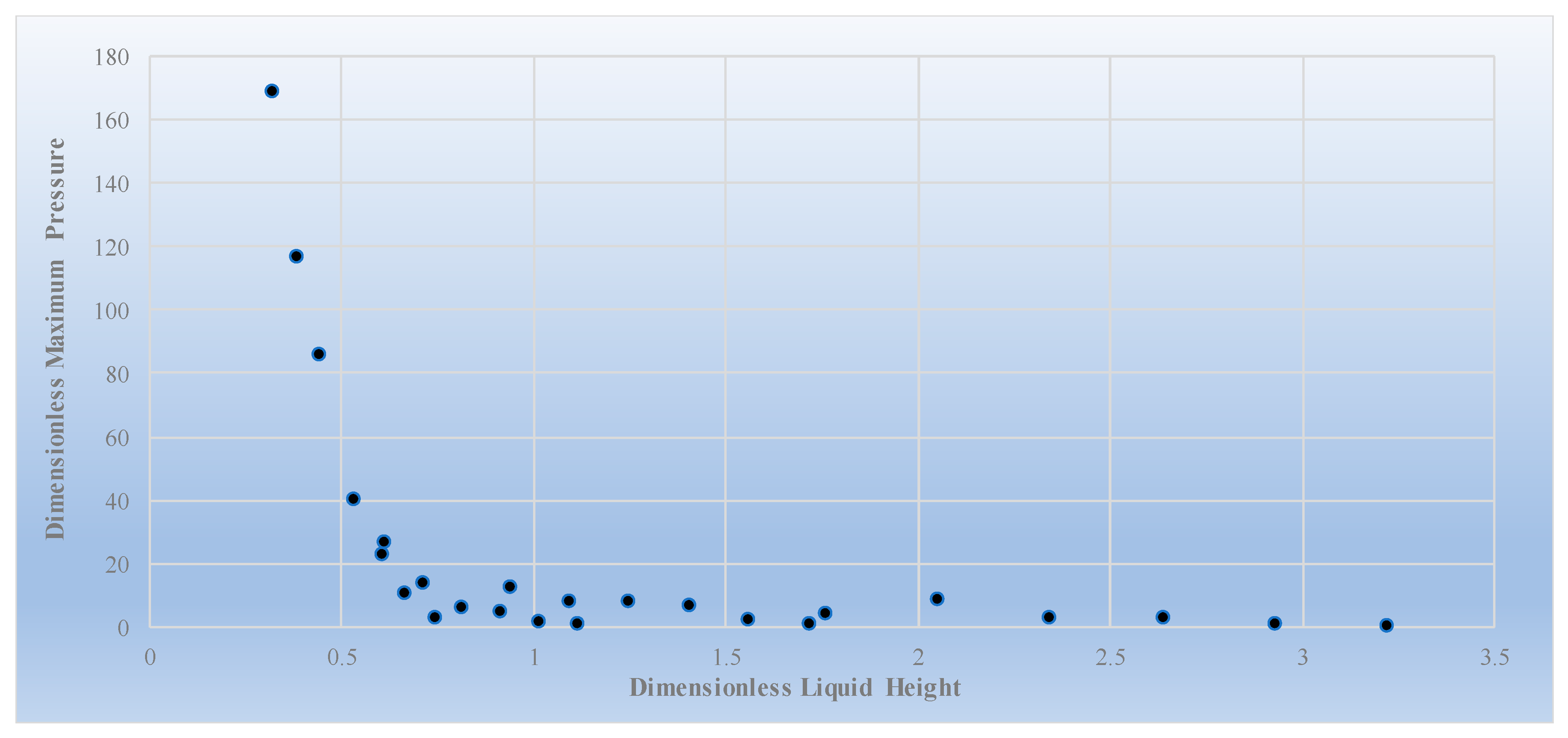
| Length | Width | Tank Height | Liquid Height | Dimensionless Liquid Height | ωi | Ti | |
|---|---|---|---|---|---|---|---|
| (mm) | (mm) | (mm) | (mm) | (hl/L) | (rad/s) | (s) | |
| Size 1 | 755 | 300 | 300 | 100 | 0.265 | 4.023 | 1.562 |
| 120 | 0.318 | 4.354 | 1.443 | ||||
| 145 | 0.384 | 4.705 | 1.335 | ||||
| 200 | 0.53 | 5.282 | 1.190 | ||||
| 230 | 0.609 | 5.510 | 1.140 | ||||
| 250 | 0.662 | 5.636 | 1.115 | ||||
| 280 | 0.742 | 5.792 | 1.085 | ||||
| Size 2 | 1978 | 779 | 1200 | 1100 | 1.112 | 3.819 | 1.645 |
| 1000 | 1.011 | 3.777 | 1.663 | ||||
| 900 | 0.910 | 3.721 | 1.689 | ||||
| 800 | 0.809 | 3.644 | 1.724 | ||||
| 700 | 0.708 | 3.540 | 1.775 | ||||
| 600 | 0.607 | 3.400 | 1.848 | ||||
| Size 3 | 1283 | 327 | 1200 | 1100 | 1.714 | 4.858 | 1.293 |
| 1000 | 1.559 | 4.845 | 1.297 | ||||
| 900 | 1.403 | 4.824 | 1.303 | ||||
| 800 | 1.247 | 4.789 | 1.312 | ||||
| 700 | 1.091 | 4.732 | 1.328 | ||||
| 600 | 0.935 | 4.640 | 1.354 | ||||
| Size 4 | 683 | 327 | 1200 | 1100 | 3.221 | 6.686 | 0.940 |
| 1000 | 2.928 | 6.686 | 0.940 | ||||
| 900 | 2.635 | 6.685 | 0.940 | ||||
| 800 | 2.343 | 6.682 | 0.940 | ||||
| 700 | 2.05 | 6.677 | 0.941 | ||||
| 600 | 1.757 | 6.662 | 0.943 |
| Data Set | MAD | ||
|---|---|---|---|
| Observed Data | Single-Gene Results | Multi-Gene Results | |
| Trained | 30.63 | 30.27 | 30.44 |
| Test | 6.32 | 17.30 | 5.90 |
| Overall | 26.08 | 25.90 | 25.56 |
| Data Set | R-Squared | RMSE | MAE | MAPE (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | % of Maximum Dimensionless Pressure | % of Mean Dimensionless Pressure | AIC | PI | |||||
| Single-Gene | Trained | 0.989 | 4.54 | 2.69 | 17.09 | 3.64 | 68% | 21.15 | 0.086 |
| Test | 0.844 | 3.23 | 14.17 | 46.30 | 3.03 | 260% | 10.55 | 0.241 | |
| Overall | 0.989 | 4.31 | 2.55 | 19.03 | 3.52 | 107% | 23.87 | 0.114 | |
| Multi-Gene | Trained | 0.992 | 3.89 | 2.30 | 14.63 | 3.28 | 76% | 21.8 | 0.073 |
| Test | 0.889 | 2.73 | 11.99 | 39.18 | 2.19 | 302% | 12.18 | 0.202 | |
| Overall | 0.992 | 3.69 | 2.18 | 16.26 | 3.06 | 121% | 24.17 | 0.082 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bahreini Toussi, I.; Mohammadian, A.; Kianoush, R. Prediction of Maximum Pressure at the Roofs of Rectangular Water Tanks Subjected to Harmonic Base Excitation Using the Multi-Gene Genetic Programming Method. Math. Comput. Appl. 2021, 26, 6. https://doi.org/10.3390/mca26010006
Bahreini Toussi I, Mohammadian A, Kianoush R. Prediction of Maximum Pressure at the Roofs of Rectangular Water Tanks Subjected to Harmonic Base Excitation Using the Multi-Gene Genetic Programming Method. Mathematical and Computational Applications. 2021; 26(1):6. https://doi.org/10.3390/mca26010006
Chicago/Turabian StyleBahreini Toussi, Iman, Abdolmajid Mohammadian, and Reza Kianoush. 2021. "Prediction of Maximum Pressure at the Roofs of Rectangular Water Tanks Subjected to Harmonic Base Excitation Using the Multi-Gene Genetic Programming Method" Mathematical and Computational Applications 26, no. 1: 6. https://doi.org/10.3390/mca26010006
APA StyleBahreini Toussi, I., Mohammadian, A., & Kianoush, R. (2021). Prediction of Maximum Pressure at the Roofs of Rectangular Water Tanks Subjected to Harmonic Base Excitation Using the Multi-Gene Genetic Programming Method. Mathematical and Computational Applications, 26(1), 6. https://doi.org/10.3390/mca26010006






