Simple Algebraic Expressions for the Prediction and Control of High-Temperature Annealed Structures by Linear Perturbation Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Phenomena Formulation
2.2. First Order Perturbation Analysis
- Volume stays constant.
- The initial geometry is an unperturbed, infinitely long void cylinder, and the surface normal points inwards, which is important for the curvature calculation and its sign.
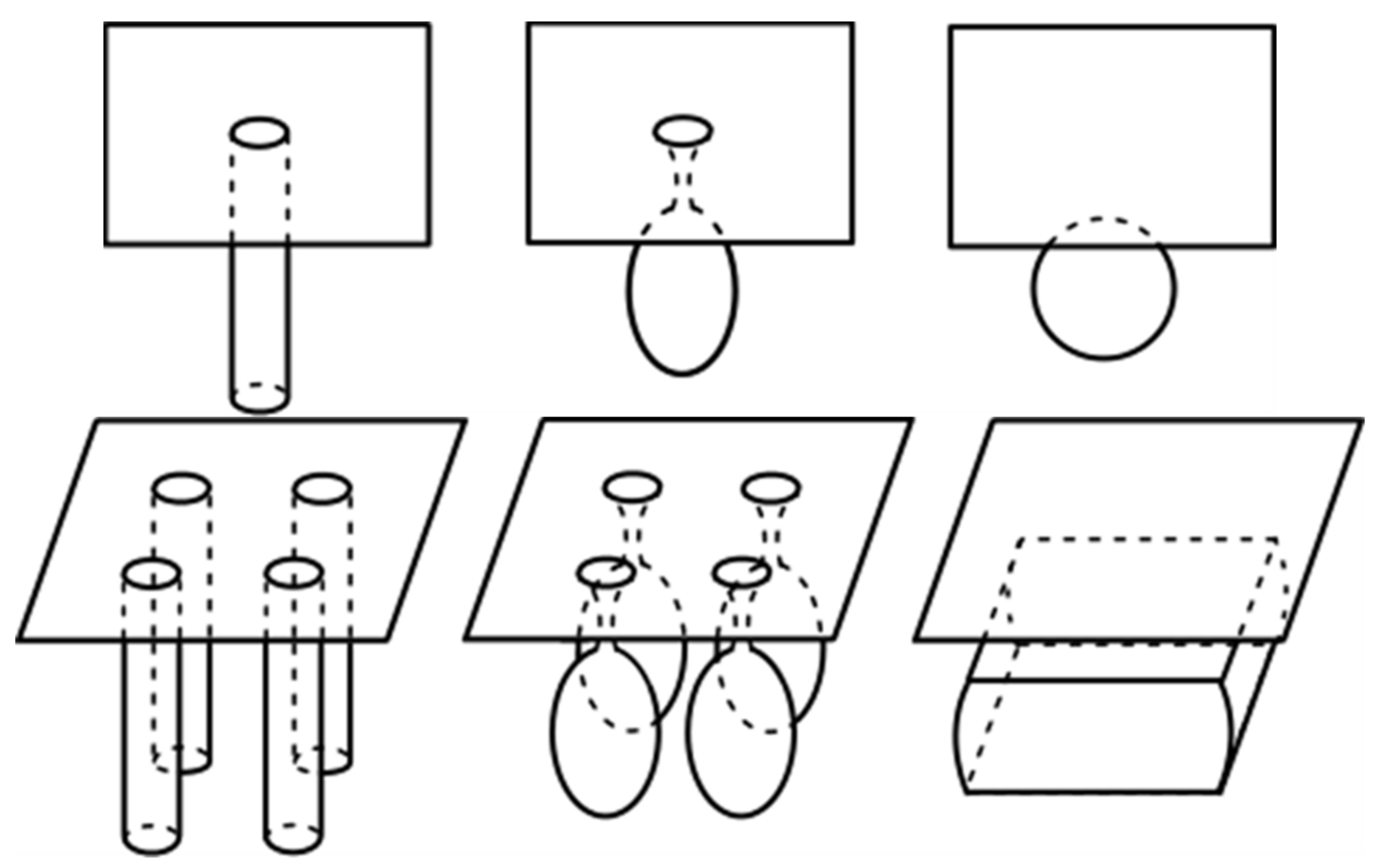
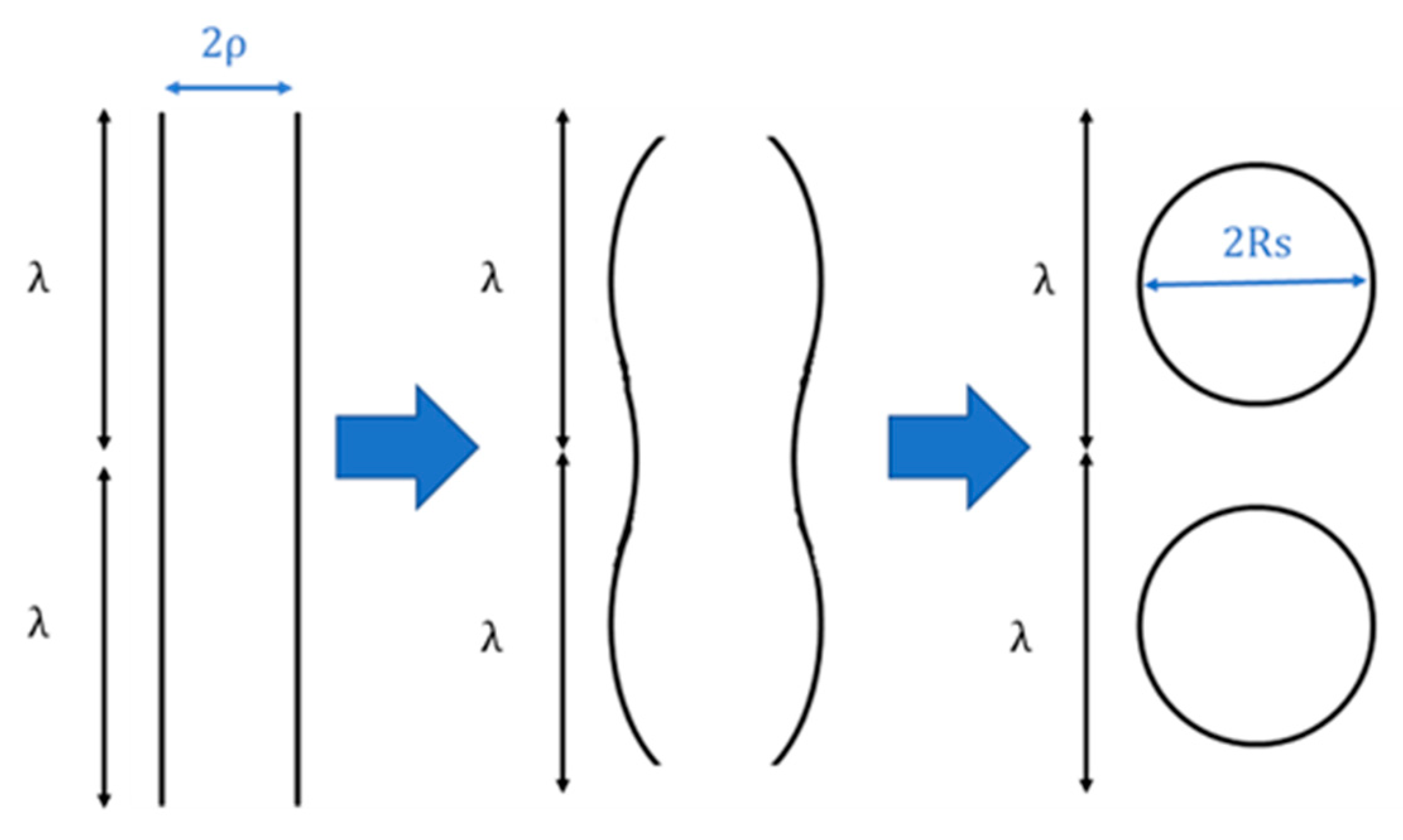
- The analyzed transformation is from an initial cylinder to a set of spheres. The evolution of the geometry is driven by an increasing sinusoidal perturbation of wavelength λ in the longitudinal direction. The evolution is schematically shown in Figure 2.
- The analysis is performed on the first seconds of the transformation. This is already provides if the initial sinusoidal disturbance shrinks or grows.
2.3. Analytical Model of the Void Shape Evolution for Finite Structures
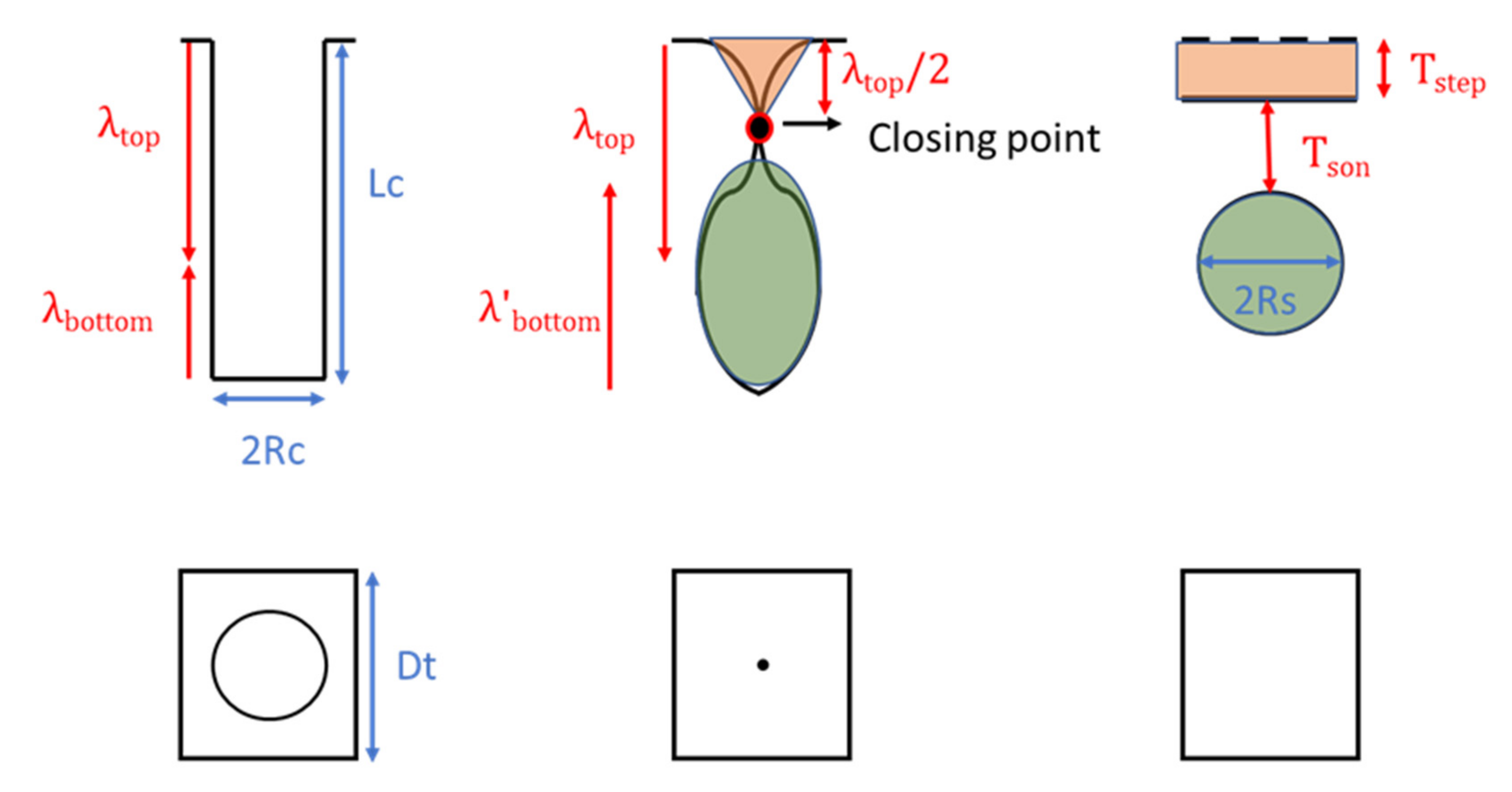
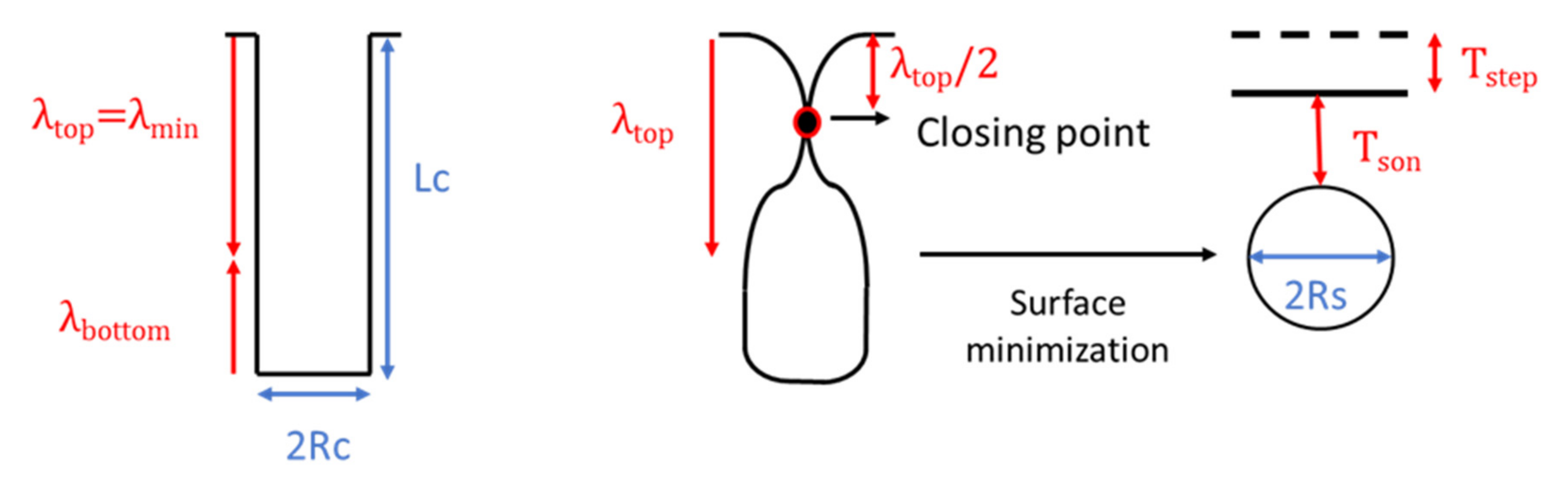
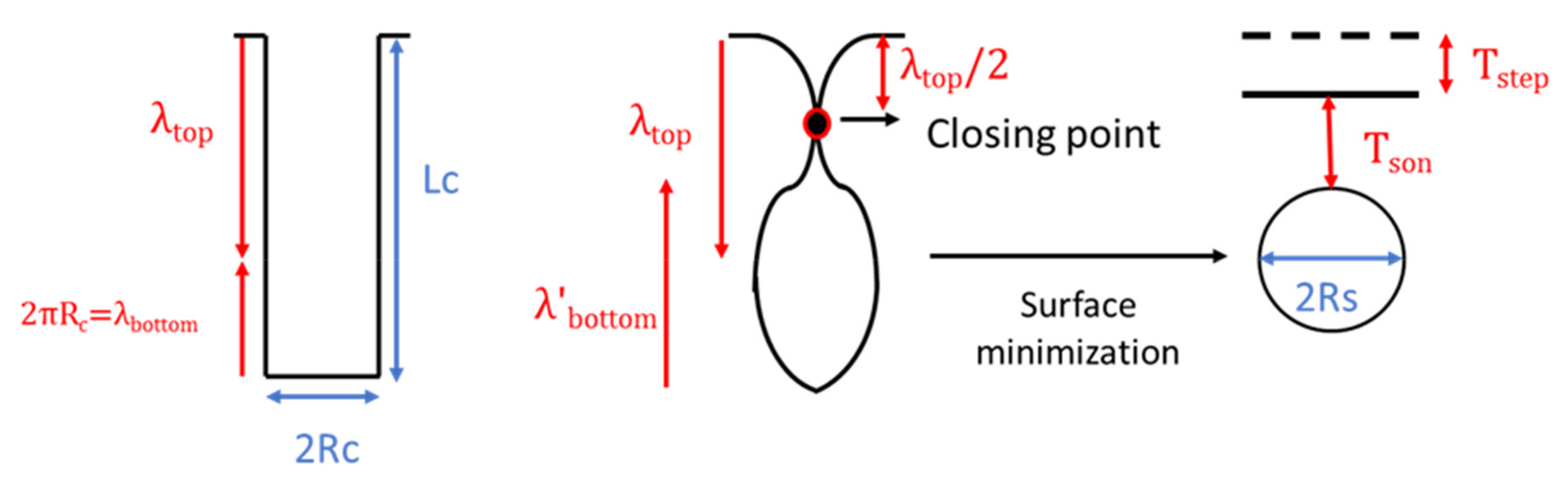
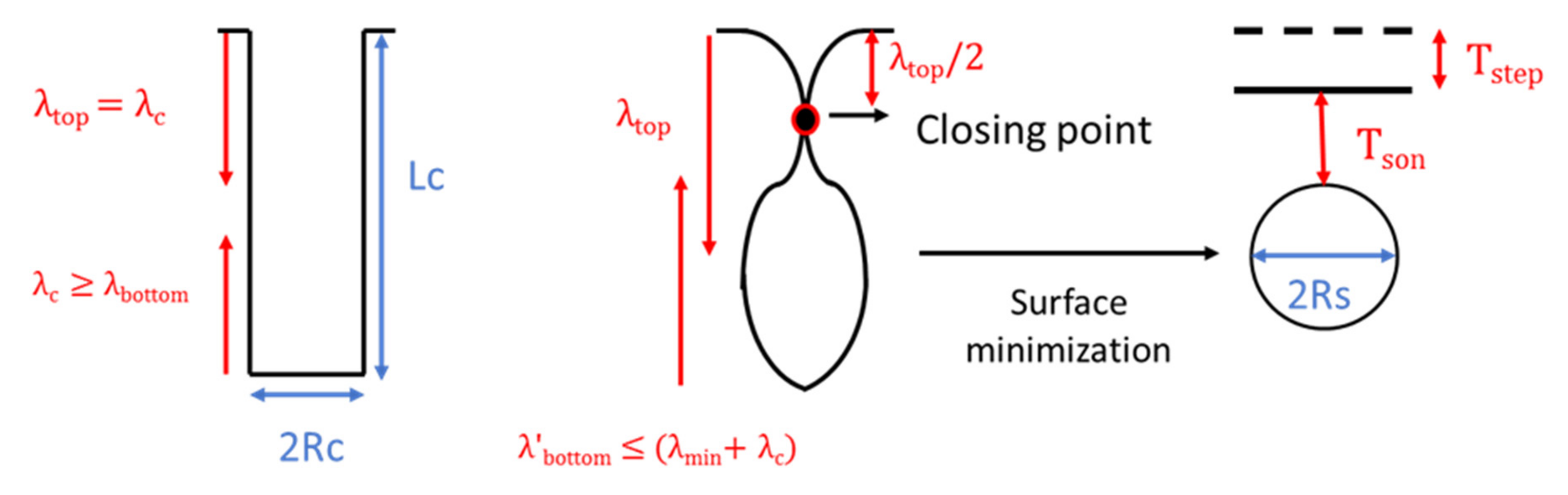
- The first transformation process is obtained through the competition between the effects at the top and at the bottom of the trench.
- The top transformation has the priority. However, a balance between both extremes must be maintained, and this is used for obtaining the corresponding expressions (see Figure 5).
- Once the wavelength at the top has been calculated, the pinch-off occurs at half the maximum wavelength, having the top surface as the reference (see Figure 5).
- The void enclosed below the closing point transforms into one or several final spheres, depending on the aspect ratio of the void. The simplest transformation is shown in Figure 5, where the complete enclosed void volume transforms into a spherical void geometry with the same volume.
- The volume left over the closing point transforms into a step, i.e., a difference of surface level with respect to the initial surface (see Figure 5).
- The only considered final equilibrium geometries are structures with constant curvatures: spheres and planes. No intermediate states can be predicted without a proper process simulation.
- Only the formation of one trench is considered, and no coalescence is assumed. This simplifies the expression of the size of the final void. The distance of the neighboring trenches is sufficient to have a void spherical transformation dominated by the aspect ratio instead of the distance to other trenches. However, the latter effect is not completely neglected, as the distance between trenches affects the step and SON-layer sizes.
3. Results and Discussion
- l1 = l2 = 0.35 µm is obtained from Figure 4 of Sato et al. [3]. In that diagram, the value “a” is given which, according to Figure 2, is the side of the base squared side.
- The length of the trench would be estimated from the parameter “b” of Figure 4 [3], as the x-axis yields the aspect ratio “b/a”. In this case, it is estimated to be LC = 1.98 µm.
- The next step is to calculate which of the proposed models must be used. That comes from the aspect ratio calculation LC/RC, which yields about 8.14. This value lies between 2π (6.28) and 4π (12.57) and thus is the model case 2. In other words, Equations (27)–(31) must be used for the calculation of the final parameters.
- The last unknown parameter is A. A is the surface area of the repeated pattern of the trench as shown in the colored area in Figure 4 of this work. The top trench area is a squared area as shown in Figure 2 of Sato et al. [3]. The information provided by Figures 2 and 3 and the work of Mizushima et al. [1] suggest that the distance between trenches “a + c” would be about 2a (which is equivalent to Dt of Table 1) and the area A would be 2a × 2a or 2l1 × 2l1 = 0.49 µm2.
- As the base of the trench is a square, the equivalent cylindrical radius is given by Equation (25) and equals RC,eq = 0.1975 µm.
- TSTEP is calculated with Equation (29) and the values of RC and A. The obtained value equals TSTEP = 0.16 µm.
- RS is calculated with Equation (30) and the values RC and LC. The obtained value equals RS = 0.34 µm.
- TSON is calculated with Equation (31) and the values LC, RC, and A. The obtained value equals TSON = 0.80 µm.
- Calculated data are then added in Table 3 and compared to the results of Sato et al. [3], Figure 4, which, after an annealing time of 10 min at 1100 °C and 10 Torr, yields the diameter of the final equilibrium spherical void. The estimated measured radius can be inferred from such Figure 4 and is RS = 0.34 µm.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mizushima, I.; Sato, T.; Taniguchi, S.; Tsunashima, Y. Empty-Space-in-Silicon Technique for Fabricating a Silicon-on-Nothing Structure. Appl. Phys. Lett. 2000, 77, 3290–3292. [Google Scholar] [CrossRef] [Green Version]
- Sato, T.; Mitsukake, K.; Mizushima, I.; Tsunashima, Y. Micro-Structure Transformation of Silicon: A Newly Developed Transformation Technology for Patterning Silicon Surfaces Using the Surface Migration of Silicon Atoms by Hydrogen Annealing. Jpn. J. Appl. Phys. 2000, 39, 5033–5038. [Google Scholar] [CrossRef]
- Sato, T.; Mizushima, I.; Taniguchi, S.; Takenaka, K.; Shimonishi, S.; Hayashi, H.; Hatano, M.; Sugihara, K.; Tsunashima, Y. Fabrication of Silicon-on-Nothing Structure by Substrate Engineering Using the Empty-Space-in-Silicon Formation Technique. Jpn. J. Appl. Phys. 2004, 43, 12. [Google Scholar] [CrossRef]
- Monfray, S.; Skotnicki, T. Silicon-on-Nothing (SON) Technology. In Proceedings of the 2006 8th International Conference on Solid-State and Integrated Circuit Technology, Shanghai, China, 23–23 October 2006; Volume 1, pp. 11–14. [Google Scholar]
- Jurczak, M.; Skotnicki, T.; Paoli, M.; Tormen, B.; Martins, J.; Regolini, J.L.; Dutartre, D.; Ribot, P.; Lenoble, D.; Pantel, R.; et al. Silicon-on-Nothing (SON)-an Innovative Process for Advanced CMOS. Electron Devices IEEE Trans. 2000, 47, 2179–2187. [Google Scholar] [CrossRef] [Green Version]
- Monfray, S.; Skotnicki, T.; Morand, Y.; Descombes, S.; Paoli, M.; Ribot, P.; Talbot, A.; Dutartre, D.; Leverd, F.; Lefriec, Y.; et al. First 80 Nm SON (Silicon-on-Nothing) MOSFETs with Perfect Morphology and High Electrical Performance. In Proceedings of the Electron Devices Meeting (IEDM’01), Washington, DC, USA, 2–5 December 2001; Volume 1, pp. 29.7.1–29.7.4. [Google Scholar]
- Monfray, S.; Boeuf, F.; Coronel, P.; Bidal, G.; Denorme, S.; Skotnicki, T. Silicon-on-Nothing (SON) Applications for Low Power Technologies. In Proceedings of the IEEE International Conference on Integrated Circuit Design and Technology and Tutorial (ICICDT 2008), Grenoble, France, 2–4 June 2008; Volume 1, pp. 1–4. [Google Scholar]
- Villani, P.; Favilla, S.; Labate, L.; Novarini, E.; Ponza, A.; Stella, R. Evaluation of Self-Heating Effects on an Innovative SOI Technology (“Venezia” Process). In Proceedings of the 17th International Symposium on Power Semiconductor Devices and ICs (ISPSD’05), Santa Barbara, CA, USA, 23–26 May 2005; Volume 1, pp. 63–66. [Google Scholar]
- Depauw, V.; Gordon, I.; Beaucarne, G.; Poortmans, J.; Mertens, R.; Celis, J.-P. Proof of Concept of an Epitaxy-Free Layer-Transfer Process for Silicon Solar Cells Based on the Reorganisation of Macropores upon Annealing. Mater. Sci. Eng. B 2009, 159–160, 286–290. [Google Scholar] [CrossRef]
- Depauw, V.; Gordon, I.; Beaucarne, G.; Poortmans, J.; Mertens, R.; Celis, J.-P. Large-Area Monocrystalline Silicon Thin Films by Annealing of Macroporous Arrays: Understanding and Tackling Defects in the Material. J. Appl. Phys. 2009, 106, 033516. [Google Scholar] [CrossRef]
- Peng, B.; Yu, T.; Yu, F. A Novel Process of Silicon-on-Nothing MOSFETs with Double Implantation. In Proceedings of the IEEE International Conference on Integration Technology (ICIT’07), Shenzhen, China, 20–24 March 2007; Volume 1, pp. 237–240. [Google Scholar]
- Bu, W.; Huang, R.; Li, M.; Tian, Y.; Wang, Y. A Novel Technique of Silicon-on-Nothing MOSFETs Fabrication by Hydrogen and Helium Co-Implantation. In Proceedings of the 7th International Conference on Solid-State and Integrated Circuits Technology, Beijing, China, 18–21 October 2004; Volume 1, pp. 269–272. [Google Scholar]
- Monfray, S.; Skotnicki, T.; Morand, Y.; Descombes, S.; Coronel, P.; Mazoyer, P.; Harrison, S.; Ribot, P.; Talbot, A.; Dutartre, D.; et al. 50 Nm-Gate All around (GAA)-Silicon on Nothing (SON)-Devices: A Simple Way to Co-Integration of GAA Transistors within Bulk MOSFET Process. In Proceedings of the Symposium on VLSI Technology, Honolulu, HI, USA, 11–13 June 2002; Volume 1, pp. 108–109. [Google Scholar]
- Hoellt, L.; Schulze, J.; Eisele, I.; Suligoj, T.; Jovanović, V.; Thompson, P.E. First Sub-30nm Vertical Silicon-on-Nothing MOSFET. Available online: https://www.academia.edu/19100324/First_sub_30nm_vertical_Silicon_On_Nothing_MOSFET (accessed on 29 May 2021).
- Sudoh, K.; Iwasaki, H.; Kuribayashi, H.; Hiruta, R.; Shimizu, R. Numerical Study on Shape Transformation of Silicon Trenches by High-Temperature Hydrogen Annealing. Jpn. J. Appl. Phys. 2004, 43, 5937. [Google Scholar] [CrossRef]
- Sudoh, K.; Iwasaki, H.; Hiruta, R.; Kuribayashi, H.; Shimizu, R. Void Shape Evolution and Formation of Silicon-on-Nothing Structures during Hydrogen Annealing of Hole Arrays on Si(001). J. Appl. Phys. 2009, 105, 083536. [Google Scholar] [CrossRef]
- Grau Turuelo, C.; Bergmann, B.; Breitkopf, C. Void Shape Evolution of Silicon Simulation: Non-Linear Three-Dimensional Curvature Calculation by First Order Analysis. Univers. J. Comput. Anal. 2014, 2, 27–45. [Google Scholar]
- Shin, S. Computation of the Curvature Field in Numerical Simulation of Multiphase Flow. J. Comput. Phys. 2007, 222, 872–878. [Google Scholar] [CrossRef]
- Engquist, B.; Tornberg, A.-K.; Tsai, R. Discretization of Dirac Delta Functions in Level Set Methods. J. Comput. Phys. 2005, 207, 28–51. [Google Scholar] [CrossRef]
- Yue, P.; Feng, J.J.; Liu, C.; Shen, J. A Diffuse-Interface Method for Simulating Two-Phase Flows of Complex Fluids. J. Fluid Mech. 2004, 515, 293–317. [Google Scholar] [CrossRef] [Green Version]
- Mullins, W.W. Theory of Thermal Grooving. J. Appl. Phys. 1957, 28, 333. [Google Scholar] [CrossRef]
- Castez, M.F.; Albano, E.V. Modeling the Decay of Nanopatterns: A Comparative Study between a Continuum Description and a Discrete Monte Carlo Approach. J. Phys. Chem. C 2007, 111, 4606–4613. [Google Scholar] [CrossRef]
- Castez, M.F. Surface-Diffusion-Driven Decay of Patterns: Beyond the Small Slopes Approximation. J. Phys Condens. Matter 2010, 22, 345007. [Google Scholar] [CrossRef] [PubMed]
- Castez, M.F. N-Fold Symmetric Two-Dimensional Shapes Evolving by Surface Diffusion. EPL (Europhys. Lett.) 2013, 104, 36003. [Google Scholar] [CrossRef]
- Madrid, M.A.; Salvarezza, R.C.; Castez, M.F. One-Dimensional Gratings Evolving through High-Temperature Annealing: Sine-Generated Solutions. J. Phys. Condens. Matter 2012, 24, 015001. [Google Scholar] [CrossRef]
- Kuribayashi, H.; Shimizu, R.; Sudoh, K.; Iwasaki, H. Hydrogen Pressure Dependence of Trench Corner Rounding during Hydrogen Annealing. J. Vac. Sci. Technol. A Vac. Surf. Film. 2004, 22, 1406. [Google Scholar] [CrossRef]
- Kuribayashi, H.; Hiruta, R.; Shimizu, R.; Sudoh, K.; Iwasaki, H. Investigation of Shape Transformation of Silicon Trenches during Hydrogen Annealing. Jpn. J. Appl. Phys. 2004, 43, L468. [Google Scholar] [CrossRef]
- Lee, M.-C.M.; Wu, M.C. Thermal Annealing in Hydrogen for 3-D Profile Transformation on Silicon-on-Insulator and Sidewall Roughness Reduction. J. Microelectromech. Syst. 2006, 15, 338–343. [Google Scholar] [CrossRef] [Green Version]
- Suo, Z. Motions of Microscopic Surfaces in Materials. In Advances in Applied Mechanics; Hutchinson, J.W., Wu, T.Y., Eds.; Elsevier: Amsterdam, The Netherlands, 1997; Volume 33, pp. 193–294. [Google Scholar]
- Mehrer, H. Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-Controlled Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 155, ISBN 3-540-71488-X. [Google Scholar]
- Rayleigh, L., XIX. On the Instability of Jets. Proc. Lond. Math. Soc. 1878, 1, 4–13. [Google Scholar] [CrossRef] [Green Version]
- Rayleigh, L., XIX. On the Instability of Cylindrical Fluid Surfaces. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1892, 34, 177–180. [Google Scholar] [CrossRef] [Green Version]
- Nichols, F.A.; Mullins, W.W. Morphological Changes of a Surface of Revolution Due to Capillarity-Induced Surface Diffusion. J. Appl. Phys. 1965, 36, 1826. [Google Scholar] [CrossRef]
- Carter, W.C.; Glaeser, A.M. The Effect of Finite Amplitude Perturbations on the Stability of Continuous Phases. Mater. Sci. Eng. 1987, 89, L41–L45. [Google Scholar] [CrossRef]
- Coleman, B.D.; Falk, R.S.; Moakher, M. Stability of Cylindrical Bodies in the Theory of Surface Diffusion. Phys. D Nonlinear Phenom. 1995, 89, 123–135. [Google Scholar] [CrossRef]
- Choy, J.-H.; Hackney, S.A.; Lee, J.K. Nonlinear Stability Analysis of the Diffusional Spheroidization of Rods. J. Appl. Phys. 1995, 77, 5647. [Google Scholar] [CrossRef]
- Yang, F. On the Interface Instability of a Cylindrical Fiber Embedded in a Matrix. Scr. Mater. 2003, 49, 571–575. [Google Scholar] [CrossRef]
- Castez, M.F. Generalized Fourier Analysis for Nanopatterns with Overhangs. EPL (Europhys. Lett.) 2010, 89, 28001. [Google Scholar] [CrossRef]
- Srolovitz, D.J.; Safran, S.A. Capillary Instabilities in Thin Films. I. Energetics. J. Appl. Phys. 1986, 60, 247. [Google Scholar] [CrossRef]
- Srolovitz, D.J.; Safran, S.A. Capillary Instabilities in Thin Films. II. Kinetics. J. Appl. Phys. 1986, 60, 255. [Google Scholar] [CrossRef]
- Mullin, J.A. Viscous Flow and Structural Relaxation in Amorphous Silicon and Amorphous Selenium Thin Films. Ph.D. Thesis, Harvard University Cambridge, Cambridge, MA, USA, 2000. [Google Scholar]
- Taylor, B. Methodus Incrementorum Directa & Inversa; Impensis Gulielmi Innys: London, UK, 1717. [Google Scholar]
- MacLaurin, C. A Treatise of Fluxions; T.W. and T. Ruddimans: Edinburgh, UK, 1742. [Google Scholar]
- Bermond, J.M.; Métois, J.J.; Egéa, X.; Floret, F. The Equilibrium Shape of Silicon. Surf. Sci. 1995, 330, 48–60. [Google Scholar] [CrossRef]
- Eaglesham, D.J.; White, A.E.; Feldman, L.C.; Moriya, N.; Jacobson, D.C. Equilibrium Shape of Si. Phys. Rev. Lett. 1993, 70, 1643. [Google Scholar] [CrossRef]
- Wilson, J.H.; Todd, J.D.; Sutton, A.P. Modelling of Silicon Surfaces: A Comparative Study. J. Phys. Condens. Matter 1990, 2, 10259–10288. [Google Scholar] [CrossRef]
- Gilmer, G.H.; Bakker, A.F. Molecular Dynamics Simulations of Steps at Crystal Surfaces. Mrs Proc. 1990, 209, 135. [Google Scholar] [CrossRef]
- Kitayama, M.; Narushima, T.; Carter, W.C.; Cannon, R.M.; Glaeser, A.M. The Wulff Shape of Alumina: I, Modeling the Kinetics of Morphological Evolution. J. Am. Ceram. Soc. 2000, 83, 2561–2571. [Google Scholar] [CrossRef]
- Hernández, D.; Trifonov, T.; Garín, M.; Alcubilla, R. “Silicon Millefeuille”: From a Silicon Wafer to Multiple Thin Crystalline Films in a Single Step. Appl. Phys. Lett. 2013, 102, 172102. [Google Scholar] [CrossRef] [Green Version]
- Garín, M.; Jin, C.; Cardador, D.; Trifonov, T.; Alcubilla, R. Controlling Plateau-Rayleigh Instabilities during the Reorganization of Silicon Macropores in the Silicon Millefeuille Process. Sci. Rep. 2017, 7, 7233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mueller, T.; Dantz, D.; von Ammon, W.; Virbulis, J.; Bethers, U. Modeling of Morphological Changes by Surface Diffusion in Silicon Trenches. ECS Trans. 2006, 2, 363–374. [Google Scholar] [CrossRef]
- Nichols, F.A. On the Spheroidization of Rod-Shaped Particles of Finite Length. J. Mater. Sci. 1976, 11, 1077–1082. [Google Scholar] [CrossRef]
- Mclean, M. The Kinetics of Spheroidization of Lead Inclusions in Aluminium. Philos. Mag. 1973, 27, 1253–1266. [Google Scholar] [CrossRef]
- McLean, M.; Loveday, M.S. In-Situ Observations of the Annealing of Liquid Lead Inclusions Entrained in an Aluminium Matrix. J. Mater. Sci. 1974, 9, 1104–1114. [Google Scholar] [CrossRef]
- Stapley, A.J.; Beevers, C.J. The Stability of Sapphire Whiskers in Nickel at Elevated Temperatures. J. Mater. Sci. 1973, 8, 1296–1306. [Google Scholar] [CrossRef]


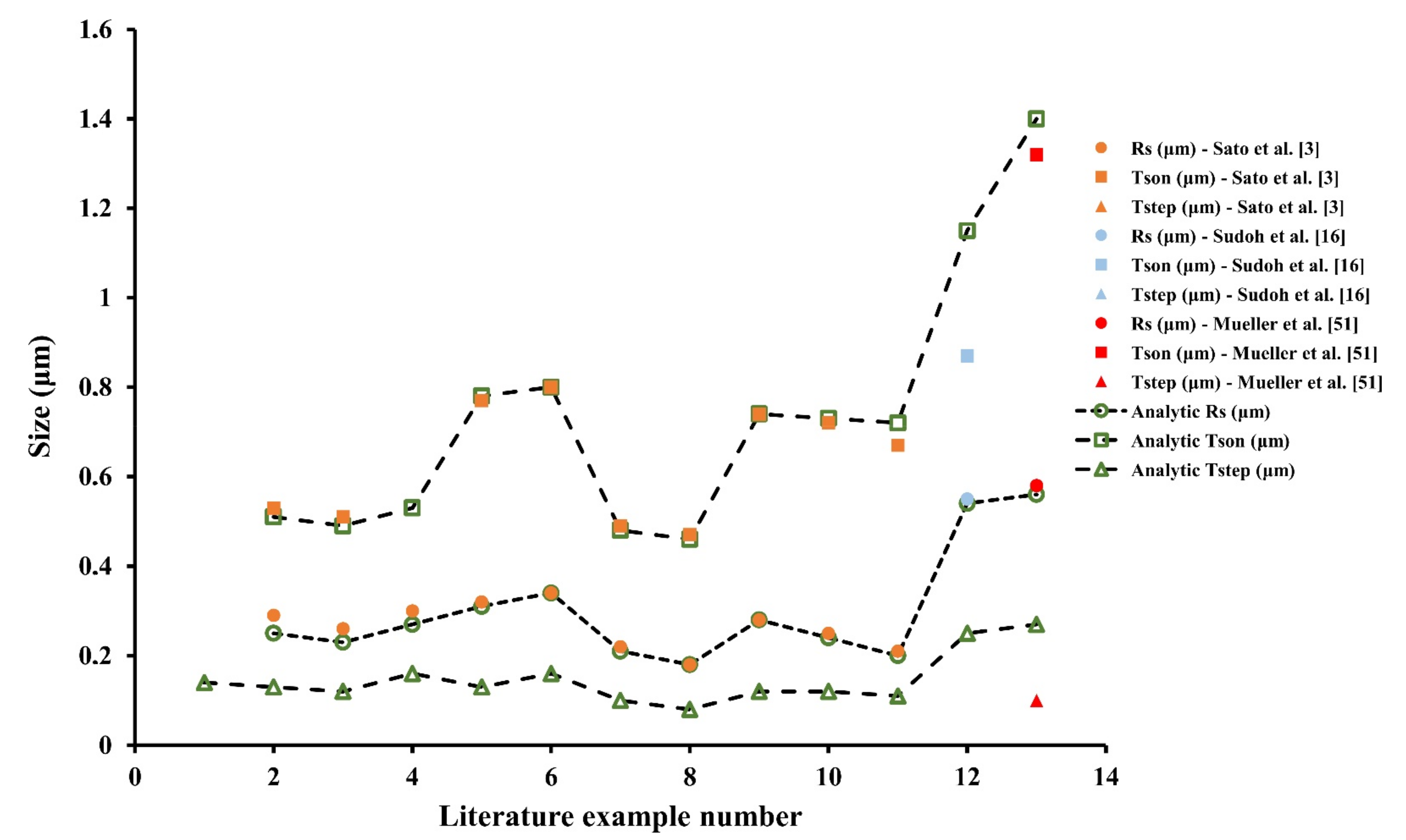
| Number | l1 [µm] | l2 [µm] | LC [μm] | LC/RC | Model Case | Dt,ave [μm] | Ref |
|---|---|---|---|---|---|---|---|
| 1 | 0.25 | 0.55 | ~1.11 | ~5.29 | 1 | ~1.06 | [1,3] |
| 2 | 0.30 | 0.30 | ~1.24 | ~7.29 | 2 | ~0.60 | [3] |
| 3 | 0.26 | 0.26 | ~1.21 | ~8.07 | 2 | ~0.52 | [3] |
| 4 | 0.35 | 0.35 | ~1.28 | ~8.14 | 2 | ~0.70 | [3] |
| 5 | 0.30 | 0.30 | ~1.92 | ~8.14 | 2 | ~0.60 | [3] |
| 6 | 0.35 | 0.35 | ~1.98 | ~9.90 | 2 | ~0.70 | [3] |
| 7 | 0.22 | 0.22 | ~1.19 | ~9.92 | 2 | ~0.44 | [3] |
| 8 | 0.17 | 0.17 | ~1.13 | ~11.30 | 2 | ~0.34 | [3] |
| 9 | 0.26 | 0.26 | ~1.81 | ~12.07 | 2 | ~0.52 | [3] |
| 10 | 0.22 | 0.22 | ~1.73 | ~14.42 | 3 | ~0.44 | [3] |
| 11 | 0.17 | 0.17 | ~1.63 | ~16.30 | 4 | ~0.34 | [3] |
| Number | LC [μm] | RC [μm] | LC/RC | Model Case | Dt,ave [μm] | Ref |
|---|---|---|---|---|---|---|
| 12 | ~2.72 | ~0.36 | ~7.56 | 2 | 1.38 | [16] |
| 13 | ~3.50 | ~0.30 | ~11.67 | 2 | 1.00 | [51] |
| Number | Source | RS [μm] | TSON [μm] | TSTEP [μm] | Ref |
|---|---|---|---|---|---|
| 1 | Literature | - | - | - | [1,3] |
| Model | - | - | 0.14 | ||
| Abs. Error | - | - | - | ||
| Rel. Error | - | - | - | ||
| 2 | Literature | ~0.29 | ~0.53 | - | [3] |
| Model | 0.25 | 0.51 | 0.13 | ||
| Abs. Error | 0.04 | 0.02 | - | ||
| Rel. Error | 14% | 4% | - | ||
| 3 | Literature | ~0.26 | ~0.51 | - | [3] |
| Model | 0.23 | 0.49 | 0.12 | ||
| Abs. Error | 0.03 | 0.02 | - | ||
| Rel. Error | 12% | 4% | - | ||
| 4 | Literature | ~0.30 | - | - | [3] |
| Model | 0.27 | 0.53 | 0.16 | ||
| Abs. Error | 0.03 | - | - | ||
| Rel. Error | 10% | - | - | ||
| 5 | Literature | ~0.32 | ~0.77 | - | [3] |
| Model | 0.31 | 0.78 | 0.13 | ||
| Abs. Error | 0.01 | 0.01 | - | ||
| Rel. Error | 4% | 2% | - | ||
| 6 | Literature | ~0.34 | ~0.80 | - | [3] |
| Model | 0.34 | 0.80 | 0.16 | ||
| Abs. Error | 0.00 | 0.00 | - | ||
| Rel. Error | 0% | 0% | - | ||
| 7 | Literature | ~0.22 | ~0.49 | - | [3] |
| Model | 0.21 | 0.48 | 0.10 | ||
| Abs. Error | 0.01 | 0.01 | - | ||
| Rel. Error | 5% | 3% | - | ||
| 8 | Literature | ~0.18 | ~0.47 | - | [3] |
| Model | 0.18 | 0.46 | 0.08 | ||
| Abs. Error | 0.00 | 0.01 | - | ||
| Rel. Error | 0% | 3% | - | ||
| 9 | Literature | ~0.28 | ~0.74 | - | [3] |
| Model | 0.28 | 0.74 | 0.12 | ||
| Abs. Error | 0.00 | 0.00 | - | ||
| Rel. Error | 0% | 0% | - | ||
| 10 | Literature | ~0.25 | ~0.72 | - | [3] |
| Model | 0.24 | 0.73 | 0.12 | ||
| Abs. Error | 0.01 | 0.01 | - | ||
| Rel. Error | 4% | 2% | - | ||
| 11 | Literature | ~0.21 | ~0.67 | - | [3] |
| Model | 0.20 | 0.72 | 0.11 | ||
| Abs. Error | 0.01 | 0.05 | - | ||
| Rel. Error | 5% | 8% | - |
| Number | Source | RS [μm] | TSON [μm] | TSTEP [μm] | Ref |
|---|---|---|---|---|---|
| 12 | Literature | ~0.55 | ~0.87 | - | [16] |
| Model | 0.54 | 1.15 | 0.24 | ||
| Abs. Error | 0.01 | 0.28 | - | ||
| Rel. Error | 2% | 33% | - | ||
| 13 | Literature | ~0.58 | ~1.32 | ~0.10 | [51] |
| Model | 0.56 | 1.40 | 0.27 | ||
| Abs. Error | 0.02 | 0.08 | 0.17 | ||
| Rel. Error | 4% | 7% | 170% |
| Number of ESS | This Work Analytical Model | Sato et al. [3] | Müller et al. [51] | Nichols et al. [52] | Grau et al. [17] | McLean et al. [53,54] | Garín et al. [50] | Stapley and Beevers [55] |
|---|---|---|---|---|---|---|---|---|
| 0 | ≤π ≈ 3.14 | ≤3.00 | ≈2.76 | - | ≤2.22 | - | ≈5.00 | ≤3.00 |
| 1 | ≤(3·21/2 + 2)π/2 ≈ 9.81 | ≤9.50 | ≈8.28 | ≤7.20 | ≤6.66 | ≤8.00 | ≈10.00 | ≤6.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grau Turuelo, C.; Breitkopf, C. Simple Algebraic Expressions for the Prediction and Control of High-Temperature Annealed Structures by Linear Perturbation Analysis. Math. Comput. Appl. 2021, 26, 43. https://doi.org/10.3390/mca26020043
Grau Turuelo C, Breitkopf C. Simple Algebraic Expressions for the Prediction and Control of High-Temperature Annealed Structures by Linear Perturbation Analysis. Mathematical and Computational Applications. 2021; 26(2):43. https://doi.org/10.3390/mca26020043
Chicago/Turabian StyleGrau Turuelo, Constantino, and Cornelia Breitkopf. 2021. "Simple Algebraic Expressions for the Prediction and Control of High-Temperature Annealed Structures by Linear Perturbation Analysis" Mathematical and Computational Applications 26, no. 2: 43. https://doi.org/10.3390/mca26020043
APA StyleGrau Turuelo, C., & Breitkopf, C. (2021). Simple Algebraic Expressions for the Prediction and Control of High-Temperature Annealed Structures by Linear Perturbation Analysis. Mathematical and Computational Applications, 26(2), 43. https://doi.org/10.3390/mca26020043







