Analytical Equations Applied to the Study of Steel Profiles under Fire According to Different Nominal Temperature-Time Curves

Abstract

Some analytical methods are available for temperature evaluation in solid bodies. These methods can be used due to their simplicity and good results. The main goal of this work is to present the temperature calculation in different cross-sections of structural hot-rolled steel profiles (IPE, HEM, L, and UAP) using the lumped capacitance method and the simplified equation from Eurocode 3. The basis of the lumped capacitance method is that the temperature of the solid body is uniform at any given time instant during a heat transient process. The profiles were studied, subjected to the fire action according to the nominal temperature–time curves (standard temperature-time curve ISO 834, external fire curve, and hydrocarbon fire curve). The obtained results allow verifying the agreement between the two methodologies and the influence in the temperature field due to the use of different nominal fire curves. This finding enables us to conclude that the lumped capacitance method is accurate and could be easily applied.

1. Introduction

Fire is a very complex phenomenon and can cause severe structural damages. A temperature–time curve evolution is always considered in fire analysis design. Temperature-time curves are analytical functions of time that give a temperature, and they are termed nominal because they do not represent a real fire but instead measure temperatures of previous fires and are therefore standardized. Since they are conventional, such relationships are thus to be used in a prescriptive regulatory environment, and any requirement that is expressed in terms of a nominal curve is prescriptive. According to Eurocode 1, fire action is defined as a temperature-time curve, which represents the time evolution of a gas temperature surrounding the structure. Eurocode 1 introduces three different nominal temperature-time curves: the standard temperature-time curve, the external temperature-time curve, and the hydrocarbon temperature-time curve. Each of these curves is used for special types of fires [1,2,3].

The standard temperature-time curve, also referred to as the ISO 834 curve, is the most common standard fire curve used internationally for fire resistance testing of components. This curve has been used in standard fire tests to rate structural and separating elements, which can be used for all fire design scenarios. The standard nominal curve ISO 834, suitable for civil structures, which are characterized by cellulosic materials, helps to define the conditions when the temperature increases according. This curve represents a fully developed fire in a compartment. The ISO curve reference is due to the ISO 834 standard. When a requirement is expressed as Rxx, where xx could be equal to 30 or 60 min, for example, the standard fire curve must be used to evaluate the fire resistance duration of the structural elements. This allows for a direct comparison between standard fire tests of components rather than indicating how long the component will survive in the fire [1,2,3,4].

The external temperature-time curve is used for the outside surface of separating external walls of a building, which are exposed to a fire that develops outside the building or to the flames coming through the windows of a compartment situated below or adjacent to the external wall. The external curve has the same behavior as the standard curve up to approximately 650 °C but after then it remains constant [1,2].

The nominal curve, if the hydrocarbons burn, is used to describe fires, and to evaluate the fire resistance of constructive elements where the temperature can increase more quickly than that of the standard nominal curve, thus reaching higher values (as with combustible liquids). The hydrocarbon temperature-time curve is used for representing the effects of a hydrocarbon-type fire. It shows that the hydrocarbon curve increases very quickly and reaches a constant value of 1100 °C after half an hour, whereas the standard curve increases more progressively but keeps on increasing with time [1,2,3].

In fire resistance, the calculation of the temperature profile developed in the element cross-sectional area, as a function of time, is called thermal analysis. In this type of analysis, it is always necessary to carry out a structural analysis since any discrepancy in the temperature field calculation can lead to the selection of an incorrect cross-sectional size element or a decrease/increase in the required thickness to fire protection [2,3,4,5]. Thermal analyses can be performed using experimental tests, simplified analytical methods, or numerical methods. The study of structural elements subjected to fire is a subject that has been extensively studied by several authors in recent years. However, it still has a significant number of aspects to be known and developed, requiring further research.

In 2006, Franssen [6] conducted a study to verify if the simplified method proposed by Eurocode 3 for temperature determination would have a significantly lower safety factor than the method proposed by the same Eurocode 3 for profiles without protection since a new correction factor for the shadow effect was introduced. The study was focused on a nominal fire situation in which the profile was exposed on all sides to the fire action. Thus, it was possible to demonstrate that the temperature field in steel profiles can differ depending on the method used, mainly for profiles with I cross-sections, since the method proposed by the new standard leads to a temperature profile with lower values. However, this temperature reduction never exceeded 14%, and it is only registered for a short period. For profiles with convex shapes, this method allows obtaining a higher temperature profile. Finally, the author reported that it was not possible to conclude that the new method has a lower security level and that it is not a consistent method for profiles with I sections.

In 2009, Wald et al. [7] carried out experimental tests in a compartment of a three-story steel structure exposed to fire before its demolition. The main objective of the study was to evaluate the temperature in the unprotected steel elements (IPN profiles) and then compare it with the values obtained by the simplified equation proposed by Eurocode 3. It was concluded that the simplified method proposed by Eurocode 3 showed good accuracy when compared to the results obtained by the experimental tests.

In 2009, Rigobello et al. [8] addressed a study to evaluate the simplified equation to calculate the temperature of the steel profiles subjected to fire proposed by the Brazilian standard NBR 14323: 1999, which is based on Eurocode 3, and compared the results with numerical simulations. The results were carried out on steel exposed on three sides to the standard fire curve ISO 834, and they concluded that the standard fire leads to satisfactory results.

In 2013, Dwaikat et al. [9] developed an easy-to-use analytical method to estimate the temperature in the cross-sectional area of protected and unprotected steel profiles subjected to fire. This method is based on the differential equation that governs heat transfer by performing the following simplifications: the temperature in the steel profile cross-section must be considered uniform, the radiation problem must be approximated to a convection problem, the temperature in the protective material must be considered equal to the temperature of the steel and fire, and the thermal properties of the steel and the protective material must be considered constant and not dependent on the temperature. To validate the developed method, the authors performed a numerical simulation in the ANSYS^® program (Engineering Simulation Software, United States) of a steel profile subjected to fire on three sides, protected by a cement-based and fireproof material (CAFCO300), usually applied by spray. Based on this study, it was possible to conclude that the proposed method can be applied to any fire curve for protected and unprotected profiles exposed to fire up to three sides, since the obtained results are quite close to the numerical method, with an error of less than 8%. In the end, the proposed method was compared with the “best-fit line” method, concluding that it obtains better results and can be applied for a longer time interval.

In 2016, Lausova et al. [10] presented a study to analyze the distribution of nonuniform temperatures in hollow square steel cross-sectional profiles. This study consisted of numerical simulations, of four different profiles under fire on three sides, using the finite element method in the ANSYS^®. The authors considered the nonlinear thermal properties of steel. The results of the numerical simulations were compared with those obtained by the simplified equation of Eurocode 3 and with experimental tests performed by the authors. It was concluded that there is a big difference between the temperature of the unexposed side and the temperatures of the sides exposed to fire and that, for profiles with the same sections, a smaller thickness decreases the temperature difference. It was also emphasized that the exact knowledge of temperature distribution is very important, especially in structures where thermal expansion is conditioned. Therefore, the obtained results indicate that no simplified equation should be used to calculate temperatures in hollow square sections exposed to fire on three sides.

In 2019, Correia et al. [11] presented a study, based a geometric and nonlinear material analysis, to propose new expressions for the calculation of the steel profile mass factor in contact with walls. In this study, 26 profiles were analyzed, with two different brick wall thicknesses and with two orientations of the core in relation to the wall, giving a total of 94 studied cases. To calculate the temperature field in the cross-sectional area of the profile, the simplified equation proposed by Eurocode 3 and four different formulas were used to calculate the mass factor. Then, using the finite element method with the ABAQUS^® program (Dassault DS Systems, France), the temperatures in the profiles’ cross-sectional area were calculated to compare the results. In the end, the authors presented correction coefficients to be applied in the Eurocode 3 formulas to obtain a more realistic approximation of the temperatures in a profile during the occurrence of a fire.

Different research using experimental and numerical methodologies are used to study the behavior of different materials under fire conditions [12,13,14,15,16,17,18]. Nevertheless, there are some cases where analytical methods can be used. Two cases are of interest for both practical uses and basic understandings of the influence of material properties on their fire behavior. Firstly, in cases where bodies can be assumed to have a uniform temperature at any instant during the transient process, so that the temperature gradient may be considered negligible, such as thin solids or metals with high conductivity. Any thermal analysis that uses this idealization can be performed using the lumped capacitance method [18,19,20,21,22,23]. Secondly, in cases when a body can be assumed semi-infinitely thick for the time span considered. Then, the surface temperature can be estimated by analytical methods if the material properties are assumed constant. The European standards also represent simplified equations for the temperature calculation of steel structures exposed to fire.

This present paper examines the temperature distribution in different ranges of hot-rolled steel profiles when submitted to fire at all four sides. The obtained results agree between the lumped capacitance method and the simplified equation from Eurocode 3, according to the use of different nominal temperature-time curves.

Discussion of results and the calculated relative error will give a clear insight into this issue. The main goal of this work is to present the temperature calculation, using both methods, in different cross-sections of structural hot-rolled steel profiles: I-beams with parallel flanges using the acronym IPE, heavy wide-flange beams, also called HEM, beams with equal or unequal angles or L profiles, and channels that have conical internal flanges or UAP.

The advantage of this work is the demonstration of two different forms of equations for the simple temperature calculation in steel members that can be used from the scientific and technical research fire community.

2. Thermal Properties

To calculate the temperatures in hot-rolled steel profiles exposed to fire, it is necessary to consider the thermal material properties. The density of steel $\rho$ is assumed to remain constant and equal to 7859 kg/m³, as defined by Eurocode 3 [24]. The specific heat capacity of steel C_s and the thermal conductivity ${\lambda }_s$ are a function of the temperature evolution, as presented in Eurocode 3 [24]. Figure 1 and Figure 2 present the steel thermal properties used in this work.

3. Nominal Temperature–Time Curves

The environment temperature evolution due to a fire is given by one nominal time-temperature curve, as represented in Figure 3, according to Eurocode 1 [3,4].

The ISO 834 curve (standard temperature–time curve) is the one that has been used in fire tests to rate structural and separating elements [1,3,4]. This curve is obtained as follows.

$${\theta }_{\infty }=20+345{\log }_{10}\left(8t+1\right)$$

(1)

The external fire curve is used for the outside surface of separating the external walls of a building [1,3,4]. This curve is a temperature-time relationship that is representative of the reduced exposure experienced by building elements and is defined by Equation (2).

$${\theta }_{\infty }=20+660\left(1-0.687e^{0.32t}-0.313e^{-3.8t}\right)$$

(2)

The hydrocarbon fire curve, used for environments where a high degree of hydrocarbons is present, as for offshore oil installations or tunnels, is given by [3,4,25] as follows.

$${\theta }_{\infty }=20+1080\left(1-0.325e^{-0.167t}-0.675e^{2.5t}\right)$$

(3)

In the equations above, $t$ is the time in min and ${\theta }_{\infty }$ is the gas temperature in the fire compartment in °C.

As represented in Figure 3, the hydrocarbon curve increases very quickly and reaches a constant value of 1100 °C after 30 min [1]. The external fire curve reaches a constant value of 680 °C after 20 min. The standard temperature–time curve gradually increases and reaches 800–1200 °C. The standard curve gives temperatures of 842 °C at 30 min, 945 °C at 60 min, and 1049 °C at 120 min [26].

4. Calculation Methods

According to the Eurocodes, there are two main types of calculation methods for steel structures exposed to fire—simple calculation methods and advanced calculation methods [27]. For the design of individual steel members exposed to fire, simple methods could be applied, often using hand calculations. The use of advanced methods is dedicated to more complex structures that require the use of computer programs [27].

In this work, two simple methods are presented. One method consisting of the simplified equation from Eurocode 3 [24], which is based on the principle that the heat entering the steel over the exposed surface area in a small-time-step is equal to the heat required to raise the temperature of the steel, assuming that the steel temperature is uniform over the cross-section [27]. Additionally, the lumped capacitance method is also considered, which is very desirable due to its simplicity and accessibility since it is an easier transient heat conduction approach that permits the temperature of the steel members to be analyzed only as a function of time. Both methods can be used for a protected or unprotected steel element on the assumption that the internal steel temperatures are constant.

Nevertheless, there are other analytical methods, using the Duhamel’s theorem and Green’s functions, to determine steel elements in fire [28]. Heat transfer analysis of fire steel elements normally requires the solution of a two-dimensional transient diffusion equation. Since heating conditions assume steel members to be fully embedded in fire, the two-dimensional problem can be approximated by the one-dimensional differential conduction equation, assuming a steel lumped capacitance [28,29,30]. Duhamel’s theorem provides a convenient approach for developing a solution to heat conduction problems with time-dependent boundary conditions by using the solution to the same problem with time-independent boundary conditions [28,29,30]. These methods are frequently used by different authors to obtain easy solutions to compare with other methodologies.

5. Simplified Equation from Eurocode 3

The temperature increases over a given time step $\mathsf{\Delta }t$ in the cross-sectional area for an unprotected hot-rolled steel profile submitted to fire, which must be determined from the simplified equation (EC3) presented in Eurocode 3 [24], according to Equation (4).

$$\Delta {\theta }_{a,t}=k_{sh}\frac{A_m/V}{C_s \rho }{\dot{h}}_{net,d}\Delta t$$

(4)

where k_sh is the correction factor for the shadow effect and is considered equal to unity for conservative results, A_m is the surface area of the member per unit length m²/m, V is the volume of the steel member per unit length m³/m, Am/V is the section factor for unprotected steel members m⁻¹, C_s is the specific heat of steel J/kgK, and $\rho$ is the density of steel, as previously referred, according to Eurocode 3 [24], $\Delta t$ is the time interval, which must not be taken as more than 5 s and ${\dot{h}}_{net,d}$ is the net heat flux per unit area, in W/m², due to radiation and convection, which should be determined according to Eurocode 1 [3,26] by the following expression.

$${\dot{h}}_{net,d}={\dot{h}}_{net,c}+{\dot{h}}_{net,r}$$

(5)

where ${\dot{h}}_{net,c}$ is the net convective heat flux per unit area W/m², ${\dot{h}}_{net,r}$ is the net radiative heat flux per unit area W/m² and their values must be obtained from Equations (6) and (7), respectively [26].

$${\dot{h}}_{net,c}={\alpha }_c\left({\theta }_{\infty }-{\theta }_m\right)$$

(6)

where ${\alpha }_c$ is the coefficient of heat transfer by convection and should be taken as 25 W/m²K for standard fires or 50 W/m²K for hydrocarbon fires, ${\theta }_{\infty }$ is the gas temperature in the vicinity of the fire exposed steel member, and ${\theta }_m$ is the surface temperature of the steel member.

$${\dot{h}}_{net,r}=\varphi .{\epsilon }_m.{\epsilon }_f.\sigma .\left[{\left({\theta }_r+273\right)}^4-{\left({\theta }_m+273\right)}^4\right]$$

(7)

where $\varphi$ is the configuration factor, which must be equal to unity, ${\epsilon }_m$ is the surface emissivity of the member, ${\epsilon }_f$ is the emissivity of the fire, generally taken as equal to unity, $\sigma$ is the Stephan Boltzmann constant, taken as 5,67 × 10⁻⁸ W/m²K⁴, and ${\theta }_r$ is the radiation temperature of the surrounding environment of the steel member, being often considered that ${\theta }_r$ = ${\theta }_{\infty }$.

Regarding the time interval, Δt, Eurocode 3-Part 1–2 [24] recommends the use of an interval equal to or less than five seconds (Δt ≤ 5 s). To understand which interval leads to the least errors, a study was performed on an Excel spreadsheet. Thus, it was considered to study that the minimum time interval to be used would be Δt = 0.5, 1, 2, 3, 4, and 5 s. To try to understand this restriction, Δt = 10 and 20 s were also studied.

Figure 4 shows the evolution of the relative error, obtained for each solution time, comparing the temperature using a time step equal to Δt = 0.5 s (assumed as reference) and a different time step. This study was carried out for different profiles, although only the IPE 400 exposed to fire on four sides is presented, according to the ISO 834 nominal fire curve.

Analyzing Figure 4, it is possible to verify that the simplified equation proposed by Eurocode 3 is very susceptible to time variation in the first 15 min, which makes it impossible to use time intervals higher than five seconds. However, after 30 min, the selected time interval does not have much effect on the obtained results since, for all studied time intervals, its error is almost zero. However, for the simplified Equation (4), a time interval Δt = 5 s was selected since the error obtained, when compared with shorter time intervals, is insignificant. The same observation was obtained in all different profiles in this study.

6. Lumped Capacitance Method

The assumption of the lumped capacitance method (LC) method or uniform temperature is a reasonable approximation when calculating the temperature of steel cross-sections exposed to fire on all four sides. This type of formula is most accurate where it is used repeatedly with sequential time steps. For the application of this method, the temperature of a solid is assumed to be spatially independent or uniform. A perfect spatially uniform transient temperature field does not exist and relatively uniform temperature distribution within the solid should be assumed when compared to the distribution between the body and its surroundings. This hypothesis is valid if the resistance to the heat conduction within the solid is small in comparison to the heat transfer resistance between the solid and ambient, with the calculated Biot number (Bi) [20,21,23]. This number plays an important role in conduction involving convection effects. The Biot number is a dimensionless parameter, and it is defined as the ratio of the convection and the conduction thermal resistance, according to Equation (8) [31].

$$B_i=\frac{L_c {\alpha }_{cr}}{{\mathsf{\lambda }}_s}$$

(8)

where $L_c$ is the characteristic length of the solid shape, in m⁻¹, defined as the ratio between the solid volume and the cross-sectional area exposed to fire, and equal to the inverse of the section factor or massivity factor $\frac{A_m}{V}$, ${\lambda }_s$ is the steel thermal conductivity, which is temperature dependent in W/mK (Figure 1), and ${\alpha }_{cr}$ is the heat transfer coefficient by convection and radiation W/m²K, which is given by the sum of the coefficient of heat transfer by convection, ${\alpha }_c$, equal to 25 W/m²K, and the coefficient of heat transfer by radiation, ${\alpha }_r$, which must be calculated according to Equation (9) [25].

$${\alpha }_r=\epsilon \sigma \left(\theta +{\theta }_{\infty }\right)\left({\theta }^2+{\theta }_{\infty }^2\right)$$

(9)

Similar to the mass factor, for prismatic bars, the characteristic length $L_c$ can be simplified according to Equation (10), which is a function of the cross-sectional area of the hot-rolled steel profile A m², the perimeter cross-section P m, and the profile length L m.

$$L_c={\left(\frac{A_m}{V}\right)}^{-1}=\frac{V}{A}=\frac{A\times L}{P\times L}=\frac{A}{P}$$

(10)

To apply this method to solids submitted to fire, it is necessary to consider the heat transfer by radiation, since a large part of the heat flow transferred to the steel members is through radiation [32]. The use of this method is generally accepted when the Biot number is smaller than unity [25], where the resistance to conduction within the solid is much less than the resistance to convection across the fluid boundary layer. This means that the assumption of uniform temperature distribution is reasonable [20]. Therefore, solid bodies with high thermal conductivity, as in the case of steel, are good candidates for the use of this method. If the temperature in the element cross-section is uniform, i.e., ${\theta }_{x,t}\cong {\theta }_t$, the solution of Equation (11) allows obtaining the temperature as a function of time according to the LC method [20].

$${\theta }_t=\left({\theta }_i-{\theta }_{\infty }\right)e^{\left(-Bi.Fo\right)}+{\theta }_{\infty }$$

(11)

where ${\theta }_t$ is the temperature for a time $t$, $\left({\theta }_i-{\theta }_{\infty }\right)$ is the temperature difference at time t = 0, $Fo$ is the Fourier number, and ${\theta }_{\infty }$ is the gas temperature in the vicinity of the fire exposed steel member.

The Fourier number is a dimensionless ratio between the heat conducted through the solid and the heat retained by the solid. A high Fourier value reveals a faster heat spread through a solid body, and it is calculated for a time after a step change in ambient temperature, according to the following equation [31]:

$$Fo=\mathsf{\alpha }\frac{ t}{L_c^2}$$

(12)

In Equation (12), $\mathsf{\alpha }$ represents the ratio of the thermal conductivity to the heat capacity, which is an important property, termed as thermal diffusivity and given in m²/s [20].

$$\mathsf{\alpha }=\frac{{\lambda }_s}{\rho C_s }$$

(13)

The characteristic length, equal to the inverse section factor, was determined for all members, as shown in

Table 1. Section factor values m⁻¹.

Profiles	IPE100	IPE300	IPE500	IPE600
$\frac{A_m}{V}$	387.3837	215.5733	150.9564	129.1536
Profiles	HEM100	HEM400	HEM700	HEM1000
$\frac{A_m}{V}$	115.9488	61.4993	66.8315	67.8309
Profiles	L 100 × 100 × 8	L 140 × 140 × 10	L 180 × 180 × 15	L 250 × 250 × 25
$\frac{A_m}{V}$	255.4960	203.8704	138.2748	85.6769
Profiles	UAP80	UAP150	UAP200	UAP300
$\frac{A_m}{V}$	302.8423	230.8237	210.7968	165.1751

, according to the chosen hot-rolled steel profiles and their cross-sectional area from the Arcelor catalog represented in

Table 2. Expressions used to calculate the section factors of IPE/HEM, L, and UAP, m⁻¹.

IPE/HEM	$\frac{A_m}{V}=\frac{P}{A}=\frac{4b+2d+4t_f-2t_w-4r+2\pi r}{h\times t_w+2\left(b\times t_f\right)-2\left(t_f\times t_w\right)+4r^2-\pi r^2}$
L	$\frac{A_m}{V}=\frac{P}{A}=\frac{2h+2b+2r_1-4r_2+2t+\frac{\pi r_1}{2}+\pi r_2}{h\times t+b\times t-\frac{\pi r_1^2}{4}+\frac{\pi r_2^2}{2}+r_1^2-2r_2^2-t^2}$
UAP	$\frac{A_m}{V}=\frac{P}{A}=\frac{h+d+4b+t_f+2r+2t_f-2t_w+\pi r}{h\times t_w+2\left(b\times t_f\right)-2\left(t_f\times t_w\right)-\frac{\pi r^2}{2}+2r^2}$

[33].

Table 1 represents the section factor $\frac{A_m}{V}$ for unprotected steel members, which measures the rate of temperature increase of a steel profile cross-section through the ratio of the heated surface area to the volume, or the heated perimeter to the cross-sectional area.

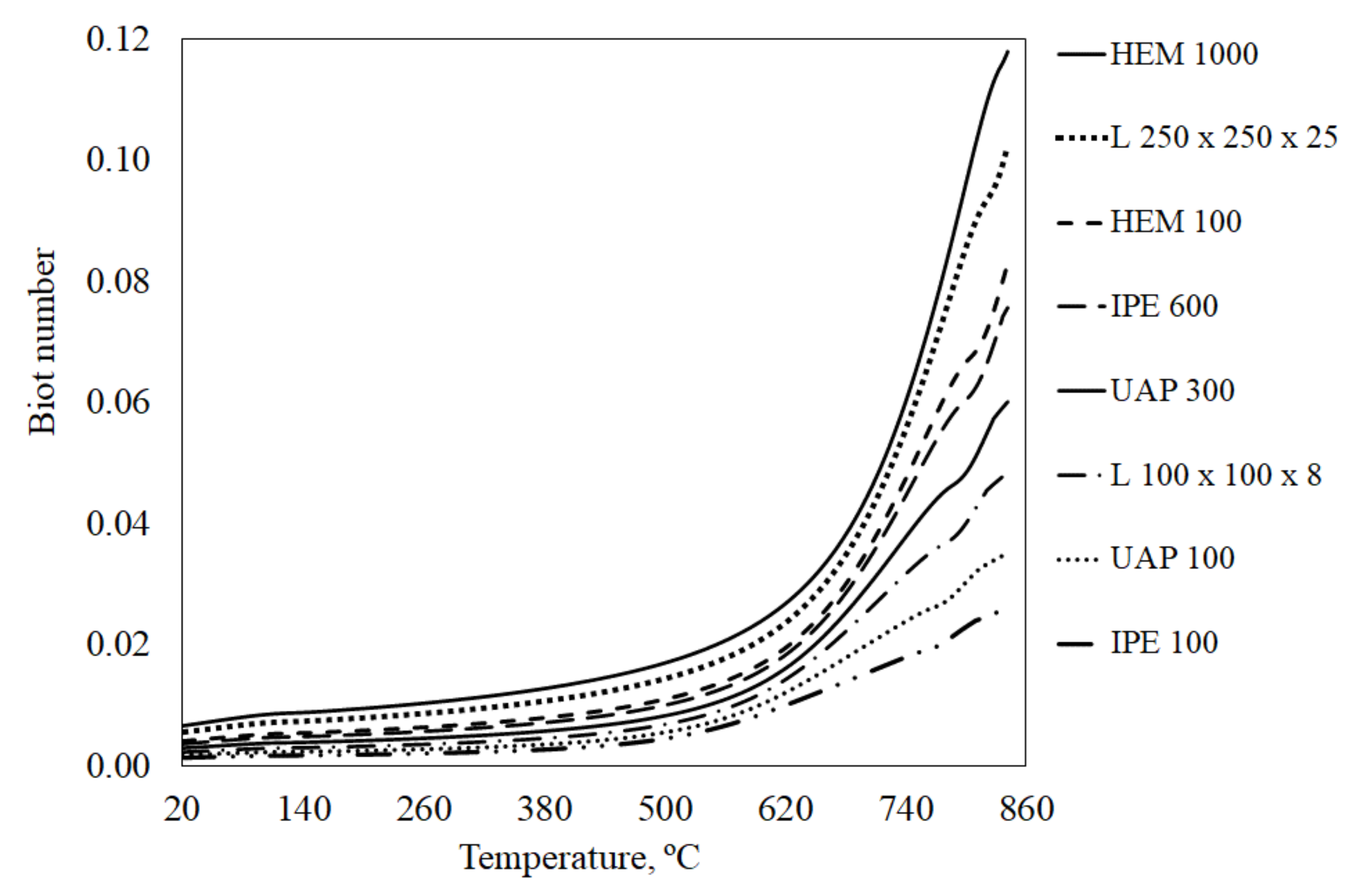
For the LC method, the Biot number was below unit in all studies, as represented in Figure 5.

The Biot number measures the temperature difference inside the solid in relation to the temperature difference between the surface of the solid and that of the surrounding environment. The lower the Biot number is, the lower this temperature difference and the more uniform the temperature field inside the solid. In this way, it is possible to consider a uniform temperature distribution for the entire cross-sectional area of the solid when the value of the Biot number is much less than the unit (Bi << 1). It is desirable to use the global capacitance method only when this condition is verified [22,23,34].

Figure 5 shows the evolution of the Biot number as a function of temperature, according to the nominal curve ISO 834, for some of the hot-rolled steel profiles in this study.

Like the simplified equation proposed by Eurocode 3, it was studied what time interval to use and how is the sensitivity of the method to the use of large time intervals. Thus, in an Excel spreadsheet, considering that the minimum time interval to use would be Δt = 0.5 s for the relative error calculation, the intervals Δt = 1, 2, 3, 4, 5, 10, and 20 s were also verified.

Figure 6 shows the relative error as a function of the fire time for each of the time intervals mentioned for an IPE 400 profile subjected to the ISO 834 standard fire curve on the four sides.

Comparing the errors obtained for the LC method with those obtained for the simplified method of Eurocode 3, it is possible to state that the LC method has less sensitivity to the use of longer time intervals. For time intervals less than 30 min, this method causes minor errors, unlike the simplified method recommended by Eurocode 3.

Even so, in this work, Δt = 5 s was used, which is the same interval used in the Eurocode 3 method.

7. Results and Discussion

Numerical and experimental investigations in different specimens from typical beam cross-sections exposed to fire were, among others, reported by [1,2,30].

Analytical methods were used and compared with the experimental data results obtained from a furnace that adopts the standard ISO fire curve. The results of comparison for the same representative specimens of steel sections HEM, HEB, HEA, IPE, and U prove reasonable accuracy between the chosen methods [30].

Numerical simulations of the thermal response of steel HE profiles subjected to the fire curve ISO were analyzed by [1,2]. The authors concluded that the temperature field on the steel cross-sectional profile exposed to all four sides shows an almost uniform temperature in each time instant [1,2].

In this work, the results obtained from the LC method were compared with the results from the EC3 method from Eurocode 3. To respond to the described objectives, an analysis was made of the temperature evolution of the profiles of each studied range exposed to fire according to the three nominal fire curves.

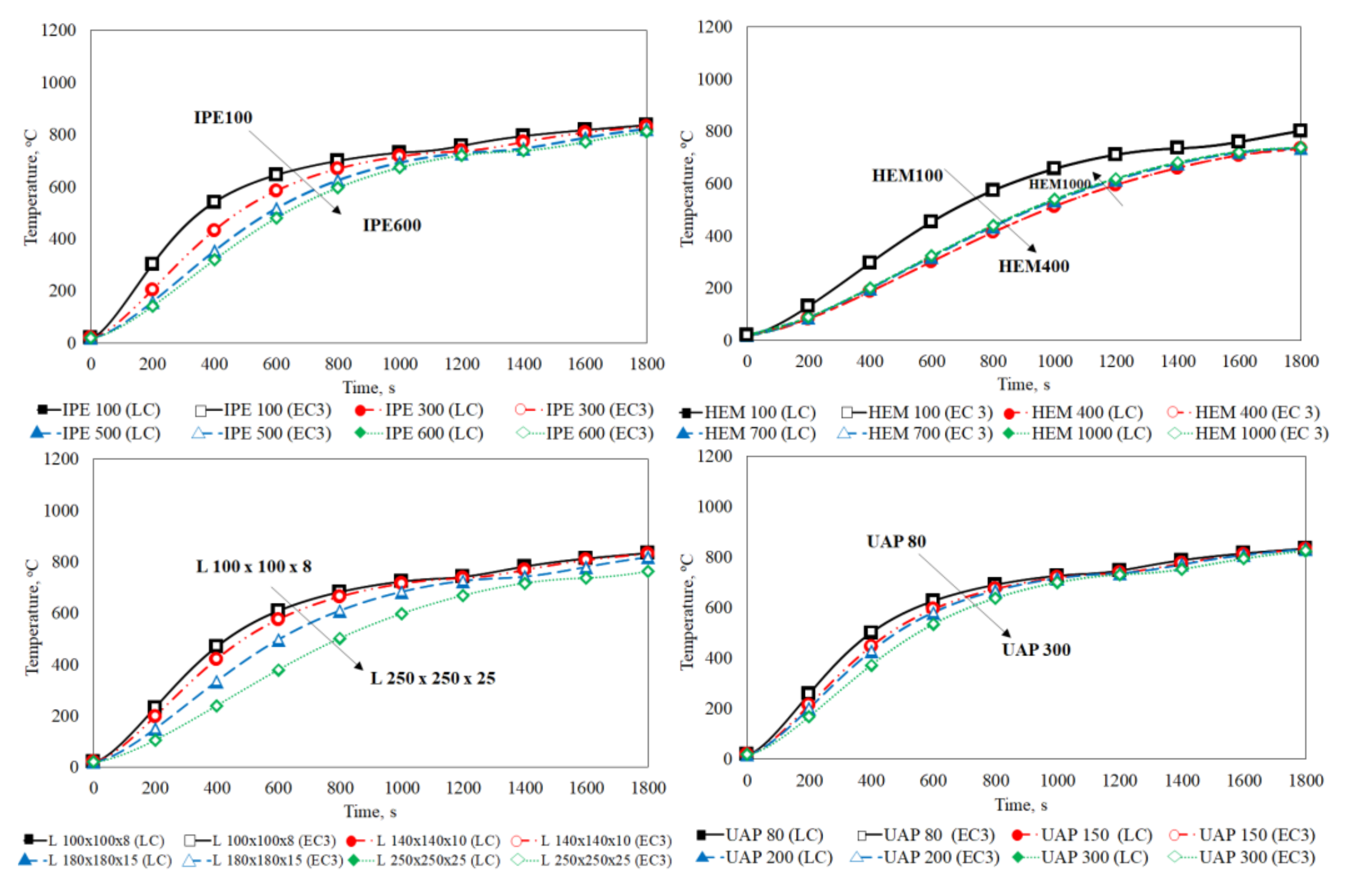
In Figure 7, Figure 8 and Figure 9, it is possible to analyze the temperature–time history for different sizes of the studied hot-rolled steel profiles.

Figure 7 represents the temperature–time history of different profiles under the ISO curve that have a similar tendency to the previous investigations.

Figure 8 represents the temperature–time history of different profiles under the external curve, and Figure 9 according to the hydrocarbon curve.

The results using the LC method agree with the results obtained from the simplified equation of Eurocode 3 for all different types and sizes of the studied profiles. It is possible to verify that, for IPE, L, and UAP hot-rolled steel profiles, when the profile size increases, the temperature distribution decreases, except for the HEM steel profile. This fact is related to the thickness of the HEM profile, which is the same for cross-section 320 and over, increasing the fire exposed surface. In IPE, L, and UAP hot-rolled steel profiles, the section factor decreases when the cross-section of the profile increases. The exception is the HEM profile, in which the section factor decreases until HEM400 and then increases.

Analyzing the graphs, it is possible to state that the thermal analyses using the LC method are close to those performed by the EC3 method since the temperature values are very close for any hot-rolled steel profile size and any nominal fire curve.

All these results add to the state-of-the-art of previous research by the authors, who formerly studied hollow tubular sections and a range of IPE profiles using numerical and analytical methodologies [1,21].

In this study, as a conclusion, hot-rolled steel profiles that have cross-sectional areas with low section factors will heat up more slowly, as referenced by K. Banerjee [34].

Figure 10 shows the relative error of the obtained results in relation to the simplified equation. The maximum error obtained is 2% in IPE100 when using the Hydrocarbon curve and for a time equal to 60 s. Nevertheless, the fire resistance might be not sensitive to so small errors.

The analysis of Figure 10 shows that the error decreases with the increase in the profile cross-section. It should also be noted that the maximum error obtained in the ISO 834 fire curves and with external elements curves is similar, due to the similarity of the heating curves in the initial moments. In all hot-rolled steel profiles, the biggest error is obtained in the hydrocarbon fire curve due to its severity and the high-temperature increase in the initial instants. Thus, it is concluded that the LC method is valid and can be used as an alternative to that proposed by Eurocode 3 (EC3 method) during the design of metal structures for this type of profile.

8. Conclusions

Regarding the use of analytical methods, it was possible to verify that the LC method can be used in design to determine the temperature evolution for profiles submitted to different fire scenarios since the results obtained agree with those of the simplified equation recommended by the Eurocode 3 for the studied profiles.

However, some limitations could arise when using the proposed approaches. The LC method is a common approximation in transient conduction heat transfer, which may be used when the resistance to heat transfer by conduction inside the body is smaller than the resistance to the heat transfer across the boundary of the body [1]. With the EC3 method, an equivalent uniform temperature distribution through the cross-section needs to be assumed. Additionally, the section factor value should not be taken less than 10 m⁻¹, because such a massive section would not have a uniform temperature, and Δt should not be taken as more than 5 s.

With the thermal analysis carried out using the analytical methods, it was possible to conclude that the lower the profile section factor is, the lower the temperatures developed in the cross-sectional area during exposure to fire. The section factor decreases with increasing cross-sectional size for all profile ranges studied, except for HEM profiles. Thus, it appears that the profiles with higher fire resistance have a larger cross-section, except for HEM profiles, since HEM 1000 has higher temperatures than HEM 320.