AutoML for Feature Selection and Model Tuning Applied to Fault Severity Diagnosis in Spur Gearboxes
Abstract
:1. Introduction
2. Background
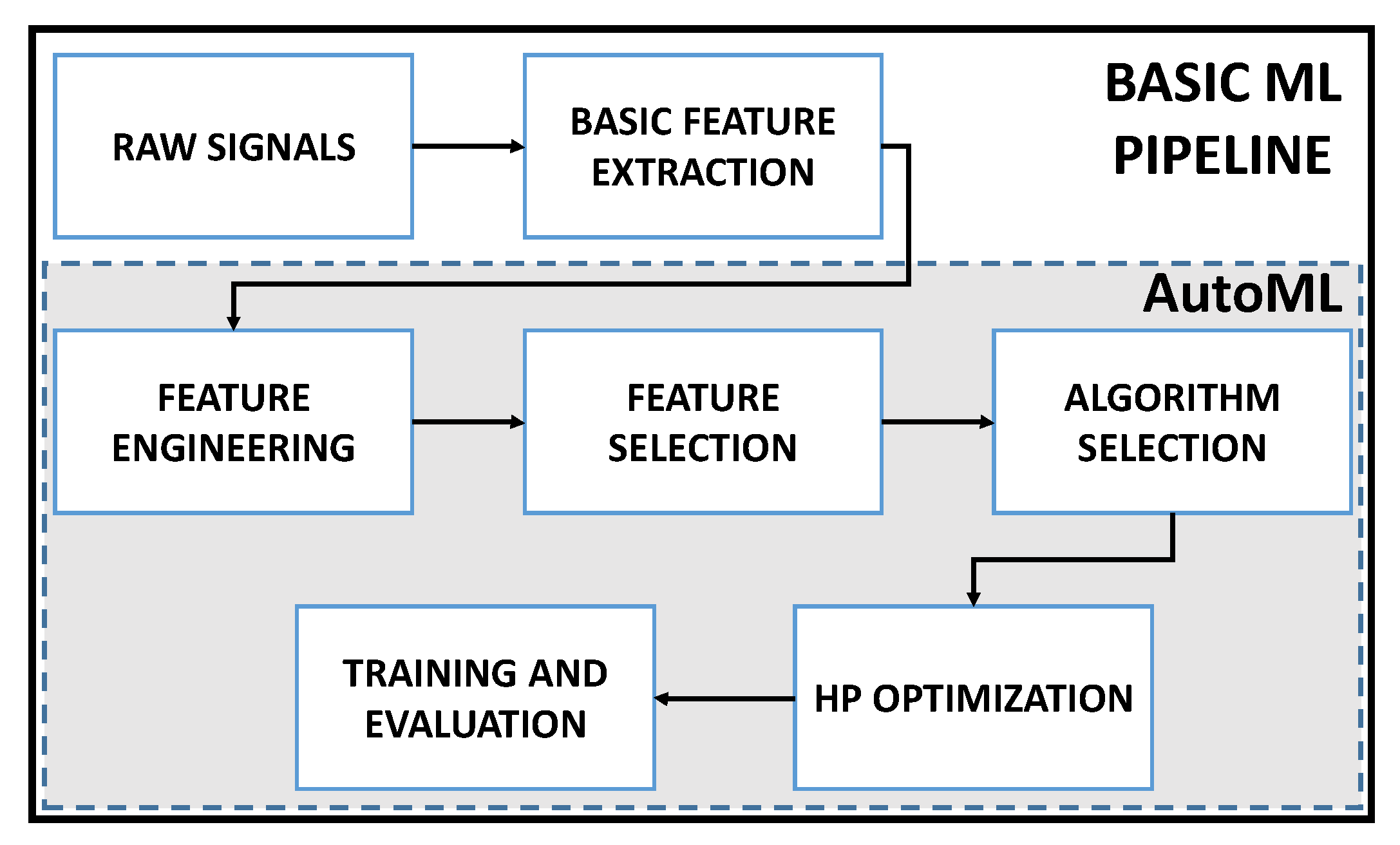
2.1. Overview of AutoML
2.2. Faults in Gearboxes
3. Previous Work
4. Case Study
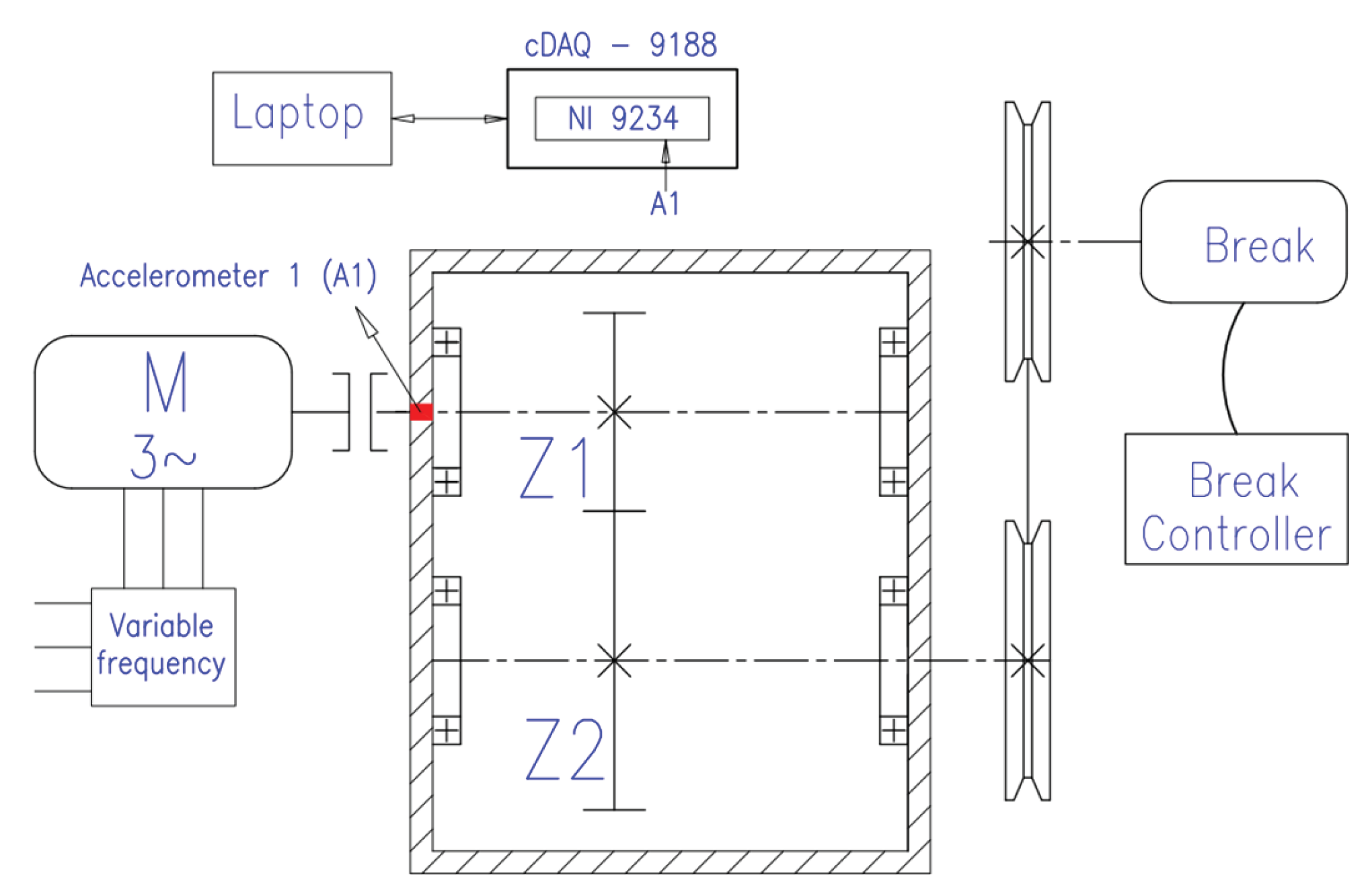
4.1. Experimental System and Data Acquisition
4.2. Dataset
- The time length of each example is 10 s. Then, the signal is composed by 500,000 samples, according to the sample frequency of the DAQ card;
- The motor rotates at constant speeds of 180 rpm, 720 rpm and 960 rpm;
- The constant load was configured for no-load (0 N m), and loads generated with constant voltage application on the magnetic brake on 5 VDC (1.44 Nm) and 10 VDC (3.84 Nm);
- Each example configured under different speed and load were repeated 15 times.
5. Experiments and Results
5.1. AutoML with H2O Driverless AI
5.1.1. System Configuration
- 1.
- Accuracy [1–10]: This setting controls the amount of search effort performed by the AutoML process to produce the most accurate pipeline possible, controlling the scope of the EA and the manner in which ensemble models are constructed. In all of our experiments, we set this to the highest value of 10;
- 2.
- Time [1–10]: This setting controls the duration of the search process and allows for early stopping using heuristics when it is set to low values. In all of our experiments, we set this to the highest value of 10;
- 3.
- Interpretability [1–10]: Guaranteeing that learned models are interpretable is one of the main open challenges in ML [75], which can be effected, for example, by model size [76]. DAI works under the assumption that model interpretability can be improved if the features used by the model are understandable to the domain expert, and if the relative number of features is kept as low as possible. This setting controls several factors, including the use of filtering features selection on the raw features, and, more importantly for our study, the amount of Feature Engineering methods used. In this work, we evaluate two extreme conditions for this setting, for each case study we perform two experiments, using a value of 1 and 10. A value of 10 filters out co-linear and uninformative feature, while also limiting the AutoML process to only use the original raw features of the problem data. On the other hand, the lower value uses all of the raw features and constructs a large set of new features using a variety of Feature Engineering methods;
- 4.
- Scoring: Depending on the type of problem, regression or classification, DAI offers a large variety of scoring functions that are to be optimized by the underlying search performed by the AutoML system, such as Classification Accuracy or Log-Loss for classification. In this work, we choose the Area Under the Receiver Operating Characteristic Curve (AUC), where optimal performance is achieved with a value of 1, and 0 otherwise. Since all case studies are multi-class problems, this measure is computed as a micro-average of the ROC curves for each class [77].
5.1.2. Evaluation of AutoML Pipelines
5.1.3. Analysis of Feature Importance
- Original: The original features in the dataset;
- Cluster Distance (CD): Uses a subset of features to cluster the samples, and uses the distance to a specific cluster as a new feature;
- Cluster Target Encoding (CTE): Also cluster the data, but computes the average value of the target feature of each cluster as a new feature;
- Interaction: Uses feature interactions as new features, based on simple arithmetic operations, namely addition, subtraction, division, and multiplication;
- Truncated SVD (TSVD): This heuristic trains a truncated SVD model on a subset of the original features, and uses the components of the SVD matrix as new features for the problem.
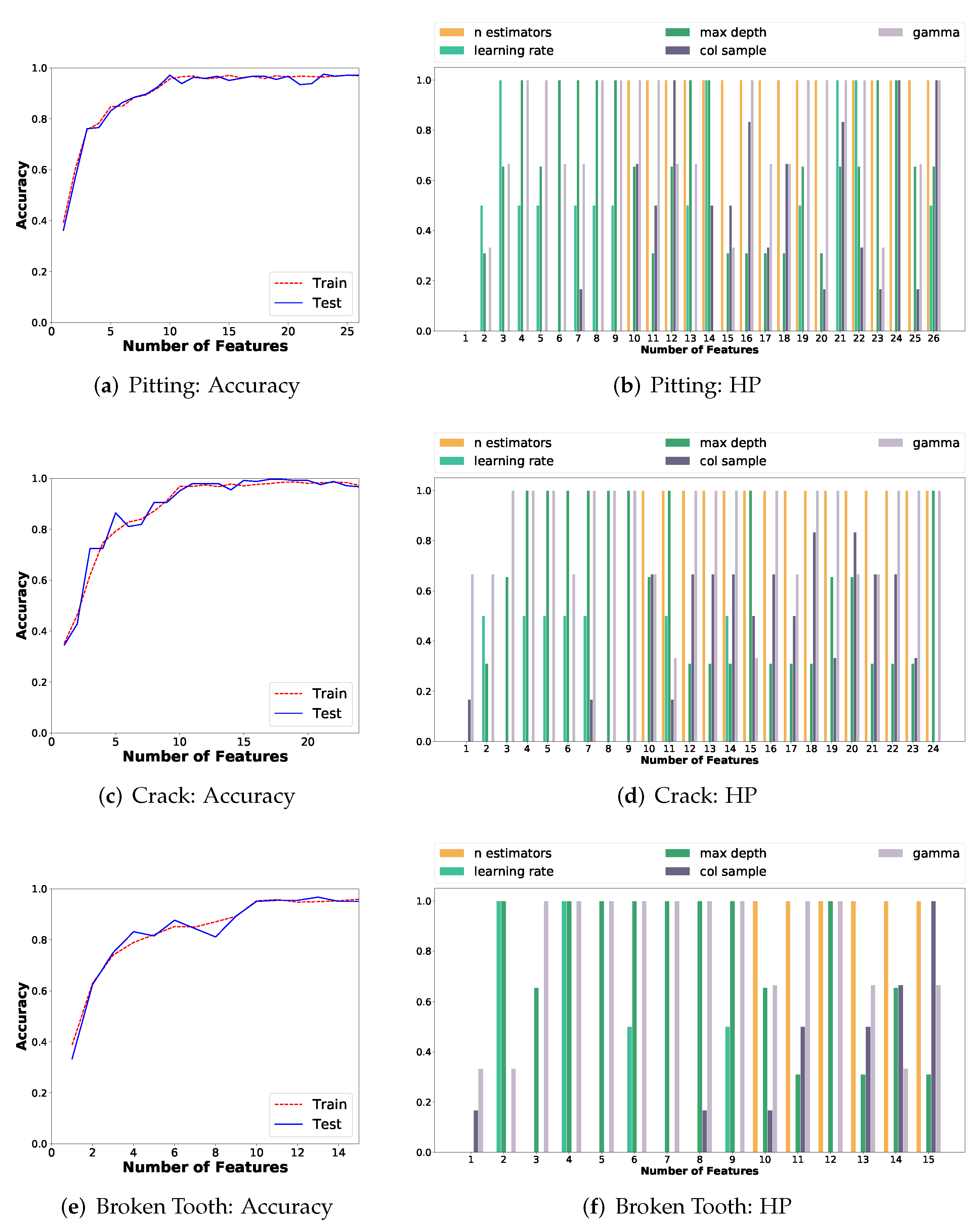
5.1.4. Feature Importance and Classification Performance
- Number of estimators (): The number of weak-learners used by the XGBoost classifier. The search range is ;
- Learning rate (): Size of each bootstrapping step, and it is critical to prevent overfitting. The search range is ;
- Max Depth (): Maximum depth of each weak-learner, which is represented as a decision tree. The search range is ;
- Feature Subsampling (): Represents the fraction of features that are subsampled by a particular learner. The search range is ;
- Gamma (): A regularization term that controls when a leaf is split in a weak-learner decision tree. The search range is .
5.2. AutoML with TPOT
5.2.1. TPOT Configuration and Results
TPOT Pitting Pipeline
- First, an RFE feature selection step that reduced the feature space to hold the number of original features;
- A filtering of the features using SelectFwe, which left a total of 27 original features. It is of note that the number of features used in this pipeline is the same as those used by H2O on the same problem (see Table 2 for Pitting with Interpretability set to 10);
- Feature transformation by PCA, followed by a robust scaling;
- Finally, modeling was carried out by the Extra Tree classifier with 100 base learners.
TPOT Crack Pipeline
- The pipeline stacked two models in this pipeline. The first model is a Multilayer Perceptron (MLP) with a learning rate of 1 and 100 hidden neurons;
- The outputs from the MLP were concatenated with the original feature set and used to train the second model, a Gradient Boosting classifier with learning rate 0.5, max depth of 7, minimum sample split of 19 and 100 base learners.
TPOT Broken Tooth Pipeline
- The pipeline stacked two models in this pipeline. The first model is a Gradient Boosting classifier with learning rate 0.5, max depth of 4, minimum sample split of 10 and 100 base learners;
- The second model is a linear SVM classifier, with a squared hinge loss function, and L1 regularization.
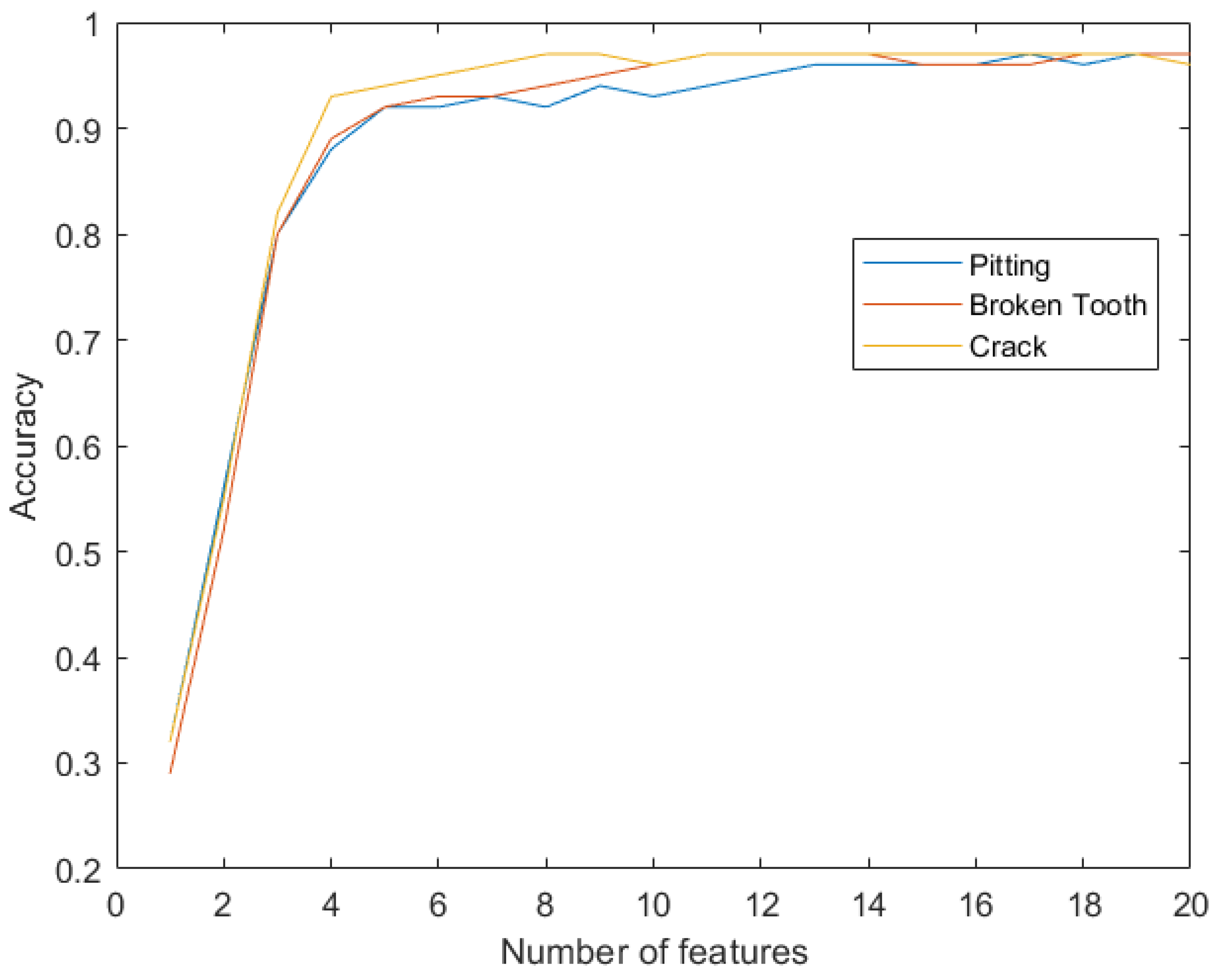
5.2.2. Analysis of Feature Selection and Feature Importance
6. Discussion
7. Summary and Conclusions
- The setting of H2O DAI in the process of feature engineering is more explicit for the user. This is particularly useful when testing the creation of new features;
- Results of the evaluation and comparison between H2O DAI and TPOT show that both platforms select common features, regardless of the selected model by each platform. The size of the feature space used by each system varies, and neither of them is consistently more or less efficient in this regard;
- Classification accuracy when using all the features, without feature selection, remains very close for both systems, over 96%;
- The accuracy achieved by AutoML can be increased relative to a hand-tuned classification model, particularly by adjusting the feature selection technique.
- Time-domain statistical features are highly informative. This is verified by the fact that the feature engineering methods provided by the AutoML platforms do not substantially increase the classification accuracy of the ML pipelines. This particularity was identified because of the use of AutoML, and this discovery reduces the requirements of computing other complex features beyond the informative ones;
- Classification accuracy over 90% is obtained with 10 features, and over 95% with more than 13 features, for each failure mode, when problem-specific features are selected based on the relative feature importance. The use of AutoML permitted to set the proper number of features, and this directly improves the generalization capability of the ML model for fault diagnosis;
- Common features for all three failures modes can be selected based on average values of feature importance across all problems. These common features are highly informative as they achieve a classification accuracy over 96%. Moreover, the common set of features are ranked as highly informative for all problems by both AutoML systems. The analysis and use of the same set of features for all three failure modes has not been previously reported in the literature;
- The accuracy of the classifiers obtained by AutoML are highly competitive with the state-of-the-art in this domain, reaching 96% of accuracy and even 99% in some failure modes. For comparison, accuracy by manual design of ML pipelines has been reported of up to 97% on the same datasets. This result verifies the power of the pipelines created from AutoML.
Author Contributions
Funding
Conflicts of Interest
References
- Lei, Y.; Lin, J.; Zuo, M.J.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Goyal, D.; Pabla, B.S.; Dhami, S.S. Condition monitoring parameters for fault diagnosis of fixed axis gearbox: A review. Arch. Comput. Methods Eng. 2017, 24, 543–556. [Google Scholar] [CrossRef]
- Randall, R.B. Vibration-Based Condition Monitoring: Industrial, Aerospace and Automotive Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Li, F.; Li, R.; Tian, L.; Chen, L.; Liu, J. Data-driven time-frequency analysis method based on variational mode decomposition and its application to gear fault diagnosis in variable working conditions. Mech. Syst. Signal Process. 2019, 116, 462–479. [Google Scholar] [CrossRef]
- Moradi, H.; Salarieh, H. Analysis of nonlinear oscillations in spur gear pairs with approximated modelling of backlash nonlinearity. Mech. Mach. Theory 2012, 51, 14–31. [Google Scholar] [CrossRef]
- Litak, G.; Friswell, M.I. Dynamics of a gear system with faults in meshing stiffness. Nonlinear Dyn. 2005, 41, 415–421. [Google Scholar] [CrossRef] [Green Version]
- Meng, Z.; Shi, G.; Wang, F. Vibration response and fault characteristics analysis of gear based on time-varying mesh stiffness. Mech. Mach. Theory 2020, 148, 103786. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhu, H.; Li, Z.; Peng, Z. The nonlinear dynamics response of cracked gear system in a coal cutter taking environmental multi-frequency excitation forces into consideration. Nonlinear Dyn. 2016, 84, 203–222. [Google Scholar] [CrossRef]
- Cabrera, D.; Sancho, F.; Li, C.; Cerrada, M.; Sánchez, R.V.; Pacheco, F.; de Oliveira, J.V. Automatic feature extraction of time-series applied to fault severity assessment of helical gearbox in stationary and non-stationary speed operation. Appl. Soft Comput. 2017, 58, 53–64. [Google Scholar] [CrossRef]
- Cerrada, M.; Li, C.; Sánchez, R.V.; Pacheco, F.; Cabrera, D.; Valente de Oliveira, J. A fuzzy transition based approach for fault severity prediction in helical gearboxes. Fuzzy Sets Syst. 2018, 337, 52–73. [Google Scholar] [CrossRef]
- Park, S.; Kim, S.; Choi, J.H. Gear fault diagnosis using transmission error and ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2018, 108, 262–275. [Google Scholar] [CrossRef]
- Wang, D. K-nearest neighbors based methods for identification of different gear crack levels under different motor speeds and loads: Revisited. Mech. Syst. Signal Process. 2016, 70–71, 201–208. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J. Gear crack level identification based on weighted K nearest neighbor classification algorithm. Mech. Syst. Signal Process. 2009, 23, 1535–1547. [Google Scholar] [CrossRef]
- Gharavian, M.; Almas Ganj, F.; Ohadi, A.; Heidari Bafroui, H. Comparison of FDA-based and PCA-based features in fault diagnosis of automobile gearboxes. Neurocomputing 2013, 121, 150–159. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J.; He, Z.; Zi, Y. A multidimensional hybrid intelligent method for gear fault diagnosis. Expert Syst. Appl. 2010, 37, 1419–1430. [Google Scholar] [CrossRef]
- Hajnayeb, A.; Ghasemloonia, A.; Khadem, S.; Moradi, M. Application and comparison of an ANN-based feature selection method and the genetic algorithm in gearbox fault diagnosis. Expert Syst. Appl. 2011, 38, 10205–10209. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, L.; Li, W. Regrouping particle swarm optimization based variable neural network for gearbox fault diagnosis. J. Intell. Fuzzy Syst. 2018, 34, 3671–3680. [Google Scholar] [CrossRef]
- Ümütlü, R.C.; Hizarci, B.; Ozturk, H.; Kiral, Z. Classification of pitting fault levels in a worm gearbox using vibration visualization and ANN. Sādhanā 2020, 45, 22. [Google Scholar] [CrossRef]
- Saravanan, N.; Siddabattuni, V.K.; Ramachandran, K. Fault diagnosis of spur bevel gear box using artificial neural network (ANN), and proximal support vector machine (PSVM). Appl. Soft Comput. 2010, 10, 344–360. [Google Scholar] [CrossRef]
- Chen, F.; Tang, B.; Chen, R. A novel fault diagnosis model for gearbox based on wavelet support vector machine with immune genetic algorithm. Measurement 2013, 46, 220–232. [Google Scholar] [CrossRef]
- Ray, P.; Mishra, D.P. Support vector machine based fault classification and location of a long transmission line. Eng. Sci. Technol. Int. J. 2016, 19, 1368–1380. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.; Chen, X.; Zhang, X.; He, Z. A novel intelligent gear fault diagnosis model based on EMD and multi-class TSVM. Measurement 2012, 45, 30–40. [Google Scholar] [CrossRef]
- Bordoloi, D.; Tiwari, R. Support vector machine based optimization of multi-fault classification of gears with evolutionary algorithms from time–frequency vibration data. Measurement 2014, 55, 1–14. [Google Scholar] [CrossRef]
- Cerrada, M.; Zurita, G.; Cabrera, D.; Sánchez, R.V.; Artés, M.; Li, C. Fault diagnosis in spur gears based on genetic algorithm and random forest. Mech. Syst. Signal Process. 2016, 70–71, 87–103. [Google Scholar] [CrossRef]
- Cabrera, D.; Sancho, F.; Sánchez, R.V.; Zurita, G.; Cerrada, M.; Li, C.; Vásquez, R.E. Fault diagnosis of spur gearbox based on random forest and wavelet packet decomposition. Front. Mech. Eng. 2015, 10, 277–286. [Google Scholar] [CrossRef]
- Muralidharan, A.; Sugumaran, V.; Soman, K.; Amarnath, M. Fault diagnosis of helical gear box using variational mode decomposition and random forest algorithm. Struct. Durab. Health Monit. 2014, 10, 55. [Google Scholar]
- Saravanan, N.; Ramachandran, K. Fault diagnosis of spur bevel gear box using discrete wavelet features and Decision Tree classification. Expert Syst. Appl. 2009, 36, 9564–9573. [Google Scholar] [CrossRef]
- Sugumaran, V.; Jain, D.; Amarnath, M.; Kumar, H. Fault Diagnosis of Helical Gear Box using Decision Tree through Vibration Signals. Int. J. Perform. Eng. 2013, 9, 221. [Google Scholar]
- Zhao, X.; Zuo, M.J.; Liu, Z. Diagnosis of pitting damage levels of planet gears based on ordinal ranking. In Proceedings of the 2011 IEEE Conference on Prognostics and Health Management, Montreal, QC, Canada, 20–23 June 2011; pp. 1–8. [Google Scholar]
- Phinyomark, A.; Limsakul, C.; Phukpattaranont, P. A Novel Feature Extraction for Robust EMG Pattern Recognition. J. Comput. 2009, 1, 71–80. [Google Scholar]
- Chowdhury, R.H.; Reaz, M.B.; Ali, M.A.B.M.; Bakar, A.A.; Chellappan, K.; Chang, T.G. Surface electromyography signal processing and classification techniques. Sensors 2013, 13, 12431–12466. [Google Scholar] [CrossRef]
- Kim, S.; Choi, J.H. Convolutional neural network for gear fault diagnosis based on signal segmentation approach. Struct. Health Monit. 2019, 18, 1401–1415. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Qu, Y.; He, D. Semi-supervised gear fault diagnosis using raw vibration signal based on deep learning. Chin. J. Aeronaut. 2020, 33, 418–426. [Google Scholar] [CrossRef]
- Jing, L.; Zhao, M.; Li, P.; Xu, X. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Singh, J.; Azamfar, M.; Ainapure, A.; Lee, J. Deep learning-based cross-domain adaptation for gearbox fault diagnosis under variable speed conditions. Meas. Sci. Technol. 2020, 31, 055601. [Google Scholar] [CrossRef]
- Cabrera, D.; Sancho, F.; Cerrada, M.; Sánchez, R.V.; Li, C. Knowledge extraction from deep convolutional neural networks applied to cyclo-stationary time-series classification. Inf. Sci. 2020, 524, 1–14. [Google Scholar] [CrossRef]
- Cabrera, D.; Sancho, F.; Long, J.; Sánchez, R.; Zhang, S.; Cerrada, M.; Li, C. Generative Adversarial Networks Selection Approach for Extremely Imbalanced Fault Diagnosis of Reciprocating Machinery. IEEE Access 2019, 7, 70643–70653. [Google Scholar] [CrossRef]
- Monteiro, R.P.; Cerrada, M.; Cabrera, D.R.; Sánchez, R.V.; Bastos-Filho, C.J. Using a support vector machine based decision stage to improve the fault diagnosis on gearboxes. Comput. Intell. Neurosci. 2019, 2019, 1383752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, Q.; Wang, M.; Chen, Y.; Dai, W.; Li, Y.F.; Tu, W.W.; Yang, Q.; Yu, Y. Taking Human out of Learning Applications: A Survey on Automated Machine Learning. arXiv 2018, arXiv:1810.13306. [Google Scholar]
- He, X.; Zhao, K.; Chu, X. AutoML: A Survey of the State-of-the-Art. arXiv 2019, arXiv:1908.00709. [Google Scholar] [CrossRef]
- Petke, J.; Haraldsson, S.O.; Harman, M.; Langdon, W.B.; White, D.R.; Woodward, J.R. Genetic Improvement of Software: A Comprehensive Survey. IEEE Trans. Evol. Comput. 2018, 22, 415–432. [Google Scholar] [CrossRef] [Green Version]
- Z-Flores, E.; Abatal, M.; Bassam, A.; Trujillo, L.; Juárez-Smith, P.; Hamzaoui, Y.E. Modeling the adsorption of phenols and nitrophenols by activated carbon using genetic programming. J. Clean. Prod. 2017, 161, 860–870. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef] [Green Version]
- Muñoz, L.; Trujillo, L.; Silva, S. Transfer learning in constructive induction with Genetic Programming. Genet. Program. Evolvable Mach. 2019, 21, 529–569. [Google Scholar] [CrossRef]
- Liang, J.; Meyerson, E.; Hodjat, B.; Fink, D.; Mutch, K.; Miikkulainen, R. Evolutionary Neural AutoML for Deep Learning. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ’19), Prague, Czech Republic, 13–17 July 2019; ACM: New York, NY, USA, 2019; pp. 401–409. [Google Scholar]
- Olson, R.S.; Bartley, N.; Urbanowicz, R.J.; Moore, J.H. Evaluation of a Tree-based Pipeline Optimization Tool for Automating Data Science. In Proceedings of the Genetic and Evolutionary Computation Conference 2016 (GECCO ’16), Denver, CO, USA, 20–24 July 2016; ACM: New York, NY, USA, 2016; pp. 485–492. [Google Scholar]
- Hall, P.; Kurka, M.; Bartz, A. Using H2O Driverless AI. Mountain View, CA. 2018. Available online: http://docs.h2o.ai (accessed on 30 November 2021).
- Real, E.; Aggarwal, A.; Huang, Y.; Le, Q.V. Regularized evolution for image classifier architecture search. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 4780–4789. [Google Scholar]
- Real, E.; Moore, S.; Selle, A.; Saxena, S.; Suematsu, Y.L.; Tan, J.; Le, Q.V.; Kurakin, A. Large-scale Evolution of Image Classifiers. In Proceedings of the 34th International Conference on Machine Learning-Olume 70 (ICML’17), Sydney, NSW, Australia, 6–11 August 2017; pp. 2902–2911. [Google Scholar]
- Assunção, F.; Lourenço, N.; Machado, P.; Ribeiro, B. Evolving the Topology of Large Scale Deep Neural Networks. In Genetic Programming; Castelli, M., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 19–34. [Google Scholar]
- Wong, C.; Houlsby, N.; Lu, Y.; Gesmundo, A. Transfer Learning with Neural AutoML. In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS’18), Montreal, QC, Canada, 3–8 December 2018; Curran Associates Inc.: Red Hook, NY, USA, 2018; pp. 8366–8375. [Google Scholar]
- Stanley, K.O.; Miikkulainen, R. Evolving Neural Networks through Augmenting Topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef]
- Stanley, K.O.; D’Ambrosio, D.B.; Gauci, J. A Hypercube-Based Encoding for Evolving Large-Scale Neural Networks. Artif. Life 2009, 15, 185–212. [Google Scholar] [CrossRef] [PubMed]
- Eiben, A.; Smith, J. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Liang, X.; Zuo, M.J.; Feng, Z. Dynamic modeling of gearbox faults: A review. Mech. Syst. Signal Process. 2018, 98, 852–876. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, F. Mesh stiffness modelling and dynamic simulation of helical gears with tooth crack propagation. Meccanica 2020, 55, 1215–1236. [Google Scholar] [CrossRef]
- Liang, X.H.; Liu, Z.L.; Pan, J.; Zuo, M.J. Spur gear tooth pitting propagation assessment using model-based analysis. Chin. J. Mech. Eng. 2017, 30, 1369–1382. [Google Scholar] [CrossRef] [Green Version]
- Dadon, I.; Koren, N.; Klein, R.; Bortman, J. A step toward fault type and severity characterization in spur gears. J. Mech. Des. 2019, 141, 083301. [Google Scholar] [CrossRef]
- Gecgel, O.; Ekwaro-Osire, S.; Dias, J.P.; Nispel, A.; Alemayehu, F.M.; Serwadda, A. Machine Learning in Crack Size Estimation of a Spur Gear Pair Using Simulated Vibration Data. In Proceedings of the 10th International Conference on Rotor Dynamics (IFToMM), Rio de Janeiro, Brazil, 23–27 September 2018; Cavalca, K.L., Weber, H.I., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 175–190. [Google Scholar]
- Joshuva, A.; Sugumaran, V. Crack detection and localization on wind turbine blade using machine learning algorithms: A data mining approach. Struct. Durab. Health Monit. 2019, 13, 181. [Google Scholar] [CrossRef] [Green Version]
- Pan, W.; He, H. An ordinal rough set model based on fuzzy covering for fault level identification. J. Intell. Fuzzy Syst. 2017, 33, 2979–2985. [Google Scholar] [CrossRef]
- Wang, W.; Galati, F.A.; Szibbo, D. LSTM Residual Signal for Gear Tooth Crack Diagnosis. In Advances in Asset Management and Condition Monitoring; Ball, A., Gelman, L., Rao, B.K.N., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 1075–1090. [Google Scholar]
- Qu, Y.; Zhang, Y.; He, M.; He, D.; Jiao, C.; Zhou, Z. Gear pitting fault diagnosis using disentangled features from unsupervised deep learning. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2019, 233, 719–730. [Google Scholar] [CrossRef]
- Elshawi, R.; Maher, M.; Sakr, S. Automated Machine Learning: State-of-The-Art and Open Challenges. arXiv 2019, arXiv:1906.02287. [Google Scholar]
- Patel, S.A.; Patel, S.P.; Adhyaru, Y.B.K.; Maheshwari, S.; Kumar, P.; Soni, M. Developing smart devices with automated Machine learning Approach: A review. In Materials Today: Proceedings; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Yi, H.; Bui, K.H.N. An automated hyperparameter search-based deep learning model for highway traffic prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 5486–5495. [Google Scholar] [CrossRef]
- Tokuyama, K.; Shimodaira, Y.; Kodama, Y.; Matsui, R.; Kusunose, Y.; Fukushima, S.; Nakai, H.; Tsuji, Y.; Toya, Y.; Matsuda, F.; et al. Soft-sensor development for monitoring the lysine fermentation process. J. Biosci. Bioeng. 2021, 132, 183–189. [Google Scholar] [CrossRef]
- Zhu, J.; Shi, H.; Song, B.; Tao, Y.; Tan, S. Information concentrated variational auto-encoder for quality-related nonlinear process monitoring. J. Process Control 2020, 94, 12–25. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Zheng, J.; Li, M. Neural Architecture Search For Fault Diagnosis. arXiv 2020, arXiv:2002.07997. [Google Scholar]
- Wang, R.; Jiang, H.; Li, X.; Liu, S. A reinforcement neural architecture search method for rolling bearing fault diagnosis. Measurement 2020, 154, 107417. [Google Scholar] [CrossRef]
- Liu, T.; Kou, L.; Yang, L.; Fan, W.; Wu, C. A physical knowledge-based extreme learning machine approach to fault diagnosis of rolling element bearing from small datasets. In Proceedings of the 2020 ACM International Joint Conference on Pervasive and Ubiquitous Computing and Proceedings of the 2020 ACM International Symposium on Wearable Computers, Virtual Conference, 12–17 September 2020; pp. 553–559. [Google Scholar]
- Listewnik, K.; Grzeczka, G.; Kłaczyński, M.; Cioch, W. An on-line diagnostics application for evaluation of machine vibration based on standard ISO 10816-1. J. Vibroeng. 2015, 17, 4248–4258. [Google Scholar]
- Carvalho, D.V.; Pereira, E.M.; Cardoso, J.S. Machine Learning Interpretability: A Survey on Methods and Metrics. Electronics 2019, 8, 832. [Google Scholar] [CrossRef] [Green Version]
- Juárez-Smith, P.; Trujillo, L.; García-Valdez, M.; Fernández de Vega, F.; Chávez, F. Local search in speciation-based bloat control for genetic programming. Genet. Program. Evolvable Mach. 2019, 20, 351–384. [Google Scholar] [CrossRef]
- Hand, D.J.; Till, R.J. A Simple Generalisation of the Area Under the ROC Curve for Multiple Class Classification Problems. Mach. Learn. 2001, 45, 171–186. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Sánchez, R.V.; Lucero, P.; Vásquez, R.E.; Cerrada, M.; Cabrera, D. A comparative feature analysis for gear pitting level classification by using acoustic emission, vibration and current signals. IFAC-PapersOnLine 2018, 51, 346–352. [Google Scholar] [CrossRef]
- Sánchez, R.V.; Lucero, P.; Vásquez, R.E.; Cerrada, M.; Macancela, J.C.; Cabrera, D. Feature ranking for multi-fault diagnosis of rotating machinery by using random forest and KNN. J. Intell. Fuzzy Syst. 2018, 34, 3463–3473. [Google Scholar] [CrossRef]
- Feurer, M.; Eggensperger, K.; Falkner, S.; Lindauer, M.; Hutter, F. Auto-Sklearn 2.0: Hands-free AutoML via Meta-Learning. arXiv 2021, arXiv:2007.04074. [Google Scholar]






| Label | Severity Level | Severity Level | Severity Level |
|---|---|---|---|
| Pitting | Crack | Broken Tooth | |
| P1 | N | N | N |
| P2 | Holes: 2 | Depth: 1 mm | 12.5% |
| Diameter: 1 mm | Width: 1 mm | ||
| Depth: 1 mm | Length: 4 mm | ||
| 4.1% | 4.9% | ||
| P3 | Holes: 2 | Depth: 1mm | 25.0% |
| Diameter: 1.5 mm | Width: 1 mm | ||
| Depth: 1.5 mm | Length: 8 mm | ||
| 7.3% | 9.8% | ||
| P4 | Holes: 4 | Depth: 1 mm | 37.5% |
| Diameter: 1.5 mm | Width: 1 mm | ||
| Depth: 1.5 mm | Length: 10 mm | ||
| 14.7% | 12.3% | ||
| P5 | Holes: 4 | Depth: 1mm | 50.0% |
| Diameter: 2 mm | Width: 1 mm | ||
| Depth: 2 mm | Length: 12 mm | ||
| 23.1% | 14.7% | ||
| P6 | Holes: 6 | Depth: 1 mm | 62.5% |
| Diameter: 2 mm | Width: 1 mm | ||
| Depth: 2 mm | Length: 16 mm | ||
| 34.6% | 19.7% | ||
| P7 | Holes: 6 | Depth: 1 mm | 62.5% |
| Diameter: 2.5 mm | Width: 1 mm | ||
| Depth: 2.5 mm | Length: 20 mm | ||
| 49.91% | 25% | ||
| P8 | Holes: 8 | Depth: 2 mm | 87.5% |
| Diameter: 2.5 mm | Width: 1.5 mm | ||
| Depth: 2.5 mm | Length: along the tooth | ||
| 66.5% | 50.0% | ||
| P9 | Holes: irregular | Depth: 4 mm | 100% |
| Diameter: irregular | Width: 1.5 mm | ||
| Depth: 2.5 mm | Length: along the tooth | ||
| 83.1% | 100% |
| Configuration | Testing Performance | Model Size | ||||||
|---|---|---|---|---|---|---|---|---|
| Problem | Interpret. | Acc. | AUC | F1 | Log-Loss | Features | Ensemble | Time |
| Pitting | 1 | 0.99(0.0025) | 0.99(0.0002) | 0.97(0.0116) | 0.09(0.0185) | 177 | 4 | 19 |
| Pitting | 10 | 0.99(0.0021) | 0.99(0.0005) | 0.96(0.0009) | 0.12(0.0253) | 27 | 1 | 8.5 |
| Crack | 1 | 0.99(0.0023) | 0.99(0.0001) | 0.98(0.0106) | 0.08(0.0176) | 131 | 4 | 18.5 |
| Crack | 10 | 0.99(0.0015) | 0.99(0.0002) | 0.98(0.0007) | 0.08(0.0197) | 25 | 2 | 14.8 |
| BT | 1 | 0.98(0.0027) | 0.99(0.0003) | 0.95(0.0124) | 0.17(0.0161) | 1019 | 3 | 19.5 |
| BT | 10 | 0.98(0.0040) | 0.99(0.0002) | 0.94(0.0180) | 0.17(0.0556) | 15 | 2 | 14.7 |
| Feature | Pitting | Crack | Broken Tooth | Average |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | |
| 0.07 | 0 | 0 | 0.02 | |
| 0.92 | 0.63 | 0.93 | 0.88 | |
| 0.52 | 0.77 | 0.20 | 0.49 | |
| 0.50 | 0.71 | 0.90 | 0.70 | |
| 0 | 0.14 | 0.57 | 0.23 | |
| 0.06 | 0 | 0 | 0.02 | |
| 0 | 0.64 | 0 | 0.02 | |
| 0.05 | 0.18 | 0 | 0.07 | |
| 0.51 | 0 | 0.61 | 0.37 | |
| 0.17 | 0.65 | 0 | 0.27 | |
| 0.14 | 0 | 0 | 0.04 | |
| 0.09 | 0 | 0 | 0.03 | |
| 0.51 | 0.38 | 0 | 0.29 | |
| 0.52 | 0.18 | 0 | 0.23 | |
| 0.11 | 0.30 | 0 | 0.13 | |
| 0.05 | 0 | 0.97 | 0.34 | |
| 0.25 | 0 | 0 | 0.08 | |
| 0 | 0.44 | 0 | 0.14 | |
| 0.63 | 0.70 | 0.52 | 0.61 | |
| 0.06 | 0.72 | 0 | 0.26 | |
| 0 | 0 | 0.49 | 0.16 | |
| 0 | 0 | 0.20 | 0.06 | |
| 0.27 | 0.16 | 0.65 | 0.36 | |
| 0.05 | 0.19 | 0 | 0.08 | |
| 0.52 | 0.65 | 0.94 | 0.70 | |
| 0.27 | 0.19 | 0 | 0.09 | |
| 0 | 0.62 | 0 | 0.20 | |
| 0.24 | 0.56 | 0.19 | 0.33 | |
| 0.05 | 0 | 0.55 | 0.20 | |
| 0.39 | 0.68 | 0.22 | 0.43 | |
| 0 | 0.18 | 0 | 0.06 | |
| 0 | 0.15 | 0 | 0.05 | |
| 0.05 | 0.77 | 0 | 0.27 |
| Configuration | Feature Importance | |||||
|---|---|---|---|---|---|---|
| Problem | Interpret. | Min | Max | Median | Mean | Std |
| Pitting | 1 | 0.149 | 1 | 0.212 | 0.259 | 0.152 |
| Pitting | 10 | 0.114 | 1 | 0.183 | 0.233 | 0.147 |
| Crack | 1 | 0.281 | 1 | 0.414 | 0.462 | 0.180 |
| Crack | 10 | 0.003 | 1 | 0.052 | 0.166 | 0.248 |
| BT | 1 | 0.003 | 1 | 0.003 | 0.182 | 0.319 |
| BT | 10 | 0.003 | 1 | 0.062 | 0.237 | 0.301 |
| Problem | Original | CD | CTE | Interaction | TSVD |
|---|---|---|---|---|---|
| Pitting | 48% | 32% | 0% | 18% | 2% |
| Broken Tooth | 32% | 30% | 0% | 36% | 2% |
| Crack | 8% | 52% | 4% | 36% | 0% |
| Number of Features | Pitting | Broken Tooth | Crack |
|---|---|---|---|
| 1 | 0.32 | 0.29 | 0.32 |
| 2 | 0.56 | 0.52 | 0.55 |
| 3 | 0.80 | 0.80 | 0.82 |
| 4 | 0.88 | 0.89 | 0.93 |
| 5 | 0.92 | 0.91 | 0.94 |
| 6 | 0.92 | 0.93 | 0.95 |
| 7 | 0.93 | 0.93 | 0.96 |
| 8 | 0.92 | 0.94 | 0.97 |
| 9 | 0.94 | 0.95 | 0.97 |
| 10 | 0.93 | 0.96 | 0.96 |
| 11 | 0.94 | 0.97 | 0.97 |
| 12 | 0.95 | 0.97 | 0.97 |
| 13 | 0.96 | 0.97 | 0.97 |
| 14 | 0.96 | 0.97 | 0.97 |
| 15 | 0.96 | 0.96 | 0.97 |
| 16 | 0.96 | 0.96 | 0.97 |
| 17 | 0.97 | 0.96 | 0.97 |
| 18 | 0.96 | 0.97 | 0.97 |
| 19 | 0.97 | 0.97 | 0.97 |
| 20 | 0.97 | 0.97 | 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerrada, M.; Trujillo, L.; Hernández, D.E.; Correa Zevallos, H.A.; Macancela, J.C.; Cabrera, D.; Vinicio Sánchez, R. AutoML for Feature Selection and Model Tuning Applied to Fault Severity Diagnosis in Spur Gearboxes. Math. Comput. Appl. 2022, 27, 6. https://doi.org/10.3390/mca27010006
Cerrada M, Trujillo L, Hernández DE, Correa Zevallos HA, Macancela JC, Cabrera D, Vinicio Sánchez R. AutoML for Feature Selection and Model Tuning Applied to Fault Severity Diagnosis in Spur Gearboxes. Mathematical and Computational Applications. 2022; 27(1):6. https://doi.org/10.3390/mca27010006
Chicago/Turabian StyleCerrada, Mariela, Leonardo Trujillo, Daniel E. Hernández, Horacio A. Correa Zevallos, Jean Carlo Macancela, Diego Cabrera, and René Vinicio Sánchez. 2022. "AutoML for Feature Selection and Model Tuning Applied to Fault Severity Diagnosis in Spur Gearboxes" Mathematical and Computational Applications 27, no. 1: 6. https://doi.org/10.3390/mca27010006
APA StyleCerrada, M., Trujillo, L., Hernández, D. E., Correa Zevallos, H. A., Macancela, J. C., Cabrera, D., & Vinicio Sánchez, R. (2022). AutoML for Feature Selection and Model Tuning Applied to Fault Severity Diagnosis in Spur Gearboxes. Mathematical and Computational Applications, 27(1), 6. https://doi.org/10.3390/mca27010006









