Fractional Modeling of Viscous Fluid over a Moveable Inclined Plate Subject to Exponential Heating with Singular and Non-Singular Kernels
Abstract
:1. Introduction
2. Mathematical Model
3. Mathematical Preliminaries
Special Functions
- Mittag-Leffler function. The Mittag-Leffler function is the generalization of the exponential function and is defined as [33]The exponential function is a special case of this function; for , we getMoreover,
- Erdelyi’s function. This function is the generalization of the Mittag-Leffler function and is described as [36]Setting , we haveFor and , we haveSimilarly, for and , we getWhen and , we havewhere [30] is known as the complementary error function.Further,
- Robotnov and Hartley function. This was presented by Hartley and Lorenzo [34] and later on studied by Robotnov for utilization in solid mechanics as well. It is confined asHere,so
- Generalized R-function. Lorenzo and Hartley [35] developed this function; it is written as:It is easy to see that , and .When , we getSimilarly, for , yieldsMoreover,
- Generalized G-function. Lorenzo and Hartley [35] also introduced this function which is the generalization of R-function and is specified as:For , we haveMoreover,Moreover,Next, we define Caputo, CF and ABC fractional operators used in this paper to fractionalize the proposed problem.
- Caputo fractional operator having power law kernel is described as:with Laplace transformation
- CF fractional operator with a non-singularized and local kernel is described as:Its Laplace transformation is obtained as:
- The Atangana–Baleanu fractional operator in a Caputo sense (ABC) with non-singularized and non-local kernel is defined in the following way:Its Laplace transformation is obtained as:where ℘ is named as the fractional parameter.
4. Solution of the Problem
4.1. Exact Solution of Heat Profile with CF Time Fractional Derivative
4.2. Exact Solution of Heat Profile with ABC Time Fractional Derivative
4.3. Exact Solution of Mass Profile with CF Time Fractional Derivative
4.4. Exact Solution of Mass Profile with ABC Time Fractional Derivative
4.5. Exact Solution of Velocity Profile with CF Time Fractional Derivative
4.6. Exact Solution of Velocity Profile with ABC Time Fractional Derivative
5. Various Cases Concerning the Motion of the Plate
5.1. Case-I: (for Variable Accelerating Plate)
5.2. Case-II: (for Oscillating Plate)
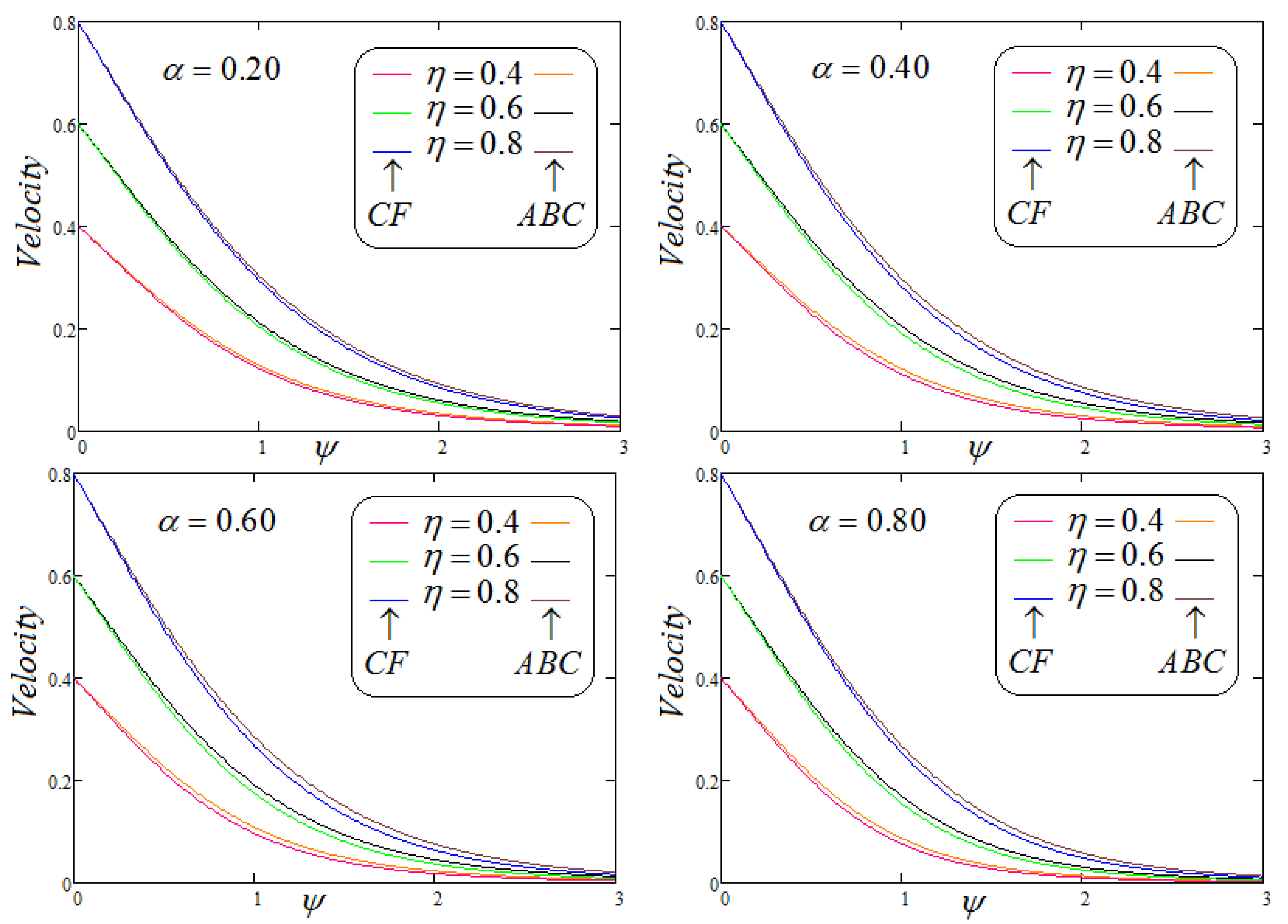
6. Results Validation
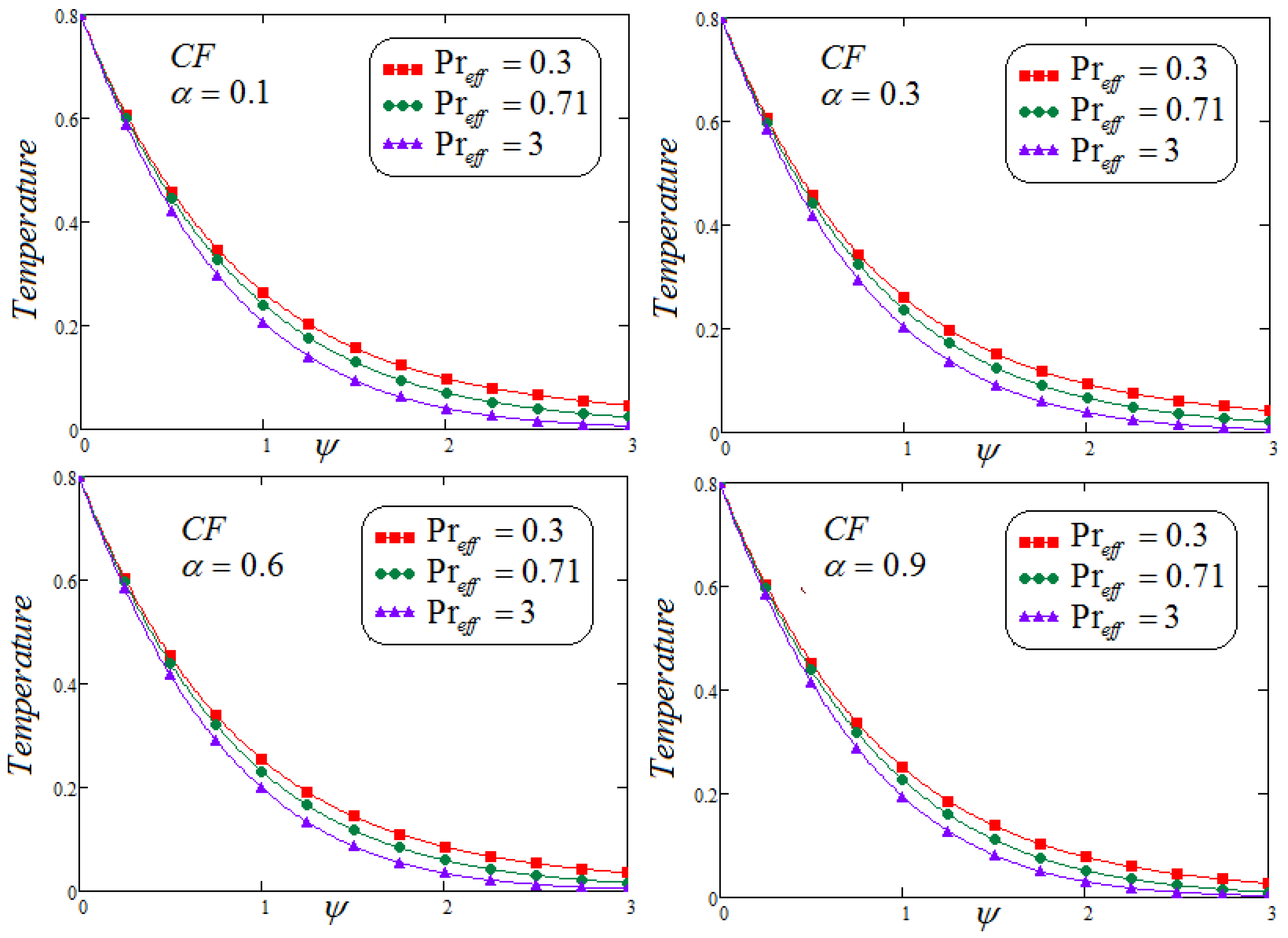
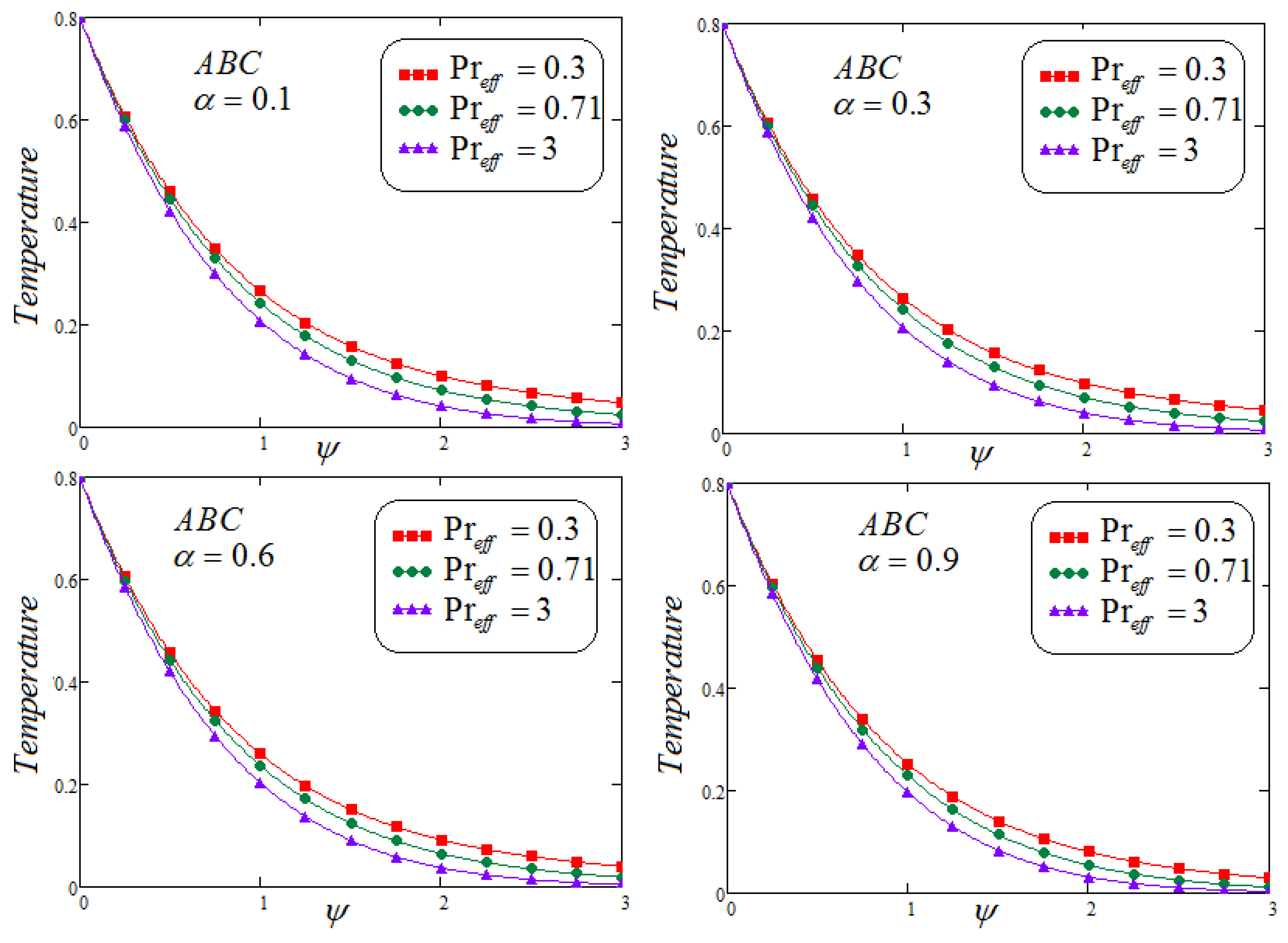
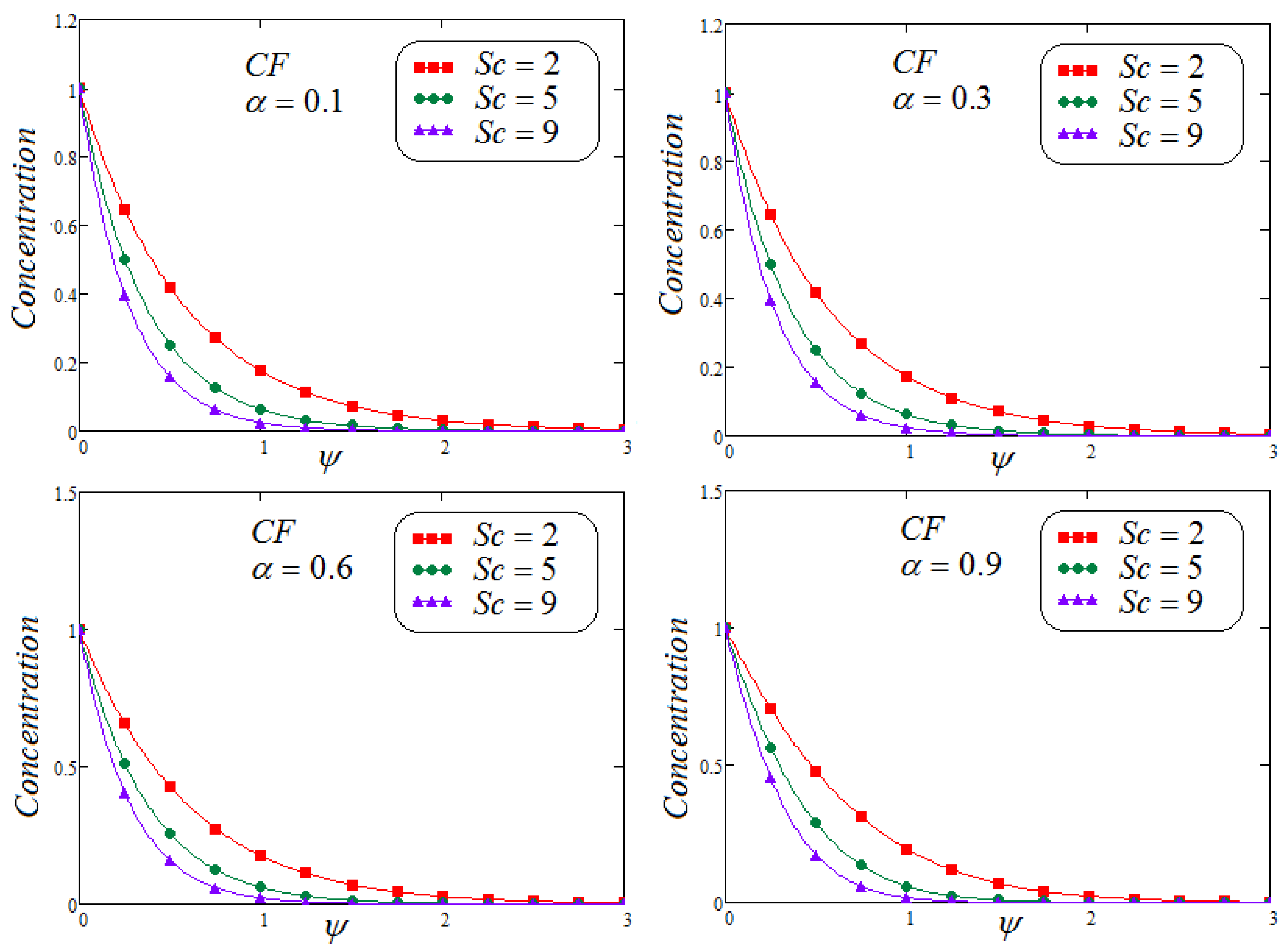
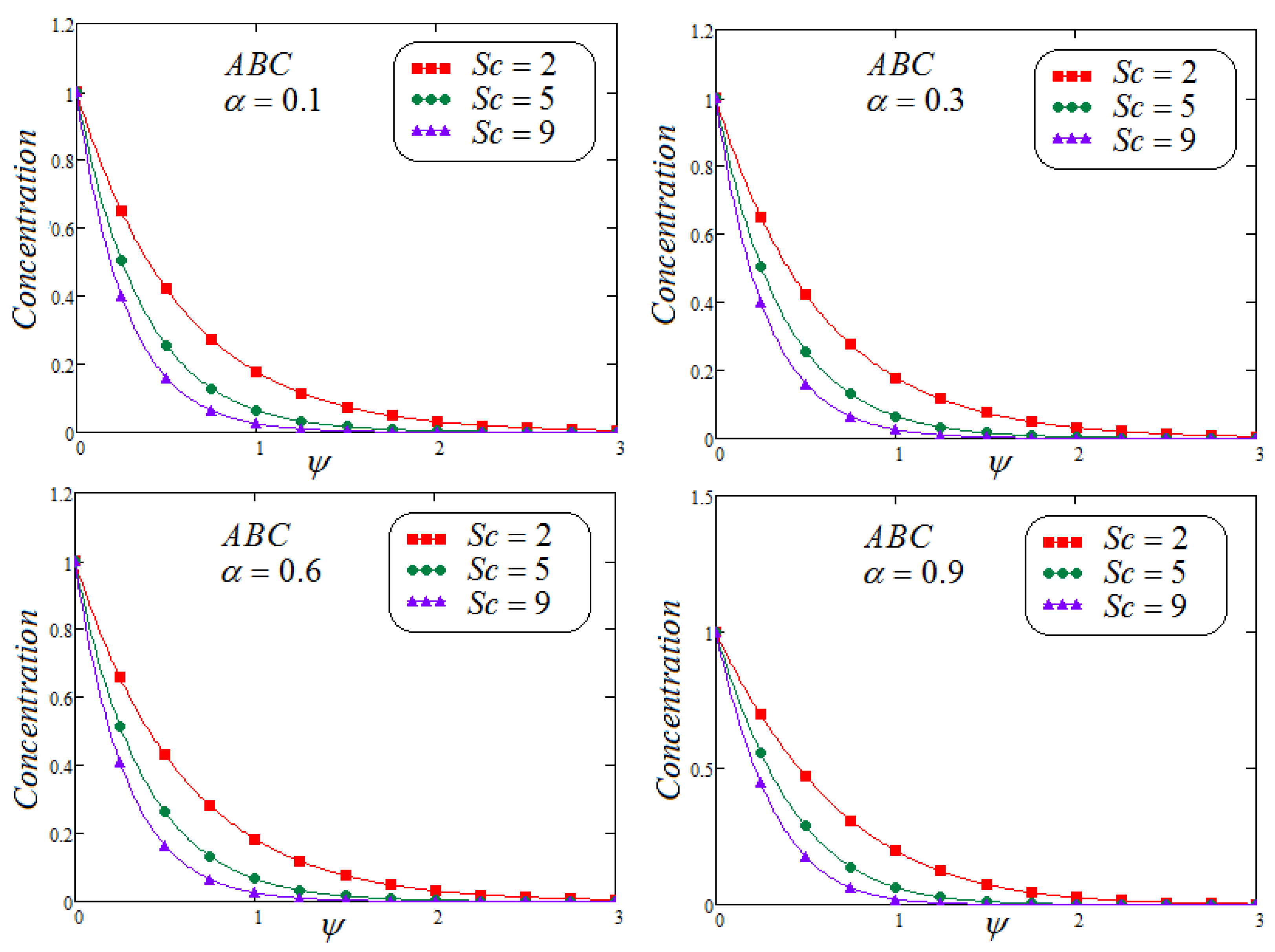
7. Results and Discussion
8. Conclusions
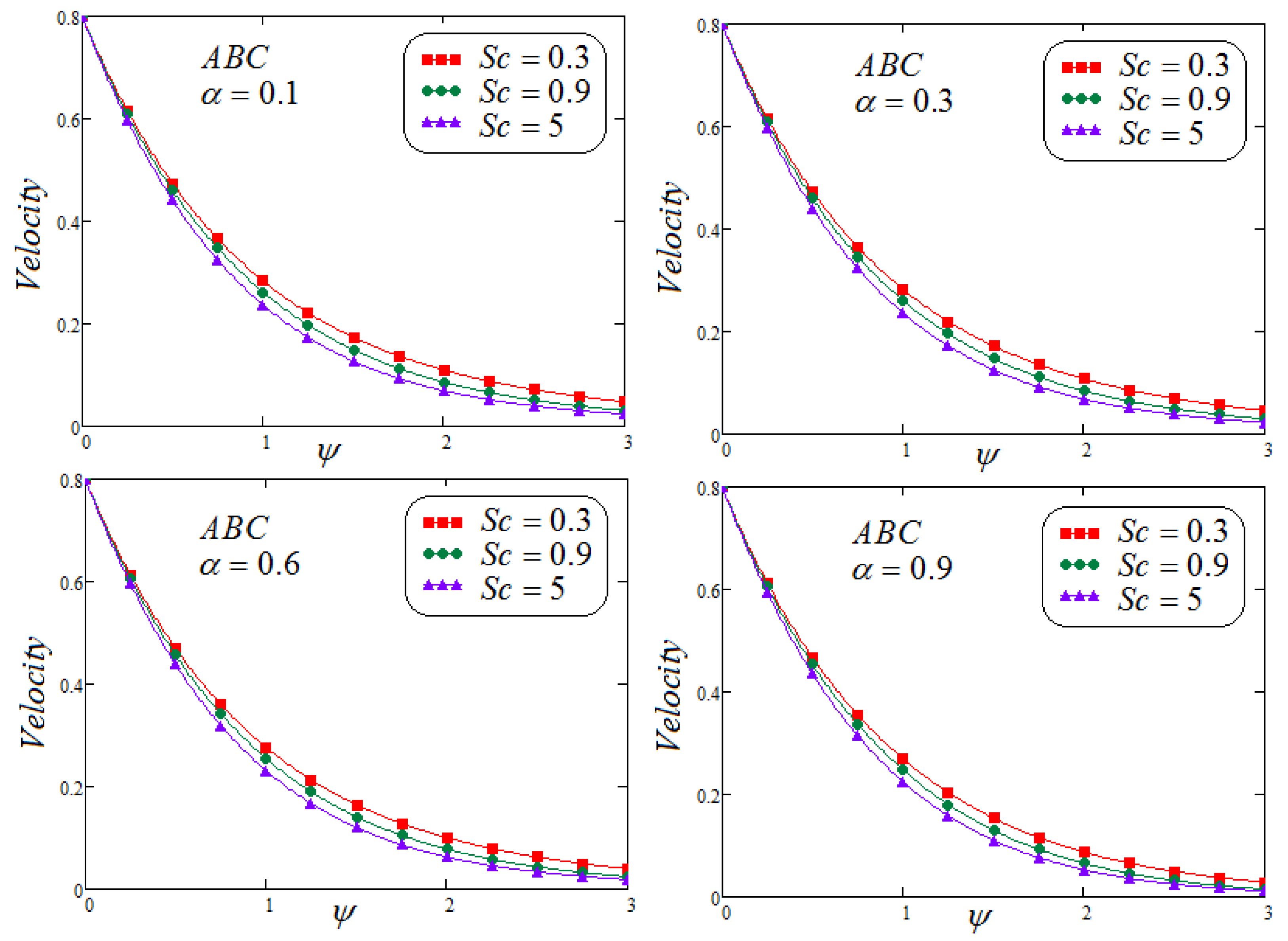
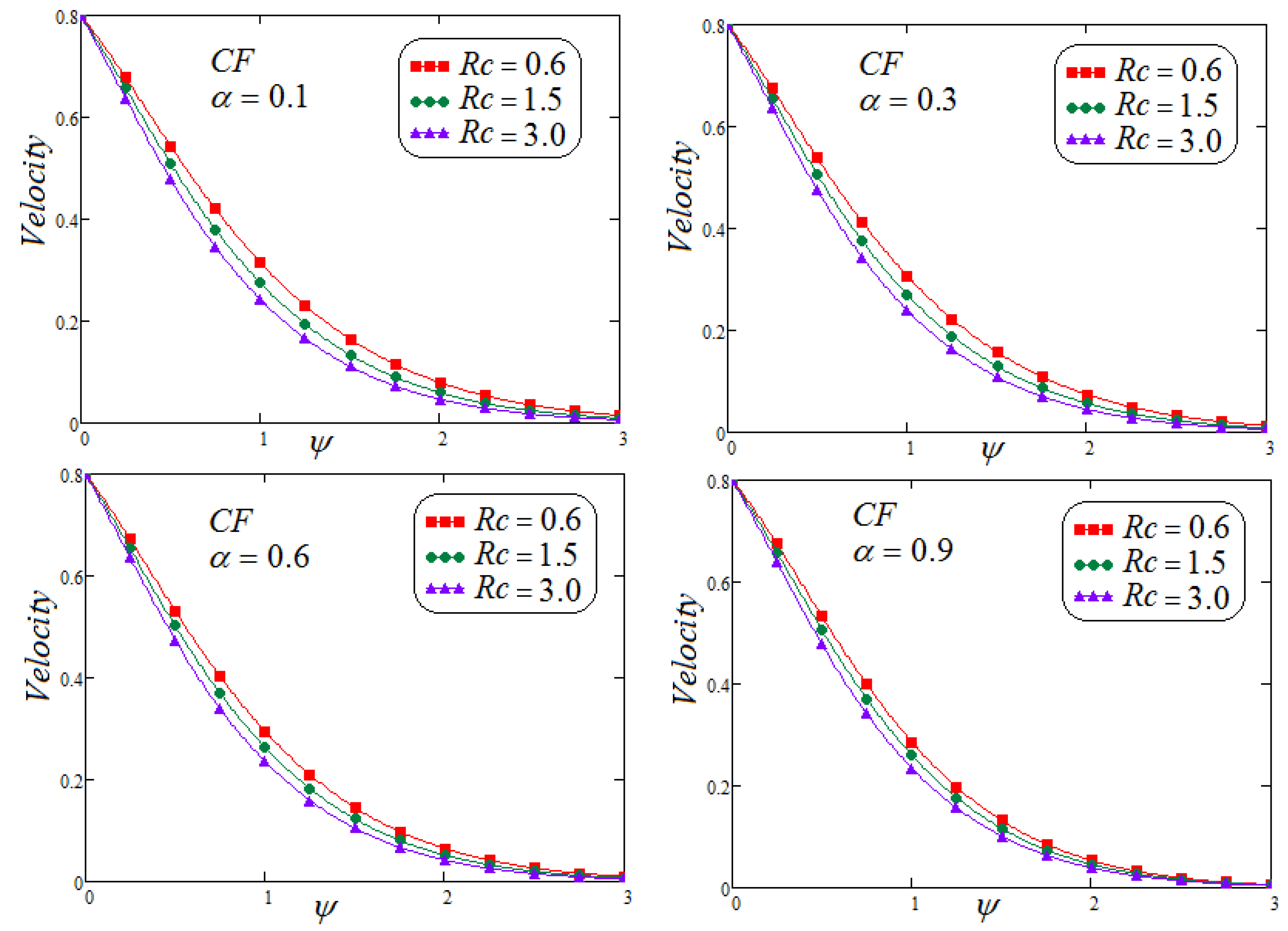
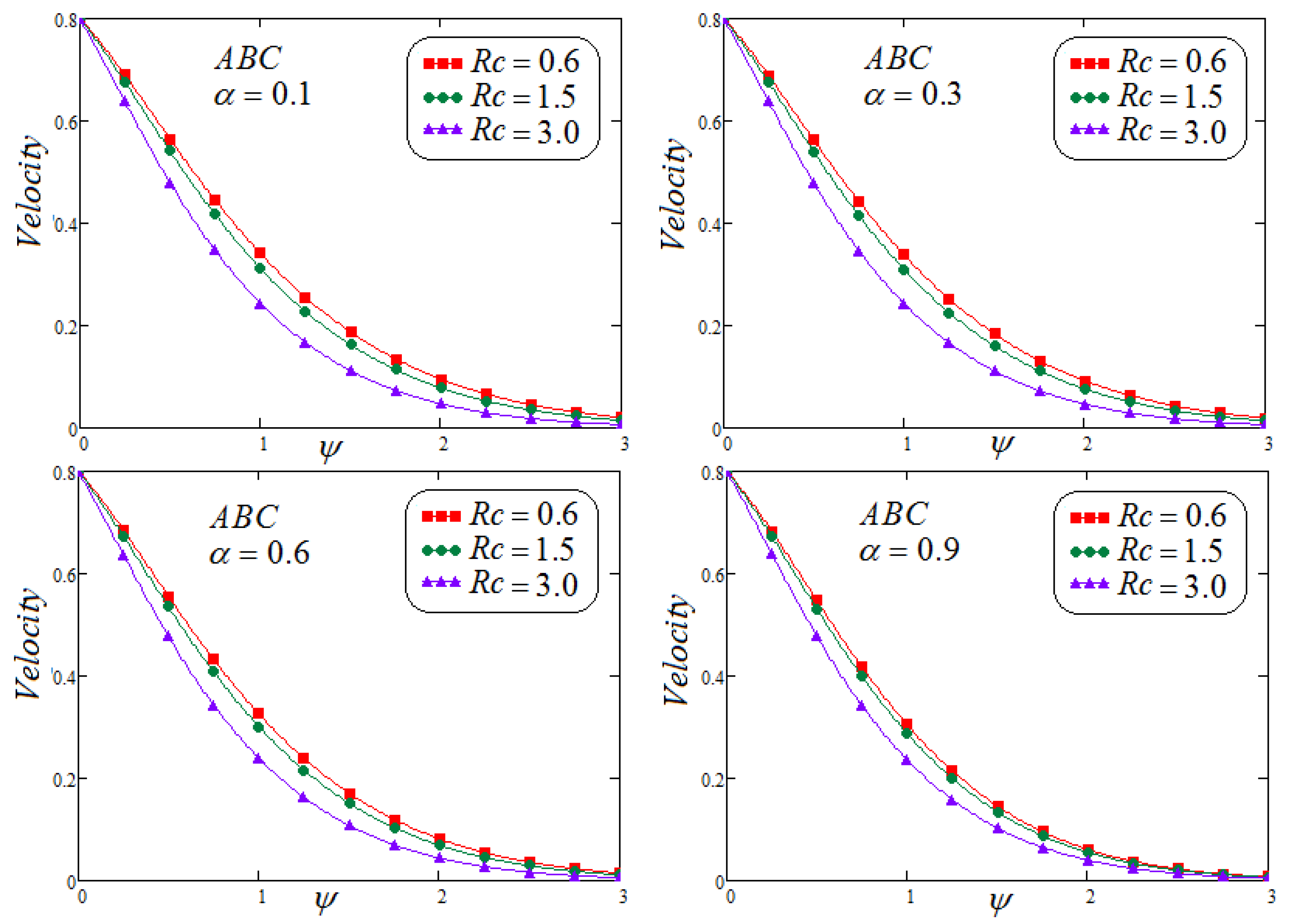
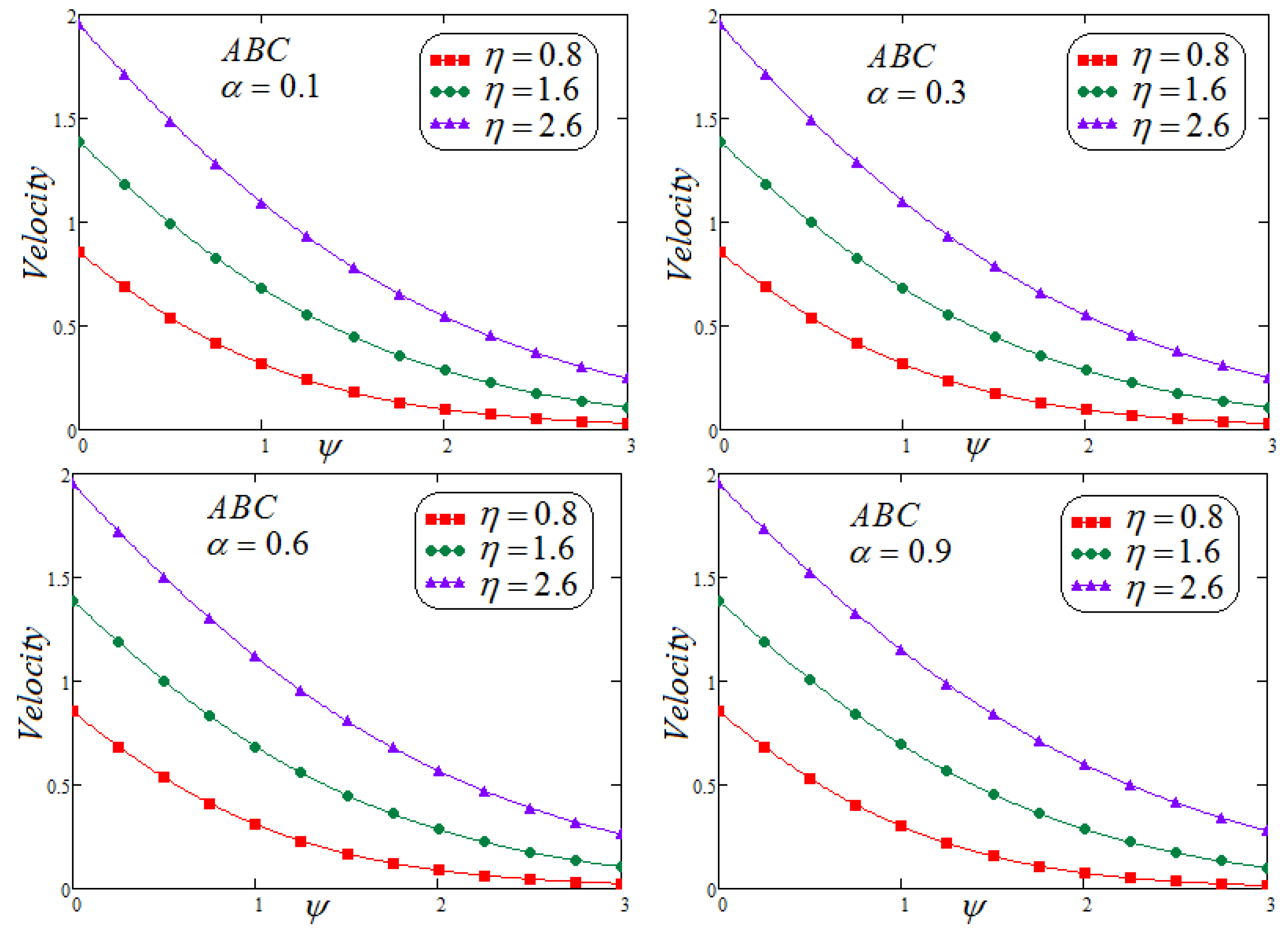
- It is detected that the velocity field declined with the larger values of . Moreover, reduction in the velocity and concentration profile are observed for growing values of for varying values of .
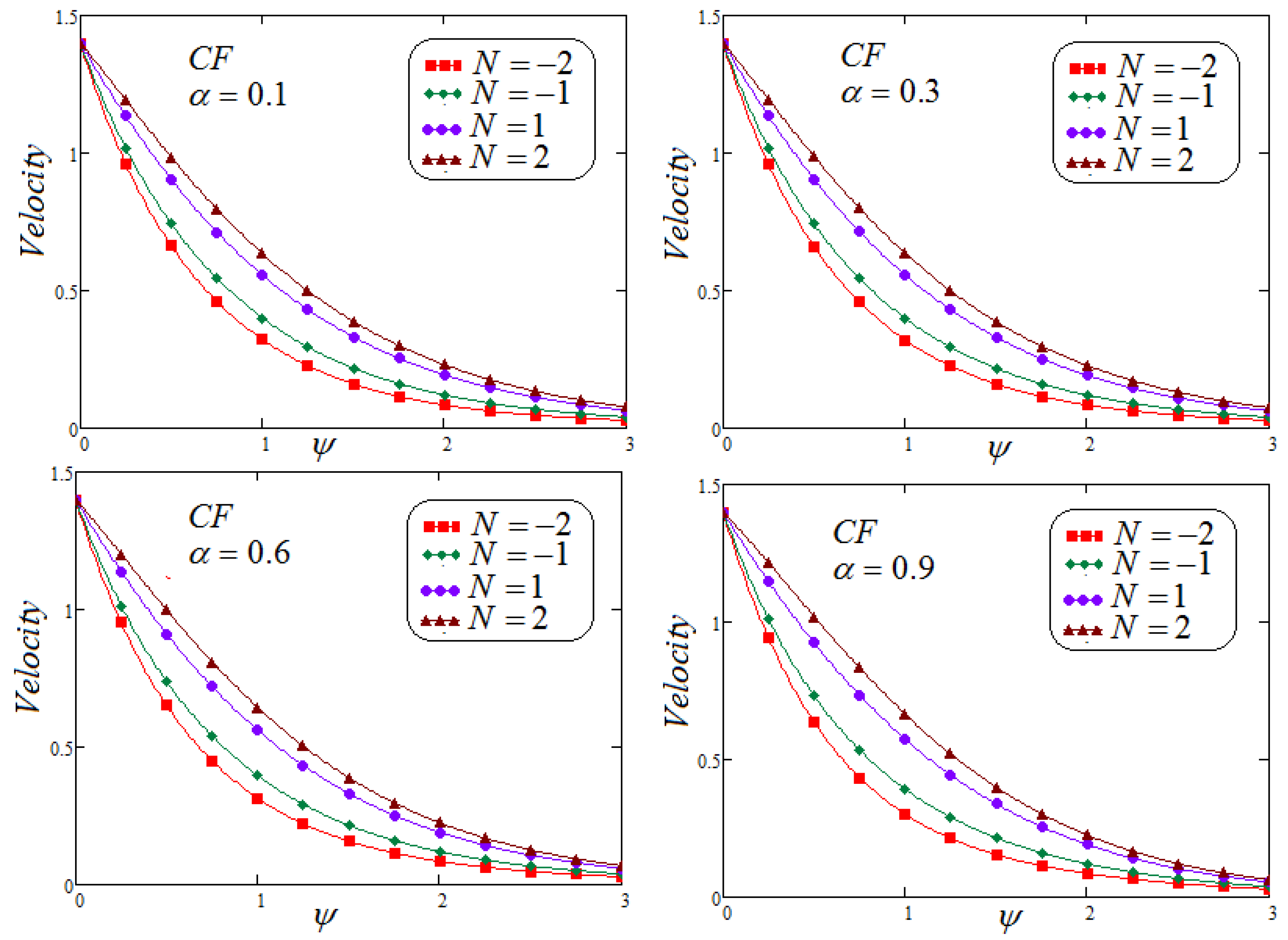
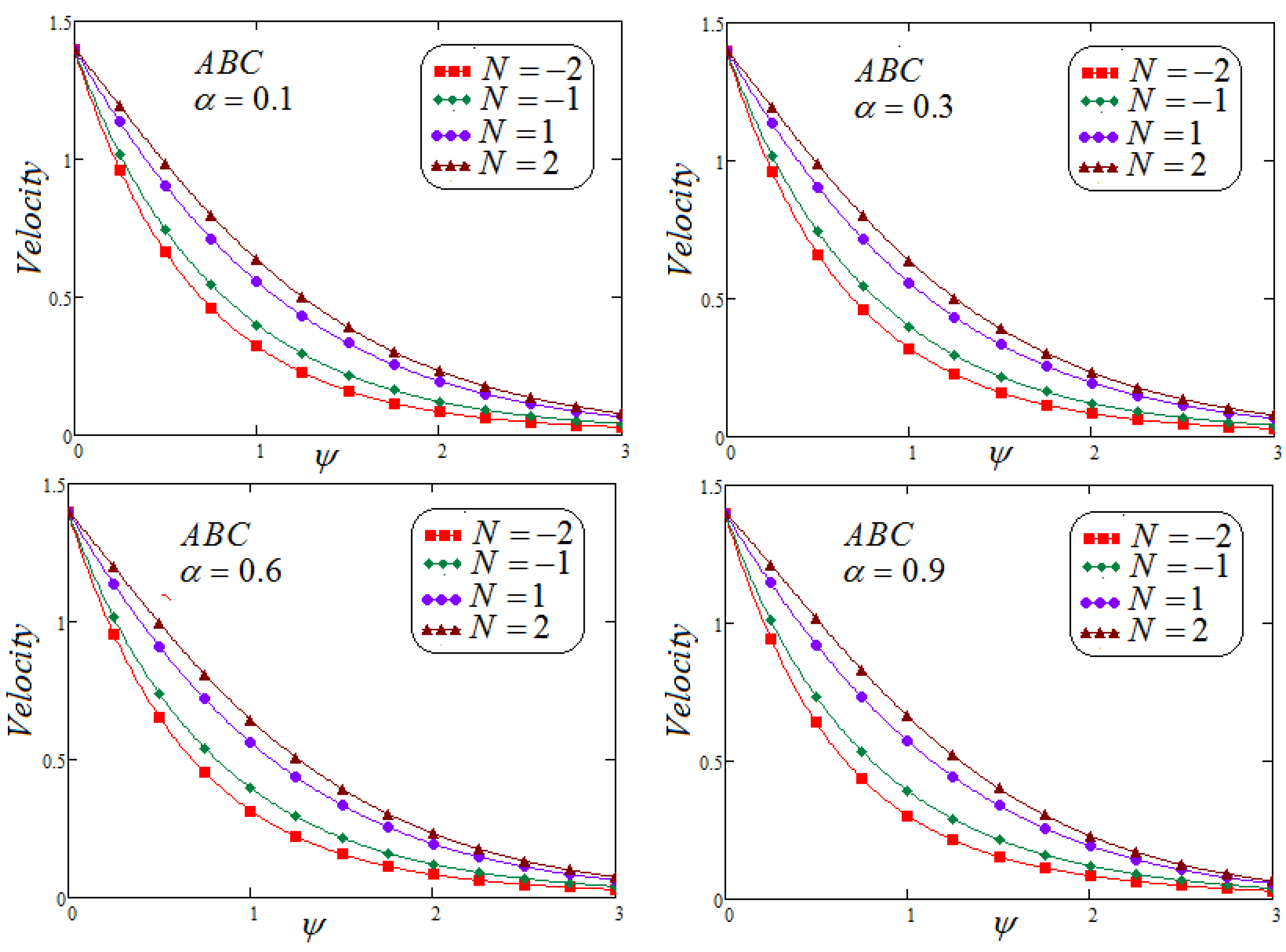
- It is found that the fluid velocity intensifies for , but the opposite trend is observed for .
- The increasing values of the time stimulate the velocity distribution.
- The accumulative values of the parameter decline in the temperature profile are noticed.
- Involvement of concentration factor of fluid velocity in the fluid movement is significant and cannot be overlooked.
- It is depicted that for both non-integer operators CF and ABC, velocity field, concentration and temperature profile represent the same behavior for parametric analysis of the proposed problem.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hartmann, J. Theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field. Fys. Med. 1937, 15, 1–27. [Google Scholar]
- Hartmann, J.; Lazarus, F. Experimental investigations on the flow of mercury in a homogeneous magnetic field. Mat. Fys. Medd. K. Dan. Vidensk. Selsk. 1937, 15, 1–46. [Google Scholar]
- Radko, T. Double-Diffusive Convection; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-0-521-88074-9. [Google Scholar]
- Huppert, H.E.; Sparks, R.S.J. Double-Diffusive Convection Due to Crystallization in Magmas. Ann. Rev. Earth Planet Sci. 1984, 12, 11–37. [Google Scholar] [CrossRef]
- Ghara, N.; Das, S.L.; Maji, S.L.; Jana, R.N. Effect of radiation on MHD free convection flow past an impulsively moving vertical plate with ramped wall temperature. Am. J. Sci. Ind. Res. 2012, 3, 376–386. [Google Scholar] [CrossRef]
- Nandkeolyar, R.R.; Das, M.; Sibanda, P. Exact solutions of unsteady MHD free convection in a heat absorbing fluid flow past flat plate with ramped wall temperature. Bound Value Probl. 2013, 247, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Vieru, D.; Fetecau, C.; Fetecau, C.; Nigar, N. Magnetohydrodynamic natural convection flow with Newtonian heating and mass diffusion over an infinite plate that applies shear stress to a viscous fluid. Z. Naturforsch. 2014, 69a, 714–724. [Google Scholar] [CrossRef] [Green Version]
- Jha, B.K.; Aina, B.; Isa, S. Fully developed MHD natural convection flow in a vertical annular microchannel: An exact solution. J. King Saud Univ.-Sci. 2015, 27, 253–259. [Google Scholar] [CrossRef] [Green Version]
- Rehman, A.U.; Riaz, M.B.; Awrejcewicz, J.; Baleanu, D. Exact solutions of thermomagetized unsteady non-singularized jeffery fluid: Effects of ramped velocity, concentration with Newtonian heating. Results Phys. 2021, 26, 104367. [Google Scholar] [CrossRef]
- Rehman, A.U.; Riaz, M.B.; Akgul, A.; Saeed, S.T.; Baleanu, D. Heat and mass transport impact on MHD second grade fluid: A comparative analysis of fractional operators. Heat Transf. 2021, 50, 7042–7064. [Google Scholar] [CrossRef]
- Seth, G.S.; Ansari, M.S.; Nandkeolyar, R. MHD natural convection flow with radiative heat transfer past an impulsively moving plate with ramped wall temperature. Heat Mass Transf. 2011, 47, 551–561. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Surender, O. Non-Darcy natural convection from a vertical plate with a uniform wall temperature and concentration in a doubly stratified porous medium. J. Appl. Mech. Tech. Phys. 2015, 56, 590–600. [Google Scholar] [CrossRef]
- Narahari, M.; Debnath, L. Unsteady magnetohydrodynamic free convection flow past an accelerated vertical plate with constant heat flux and heat generation or absorptio. Z. Angew. Math. Mech. 2013, 93, 38–49. [Google Scholar] [CrossRef]
- Shah, N.A.; Zafar, A.A.; Akhtar, S. General solution for MHD-free convection flow over a vertical plate with ramped wall temperature and chemical reaction. Arab. J. Math. 2018, 7, 49–60. [Google Scholar] [CrossRef] [Green Version]
- Shah, N.A.; Zafar, A.A.; Fetecau, C.; Naseem, A. Effects of Exponential Heating on Double-Diffusive Free Convection Flows on a Moving Vertical Plate. Math. Rep. 2019. accepted for publication. [Google Scholar]
- Sparrow, E.M.; Husar, R.B. Longitudinal vortices in Natural convection flow on inclined plates. J. Fluid Mech. 1969, 37, 251–255. [Google Scholar] [CrossRef]
- Siddiqa, S.; Asghar, S.; Hossain, M.A. Natural convection flow over an inclined flat plate with internal heat generation and variable viscosity. Math. Comput. Model. 2010, 52, 1739–1751. [Google Scholar] [CrossRef]
- Saeed, S.T.; Riaz, M.B.; Baleanu, D.; Akgul, A.; Husnine, S.M. Exact Analysis of Second Grade Fluid with Generalized Boundary Conditions. Intell. Autom. Soft Comput. 2021, 28, 547–559. [Google Scholar] [CrossRef]
- Saeed, S.T.; Riaz, M.B.; Baleanu, D.; Abro, K.A. A Mathematical Study of Natural Convection Flow Through a Channel with Non-Singular Kernels: An Application to Transport Phenomena. Alex. Eng. J. 2020, 59, 2269–2281. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivative with non local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Jhangeer, A.; Munawar, M.; Riaz, M.B.; Baleanu, D. Construction of traveling waves patterns of (1 + n)-dimensional modified Zakharov–Kuznetsov equation in plasma physics. Results Phys. 2020, 19, 103330. [Google Scholar] [CrossRef]
- Iftikhar, N.; Baleanu, D.; Riaz, M.B.; Husnine, S.M. Heat and Mass Transfer of Natural Convective Flow with Slanted Magnetic Field via Fractional Operators. J. Appl. Comput. Mech. 2021, 7, 189–212. [Google Scholar] [CrossRef]
- Riaz, M.B.; Saeed, S.T.; Baleanu, D.; Ghalib, M.M. Computational results with non-singular and non-local kernel flow of viscous fluid in vertical permeable medium with variant temperature. Front. Phys. 2020, 8, 275. [Google Scholar] [CrossRef]
- Riaz, M.B.; Saeed, S.T.; Baleanu, D. Role of Magnetic field on the Dynamical Analysis of second grade fluid in optimal solution subject to non-integer Differentiable Operators. J. Appl. Comput. Mech. 2021, 7, 54–68. [Google Scholar]
- Rehman, A.U.; Riaz, M.B.; Saeed, S.T.; Yao, S. Dynamical Analysis of Radiation and Heat Transfer on MHD Second Grade Fluid. Comput. Modeling Eng. Sci. 2021, 129, 689–703. [Google Scholar] [CrossRef]
- Riaz, M.B.; Abro, K.A.; Abualnaja, K.M.; Akgül, A.; Rehman, A.U.; Abbas, M.; Hamed, Y.S. Exact solutions involving special functions for unsteady convective flow of magnetohydrodynamic second grade fluid with ramped conditions. Adv. Differ. Equ. 2021, 2021, 408. [Google Scholar] [CrossRef]
- Jhangeer, A.; Hussain, A.; Rehman, M.J.U.; Baleanu, D.; Riaz, M.B. Quasi-periodic, chaotic and travelling wave structures of modified Gardner equation. Chaos Solitons Fractals 2021, 143, 110578. [Google Scholar] [CrossRef]
- Iftikhar, N.; Husnine, S.M.; Riaz, M.B. Heat and mass transfer in MHD Maxwell Fluid over an infinite vertical plate. J. Prime Res. Math. 2019, 15, 63–80. [Google Scholar]
- Narahari, N.; Dutta, B.K. Effects of thermal radiation and mass diffusion on free convection flow near a vertical plate with Newtonian heating. Chem. Eng. Commun. 2012, 199, 628–643. [Google Scholar] [CrossRef]
- Rainville, E.D. Special Functions; Macmillan Co.: New York, NY, USA, 1960. [Google Scholar]
- Kurulay, M.; Bayram, M. Some properties of the Mittag-Leffler functions and their relation with the Wright functions. Adv. Differ. Equ. 2012, 2012, 181. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Li, K. A note on property of the Mittag-Leffler function. J. Math. Anal. Appl. 2010, 370, 635–638. [Google Scholar] [CrossRef] [Green Version]
- Mittag-Leffler, M.G. Sur la nouvelle fonction Eα(x). Proc. Paris Acad. Sci. 1903, 137, 554–558. [Google Scholar]
- Hartley, T.T.; Lorenzo, C.F. A Solution to the Fundamental Linear Fractional Order Differential Equation; NASA/TP–1998-208963; NASA: Washington, DC, USA, 1998.
- Lorenzo, C.F.; Hartley, T.T. Generalized functions for fractional calculus. Phys. Rev. E 2013, 8, 1199–1204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erdelyi, A.; Magnus, W.; Oberhettinger, F.; Tricimi, F.G. Table of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954; Volume 12. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Tokis, J.N. A class of exact solutions of the unsteady magneto hydrodynamic free-convection flows. Astrophys. Space Sci. 1985, 112, 413–422. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, A.U.; Riaz, M.B.; Rehman, W.; Awrejcewicz, J.; Baleanu, D. Fractional Modeling of Viscous Fluid over a Moveable Inclined Plate Subject to Exponential Heating with Singular and Non-Singular Kernels. Math. Comput. Appl. 2022, 27, 8. https://doi.org/10.3390/mca27010008
Rehman AU, Riaz MB, Rehman W, Awrejcewicz J, Baleanu D. Fractional Modeling of Viscous Fluid over a Moveable Inclined Plate Subject to Exponential Heating with Singular and Non-Singular Kernels. Mathematical and Computational Applications. 2022; 27(1):8. https://doi.org/10.3390/mca27010008
Chicago/Turabian StyleRehman, Aziz Ur, Muhammad Bilal Riaz, Wajeeha Rehman, Jan Awrejcewicz, and Dumitru Baleanu. 2022. "Fractional Modeling of Viscous Fluid over a Moveable Inclined Plate Subject to Exponential Heating with Singular and Non-Singular Kernels" Mathematical and Computational Applications 27, no. 1: 8. https://doi.org/10.3390/mca27010008
APA StyleRehman, A. U., Riaz, M. B., Rehman, W., Awrejcewicz, J., & Baleanu, D. (2022). Fractional Modeling of Viscous Fluid over a Moveable Inclined Plate Subject to Exponential Heating with Singular and Non-Singular Kernels. Mathematical and Computational Applications, 27(1), 8. https://doi.org/10.3390/mca27010008






