A SARS-CoV-2 Fractional-Order Mathematical Model via the Modified Euler Method
Abstract
1. Introduction
2. Mathematical Model
3. Basic Definitions and Theorems
4. Existences and Uniqueness
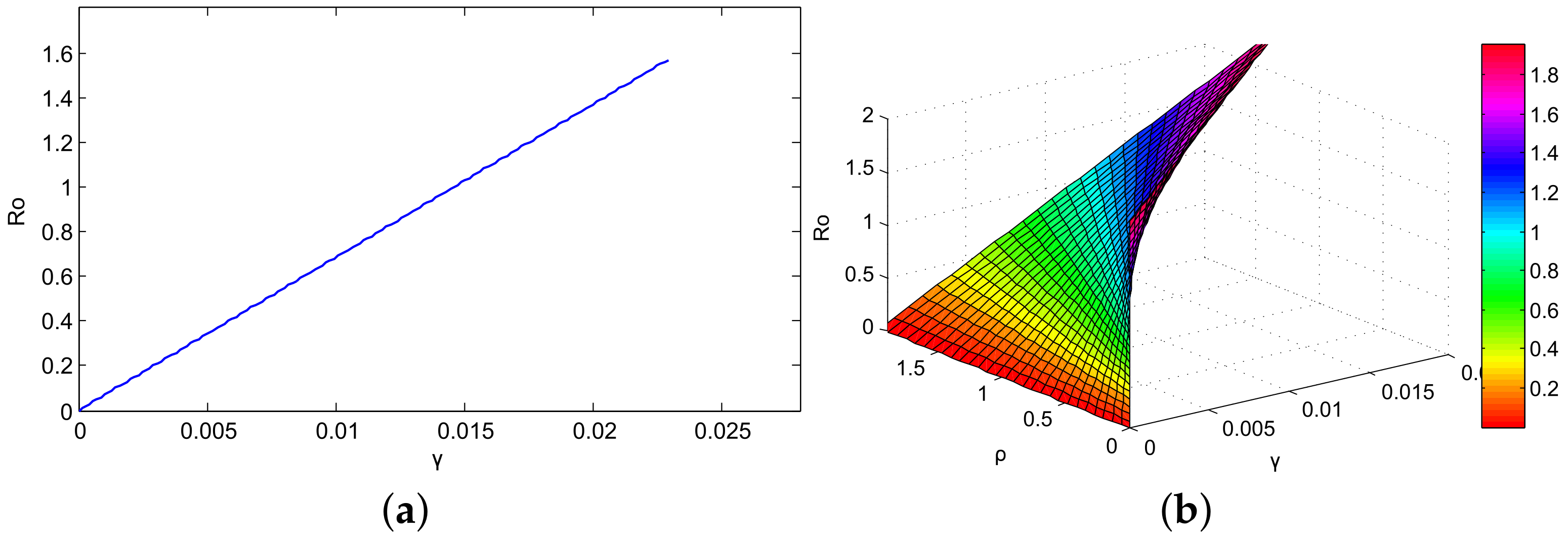
5. Steady State and Derivation of Reproduction Number
6. Local Stability
7. Global Stability
8. Algorithm for the Solution
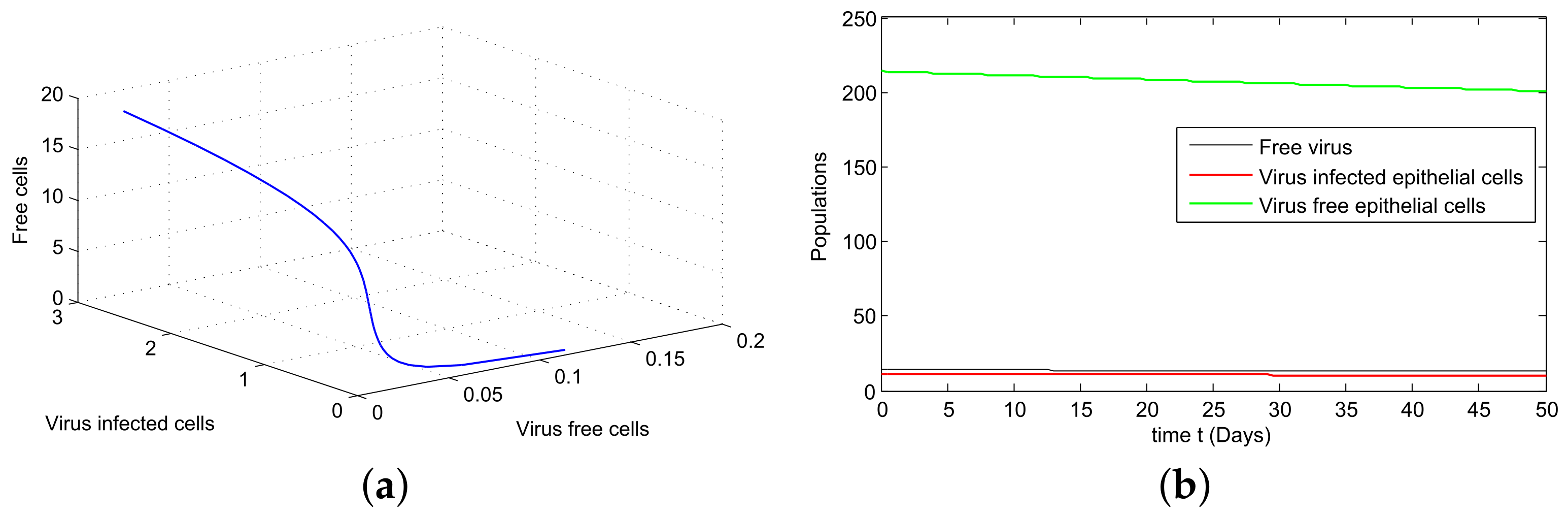
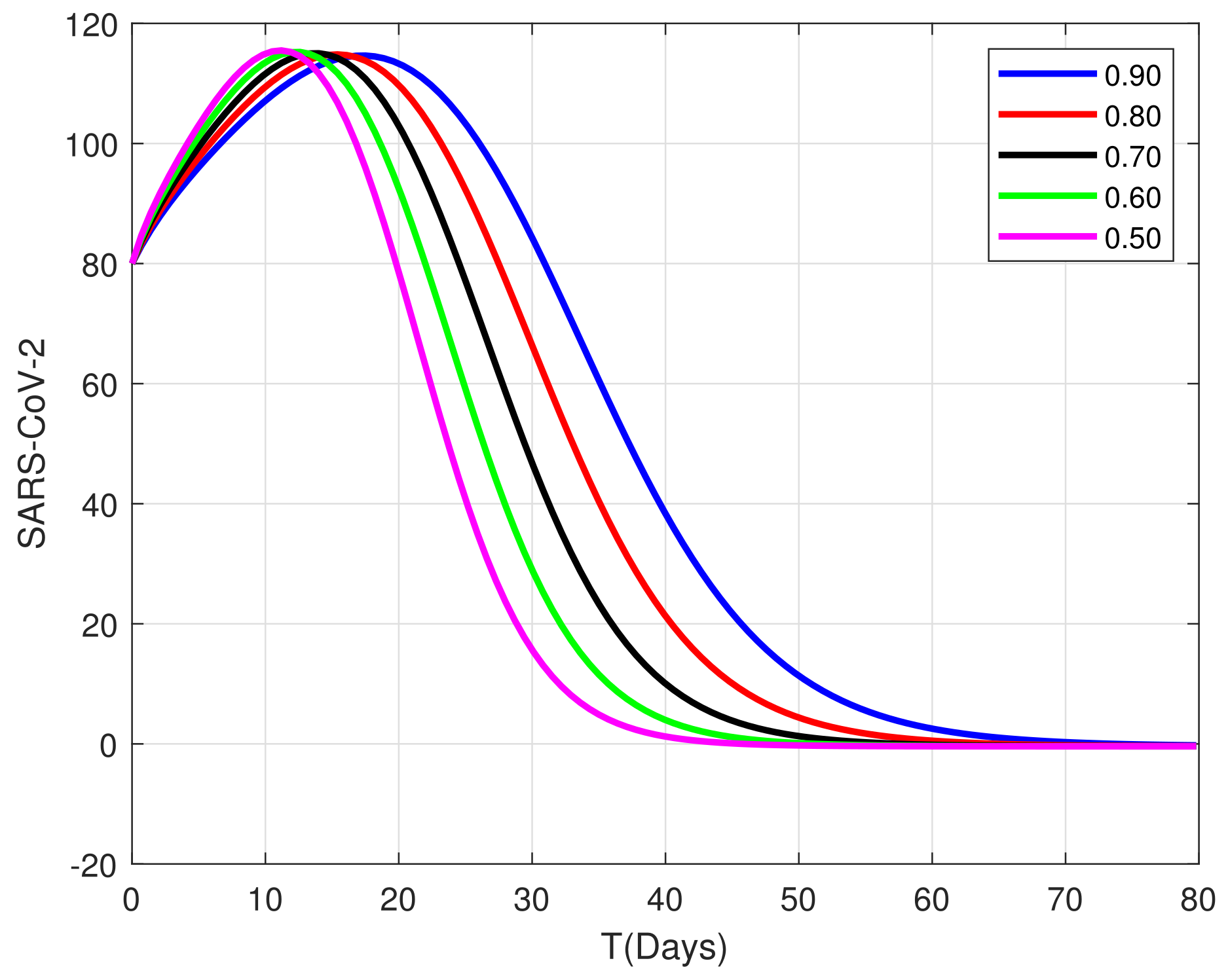
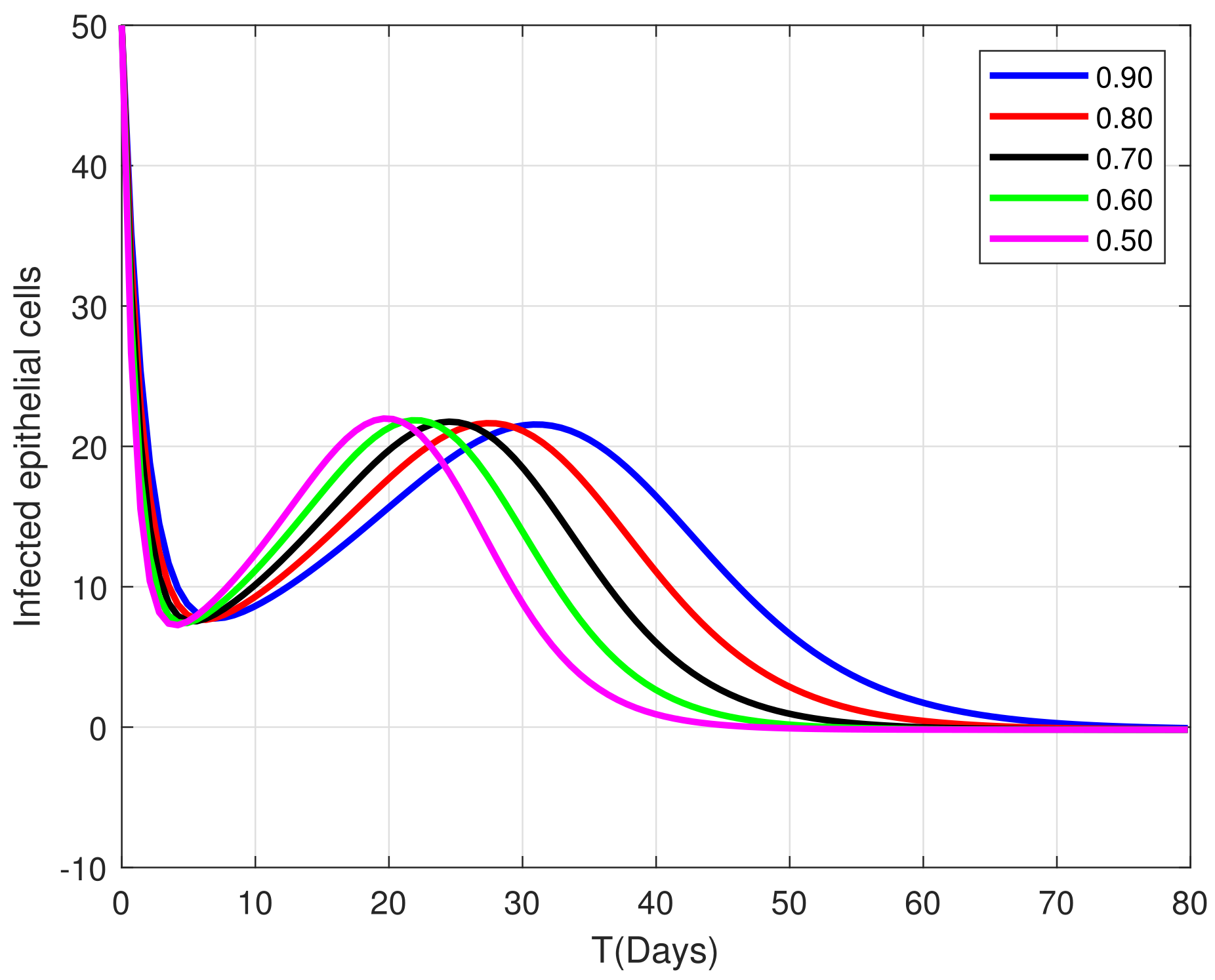
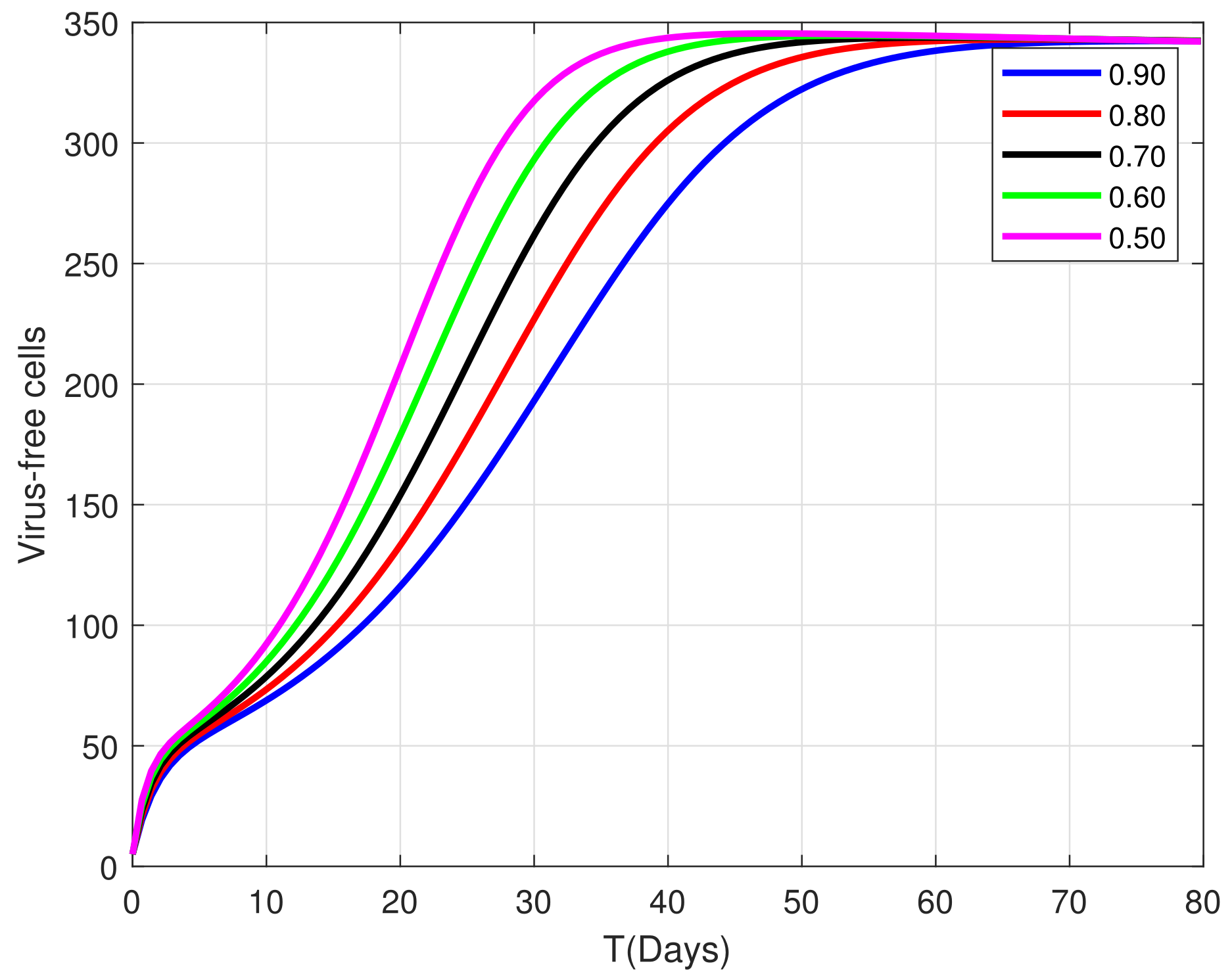
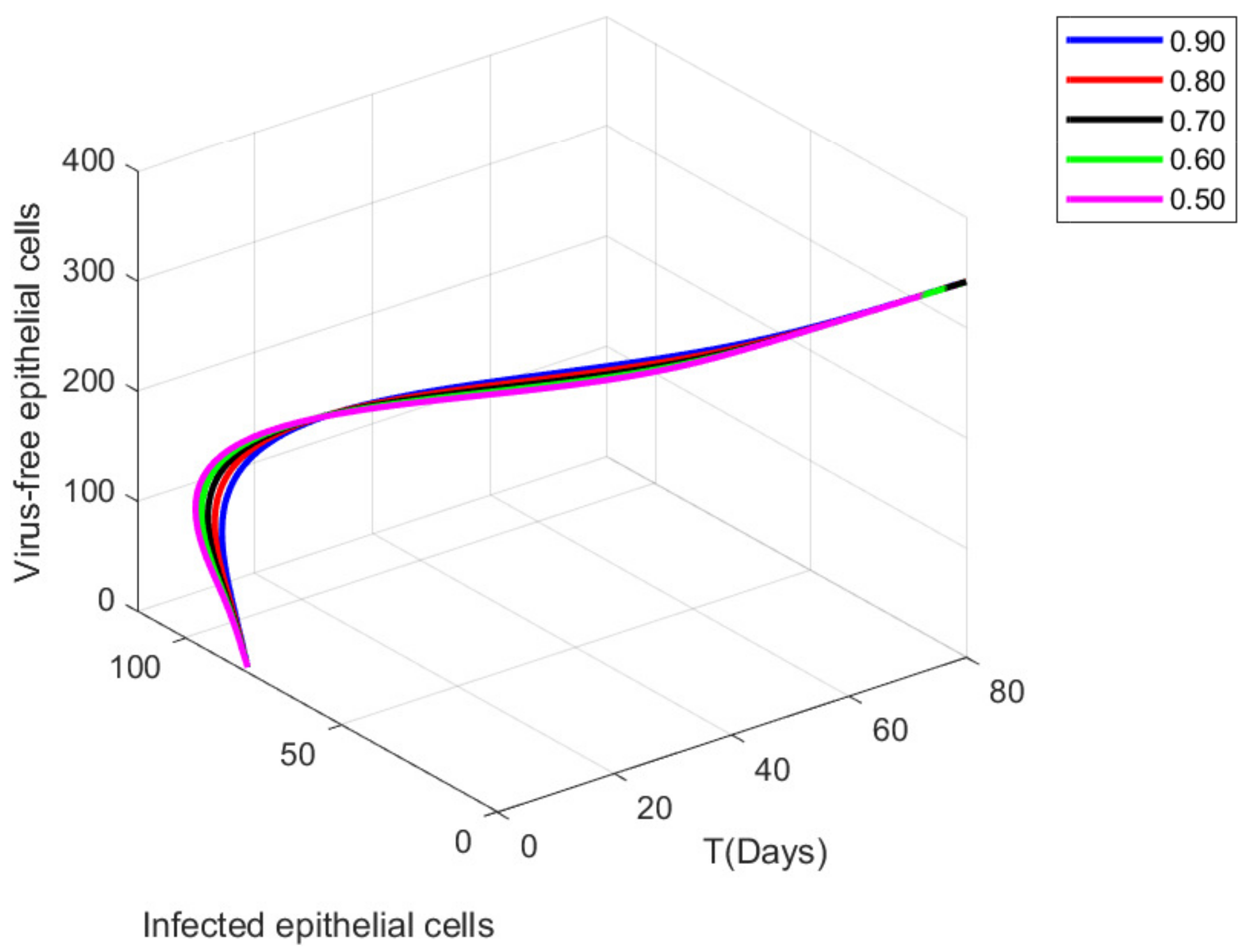
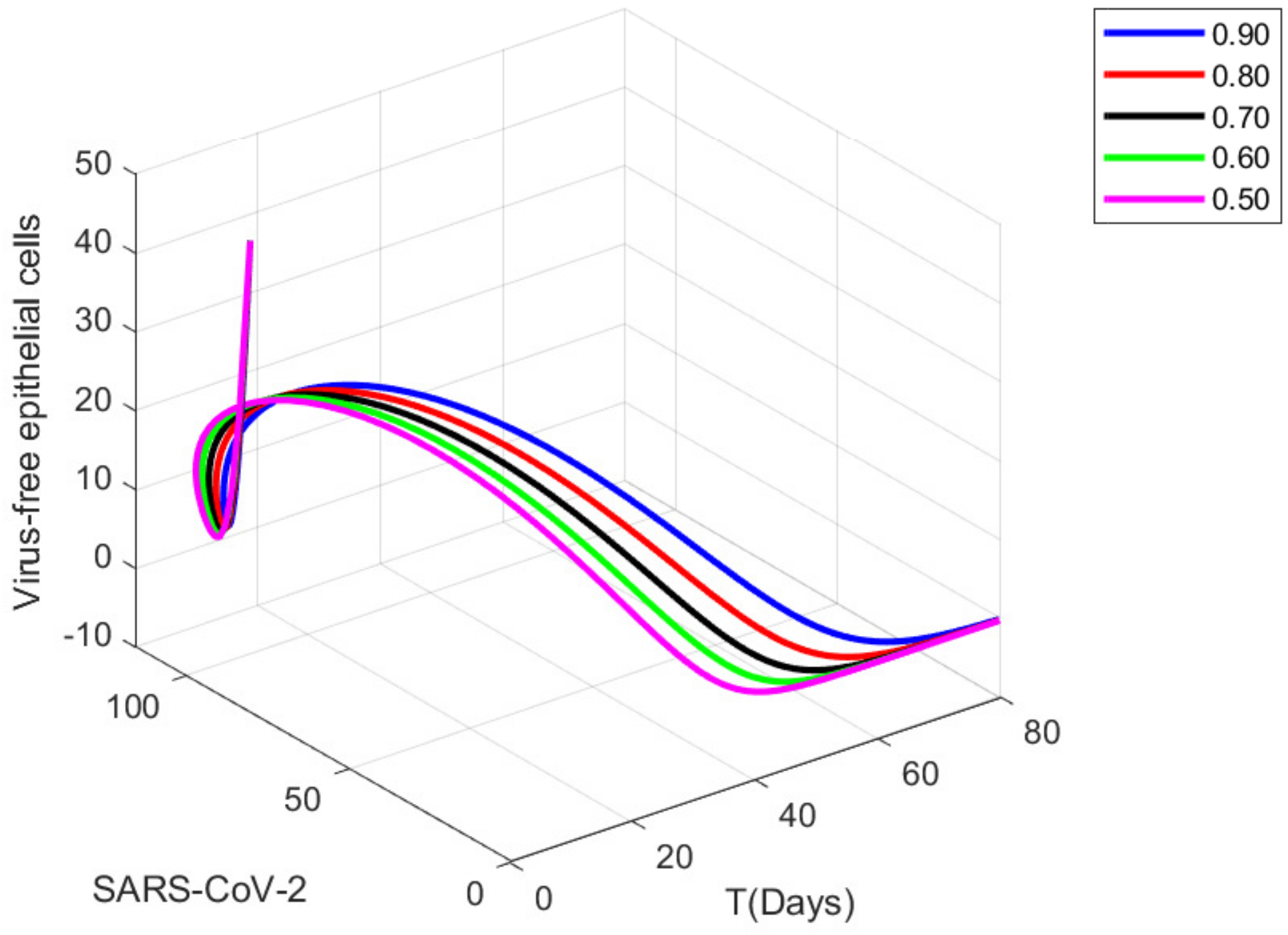
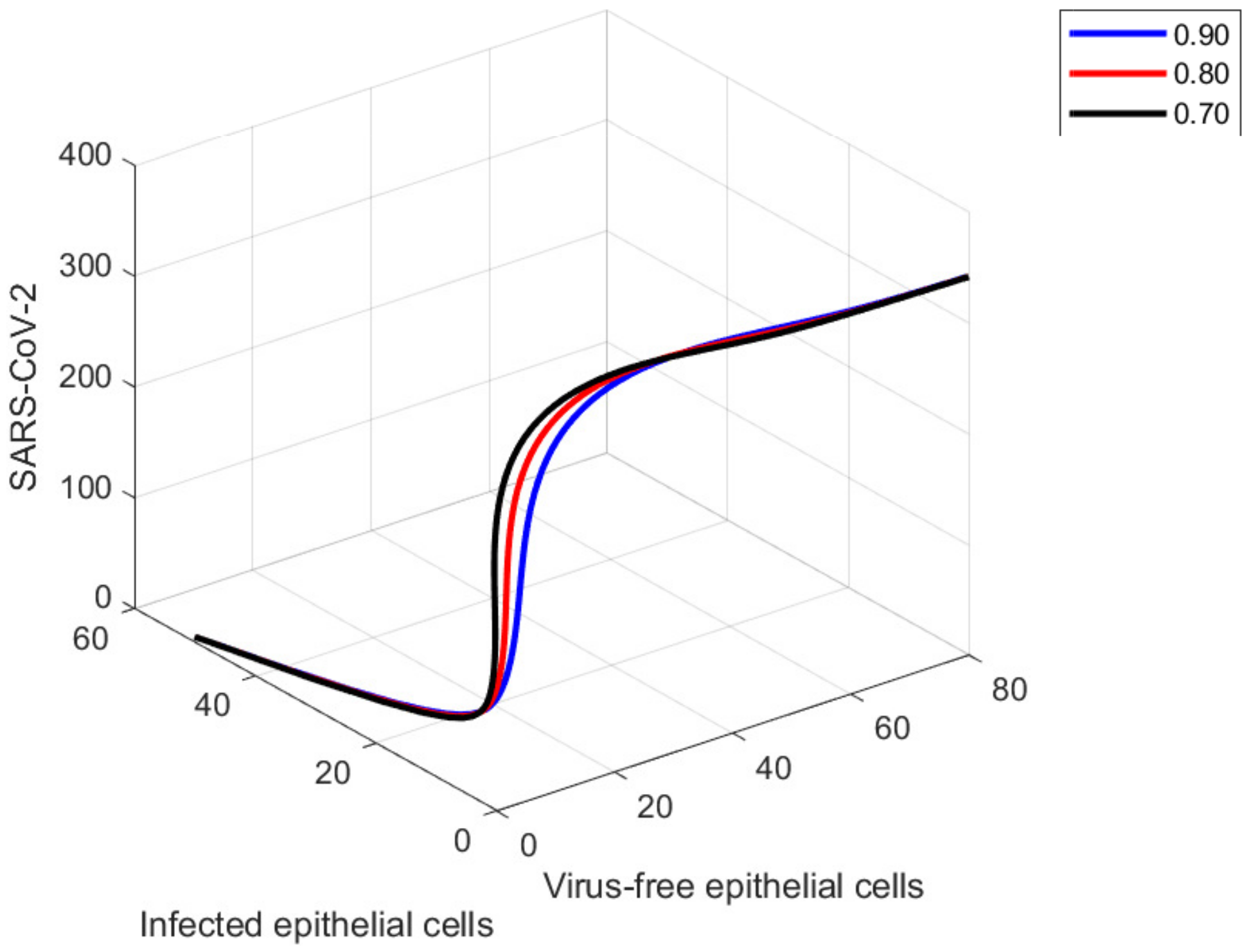
9. Graphical Representations
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reusken, C.B.; Buiting, A.; Bleeker-Rovers, C.; Diederen, B.; Hooiveld, M.; Friesema, I.; Koopmans, M.; Kortbeek, T.; Lutgens, S.P.; Meijer, A.; et al. Rapid assessment of regional SARS-CoV-2 community transmission through a convenience sample of healthcare workers, the Netherlands, March 2020. Eurosurveillance 2020, 25, 2000334. [Google Scholar] [CrossRef]
- Zhou, P.; Yang, X.L.; Wang, X.G.; Hu, B.; Zhang, L.; Zhang, W.; Si, H.R.; Zhu, Y.; Li, B.; Huang, C.L.; et al. Discovery of a novel coronavirus associated with the recent pneumonia outbreak in humans and its potential bat origin. BioRxiv 2020, 22, 914952. [Google Scholar]
- Miron, V.D. COVID-19 in the pediatric population and parental perceptions. Germs 2020, 10, 294. [Google Scholar] [CrossRef] [PubMed]
- Liang, K. Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS. Infect. Genet. Evol. 2020, 82, 104306. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Xu, J.; Liu, J.; Zhou, Y. The within-host viral kinetics of SARS-CoV-2. bioRxiv 2020, 17, 234. [Google Scholar] [CrossRef]
- Mason, R.J. Pathogenesis of COVID-19 from a cell biology perspective. Eur. Respir. J. 2020, 55, 2000607. [Google Scholar] [CrossRef]
- World Health Orgnization. Naming the Coronavirus Disease (COVID-19) and the Virus That Causes It. 2020. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/technical-guidance/naming-the-coronavirus-disease-(covid-2019)-and-the-virus-that-causes-it (accessed on 22 September 2022).
- Yang, C.; Wang, J. A mathematical model for the novel coronavirus epidemic in Wuhan, China. Math. Biosci. Eng. 2020, 17, 2853–2861. [Google Scholar] [CrossRef]
- Sinan, M.; Leng, J.; Anjum, M.; Fiaz, M. Asymptotic behavior and semi-analytic solution of a novel compartmental biological model. Math. Model. Numer. Simul. Appl. 2022, 2, 88–107. [Google Scholar] [CrossRef]
- Tang, B.; Bragazzi, N.L.; Li, Q.; Tang, S.; Xiao, Y.; Wu, J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov). Infect. Dis. Model. 2020, 5, 248–255. [Google Scholar] [CrossRef]
- Kochańczyk, M.; Grabowski, F.; Lipniacki, T. Dynamics of COVID-19 pandemic at constant and time-dependent contact rates. Math. Model. Nat. Phenom. 2020, 15, 28. [Google Scholar] [CrossRef]
- Naik, P.A.; Yavuz, M.; Qureshi, S.; Zu, J.; Townley, S. Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. Eur. Phys. J. Plus 2020, 135, 1–42. [Google Scholar] [CrossRef]
- Allegretti, S.; Bulai, I.M.; Marino, R.; Menandro, M.A.; Parisi, K. Vaccination effect conjoint to fraction of avoided contacts for a Sars-Cov-2 mathematical model. Math. Model. Numer. Simul. Appl. 2021, 1, 56–66. [Google Scholar] [CrossRef]
- Özköse, F.; Yavuz, M.; Şenel, M.T.; Habbireeh, R. Fractional order modelling of omicron SARS-CoV-2 variant containing heart attack effect using real data from the United Kingdom. Chaos Solitons Fractals 2022, 157, 111954. [Google Scholar] [CrossRef]
- Haq, I.U.; Ali, N.; Nisar, K.S. An optimal control strategy and Grünwald-Letnikov finite-difference numerical scheme for the fractional-order COVID-19 model. Math. Model. Numer. Simul. Appl. 2022, 2, 108–116. [Google Scholar] [CrossRef]
- Özköse, F.; Yavuz, M. Investigation of interactions between COVID-19 and diabetes with hereditary traits using real data: A case study in Turkey. Comput. Biol. Med. 2022, 141, 105044. [Google Scholar] [CrossRef]
- Ikram, R.; Khan, A.; Zahri, M.; Saeed, A.; Yavuz, M.; Kumam, P. Extinction and stationary distribution of a stochastic COVID-19 epidemic model with time-delay. Comput. Biol. Med. 2022, 141, 105115. [Google Scholar] [CrossRef]
- Naik, P.A.; Eskandari, Z.; Yavuz, M.; Zu, J. Complex dynamics of a discrete-time Bazykin–Berezovskaya prey-predator model with a strong Allee effect. J. Comput. Appl. Math. 2022, 413, 114401. [Google Scholar] [CrossRef]
- Moussouni, N.; Aliane, M. Optimal control of COVID-19. Int. J. Optim. Control Theor. Appl. 2021, 11, 114–122. [Google Scholar] [CrossRef]
- Hamou, A.A.; Rasul, R.R.; Hammouch, Z.; Özdemir, N. Analysis and dynamics of a mathematical model to predict unreported cases of COVID-19 epidemic in Morocco. Comput. Appl. Math. 2022, 41, 1–33. [Google Scholar] [CrossRef]
- Evirgen, F. Transmission of Nipah virus dynamics under Caputo fractional derivative. J. Comput. Appl. Math. 2023, 418, 114654. [Google Scholar] [CrossRef]
- Du, S.Q.; Yuan, W. Mathematical modeling of interaction between innate and adaptive immune responses in COVID-19 and implications for viral pathogenesis. J. Med. Virol. 2020, 92, 1615–1628. [Google Scholar] [CrossRef]
- Abuin, P.; Anderson, A.; Ferramosca, A.; Hernandez-Vargas, E.A.; Gonzalez, A.H. Characterization of SARS-CoV-2 dynamics in the host. Annu. Rev. Control 2020, 50, 457–468. [Google Scholar] [CrossRef]
- Nath, B.J.; Dehingia, K.; Mishra, V.N.; Chu, Y.M.; Sarmah, H.K. Mathematical analysis of a within-host model of SARS-CoV-2. Adv. Differ. Equ. 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Agarwal, P.; Deniz, S.; Jain, S.; Alderremy, A.A.; Aly, S. A new analysis of a partial differential equation arising in biology and population genetics via semi analytical techniques. Phys. A Stat. Mech. Appl. 2020, 542, 122769. [Google Scholar] [CrossRef]
- Lei, S.; Jiang, F.; Su, W.; Chen, C.; Chen, J.; Mei, W.; Zhan, L.Y.; Jia, Y.; Zhang, L.; Liu, D.; et al. Clinical characteristics and outcomes of patients undergoing surgeries during the incubation period of COVID-19 infection. EClinicalMedicine 2020, 21, 100331. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef]
- Chan, J.F.W.; Yuan, S.; Kok, K.H.; To, K.K.W.; Chu, H.; Yang, J.; Xing, F.; Liu, J.; Yip, C.C.Y.; Poon, R.W.S.; et al. A familial cluster of pneumonia associated with the 2019 novel coronavirus indicating person-to-person transmission: A study of a family cluster. Lancet 2020, 395, 514–523. [Google Scholar] [CrossRef]
- Letko, M.; Munster, V. Functional assessment of cell entry and receptor usage for lineage B β-coronaviruses, including 2019-nCoV. bioRxiv 2020. [Google Scholar] [CrossRef]
- Liu, J.; Liao, X.; Qian, S.; Yuan, J.; Wang, F.; Liu, Y.; Wang, Z.; Wang, F.S.; Liu, L.; Zhang, Z. Community transmission of severe acute respiratory syndrome coronavirus 2, Shenzhen, China, 2020. Emerg. Infect. Dis. 2020, 26, 1320. [Google Scholar] [CrossRef]
- Agarwal, P.; Nieto, J.J.; Ruzhansky, M.; Torres, D.F. Analysis of Infectious Disease Problems (Covid-19) and Their Global Impact; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Yavuz, M.; Coşar, F.Ö.; Günay, F.; Özdemir, F.N. A new mathematical modeling of the COVID-19 pandemic including the vaccination campaign. J Model. Simul. 2021, 9, 299–321. [Google Scholar] [CrossRef]
- Tuite, A.R.; Fisman, D.N.; Greer, A.L. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. CMAJ 2020, 192, E497–E505. [Google Scholar] [CrossRef] [PubMed]
- Marovich, M.; Mascola, J.R.; Cohen, M.S. Monoclonal antibodies for prevention and treatment of COVID-19. JAMA 2020, 324, 131–132. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Fan, Y.; Lai, Y.; Han, T.; Li, Z.; Zhou, P.; Pan, P.; Wang, W.; Hu, D.; Liu, X.; et al. Coronavirus infections and immune responses. J. Med. Virol. 2020, 92, 424–432. [Google Scholar] [CrossRef] [PubMed]
- Harapan, H.; Itoh, N.; Yufika, A.; Winardi, W.; Keam, S.; Te, H.; Megawati, D.; Hayati, Z.; Wagner, A.L.; Mudatsir, M. Coronavirus disease 2019 (COVID-19): A literature review. J. Infect. Public Health 2020, 13, 667–673. [Google Scholar] [CrossRef]
- Chen, T.M.; Rui, J.; Wang, Q.P.; Zhao, Z.Y.; Cui, J.A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 1–8. [Google Scholar] [CrossRef]
- Ahmed, I.; Baba, I.A.; Yusuf, A.; Kumam, P.; Kumam, W. Analysis of Caputo fractional-order model for COVID-19 with lockdown. Adv. Differ. Equ. 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Baba, I.A.; Nasidi, B.A. Fractional order model for the role of mild cases in the transmission of COVID-19. Chaos Solitons Fractals 2021, 142, 110374. [Google Scholar] [CrossRef]
- Hamdan, N.; Kilicman, A. Analysis of the fractional order dengue transmission model: A case study in Malaysia. Adv. Differ. Equ. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Khan, M.; Khan, A.; Elsonbaty, A.; Elsadany, A. Modeling and simulation results of a fractional dengue model. Eur. Phys. J. Plus 2019, 134, 379. [Google Scholar] [CrossRef]
- Hammouch, Z.; Yavuz, M.; Özdemir, N. Numerical solutions and synchronization of a variable-order fractional chaotic system. Math. Model. Numer. Simul. Appl. 2021, 1, 11–23. [Google Scholar] [CrossRef]
- Din, A.; Abidin, M.Z. Analysis of fractional-order vaccinated Hepatitis-B epidemic model with Mittag-Leffler kernels. Math. Model. Numer. Simul. Appl. 2022, 2, 59–72. [Google Scholar] [CrossRef]
- Kalidass, M.; Zeng, S.; Yavuz, M. Stability of Fractional-Order Quasi-Linear Impulsive Integro-Differential Systems with Multiple Delays. Axioms 2022, 11, 308. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Lee, H.Y.; Topham, D.J.; Park, S.Y.; Hollenbaugh, J.; Treanor, J.; Mosmann, T.R.; Jin, X.; Ward, B.M.; Miao, H.; Holden-Wiltse, J.; et al. Simulation and prediction of the adaptive immune response to influenza A virus infection. J. Virol. 2009, 83, 7151–7165. [Google Scholar] [CrossRef]
- Higazy, M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals 2020, 138, 110007. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Al-Mdallal, Q.M.; Khan, H.; Shah, K.; Khan, A. Fractional Order Mathematical Modeling of COVID-19 Transmission; Elsevier: Amsterdam, The Netherlands, 2020; Volume 139, p. 110256. [Google Scholar]
- Joshi, H.; Jha, B.K. Chaos of calcium diffusion in Parkinson’s infectious disease model and treatment mechanism via Hilfer fractional derivative. Math. Model. Numer. Simul. Appl. 2021, 1, 84–94. [Google Scholar]
- Yavuz, M.; Sene, N.; Yıldız, M. Analysis of the influences of parameters in the fractional second-grade fluid dynamics. Mathematics 2022, 10, 1125. [Google Scholar] [CrossRef]
- Kilbas, A.; Trujillo, J. Differential equations of fractional order: Methods, results and problems. II. Appl. Anal. 2002, 81, 435–493. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef]
- Ahmed, E.; Elgazzar, A. On fractional order differential equations model for nonlocal epidemics. Phys. A Stat. Mech. Its Appl. 2007, 379, 607–614. [Google Scholar] [CrossRef]
- Ahmady, N.; Allahviranloo, T.; Ahmady, E. A modified Euler method for solving fuzzy differential equations under generalized differentiability. Comput. Appl. Math. 2020, 39, 1–21. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haq, I.U.; Yavuz, M.; Ali, N.; Akgül, A. A SARS-CoV-2 Fractional-Order Mathematical Model via the Modified Euler Method. Math. Comput. Appl. 2022, 27, 82. https://doi.org/10.3390/mca27050082
Haq IU, Yavuz M, Ali N, Akgül A. A SARS-CoV-2 Fractional-Order Mathematical Model via the Modified Euler Method. Mathematical and Computational Applications. 2022; 27(5):82. https://doi.org/10.3390/mca27050082
Chicago/Turabian StyleHaq, Ihtisham Ul, Mehmet Yavuz, Nigar Ali, and Ali Akgül. 2022. "A SARS-CoV-2 Fractional-Order Mathematical Model via the Modified Euler Method" Mathematical and Computational Applications 27, no. 5: 82. https://doi.org/10.3390/mca27050082
APA StyleHaq, I. U., Yavuz, M., Ali, N., & Akgül, A. (2022). A SARS-CoV-2 Fractional-Order Mathematical Model via the Modified Euler Method. Mathematical and Computational Applications, 27(5), 82. https://doi.org/10.3390/mca27050082








