Comparison of Two Aspects of a PDE Model for Biological Network Formation
Abstract
1. Introduction
2. Mathematical Model
3. Numerical Schemes
3.1. Space Discretization
3.2. Time Discretization: Symmetric ADI Method
3.2.1. Time Discretization for the Conductivity Vector
3.2.2. Time Discretization for the Conductivity Tensor
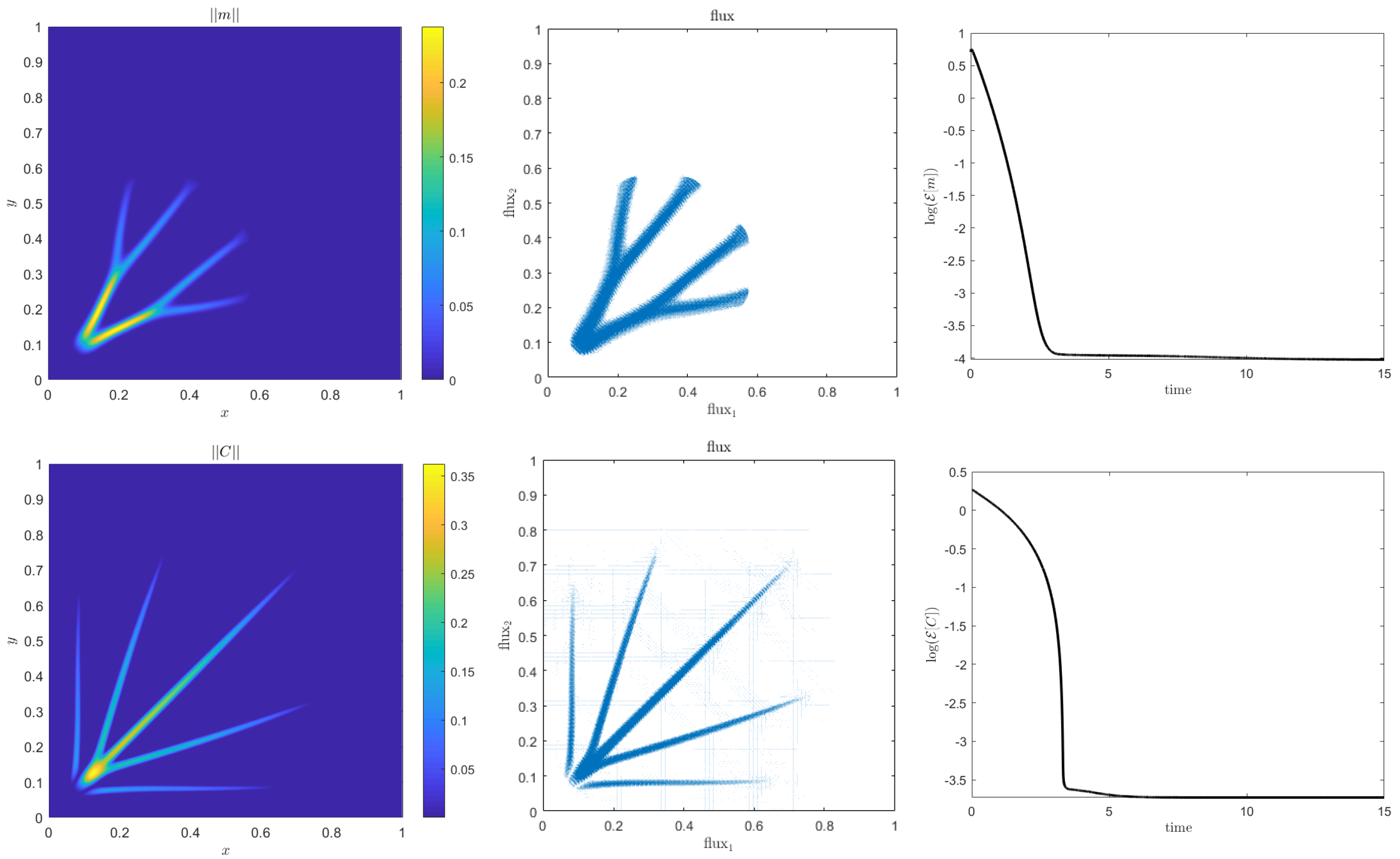
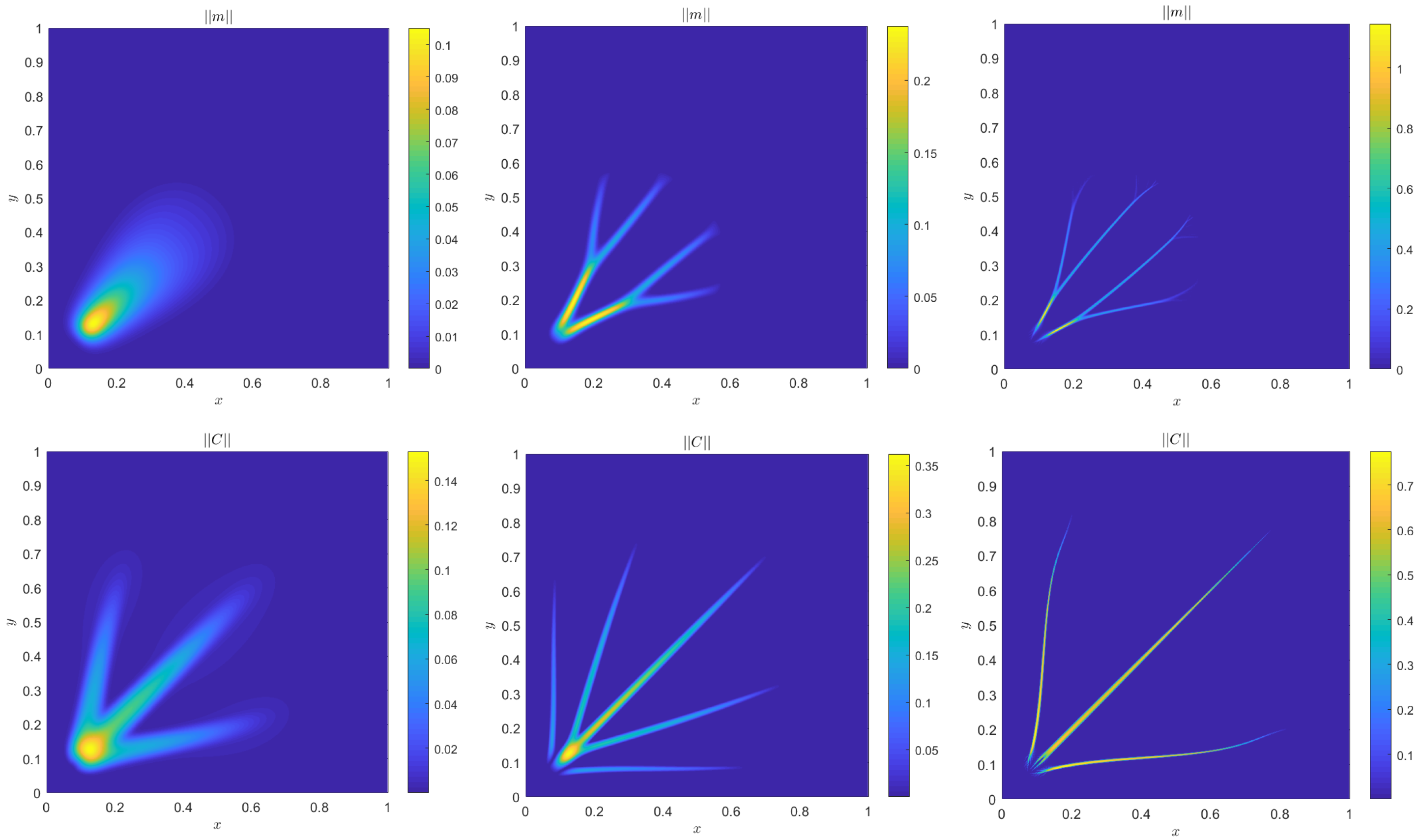
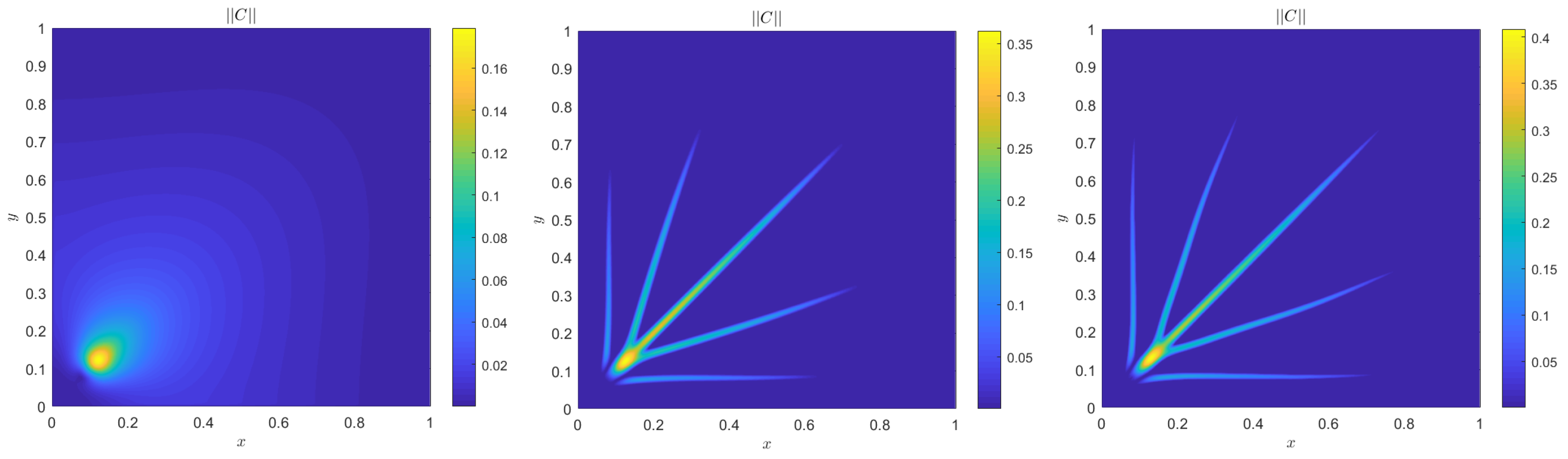
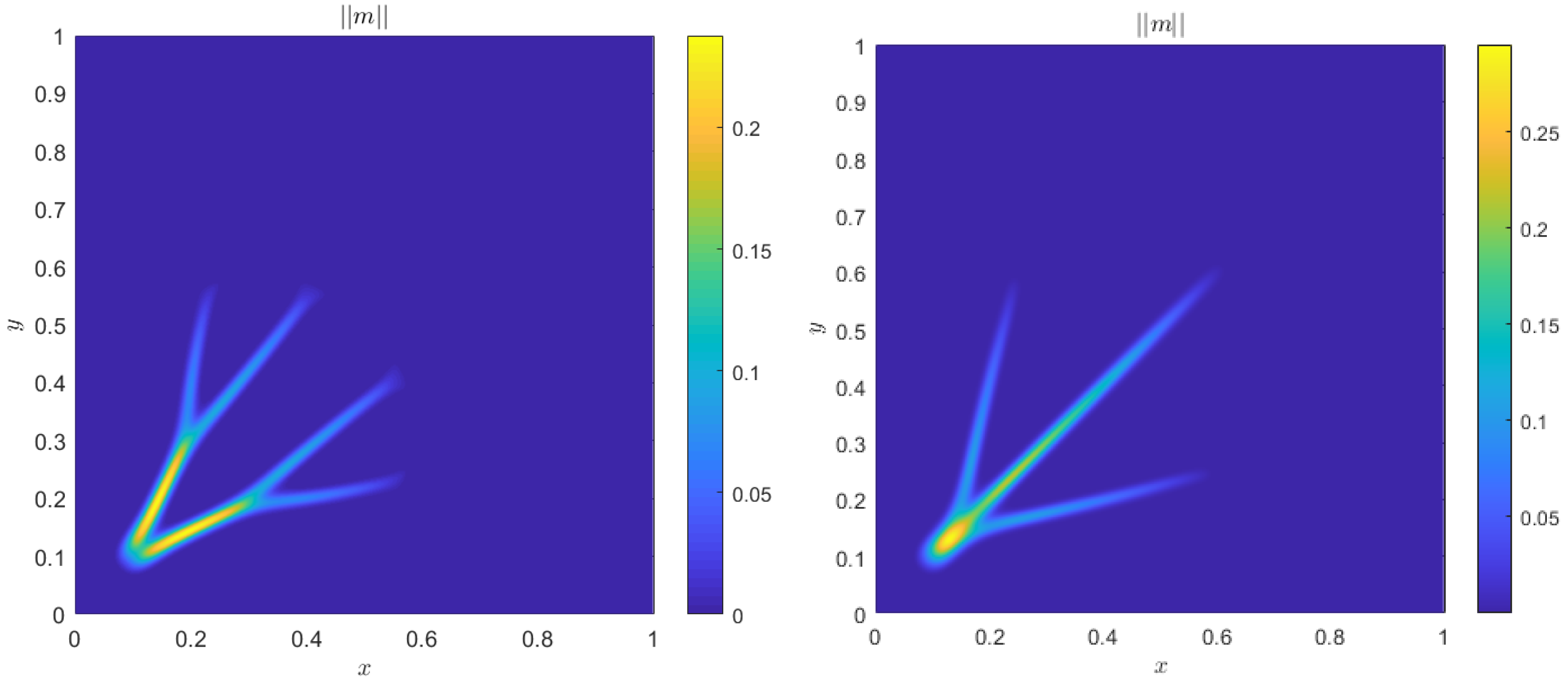
4. Numerical Results
4.1. Accuracy Tests and Qualitative Agreements
4.2. Quantitative Agreement
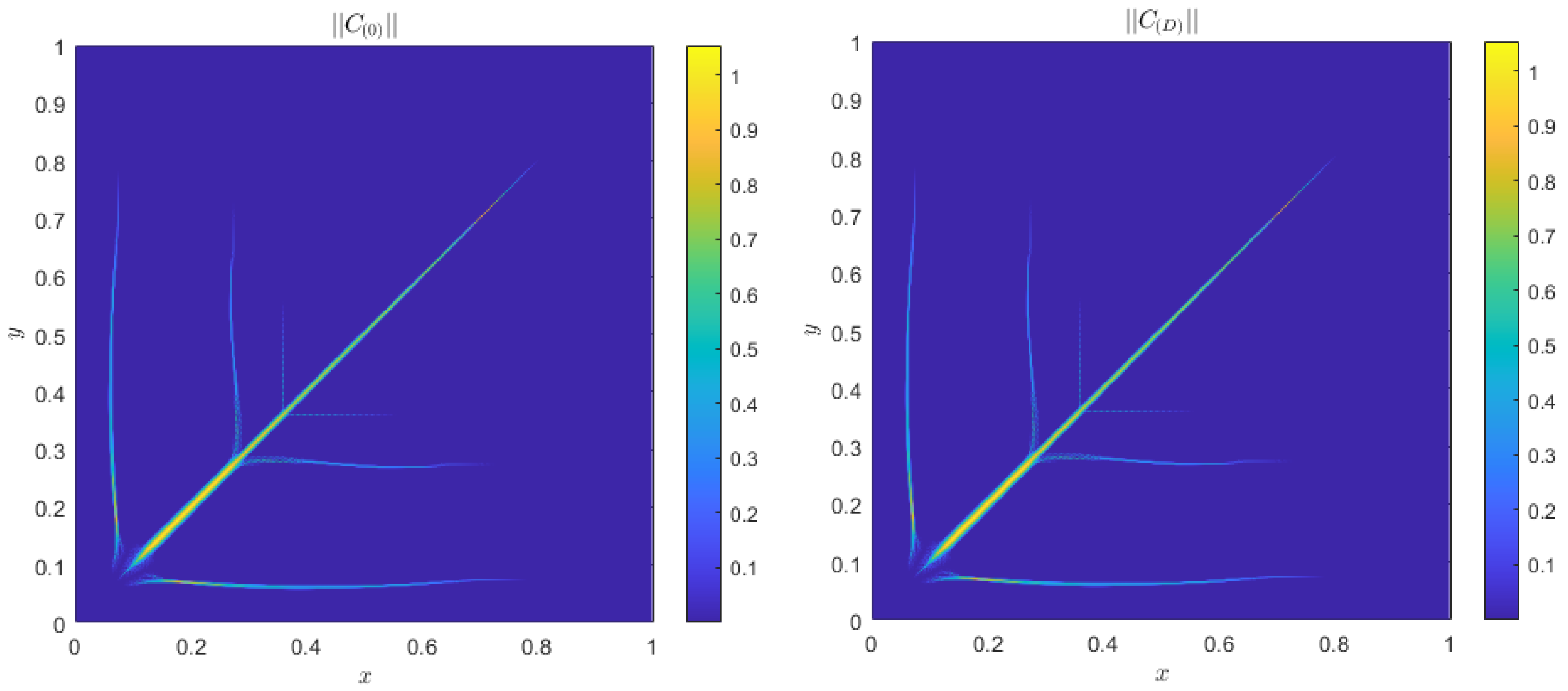
Alternative Boundary Conditions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, D.; Cai, D. Adaptation and optimization of biological transport networks. Phys. Rev. Lett. 2013, 111, 138701. [Google Scholar] [CrossRef] [PubMed]
- Katifori, E.; Szöllosi, G.J.; Magnasco, M.O. Damage and fluctuations induce loops in optimal transport networks. Phys. Rev. Lett. 2010, 104, 048704. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Cai, D. An optimization principle for initiation and adaptation of biological transport networks. Commun. Math. Sci. 2019, 17, 1427–1436. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application des Principes à Suivre et des Formules à Employer Dans les Questions de Distribution d’eau: Ouvrage Terminé par un Appendice Relatif aux Fournitures d’eau de Plusieurs Villes, au Filtrage des Eaux et à la Fabrication des Tuyaux de Fonte, de Plomb, de tôle et de Bitume; Dalmont, V., Ed.; Typographie Hennuyer: Paris, France, 1856. [Google Scholar]
- Neuman, S.P. Theoretical derivation of Darcy’s law. Acta Mech. 1977, 25, 153–170. [Google Scholar] [CrossRef]
- Fang, D.; Jin, S.; Markowich, P.; Perthame, B. Implicit and Semi-implicit Numerical Schemes for the Gradient Flow of the Formation of Biological Transport Networks. SMAI J. Comput. Math. 2019, 5, 229–249. [Google Scholar] [CrossRef]
- Haskovec, J.; Markowich, P.; Perthame, B. Mathematical Analysis of a PDE System for Biological Network Formation. Commun. Partial. Differ. Equ. 2015, 40, 918–956. [Google Scholar] [CrossRef]
- Haskovec, J.; Markowich, P.; Perthame, B.; Schlottbom, M. Notes on a PDE system for biological network formation. Nonlinear Anal. 2016, 138, 127–155. [Google Scholar] [CrossRef]
- Albi, G.; Artina, M.; Foransier, M.; Markowich, P.A. Biological transportation networks: Modeling and simulation. Anal. Appl. 2016, 14, 185–206. [Google Scholar] [CrossRef]
- Haskovec, J.; Markowich, P.; Portaro, S. Emergence of biological transportation networks as a self-regulated process. arXiv 2022, arXiv:2207.03542. [Google Scholar]
- Haskovec, J.; Markowich, P.; Pilli, G. Tensor PDE model of biological network formation. Commun. Math. Sci. 2022, 20, 1173–1191. [Google Scholar] [CrossRef]
- Wesseling, P. Principles of Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Richardson, L.F. IX. The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1911, 210, 307–357. [Google Scholar]



| c | D | r | ||||||
|---|---|---|---|---|---|---|---|---|
| Accuracy m | TestA: | 0.5 | 1 | 0.01 | - | 0.75 | 0.1 | 1 |
| Accuracy | TestB: | 1 | 1 | 0.01 | 0.1 | 1.75 | 0.1 | 1 |
| Accuracy m | TestC: | 0.5 | 5 | 0.01 | - | 0.75 | 0.01 | 1 |
| TestG: | 0.75 | 5 | 0.05 | 0.75 | 0.005 | 15 | ||
| TestD: | 0.75 | 5 | 0.01 | 0.75 | 0.005 | 15 | ||
| TestE: | 0.75 | 5 | 0.001 | 0.75 | 0.005 | 15 | ||
| TestH: | 0.75 | 5 | 0.01 | 1 | 0.005 | 15 | ||
| TestD: | 0.75 | 5 | 0.01 | 0.75 | 0.005 | 15 | ||
| TestF: | 0.75 | 5 | 0.01 | 0.5 | 0.005 | 15 | ||
| TestI: | 0.75 | 5 | 0.01 | 0.75 | 0.005 | 15 | ||
| TestD: | 0.75 | 5 | 0.01 | 0.75 | 0.005 | 15. | ||
| TestL: | 0.75 | 5 | 0.01 | 0.75 | 0.005 | 15 |
| N | Error | Order | N | Error | Order |
|---|---|---|---|---|---|
| 20 | - | - | 20 | - | - |
| 40 | 0.036030 | - | 40 | 0.036012 | - |
| 80 | 0.0492860 | −0.4520 | 80 | 0.0493010 | −0.4531 |
| 160 | 0.01454106 | 1.7610 | 160 | 0.01456192 | 1.7594 |
| 320 | 0.00690830 | 1.0737 | 320 | 0.00691103 | 1.0752 |
| 640 | 0.001529779 | 2.1750 | 640 | 0.001528055 | 2.1772 |
| N | Error | Order |
|---|---|---|
| 25 | - | - |
| 50 | - | |
| 100 | 0.97 | |
| 200 | 1.56 | |
| 400 | 1.92 | |
| 800 | 2.50 |
| r | N | |||||||
|---|---|---|---|---|---|---|---|---|
| set of parameters | TestM: | 1, 0.5 | , 1 | 0.1 | 1.75, 0.75 | 0.1 | 600 |
| Time | 0.01 | 0.02 | 0.04 | 0.08 | 0.16 | 0.32 | 0.64 |
|---|---|---|---|---|---|---|---|
| 0.0348 | 0.0538 | 0.0697 | 0.0982 | 0.1509 | 0.2611 | 0.5320 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Astuto, C.; Boffi, D.; Haskovec, J.; Markowich, P.; Russo, G. Comparison of Two Aspects of a PDE Model for Biological Network Formation. Math. Comput. Appl. 2022, 27, 87. https://doi.org/10.3390/mca27050087
Astuto C, Boffi D, Haskovec J, Markowich P, Russo G. Comparison of Two Aspects of a PDE Model for Biological Network Formation. Mathematical and Computational Applications. 2022; 27(5):87. https://doi.org/10.3390/mca27050087
Chicago/Turabian StyleAstuto, Clarissa, Daniele Boffi, Jan Haskovec, Peter Markowich, and Giovanni Russo. 2022. "Comparison of Two Aspects of a PDE Model for Biological Network Formation" Mathematical and Computational Applications 27, no. 5: 87. https://doi.org/10.3390/mca27050087
APA StyleAstuto, C., Boffi, D., Haskovec, J., Markowich, P., & Russo, G. (2022). Comparison of Two Aspects of a PDE Model for Biological Network Formation. Mathematical and Computational Applications, 27(5), 87. https://doi.org/10.3390/mca27050087







