Effect of Chrome and Vanadium on the Behavior of Hydrogen and Helium in Tungsten
Abstract
:1. Introduction
2. Methodology
3. Results and Discussion
3.1. The Energetics and Stability of the Binary W-Cr and W-V Alloys
3.2. Mechanical Properties of the W-Cr and W-V Alloys
3.3. The Formation Energies of H and He in W
3.4. The Interaction of H-Cr, H-V, He-Cr, and He-V
3.5. The Competition between Vacancy and Cr or Vacancy and V Atoms
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, G.Y.; Juslin, N.; Wirth, B.D. First-principles study of vacancy, interstitial, noble gas atom interstitial and vacancy clusters in bcc-W. Comput. Mater. Sci. 2016, 123, 121–130. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Jin, S.; Lu, G.H.; Wang, L. High hydrogen retention in the sub-surfaces of tungsten plasma facing materials: A theoretical insight. Scr. Mater. 2016, 122, 14–17. [Google Scholar] [CrossRef]
- Roth, J.; Schmid, K. Hydrogen in tungsten as plasma-facing material. Phys. Scr. 2011, 2011, 1972–1978. [Google Scholar] [CrossRef] [Green Version]
- Rieth, M.; Boutard, J.L.; Dudarev, S.L.; Ahlgren, T.; Antusch, S.; Baluc, N.; Barthe, M.F.; Becquart, C.S.; Ciupinski, L.; Correia, J.B. Review on the EFDA programme on tungsten materials technology and science. J. Nucl. Mater. 2011, 417, 463–467. [Google Scholar] [CrossRef]
- Zhou, Z.; Ma, Y.; Du, J.; Linke, J. Fabrication and characterization of ultra-fine grained tungsten by resistance sintering under ultra-high pressure. Mater. Sci. Eng. A 2009, 505, 131–135. [Google Scholar] [CrossRef]
- Causey, R.; Wilson, K.; Venhaus, T.; Wampler, W.R. Tritium retention in tungsten exposed to intense fluxes of 100 eV tritons. J. Nucl. Mater. 1999, 266, 467–471. [Google Scholar] [CrossRef] [Green Version]
- Wurster, S.; Baluc, N.; Battabyal, M.; Crosby, T.; Du, J.; García-Rosales, C.; Hasegawa, A.; Hoffmann, A.; Kimura, A.; Kurishita, H. Recent progress in R and D on tungsten alloys for divertor structural and plasma facing materials. J. Nucl. Mater. 2013, 442, S181–S189. [Google Scholar] [CrossRef] [Green Version]
- Margevicius, R.W.; Riedle, J.; Gumbsch, P. Fracture toughness of polycrystalline tungsten under mode I and mixed mode I/II loading. Mater. Sci. Eng. A 1999, 270, 197–209. [Google Scholar] [CrossRef]
- Gumbsch, P. Brittle fracture and the brittle-to-ductile transition of tungsten. J. Nucl. Mater. 2003, 323, 304–312. [Google Scholar] [CrossRef]
- Ma, Y.; Han, Q.F.; Zhou, Z.Y.; Liu, Y.L. First-principles investigation on mechanical behaviors of W-Cr/Ti binary alloys. J. Nucl. Mater. 2016, 468, 105–112. [Google Scholar] [CrossRef]
- Arshad, K.; Guo, W.; Wang, J.; Zhao, M.Y.; Yuan, Y.; Zhang, Y.; Wang, B.; Zhou, Z.J.; Lu, G.H. Influence of vanadium precursor powder size on microstructures and properties of W–V alloy. Int. J. Refract. Met. Hard Mater. 2015, 50, 59–64. [Google Scholar] [CrossRef]
- Liu, X.; Lian, Y.; Chen, L.; Chen, Z.; Chen, J.; Duan, X.; Fan, J.; Song, J. Experimental and numerical simulations of ELM-like transient damage behaviors to different grade tungsten and tungsten alloys. J. Nucl. Mater. 2014, 463, 166–169. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, B.; Fu, B.Q.; Greuner, H.; Böswirth, B.; Xu, H.Y.; Li, C.; Jia, Y.Z.; Qu, S.L.; Luo, G.N. Suppression of cavitation in melted tungsten by doping with lanthanum oxide. Nucl. Fusion 2014, 54, 083026. [Google Scholar] [CrossRef]
- Gilbert, M.R.; Sublet, J.C. Neutron-induced transmutation effects in W and W-alloys in a fusion environment. Nucl. Fusion 2011, 51, 43005–43017. [Google Scholar] [CrossRef] [Green Version]
- Muzyk, M.; Nguyenmanh, D.; Kurzydłowski, K.J.; Baluc, N.L.; Dudarev, S.L. Phase stability, point defects, and elastic properties of W-V and W-Ta alloys. Phys. Rev. B 2011, 84, 4115. [Google Scholar] [CrossRef] [Green Version]
- Nguyen Manh, D.; Muzyk, M.; Kurzydlowski, K.J.; Baluc, N.L.; Rieth, M.; Dudarev, S.L. First-Principles Modeling of Tungsten-Based Alloys for Fusion Power Plant Applications. Key Eng. Mater. 2011, 465, 15–20. [Google Scholar] [CrossRef]
- Xu, H.; He, L.L.; Pei, Y.F.; Jiang, C.Z.; Li, W.Q.; Xiao, X.H. Recent progress of radiation response in nanostructured tungsten for nuclear application. Tungsten 2021, 3, 20–37. [Google Scholar] [CrossRef]
- Golubeva, A.; Mayer, M.; Roth, J.; Kurnaev, V.; Ogorodnikova, O. Deuterium retention in rhenium-doped tungsten. J. Nucl. Mater. 2007, 363, 893–897. [Google Scholar] [CrossRef] [Green Version]
- Tyburska Pschel, B.; Alimov, V.K. On the reduction of deuterium retention in damaged Re-doped W. Nucl. Fusion 2013, 53, 8–10. [Google Scholar] [CrossRef]
- Alimov, V.K.; Hatano, Y.; Sugiyama, K.; Balden, M.; Oyaidzu, M.; Akamaru, S.; Tada, K.; Kurishita, H.; Hayashi, T.; Matsuyama, M. Surface morphology and deuterium retention in tungsten and tungsten–rhenium alloy exposed to low-energy, high flux D plasma. J. Nucl. Mater. 2014, 454, 136–141. [Google Scholar] [CrossRef]
- Schmid, K.; Rieger, V.; Manhard, A. Comparison of hydrogen retention in W and W/Ta alloys. J. Nucl. Mater. 2012, 426, 247–253. [Google Scholar] [CrossRef] [Green Version]
- Zayachuk, Y.; Hoen, M.H.J.T.; Emmichoven, Z.P.A.; Uytdenhouwen, I.; Oost, G.V. Deuterium retention in tungsten and tungsten–tantalum alloys exposed to high-flux deuterium plasmas. Nucl. Fusion 2012, 52, 1299–1304. [Google Scholar] [CrossRef] [Green Version]
- Zayachuk, Y.; Hoen, M.H.J.T.; Emmichoven, P.A.Z.V.; Terentyev, D.; Uytdenhouwen, I.; Van Oost, G. Surface modification of tungsten and tungsten—Tantalum alloys exposed to high-flux deuterium plasma and its impact on deuterium retention. Nucl. Fusion 2013, 53, 13013–13019. [Google Scholar] [CrossRef] [Green Version]
- Zayachuk, Y.; Manhard, A.; t Hoen, M.H.J.; Jacob, W.; van Emmichoven, P.A.; Van Oost, G. Depth profiling of the modification induced by high-flux deuterium plasma in tungsten and tungsten-tantalum alloys. Nucl. Fusion 2014, 54, 25–36. [Google Scholar] [CrossRef] [Green Version]
- Grigorev, P.; Zinovev, A.; Terentyev, D.; Bonny, G.; Zhurkin, E.E.; Van Oost, G.; Noterdaeme, J.M. Molecular dynamics simulation of hydrogen and helium trapping in tungsten. J. Nucl. Mater. 2018, 508, 451–458. [Google Scholar] [CrossRef] [Green Version]
- Qiu, M.; Zhai, L.; Cui, J.; Fu, B.; Li, M.; Hou, Q. Diffusion behavior of hydrogen isotopes in tungsten revisited by molecular dynamics simulations. Chin. Phys. B 2018, 27, 073103. [Google Scholar] [CrossRef]
- Wei, G.; Ren, F.; Fang, J.; Hu, W.; Gao, F.; Qin, W.; Cheng, T.; Wang, Y.; Jiang, C.; Deng, H. Understanding the release of helium atoms from nanochannel tungsten: A molecular dynamics simulation. Nucl. Fusion 2019, 59, 076020. [Google Scholar] [CrossRef]
- Fu, B.; Qiu, M.; Cui, J.; Li, M.; Hou, Q. The trapping and dissociation process of hydrogen in tungsten vacancy: A molecular dynamics study. J. Nucl. Mater. 2018, 508, 278–285. [Google Scholar] [CrossRef]
- Granberg, F.; Byggmästar, J.; Nordlund, K. Molecular dynamics simulations of high-dose damage production and defect evolution in tungsten. J. Nucl. Mater. 2021, 556, 153158. [Google Scholar] [CrossRef]
- Jun, W.; BaoLing, Z.; YuLu, Z.; Qing, H. Molecular dynamics simulation of helium behavior in tungsten matrix. Acta Phys. Sin. 2011, 60, 524–529. [Google Scholar]
- Li, X.C.; Liu, Y.N.; Yu, Y.; Luo, G.N.; Shu, X.; Lu, G.H. Helium defects interactions and mechanism of helium bubble growth in tungsten: A molecular dynamics simulation. J. Nucl. Mater. 2014, 451, 356–360. [Google Scholar] [CrossRef]
- Li, X.C.; Shu, X.; Tao, P.; Yu, Y.; Niu, G.J.; Xu, Y.; Gao, F.; Luo, G.N. Molecular dynamics simulation of helium cluster diffusion and bubble formation in bulk tungsten. J. Nucl. Mater. 2014, 455, 544–548. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Xu, Q.; Hong, R.; Li, Q.; Luo, G.N. Molecular dynamics simulation of low-energy atomic hydrogen on tungsten surface. Fusion Eng. Des. 2010, 85, 1517–1520. [Google Scholar] [CrossRef]
- Fu, B.Q.; Lai, W.S.; Yuan, Y.; Xu, H.Y.; Liu, W. Study of interaction between low energetic hydrogen and tungsten surface by molecular dynamics simulations. Nucl. Instrum. Methods Phys. Res. Sect. B 2013, 303, 162–164. [Google Scholar] [CrossRef]
- Li, M.; Cui, J.; Wang, J.; Hou, Q. Molecular dynamics simulations of cumulative helium bombardments on tungsten surfaces. Nucl. Instrum. Methods Phys. Res. Sect. B 2013, 337, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.N.; Yu, Y.; Shu, X.; Lu, G.H. Molecular dynamics simulations of hydrogen diffusion behaviour at tungsten surface. Mater. Res. Innov. 2014, 18, S4-1040–S4-1044. [Google Scholar] [CrossRef]
- Yu, X.; Gou, F. Molecular Dynamics Study on the Diffusion Properties of Hydrogen Atoms in Bulk Tungsten. Plasma Sci. Technol. 2013, 15, 710–715. [Google Scholar] [CrossRef]
- Ding, Y.; Ma, C.; Li, M.; Hou, Q. Molecular dynamics study on the interactions between helium projectiles and helium bubbles pre-existing in tungsten surfaces. Nucl. Instrum. Methods Phys. Res. Sect. B 2016, 368, 50–59. [Google Scholar] [CrossRef]
- Cui, J.; Li, M.; Wang, J.; Hou, Q. Molecular dynamics study of helium bubble pressure in tungsten. Nucl. Instrum. Methods Phys. Res. Sect. B 2014, 352, 104–106. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, Z.; Huang, M.; Zhang, X.; Ouyang, X. Effects of H and He on the clustering behavior of transmutation elements in tungsten. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms. 2020, 470, 48–55. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, Z.; Huang, M.; Ouyang, X. Effects of transmutation elements in tungsten. Comput. Mater. Sci. 2019, 162, 133–139. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Zhang, Z.; Li, Y.; Ouyang, X. First-principles study on various point defects formed by hydrogen and helium atoms in tungsten. Sci. Technol. Nucl. Install. 2017, 2017, 6547939. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Zhao, J. First-principles study of hydrogen in perfect tungsten crystal. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 3170–3174. [Google Scholar] [CrossRef]
- Lee, S.C.; Choi, J.H.; Lee, J.G. Energetics of He and H atoms with vacancies in tungsten: First-principles approach. J. Nucl. Mater. 2009, 383, 244–246. [Google Scholar] [CrossRef]
- Liu, Y.L.; Zhang, Y.; Luo, G.N.; Lu, G.H. Structure, stability and diffusion of hydrogen in tungsten: A first-principles study. J. Nucl. Mater. 2009, 390–391, 1032–1034. [Google Scholar] [CrossRef]
- Hu, Y.J.; Shang, S.L.; Wang, Y.; Darling, K.A.; Butler, B.G.; Kecskes, L.J.; Liu, Z.K. Effects of alloying elements and temperature on the elastic properties of W-based alloys by first-principles calculations. J. Alloys Compd. 2016, 671, 267–275. [Google Scholar] [CrossRef] [Green Version]
- Kong, X.S.; Wu, X.; Liu, C.S.; Fang, Q.F.; Hu, Q.M.; Chen, J.L.; Luo, G.N. First-principles calculations of transition metal solute interactions with hydrogen in tungsten. Nucl. Fusion 2016, 56, 026004. [Google Scholar] [CrossRef]
- Ma, Y.T.; Zhang, Y.; Lu, G.H.; Zhu, K.; Zhao, Z.; Cheng, L.; Wang, B.; Long, Z.; Chen, C.; Luo, G.N. The effect of cerium doping on helium implantation behavior in tungsten. Nucl. Instrum. Methods Phys. Res. Sect. B 2013, 307, 55–59. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, K.; Zhao, Q.; Huang, M.; Ouyang, X. Effects of noble metal doping on hydrogen sensing performances of monolayer MoS2. Mater. Res. Express 2019, 7, 015501. [Google Scholar] [CrossRef]
- Yi, Y.U.; Shu, X.L.; Liu, Y.N.; Niu, L.L.; Jin, S.; Fei, G.; Guanghong, L.U. Effect of hydrogen on grain boundary migration in tungsten. Sci. China Phys. Mech. 2015, 58, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.B.; Liu, Y.L.; Jin, S.; Zhang, Y.; Luo, G.N.; Lu, G.H. Investigating behaviours of hydrogen in a tungsten grain boundary by first principles: From dissolution and diffusion to a trapping mechanism. Nucl. Fusion 2010, 50, 275–282. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef] [Green Version]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krestallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Yue, W. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Chevary, J.; Vosko, S.; Jackson, K.A.; Pederson, M.R.; Singh, D.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Iikura, H.; Tsuneda, T.; Yanai, T.; Hirao, K. A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 2001, 115, 3540–3544. [Google Scholar] [CrossRef]
- Ortmann, F.; Bechstedt, F.; Schmidt, W. Semiempirical van der Waals correction to the density functional description of solids and molecular structures. Phys. Rev. B 2006, 73, 205101. [Google Scholar] [CrossRef] [Green Version]
- Söderlind, P.; Eriksson, O.; Wills, J.; Boring, A. Theory of elastic constants of cubic transition metals and alloys. Phys. Rev. B 1993, 48, 5844. [Google Scholar] [CrossRef]
- Becquart, C.; Domain, C. Ab initio calculations about intrinsic point defects and He in W. Nucl. Instrum. Methods Phys. Res. Sect. B 2007, 255, 23–26. [Google Scholar] [CrossRef]
- Ren, C.; Fang, Z.Z.; Koopman, M.; Butler, B.; Paramore, J.; Middlemas, S. Methods for improving ductility of tungsten-a review. Int. J. Refract. Met. Hard Mater. 2018, 75, 170–183. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Skinner, C.H.; Haasz, A.A.; Almov, V.K.H.; Bekris, N.; Causey, R.A.; Clark, R.E.H.; Coad, J.P.; Davis, J.W.; Doerner, R.P.; Mayer, M. Recent advances on hydrogen retention in iter’s plasma-facing materials: Beryllium, carbon. And tungsten. Fusion Sci. Technol. 2008, 54, 891–945. [Google Scholar] [CrossRef]
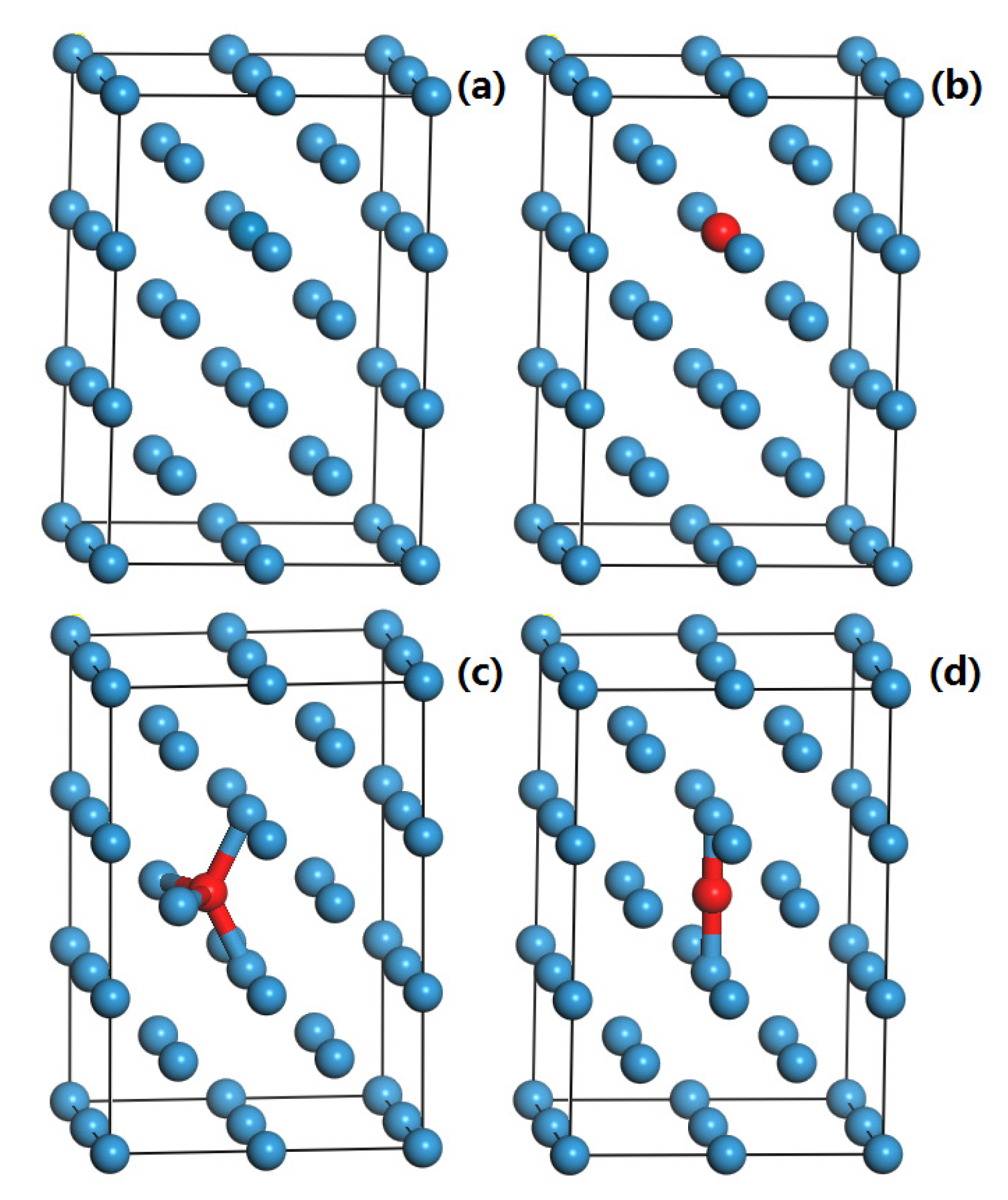
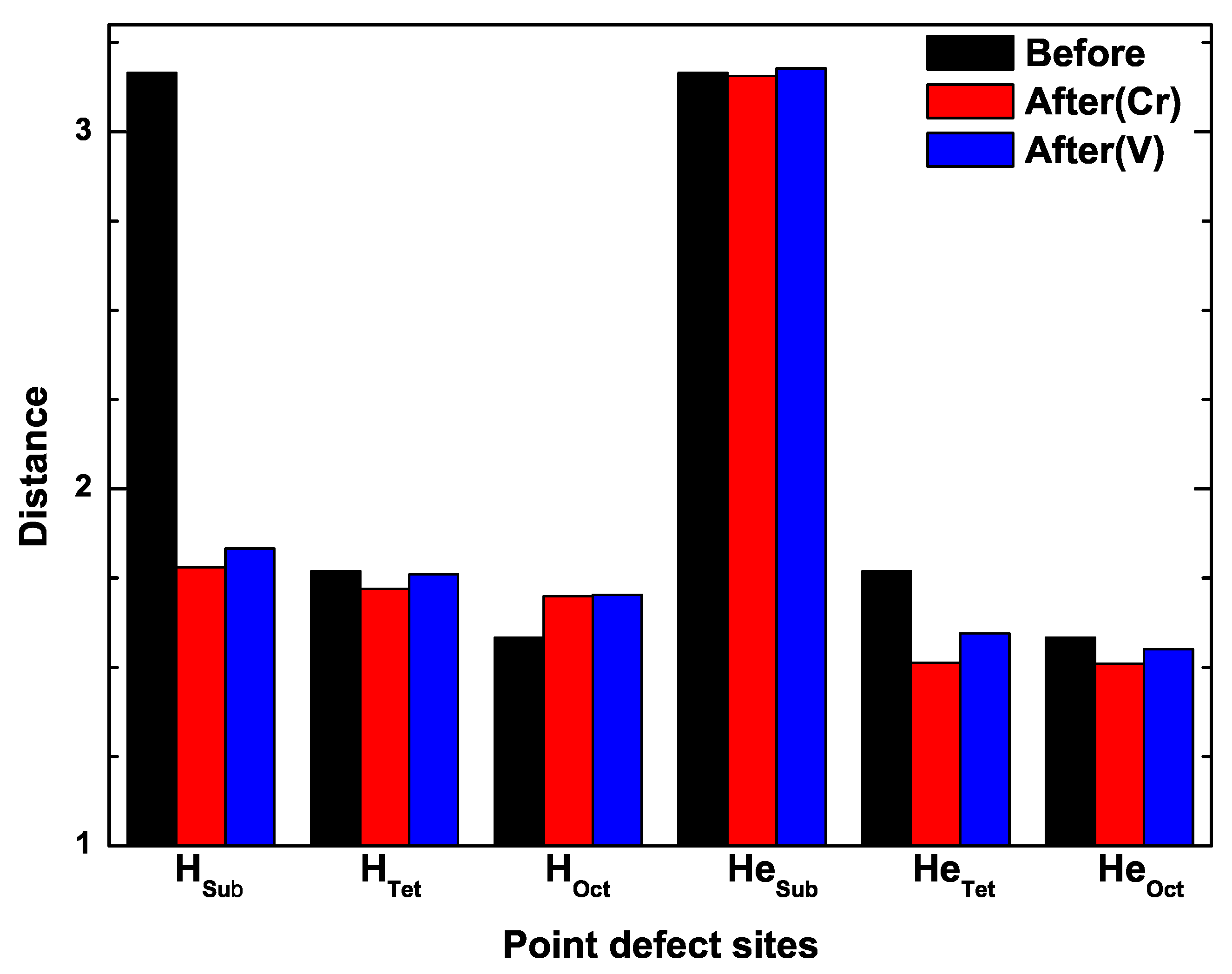
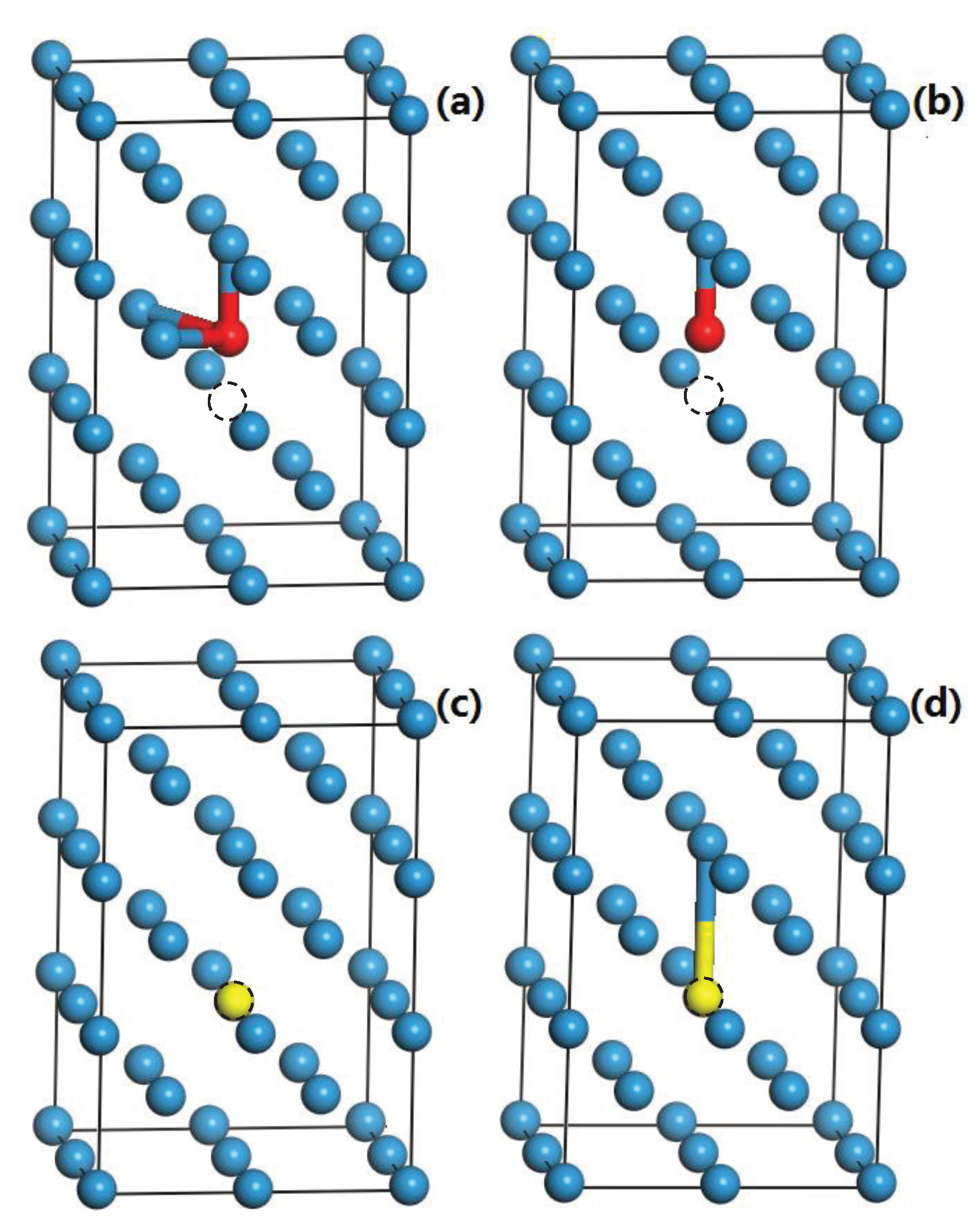
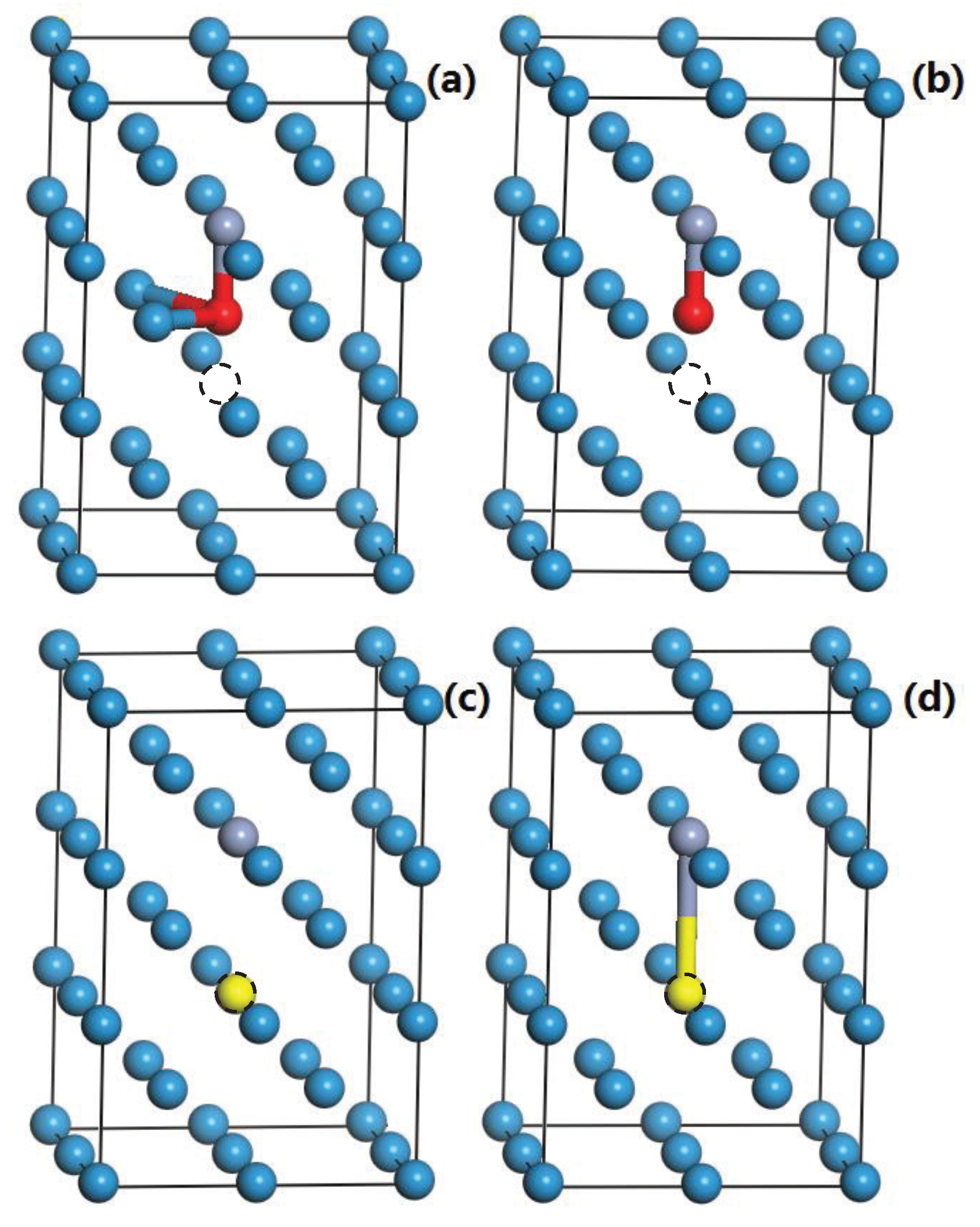
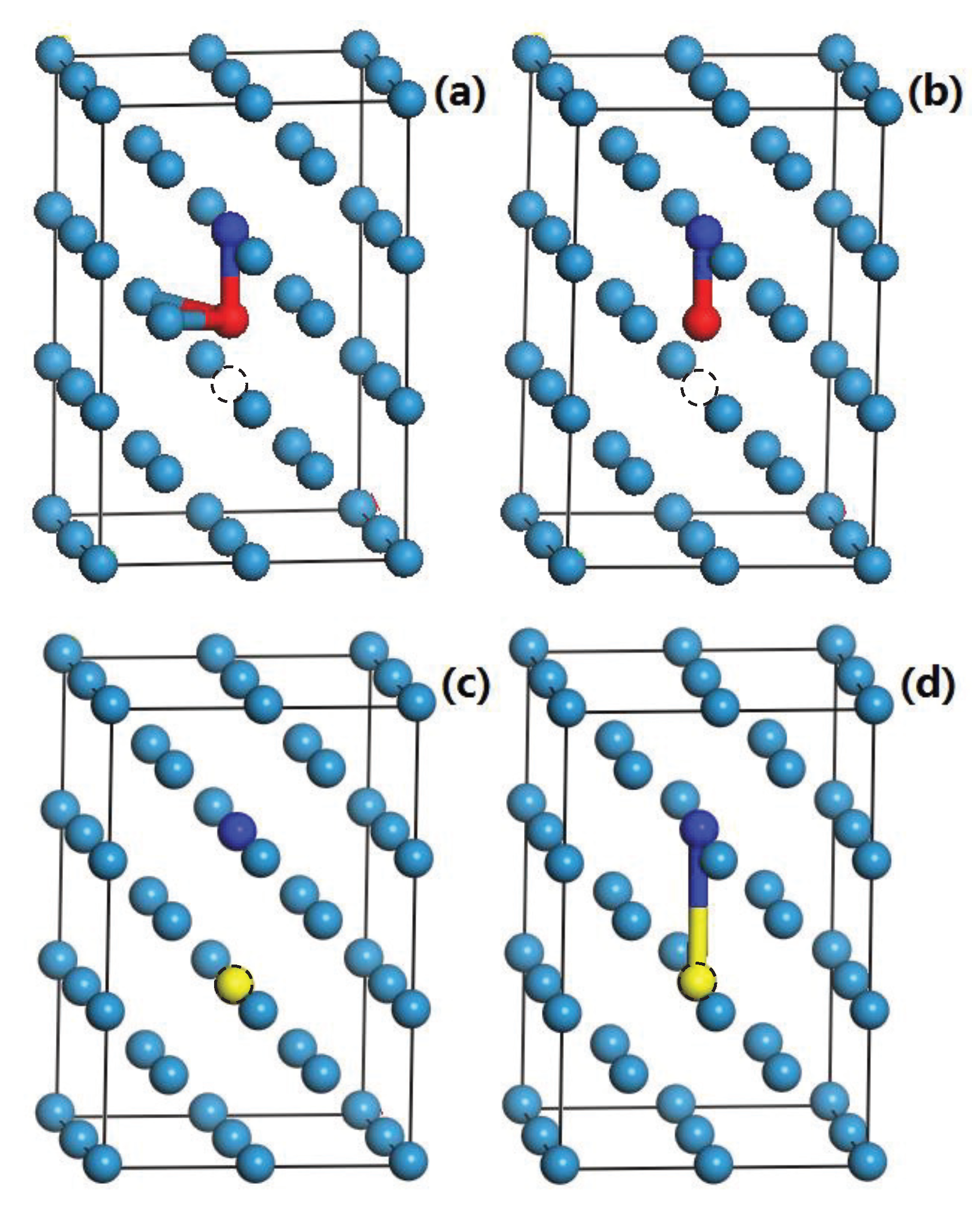
| Crystal | ||
|---|---|---|
| W | 0 | |
| W-Cr | 3.683 | |
| W-V |
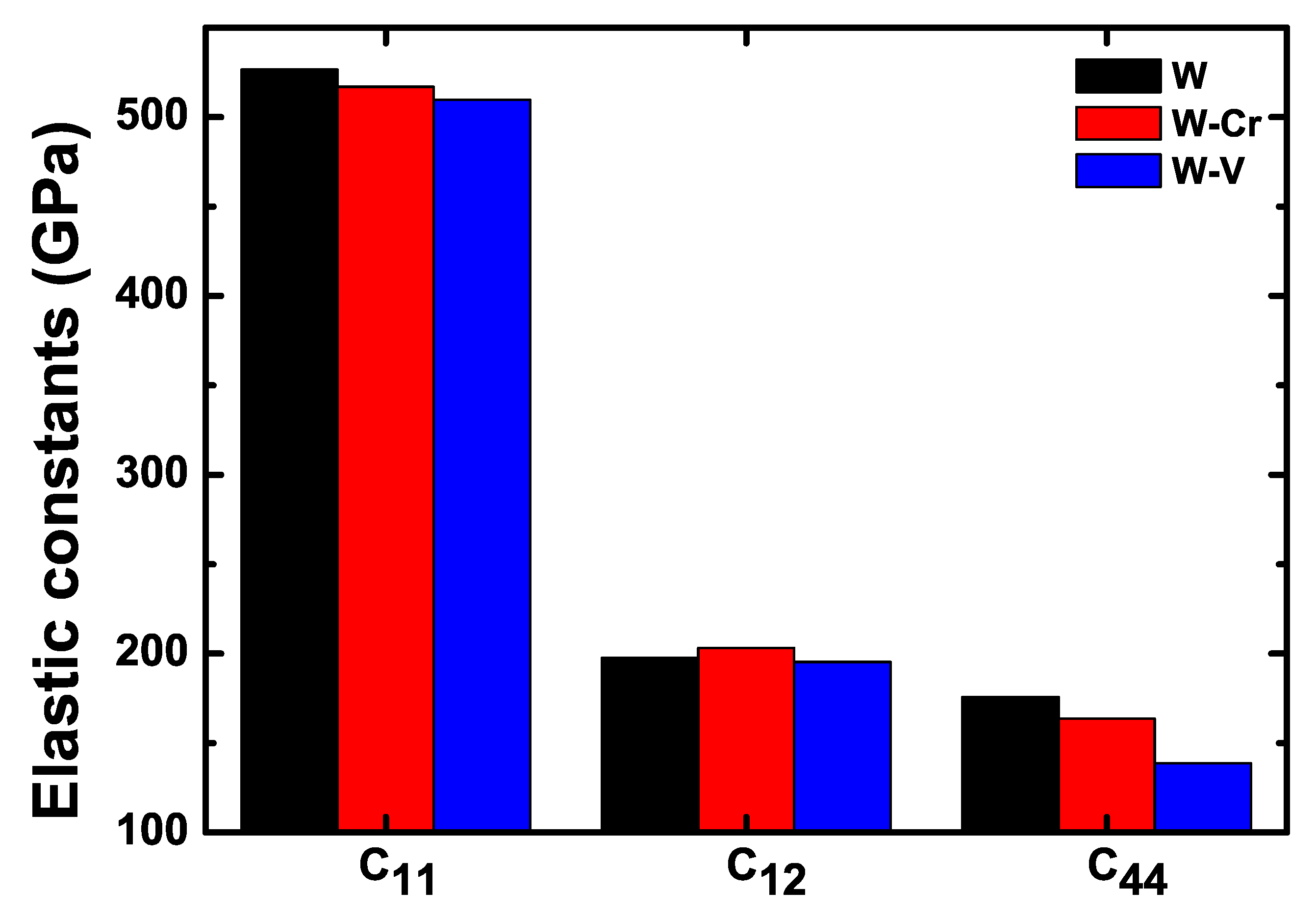
| Parameters | a | |||
|---|---|---|---|---|
| W | 3.15 (0.3%) | 526.48 (1.2%) | 197.60 (3.6%) | 175.80 (7.8%) |
| Cal [61] | 3.17 (0.3%) | 536.32 (0.6%) | 202.25 (1.3%) | 138.70 (14.9%) |
| Exp [60] | 3.16 | 533 | 205 | 163 |
| W-Cr | 3.17 | 516.92 | 203.25 | 153.68 |
| W-V | 3.17 | 509.75 | 195.39 | 138.62 |
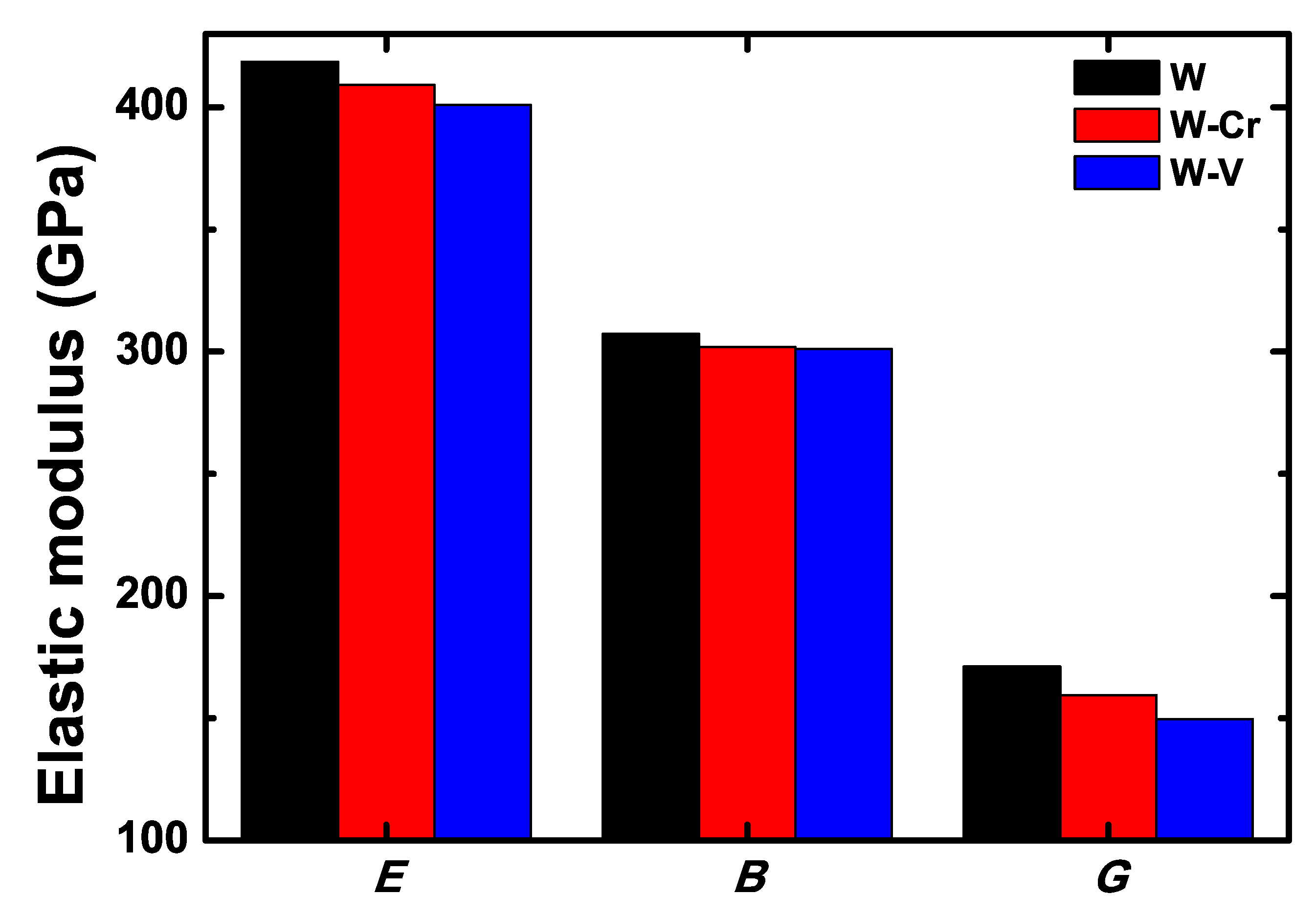
| Parameters | B | E | G | ||
|---|---|---|---|---|---|
| W | 307.23 (2.2%) | 418.63 (0.2%) | 171.16 (4.7%) | 0.27 (3.6%) | 0.56 (3.6%) |
| Cal [61] | 313.61 (0.2%) | 386.83 (7.4%) | 149.42 (8.5%) | 0.29 (3.6%) | 0.48 (12.5%) |
| Exp [60] | 314.33 | 417.80 | 163.40 | 0.28 | 0.54 |
| W-Cr | 301.86 | 409.11 | 159.44 | 0.27 | 0.53 |
| W-V | 301.05 | 400.89 | 149.69 | 0.28 | 0.50 |
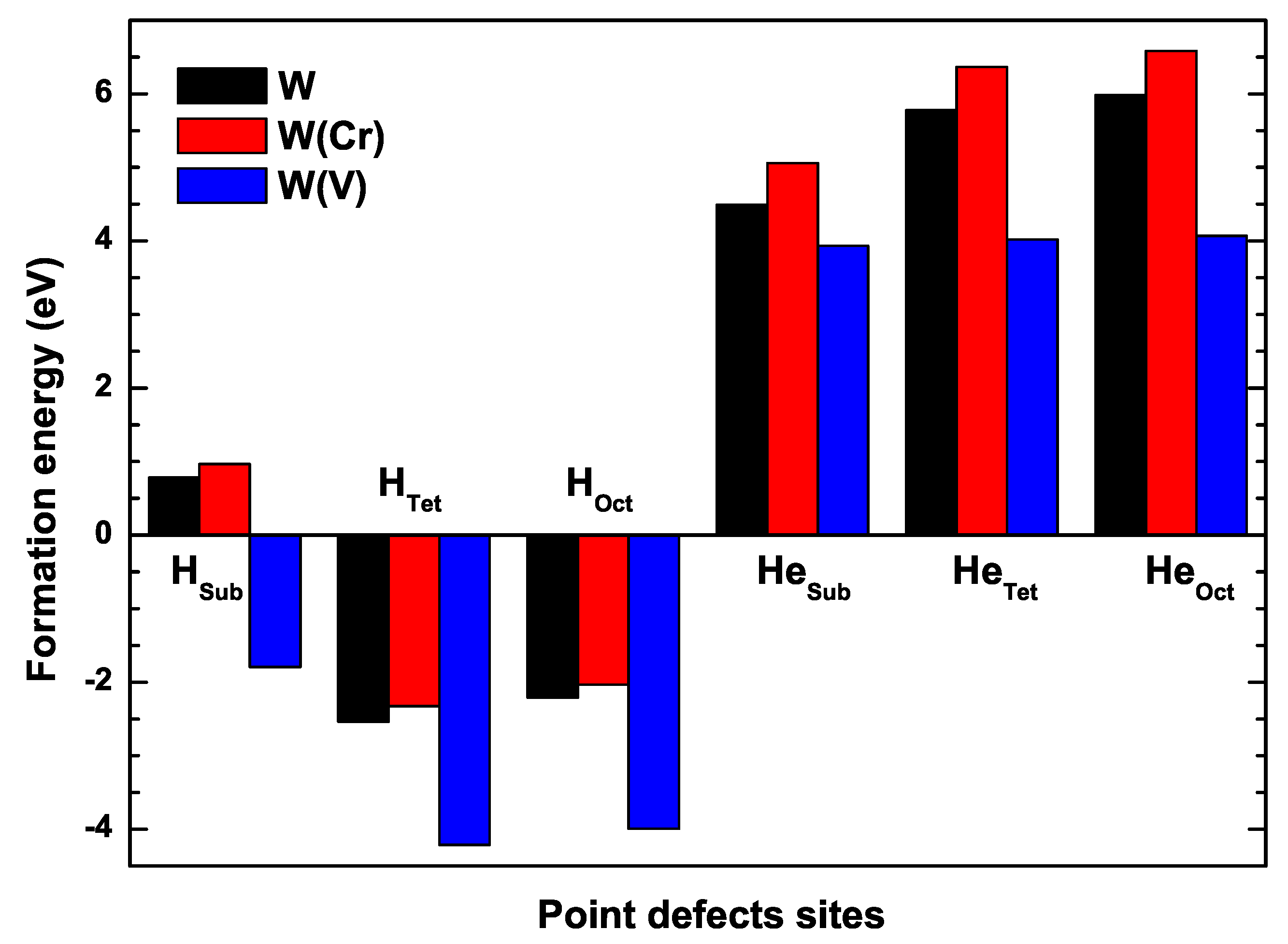
| Configuration | H | H | H | He | He | He |
|---|---|---|---|---|---|---|
| This paper | 0.782 | 4.49 | 5.775 | 5.984 | ||
| Cal [44] | 0.92 (16.2%) | (2.6%) | (6.6%) | 5.00 (10.8%) | 6.23 (7.6%) | 6.48 (8.0%) |
| Cal [61,64] | 0.78 (0.3%) | (3.9%) | (7.1%) | 4.70 (4.6%) | 6.16 (6.5%) | 6.38 (6.4%) |
| Configuration | H | H | H | He | He | He |
| 0.965 | 5.059 | 6.365 | 6.583 | |||
| Configuration | H | H | H | He | He | He |
| 3.93 | 4.02 | 4.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhang, Z.; Li, Y.; Zhao, Q.; Huang, M.; Ouyang, X. Effect of Chrome and Vanadium on the Behavior of Hydrogen and Helium in Tungsten. Math. Comput. Appl. 2023, 28, 81. https://doi.org/10.3390/mca28040081
Li M, Zhang Z, Li Y, Zhao Q, Huang M, Ouyang X. Effect of Chrome and Vanadium on the Behavior of Hydrogen and Helium in Tungsten. Mathematical and Computational Applications. 2023; 28(4):81. https://doi.org/10.3390/mca28040081
Chicago/Turabian StyleLi, Meicong, Zheng Zhang, Yangyang Li, Qiang Zhao, Mei Huang, and Xiaoping Ouyang. 2023. "Effect of Chrome and Vanadium on the Behavior of Hydrogen and Helium in Tungsten" Mathematical and Computational Applications 28, no. 4: 81. https://doi.org/10.3390/mca28040081
APA StyleLi, M., Zhang, Z., Li, Y., Zhao, Q., Huang, M., & Ouyang, X. (2023). Effect of Chrome and Vanadium on the Behavior of Hydrogen and Helium in Tungsten. Mathematical and Computational Applications, 28(4), 81. https://doi.org/10.3390/mca28040081







