Data-Driven Active Learning Control for Bridge Cranes
Abstract
:1. Introduction
2. Problem Formulation
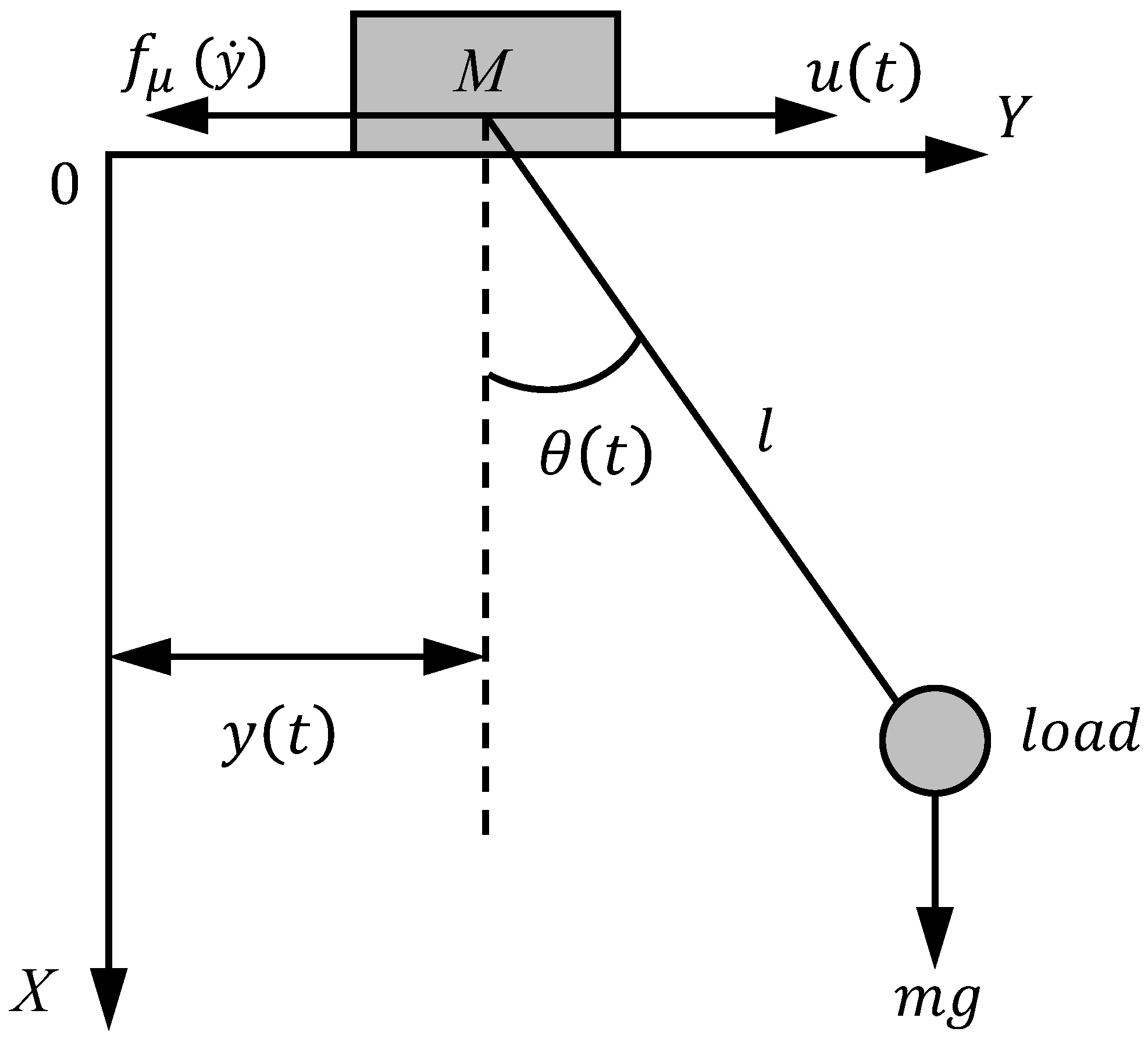
2.1. Bridge Crane Dynamics
2.2. Koopman Operator Theory
3. Control
3.1. Objective Function Design
3.2. Linear Quadratic Optimal Tracking
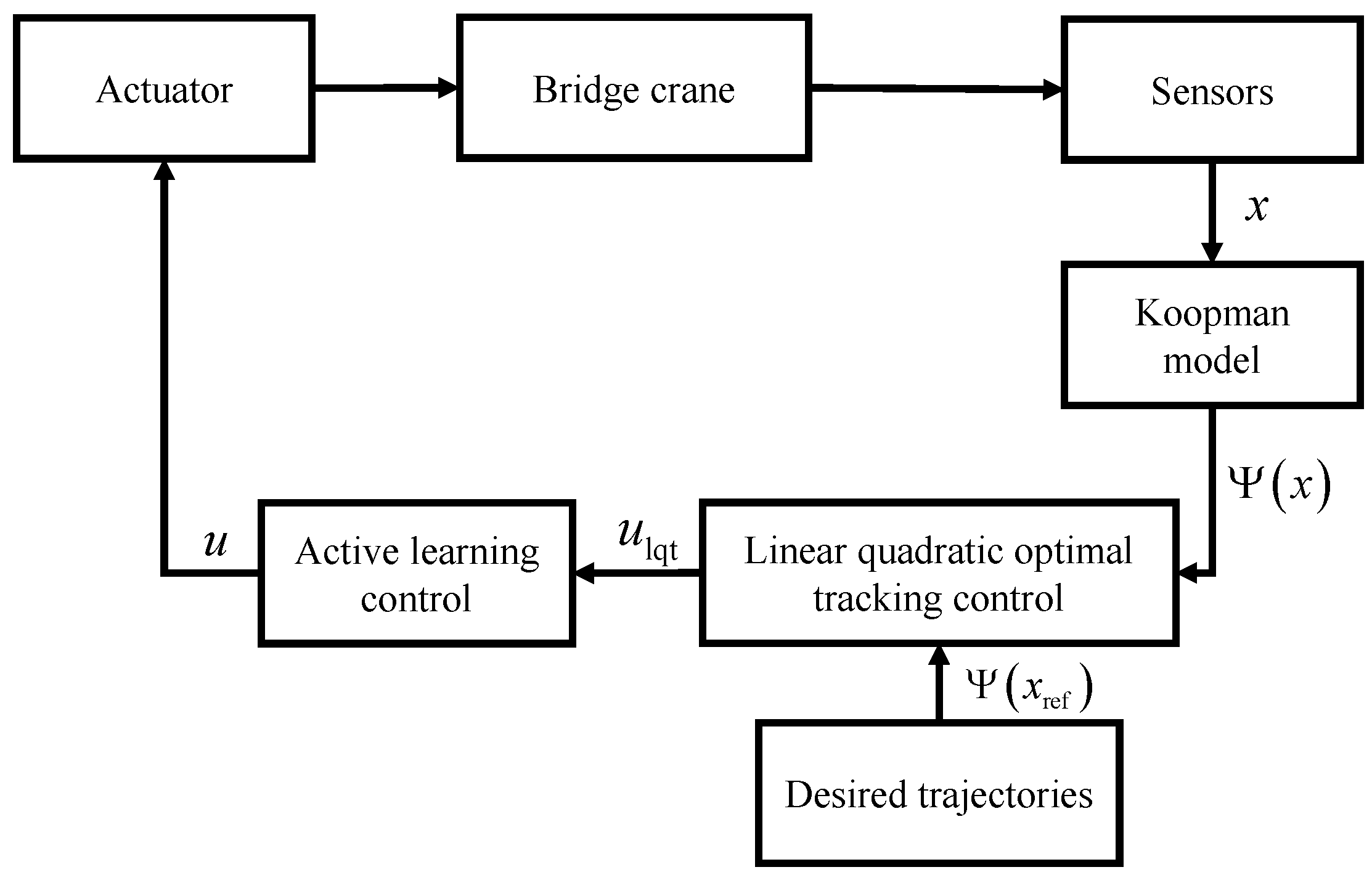
3.3. Active Learning Controller
- Step 1.
- Define a set of observable functions; given an initial approximate continuous-time operator, construct the Koopman model.
- Step 2.
- Pre-set the desired trajectory and lift it using the observable function.
- Step 3.
- Design the linear quadratic optimal tracking controller based on the Koopman model and the desired trajectory.
- Step 4.
- Consider both the learning and running costs, design an active learning controller based on the linear quadratic optimal tracking controller.
- Step 5.
- Apply the active learning controller to the bridge crane at the current time and obtain the output after the control is applied.
- Step 6.
- Update the approximate continuous-time operator using the online input and output data.
- Step 7.
- Reconstruct the Koopman model using the updated continuous-time operator and repeat Steps 3–7.
4. Simulation
4.1. Performance Evaluation for Active Learning Controller without Training in Advance
4.2. Comparative Study
4.2.1. CSMC Controller
4.2.2. PID Controller
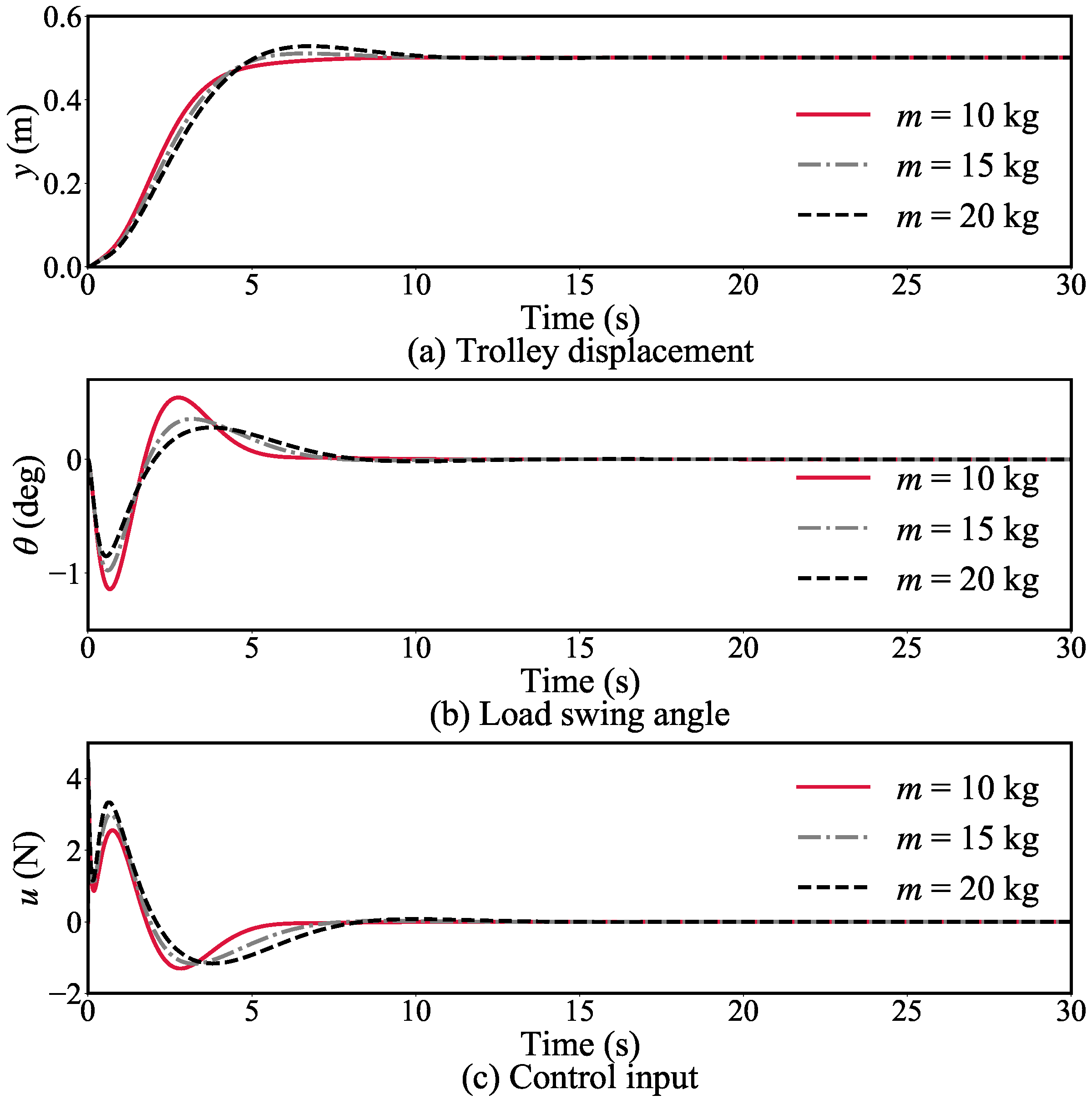
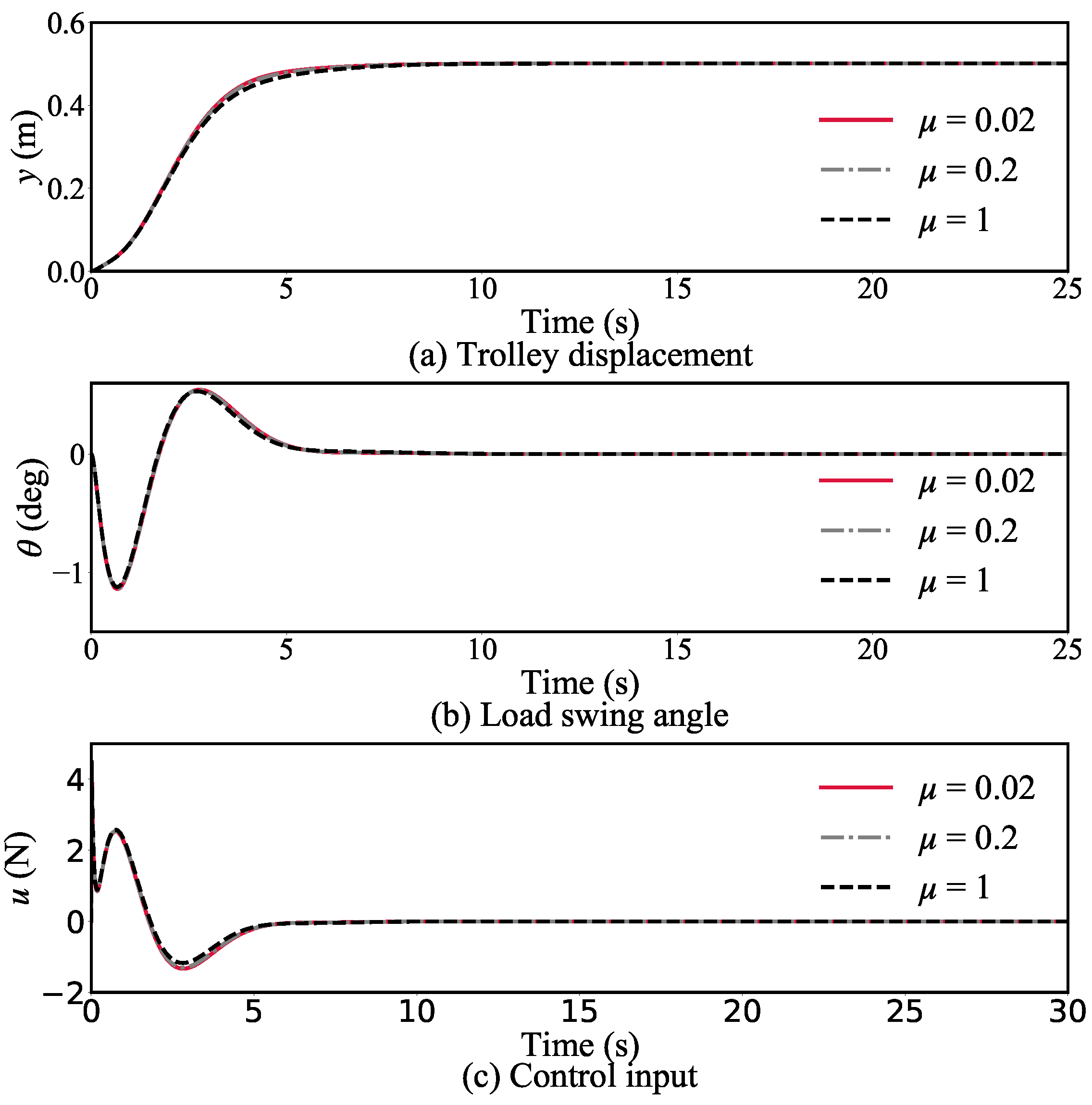
4.3. Robustness Study
4.3.1. Simulation Group 1
4.3.2. Simulation Group 2
4.3.3. Simulation Group 3
4.4. Performance with Dead Zone
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, T.L.; Tan, N.L.; Zhang, X.; Li, G.; Su, S.; Zhou, J.; Qiu, J.; Wu, Z.; Zhai, Y.; Donida, L.R.; et al. A Time-Varying Sliding Mode Control Method for Distributed-Mass Double Pendulum Bridge Crane With Variable Parameters. IEEE Access 2021, 9, 75981–75992. [Google Scholar] [CrossRef]
- Tysse, G.O.; Cibicik, A.; Tingelstad, L.; Egeland, O. Lyapunov-based damping controller with nonlinear MPC control of payload position for a knuckle boom crane. Automatica 2022, 140, 110219. [Google Scholar] [CrossRef]
- Roman, R.C.; Precup, R.E.; Petriu, E.M. Hybrid data-driven fuzzy active disturbance rejection control for tower crane systems. Eur. J. Control 2021, 58, 373–387. [Google Scholar] [CrossRef]
- Rigatos, G.; Siano, P.; Abbaszadeh, M. Nonlinear H-infinity control for 4-DOF underactuated overhead cranes. Trans. Inst. Meas. Control 2018, 40, 2364–2377. [Google Scholar] [CrossRef]
- Hou, Z.S.; Bu, X.H. Model free adaptive control with data dropouts. Expert Syst. Appl. 2011, 38, 10709–10717. [Google Scholar] [CrossRef]
- Furqan, M.; Cheng, S. Data-driven optimal PID type ILC for a class of nonlinear batch process. Int. J. Syst. Sci. 2021, 52, 263–276. [Google Scholar] [CrossRef]
- Chi, R.H.; Li, H.Y.; Shen, D.; Hou, Z.S.; Huang, B. Enhanced P-Type Control: Indirect Adaptive Learning From Set-Point Updates. IEEE Trans. Autom. Control 2023, 68, 1600–1613. [Google Scholar] [CrossRef]
- Estakhrouiyeh, M.R.; Gharaveisi, A.; Vali, M. Fractional order Proportional-Integral-Derivative Controller parameter selection based on iterative feedback tuning. Case study: Ball Levitation system. Trans. Inst. Meas. Control 2018, 40, 1776–1787. [Google Scholar] [CrossRef]
- Yuan, Y.; Tang, L.X. Novel time-space network flow formulation and approximate dynamic programming approach for the crane scheduling in a coil warehouse. Eur. J. Oper. Res. 2017, 262, 424–437. [Google Scholar] [CrossRef]
- Williams, M.O.; Hemati, M.S.; Dawson, S.T.M.; Kevrekidis, I.G.; Rowley, C.W. Extending Data-Driven Koopman Analysis to Actuated Systems. IFAC-PapersOnLine 2016, 49, 704–709. [Google Scholar] [CrossRef]
- Proctor, J.L.; Brunton, S.L.; Kutz, J.N. Generalizing Koopman Theory to Allow for Inputs and Control. SIAM J. Appl. Dyn. Syst. 2018, 17, 909–930. [Google Scholar] [CrossRef] [PubMed]
- Maksakov, A.; Golovin, I.; Shysh, M.; Palis, S. Data-driven modeling for damping and positioning control of gantry crane. Mech. Syst. Signal. Pract. 2023, 197, 110368. [Google Scholar] [CrossRef]
- Brunton, S.L.; Brunton, B.W.; Proctor, J.L.; Kutz, J.N. Koopman Invariant Subspaces and Finite Linear Representations of Nonlinear Dynamical Systems for Control. PLoS ONE 2016, 2, e0150171. [Google Scholar] [CrossRef] [PubMed]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data–driven approximation of the Koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Kaiser, E.; Kutz, J.N.; Brunton, S.L. Data-driven discovery of Koopman eigenfunctions for control. Mach. Learn. Sci. Technol. 2021, 2, 035023. [Google Scholar] [CrossRef]
- Maksakov, A.; Golovin, I.; Palis, S. Koopman–based data-driven control for large gantry cranes. In Proceedings of the 2022 IEEE 3rd KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 3–7 October 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Baranes, A.; Oudeyer, P.Y. Active learning of inverse models with intrinsically motivated goal exploration in robots. Robot. Auton. Syst. 2013, 61, 49–73. [Google Scholar] [CrossRef]
- Kober, J.; Bagnell, J.A.; Peter, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Abraham, I.; Murphey, T.D. Active Learning of Dynamics for Data-Driven Control Using Koopman Operators. IEEE Trans. Robot. 2019, 35, 1071–1083. [Google Scholar] [CrossRef]
- Wilson, A.D.; Schultz, J.A.; Ansari, A.R.; Murphey, T.D. Dynamic task execution using active parameter identification with the Baxter research robot. IEEE Trans. Autom. Sci. Eng. 2017, 14, 391–397. [Google Scholar] [CrossRef]
- Wilson, A.D.; Schultz, J.A.; Murphey, T.D. Trajectory synthesis for Fisher information maximization. IEEE Trans. Robot. 2014, 30, 1358–1370. [Google Scholar] [CrossRef] [PubMed]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Tim, H.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning (PMLR), New York, NY, USA, 20–22 June 2016; pp. 1928–1937. [Google Scholar]
- Cutler, M.; Walsh, T.J.; How, J.P. Real–World Reinforcement Learning via Multifidelity Simulators. IEEE Trans. Robot. 2015, 31, 655–671. [Google Scholar] [CrossRef]
- Ding, F.; Wang, X.H.; Chen, Q.J.; Xiao, Y. Recursive Least Squares Parameter Estimation for a Class of Output Nonlinear Systems Based on the Model Decomposition. Circuits Syst. Signal Process. 2016, 35, 3323–3338. [Google Scholar] [CrossRef]
- Williams, G.; Wagener, N.; Goldfain, B.; Drews, P.; Rehg, J.M.; Boots, B.; Theodorou, E.A. Information theoretic MPC for model-based reinforcement learning. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1714–1721. [Google Scholar] [CrossRef]
- Bonnet, V.; Fraisse, P.; Crosnier, A.; Gautier, M.; González, A.; Venture, G. Optimal exciting dance for identifying inertial parameters of an anthropomorphic structure. IEEE Trans. Robot. 2016, 32, 823–836. [Google Scholar] [CrossRef]
- Jovic, J.; Escande, A.; Ayusawa, K.; Yoshida, E.; Kheddar, A.; Venture, G. Humanoid and human inertia parameter identification using hierarchical optimization. IEEE Trans. Robot. 2016, 32, 726–735. [Google Scholar] [CrossRef]
- Korda, M.; Mezić, I. Linear predictors for nonlinear dynamical systems: Koopman operator meets model predictive control. Automatica 2018, 93, 149–160. [Google Scholar] [CrossRef]
- Arbabi, H.; Korda, M.; Mezić, I. A Data-Driven Koopman Model Predictive Control Framework for Nonlinear Partial Differential Equations. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 7–19 December 2018; pp. 6409–6414. [Google Scholar] [CrossRef]
- Antsaklis, P.J.; Michel, A.N. A Linear System; Springer: New York, NY, USA, 2006. [Google Scholar]
- Pukelsheim, F. Optimal Design of Experiments; SIAM: Philadelphia, PA, USA, 2006. [Google Scholar]
- Nahi, N.E.; Napjus, G.A. Design of optimal probing signals for vector parameter estimation. In Proceedings of the 1971 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 15–17 December 1971; pp. 162–168. [Google Scholar] [CrossRef]
- Egerstedt, M.; Wardi, Y.; Delmotte, F. Optimal control of switching times in switched dynamical systems. In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No.03CH37475), Maui, HI, USA, 9–12 December 2003; pp. 2138–2143. [Google Scholar] [CrossRef]
- Sun, Z.; Ling, Y.; Tang, X.; Zhou, Y.; Sun, Z.X. Designing and application of type-2 fuzzy PID control for overhead crane systems. Int. J. Intell. Robot. 2021, 5, 10–22. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Mass of trolley | 5 |
| Mass of load | 10 |
| Gravitational acceleration | |
| Length of hoisting rope | 1 |
| Friction coefficient | |
| Predicted horizons | 0.1 |
| Sampling interval | 0.01 |
| Dimension of the Koopman model L | 78 |
| State penalty weight matrix Q | |
| Control weight matrix | 1 |
| Initial information weight | 200 |
| Regularization weight | 100 |
| Terminal cost | 0 |
| Controller | Parameters | Value |
|---|---|---|
| CSMC controller | 0.3 | |
| 10 | ||
| 0.001 | ||
| K | 10 | |
| PID controller | 4 | |
| 0.001 | ||
| 25 | ||
| −0.1 | ||
| 0.1 | ||
| −1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Lou, X. Data-Driven Active Learning Control for Bridge Cranes. Math. Comput. Appl. 2023, 28, 101. https://doi.org/10.3390/mca28050101
Lin H, Lou X. Data-Driven Active Learning Control for Bridge Cranes. Mathematical and Computational Applications. 2023; 28(5):101. https://doi.org/10.3390/mca28050101
Chicago/Turabian StyleLin, Haojie, and Xuyang Lou. 2023. "Data-Driven Active Learning Control for Bridge Cranes" Mathematical and Computational Applications 28, no. 5: 101. https://doi.org/10.3390/mca28050101
APA StyleLin, H., & Lou, X. (2023). Data-Driven Active Learning Control for Bridge Cranes. Mathematical and Computational Applications, 28(5), 101. https://doi.org/10.3390/mca28050101






