Asymptotic Behavior of Solutions to a Nonlinear Swelling Soil System with Time Delay and Variable Exponents
Abstract
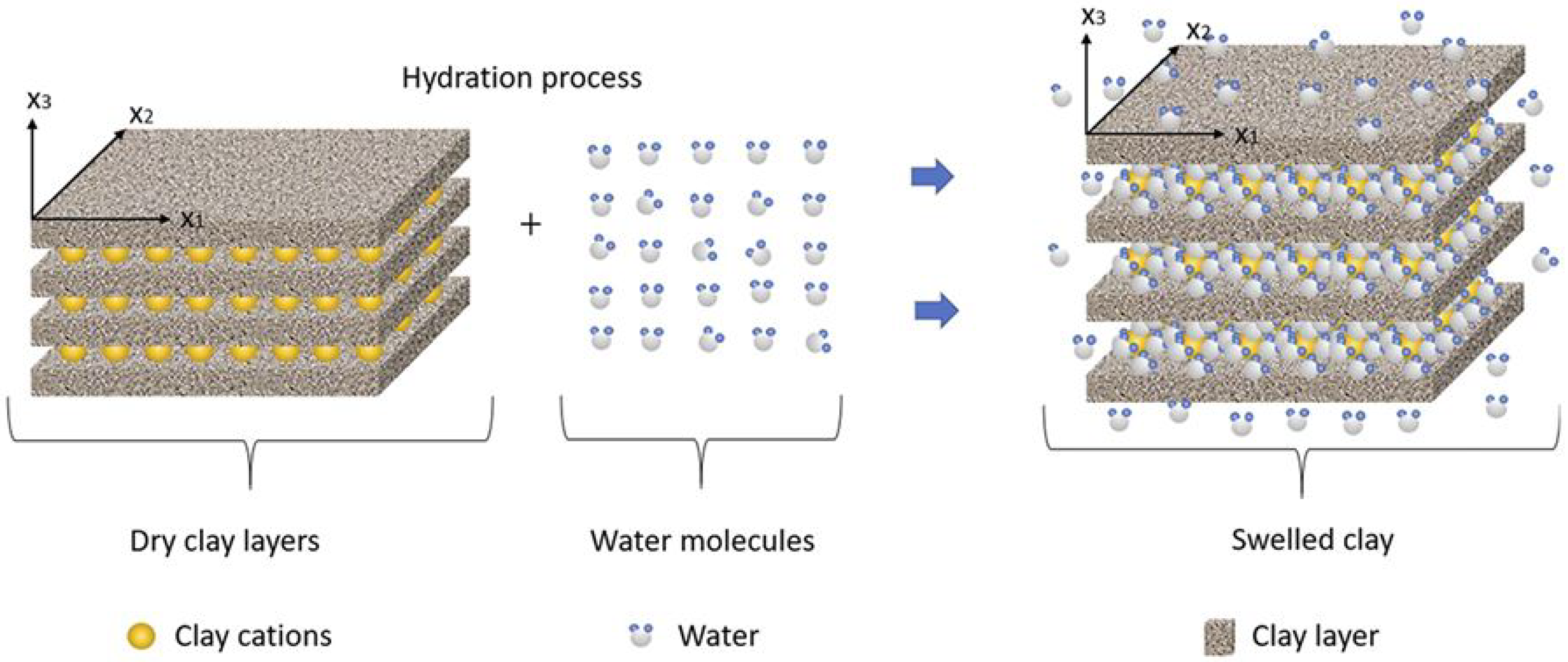
:1. Introduction
2. Preliminary and Assumptions
3. The Main Results
4. Technical Lemmas
5. Proofs of Theorems 2 and 3
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nelson, J.; Miller, D.J. Expansive Soils: Problems and Practice in Foundation and Pavement Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Ie, D. On the theory of mixtures of thermoelastic solids. J. Therm. Stress. 1991, 14, 389–408. [Google Scholar]
- Quintanilla, R. Exponential stability for one-dimensional problem of swelling porous elastic soils with fluid saturation. J. Comput. Appl. Math. 2002, 145, 525–533. [Google Scholar] [CrossRef]
- Wang, J.-M.; Guo, B.-Z. On the stability of swelling porous elastic soils with fluid saturation by one internal damping. IMA J. Appl. Math. 2006, 71, 565–582. [Google Scholar] [CrossRef]
- Ramos, A.; Freitas, M.; Almeida, D., Jr.; Noé, A.; Santos, M.D. Stability results for elastic porous media swelling with nonlinear damping. J. Math. Phys. 2020, 61, 1–10. [Google Scholar] [CrossRef]
- Apalara, T.A. General stability result of swelling porous elastic soils with a viscoelastic damping. Z. Für Angew. Math. Und Phys. 2020, 71, 1–10. [Google Scholar] [CrossRef]
- Al-Mahdi, A.M.; Al-Gharabli, M.M.; Alahyane, M. Theoretical and numerical stability results for a viscoelastic swelling porous-elastic system with past history. AIMS Math. 2021, 6, 11921–11949. [Google Scholar] [CrossRef]
- Pamplona, P.X.; Rivera, J.E.M.; Quintanilla, R. Stabilization in elastic solids with voids. J. Math. Anal. Appl. 2009, 350, 37–49. [Google Scholar] [CrossRef]
- Magaña, A.; Quintanilla, R. On the time decay of solutions in porous-elasticity with quasi-static microvoids. J. Math. Anal. Appl. 2007, 331, 617–630. [Google Scholar] [CrossRef]
- Muñoz-Rivera, J.; Quintanilla, R. On the time polynomial decay in elastic solids with voids. J. Math. Anal. Appl. 2008, 338, 1296–1309. [Google Scholar] [CrossRef]
- Soufyane, A. Energy decay for porous-thermo-elasticity systems of memory type. Appl. Anal. 2008, 87, 451–464. [Google Scholar] [CrossRef]
- Messaoudi, S.A.; Fareh, A. General decay for a porous-thermoelastic system with memory: The case of nonequal speeds. Acta Math. Sci. 2013, 33, 23–40. [Google Scholar] [CrossRef]
- Apalara, T.A. General decay of solutions in one-dimensional porous-elastic system with memory. J. Math. Anal. Appl. 2019, 469, 457–471. [Google Scholar] [CrossRef]
- Apalara, T.A. A general decay for a weakly nonlinearly damped porous system. J. Dyn. Control Syst. 2019, 25, 311–322. [Google Scholar] [CrossRef]
- Feng, B.; Apalara, T.A. Optimal decay for a porous elasticity system with memory. J. Math. Anal. Appl. 2019, 470, 1108–1128. [Google Scholar] [CrossRef]
- Feng, B.; Yin, M. Decay of solutions for a one-dimensional porous elasticity system with memory: The case of non-equal wave speeds. Math. Mech. Solids 2019, 24, 2361–2373. [Google Scholar] [CrossRef]
- Casas, P.S.; Quintanilla, R. Exponential decay in one-dimensional porous-thermo-elasticity. Mech. Res. Commun. 2005, 32, 652–658. [Google Scholar] [CrossRef]
- Santos, M.; Campelo, A.; Júnior, D.A. On the decay rates of porous elastic systems. J. Elast. 2017, 127, 79–101. [Google Scholar] [CrossRef]
- Apalara, T.A. General stability of memory-type thermoelastic timoshenko beam acting on shear force. Contin. Mech. Thermodyn. 2018, 30, 291–300. [Google Scholar] [CrossRef]
- Richard, J.-P. Time-delay systems: An overview of some recent advances and open problems. Automatica 2003, 39, 1667–1694. [Google Scholar] [CrossRef]
- Gu, K.; Chen, J.; Kharitonov, V.L. Stability of Time-Delay Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Fridman, E. Introduction to Time-Delay Systems: Analysis and Control; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Datko, R.; Lagnese, J.; Polis, M. An example on the effect of time delays in boundary feedback stabilization of wave equations. SIAM J. Control Optim. 1986, 24, 152–156. [Google Scholar] [CrossRef]
- Acerbi, E.; Mingione, G. Regularity results for stationary electro-rheological fluids. Arch. Ration. Mech. Anal. 2002, 164, 213–259. [Google Scholar] [CrossRef]
- Ruzicka, M. Electrorheological Fluids: Modeling and Mathematical Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Antontsev, S. Wave equation with p(x, t)-laplacian and damping term: Existence and blow-up. Differ. Equ. Appl. 2011, 3, 503–525. [Google Scholar] [CrossRef]
- Antontsev, S. Wave equation with p(x, t)-laplacian and damping term: Blow-up of solutions. C. R. Mécanique 2011, 339, 751–755. [Google Scholar] [CrossRef]
- Messaoudi, S.A.; Talahmeh, A.A. A blow-up result for a nonlinear wave equation with variable-exponent nonlinearities. Appl. Anal. 2017, 96, 1509–1515. [Google Scholar] [CrossRef]
- Messaoudi, S.A.; Talahmeh, A.A.; Al-Smail, J.H. Nonlinear damped wave equation: Existence and blow-up. Comput. Math. Appl. 2017, 74, 3024–3041. [Google Scholar] [CrossRef]
- Sun, L.; Ren, Y.; Gao, W. Lower and upper bounds for the blow-up time for nonlinear wave equation with variable sources. Comput. Math. Appl. 2016, 71, 267–277. [Google Scholar] [CrossRef]
- Messaoudi, S.A.; Al-Gharabli, M.M.; Al-Mahdi, A.M. On the decay of solutions of a viscoelastic wave equation with variable sources. Math. Methods Appl. Sci. 2020, 8389–8411. [Google Scholar] [CrossRef]
- Al-Mahdi, A.M.; Al-Gharabli, M.M.; Zahri, M. Theoretical and computational decay results for a memory type wave equation with variable-exponent nonlinearity. Math. Control Relat. Fields 2023, 13, 605–630. [Google Scholar] [CrossRef]
- Nicaise, S.; Pignotti, C. Stability and instability results of the wave equation with a delay term in the boundary or internal feedbacks. SIAM J. Control Optim. 2006, 45, 1561–1585. [Google Scholar] [CrossRef]
- Al-Mahdi, A.M.; Kafini, M.; Hassan, J.H.; Alahyane, M. Well-posedness, theoretical and numerical stability results of a memory-type porous thermoelastic system. Z. Für Angew. Math. Und Phys. 2022, 73, 1–25. [Google Scholar] [CrossRef]
- Kafini, M.; Messaoudi, S. On the decay and global nonexistence of solutions to a damped wave equation with variableexponent nonlinearity and delay. In Annales Polonici Mathematici; Instytut Matematyczny Polskiej Akademii Nauk: Warsaw, Poland, 2019; Volume 122, pp. 49–70. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kafini, M.M.; Al-Gharabli, M.M.; Al-Mahdi, A.M. Asymptotic Behavior of Solutions to a Nonlinear Swelling Soil System with Time Delay and Variable Exponents. Math. Comput. Appl. 2023, 28, 94. https://doi.org/10.3390/mca28050094
Kafini MM, Al-Gharabli MM, Al-Mahdi AM. Asymptotic Behavior of Solutions to a Nonlinear Swelling Soil System with Time Delay and Variable Exponents. Mathematical and Computational Applications. 2023; 28(5):94. https://doi.org/10.3390/mca28050094
Chicago/Turabian StyleKafini, Mohammad M., Mohammed M. Al-Gharabli, and Adel M. Al-Mahdi. 2023. "Asymptotic Behavior of Solutions to a Nonlinear Swelling Soil System with Time Delay and Variable Exponents" Mathematical and Computational Applications 28, no. 5: 94. https://doi.org/10.3390/mca28050094
APA StyleKafini, M. M., Al-Gharabli, M. M., & Al-Mahdi, A. M. (2023). Asymptotic Behavior of Solutions to a Nonlinear Swelling Soil System with Time Delay and Variable Exponents. Mathematical and Computational Applications, 28(5), 94. https://doi.org/10.3390/mca28050094





