Simulation of a Thermal Recuperative Incinerator of VOCs with a Special Focus on the Heat Exchanger
Abstract
:1. Introduction
2. Materials and Methods
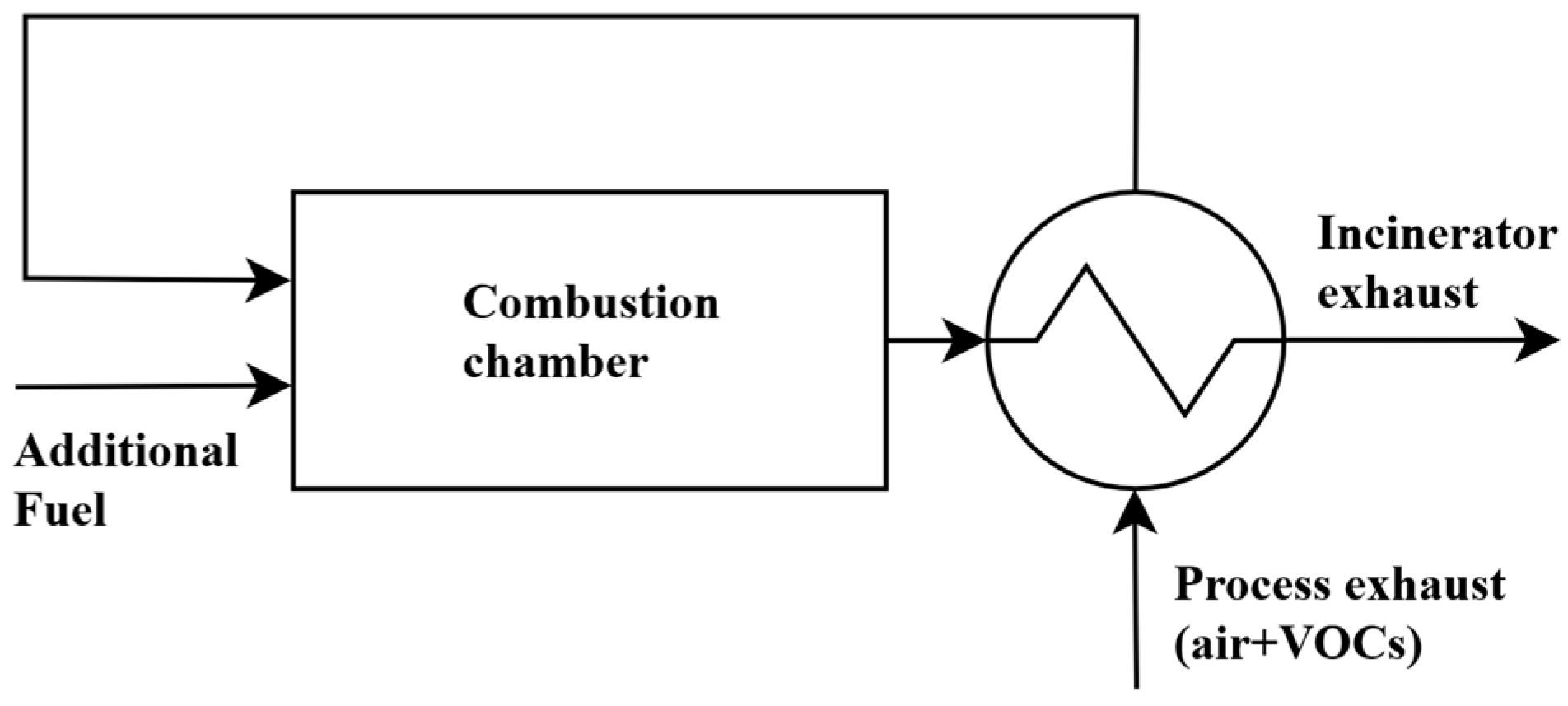
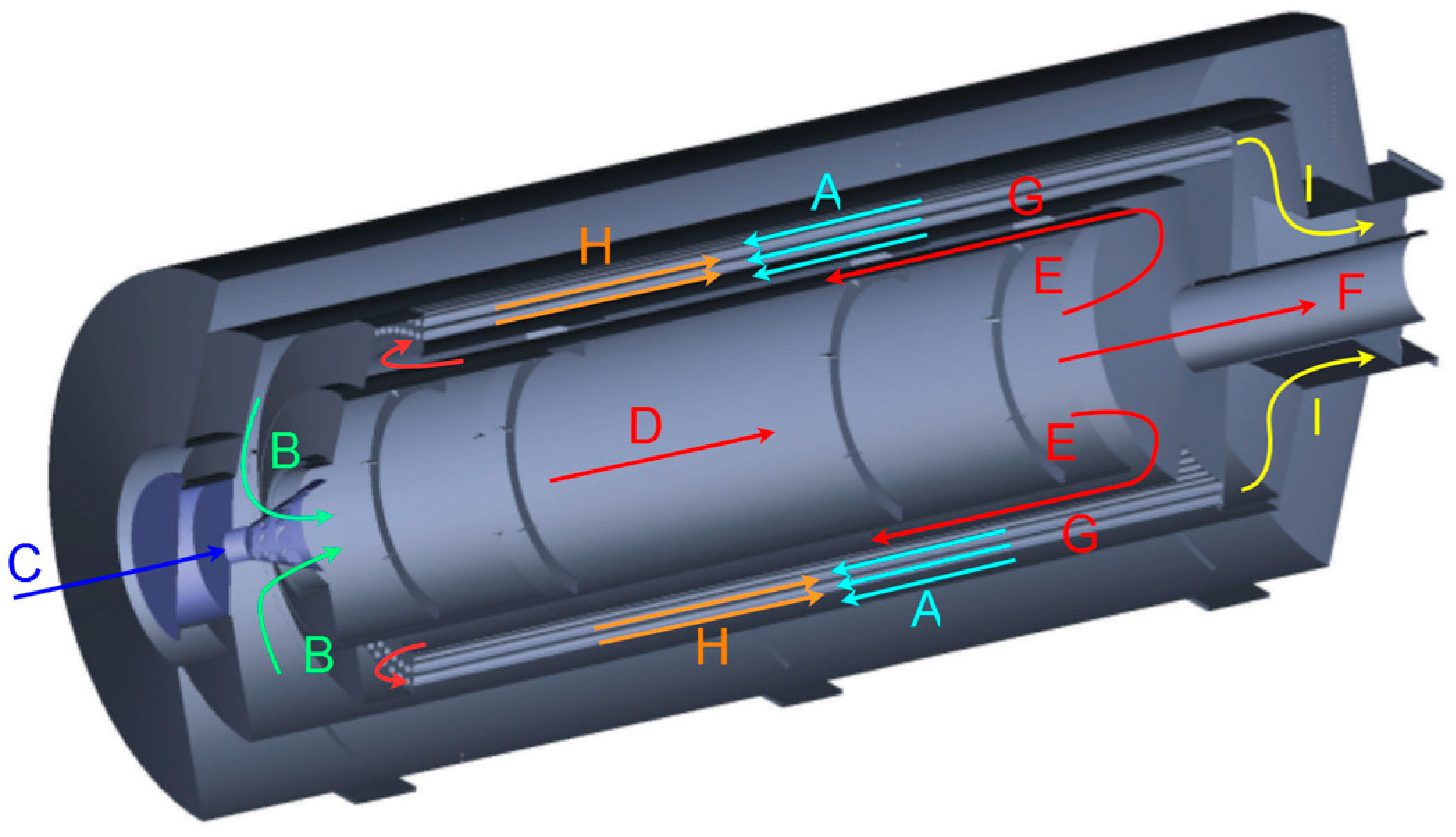
2.1. Thermal Recuperative Incinerator
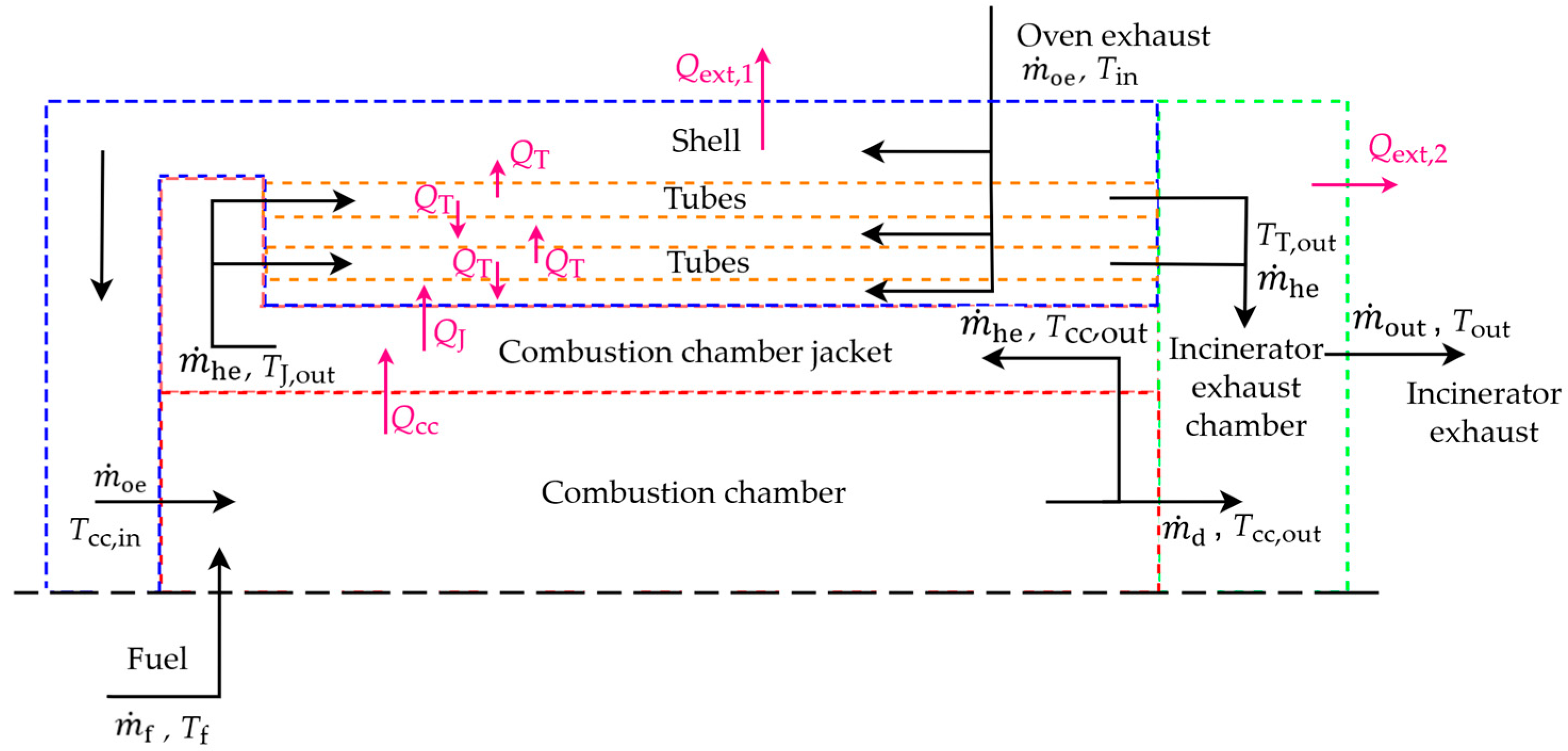
2.2. Mathematical Model
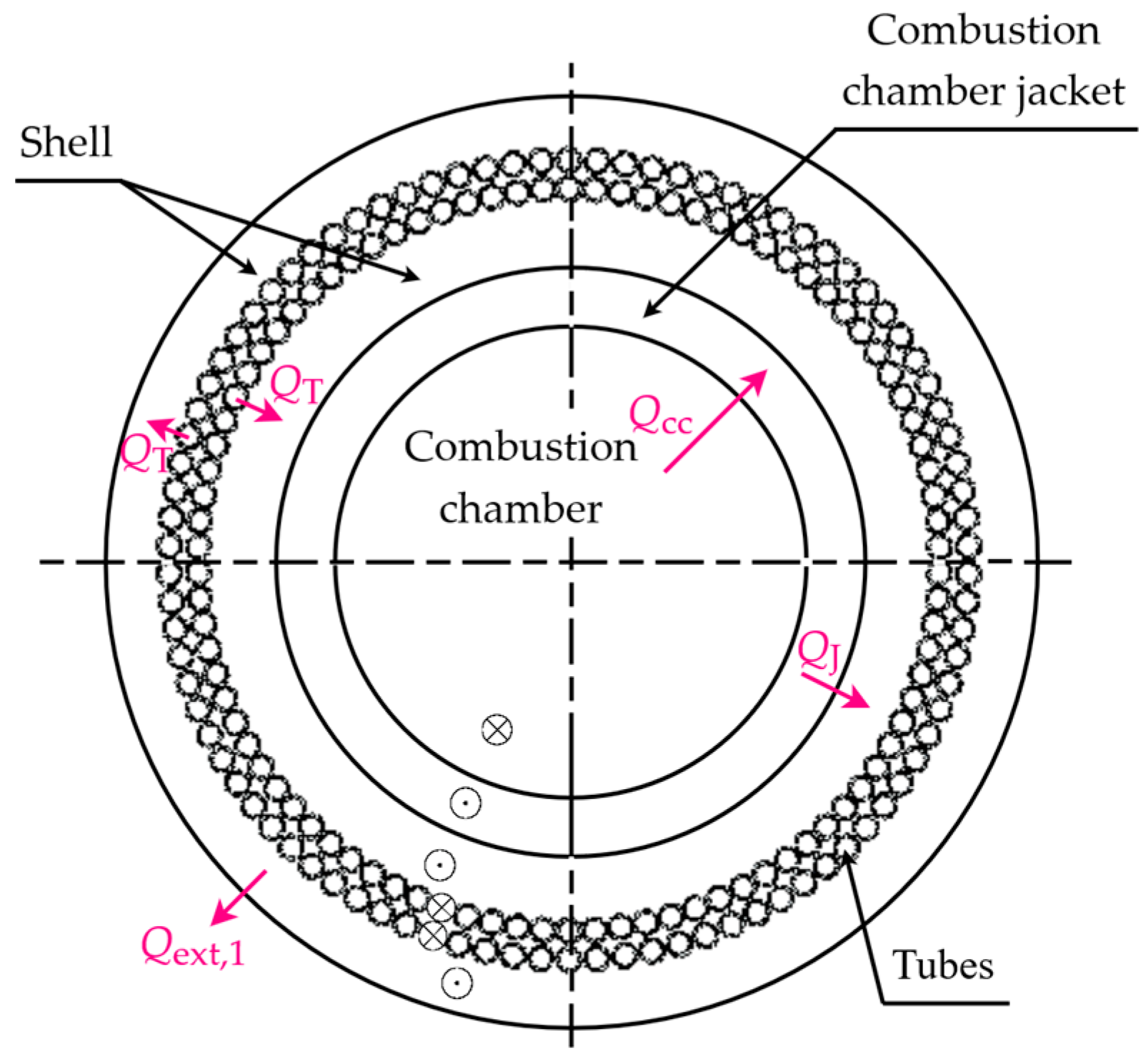
2.2.1. Combustion Chamber
2.2.2. Combustion Chamber Jacket and Shell Modeled as a Co-Current Heat Exchanger
2.2.3. Shell and Tubes Modeled as a Counter-Current Heat Exchanger
2.2.4. Tubes
2.2.5. Incinerator Exhaust Chamber
2.2.6. Thermal Resistances
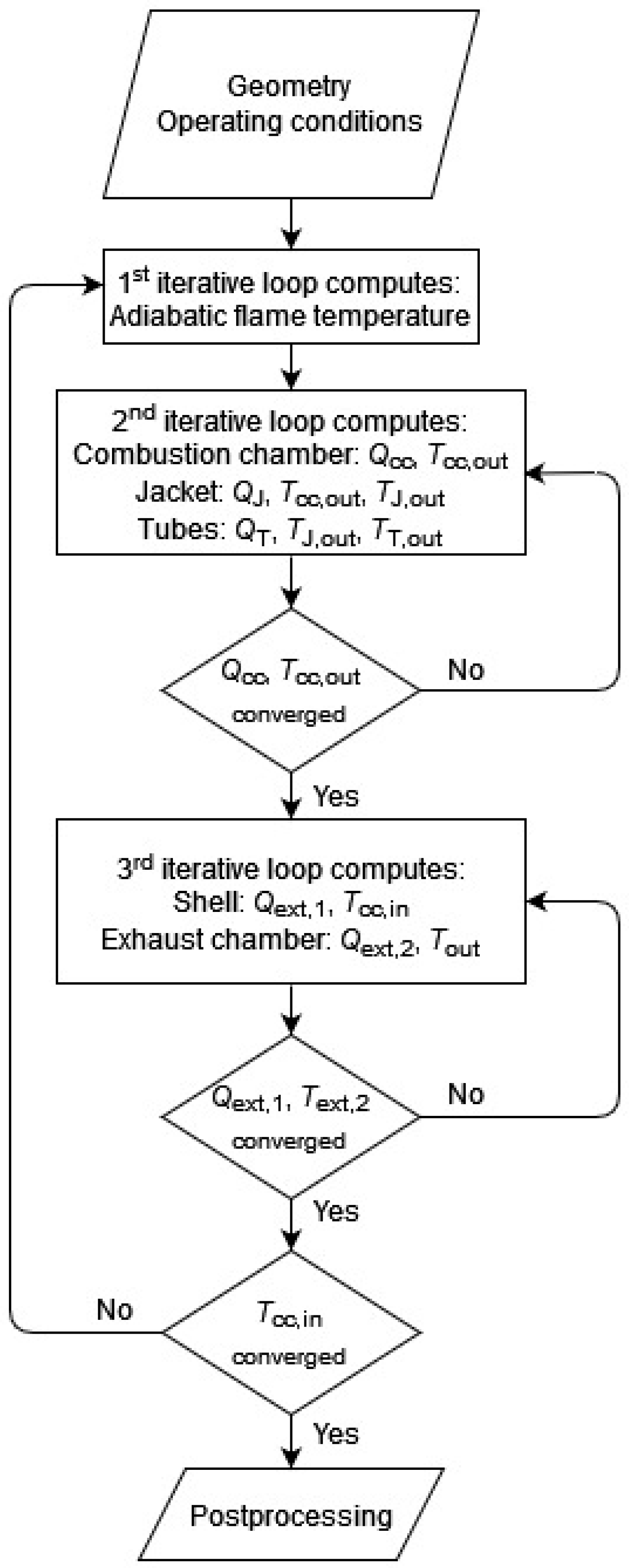
2.2.7. Fluid Properties, Numerical Procedure and Post-Processing
3. Results
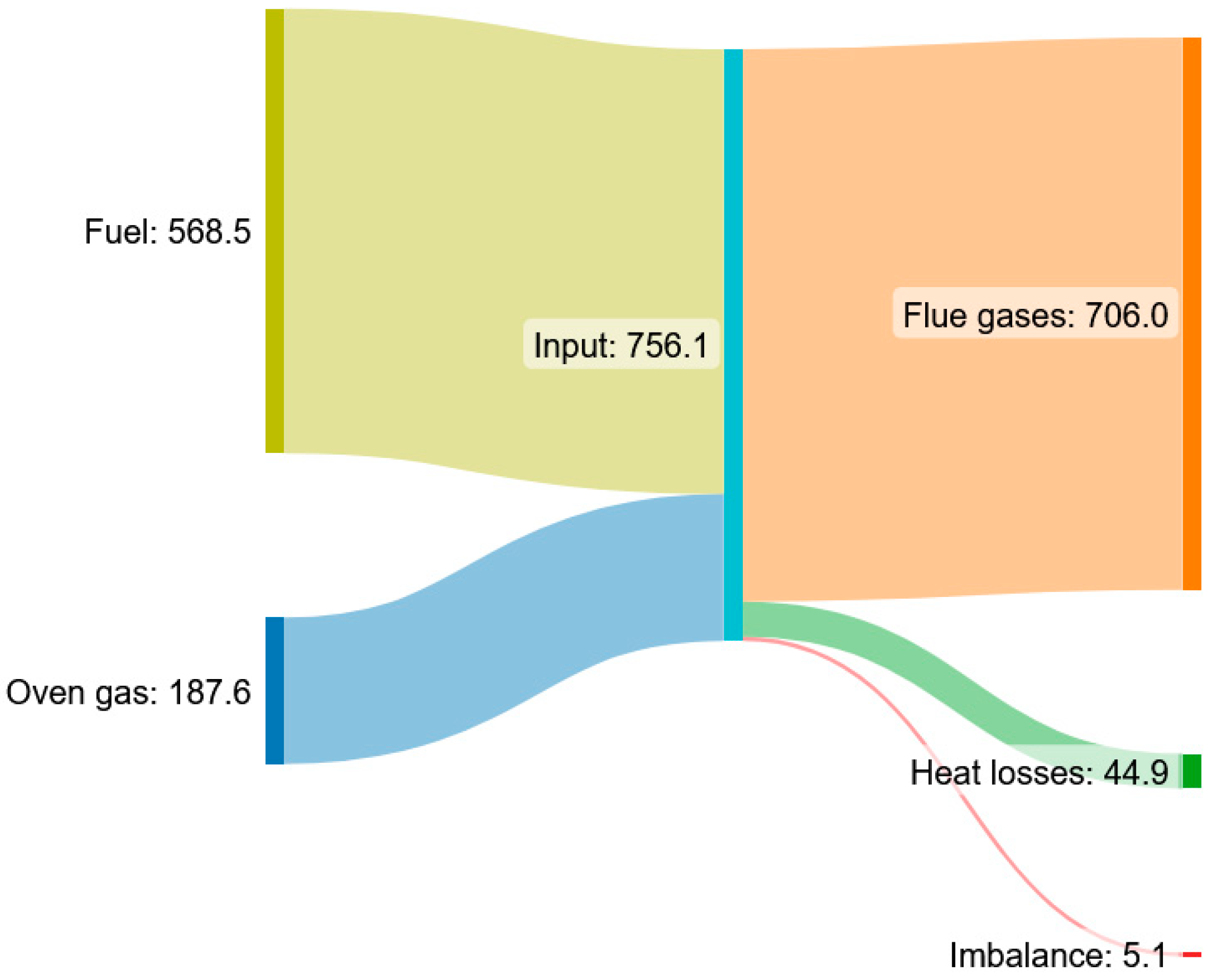
3.1. Model Validation
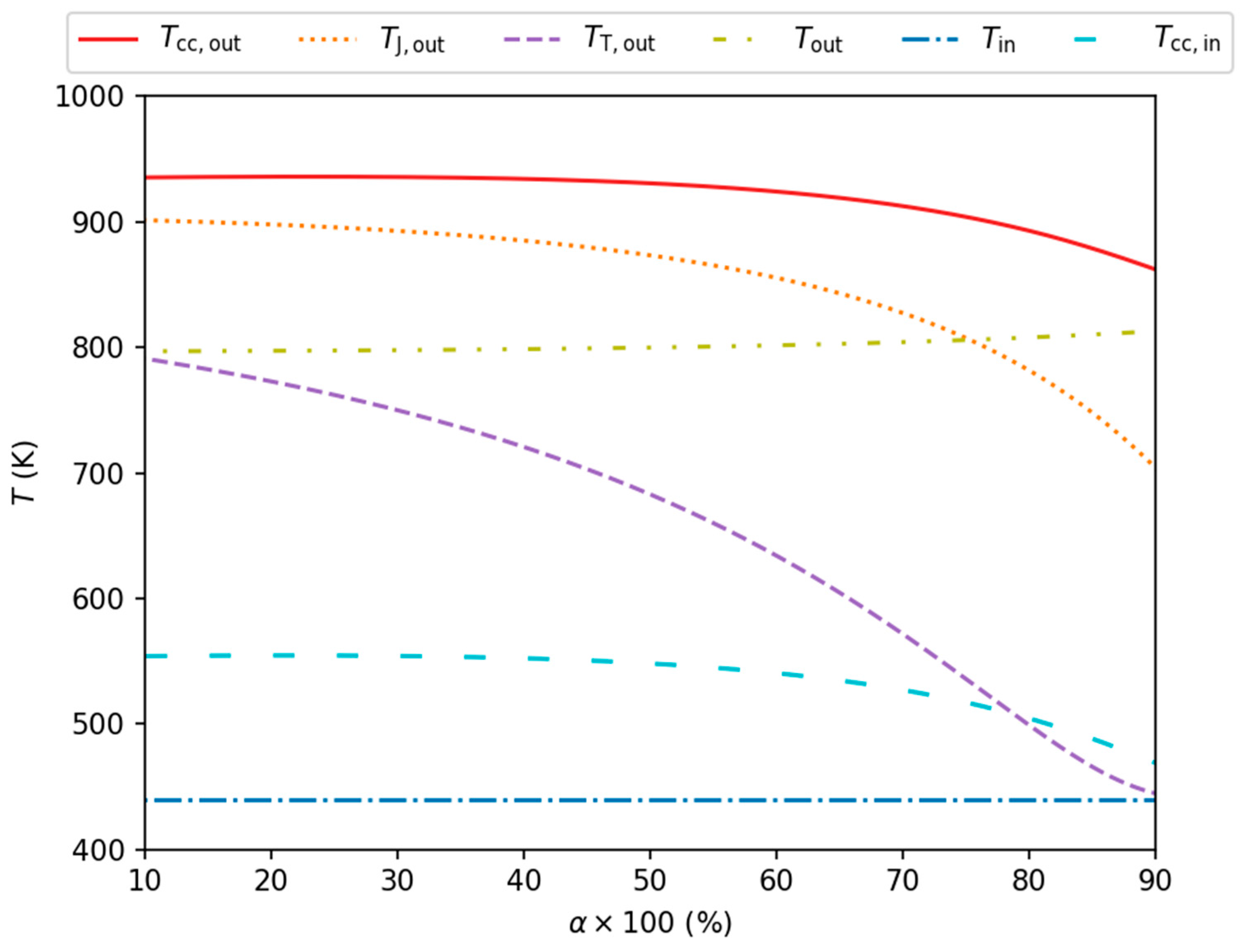
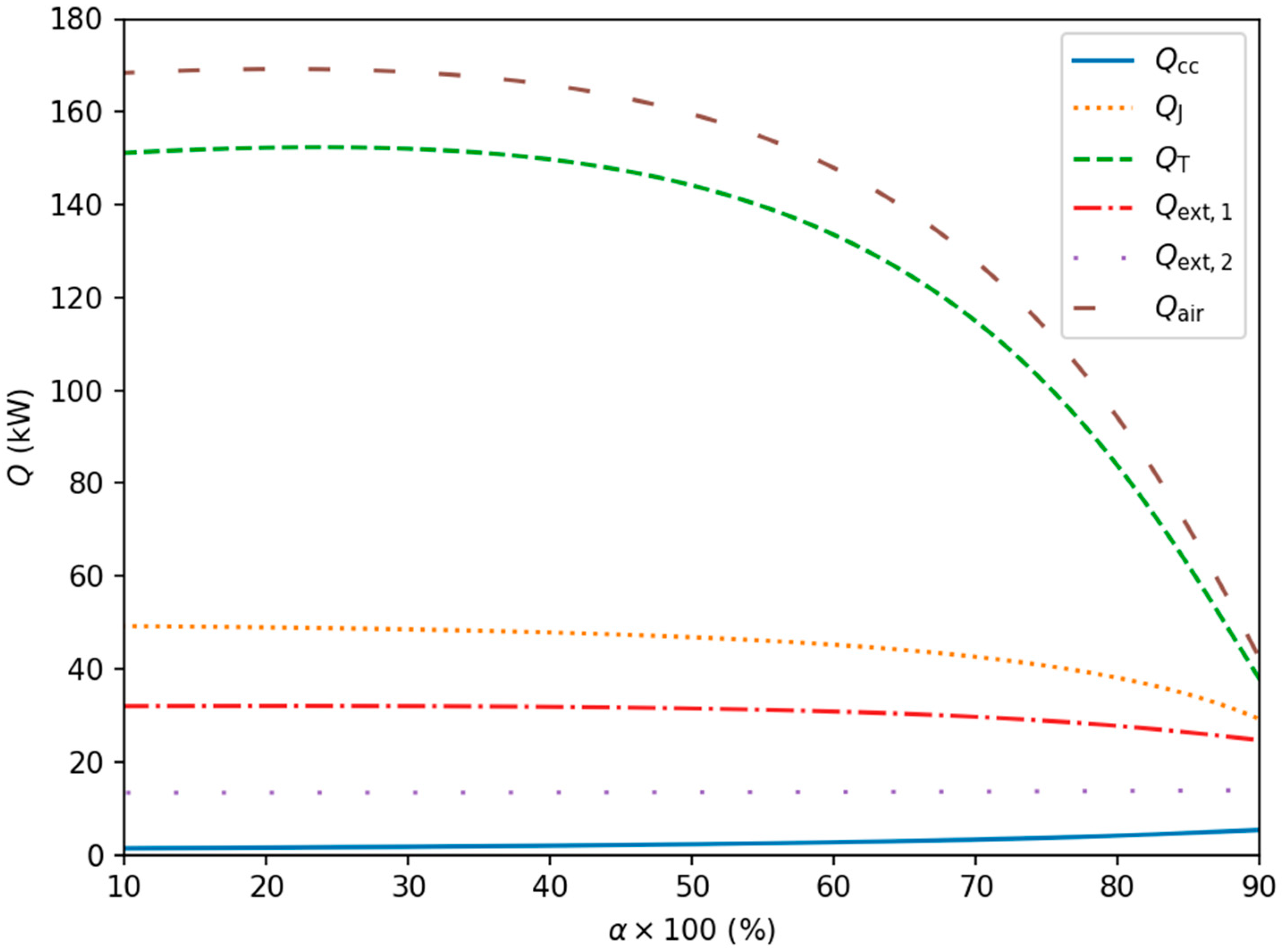
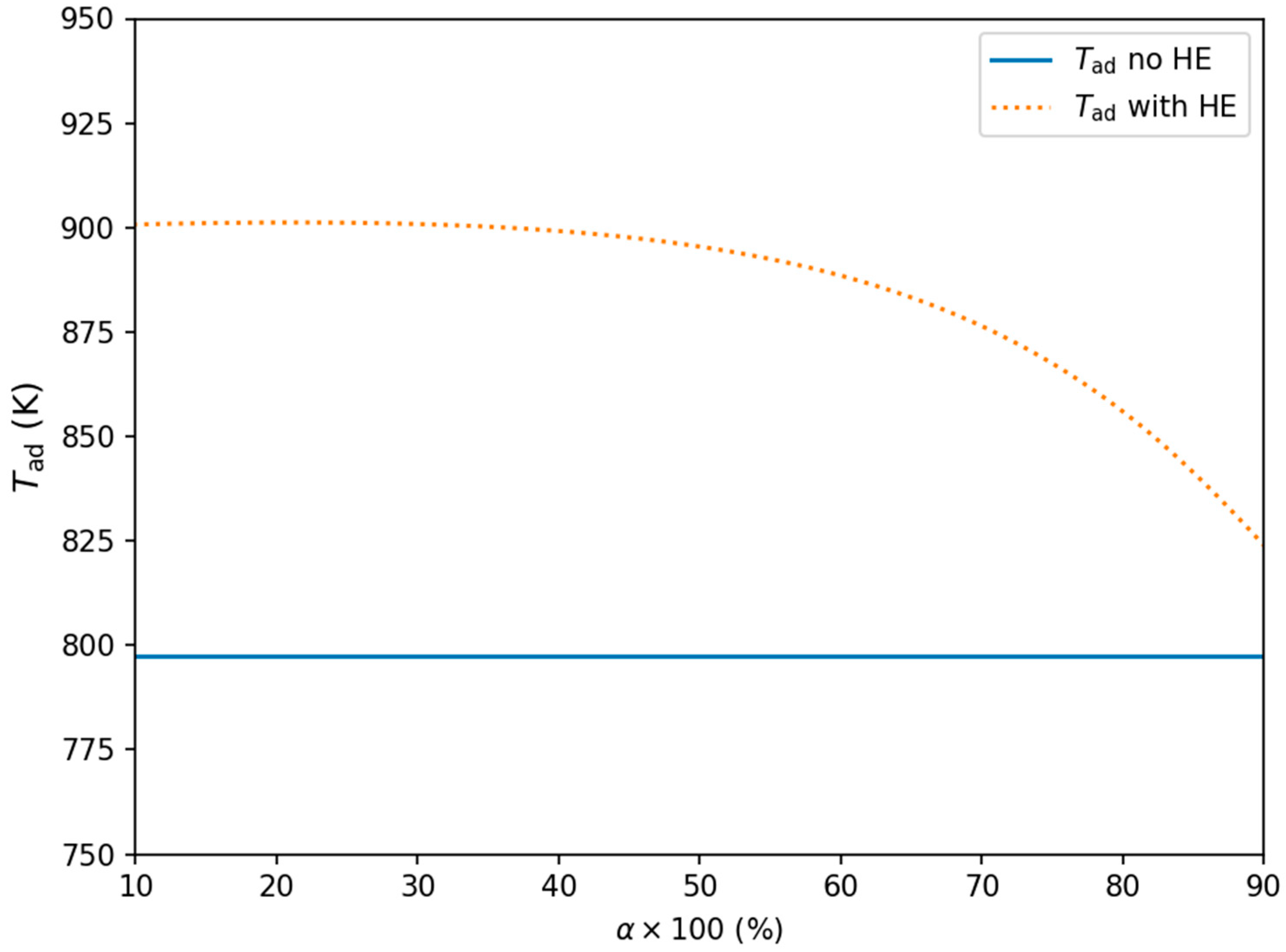
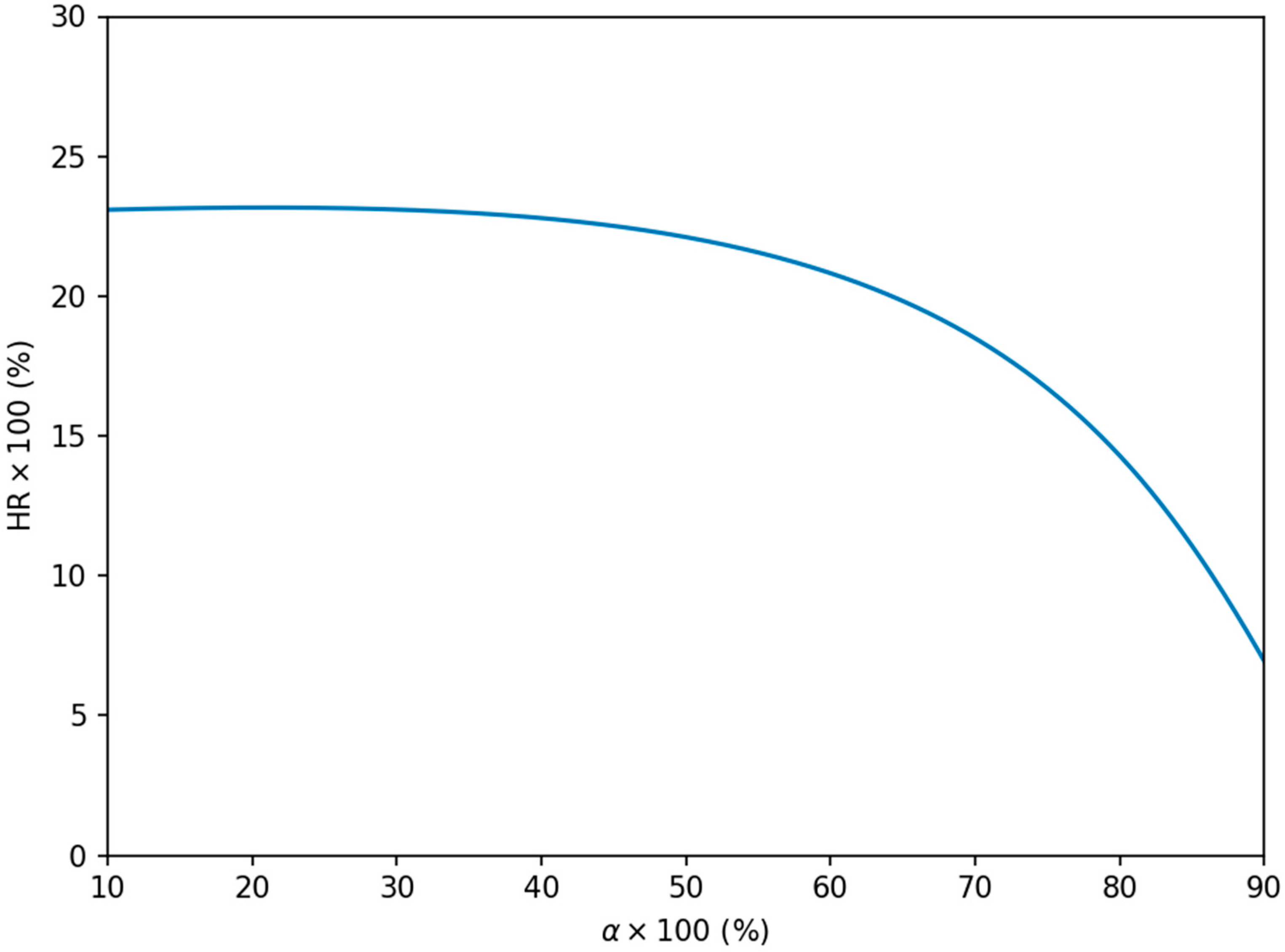
3.2. Influence of the Varying Level of Heat Recovery
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whitall, K.L. Air Pollution Control in the Finishing Industry. Met. Finish. 1999, 97, 409–419. [Google Scholar] [CrossRef]
- Salvador, S.; Commandré, J.-M.; Kara, Y. Thermal Recuperative Incineration of VOCs: CFD Modelling and Experimental Validation. Appl. Therm. Eng. 2006, 26, 2355–2366. [Google Scholar] [CrossRef]
- Granadero, D.; Garcia-Muñoz, A.; Adam, R.; Omil, F.; Feijoo, G. Evaluation of Abatement Options to Reduce Formaldehyde Emissions in Vehicle Assembly Paint Shops Using the Life Cycle Methodology. Clean. Environ. Syst. 2023, 11, 100139. [Google Scholar] [CrossRef]
- Giampieri, A.; Ling-Chin, J.; Ma, Z.; Smallbone, A.; Roskilly, A.P. A Review of the Current Automotive Manufacturing Practice from an Energy Perspective. Appl. Energy 2020, 261, 114074. [Google Scholar] [CrossRef]
- Chronopoulos, G.; Cakmak, G.-E.; Tempany, P.; Klein, G.; Brinkmann, T.; Zerger, B.; Roudier, S. Best Available Techniques (BAT) Reference Document on Surface Treatment Using Organic Solvents Including Preservation of Wood and Wood Products with Chemicals: Industrial Emissions Directive 2010/75/EU (Integrated Pollution Prevention and Control); Publications Office of the European Union: Luxembourg, 2020. [Google Scholar]
- Sorrels, J.L.; Baynham, A.; Randall, D.; Hancy, C. Incinerators and Oxidizers. In EPA Air Pollution Control Cost Manual; United States Environmental Protection Agency: Washington, DC, USA, 2017; pp. 2.1–2.67. [Google Scholar]
- Shah, R.K.; Sekulic, D.P. Fundamentals of Heat Exchanger Design; Wiley and Sons: New York, NY, USA, 2003. [Google Scholar]
- Arsenyeva, O.P.; Tovazhnyansky, L.L.; Kapustenko, P.O.; Khavin, G.L. Optimal Design of Plate-and-Frame Heat Exchangers for Efficient Heat Recovery in Process Industries. Energy 2011, 36, 4588–4598. [Google Scholar] [CrossRef]
- Yang, Z.; Ma, Y.; Zhang, N.; Smith, R. Design Optimization of Shell and Tube Heat Exchangers Sizing with Heat Transfer Enhancement. Comput. Chem. Eng. 2020, 137, 106821. [Google Scholar] [CrossRef]
- Chen, L.-Y.; Adi, V.S.K.; Laxmidewi, R. Shell and Tube Heat Exchanger Flexible Design Strategy for Process Operability. Case Stud. Therm. Eng. 2022, 37, 102163. [Google Scholar] [CrossRef]
- Li, N.; Chen, J.; Cheng, T.; Klemeš, J.J.; Varbanov, P.S.; Wang, Q.; Yang, W.; Liu, X.; Zeng, M. Analysing Thermal-Hydraulic Performance and Energy Efficiency of Shell-and-Tube Heat Exchangers with Longitudinal Flow Based on Experiment and Numerical Simulation. Energy 2020, 202, 117757. [Google Scholar] [CrossRef]
- Arsenyeva, O.; Perevertaylenko, O.; Tovazhnyanskyy, L.; Arsenyev, P.; Kapustenko, P. Experimental Investigation of Thermal and Hydraulic Performance of Panel Plate Heat Exchangers. Therm. Sci. Eng. Prog. 2023, 43, 101984. [Google Scholar] [CrossRef]
- Fetuga, I.A.; Olakoyejo, O.T.; Abolarin, S.M.; Gbegudu, J.K.; Onwuegbusi, A.; Adelaja, A.O. Numerical Analysis of Thermal Performance of Waste Heat Recovery Shell and Tube Heat Exchangers on Counter-Flow with Different Tube Configurations. Alex. Eng. J. 2023, 64, 859–875. [Google Scholar] [CrossRef]
- Kolta, T. Selecting Equipment to Control Air Pollution from Automotive Painting Operations; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 1992; pp. 1–18. [Google Scholar]
- Zhuo, W.; Zhou, B.; Zhang, Z.; Zhou, H.; Dai, B. Process Modeling and Exergy Analysis for a Typical VOC Thermal Conversion Plant. Energies 2022, 15, 3522. [Google Scholar] [CrossRef]
- Crawmer, J.K.T.; Chen, C.-H.; Richard, B.M.; Pearlman, H.G.; Edwards, T.V.; Ronney, P.D. An Innovative Volatile Organic Compound Incinerator. In Proceedings of the 36th International Conference on Thermal Treatment Technologies & Hazardous Waste Combustors, Houston, TX, USA, 8 March 2017. [Google Scholar]
- Fuligno, L.; Micheli, D.; Poloni, C. An Integrated Approach for Optimal Design of Micro Gas Turbine Combustors. J. Therm. Sci. 2009, 18, 173–184. [Google Scholar] [CrossRef]
- Vézina, G.; Fortier-Topping, H.; Bolduc-Teasdale, F.; Rancourt, D.; Picard, M.; Plante, J.-S.; Brouillette, M.; Fréchette, L. Design and Experimental Validation of a Supersonic Concentric Micro Gas Turbine. J. Turbomach. 2016, 138, 021007. [Google Scholar] [CrossRef]
- Payri, F.; Olmeda, P.; Martín, J.; García, A. A Complete 0D Thermodynamic Predictive Model for Direct Injection Diesel Engines. Appl. Energy 2011, 88, 4632–4641. [Google Scholar] [CrossRef]
- Siccinio, M.; Fable, E.; Lackner, K.; Scarabosio, A.; Wenninger, R.P.; Zohm, H. A 0D Stationary Model for the Evaluation of the Degree of Detachment on the Divertor Plates. Plasma Phys. Control. Fusion 2016, 58, 125011. [Google Scholar] [CrossRef]
- Li, R.C.; Zhu, G.G.; Men, Y. A Two-Zone Reaction-Based Combustion Model for a Spark-Ignition Engine. Int. J. Engine Res. 2021, 22, 109–124. [Google Scholar] [CrossRef]
- Chinnici, A.; Tian, Z.F.; Lim, J.H.; Nathan, G.J.; Dally, B.B. Comparison of System Performance in a Hybrid Solar Receiver Combustor Operating with MILD and Conventional Combustion. Part I: Solar-Only and Combustion-Only Employing Conventional Combustion. Sol. Energy 2017, 147, 489–503. [Google Scholar] [CrossRef]
- Arpino, F.; Cortellessa, G.; Canale, L.; Dell’Isola, M.; Ficco, G.; Moretti, L.; Zuena, F.; Rinaldi, F. A 0D-3D Approach for Numerical Analysis of Waste to Energy Plants: A Case Study. J. Phys. Conf. Ser. 2021, 1868, 012023. [Google Scholar] [CrossRef]
- Mohammadkhani, F.; Yari, M. A 0D Model for Diesel Engine Simulation and Employing a Transcritical Dual Loop Organic Rankine Cycle (ORC) for Waste Heat Recovery from Its Exhaust and Coolant: Thermodynamic and Economic Analysis. Appl. Therm. Eng. 2019, 150, 329–347. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics, 8th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014; ISBN 1-118-41293-1. [Google Scholar]
- Bergman, T.L.; Incropera, F.P.; Lavine, A.S.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Švantner, M.; Honnerová, P.; Veselý, Z. The Influence of Furnace Wall Emissivity on Steel Charge Heating. Infrared Phys. Technol. 2016, 74, 63–71. [Google Scholar] [CrossRef]
- Kays, W.M.; London, A.L. Compact Heat Exchangers, 2nd ed.; McGraw-Hill Book Company: New York, NY, USA, 1964. [Google Scholar]
- White, F.M. Fluid Mechanics, 8th ed.; McGraw-Hill: New York, NY, USA, 2017. [Google Scholar]
- Gnielinski, V. Neue Gleichungen für den Wärme-und den Stoffübergang in turbulent durchströmten Rohren und Kanälen. Forsch. Im Ingenieurwesen A 1975, 41, 8–16. [Google Scholar] [CrossRef]
- Gnielinski, V. On Heat Transfer in Tubes. Int. J. Heat Mass Transf. 2013, 63, 134–140. [Google Scholar] [CrossRef]
- Gnielinski, V. Heat Transfer Coefficients for Turbulent Flow in Concentric Annular Ducts. Heat Transf. Eng. 2009, 30, 431–436. [Google Scholar] [CrossRef]
- Gnielinski, V. Turbulent Heat Transfer in Annular Spaces—A New Comprehensive Correlation. Heat Transf. Eng. 2015, 36, 787–789. [Google Scholar] [CrossRef]
- Kim, W.K.; Martin, H.; Gnielinski, V. Pressure Drop and Heat Transfer in Shell-and-Tube Heat Exchangers without Baffles Part I. The Graetz-Nusselt Problem in a Cylindrical Shell Containing a Bundle of Seven Tubes. Chem. Eng. Process. 1993, 32, 99–110. [Google Scholar] [CrossRef]
- Gaddis, E.S.; Gnielinski, V. Pressure Drop on the Shell Side of Shell-and-Tube Heat Exchangers with Segmental Baffles. Chem. Eng. Process. 1997, 36, 149–159. [Google Scholar] [CrossRef]
- Turns, S.R. An Introduction to Combustion. In Concepts and Applications, 3rd ed.; McGraw-Hill: New York, NY, USA, 2013. [Google Scholar]
- van der Vaart, D.R.; Marchand, E.G.; Bagely-Pride, A. Thermal and Catalytic Incineration of Volatile Organic Compounds. Crit. Rev. Environ. Sci. Technol. 1994, 24, 203–236. [Google Scholar] [CrossRef]
- Trinks, W.; Mawhinney, M.H.; Shannon, R.A.; Reed, R.J.; Garvey, J.R. Industrial Furnaces, 6th ed.; John Wiley & Sons: New Jersey, NJ, USA, 2004. [Google Scholar]
- Mullinger, P.; Jenkins, B. Industrial and Process Furnaces: Principles, Design and Operation, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2014; ISBN 978-0-08-099377-5. [Google Scholar]
- EPA Incinerator-Recuperative Type. In Air Pollution Control Technology Fact Sheet; United States Environmental Protection Agency: Washington, DC, USA, 2003; pp. 1–6. Available online: https://www3.epa.gov/ttncatc1/dir1/frecup.pdf (accessed on 20 December 2023).
- Zaversky, F.; Sánchez, M.; Astrain, D. Object-Oriented Modeling for the Transient Response Simulation of Multi-Pass Shell-and-Tube Heat Exchangers as Applied in Active Indirect Thermal Energy Storage Systems for Concentrated Solar Power. Energy 2014, 65, 647–664. [Google Scholar] [CrossRef]
| Input Variables | Output Variables/Measurements |
|---|---|
| , , , Tin, Tf, α | Tcc,out, Tout |
| Variables | Measurements | Model Results | Relative Error (%) |
|---|---|---|---|
| Tf (K) | 305.87 ± 1.52 | - | - |
| (kg·s−1) | 1.04 × 10−2 ± 1.5 × 10−4 | - | - |
| Tin (K) | 439.65 ± 6.6 × 10−1 | - | - |
| (kg·s−1) | 1.31 ± 1.0 × 10−2 | - | - |
| (kgC·s−1) | 1.08 × 10−3 | - | - |
| α (-) | 0.5 | - | - |
| Tcc,out (K) | 911.45 ± 2.05 | 930.74 | 2.12 |
| Tout (K) | 733.85 ± 1.84 | 799.85 | 8.99 |
| XO2 (%) | 18.2 ± 0.0 | 17.6 | 3.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zdanowski, F.; Malico, I.; Canhoto, P.; Lima, R.P. Simulation of a Thermal Recuperative Incinerator of VOCs with a Special Focus on the Heat Exchanger. Math. Comput. Appl. 2024, 29, 1. https://doi.org/10.3390/mca29010001
Zdanowski F, Malico I, Canhoto P, Lima RP. Simulation of a Thermal Recuperative Incinerator of VOCs with a Special Focus on the Heat Exchanger. Mathematical and Computational Applications. 2024; 29(1):1. https://doi.org/10.3390/mca29010001
Chicago/Turabian StyleZdanowski, Francisco, Isabel Malico, Paulo Canhoto, and Rui Pedro Lima. 2024. "Simulation of a Thermal Recuperative Incinerator of VOCs with a Special Focus on the Heat Exchanger" Mathematical and Computational Applications 29, no. 1: 1. https://doi.org/10.3390/mca29010001
APA StyleZdanowski, F., Malico, I., Canhoto, P., & Lima, R. P. (2024). Simulation of a Thermal Recuperative Incinerator of VOCs with a Special Focus on the Heat Exchanger. Mathematical and Computational Applications, 29(1), 1. https://doi.org/10.3390/mca29010001






