Abstract
:1. Introduction
2. Preliminaries
2.1. Notation
2.2. Problem Formulation
- for , the errors and converge asymptotically to zero.
- for we solve the .
3. Adaptive Observer Design
Stability of the Observer
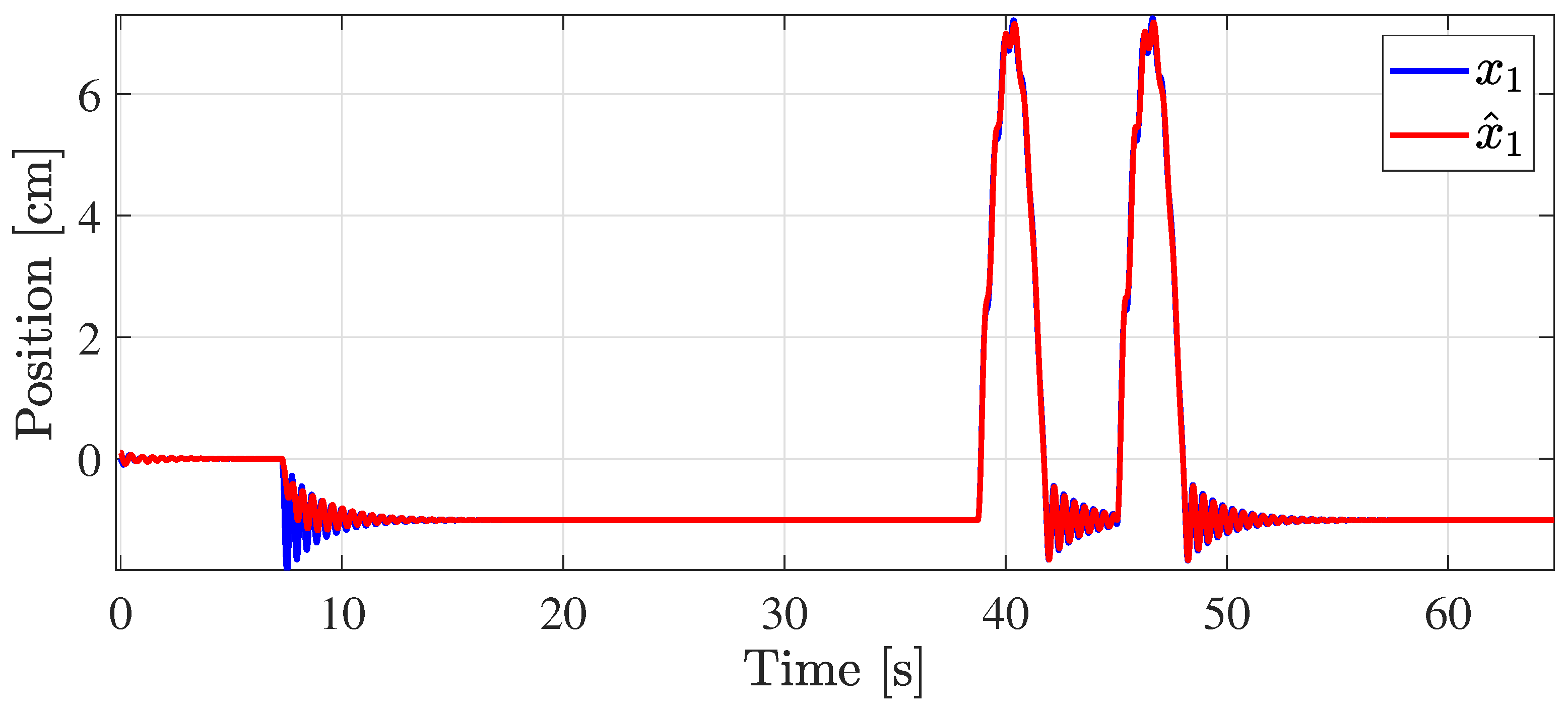
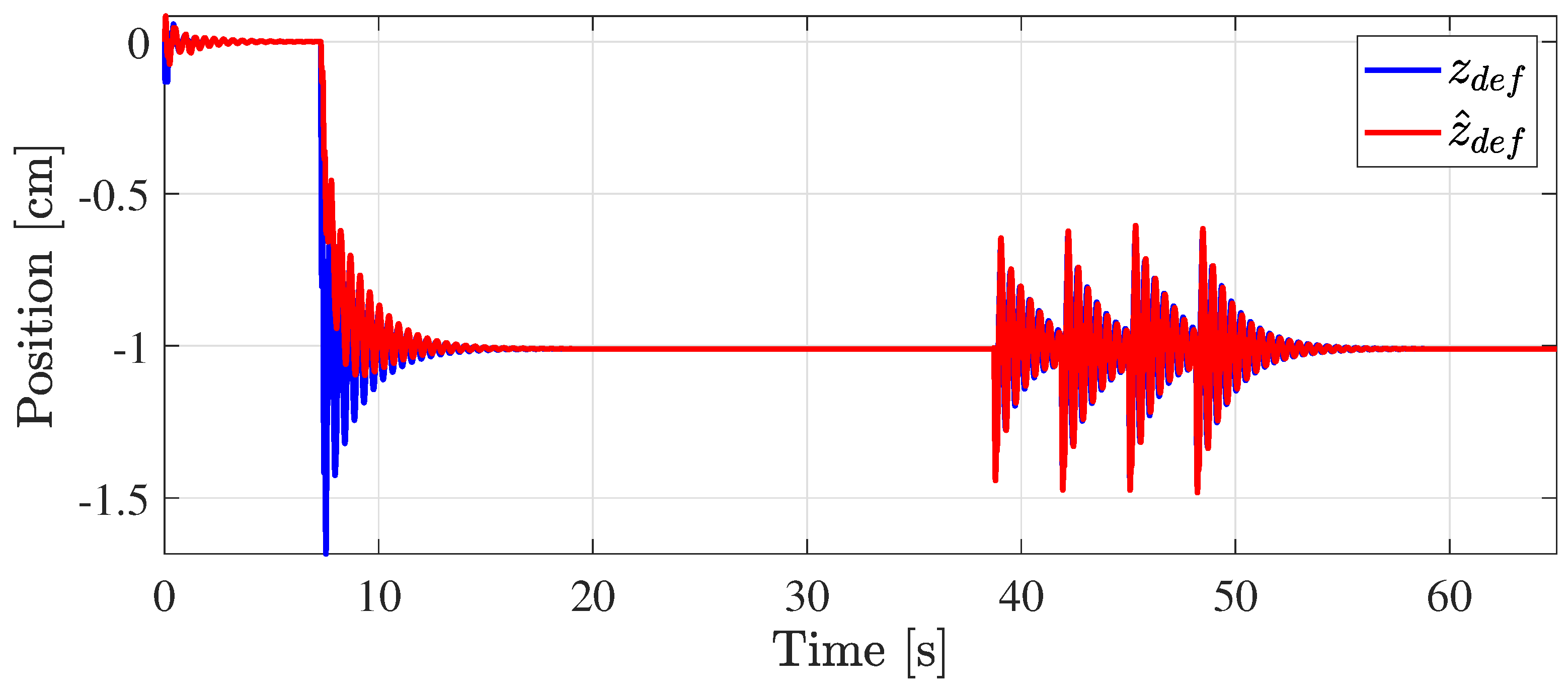
4. Application to a Semi-Active Automotive Suspension
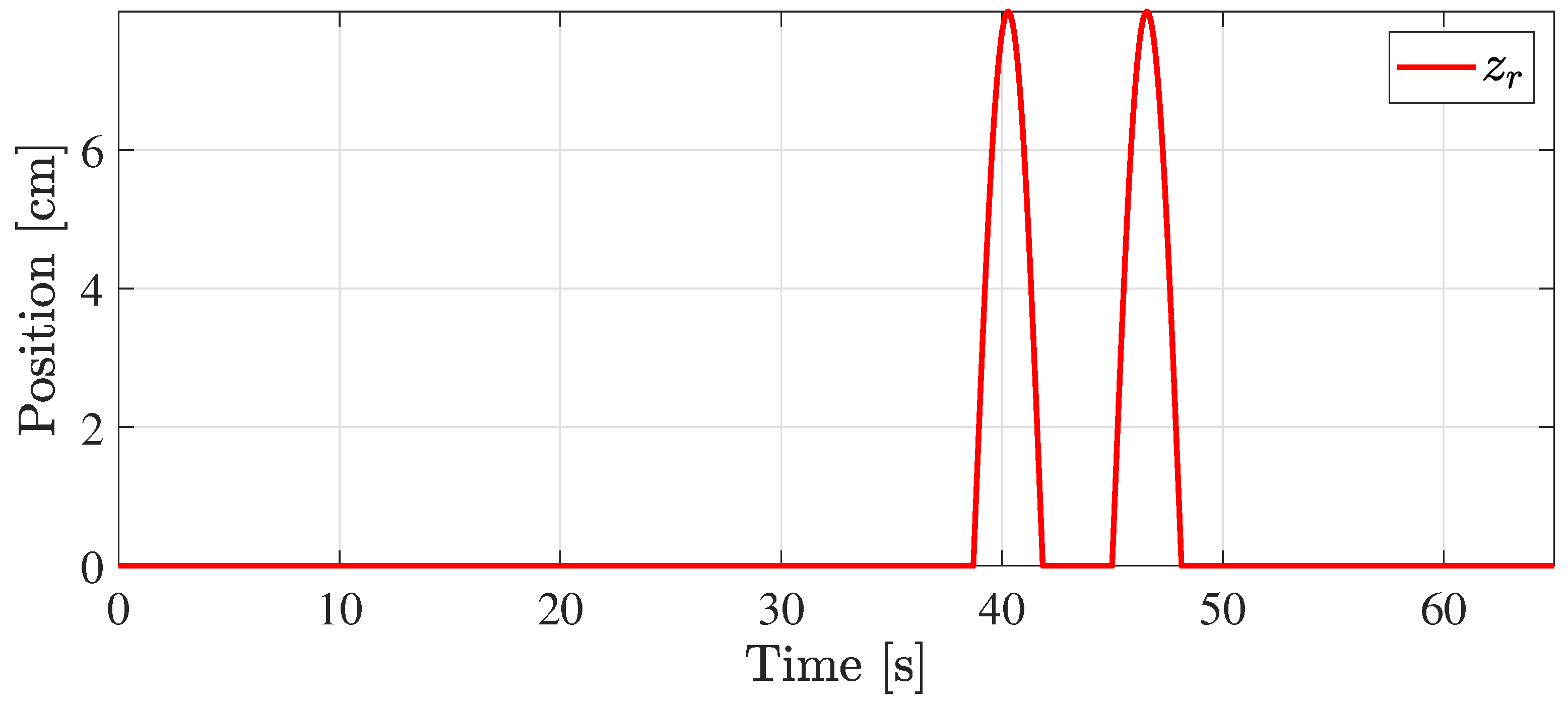
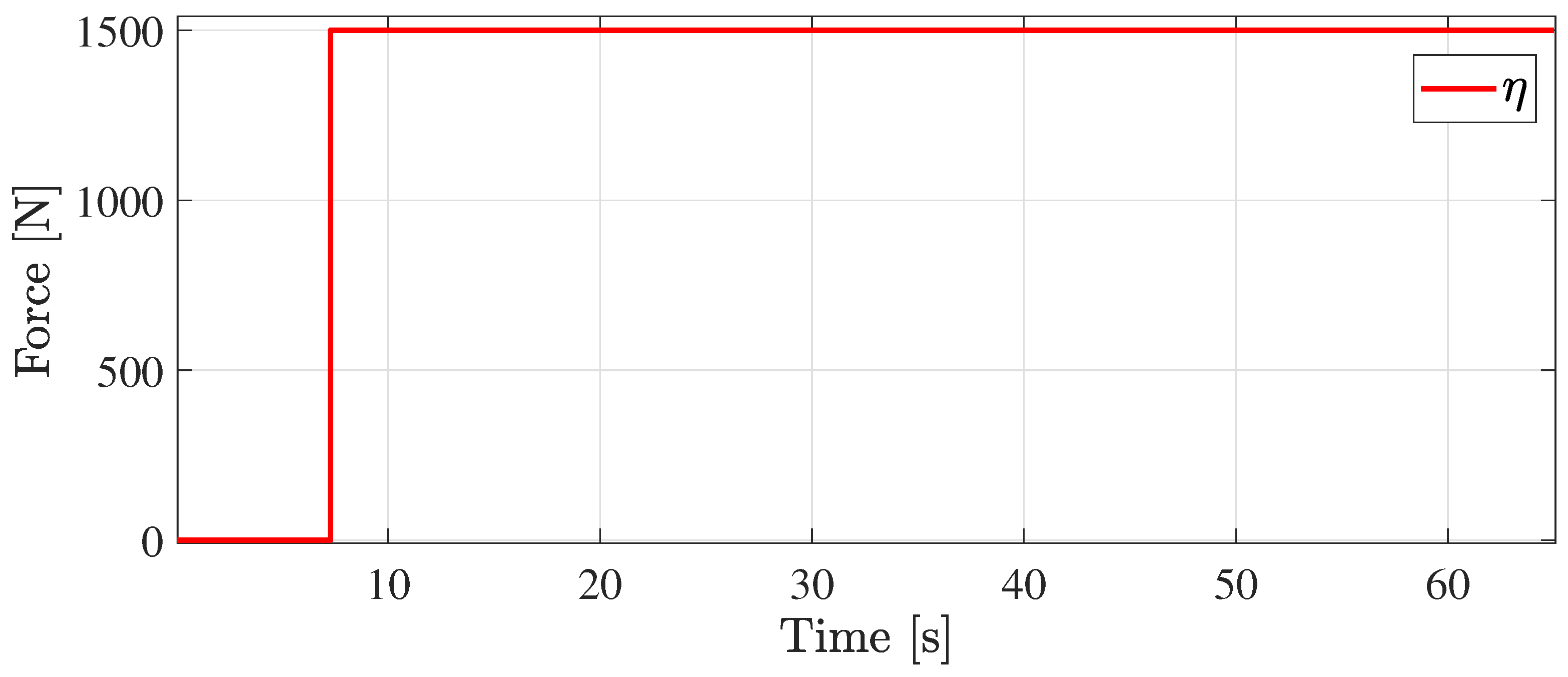
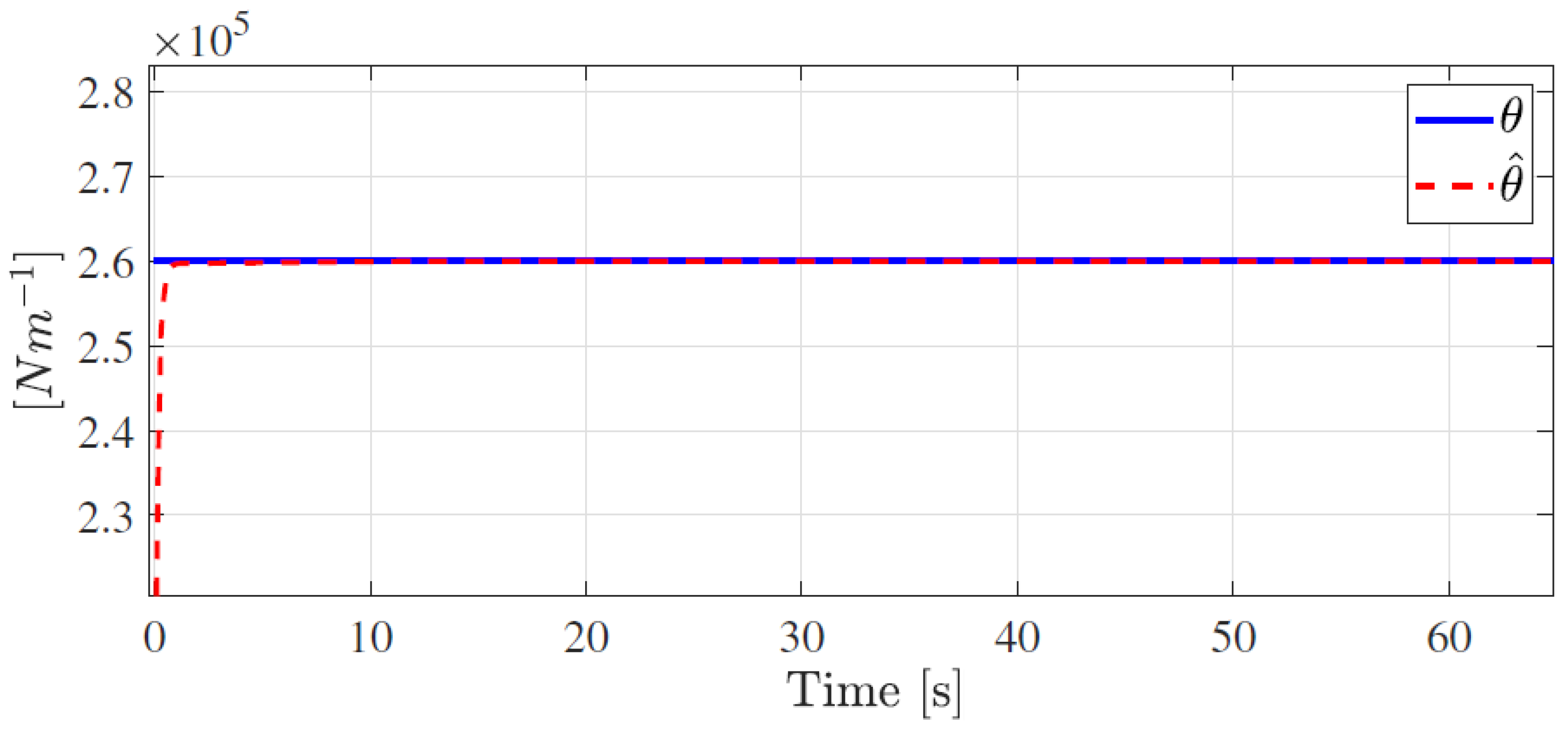
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thau, F. Observing the state of non-linear dynamic systems. Int. J. Control 1973, 17, 471–479. [Google Scholar] [CrossRef]
- Zemouche, A.; Rajamani, R.; Trinh, H.; Zasadzinski, M. A new LMI based observer design method for Lipschitz nonlinear systems. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 2011–2016. [Google Scholar]
- Zemouche, A.; Rajamani, R.; Kheloufi, H.; Bedouhene, F. Robust observer-based stabilization of Lipschitz nonlinear uncertain systems via LMIs-discussions and new design procedure. Int. J. Robust Nonlinear Control 2017, 27, 1915–1939. [Google Scholar] [CrossRef]
- Shaheen, B.; Nazir, M.S.; Rehan, M.; Ahmad, S. Robust generalized observer design for uncertain one-sided Lipschitz systems. Appl. Math. Comput. 2020, 365, 124588. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H. State-Based Dynamic Event-Triggered Observer for One-Sided Lipschitz Nonlinear Systems with Disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2326–2330. [Google Scholar] [CrossRef]
- Mu, Y.; Zhang, H.; Yan, Y.; Wu, Z. A design framework of nonlinear PD observer for one-sided Lipschitz singular systems with disturbances. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3304–3308. [Google Scholar] [CrossRef]
- Besançon, G. Remarks on nonlinear adaptive observer design. Syst. Control Lett. 2000, 41, 271–280. [Google Scholar] [CrossRef]
- Zhang, J.; Swain, A.K.; Nguang, S.K. Robust adaptive descriptor observer design for fault estimation of uncertain nonlinear systems. J. Frankl. Inst. 2014, 351, 5162–5181. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Q.; Zhang, H.; Han, J. H-Infinity Observer for Vehicle Steering System with Uncertain Parameters and Actuator Fault. Actuators 2022, 11, 43. [Google Scholar] [CrossRef]
- Mu, Y.; Zhang, H.; Ren, H.; Cai, Y. Fuzzy adaptive observer-based fault and disturbance reconstructions for TS fuzzy systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2453–2457. [Google Scholar]
- Xiong, X.; Pal, A.K.; Liu, Z.; Kamal, S.; Huang, R.; Lou, Y. Discrete-time adaptive super-twisting observer with predefined arbitrary convergence time. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2057–2061. [Google Scholar] [CrossRef]
- Qin, Q.; Gao, G.; Zhong, J. Finite-Time Adaptive Extended State Observer-Based Dynamic Sliding Mode Control for Hybrid Robots. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3784–3788. [Google Scholar] [CrossRef]
- Li, W.; Yao, X.; Krstic, M. Adaptive-gain observer-based stabilization of stochastic strict-feedback systems with sensor uncertainty. Automatica 2020, 120, 109112. [Google Scholar] [CrossRef]
- Yan, S.; Sun, W.; Yu, X.; Gao, H. Adaptive Sensor Fault Accommodation for Vehicle Active Suspensions via Partial Measurement Information. IEEE Trans. Cybern. 2021, 52, 12290–12301. [Google Scholar] [CrossRef] [PubMed]
- Bzioui, S.; Channa, R. An Adaptive Observer Design for Nonlinear Systems Affected by Unknown Disturbance with Simultaneous Actuator and Sensor Faults. Application to a CSTR. Biointerface Res. Appl. Chem. 2021, 12, 4847–4856. [Google Scholar]
- Bonargent, T.; Menard, T.; Gehan, O.; Pigeon, E. Adaptive observer design for a class of Lipschitz nonlinear systems with multirate outputs and uncertainties: Application to attitude estimation with gyro bias. Int. J. Robust Nonlinear Control 2021, 31, 3137–3162. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Y.; Song, R.; Ma, X.; Li, Y. Adaptive neural control for mobile manipulator systems based on adaptive state observer. Neurocomputing 2022, 489, 504–520. [Google Scholar] [CrossRef]
- Sleiman, M.; Bouyekhf, R.; Al Chami, Z.; El Moudni, A. Uncertainty observer and stabilization for transportation network with constraints. J. Appl. Math. Comput. 2022, 68, 1107–1133. [Google Scholar] [CrossRef]
- Perrier, M.; De Azevedo, S.F.; Ferreira, E.; Dochain, D. Tuning of observer-based estimators: Theory and application to the on-line estimation of kinetic parameters. Control Eng. Pract. 2000, 8, 377–388. [Google Scholar] [CrossRef]
- Astorga, C.M.; Othman, N.; Othman, S.; Hammouri, H.; McKenna, T.F. Nonlinear continuous–discrete observers: Application to emulsion polymerization reactors. Control Eng. Pract. 2002, 10, 3–13. [Google Scholar] [CrossRef]
- Arcak, M.; Gorgun, H.; Pedersen, L.M.; Varigonda, S. A nonlinear observer design for fuel cell hydrogen estimation. IEEE Trans. Control Syst. Technol. 2004, 12, 101–110. [Google Scholar] [CrossRef]
- Astorga-Zaragoza, C.M.; Zavala-Río, A.; Alvarado, V.; Méndez, R.M.; Reyes-Reyes, J. Performance monitoring of heat exchangers via adaptive observers. Measurement 2007, 40, 392–405. [Google Scholar] [CrossRef]
- Ramos-Hernández, E.; Astorga-Zaragoza, C.; Reyes, J.R.; Ramırez-Rasgado, F.; Osorio-Gordillo, G.; Ruiz-Acosta, S. Estimation of Process Variables in a Steam Distillation Plant. Congreso Nacional de Control Automático. 2023. Available online: https://revistadigital.amca.mx/wp-content/uploads/2023/12/0103.pdf (accessed on 29 May 2024).
- Farza, M.; M’saad, M.; Menard, T.; Ltaief, A.; Maatoug, T. Adaptive observer design for a class of nonlinear systems. Application to speed sensorless induction motor. Automatica 2018, 90, 239–247. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, M.; Guo, Z.; Huang, X.; Zhang, Y.; Zhang, Z. Adaptive state-observer for monitoring flexible nuclear reactors. Energy 2019, 171, 893–909. [Google Scholar] [CrossRef]
- Zhong, J.; Feng, Y.; Chen, X.; Zeng, C. Observer-based piecewise control of reaction–diffusion systems with the non-collocated output feedback. J. Appl. Math. Comput. 2023, 69, 4187–4211. [Google Scholar] [CrossRef]
- de Jesús Rubio, J.; Lughofer, E.; Pieper, J.; Cruz, P.; Martinez, D.I.; Ochoa, G.; Islas, M.A.; Garcia, E. Adapting H-infinity controller for the desired reference tracking of the sphere position in the Maglev process. Inf. Sci. 2021, 569, 669–686. [Google Scholar] [CrossRef]
- Asad, M.; Rehan, M.; Ahn, C.K.; Tufail, M.; Basit, A. Distributed State and Parameter Estimation over Wireless Sensor Networks under Energy Constraints. IEEE Trans. Netw. Sci. Eng. 2024, 11, 2976–2988. [Google Scholar] [CrossRef]
- Chen, C.; Sun, F.; Xiong, R.; He, H. A Novel Dual H Infinity Filters Based Battery Parameter and State Estimation Approach for Electric Vehicles Application. Energy Procedia 2016, 103, 375–380. [Google Scholar] [CrossRef]
- Gong, X.; Suh, J.; Lin, C. A novel method for identifying inertial parameters of electric vehicles based on the dual H infinity filter. Veh. Syst. Dyn. 2019, 58, 28–48. [Google Scholar] [CrossRef]
- Xu, S. Robust filtering for a class of discrete-time uncertain nonlinear systems with state delay. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 1853–1859. [Google Scholar]
- Ekramian, M.; Hosseinnia, S.; Sheikholeslam, F. Observer design for non-linear systems based on a generalised Lipschitz condition. IET Control Theory Appl. 2011, 5, 1813–1818. [Google Scholar] [CrossRef]
- Ekramian, M.; Sheikholeslam, F.; Hosseinnia, S.; Yazdanpanah, M.J. Adaptive state observer for Lipschitz nonlinear systems. Syst. Control Lett. 2013, 62, 319–323. [Google Scholar] [CrossRef]
- Guo, S.; Yang, S.; Pan, C. Dynamic modeling of magnetorheological damper behaviors. J. Intell. Mater. Syst. Struct. 2006, 17, 3–14. [Google Scholar] [CrossRef]
- Tudon-Martinez, J.C.; Morales-Menéndez, R.; Ramirez-Mendoza, R.; Sename, O.; Dugard, L. Fault tolerant control in a semi-active suspension. IFAC Proc. Vol. 2012, 45, 1173–1178. [Google Scholar] [CrossRef]
- Khalil, H.K.; Grizzle, J.W. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002; Volume 3, Available online: https://nasim.hormozgan.ac.ir/ostad/UploadedFiles/863740/863740-8707186354456456.pdf (accessed on 29 May 2024).
- Zhao, J.; Mili, L. A decentralized H-infinity unscented Kalman filter for dynamic state estimation against uncertainties. IEEE Trans. Smart Grid 2018, 10, 4870–4880. [Google Scholar] [CrossRef]
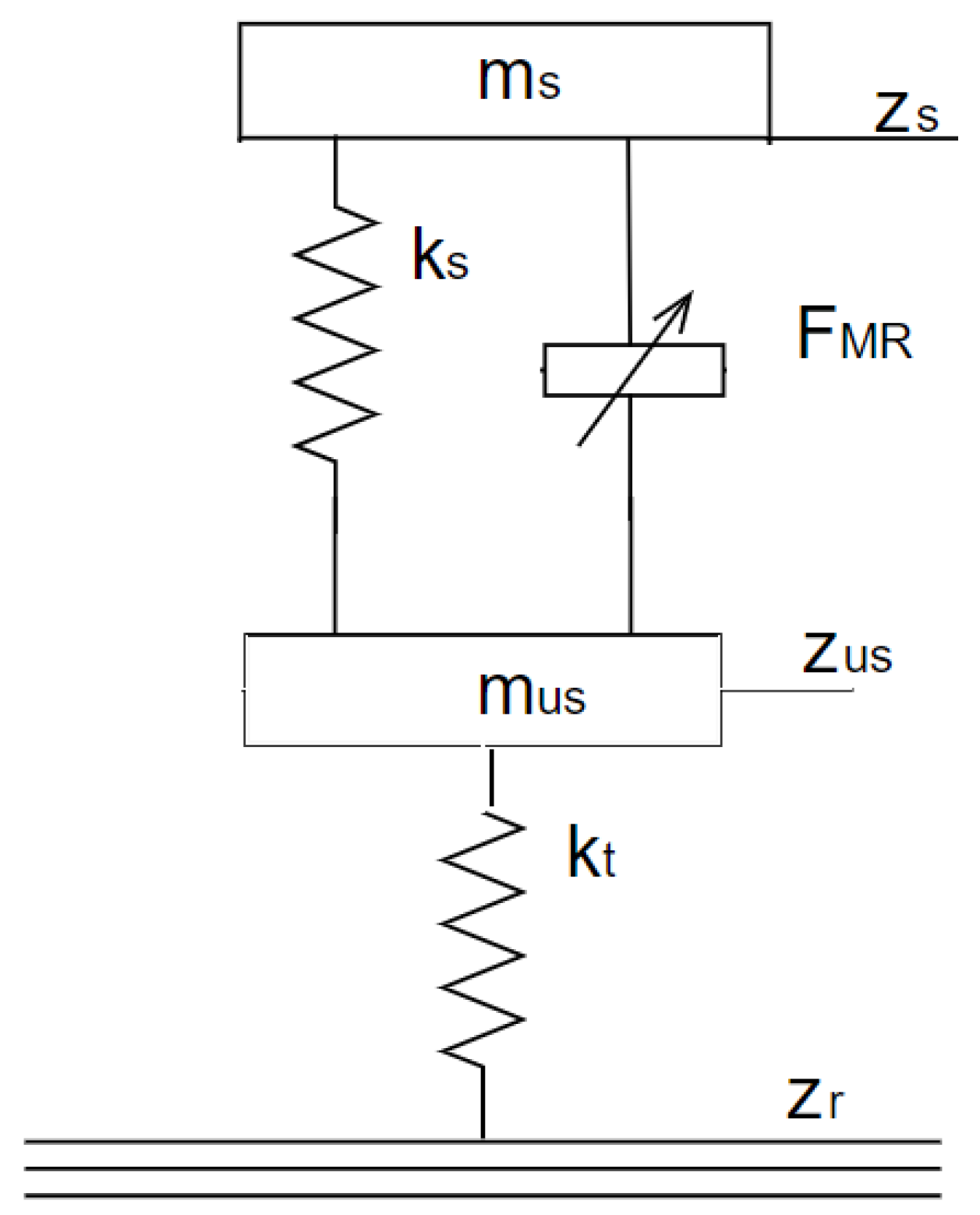

| Parameter | Description | Value | Units |
|---|---|---|---|
| , | Pre-effort zone of | , | (Ns)/m |
| , | Post-effort zone of | , | (Ns)/m |
| Damping force | N/A | ||
| I | Electric current | 2 | A |
| Spring stiffness coefficient | 86,378 | N/m | |
| Tire stiffness coefficient | 260,000 | N/m | |
| Suspended mass and Unsprung (tire) mass | 470, 110 | kg | |
| Variable | Description | Role | Units |
| Vertical damper position | output | m | |
| Vertical damper speed | m/s | ||
| Road profile | input | m | |
| Vertical displacement of , | outputs and | m | |
| Vertical speed of , | state and | m/s | |
| Vertical acceleration of , | and | m2/s | |
| Shock absorber hysteresis | nonlinear function | ||
| Force MR | damping force | N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarado-Méndez, P.E.; Astorga-Zaragoza, C.M.; Osorio-Gordillo, G.L.; Aguilera-González, A.; Vargas-Méndez, R.; Reyes-Reyes, J.
Alvarado-Méndez PE, Astorga-Zaragoza CM, Osorio-Gordillo GL, Aguilera-González A, Vargas-Méndez R, Reyes-Reyes J.
Alvarado-Méndez, Pedro Eusebio, Carlos M. Astorga-Zaragoza, Gloria L. Osorio-Gordillo, Adriana Aguilera-González, Rodolfo Vargas-Méndez, and Juan Reyes-Reyes.
2024. "






