Modeling of the Human Cardiovascular System: Implementing a Sliding Mode Observer for Fault Detection and Isolation
Abstract
:1. Introduction
2. Cardiovascular System Model
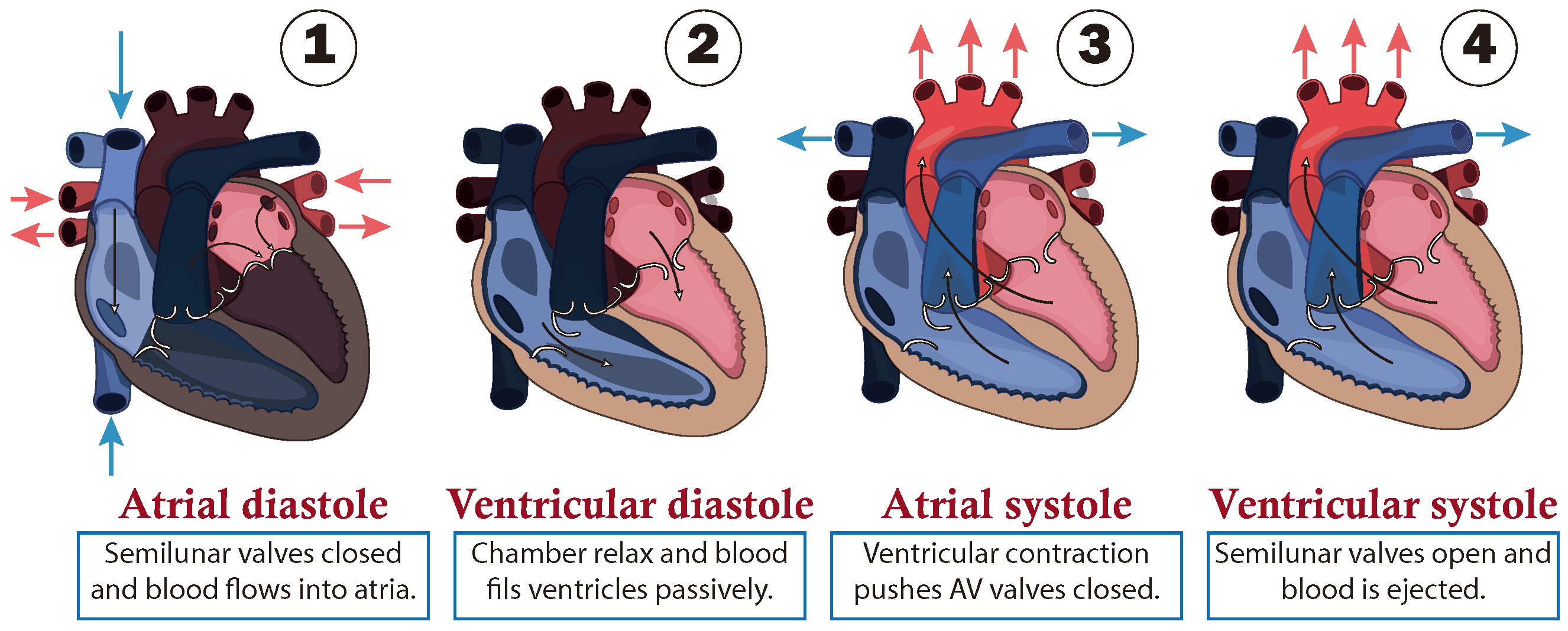
2.1. Anatomy and Physiology of the Cardiac Cycle
- Blood circulation pathway
- Cardiac cycle phases
- (1)
- The first stage is atrial diastole and the beginning of ventricular systole, during which the atria relax while the ventricles contract and the atrioventricular valves close. This increases the pressure inside the ventricles but not enough to open the semilunar valves.
- (2)
- The second stage is ventricular diastole, when the pressure inside the ventricles rapidly decreases, the atrioventricular valves open, and the chambers passively fill due to their relaxation combined with atrial systole, during which the atria contract to fill the ventricles.
- (3)
- The third stage is atrial systole, during which the pressure in the ventricles rises until it exceeds that of the arteries. This leads to the opening of the semilunar valves and the ejection of blood into the pulmonary artery, marking the beginning of systemic circulation.
- (4)
- The last stage marks the end of ventricular systole and the start of the ventricular and atrial diastole. During this phase, the pressure in the ventricles decreases rapidly, and all chambers passively fill due to their relaxation. This transition leads into a new cardiac cycle, beginning with atrial systole.
2.2. Valve Pathologies
3. Description of the Cardiovascular System Model
3.1. Equivalent Electric Model
3.2. Elastance
3.3. Presentation of the Mathematical Model of the Cardiovascular System
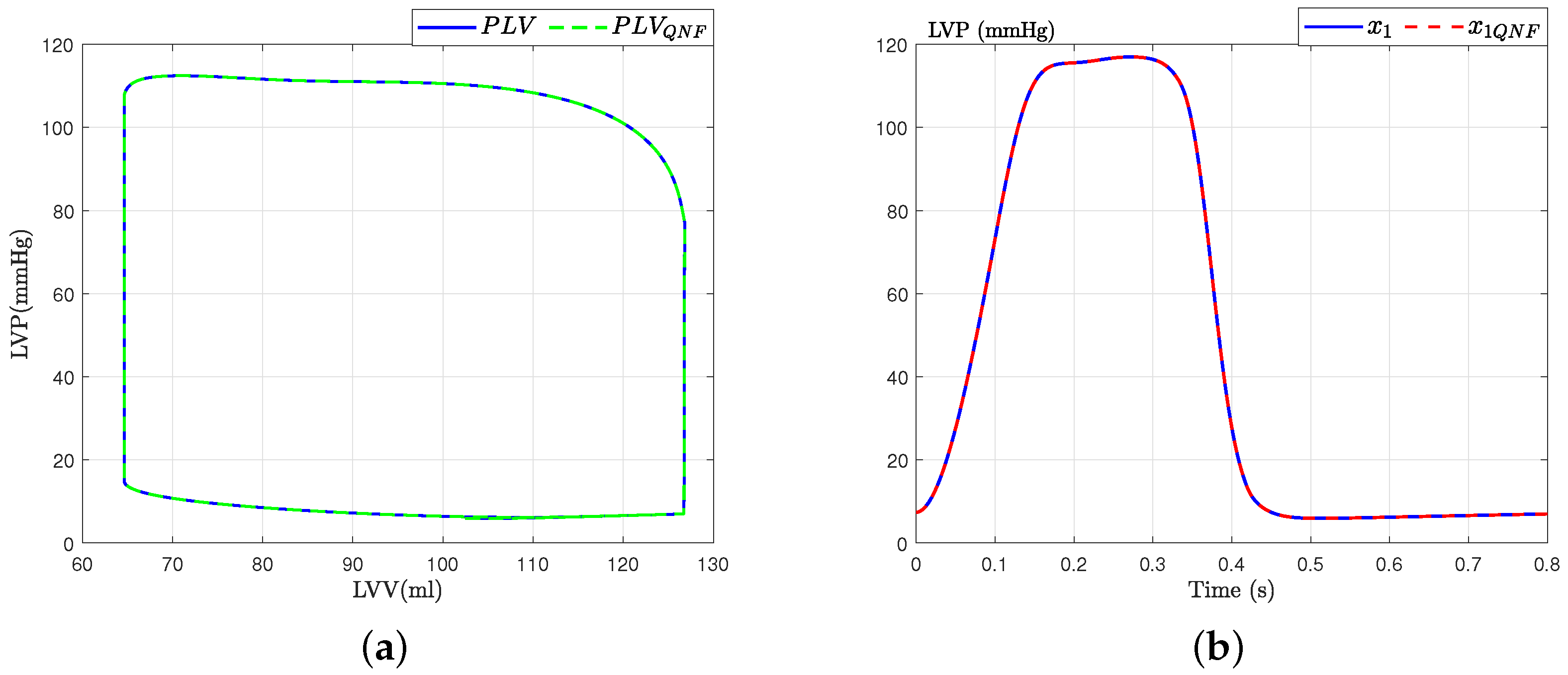
3.4. Quadratic Normal Form of the CVS [25]
3.5. Validation of the Quadratic Normal Form of the CVS Model
4. Sliding Mode Observer Design
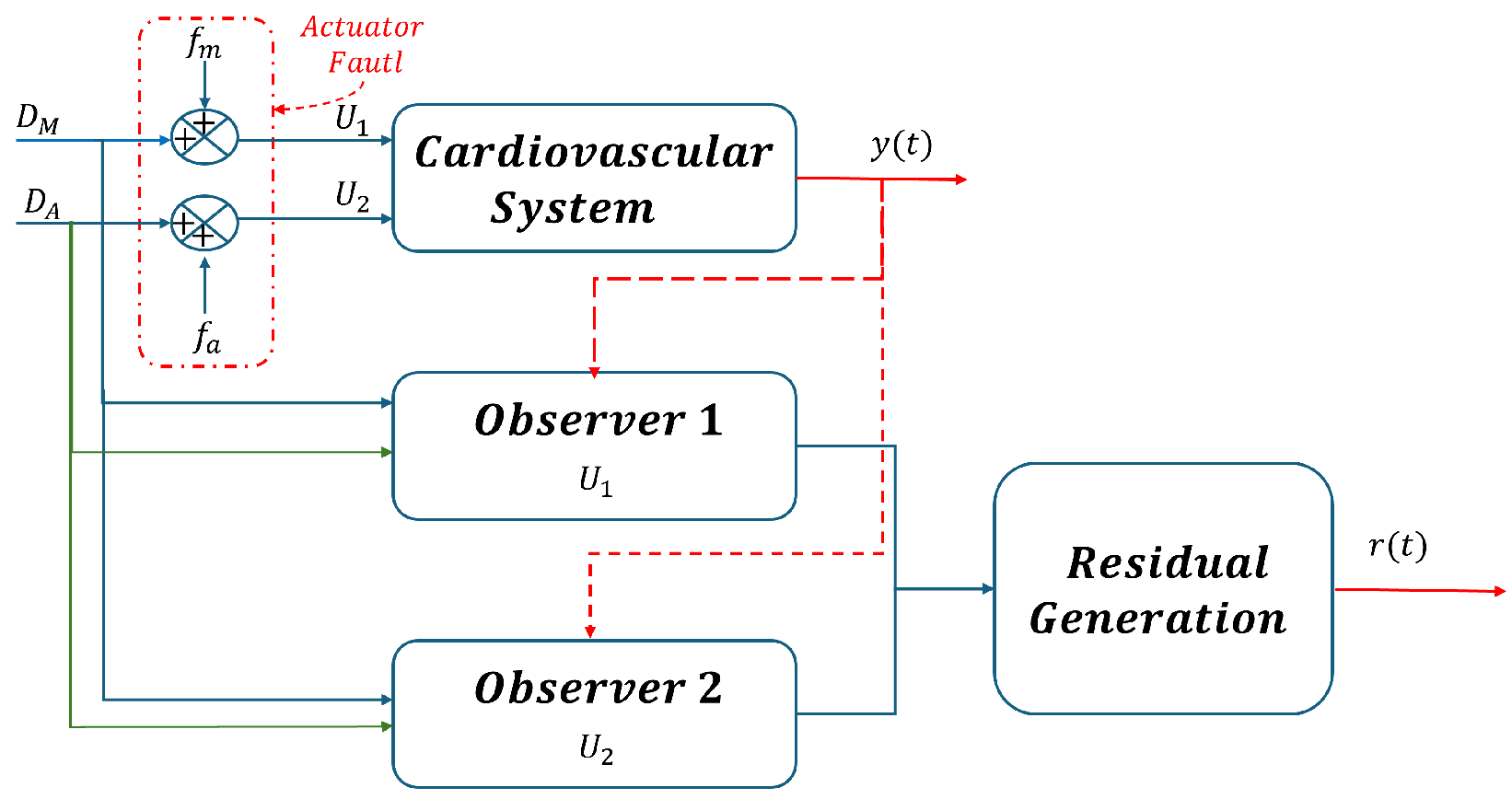
5. Model for Anomaly Detection
5.1. Residual Generation of Anomalies
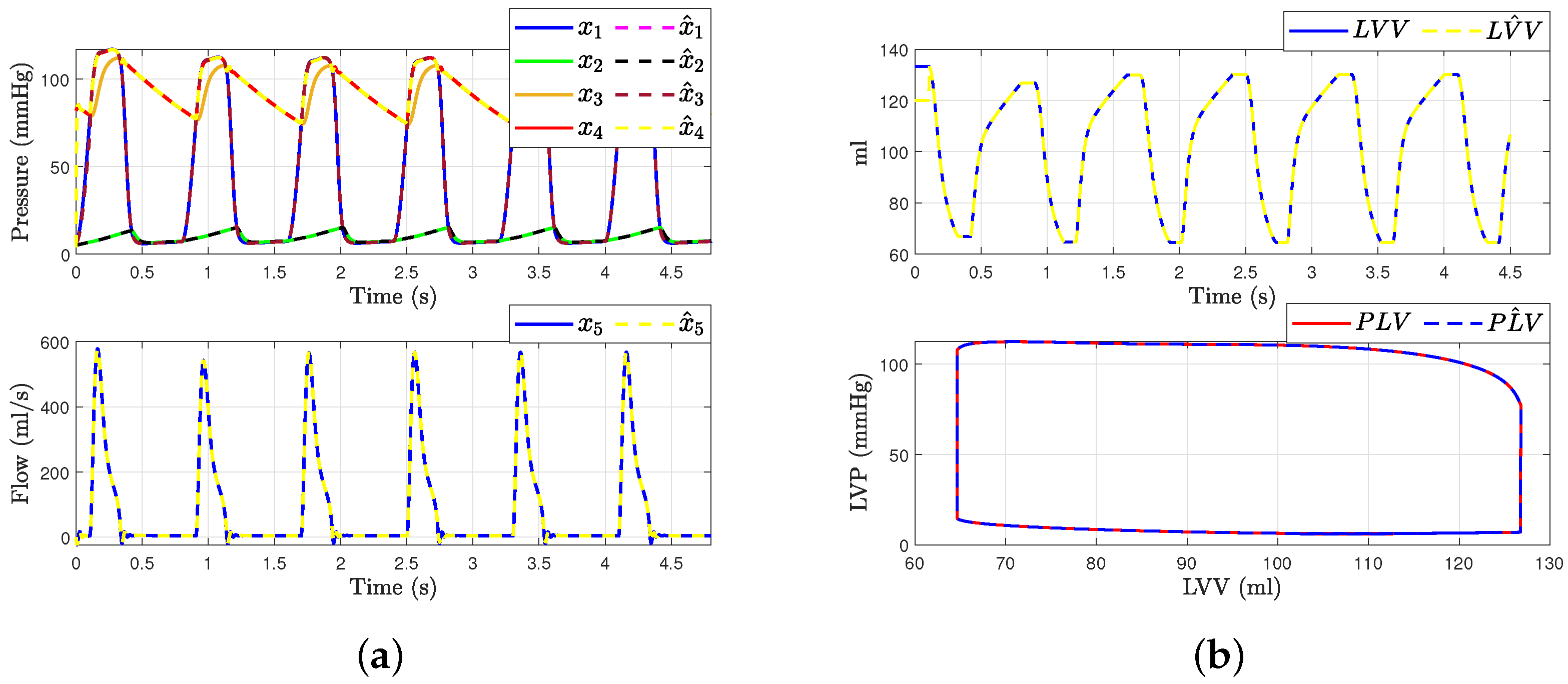
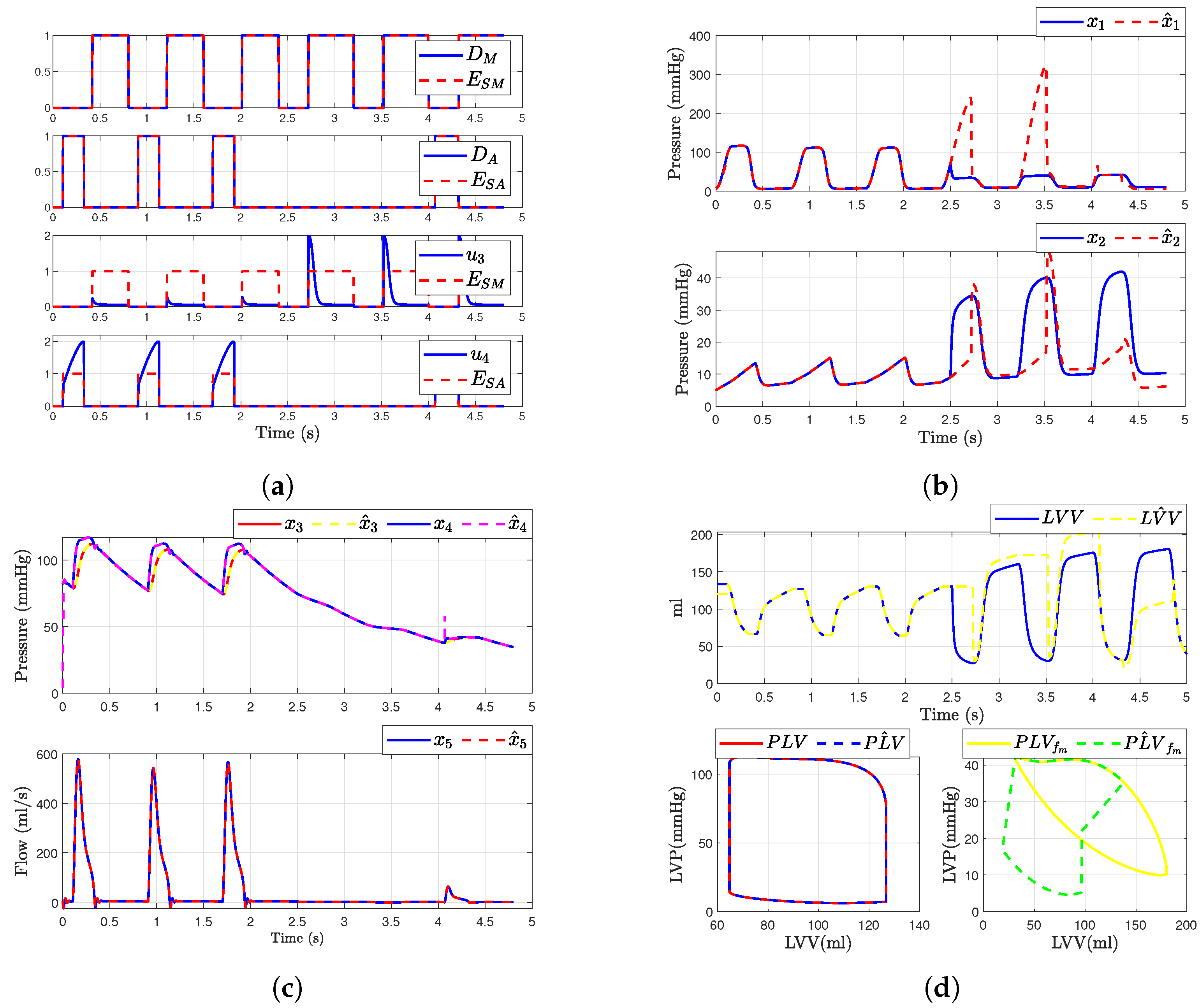
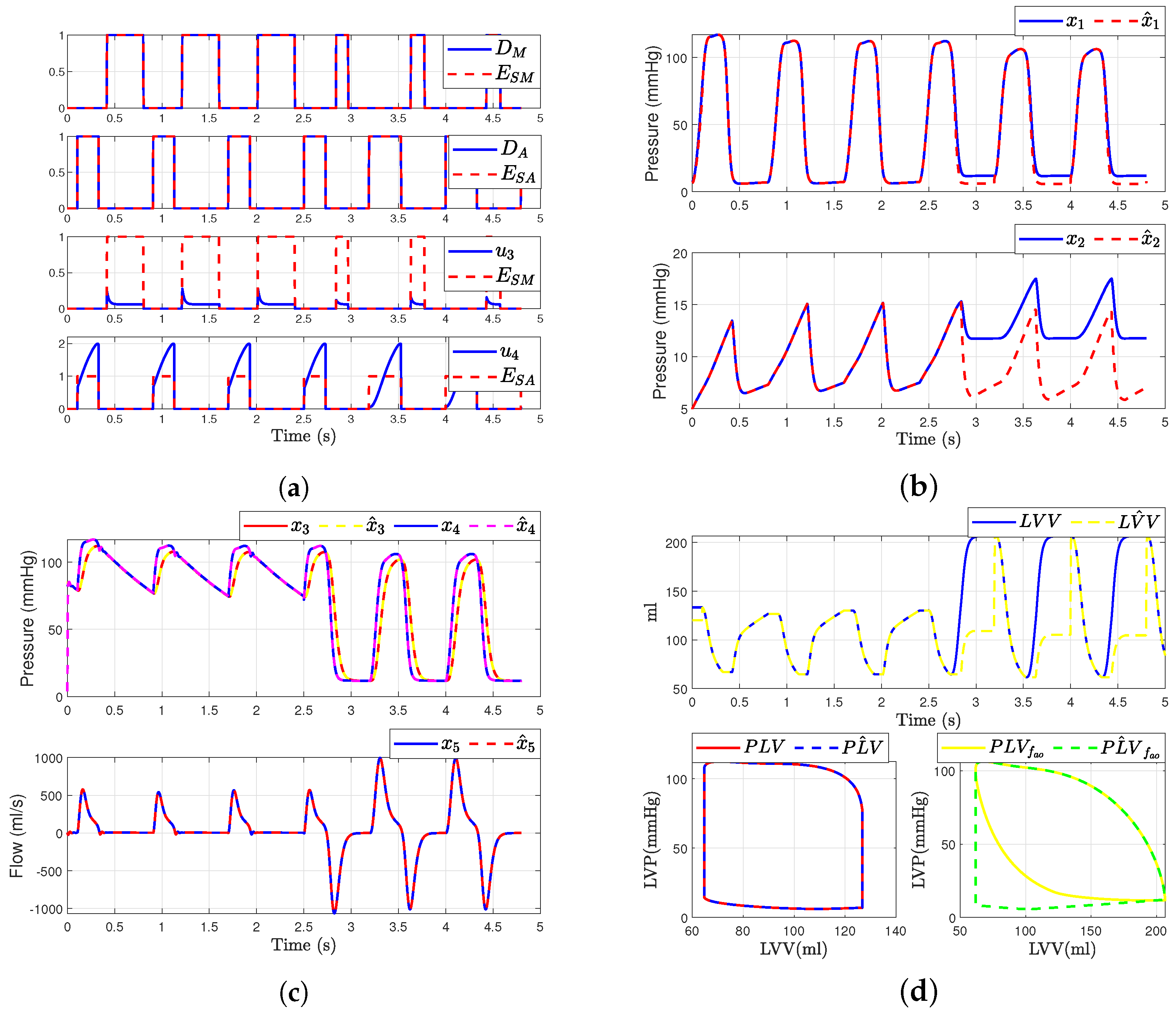
5.2. Simulation Results
5.3. Scenario 1: Mitral Regurgitation
5.4. Case 2: Aortic Regurgitation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CVD | Cardiovascular disease |
| WHO | World Health Organization |
| CVS | Cardiovascular system |
| LVP | Left ventricular pressure |
| LV | Left ventricle |
| LVV | Left ventricular volume |
| EDV | End-diastolic volume |
| ESV | End-systolic volume |
| SMO | Sliding mode observer |
| FDI | Fault detection and isolation |
| PV | Pressure–volume |
| PVA | Pressure–volume area |
| LA | Left atria |
| Heart rate | |
| LAP | Left atrial pressure |
| AoP | Ascending aorta pressure |
| F | Total flow |
References
- World Health Organization. Cardiovascular Diseases (CVDs). Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 8 May 2024).
- Chen, C.; Ting, C.-T.; Nussbacher, A.; Nevo, E.; Kass, D.A.; Pak, P.; Wang, S.-P.; Chang, M.; Yin, F.C.P. Validation of carotid artery tonometry as a means of estimating augmentation index of ascending aortic pressure. Hypertension 1996, 27, 168–175. [Google Scholar] [CrossRef]
- Fónod, R.; Krokavec, D. Actuator fault estimation using neuro-sliding mode observers. In Proceedings of the IEEE 16th International Conference on Intelligent Engineering Systems (INES), Lisbon, Portugal, 13–15 June 2012; pp. 405–410. [Google Scholar]
- Ledezma, F.D.; Laleg-Kirati, T.M. Detection of Cardiovascular Anomalies: Hybrid Systems Approach. IFAC Proc. Vol. 2012, 45, 222–227. [Google Scholar] [CrossRef]
- Laleg-Kirati, T.M.; Belkhatir, Z.; Ledezma, F.D. Application of Hybrid Dynamical Theory to the Cardiovascular System. In Hybrid Dynamical Systems; Djemai, M., Defoort, M., Eds.; Springer: Cham, Switzerland, 2015; pp. 315–328. [Google Scholar]
- Traver, J.; Nuevo-Gallardo, C.; Tejado, I.; Fernández-Portales, J.; Ortega-Morán, J.F.; Pagador, J.B.; Vinagre, B.M. Cardiovascular circulatory system and left carotid model: A fractional approach to disease modeling. Fractal Fract. 2022, 6, 64. [Google Scholar] [CrossRef]
- Diaz Ledezma, F.; Laleg-Kirati, T.M. A first approach on fault detection and isolation for cardiovascular anomalies detection. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 5788–5793. [Google Scholar]
- El Khaloufi, G.; Chaibi, N.; Alaoui, S.; Boumhidi, I.; Driss, E.-J. Design of Observer for Cardiovascular Anomalies Detection: An LMI approach. In Proceedings of the 2022 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 18–20 May 2022. [Google Scholar]
- Ghasemi, Z.; Jeon, W.; Kim, C.-S.; Gupta, A.; Rajamani, R.; Hahn, J.-O. Observer-based deconvolution of deterministic input in coprime multichannel systems with its application to noninvasive central blood pressure monitoring. J. Dyn. Syst. Meas. Control 2020, 142, 091006. [Google Scholar] [CrossRef] [PubMed]
- Ortiz-Rangel, E.; Guerrero-Ramírez, G.V.; García-Beltrán, C.D.; Guerrero-Lara, M.; Adam-Medina, M.; Astorga-Zaragoza, C.M.; Reyes-Reyes, J.; Posada-Gómez, R. Dynamic modeling and simulation of the human cardiovascular system with PDA. Biomed. Signal Process. Control 2022, 71, 103151. [Google Scholar] [CrossRef]
- Laubscher, R.; van der Merwe, J.; Liebenberg, J.; Herbst, P. Dynamic simulation of aortic valve stenosis using a lumped parameter cardiovascular system model with flow regime dependent valve pressure loss characteristics. Med. Eng. Phys. 2022, 106, 103838. [Google Scholar] [CrossRef] [PubMed]
- Simaan, M.A.; Ferreira, A.; Chen, S.; Antaki, J.F.; Galati, D.G. A dynamical state space representation and performance analysis of a feedback-controlled rotary left ventricular assist device. IEEE Trans. Control. Syst. Technol. 2018, 17, 15–28. [Google Scholar] [CrossRef]
- Ferreira, A.; Chen, S.; Simaan, M.A.; Boston, J.R.; Antaki, J.F. A nonlinear state-space model of a combined cardiovascular system and a rotary pump. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 897–902. [Google Scholar]
- Korakianitis, T.; Shi, Y. A concentrated parameter model for the human cardiovascular system including heart valve dynamics and atrioventricular interaction. Med. Eng. Phys. 2006, 28, 613–628. [Google Scholar] [CrossRef] [PubMed]
- Simaan, M.A. Modeling and control of the heart left ventricle supported with a rotary assist device. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2656–2661. [Google Scholar]
- Astorga-Zaragoza, C. Observer-based monitoring of the cardiovascular system. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 501–505. [Google Scholar] [CrossRef]
- Belkhatir, Z.; Laleg-Kirati, T.-M.; Tadjine, M. Residual generator for cardiovascular anomalies detection. In Proceedings of the European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 1862–1868. [Google Scholar]
- Ramírez-Rasgado, F.; Hernández-González, O.; Astorga-Zaragoza, C.M.; Farza, M.; Barreto-Arenas, O.; Guerrero-Sánchez, M.E. Observer-based supervision of the cardiovascular system with delayed measurements. In Proceedings of the Congreso Nacional de Control Automático, Tuxtla Gutiérrez, Mexico, 12–14 October 2022. [Google Scholar]
- Serrano-Cruz, D.; Boutat-Baddas, L.; Darouach, M.; Zaragoza, C.M.A.; Ramirez, G.V.G. Sliding mode observer design for fault estimation in cardiovascular system. In Proceedings of the Congreso Nacional de Control Automático, Acapulco, Mexico, 25–27 October 2023. [Google Scholar]
- Simaan, M.A. Rotary heart assist devices. In Springer Handbook of Automation; Nof, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1409–1422. [Google Scholar]
- Mensah, G.A.; Roth, G.A.; Fuster, V. The global burden of cardiovascular diseases and risk factors: 2020 and beyond. J. Am. Coll. Cardiol. 2019, 74, 2529–2532. [Google Scholar] [CrossRef] [PubMed]
- Aluru, J.S.; Barsouk, A.; Saginala, K.; Rawla, P.; Barsouk, A. Valvular heart disease epidemiology. Med. Sci. 2022, 10, 32. [Google Scholar] [CrossRef] [PubMed]
- Hollenberg, S.M. Valvular Heart Disease in Adults: Etiologies, Classification, and Diagnosis. FP Essent. 2017, 457, 11–16. [Google Scholar] [PubMed]
- Manoliu, V. Modeling cardiovascular hemodynamics in a model with nonlinear parameters. In Proceedings of the E-Health and Bioengineering Conference (EHB), Iasi, Romania, 19–21 November 2015; pp. 1–4. [Google Scholar]
- Boutat-Baddas, L.; Boutat, D.; Barbot, J.; Tauleigne, R. Quadratic observability normal form. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No.01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 3, pp. 2942–2947. [Google Scholar]
- Boutat-Baddas, L. Analyse des singularités d’observabilité et de détectabilité: Application à la synchronisation des circuits éléctroniques chaotiques. Ph.D. Thesis, Université de Cergy-Pontoise, Cergy, France, 2002. [Google Scholar]
- Serrano-Cruz, D.A.; Boutat-Baddas, L.; Darouach, M.; Astorga-Zaragoza, C.-M. Observer design for a nonlinear cardiovascular system. In Proceedings of the 9th International Conference on Systems and Control, Caen, France, 24–26 November 2021; pp. 294–299. [Google Scholar]
- Barbot, J.; Boukhobza, T.; Djemai, M. Sliding mode observer for triangular input form. In Proceedings of the 35th IEEE Conference on Decision and Control, Kobe, Japan, 13 December 1996; Volume 2, pp. 1489–1490. [Google Scholar]
- Barbot, J.; Floquet, T. Iterative higher order sliding mode observer for nonlinear systems with unknown inputs. Dyn. Contin. Discret. Impuls. Syst. 2010, 17, 1019–1033. [Google Scholar]
- Floquet, T.; Barbot, J.-P. Super Twisting Algorithm-Based Step-by-Step Sliding Mode Observers for Nonlinear Systems with Unknown Inputs. Int. J. Syst. Sci. 2007, 38, 803–815. [Google Scholar] [CrossRef]
- Draženović, B. The invariance conditions in variable structure systems. Automatica 1969, 5, 287–295. [Google Scholar] [CrossRef]



| Variables | Abbreviation | Physiological Meaning (Unit) |
|---|---|---|
| LVP(t) | Left ventricular pressure (mmHg) | |
| LAP(t) | Left atrial pressure (mmHg) | |
| AP(t) | Descending arterial pressure (mmHg) | |
| Ascending aortic pressure (mmHg) | ||
| F(t) | Total aortic flow (mL/s) |
| Parameter | Value | Physiological Meaning |
|---|---|---|
| Systemic compliance | ||
| Left atrial compliance | ||
| Aortic compliance | ||
| Inertia of blood in aorta | ||
| Characteristic resistance | ||
| Mitral valve resistance | ||
| Aortic valve resistance | ||
| Left Ventricle | ||
| 2 | Maximum volume in diastole | |
| 0.06 | Minimum volume in diastole | |
| 10 | Reference volume at zero pressure (mL) | |
| 75 | Heart rate (bpm) | |
| Elastance | ||
| 1.17 | Shape parameter | |
| 0.7 | Shape parameter | |
| 1.55 | Amplitude | |
| 1.9 | Ascending slope of the LV relaxation time | |
| 21.9 | Descending slope of the LV relaxation time |
| Residuals/Faults | Anomalie on | Anomalie on |
|---|---|---|
| 0 | 0 | |
| 0 | 0 | |
| 1 | 1 | |
| 0 | 0 | |
| 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serrano-Cruz, D.A.; Boutat-Baddas, L.; Darouach, M.; Astorga-Zaragoza, C.M.; Guerrero Ramírez, G.V. Modeling of the Human Cardiovascular System: Implementing a Sliding Mode Observer for Fault Detection and Isolation. Math. Comput. Appl. 2024, 29, 57. https://doi.org/10.3390/mca29040057
Serrano-Cruz DA, Boutat-Baddas L, Darouach M, Astorga-Zaragoza CM, Guerrero Ramírez GV. Modeling of the Human Cardiovascular System: Implementing a Sliding Mode Observer for Fault Detection and Isolation. Mathematical and Computational Applications. 2024; 29(4):57. https://doi.org/10.3390/mca29040057
Chicago/Turabian StyleSerrano-Cruz, Dulce A., Latifa Boutat-Baddas, Mohamed Darouach, Carlos M. Astorga-Zaragoza, and Gerardo V. Guerrero Ramírez. 2024. "Modeling of the Human Cardiovascular System: Implementing a Sliding Mode Observer for Fault Detection and Isolation" Mathematical and Computational Applications 29, no. 4: 57. https://doi.org/10.3390/mca29040057
APA StyleSerrano-Cruz, D. A., Boutat-Baddas, L., Darouach, M., Astorga-Zaragoza, C. M., & Guerrero Ramírez, G. V. (2024). Modeling of the Human Cardiovascular System: Implementing a Sliding Mode Observer for Fault Detection and Isolation. Mathematical and Computational Applications, 29(4), 57. https://doi.org/10.3390/mca29040057







