Numerical Modelling of Corrugated Paperboard Boxes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Box Geometry And Features
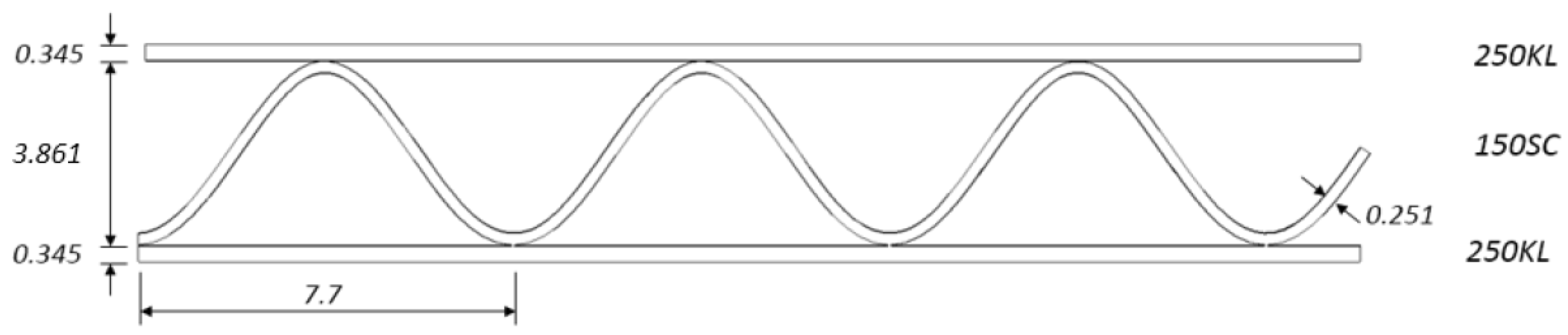
2.2. Paperboard Geometry
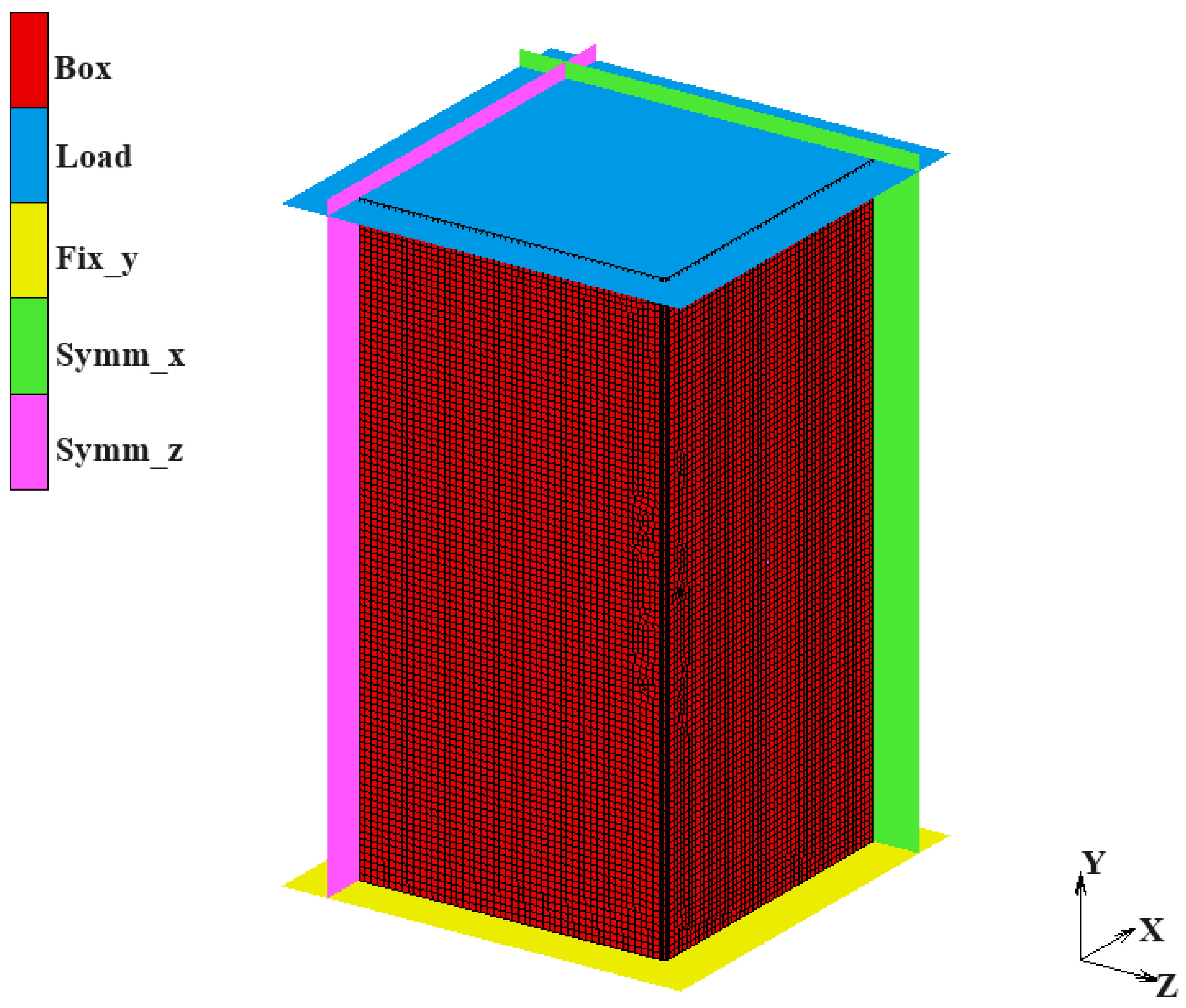
2.3. Four-Point Bending Tests
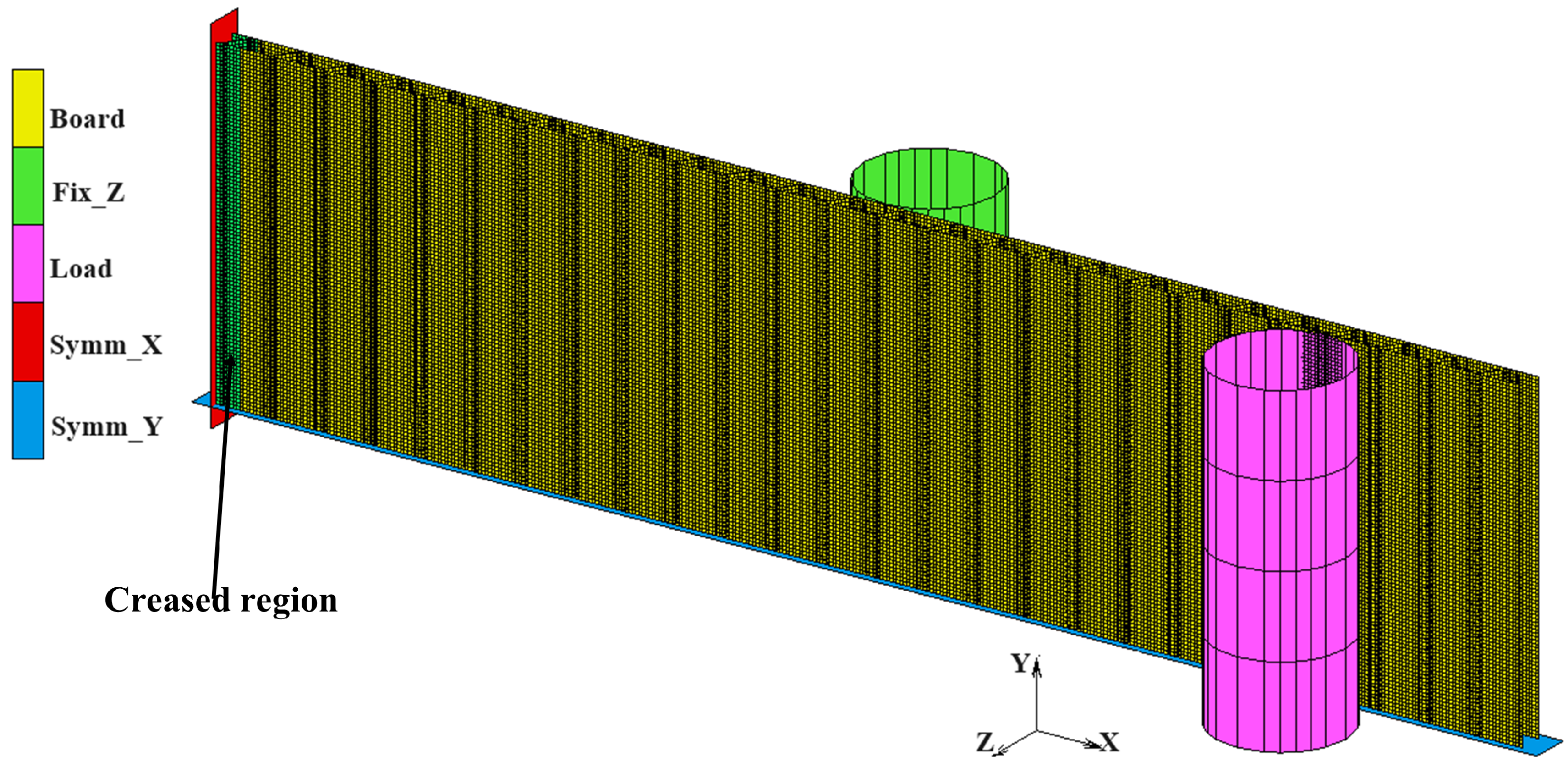
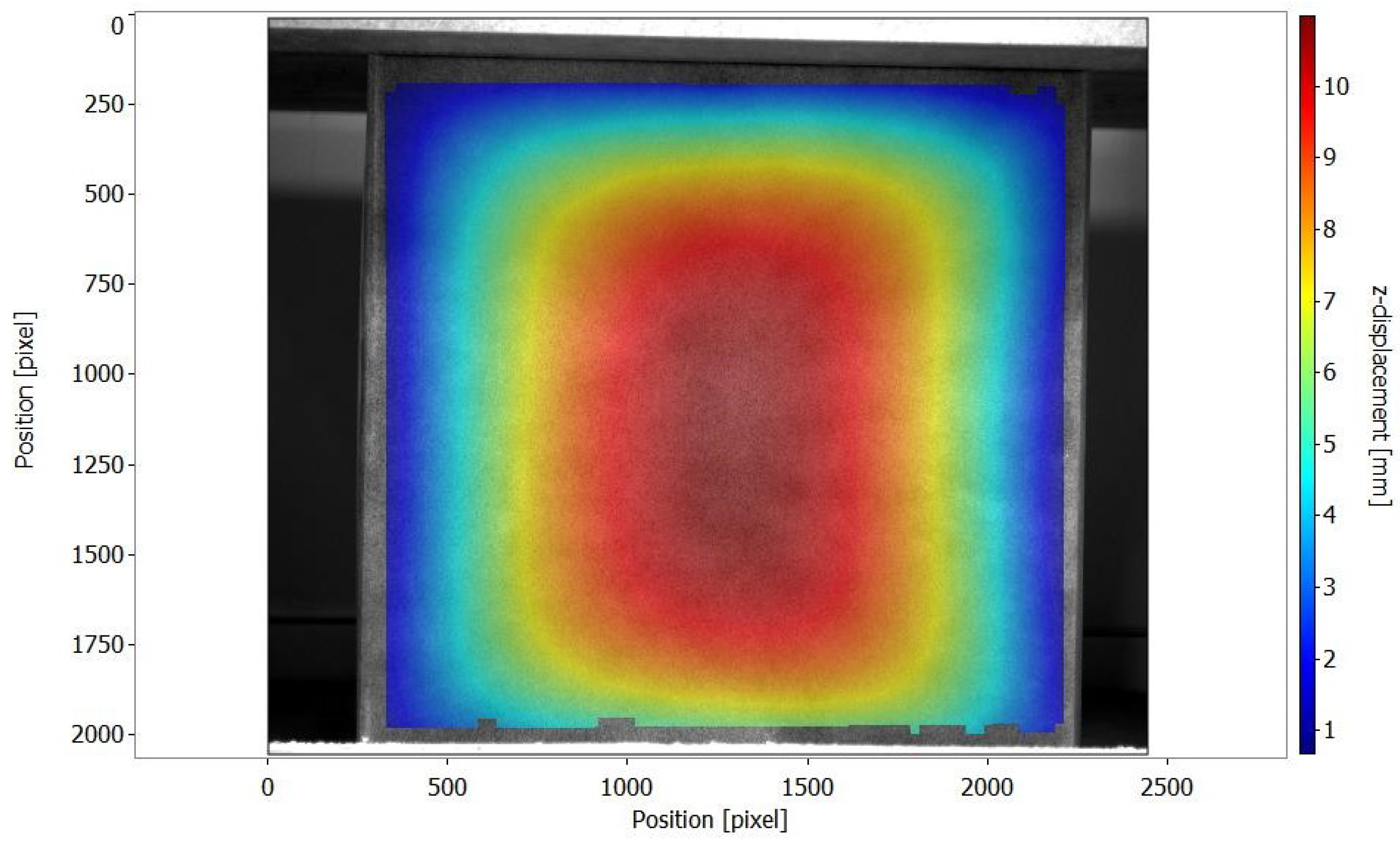
2.4. Box Compression Tests
2.5. Finite Element Modelling
2.5.1. Four-Point Bending Tests
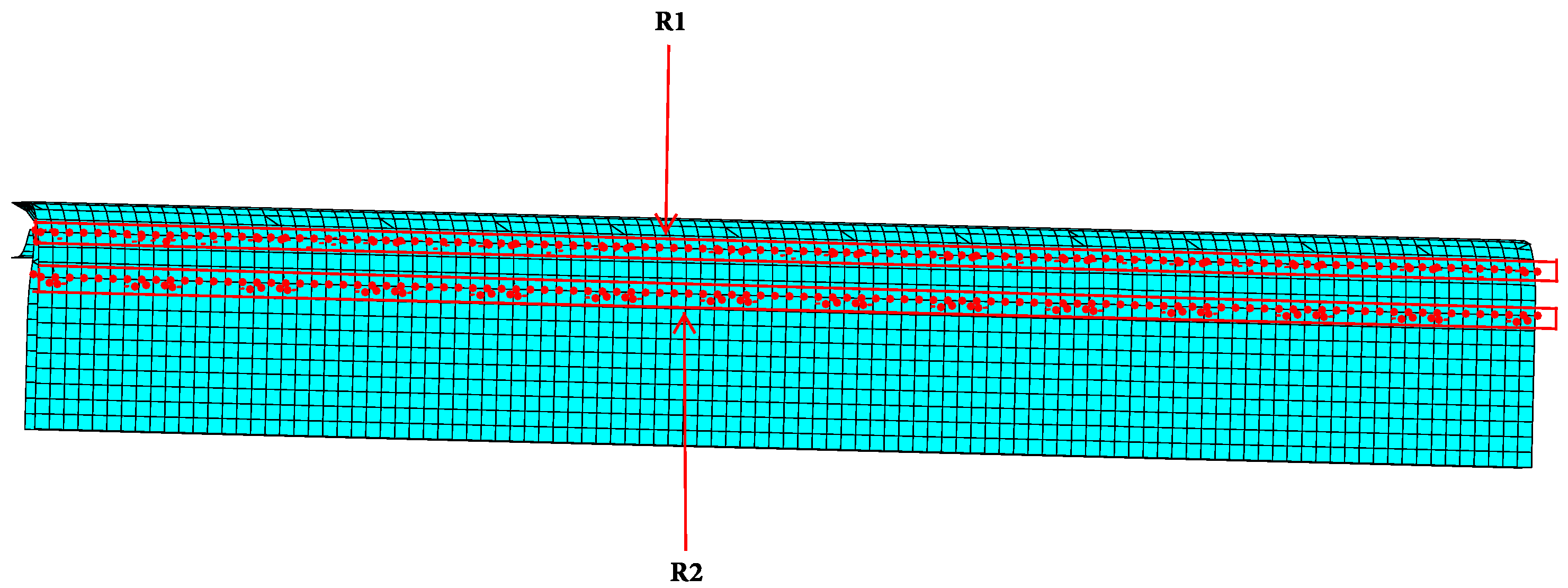
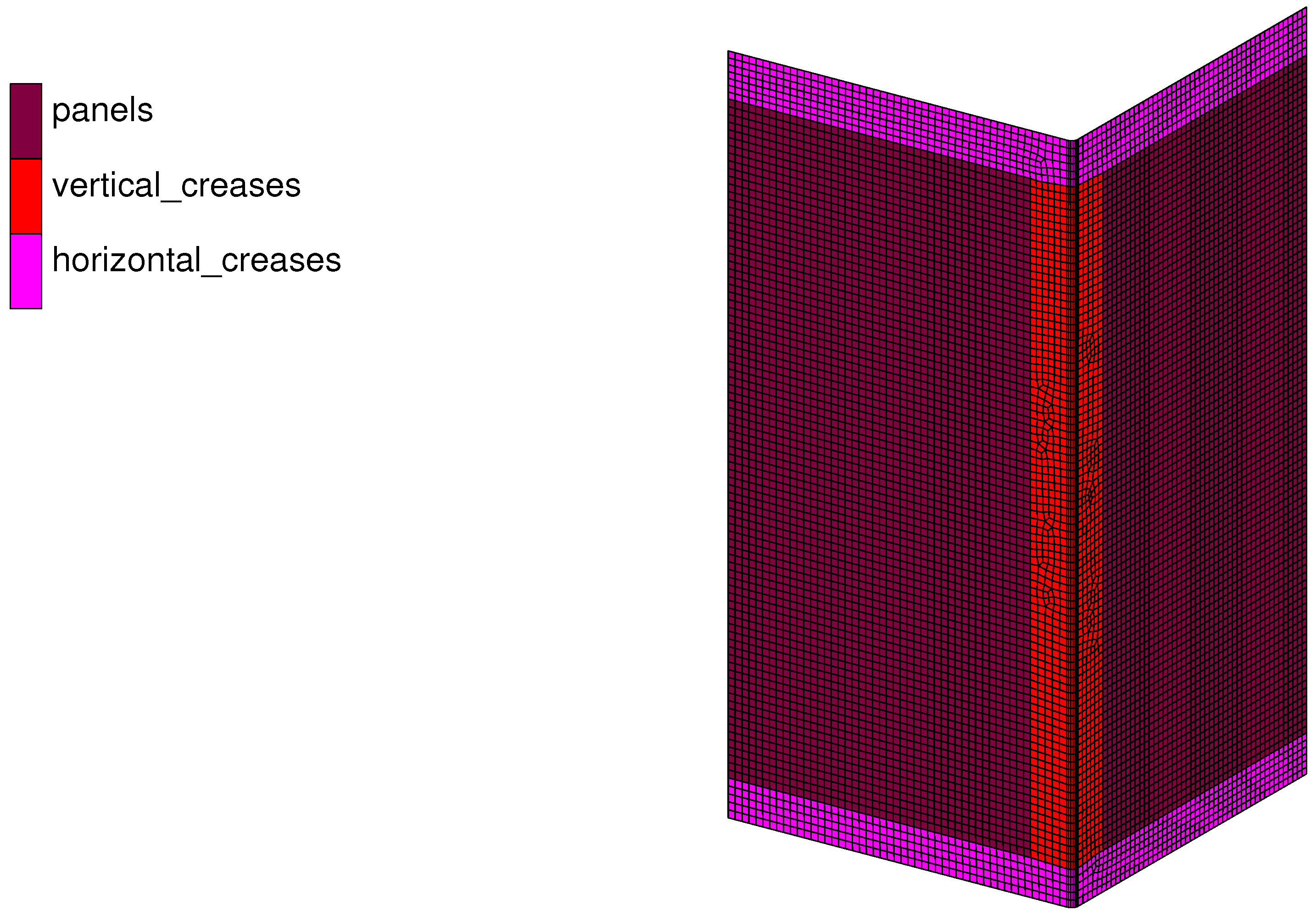
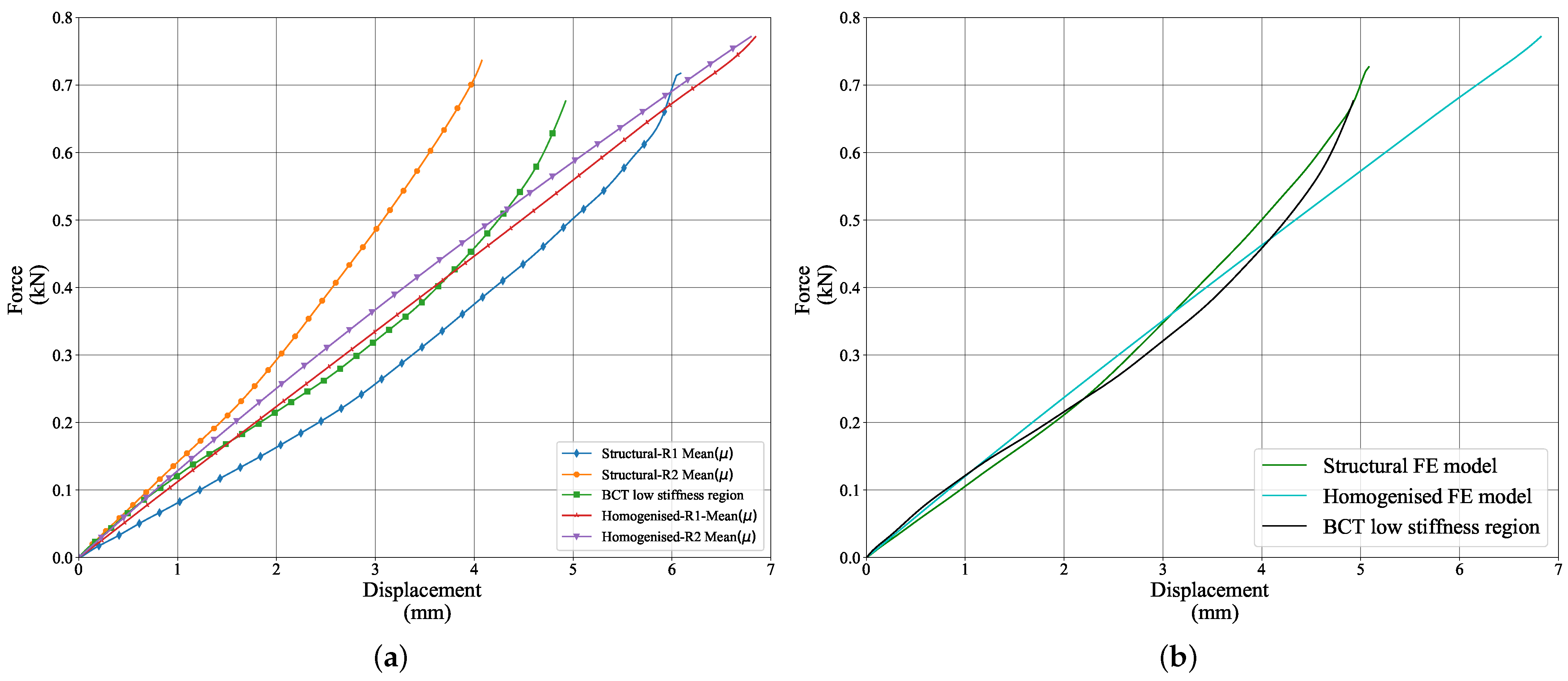
2.5.2. Horizontal Creases
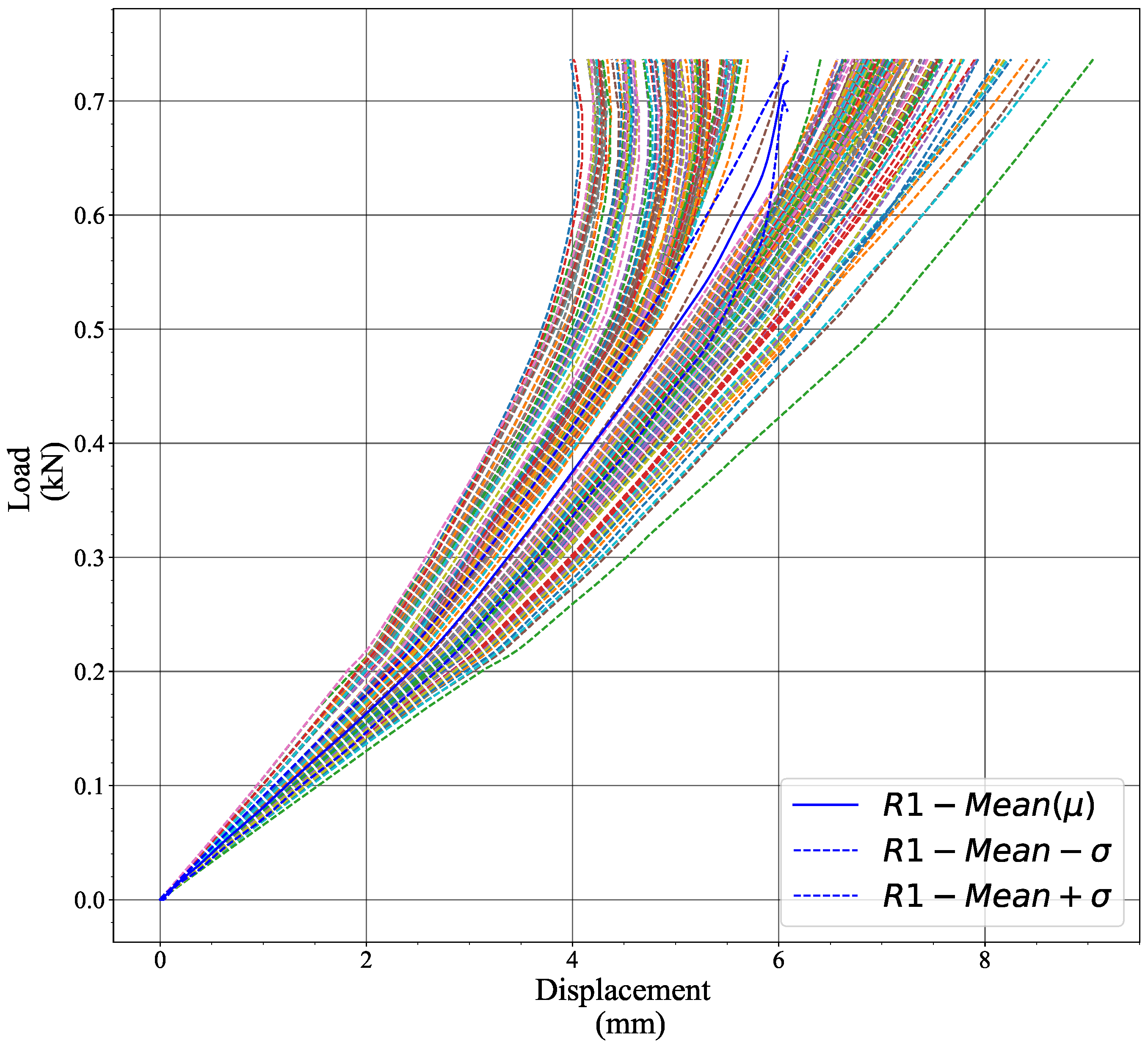
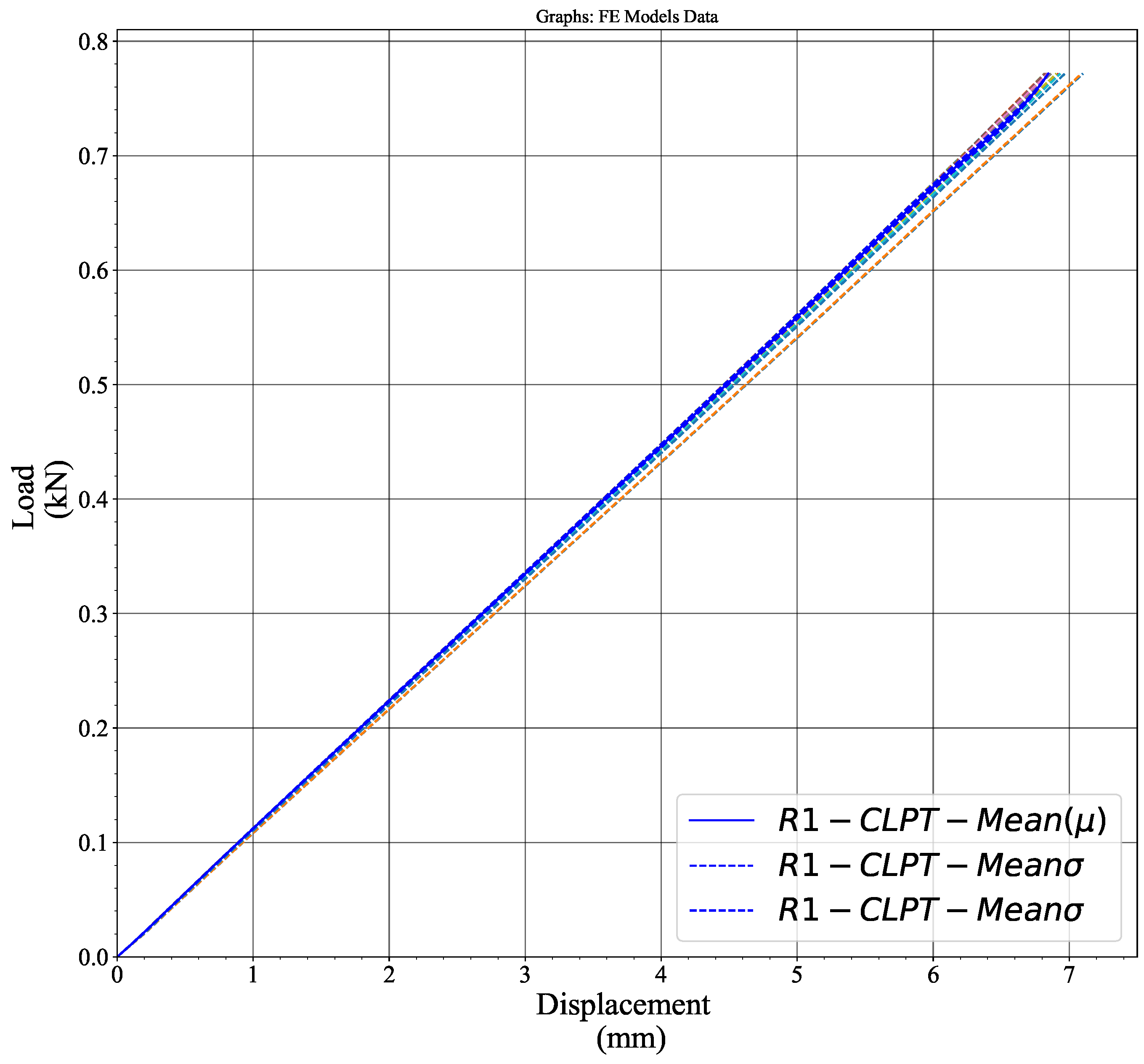
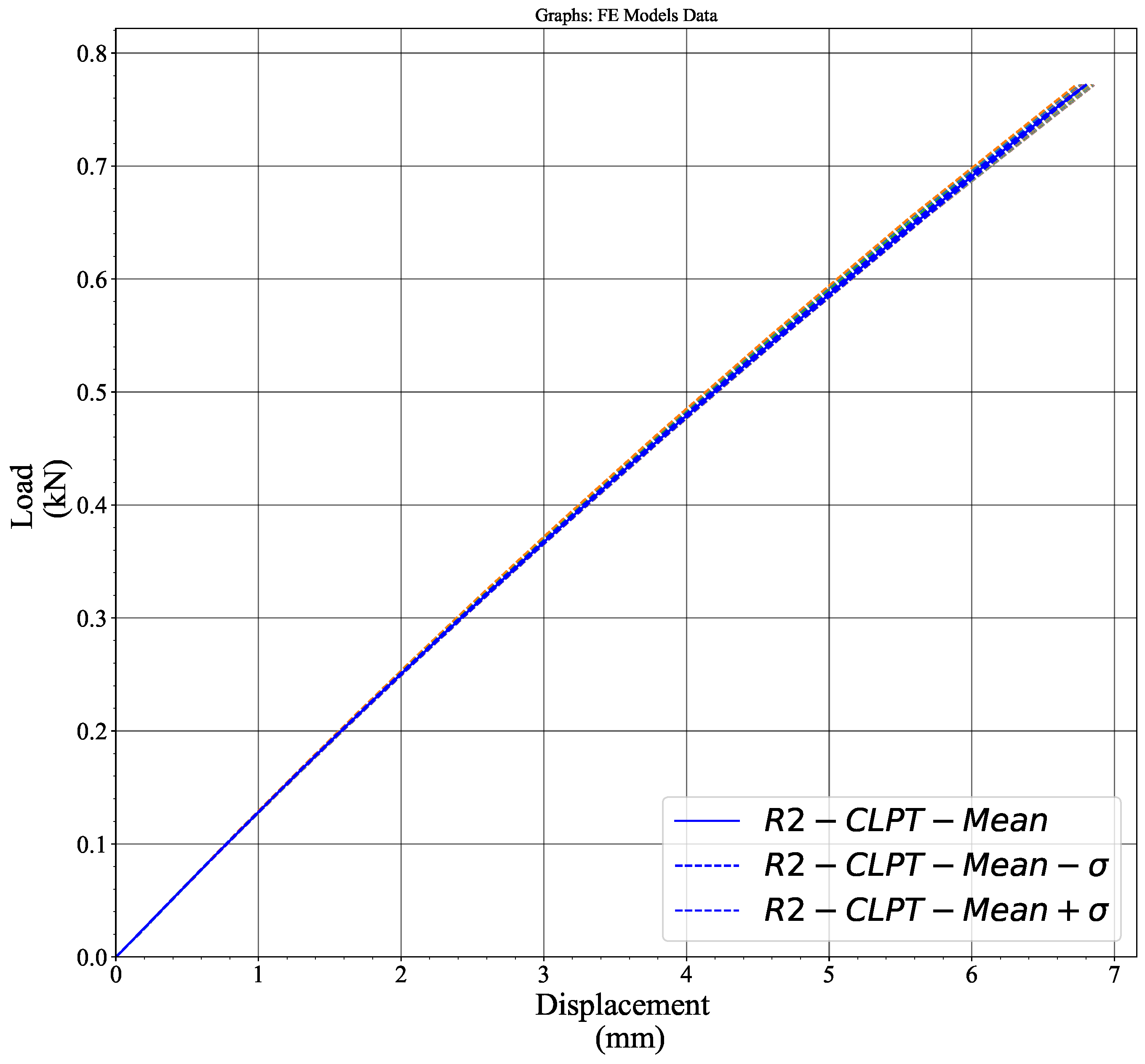
- The section marked as R1 on Figure 10 consists of all the nodes, including both liners and fluting, shown in red along the X-axis at the centre of the crease. The section labelled R2 includes all the nodes, with liners and fluting, positioned along the X-axis 5mm below R1.
- The overall average load–displacement curve for the creased region was obtained by averaging the previously calculated average curves of sections R1 and R2.
2.5.3. Box Compression Tests
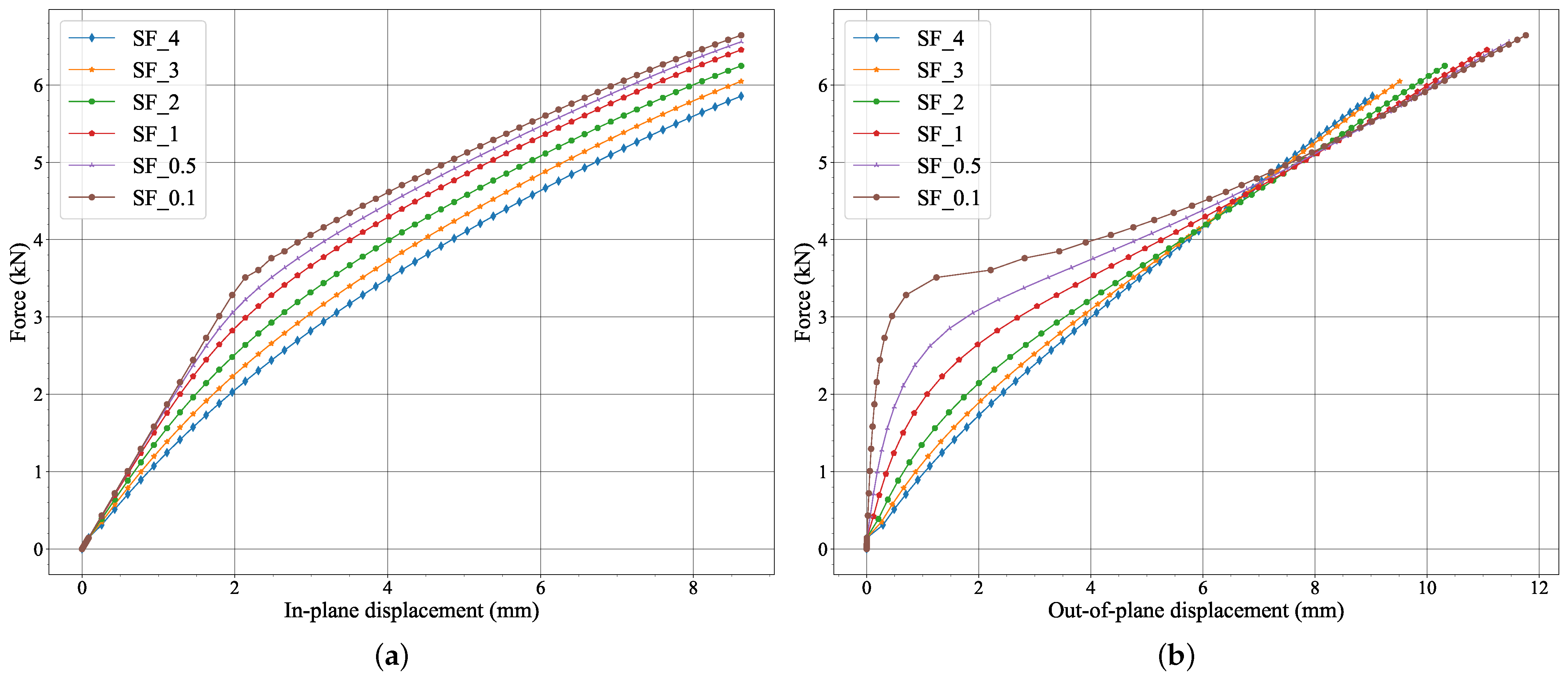
2.6. Optimisation of FE Models
3. Results and Discussion
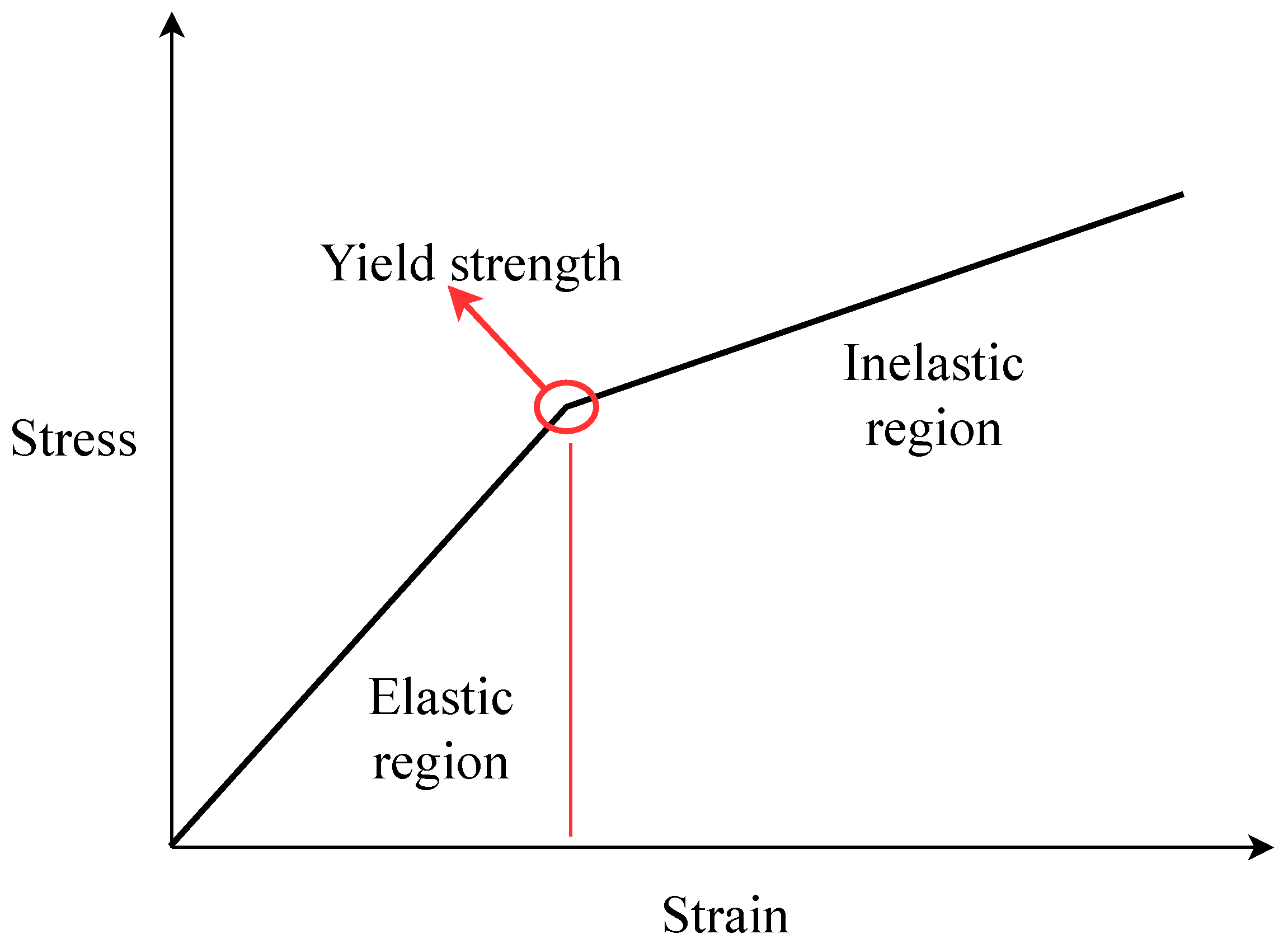
3.1. Inverse Analysis
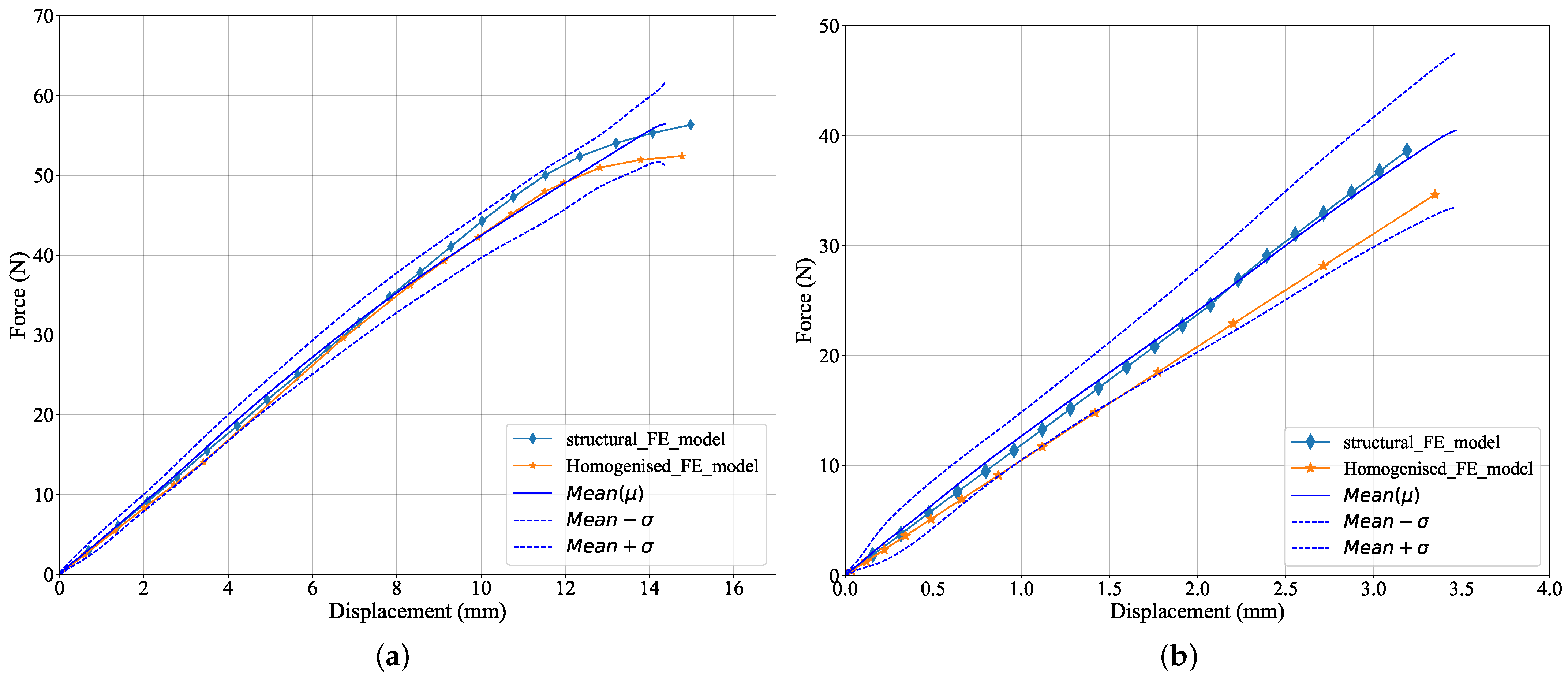
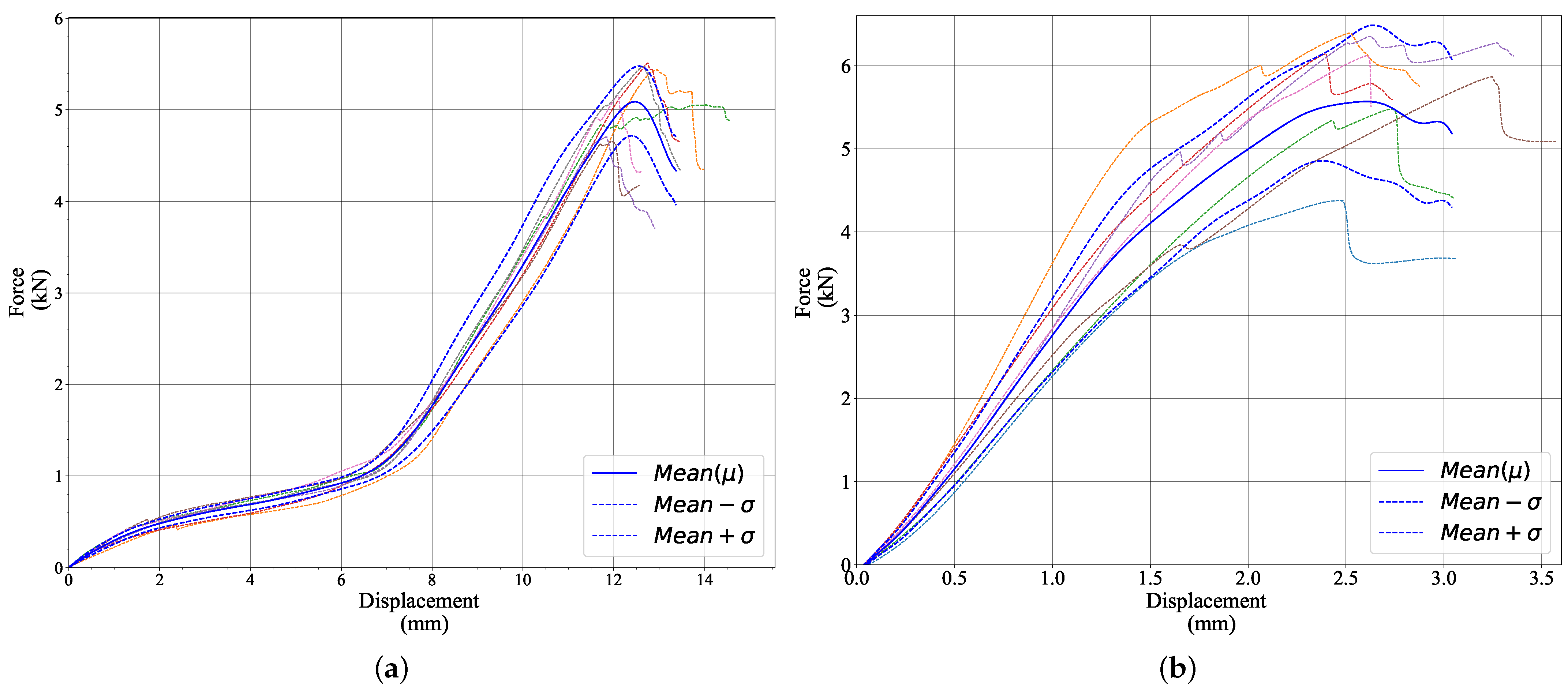
3.2. Four-Point Bending Tests
Four-Point Bending Models with Creases
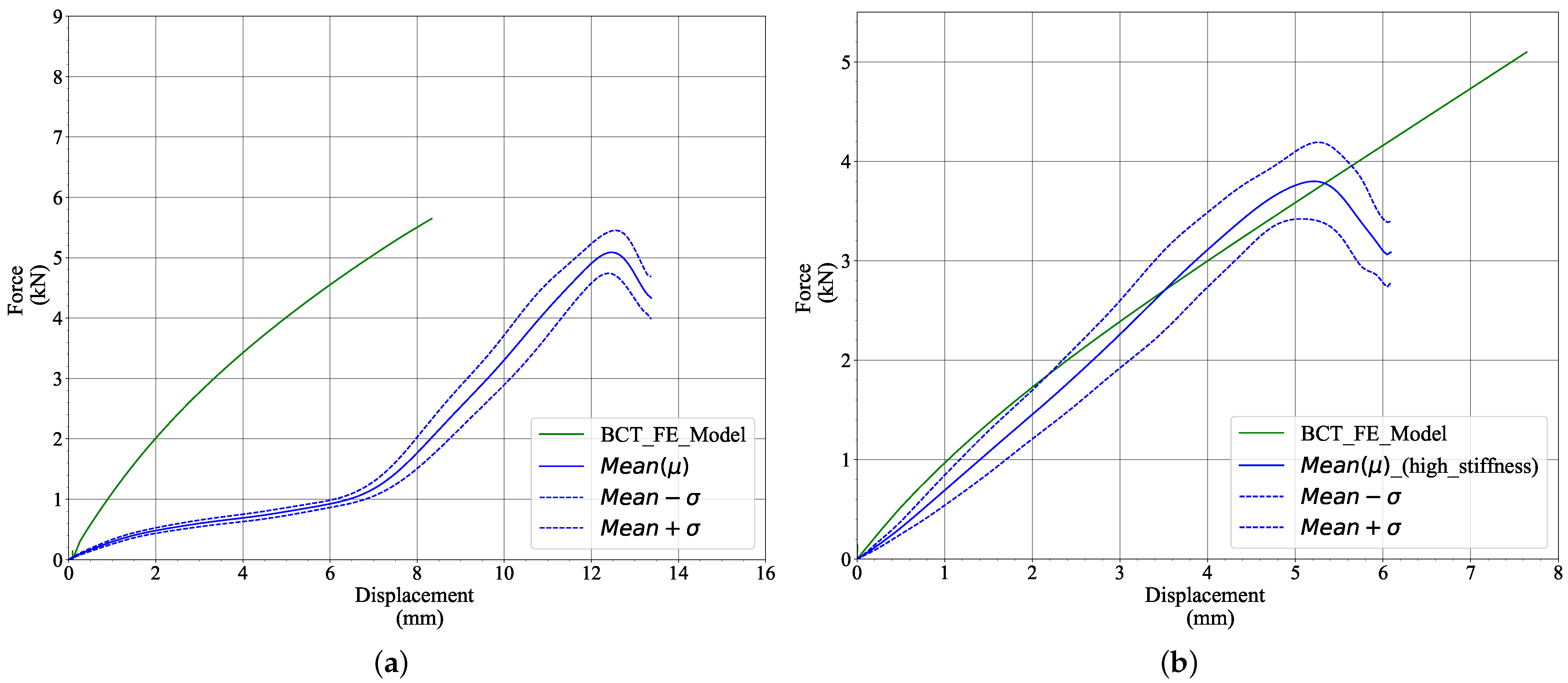
3.3. Horizontal Creases
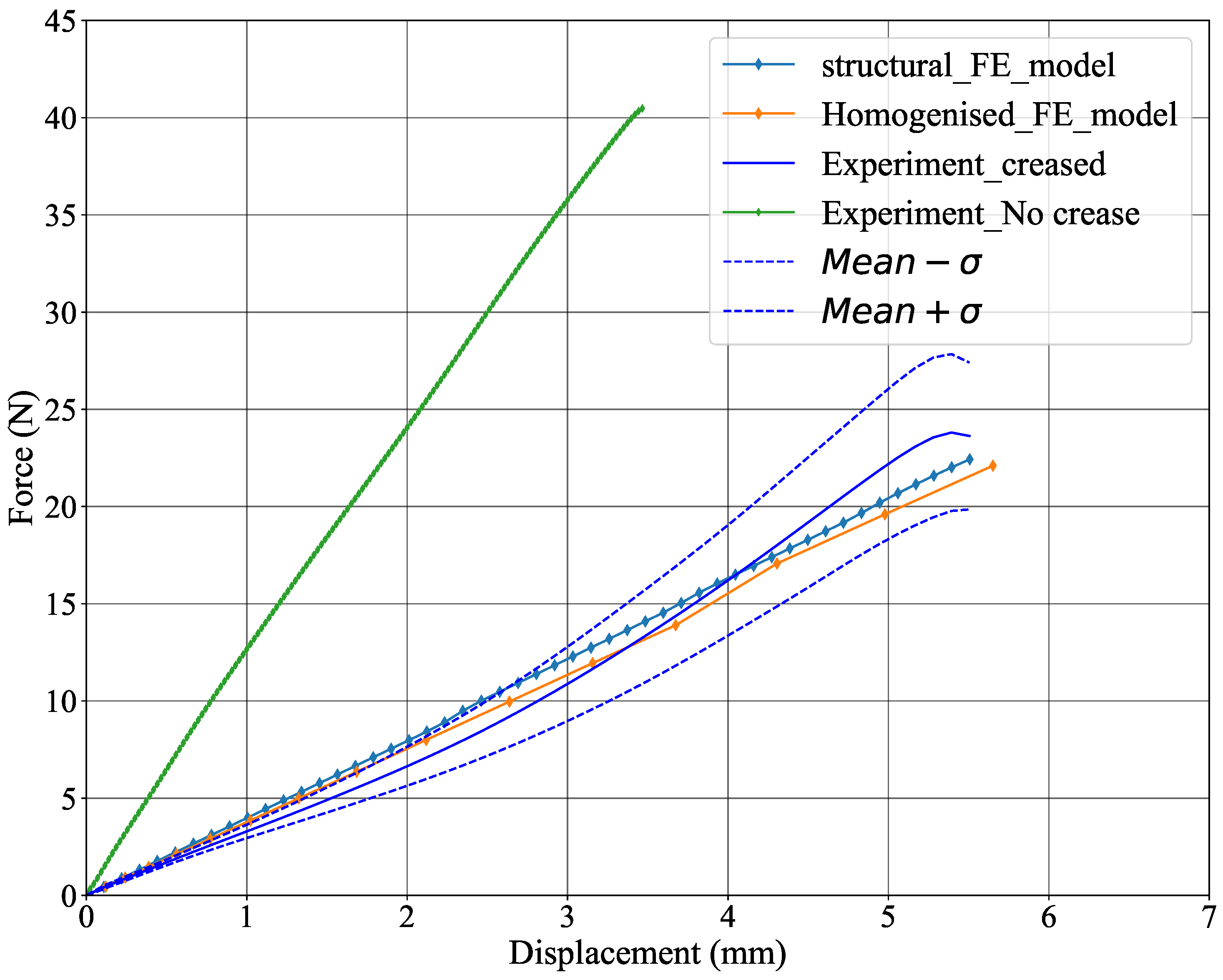
3.4. Box Compression Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Optimisation of FE Models
| Liners | Core | ||||||
|---|---|---|---|---|---|---|---|
(MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | ||
| Reference Properties (CLPT) | 3348 | 1155 | 761 | 2355 | 1459 | 718 | |
| Starting Points | 1 | 2381.00 | 836.52 | 675.33 | 1301.52 | 1363.04 | 510.74 |
| 2 | 2377.48 | 887.75 | 587.75 | 1229.44 | 1246.11 | 589.97 | |
| 3 | 2376.76 | 894.70 | 624.94 | 1539.98 | 1260.08 | 687.67 | |
| 4 | 2376.09 | 953.34 | 695.15 | 1487.81 | 1166.38 | 467.30 | |
| 5 | 2376.03 | 1053.82 | 523.57 | 1595.70 | 1303.57 | 654.72 | |
| 6 | 2376.82 | 996.01 | 508.96 | 1691.96 | 1099.60 | 562.57 | |
| 7 | 2378.80 | 1107.63 | 543.37 | 1272.20 | 1159.50 | 529.69 | |
| 8 | 2380.87 | 1108.82 | 719.50 | 1677.84 | 1018.65 | 663.07 | |
| 9 | 2380.10 | 1034.11 | 533.16 | 1287.35 | 1375.94 | 674.46 | |
| 10 | 2380.62 | 927.75 | 619.02 | 1204.64 | 976.10 | 623.06 | |
| Average | 2378.46 | 980.04 | 603.07 | 1428.84 | 1196.90 | 596.33 | |
| Standard Deviation | 1.94 | 90.18 | 72.01 | 180.47 | 130.30 | 72.54 | |
| Liners | Core | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | Initial Yield Stress | Yield Stress (5% Plastic Strain) | (MPa) | (MPa) | (MPa) | Initial Yield Stress | Yield Stress (5% Plastic Strain) | ||
| Reference Properties (CLPT) | 6695 | 2310 | 1522 | 17.44 | 21.96 | 73 | 219 | 15 | 14.02 | 22.43 | |
| Starting Points | 1 | 5370.18 | 1878.22 | 1287.31 | 13.53 | 24.59 | 59.07 | 255.20 | 14.32 | 12.63 | 21.35 |
| 2 | 5368.30 | 1866.05 | 1548.02 | 13.61 | 20.14 | 58.77 | 258.57 | 12.75 | 15.08 | 18.99 | |
| 3 | 5371.31 | 1872.71 | 1283.49 | 11.90 | 20.50 | 58.97 | 258.21 | 13.62 | 11.69 | 21.39 | |
| 4 | 5371.33 | 1867.72 | 1445.36 | 13.47 | 18.72 | 60.86 | 262.27 | 17.29 | 13.06 | 26.72 | |
| 5 | 5363.46 | 1888.13 | 1287.31 | 13.46 | 21.88 | 59.31 | 247.31 | 14.73 | 13.84 | 25.00 | |
| 6 | 5359.69 | 1891.32 | 1548.02 | 13.48 | 23.74 | 59.86 | 245.22 | 16.17 | 16.69 | 25.18 | |
| 7 | 5370.01 | 1910.87 | 1283.49 | 13.66 | 17.86 | 58.45 | 235.11 | 12.39 | 14.16 | 20.17 | |
| 8 | 5361.84 | 1887.49 | 1445.36 | 13.49 | 25.65 | 63.21 | 251.98 | 17.87 | 17.20 | 27.48 | |
| 9 | 5371.72 | 1887.40 | 1222.86 | 13.57 | 24.26 | 58.69 | 248.96 | 15.58 | 16.18 | 23.68 | |
| 10 | 5361.50 | 1887.43 | 1571.67 | 13.44 | 22.69 | 61.63 | 251.27 | 16.07 | 14.68 | 22.50 | |
| Average | 5366.93 | 1883.73 | 1426.54 | 13.36 | 22.00 | 59.88 | 251.41 | 15.08 | 14.52 | 23.25 | |
| Standard Deviation | 4.51 | 12.55 | 156.74 | 0.49 | 2.49 | 1.47 | 7.46 | 1.75 | 1.71 | 2.69 | |
| Liners | Core | ||||||
|---|---|---|---|---|---|---|---|
(MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | ||
| Reference Properties (CLPT) | 2379 | 980 | 603 | 73 | 219 | 15 | |
| Starting Points | 1 | 4016.23 | 925.60 | 806.87 | 45.38 | 99.47 | 11.84 |
| 2 | 3660.87 | 937.30 | 699.34 | 47.70 | 98.89 | 9.09 | |
| 3 | 3696.56 | 1027.19 | 889.57 | 60.06 | 134.39 | 10.42 | |
| 4 | 2820.84 | 940.75 | 636.58 | 52.65 | 98.68 | 9.95 | |
| 5 | 3157.76 | 1011.55 | 768.91 | 55.65 | 126.42 | 9.50 | |
| 6 | 3413.91 | 1066.66 | 868.27 | 41.74 | 113.04 | 11.28 | |
| 7 | 2942.90 | 971.99 | 848.18 | 58.48 | 111.32 | 12.88 | |
| 8 | 3029.87 | 1001.44 | 749.27 | 43.45 | 133.36 | 11.74 | |
| 9 | 3886.09 | 1015.50 | 728.78 | 50.74 | 121.27 | 12.59 | |
| 10 | 3280.73 | 990.93 | 640.59 | 54.27 | 123.24 | 10.76 | |
| Average | 3390.57 | 982.89 | 763.64 | 51.01 | 116.01 | 11 | |
| Standard Deviation | 390.59 | 34.75 | 85.26 | 5.99 | 13.13 | 1.22 | |
| Liners | Core | ||||||
|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | (MPa) | ||
| Reference Properties (CLPT) | 2379 | 980 | 602 | 73 | 219 | 15 | |
| Starting Points | 1 | 3990.33 | 1357.28 | 835.00 | 59.93 | 133.30 | 9.54 |
| 2 | 3982.04 | 1379.64 | 890.32 | 60.58 | 145.91 | 12.85 | |
| 3 | 3980.88 | 1368.87 | 890.31 | 60.52 | 147.22 | 12.79 | |
| 4 | 3981.73 | 1374.11 | 901.81 | 60.94 | 147.91 | 10.85 | |
| 5 | 3999.99 | 1286.03 | 831.69 | 60.28 | 100.10 | 10.51 | |
| 6 | 3980.45 | 1382.31 | 838.01 | 60.12 | 147.94 | 11.18 | |
| 7 | 3977.82 | 1380.82 | 911.86 | 60.53 | 147.78 | 12.99 | |
| 8 | 3984.08 | 1369.76 | 897.24 | 60.64 | 143.50 | 12.48 | |
| 9 | 3992.53 | 1344.99 | 844.59 | 58.53 | 145.09 | 11.96 | |
| 10 | 3977.39 | 1381.33 | 892.72 | 60.62 | 144.63 | 12.88 | |
| Average | 3984.72 | 1362.52 | 873.36 | 60.27 | 140.34 | 11.80 | |
| Standard Deviation | 6.90 | 27.90 | 30.16 | 0.64 | 14.03 | 1.15 | |
Appendix B. Horizontal Crease Stiffness Determination

References
- Han, J.; Park, J.M. Finite element analysis of vent/hand hole designs for corrugated fibreboard boxes. Packag. Technol. Sci. 2007, 20, 39–47. [Google Scholar] [CrossRef]
- Fadiji, T.; Ambaw, A.; Coetzee, C.J.; Berry, T.M.; Opara, U.L. Application of finite element analysis to predict the mechanical strength of ventilated corrugated paperboard packaging for handling fresh produce. Biosyst. Eng. 2018, 174, 260–281. [Google Scholar] [CrossRef]
- Starke, M.M. Material and Structural Modeling of Corrugated Paperboard Packaging for Horticultural Produce. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2020. [Google Scholar]
- Beldie, L.; Sandberg, G.; Sandberg, L. Paperboard packages exposed to static loads–finite element modeling and experiments. Packag. Technol. Sci. Int. 2001, 14, 171–178. [Google Scholar] [CrossRef]
- Renman, M. Test fixture for eccentricity and stiffness of corrugated board. Exp. Mech. 1996, 36, 262–268. [Google Scholar] [CrossRef]
- Frank, B. Corrugated box compression—A literature survey. Packag. Technol. Sci. Int. 2014, 27, 105–128. [Google Scholar] [CrossRef]
- Aduke, R.; Venter, M.; Coetzee, C. An Analysis of Numerical Homogenisation Methods Applied on Corrugated Paperboard. Math. Comput. Appl. 2022, 27, 108. [Google Scholar] [CrossRef]
- Jekel, C.F.; Venter, G.; Venter, M.P. Obtaining a hyperelastic non-linear orthotropic material model via inverse bubble inflation analysis. Struct. Multidiscip. Optim. 2016, 4, 927–935. [Google Scholar] [CrossRef]
- Garbowski, T.; Maier, G.; Novati, G. On calibration of orthotropic elastic-plastic constitutive models for paper foils by biaxial tests and inverse analyses. Struct. Multidiscip. Optim. 2012, 46, 111–128. [Google Scholar] [CrossRef]
- Helena, F. Investigating an Inverse Finite Element Approach for Characterising Soft Materials. Master’s Thesis, Stellenbosch University, Stellenbosch, South Africa, 2020. [Google Scholar]
- Murdock, K.; Martin, C.; Sun, W. Characterization of mechanical properties of pericardium tissue using planar biaxial tension and flexural deformation. J. Mech. Behav. Biomed. Mater. 2018, 77, 148–156. [Google Scholar] [CrossRef] [PubMed]
- Hagman, A. Investigations of In-Plane Properties of Paperboard. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2013. [Google Scholar]
- BS EN 20187:199; Paper, Board, and Pulps—Standard Atmosphere for Conditioning and Testing and Procedure for Monitoring the Atmosphere and Conditioning of Samples. British Standards Institution: London, UK, 1990. Available online: https://www.iso.org/standard/4037.html (accessed on 12 February 2023).
- Cillie, J.; Coetzee, C. Experimental and Numerical Investigation of the In-Plane Compression of Corrugated Paperboard Panels. Math. Comput. Appl. 2022, 27, 108. [Google Scholar] [CrossRef]
- ISO 5628:1990; Paper and Board—Determination of Bending Stiffness by Static Methods. International Organization for Standardization: Geneva, Switzerland, 1990. Available online: https://www.iso.org/standard/11703.html (accessed on 12 February 2023).
- McKee, R.; Gander, J.; Wachuta, J. Compression strength formula for corrugated boxes. Paperboard Packag. 1963, 48, 149–159. [Google Scholar]
- Mann, R.W.; Baum, G.A.; Habeger, C.C., Jr. Determination of All Nine Orthotropic Elastic Constants for Machine-Made Paper. Available online: https://smartech.gatech.edu/bitstream/handle/1853/3101/tps-084.pdf (accessed on 12 February 2023).
- Baum, G. Orthotropic elastic constants of paper. TAPPI J. 1981, 64, 97–101. [Google Scholar]
- Nordstrand, T.M. Parametric study of the post-buckling strength of structural core sandwich panels. Compos. Struct. 1995, 30, 441–451. [Google Scholar] [CrossRef]
- Mrówczyński, D.; Garbowski, T.; Knitter-Piątkowska, A. Estimation of the compressive strength of corrugated board boxes with shifted creases on the flaps. Materials 2021, 14, 5181. [Google Scholar] [CrossRef] [PubMed]
- Haj-Ali, R.; Choi, J.; Wei, B.S.; Popil, R.; Schaepe, M. Refined nonlinear finite element models for corrugated fiberboards. Compos. Struct. 2009, 4, 321–333. [Google Scholar] [CrossRef]
- Šarčević, I.; Gregor-Svetec, D.; Banić, D. Effect of perforations on the loss of corrugated cardboard bending stiffness. In Proceedings of the 11th International Symposium on Graphic Engineering and Design, Novi Sad, Serbia, 3–5 November 2022. [Google Scholar]
- Smedman, O. Factors Affecting the Relative Crease Strength of Paperboard. Master’s Thesis, Lund University, Lund, Sweden, 2017. [Google Scholar]
- Kueh, C.; Navaranjan, N.; Duke, M. The effect of in-plane boundary conditions on the post-buckling behaviour of rectangular corrugated paperboard panels. Comput. Struct. 2012, 104, 55–62. [Google Scholar] [CrossRef]









| Paper Type | Liners (250KL) | Corrugated Core (150SC) | Homogenised Core (CLPT) |
|---|---|---|---|
| (MPa) | 6695 | 4709 | 73 |
| (MPa) | 2310 | 2918 | 219 |
| (MPa) | 35 | 42 | 3000 |
| 0.50 | 0.37 | 0.07 | |
| 0.01 | 0.01 | 0.01 | |
| 0.01 | 0.01 | 0.01 | |
| (MPa) | 1522 | 1435 | 15 |
| (MPa) | 122 | 86 | 6 |
| (MPa) | 66 | 83 | 7 |
| Thickness (mm) | 0.345 | 0.251 | 4.4 (effective thickness of the board) |
| Paper Type | Liners (250KL) | Corrugated Core (150SC) | Homogenised Core (150SC) |
|---|---|---|---|
| (MPa) | 2378 | 1429 | 51 |
| (MPa) | 980 | 1197 | 116 |
| (MPa) | 13 | 8 | 3000 |
| 0.50 | 0.37 | 0.02 | |
| 0.01 | 0.01 | 0.01 | |
| 0.01 | 0.01 | 0.01 | |
| (MPa) | 603 | 596 | 11 |
| (MPa) | 43 | 26 | 1 |
| (MPa) | 28 | 34 | 3 |
| Thickness (mm) | 0.345 | 0.251 | 4.4 |
| Type | (MPa) | (MPa) | (MPa) | (MPa) |
|---|---|---|---|---|
| Liners (250KL) | 26.11 | 17.44 | 17.44 | 19.61 |
| Fluting (150C-SC) | 32.65 | 14.02 | 14.02 | 18.68 |
| Layer | (MPa) | (MPa) | (MPa) | Initial Yield Stress (MPa) | Yield Stress (5% Strain) (MPa) |
|---|---|---|---|---|---|
| Normal Sample (un-creased sample) | |||||
| Liners | 5364 | 1884 | 1427 | 13.36 | 22 |
| Homogenised core | 60 | 251 | 15 | 14.52 | 23.25 |
| Vertical creases | |||||
| Liners | 3390 | 983 | 764 | - | - |
| Homogenised core | 51 | 116 | 11 | - | - |
| Horizontal creases | |||||
| Liners | 3985 | 1363 | 873 | - | - |
| Homogenised core | 60 | 140 | 12 | - | - |
| MD | CD | |||||
|---|---|---|---|---|---|---|
| Sample Type | Exp | Structural FE Model | Homogenised FE Model | Exp | Structural FE Model | Homogenised FE Model |
| Normal sample (without crease) | ||||||
| Error (%) | − | 4 | 11 | − | 4 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aduke, R.N.; Venter, M.P.; Coetzee, C.J. Numerical Modelling of Corrugated Paperboard Boxes. Math. Comput. Appl. 2024, 29, 70. https://doi.org/10.3390/mca29040070
Aduke RN, Venter MP, Coetzee CJ. Numerical Modelling of Corrugated Paperboard Boxes. Mathematical and Computational Applications. 2024; 29(4):70. https://doi.org/10.3390/mca29040070
Chicago/Turabian StyleAduke, Rhoda Ngira, Martin P. Venter, and Corné J. Coetzee. 2024. "Numerical Modelling of Corrugated Paperboard Boxes" Mathematical and Computational Applications 29, no. 4: 70. https://doi.org/10.3390/mca29040070





