Enhanced Forecasting of Equity Fund Returns Using Machine Learning
Abstract
:1. Introduction
2. Related Work
3. Methodology
3.1. Data Description and Data Preparation
3.1.1. Aggregating Daily Data into Monthly Intervals
3.1.2. Data Transformation
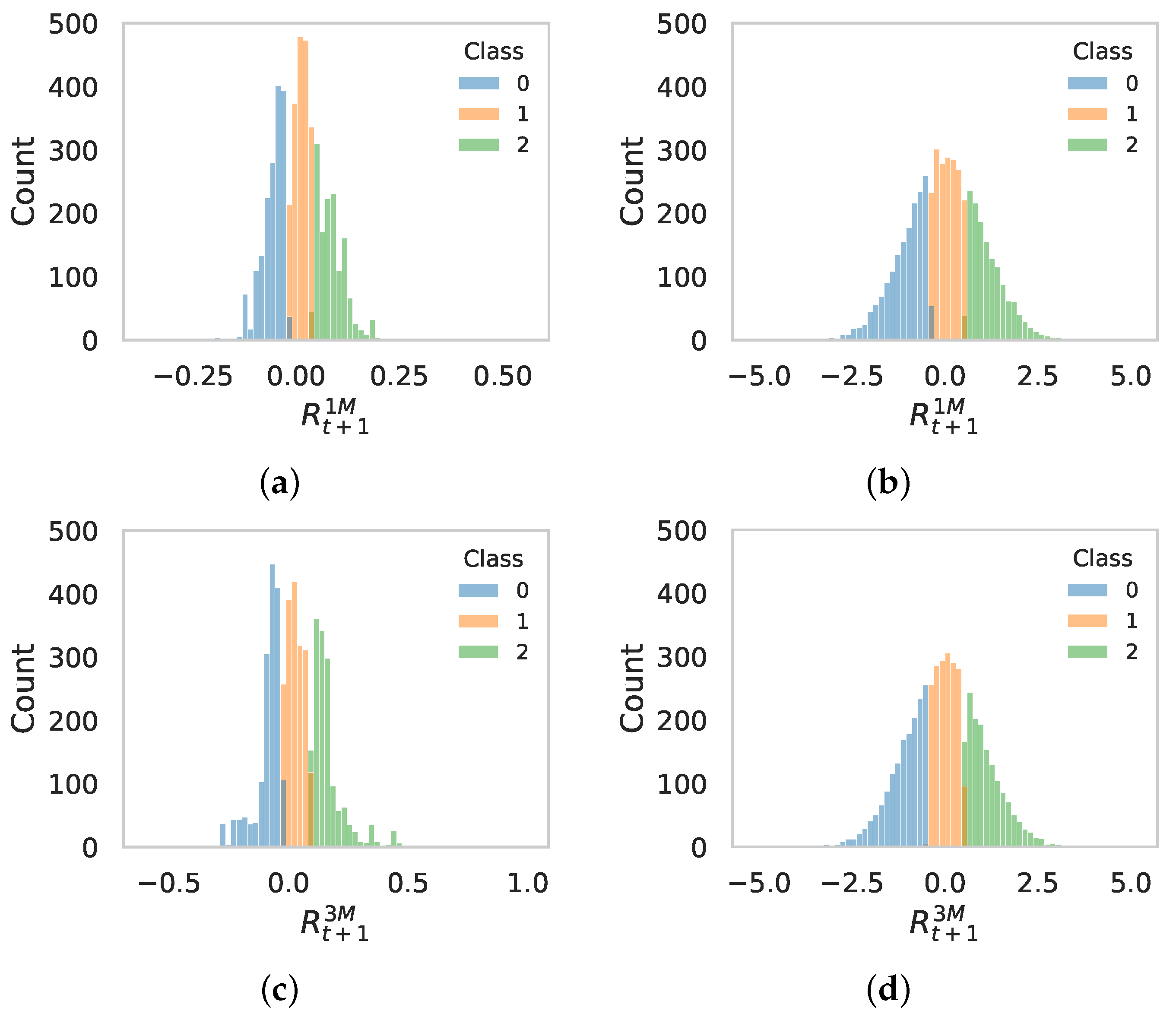
3.2. Labels Definition
3.3. Feature Engineering
3.4. Model Setup
- Accuracy: The proportion of correct predictions out of all predictions.
- AUC (Area Under the Curve): A metric that summarizes the performance of a binary classifier in terms of the false positive rate (FPR) and the true positive rate (TPR).
- Recall: The proportion of positive instances that were correctly identified.
- Precision: The proportion of positive predictions that were actually positive.
- F1-score: The harmonic mean of precision and recall.
- Kappa: A metric that measures the agreement between the predictions of the model and the true labels, corrected for chance.
- MCC (Matthews Correlation Coefficient): A metric that balances the true positive rate and the false positive rate.
- Time (TT): The time taken to fit the model and make predictions.
- Confusion matrices: Show the actual versus predicted classifications for each class, including true positives, false positives, true negatives, and false negatives.
3.5. Computational Resources
4. Results
4.1. Feature Importance
4.2. Validation of Classifier Forecasts on Unseen Data
5. Discussion
5.1. Random Forest Classifier
5.2. Extra Trees Classifier
5.3. Light Gradient Boosting Machine
5.4. Feature Importance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Bank. Brazil Overview. Available online: https://www.worldbank.org/en/country/brazil/overview (accessed on 5 July 2024).
- Apex-Brasil. Legal Structure-VCPE Funds in Brazil. Available online: https://www.apexbrasil.com.br/uploads/Legal%20Structure%20-%20VCPE%20Funds%20in%20Brazil.pdf (accessed on 12 July 2024).
- Bodie, Z.; Kane, A.; Marcus, A. Investments, 13th ed.; McGraw-Hill Education: New York, NY, USA, 2024. [Google Scholar]
- Lewellen, J. The Cross-section of Expected Stock Returns. Crit. Financ. Rev. 2015, 4, 1–44. [Google Scholar] [CrossRef]
- Gu, S.; Kelly, B.; Xiu, D. Empirical Asset Pricing via Machine Learning. Rev. Financ. Stud. 2020, 33, 2223–2273. [Google Scholar] [CrossRef]
- Zhou, Y.; Xie, C.; Wang, G.J.; Zhu, Y.; Uddin, G.S. Analysing and forecasting co-movement between innovative and traditional financial assets based on complex network and machine learning. Res. Int. Bus. Financ. 2023, 64, 101846. [Google Scholar] [CrossRef]
- Kelly, B.; Malamud, S.; Zhou, K. The Virtue of Complexity in Return Prediction. J. Financ. 2024, 79, 459–503. [Google Scholar] [CrossRef]
- Kelly, B.; Xiu, D. Financial Machine Learning. Found. Trends® Financ. 2023, 13, 205–363. [Google Scholar] [CrossRef]
- Selvamuthu, D.; Kumar, V.; Mishra, A. Indian stock market prediction using artificial neural networks on tick data. Financ. Innov. 2019, 5, 16. [Google Scholar] [CrossRef]
- Asere, G.; Nuga, K. Examining the Potential of Artificial Intelligence and Machine Learning in Predicting Trends and Enhancing Investment Decision-Making. Sci. J. Eng. Technol. 2024, 1, 15–20. [Google Scholar] [CrossRef]
- Bouslimi, J.; Boubaker, S.; Tissaoui, K. Forecasting of Cryptocurrency Price and Financial Stability: Fresh Insights based on Big Data Analytics and Deep Learning Artificial Intelligence Techniques. Eng. Technol. Appl. Sci. Res. 2024, 14, 14162–14169. [Google Scholar] [CrossRef]
- Wade, T. Transformers and Tradition: Using Generative AI and Deep Learning for Financial Markets Prediction. Ph.D. Thesis, London School of Economics and Political Science, London, UK, 2024. [Google Scholar]
- Kouki, F. Design of Single Valued Neutrosophic Hypersoft Set VIKOR Method for Hedge Fund Return Prediction. J. Int. J. Neutrosophic Sci. 2024, 24, 317. [Google Scholar] [CrossRef]
- Li, Y.; Xue, H.; Wei, S.; Wang, R.; Liu, F. A Machine Learning Approach for Investigating the Determinants of Stock Price Crash Risk: Exploiting Firm and CEO Characteristics. Systems 2024, 12, 143. [Google Scholar] [CrossRef]
- Lee, T.H.; Hsieh, W.Y. Forecasting relative returns for SP 500 stocks using machine learning. Financ. Innov. 2024, 10, 45. [Google Scholar]
- Raza, H.; Akhtar, Z. Predicting stock prices in the Pakistan market using machine learning and technical indicators. Mod. Financ. 2024, 2, 46–63. [Google Scholar] [CrossRef]
- Liu, H.; Huang, S.; Wang, P.; Li, Z. A review of data mining methods in financial markets. Data Sci. Financ. Econ. 2021, 1, 362–392. [Google Scholar] [CrossRef]
- Agrawal, L.; Adane, D. Improved Decision Tree Model for Prediction in Equity Market Using Heterogeneous Data. IETE J. Res. 2021, 69, 6065–6074. [Google Scholar] [CrossRef]
- Nabi, K.; Saeed, A. A Novel Approach for Stock Price Prediction Using Gradient Boosting Machine with Feature Engineering (GBM-wFE). Kirkuk J. Appl. Res. 2020, 5, 259–275. [Google Scholar] [CrossRef]
- Anupama, K.; Khandelwal, A.; Mohapatra, D.P. Prediction of stock price movement using an improved NSGA-II-RF algorithm with a three-stage feature engineering process. PLoS ONE 2023, 18, e0287754. [Google Scholar]
- Maldonado, S.; Lopez, J.; Izquierdo, J. Survey of feature selection and extraction techniques for stock market prediction. Financ. Innov. 2022, 8, 41. [Google Scholar]
- B3. IBOVESPA. Available online: https://www.b3.com.br/en_us/market-data-and-indices/indices/broad-indices/ibovespa.htm (accessed on 7 November 2024).
- do Brasil, B.C. Taxa SELIC. Available online: https://www.bcb.gov.br/en/monetarypolicy/selicrate (accessed on 7 November 2024).
- Retorno, M. Mais Retorno-Informações e Análises Financeiras. Available online: https://maisretorno.com/ (accessed on 7 November 2024).






| Return | Volatility | Beta | Track | Sharpe | Sortino | Info | Treynor | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Error | Ratio | Ratio | Ratio | Index | |||||||||||
| Shifted | |||||||||||||||
| Date | 1-M | 1-M | 3-M | ⋯ | 1-M | 3-M | ⋯ | 1-M | 3-M | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-01 | −0.032 | 0.061 | −0.003 | ⋯ | 0.402 | 0.399 | ⋯ | 1.295 | 1.125 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-02 | −0.071 | −0.032 | 0.002 | ⋯ | 0.361 | 0.387 | ⋯ | 1.174 | 1.214 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-03 | 0.131 | −0.071 | −0.045 | ⋯ | 0.309 | 0.336 | ⋯ | 0.927 | 1.044 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-04 | 0.092 | 0.131 | 0.036 | ⋯ | 0.334 | 0.333 | ⋯ | 0.920 | 1.007 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-05 | 0.190 | 0.092 | 0.145 | ⋯ | 0.300 | 0.315 | ⋯ | 0.791 | 0.893 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-06 | 0.049 | 0.190 | 0.470 | ⋯ | 0.376 | 0.333 | ⋯ | 1.290 | 0.979 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-07 | 0.060 | 0.049 | 0.363 | ⋯ | 0.286 | 0.314 | ⋯ | 1.339 | 1.087 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | |
| 23-08 | 0.078 | 0.060 | 0.284 | ⋯ | 0.233 | 0.299 | ⋯ | 1.155 | 1.236 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-09 | 0.003 | 0.078 | 0.199 | ⋯ | 0.222 | 0.245 | ⋯ | 0.236 | 0.926 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-10 | 0.069 | 0.003 | 0.164 | ⋯ | 0.371 | 0.280 | ⋯ | 0.194 | 0.604 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-11 | 0.036 | 0.069 | 0.156 | ⋯ | 0.228 | 0.281 | ⋯ | 0.179 | 0.327 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 23-12 | 0.083 | 0.036 | 0.111 | ⋯ | 0.221 | 0.280 | ⋯ | 1.157 | 0.420 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 24-01 | −0.008 | 0.083 | 0.187 | ⋯ | 0.204 | 0.216 | ⋯ | 0.805 | 0.566 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| 24-02 | −0.068 | −0.008 | 0.113 | ⋯ | 0.282 | 0.234 | ⋯ | 0.981 | 0.903 | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| Data | Class 0 | Class 1 | Class 2 | |
|---|---|---|---|---|
| count | 4970 | 1683 | 1874 | 1413 |
| mean | 0.009669 | −0.057537 | 0.012153 | 0.086422 |
| std | 0.063632 | 0.028733 | 0.016729 | 0.040091 |
| min | −0.371327 | −0.371327 | −0.022107 | 0.041519 |
| 25% | −0.037126 | −0.073548 | −0.001007 | 0.056562 |
| 50% | 0.008172 | −0.050458 | 0.011537 | 0.080719 |
| 75% | 0.048322 | −0.036692 | 0.027170 | 0.106506 |
| max | 0.565069 | −0.022210 | 0.041356 | 0.565069 |
| Data | Class 0 | Class 1 | Class 2 | |
|---|---|---|---|---|
| count | 4970 | 1623 | 1814 | 1533 |
| mean | 0.033659 | −0.087063 | 0.029746 | 0.166100 |
| std | 0.116011 | 0.056746 | 0.032603 | 0.077302 |
| min | −0.609930 | −0.609930 | −0.024153 | 0.091768 |
| 25% | −0.049681 | −0.098293 | 0.002937 | 0.119454 |
| 50% | 0.024955 | −0.071773 | 0.027164 | 0.144124 |
| 75% | 0.114138 | −0.051058 | 0.056815 | 0.174111 |
| max | 1.004956 | −0.024403 | 0.091638 | 1.004956 |
| Model | Accuracy | AUC | Recall | Prec. | F1 | Kappa | MCC | TT (Sec) |
|---|---|---|---|---|---|---|---|---|
| Light Gradient Boosting Machine | 0.9218 | 0.9855 | 0.9218 | 0.9225 | 0.9217 | 0.8818 | 0.8822 | 353.3480 |
| Random Forest Classifier | 0.9160 | 0.9850 | 0.9160 | 0.9170 | 0.9161 | 0.8731 | 0.8735 | 0.2710 |
| Extra Trees Classifier | 0.9142 | 0.9851 | 0.9142 | 0.9150 | 0.9142 | 0.8704 | 0.8708 | 0.1890 |
| Gradient Boosting Classifier | 0.8911 | 0.9725 | 0.8911 | 0.8918 | 0.8909 | 0.8355 | 0.8360 | 2.3540 |
| Quadratic Discriminant Analysis | 0.8627 | 0.9383 | 0.8627 | 0.8638 | 0.8627 | 0.7928 | 0.7933 | 0.1410 |
| K Neighbors Classifier | 0.8599 | 0.9560 | 0.8599 | 0.8634 | 0.8598 | 0.7881 | 0.7898 | 0.3230 |
| Decision Tree Classifier | 0.8436 | 0.8812 | 0.8436 | 0.8445 | 0.8436 | 0.7636 | 0.7640 | 0.1650 |
| Logistic Regression | 0.8081 | 0.9133 | 0.8081 | 0.8082 | 0.8074 | 0.7105 | 0.7112 | 0.5070 |
| Model | Accuracy | AUC | Recall | Prec. | F1 | Kappa | MCC | TT (Sec) |
|---|---|---|---|---|---|---|---|---|
| Extra Trees Classifier | 0.9253 | 0.9879 | 0.9253 | 0.9259 | 0.9251 | 0.8878 | 0.8882 | 0.1980 |
| Light Gradient Boosting Machine | 0.9250 | 0.9880 | 0.9250 | 0.9254 | 0.9249 | 0.8874 | 0.8877 | 341.5240 |
| Random Forest Classifier | 0.9210 | 0.9868 | 0.9210 | 0.9214 | 0.9209 | 0.8813 | 0.8816 | 0.3060 |
| Gradient Boosting Classifier | 0.9039 | 0.9778 | 0.9039 | 0.9047 | 0.9037 | 0.8556 | 0.8561 | 2.4840 |
| Quadratic Discriminant Analysis | 0.8727 | 0.9447 | 0.8727 | 0.8737 | 0.8728 | 0.8086 | 0.8090 | 0.1530 |
| Decision Tree Classifier | 0.8707 | 0.9020 | 0.8707 | 0.8714 | 0.8706 | 0.8056 | 0.8060 | 0.1880 |
| K Neighbors Classifier | 0.8644 | 0.9600 | 0.8644 | 0.8665 | 0.8641 | 0.7962 | 0.7975 | 0.3520 |
| Logistic Regression | 0.8287 | 0.9368 | 0.8287 | 0.8291 | 0.8284 | 0.7425 | 0.7430 | 0.5630 |
| Months Ahead | Model | Precision | Recall | F1-Score | |
|---|---|---|---|---|---|
| Class 0 | one | LightGBM | 0.281 | 0.730 | 0.405 |
| Random Forest | 0.330 | 0.854 | 0.475 | ||
| Extra Trees | 0.297 | 0.820 | 0.434 | ||
| two | LightGBM | 0.270 | 0.673 | 0.386 | |
| Random Forest | 0.300 | 0.772 | 0.433 | ||
| Extra Trees | 0.277 | 0.525 | 0.361 | ||
| Class 2 | one | LightGBM | 0.846 | 0.169 | 0.283 |
| Random Forest | 0.750 | 0.185 | 0.297 | ||
| Extra Trees | 0.824 | 0.215 | 0.341 | ||
| two | LightGBM | 1.000 | 0.305 | 0.467 | |
| Random Forest | 0.938 | 0.316 | 0.472 | ||
| Extra Trees | 0.944 | 0.358 | 0.519 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bargos, F.F.; Claro Romão, E. Enhanced Forecasting of Equity Fund Returns Using Machine Learning. Math. Comput. Appl. 2025, 30, 9. https://doi.org/10.3390/mca30010009
Bargos FF, Claro Romão E. Enhanced Forecasting of Equity Fund Returns Using Machine Learning. Mathematical and Computational Applications. 2025; 30(1):9. https://doi.org/10.3390/mca30010009
Chicago/Turabian StyleBargos, Fabiano Fernandes, and Estaner Claro Romão. 2025. "Enhanced Forecasting of Equity Fund Returns Using Machine Learning" Mathematical and Computational Applications 30, no. 1: 9. https://doi.org/10.3390/mca30010009
APA StyleBargos, F. F., & Claro Romão, E. (2025). Enhanced Forecasting of Equity Fund Returns Using Machine Learning. Mathematical and Computational Applications, 30(1), 9. https://doi.org/10.3390/mca30010009







