The Weighted Flexible Weibull Model: Properties, Applications, and Analysis for Extreme Events
Abstract
:1. Introduction
- This study is a pioneer in the use of weighted distributions in actuarial risk modeling, filling a critical research gap and providing a fresh perspective on risk evaluation.
- Actuarial risk metrics are applied beyond traditional financial contexts to medical data, specifically for assessing COVID-19 risk and managing datasets with extreme values. This cross-disciplinary approach highlights the adaptability of actuarial methods in diverse fields.
- A new estimation techniques and a sequential sampling plan based on truncated life testing are introduced, enhancing the precision and efficiency of risk assessment models.
- While the original discussion on PORT-VaR is too general, we have now expanded on its significance and provided a more detailed analysis of its applicability in modern risk assessment scenarios.
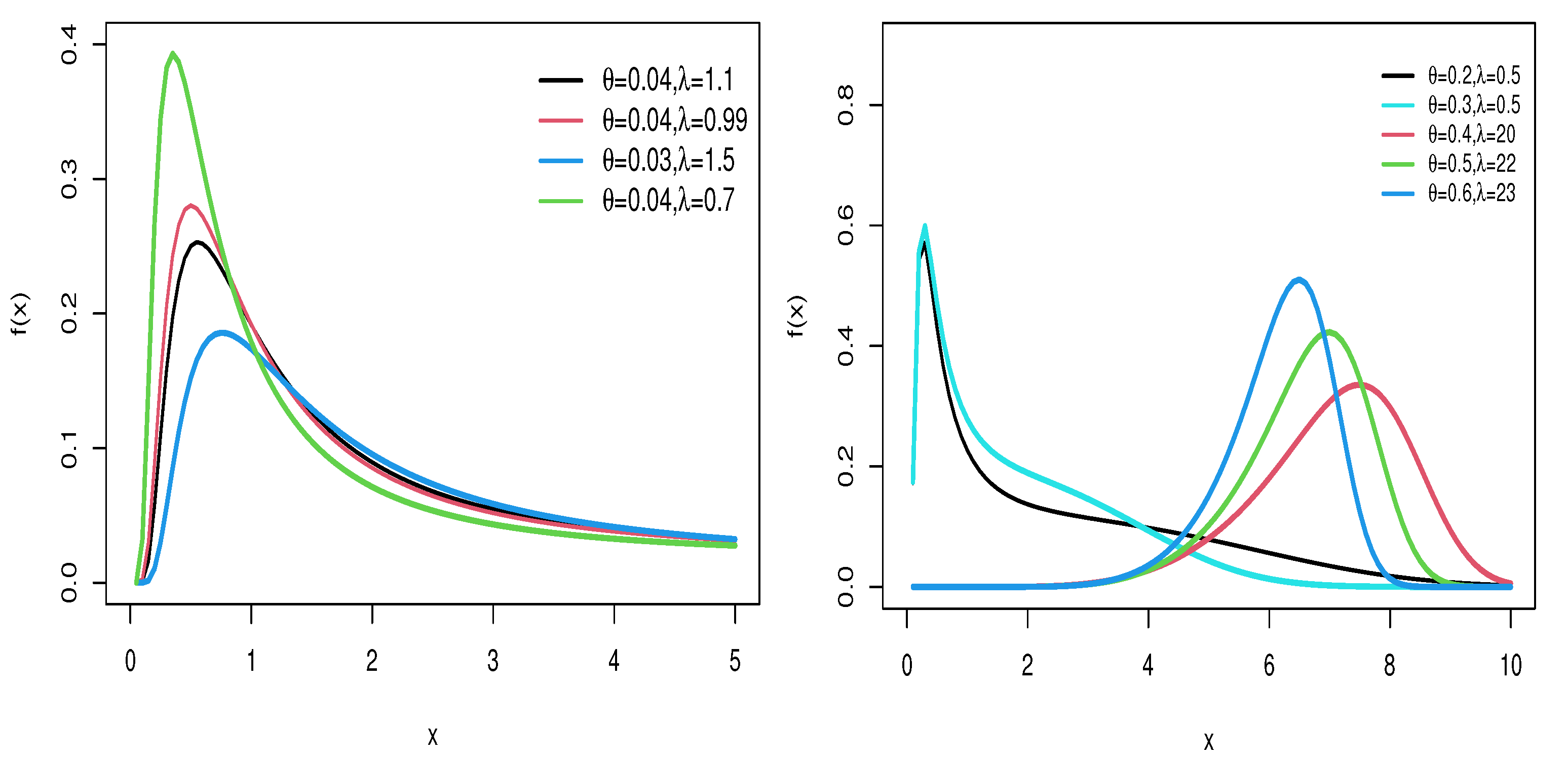
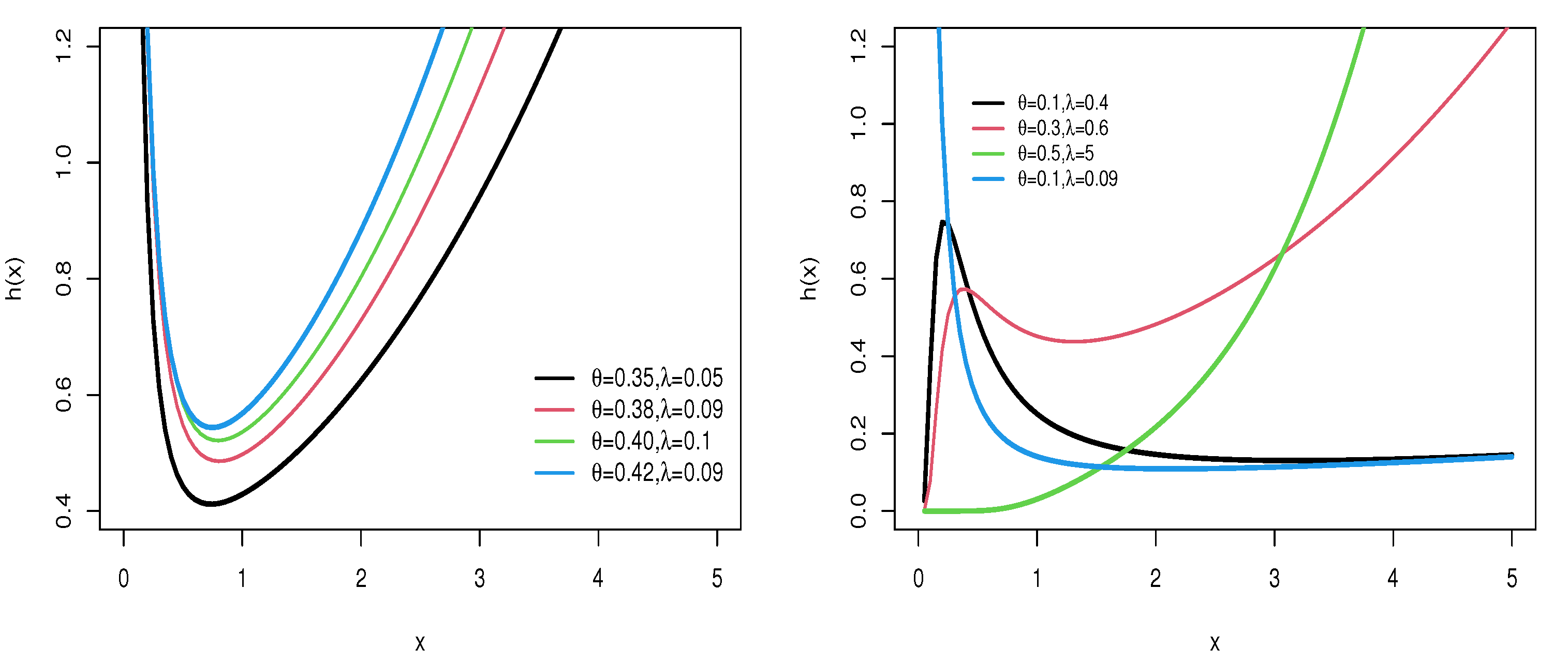
2. The WFW Distribution
3. Properties
3.1. Asymptotic Properties
3.2. Moments and Generating Function
3.3. Moment Generating Function
4. Entropy
4.1. Cumulative Entropy
4.2. Cumulative Residual Entropy
4.3. Rényi Entropy
5. Estimation Methods
5.1. Maximum Likelihood Estimation Method
5.2. Least Squares Estimation Method
5.3. Weighted Least Squares Estimation
5.4. Cramer–Von Mises Estimator
5.5. Anderson–Darling Estimator
6. Simulations
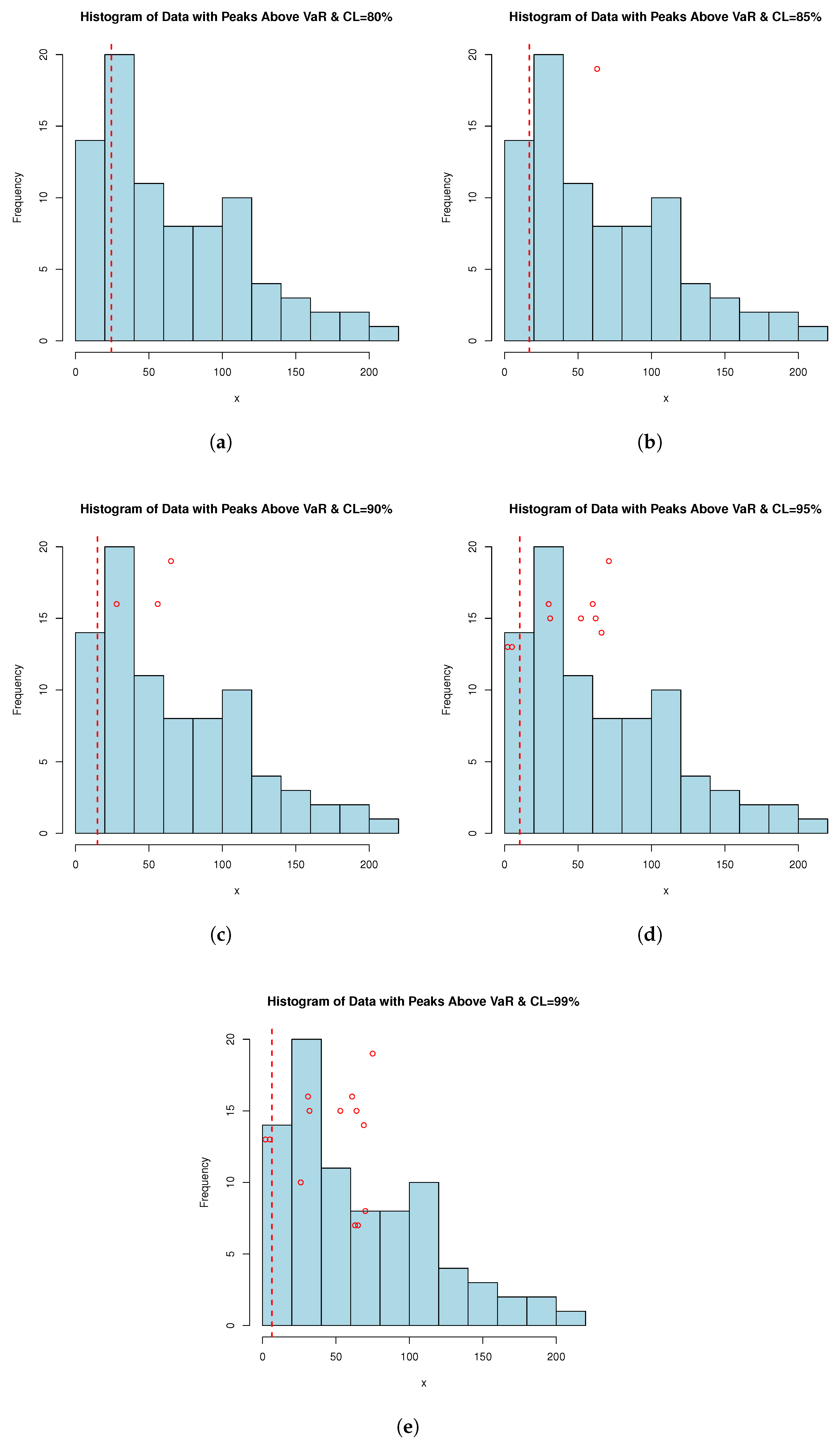
7. Risk Indicators
7.1. The Mean of Order P and Optimal Order of P
7.2. The PORT-VaR Estimator
- Gather relevant data that capture extreme events or rare occurrences. Clean and preprocess the data to ensure quality and suitability for analysis.
- Choose an appropriate statistical model.
- Select a threshold above which extreme events are considered for analysis. This threshold is crucial and should be based on domain expertise and risk management goals.
- Identify all data points that exceed the chosen threshold to form the PORT subset.
- Estimate the VaR for each peak in the PORT subset, where VaR represents the maximum expected loss at a specified confidence level based on extreme value modeling.
- Analyze the distribution of PORT-VaR estimates to quantify the tail risk associated with extreme events. Assess the impact of these events on overall risk exposure.
- Utilize PORT-VaR results to inform risk management strategies, such as setting reserves, determining insurance premiums, or implementing risk mitigation measures.
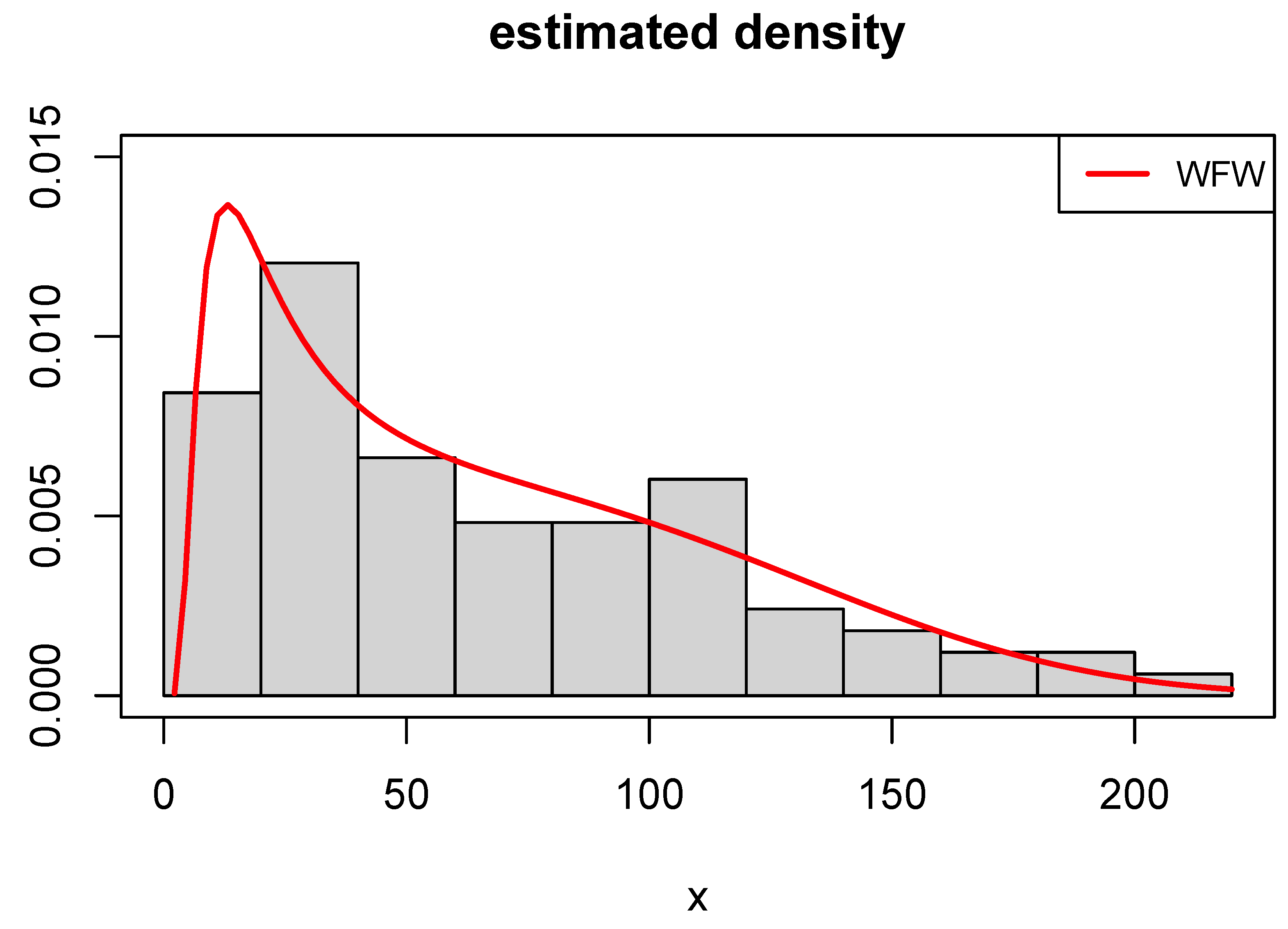
8. Applications
8.1. Failure Times Dataset
8.2. COVID-19 Mortality Dataset
8.3. COVID-19 Times Dataset
9. Assessments and Risk Analysis Under Real Data
9.1. Assessments and Optimal Order of P
9.2. VaR, TVaR and PORT-VaR Estimators for Extreme Failure Times
9.3. VaR, TVaR, and PORT-VaR Estimators for Extreme COVID-19 Deaths
10. Conclusions and Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.S.; Lai, S.B.; Wen, C.T. The influence of green innovation performance on corporate advantage in Taiwan. J. Bus. Ethics 2006, 67, 331–339. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Ortega, E.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Famoye, F.; Lee, C.; Olumolade, O. The beta-Weibull distribution. J. Stat. Appl. 2005, 4, 121–136. [Google Scholar]
- Xie, M.; Tang, Y.; Goh, T.N. A modified Weibull extension with bathtub-shaped failure rate function. Reliab. Eng. Syst. Saf. 2002, 76, 279–285. [Google Scholar] [CrossRef]
- Xie, M.; Lai, C.D. Reliability analysis using an additive Weibull model with bathtub-shaped failure rate function. Reliab. Eng. Syst. Saf. 1996, 52, 87–93. [Google Scholar] [CrossRef]
- Mustafa, A.; El-Desouky, B.S.; AL-Garash, S. The Marshall-Olkin Flexible Weibull Extension Distribution. arXiv 2016, arXiv:1609.08997. [Google Scholar]
- Bebbington, M.; Lai, C.D.; Zitikis, R. A flexible Weibull extension. Reliab. Syst. Saf. 2007, 92, 719–726. [Google Scholar] [CrossRef]
- Mustafa, A.; El-Desouky, B.S.; Al-Garash, S. The exponentiated generalized flexible Weibull extension distribution. Fundam. J. Math. Math. Sci. 2016, 6, 75–98. [Google Scholar]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Zekri, A.R.N.; Youssef, A.S.E.D.; El-Desouky, E.D.; Ahmed, O.S.; Lotfy, M.M.; Nassar, A.A.M.; Bahnassey, A.A. Serum microRNA panels as potential biomarkers for early detection of hepatocellular carcinoma on top of HCV infection. Tumor Biol. 2016, 37, 12273–12286. [Google Scholar] [CrossRef]
- Alizadeh, M.; Afshari, M.; Cordeiro, G.M.; Ramaki, Z.; Contreras-Reyes, J.E.; Dirnik, F.; Yousof, H.M. A Weighted Lindley Claims Model with Applications to Extreme Historical Insurance Claims. Stats 2025, 8, 8. [Google Scholar] [CrossRef]
- Kharazmi, O.; Contreras-Reyes, J.E.; Balakrishnan, N. Optimal information, Jensen-RIG function and α-Onicescu’s correlation coefficient in terms of information generating functions. Phys. A 2023, 609, 128362. [Google Scholar] [CrossRef]
- Kuschel, K.; Carrasco, R.; Idrovo-Aguirre, B.J.; Duran, C.; Contreras-Reyes, J.E. Preparing Cities for Future Pandemics: Unraveling the influence of urban and housing variables on COVID-19 incidence in Santiago de Chile. Healthcare 2023, 11, 2259. [Google Scholar] [CrossRef] [PubMed]
- Zwillinger, D. Table of Integrals, Series, and Products; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Ferreira, A.A.; Cordeiro, G.M. The gamma flexible Weibull distribution: Properties and Applications. Span. J. Stat. 2023, 4, 55–71. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Chaudhry, M.A.; Zubair, S.M. Generalized incomplete gamma functions with applications. J. Comput. Appl. Math. 1994, 55, 99–124. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. On cumulative entropies. J. Stat. Inference 2009, 139, 4072–4087. [Google Scholar] [CrossRef]
- Kharazmi, O.; Contreras-Reyes, J.E. Fractional cumulative residual inaccuracy information measure and its extensions with application to chaotic maps. Int. J. Bifurc. Chaos 2024, 34, 2450006. [Google Scholar] [CrossRef]
- Kharazmi, O.; Yalcin, F.; Contreras-Reyes, J.E. Cumulative residual Fisher information based on finite and infinite mixture models. Fluct. Noise Lett. 2025. [Google Scholar] [CrossRef]
- Psarrakos, G.; Toomaj, A. On the generalized cumulative residual entropy with applications in actuarial science. J. Comput. Appl. Math. 2017, 309, 186–199. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1961; Volume 4, pp. 547–562. [Google Scholar]
- Contreras-Reyes, J.E. Mutual information matrix based on Rényi entropy and application. Nonlinear Dyn. 2022, 110, 623–633. [Google Scholar] [CrossRef]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Team, R.C. Package ‘caret’. R J. 2020, 223, 48. [Google Scholar]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024; Available online: http://www.R-project.org (accessed on 17 February 2025).
- Alizadeh, M.; Afshari, M.; Contreras-Reyes, J.E.; Mazarei, D.; Yousof, H.M. The Extended Gompertz Model: Applications, Mean of Order P Assessment and Statistical Threshold Risk Analysis Based on Extreme Stresses Data. IEEE Trans. Reliab. 2024. [Google Scholar] [CrossRef]
- Rice, J.A. Mathematical Statistics and Data Analysis; Thomson/Brooks/Cole: Belmont, CA, USA, 2007; Volume 371. [Google Scholar]
- Szubzda, F.; Chlebus, M. Comparison of Block Maxima and Peaks Over Threshold Value-at-Risk models for market risk in various economic conditions. Cent. Econ. J. 2019, 6, 70–85. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K. Exponentiated Weibull family for analyzing bathtub failure-rate data. IEEE Trans. Reliab. 1993, 42, 299–302. [Google Scholar] [CrossRef]
- Lai, C.D.; Xie, M.; Murthy, D.N.P. A modified Weibull distribution. IEEE Trans. Reliab. 2003, 52, 33–37. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Vasconcelos, J.C.S.; dos Santos, D.P.; Ortega, E.M.; Sermarini, R.A. Three mixed-effects regression models using an extended Weibull with applications on games in differential and integral calculus. Braz. J. Probability Stat. 2022, 36, 751–770. [Google Scholar] [CrossRef]
- Paranaíba, P.F.; Ortega, E.M.; Cordeiro, G.M.; Pascoa, M.A.D. The Kumaraswamy Burr XII distribution: Theory and practice. J. Stat. Comput. Simul. 2013, 83, 2117–2143. [Google Scholar] [CrossRef]
- Marinho, P.R.D.; Silva, R.B.; Bourguignon, M.; Cordeiro, G.M.; Nadarajah, S. AdequacyModel: An R package for probability distributions and general purpose optimization. PLoS ONE 2019, 14, e0221487. [Google Scholar] [CrossRef]
- Murthy, D.P.; Xie, M.; Jiang, R. Weibull Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Ahmad, Z.; Almaspoor, Z.; Khan, F.; El-Morshedy, M. On predictive modeling using a new flexible Weibull distribution and machine learning approach: Analyzing the COVID-19 data. Mathematics 2022, 10, 1792. [Google Scholar] [CrossRef]
- Brown, A.; Williams, R. Equity implications of ride-hail travel during COVID-19 in California. Transp. Res. Rec. 2023, 2677, 1–14. [Google Scholar] [CrossRef]
- Mohamed, H.S.; Cordeiro, G.M.; Minkah, R.; Yousof, H.M.; Ibrahim, M. A size-of-loss model for the negatively skewed insurance claims data: Applications, risk analysis using different methods and statistical forecasting. J. Appl. Stat. 2024, 51, 348–369. [Google Scholar] [CrossRef] [PubMed]
- Golinelli, D.; Boetto, E.; Carullo, G.; Nuzzolese, A.G.; Landini, M.P.; Fantini, M.P. Adoption of digital technologies in health care during the COVID-19 pandemic: Systematic review of early scientific literature. J. Medical Internet Res. 2020, 22, e22280. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, E.B.; Souissi, M.N.; Baccar, A.; Bouri, A. CEO’s personal characteristics, ownership and investment cash flow sensitivity: Evidence from NYSE panel data firms. J. Econ. Financ. Adm. Sci. 2014, 19, 98–103. [Google Scholar] [CrossRef]

| 10.923 | 10.773 | 11.439 | 10.040 | |
| 243.831 | 240.959 | 254.236 | 228.0944 | |
| 6860.908 | 6783.186 | 7146.237 | 6440.962 | |
| 219054.8 | 216538.5 | 228340.1 | 205525.1 | |
| 11.15824 | 11.17569 | 11.106 | 11.282 | |
| 1.063338 | 1.071 | 1.032 | 1.11053 | |
| 3.29815 | 3.309 | 3.257 | 3.352 | |
| 6.2996 | 5.980 | 7.174612 | 5.642 | |
| 40.71086 | 36.776 | 52.5268 | 32.84342 | |
| 268.776 | 231.495 | 391.2338 | 196.1263 | |
| 1807.249 | 1486.404 | 2957.79 | 1196.871 | |
| 1.012774 | 1.0074 | 1.025543 | 1.001466 | |
| −0.5871091 | −0.5543 | −0.6650084 | −0.5167628 | |
| 3.301012 | 3.227 | 3.492299 | 3.147694 | |
| 7.0534 | 5.565 | 6.869 | 6.119 | |
| 51.317 | 33.453 | 49.785 | 39.985 | |
| 383.059 | 213.284 | 376.477 | 274.881 | |
| 2922.048 | 1425.085 | 2947.551 | 1968.856 | |
| 1.251 | 1.574 | 1.612 | 1.591 | |
| −0.516 | −0.127 | −0.294 | 0.20 | |
| 3.147 | 2.603 | 2.776 | 2.672 | |
| 0.631 | 0.849 | 1.022 | 1.169 | |
| 0.487 | 0.815 | 1.142 | 1.468 | |
| 0.430 | 0.854 | 1.364 | 1.947 | |
| 0.416 | 0.958 | 1.719 | 2.697 | |
| 0.297 | 0.305 | 0.311 | 0.316 | |
| 0.381 | 0.105 | −0.055 | −0.167 | |
| 2.555 | 2.498 | 2.555 | 2.638 |
| Bias for | n | MLEs | LSEs | WLSEs | CMEs | ADEs | RTADEs |
| 20 | 0.0707 | 0.0039 | 0.0129 | 0.0812 | 0.0255 | 0.0440 | |
| 50 | 0.0256 | 0.0013 | 0.0077 | 0.0304 | 0.0099 | 0.0169 | |
| 100 | 0.0099 | −0.0020 | 0.0028 | 0.0122 | 0.0028 | 0.0052 | |
| 200 | 0.0050 | −0.0014 | 0.0010 | 0.0057 | 0.0009 | 0.0008 | |
| 500 | 0.0024 | 0.0006 | 0.0016 | 0.0035 | 0.0012 | 0.0016 | |
| Bias for | n | MLEs | LSEs | WLSEs | CMEs | ADEs | RTADEs |
| 20 | 0.1061 | 0.0202 | 0.0311 | 0.1116 | 0.0444 | 0.0839 | |
| 50 | 0.0396 | 0.0101 | 0.0178 | 0.0445 | 0.0190 | 0.0343 | |
| 100 | 0.0174 | 0.0011 | 0.0073 | 0.0179 | 0.0066 | 0.0122 | |
| 200 | 0.0061 | −0.0039 | −0.0003 | 0.0044 | −0.0008 | −0.0004 | |
| 500 | 0.0027 | 0.0000 | 0.0013 | 0.0033 | 0.0006 | 0.0016 | |
| MSE for | n | MLEs | LSEs | WLSEs | CMEs | ADEs | RTADEs |
| 20 | 0.1948 | 0.2158 | 0.2010 | 0.2538 | 0.1827 | 0.1958 | |
| 50 | 0.1045 | 0.1258 | 0.1145 | 0.1342 | 0.1087 | 0.1115 | |
| 100 | 0.0661 | 0.0841 | 0.0751 | 0.0866 | 0.0725 | 0.0749 | |
| 200 | 0.0474 | 0.0589 | 0.0528 | 0.0597 | 0.0517 | 0.0532 | |
| 500 | 0.0288 | 0.0379 | 0.0326 | 0.0382 | 0.0323 | 0.0326 | |
| MSE for | n | MLEs | LSEs | WLSEs | CMEs | ADEs | RTADEs |
| 20 | 0.3333 | 0.3366 | 0.3248 | 0.3865 | 0.3087 | 0.3622 | |
| 50 | 0.1778 | 0.2027 | 0.1898 | 0.2146 | 0.1835 | 0.2102 | |
| 100 | 0.1268 | 0.1452 | 0.1358 | 0.1489 | 0.1334 | 0.1513 | |
| 200 | 0.0838 | 0.0964 | 0.0895 | 0.0973 | 0.0888 | 0.0989 | |
| 500 | 0.0509 | 0.0598 | 0.0546 | 0.0601 | 0.0543 | 0.0608 |
| Bias for | n | MLEs | LSEs | WLSEs | CMEs | ADEs | RTADEs |
| 20 | 0.03848 | 0.01386 | 0.01524 | 0.05298 | 0.01992 | 0.02619 | |
| 50 | 0.01225 | −0.00096 | 0.00260 | 0.01317 | 0.00367 | 0.00728 | |
| 100 | 0.00644 | 0.00041 | 0.00234 | 0.00738 | 0.00261 | 0.00440 | |
| 200 | 0.00465 | 0.00161 | 0.00267 | 0.00507 | 0.00262 | 0.00313 | |
| 500 | 0.00070 | −0.00075 | −0.00008 | 0.00062 | −0.00026 | 0.00003 | |
| Bias for | n | MLEs | LSEs | WLSEs | CMEs | ADEs | RTADEs |
| 20 | 0.11110 | 0.03352 | 0.03706 | 0.13005 | 0.05047 | 0.09532 | |
| 50 | 0.03963 | 0.00562 | 0.01467 | 0.04093 | 0.01528 | 0.03732 | |
| 100 | 0.02875 | 0.01374 | 0.01831 | 0.03127 | 0.01813 | 0.02871 | |
| 200 | 0.01243 | 0.00486 | 0.00786 | 0.01346 | 0.00739 | 0.01084 | |
| 500 | 0.00199 | −0.00221 | −0.00043 | 0.00119 | −0.00115 | 0.00058 | |
| MSE for | n | MLEs | LSEs | WLSEs | CMEs | ADEs | RTADEs |
| 20 | 0.09613 | 0.11221 | 0.10429 | 0.13553 | 0.09246 | 0.09473 | |
| 50 | 0.05239 | 0.06250 | 0.05693 | 0.06627 | 0.05443 | 0.05605 | |
| 100 | 0.03401 | 0.04156 | 0.03730 | 0.04300 | 0.03626 | 0.03730 | |
| 200 | 0.02483 | 0.02923 | 0.02625 | 0.02989 | 0.02604 | 0.02644 | |
| 500 | 0.01552 | 0.01908 | 0.01687 | 0.01915 | 0.01676 | 0.01702 | |
| MSE for | n | MLEs | LSEs | WLSEs | CMEs | ADEs | RTADEs |
| 20 | 0.36420 | 0.37965 | 0.36290 | 0.43784 | 0.34708 | 0.43814 | |
| 50 | 0.19811 | 0.22821 | 0.21303 | 0.24043 | 0.20657 | 0.25621 | |
| 100 | 0.14033 | 0.16054 | 0.15059 | 0.16596 | 0.14732 | 0.17763 | |
| 200 | 0.09688 | 0.10939 | 0.10210 | 0.11110 | 0.10170 | 0.11767 | |
| 500 | 0.05945 | 0.07042 | 0.06431 | 0.07066 | 0.06398 | 0.07407 |
| Model | MLE (SE) | ||||
|---|---|---|---|---|---|
| WFW | 0.109 | 0.146 | |||
| GFW | 1.362 | 0.109 | 0.126 | ||
| FW | 0.099 | 0.183 | |||
| MW | 0.496 | 0.034 | 0.562 | ||
| EW | 0.290 | 0.770 | 0.785 | ||
| KwBXII | 0.121 | 2.199 | 4.381 | 1.193 | 21.015 |
| BW | 0.708 | 0.703 | 0.412 | 0.819 | |
| Model | AIC | CAIC | BIC | HQIC | ||
|---|---|---|---|---|---|---|
| WFW | 0.041 | 0.267 | 192.294 | 192.55 | 196.118 | 193.750 |
| GFW | 0.042 | 0.257 | 193.850 | 194.372 | 199.586 | 196.035 |
| FW | 0.079 | 0.414 | 195.846 | 196.101 | 199.670 | 197.302 |
| MW | 0.130 | 0.850 | 208.727 | 209.249 | 214.463 | 210.912 |
| EW | 0.150 | 0.946 | 210.713 | 211.234 | 216.449 | 212.897 |
| BW | 0.149 | 0.942 | 212.696 | 213.585 | 220.344 | 215.608 |
| KwBXII | 1.132 | 0.870 | 213.086 | 214.450 | 222.646 | 216.726 |
| Model | MLE (SE) | ||||
|---|---|---|---|---|---|
| WFW | 0.010 | 23.243 | |||
| GFW | 1.702 | 0.010 | 14.005 | ||
| FW | 0.008 | 32.812 | |||
| MW | 0.005 | 0.003 | 1.161 | ||
| EW | 0.013 | 1.418 | 0.986 | ||
| KwBXII | 10.526 | 72.271 | 0.327 | 1.393 | 40.836 |
| BW | 3.697 | 3.665 | 0.011 | 0.615 | |
| Model | AIC | CAIC | BIC | HQIC | ||
|---|---|---|---|---|---|---|
| WFW | 0.029 | 0.212 | 853.026 | 853.176 | 857.864 | 854.969 |
| GFW | 0.034 | 0.241 | 855.333 | 855.637 | 862.590 | 858.248 |
| FW | 0.095 | 0.596 | 859.516 | 859.666 | 864.353 | 861.459 |
| MW | 0.057 | 0.348 | 858.767 | 859.071 | 866.024 | 861.682 |
| EW | 0.059 | 0.351 | 858.690 | 858.994 | 865.946 | 861.605 |
| BW | 0.088 | 0.544 | 863.876 | 864.389 | 873.551 | 867.763 |
| KwBXII | 0.083 | 0.508 | 864.870 | 865.649 | 876.964 | 869.728 |
| Model | Parameter 1 | Parameter 2 | Parameter 3 | Parameter 4 |
|---|---|---|---|---|
| WFW | 0.127 (0.015) | 3.951 (0.931) | ||
| GFW | 0.3418 (0.566) | 0.1315 (0.07) | 16.38 (24.75) | |
| FW | 0.1199 (0.018) | 5.596 (1.056) | ||
| EW | 4.084 (3.476) | 1.188 (0.679) | 2.508 (3.049) | |
| KwW | 100 (1472.02) | 100 (960.966) | 2.444 (13.220) | 0.1249 (0.6912) |
| W | 6.9637 (0.715) | 1.879 (0.262) | ||
| LNORM | 1.6471 (0.112) | 0.611 (0.078) |
| Model | AIC | CAIC | BIC | HQIC |
|---|---|---|---|---|
| WFW | 157.7342 | 158.1787 | 159.5366 | 158.6308 |
| GFW | 158.677 | 159.6 | 162.8806 | 160.0217 |
| FW | 158.810 | 158.2553 | 160.6132 | 158.7073 |
| KwW | 161.3179 | 162.9179 | 166.9226 | 163.1109 |
| W | 158.0685 | 158.5129 | 160.8709 | 158.965 |
| LNORM | 158.4702 | 159 | 161.2726 | 159.3667 |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| TMV | 1.001314 | ||||
| MSE | 0.9983274 | 0.9983274 | 0.9983274 | 0.9983274 | 0.9983274 |
| Bias | 0.9991634 | 0.9991634 | 0.9991634 | 0.9991634 | 0.9991634 |
| TMV | 0.9973669 | ||||
| MSE | 0.9947407 | 0.9947407 | 0.9947407 | 0.9947407 | 0.9947407 |
| Bias | 0.9973669 | 0.9973669 | 0.9973669 | 0.9973669 | 0.9973669 |
| TMV | 0.9978629 | ||||
| MSE | 0.9957304 | 0.9957304 | 0.9957304 | 0.9957303 | 0.9957296 |
| Bias | 0.9978629 | 0.9978629 | 0.9978629 | 0.9978629 | 0.9978625 |
| TMV | 0.9988142 | ||||
| MSE | 0.9976297 | 0.9976297 | 0.9976297 | 0.9976297 | 0.9976297 |
| Bias | 0.9988142 | 0.9988142 | 0.9988142 | 0.9988142 | 0.9988142 |
| CLs | N. of PORT | VaR | TVaR | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|---|---|---|---|
| 80% | 40 | 3.490 | 1.5764 | 0.148 | 0.586 | 3.067 | 4.158 | 6.410 | 15.08 |
| 85% | 42 | 3.019 | 1.035 | 0.114 | 0.571 | 2.931 | 3.965 | 5.929 | 15.08 |
| 90% | 45 | 1.491 | 0.593 | 0.086 | 0.381 | 2.054 | 3.708 | 4.893 | 15.08 |
| 95% | 47 | 0.744 | 0.375 | 0.0740 | 0.3205 | 2.0060 | 3.5530 | 4.7135 | 15.08 |
| 99% | 94 | 0.321 | 0.130 | 0.058 | 0.254 | 1.600 | 3.410 | 4.534 | 15.08 |
| CL | N. of PORT | VaR | TVaR | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|---|---|---|---|
| 80% | 66 | 24.4 | 30.375 | 25.00 | 40.25 | 72.50 | 81.74 | 107.75 | 201.00 |
| 85% | 70 | 16.9 | 11.769 | 19.00 | 38.00 | 70.50 | 78.29 | 107.00 | 201.00 |
| 90% | 72 | 15 | 11 | 16.00 | 37.50 | 68.00 | 76.56 | 107.00 | 201.00 |
| 95% | 78 | 10.3 | 7.2 | 13.00 | 32.50 | 58.50 | 71.76 | 103.25 | 201.00 |
| 99% | 82 | 6.46 | 4 | 7.00 | 30.25 | 57.50 | 68.65 | 101.00 | 201.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramaki, Z.; Alizadeh, M.; Tahmasebi, S.; Afshari, M.; Contreras-Reyes, J.E.; Yousof, H.M. The Weighted Flexible Weibull Model: Properties, Applications, and Analysis for Extreme Events. Math. Comput. Appl. 2025, 30, 42. https://doi.org/10.3390/mca30020042
Ramaki Z, Alizadeh M, Tahmasebi S, Afshari M, Contreras-Reyes JE, Yousof HM. The Weighted Flexible Weibull Model: Properties, Applications, and Analysis for Extreme Events. Mathematical and Computational Applications. 2025; 30(2):42. https://doi.org/10.3390/mca30020042
Chicago/Turabian StyleRamaki, Ziaurrahman, Morad Alizadeh, Saeid Tahmasebi, Mahmoud Afshari, Javier E. Contreras-Reyes, and Haitham M. Yousof. 2025. "The Weighted Flexible Weibull Model: Properties, Applications, and Analysis for Extreme Events" Mathematical and Computational Applications 30, no. 2: 42. https://doi.org/10.3390/mca30020042
APA StyleRamaki, Z., Alizadeh, M., Tahmasebi, S., Afshari, M., Contreras-Reyes, J. E., & Yousof, H. M. (2025). The Weighted Flexible Weibull Model: Properties, Applications, and Analysis for Extreme Events. Mathematical and Computational Applications, 30(2), 42. https://doi.org/10.3390/mca30020042









