Long-Range Non-Line-of-Sight Imaging Based on Projected Images from Multiple Light Fields
Abstract
:1. Introduction
2. Materials and Methods
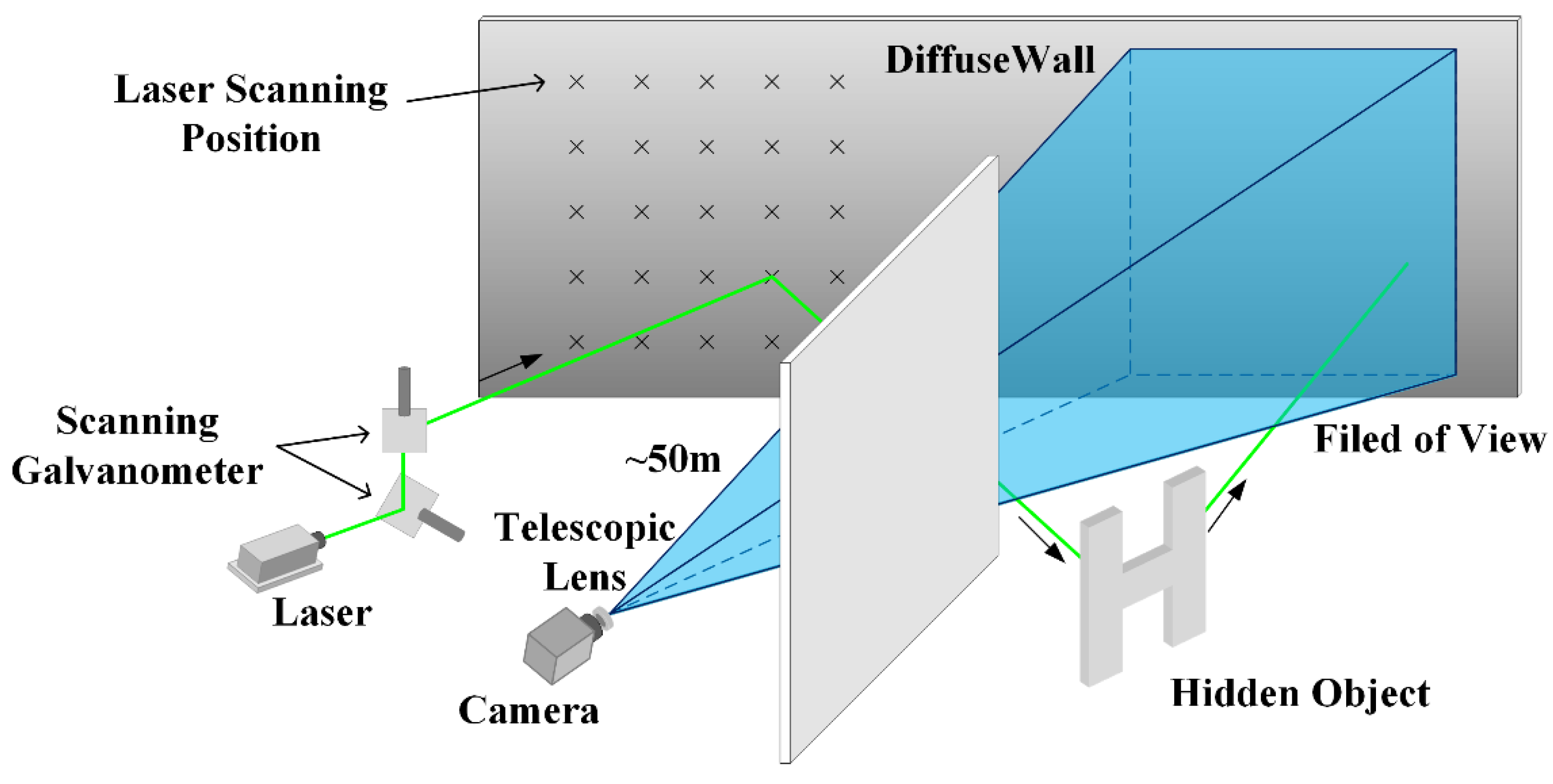
2.1. NLOS Imaging System Setup
2.2. Theory
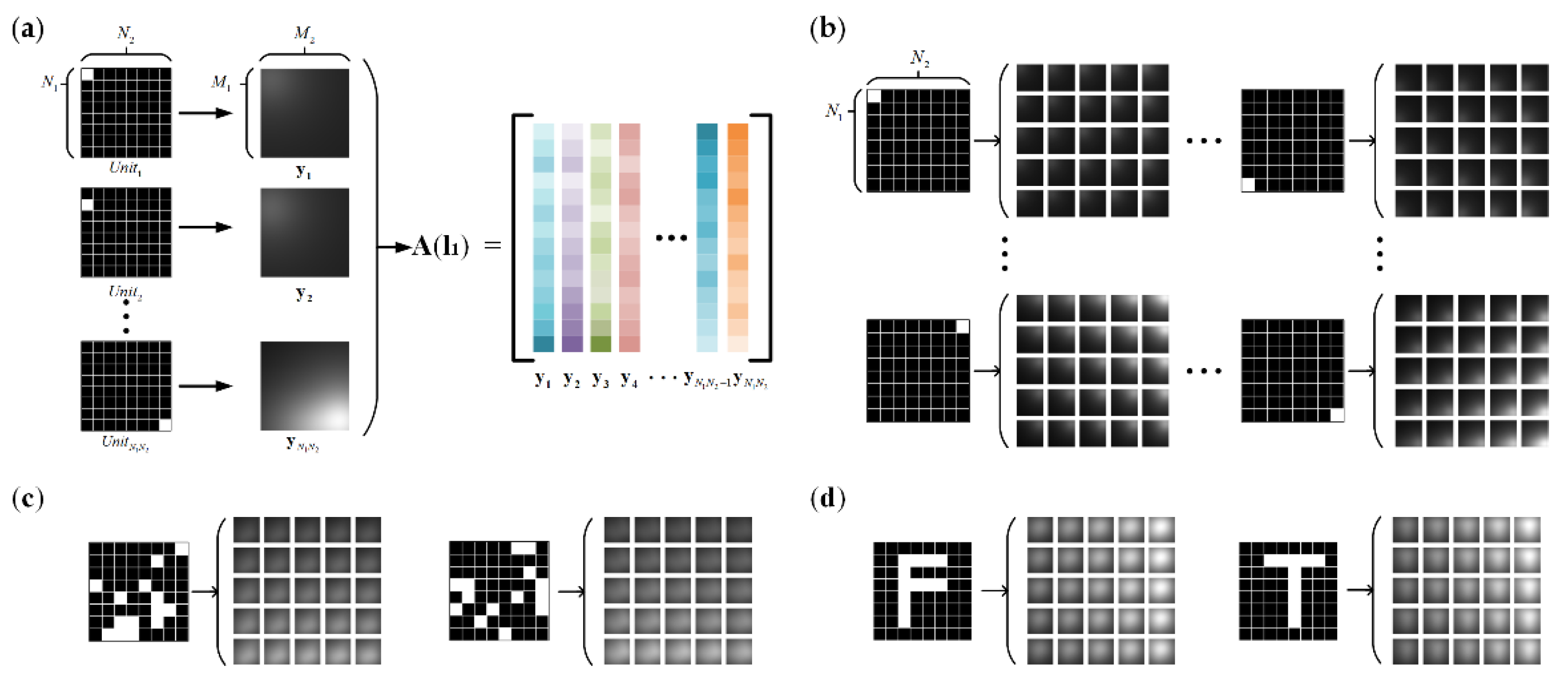
2.2.1. Projected Image Formulation Model
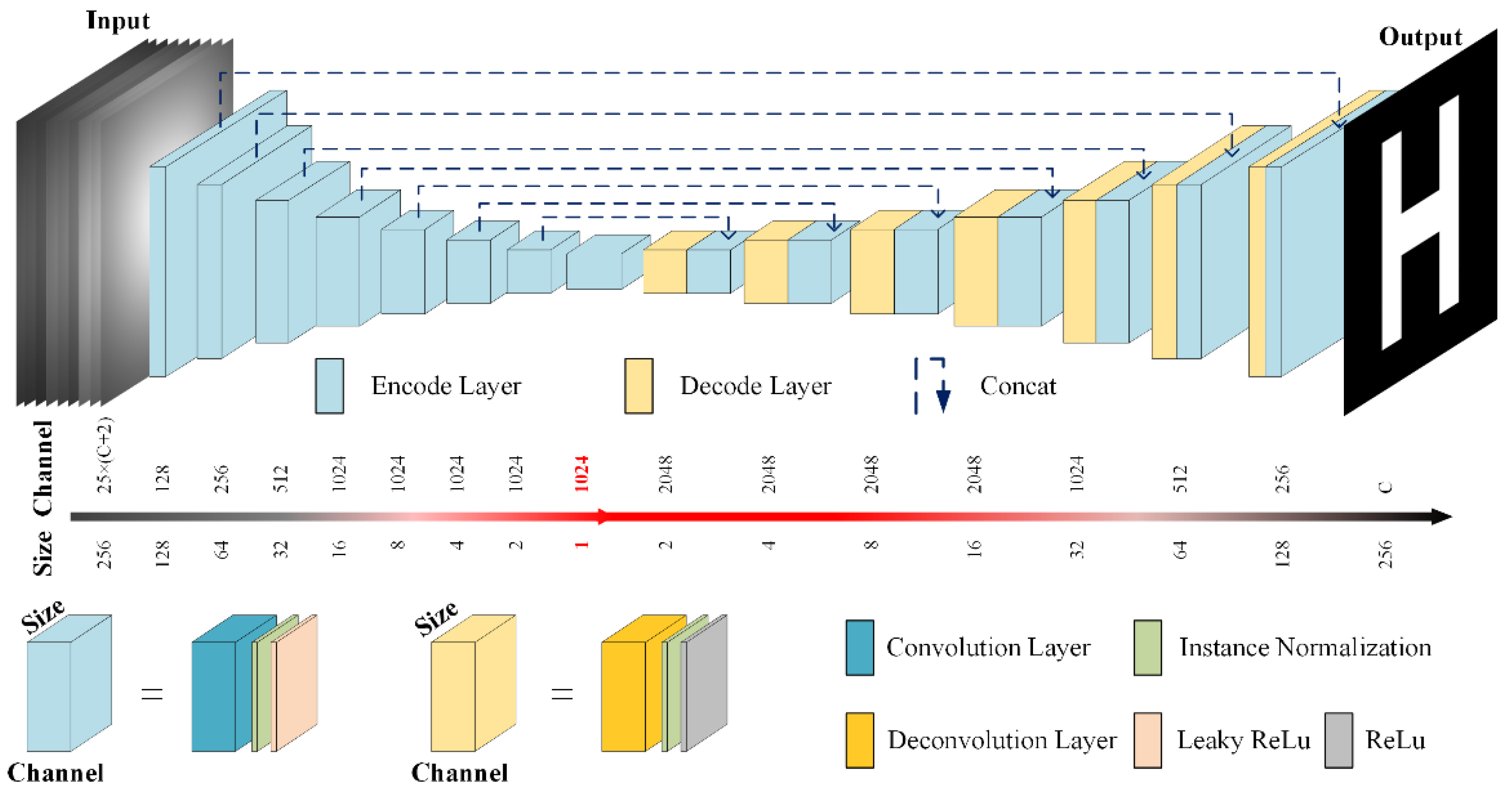
2.2.2. Deep Learning Based Reconstruction Model
3. Results and Discussion
3.1. Simulation Results
3.1.1. Projected Image Simulation
3.1.2. Target Reconstruction with Simulated Data
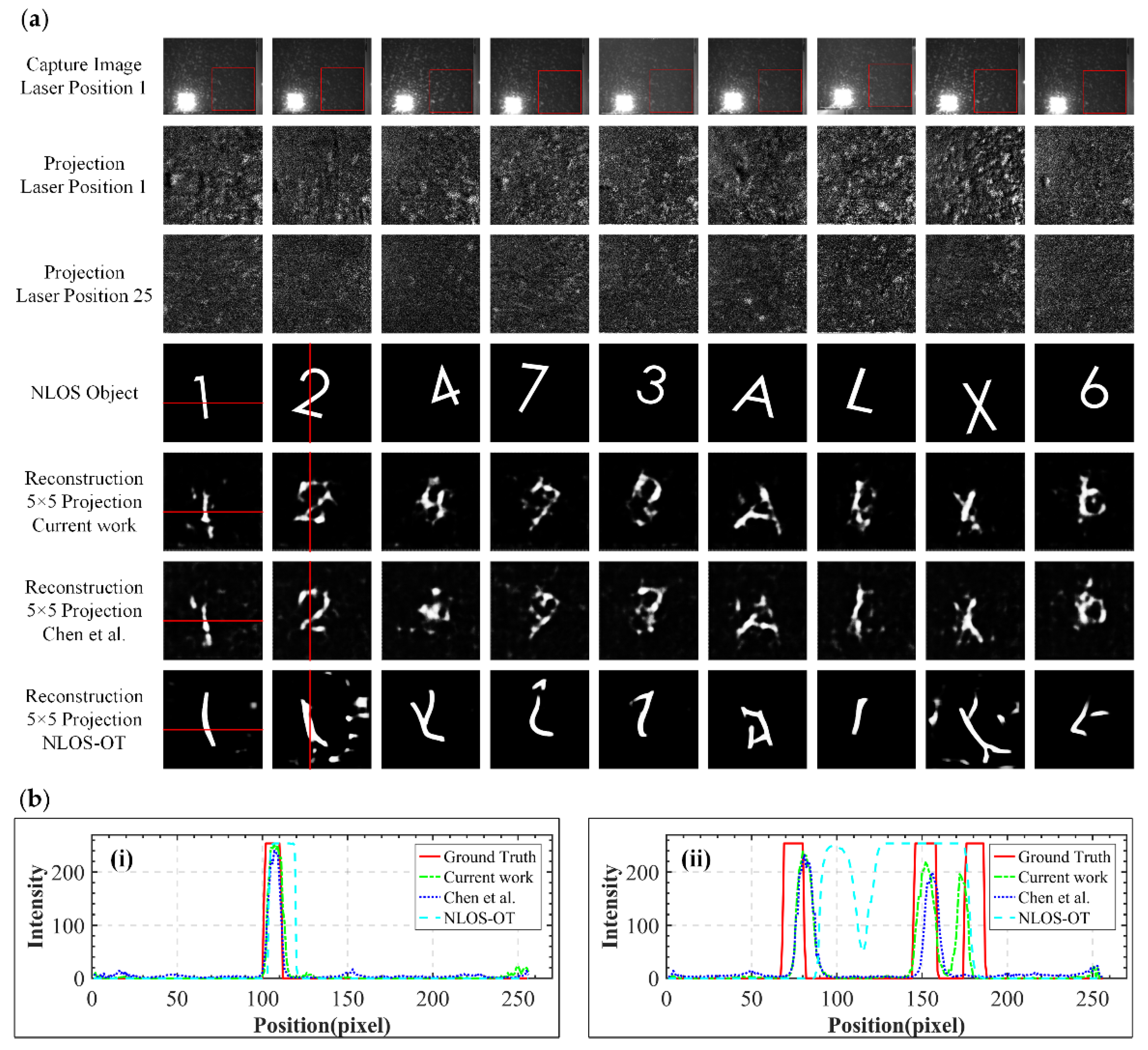
3.2. Experimental Results
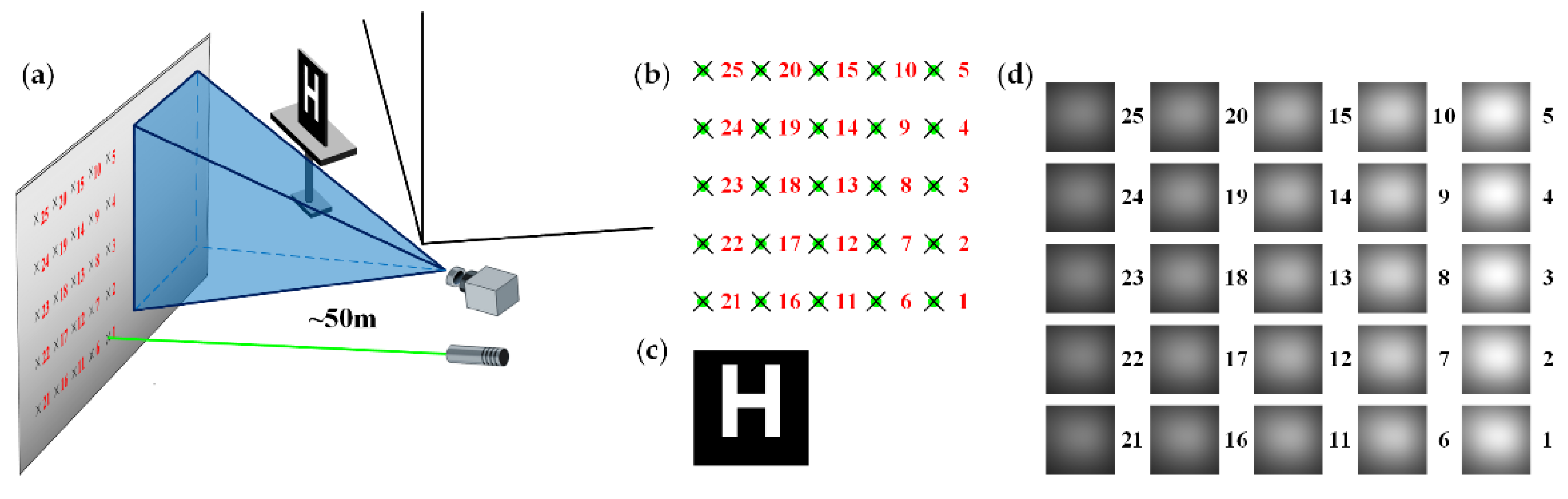
3.2.1. Experimental Setup
3.2.2. Target Reconstruction with Captured Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Velten, A.; Willwacher, T.; Gupta, O.; Veeraraghavan, A.; Bawendi, M.G.; Raskar, R. Recovering three-dimensional shape around a corner using ultrafast time-of-flight imaging. Nat. Commun. 2012, 3, 745. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arellano, V.; Gutiérrez, D.; Jarabo, A. Fast back-projection for non-line of sight reconstruction. In Proceedings of the ACM SIGGRAPH 2017 Posters, Los Angeles, CA, USA, 30 July–3 August 2017. [Google Scholar]
- Chan, S.; Warburton, R.E.; Gariepy, G.; Leach, J.; Faccio, D. Non-line-of-sight tracking of people at long range. Opt. Express 2017, 25, 10109–10117. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.; Xie, J.; Zhang, S.; Zhang, Z.J.; Yuan, Z. Reconstruction of multiple non-line-of-sight objects using back projection based on ellipsoid mode decomposition. Opt. Express 2018, 26, 20089. [Google Scholar] [CrossRef] [PubMed]
- Jin, C.; Xie, J.; Zhang, S.; Zhang, Z.J.; Yuan, Z. Richardson–Lucy deconvolution of time histograms for high-resolution non-line-of-sight imaging based on a back-projection method. Opt. Lett. 2018, 43, 5885. [Google Scholar] [CrossRef] [PubMed]
- Marco, L.M.; Fiona, K.; Eric, B.; Jonathan, J.; Talha, S.; Andreas, V. Error Backprojection Algorithms for Non-Line-of-Sight Imaging. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 1615–1626. [Google Scholar]
- O’Toole, M.; Lindell, D.B.; Wetzstein, G. Confocal non-line-of-sight imaging based on the light-cone transform. Nature 2018, 555, 338–341. [Google Scholar] [CrossRef]
- Heide, F.; O’Toole, M.; Zang, K.; Lindell, D.B.; Wetzstein, G. Non-line-of-sight Imaging with Partial Occluders and Surface Normals. ACM Trans. Graph. 2019, 38, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Wang, X.; Yuan, Y.; Gu, S.; Shen, Y. Improved algorithm of non-line-of-sight imaging based on the Bayesian statistics. JOSA A 2019, 36, 834–838. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, X.; Li, Y.; Sun, Z.; Zhang, W. Edge re-projection method for high-quality edge reconstruction in non-line-of-sight imaging. Appl. Opt. 2020, 59, 1793–1800. [Google Scholar] [CrossRef]
- Young, S.I.; Lindell, D.B.; Girod, B.; Taubman, D.; Wetzstein, G. Non-Line-of-Sight Surface Reconstruction Using the Directional Light-Cone Transform. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1404–1413. [Google Scholar]
- Wu, C.; Liu, J.; Huang, X.; Li, Z.P.; Pan, J.W. Non-line-of-sight imaging over 1.43 km. Proc. Natl. Acad. Sci. USA 2021, 118, e2024468118. [Google Scholar] [CrossRef]
- Tanaka, K.; Mukaigawa, Y.; Kadambi, A. Polarized Non-Line-of-Sight Imaging. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 2133–2142. [Google Scholar]
- Torralba, A.; Freeman, W.T. Accidental pinhole and pinspeck cameras: Revealing the scene outside the picture. In Proceedings of the 2012 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Bouman, K.L.; Ye, V.; Yedidia, A.B.; Durand, F.; Freeman, W.T. Turning Corners into Cameras: Principles and Methods. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Saunders, C.; Murray-Bruce, J.; Goyal, V.K. Computational periscopy with an ordinary digital camera. Nature 2019, 565, 472–475. [Google Scholar] [CrossRef] [PubMed]
- Seidel, S.W.; Ma, Y.; Murray-Bruce, J.; Saunders, C.; Goyal, V.K. Corner Occluder Computational Periscopy: Estimating a Hidden Scene from a Single Photograph. In Proceedings of the 2019 IEEE International Conference on Computational Photography (ICCP), Tokyo, Japan, 15–17 May 2019. [Google Scholar]
- Yedidia, A.B.; Baradad, M.; Thrampoulidis, C.; Freeman, W.T.; Wornell, G.W. Using unknown occluders to recover hidden scenes. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition(CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 12231–12239. [Google Scholar]
- Saunders, C.; Bose, R.; Murray-Bruce, J.; Goyal, V.K. Multi-depth computational periscopy with an ordinary camera. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 9299–9305. [Google Scholar]
- Seidel, S.W.; Murray-Bruce, J.; Ma, Y.; Yu, C.; Goyal, V.K. Two-Dimensional Non-Line-of-Sight Scene Estimation from a Single Edge Occluder. IEEE Trans. Comput. Imaging 2021, 7, 58–72. [Google Scholar] [CrossRef]
- Caramazza, P.; Boccolini, A.; Buschek, D.; Hullin, M.; Higham, C.F.; Henderson, R.; Murray-Smith, R.; Faccio, D. Neural network identification of people hidden from view with a single-pixel, single-photon detector. Sci. Rep. 2018, 8, 11945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aittala, M.; Sharma, P.; Murmann, L.; Yedidia, A.B.; Wornell, G.W.; Freeman, W.T.; Durand, F. Computational mirrors: Blind inverse light transport by deep matrix factorization. arXiv 2019, arXiv:1912.02314. [Google Scholar]
- Chen, W.; Daneau, S.; Mannan, F.; Heide, F. Steady-state non-line-of-sight imaging. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 6790–6799. [Google Scholar]
- Musarra, G.; Caramazza, P.; Turpin, A.; Lyons, A.; Higham, C.F.; Murray-Smith, R.; Faccio, D. Detection, identification, and tracking of objects hidden from view with neural networks. In Proceedings of the Advanced Photon Counting Techniques XIII, Baltimore, MD, USA, 17–18 April 2019; p. 1097803. [Google Scholar]
- Chen, W.; Wei, F.; Kutulakos, K.N.; Rusinkiewicz, S.; Heide, F. Learned feature embeddings for non-line-of-sight imaging and recognition. ACM Trans. Graph. (TOG) 2020, 39, 1–18. [Google Scholar] [CrossRef]
- Chopite, J.G.; Hullin, M.B.; Wand, M.; Iseringhausen, J. Deep non-line-of-sight reconstruction. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 960–969. [Google Scholar]
- Metzler, C.A.; Heide, F.; Rangarajan, P.; Balaji, M.M.; Viswanath, A.; Veeraraghavan, A.; Baraniuk, R.G. Deep-inverse correlography: Towards real-time high-resolution non-line-of-sight imaging. Optica 2020, 7, 63–71. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, C.-Y.; Liu, Z. Non-line-of-sight imaging off a phong surface through deep learning. arXiv 2020, arXiv:2005.00007. [Google Scholar]
- Zhu, D.; Cai, W. Fast Non-line-of-sight Imaging with Two-step Deep Remapping. arXiv 2021, arXiv:2101.10492. [Google Scholar] [CrossRef]
- Geng, R.; Hu, Y.; Lu, Z.; Yu, C.; Li, H.; Zhang, H.; Chen, Y. Passive Non-Line-of-Sight Imaging Using Optimal Transport. IEEE Trans. Image Process. 2022, 31, 110–124. [Google Scholar] [CrossRef]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef] [Green Version]
- Rick Chang, J.; Li, C.-L.; Poczos, B.; Vijaya Kumar, B.; Sankaranarayanan, A.C. One network to solve them all--solving linear inverse problems using deep projection models. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5888–5897. [Google Scholar]
- Shah, V.; Hegde, C. Solving linear inverse problems using gan priors: An algorithm with provable guarantees. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 4609–4613. [Google Scholar]
- Wang, F.; Eljarrat, A.; Müller, J.; Henninen, T.R.; Erni, R.; Koch, C.T. Multi-resolution convolutional neural networks for inverse problems. Sci. Rep. 2020, 10, 5730. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Phong, B.T. Illumination for computer generated pictures. Commun. ACM 1975, 18, 311–317. [Google Scholar] [CrossRef] [Green Version]
- Akkoul, S.; Ledee, R.; Leconge, R.; Leger, C.; Harba, R.; Pesnel, S.; Lerondel, S.; Lepape, A.; Vilcahuaman, L. Comparison of image restoration methods for bioluminescence imaging. In Proceedings of the International Conference on Image and Signal Processing, Cherbourg-Octeville, France, 1–3 July 2008; pp. 163–172. [Google Scholar]
- Poggio, T.; Girosi, F. Networks for approximation and learning. Proc. IEEE 1990, 78, 1481–1497. [Google Scholar] [CrossRef]
- Van Loan, C.F. Generalizing the singular value decomposition. SIAM J. Numer. Anal. 1976, 13, 76–83. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. Siam J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]


| Method | SSIM | PSNR (dB) | Rebuild Rate (FPS) |
|---|---|---|---|
| NLOS-OT | 0.7251 | 7.29 | 8.14 |
| Chen et al. | 0.8802 | 17.89 | 14.18 |
| Current work | 0.9193 | 18.77 | 14.16 |
| Method | SSIM | PSNR (dB) | Rebuild Rate (FPS) |
|---|---|---|---|
| NLOS-OT | 0.8641 | 12.26 | 7.91 |
| Chen et al. | 0.3583 | 13.76 | 15.05 |
| Current work | 0.8154 | 13.81 | 14.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Li, M.; Chen, T.; Zhan, S. Long-Range Non-Line-of-Sight Imaging Based on Projected Images from Multiple Light Fields. Photonics 2023, 10, 25. https://doi.org/10.3390/photonics10010025
Chen X, Li M, Chen T, Zhan S. Long-Range Non-Line-of-Sight Imaging Based on Projected Images from Multiple Light Fields. Photonics. 2023; 10(1):25. https://doi.org/10.3390/photonics10010025
Chicago/Turabian StyleChen, Xiaojie, Mengyue Li, Tiantian Chen, and Shuyue Zhan. 2023. "Long-Range Non-Line-of-Sight Imaging Based on Projected Images from Multiple Light Fields" Photonics 10, no. 1: 25. https://doi.org/10.3390/photonics10010025
APA StyleChen, X., Li, M., Chen, T., & Zhan, S. (2023). Long-Range Non-Line-of-Sight Imaging Based on Projected Images from Multiple Light Fields. Photonics, 10(1), 25. https://doi.org/10.3390/photonics10010025





