A Bound State in the Continuum Supported by a Trimeric Metallic Metasurface
Abstract
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, J.; Zhang, Y. Metasurfaces in terahertz waveband. J. Phys. D Appl. Phys. 2017, 50, 464004. [Google Scholar] [CrossRef]
- Deng, Z.-L.; Shi, T.; Krasnok, A.; Li, X.; Alù, A. Observation of localized magnetic plasmon skyrmions. Nat. Commun. 2022, 13, 8. [Google Scholar] [CrossRef] [PubMed]
- An, Y.; Fu, T.; Liu, Q.; Ouyang, Z. High-Q Fano resonance based on degenerate modes in a single dielectric point-defect photonic crystal cavity with x–y asymmetry. Appl. Phys. Express 2020, 13, 032006. [Google Scholar] [CrossRef]
- Amin, M.; Ramzan, R.; Siddiqui, O. Fano resonance based ultra high-contrast electromagnetic switch. Appl. Phys. Lett. 2017, 110, 181904. [Google Scholar] [CrossRef]
- Pu, M.; Hu, C.; Huang, C.; Wang, C.; Zhao, Z.; Wang, Y.; Luo, X. Investigation of Fano resonance in planar metamaterial with perturbed periodicity. Opt. Express 2013, 21, 992–1001. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Y.; Lin, Y.; Xiang, J.; Feng, T.; Cao, Q.; Li, J.; Lan, S.; Liu, J. High-Q Quasibound States in the Continuum for Nonlinear Metasurfaces. Phys. Rev. Lett. 2019, 123, 253901. [Google Scholar] [CrossRef]
- Wang, X.; Duan, J.; Chen, W.; Zhou, C.; Liu, T.; Xiao, S. Controlling light absorption of graphene at critical coupling through magnetic dipole quasi-bound states in the continuum resonance. Phys. Rev. B 2020, 102, 155432. [Google Scholar] [CrossRef]
- Doeleman, H.M.; Monticone, F.; den Hollander, W.; Alù, A.; Koenderink, A.F. Experimental observation of a polarization vortex at an optical bound state in the continuum. Nat. Photonics 2018, 12, 397–401. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Yesilkoy, F.; Arvelo, E.R.; Jahani, Y.; Liu, M.; Tittl, A.; Cevher, V.; Kivshar, Y.; Altug, H. Ultrasensitive hyperspectral imaging and biodetection enabled by dielectric metasurfaces. Nat. Photonic 2019, 13, 390–396. [Google Scholar] [CrossRef]
- Han, S.; Cong, L.; Srivastava, Y.K.; Qiang, B.; Rybin, M.V.; Kumar, A.; Jain, R.; Lim, W.X.; Achanta, V.G.; Prabhu, S.S.; et al. All-Dielectric Active Terahertz Photonics Driven by Bound States in the Continuum. Adv. Mater. 2019, 31, e1901921. [Google Scholar] [CrossRef]
- Bogdanov, A.A.; Koshelev, K.L.; Kapitanova, P.V.; Rybin, M.V.; Gladyshev, S.A.; Sadrieva, Z.F.; Samusev, K.B.; Kivshar, Y.S.; Limonov, M.F. Bound states in the continuum and Fano resonances in the strong mode coupling regime. Adv. Photonics 2019, 1, 016001. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric Metasurfaces with High-Q Resonances Governed by Bound States in the Continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
- Tittl, A.; Leitis, A.; Liu, M.; Yesilkoy, F.; Choi, D.Y.; Neshev, D.N.; Kivshar, Y.S.; Altug, H. Imaging based molecular barcoding with pixelated dielectric metasurfaces. Science 2018, 360, 1105–1109. [Google Scholar] [CrossRef]
- Koshelev, K.; Kruk, S.; Melik-Gaykazyan, E.; Choi, J.H.; Bogdanov, A.; Park, H.G.; Kivshar, Y. Subwavelength dielectric resonators for nonlinear nanophotonics. Science 2020, 367, 288–292. [Google Scholar] [CrossRef]
- Cong, L.; Singh, R. Symmetry-Protected Dual Bound States in the Continuum in Metamaterials. Adv. Opt. Mater. 2019, 7, 1900383. [Google Scholar] [CrossRef]
- Deng, Z.-L.; Li, X.; Fu, T.; Wang, G.P. Fano Resonance in a Metasurface Composed of Graphene Ribbon Superlattice. IEEE Photonics J. 2017, 9, 4801107. [Google Scholar] [CrossRef]
- Limonov, M.F.; Rybin, M.V.; Poddubny, A.N.; Kivshar, Y.S. Fano resonances in photonics. Nat. Photonics 2017, 11, 543–554. [Google Scholar] [CrossRef]
- Fang, C.; Yang, Q.; Yuan, Q.; Gan, X.; Zhao, J.; Shao, Y.; Liu, Y.; Han, G.; Hao, Y. High Q resonances governed by the quasi-bound states in the continuum in all-dielectric metasurfaces. Opto-Electron. Adv. 2021, 4, 200030. [Google Scholar] [CrossRef]
- Fu, T.; Liu, F.; An, Y.; Li, Q.; Li, H.; Sun, T.; Xiao, G.; Muhammad, N. Separately tuning of double Fano resonances in facile asymmetric slit metasurface. Appl. Phys. Express 2020, 13, 052009. [Google Scholar] [CrossRef]
- Kim, S.; Kim, K.H.; Cahoon, J.F. Optical Bound States in the Continuum with Nanowire Geometric Superlattices. Phys. Rev. Lett. 2019, 122, 187402. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.J.; Zhao, Q.; He, J. Fano interferences of electromagnetic modes in dielectric nanoblock dimers. J. Appl. Phys. 2019, 125, 063103. [Google Scholar] [CrossRef]
- Manna, U.; Sugimoto, H.; Eggena, D.; Coe, B.; Wang, R.; Biswas, M.; Fujii, M. Selective excitation and enhancement of multipolar resonances in dielectric nanospheres using cylindrical vector beams. J. Appl. Phys. 2020, 127, 033101. [Google Scholar]
- Luk’Yanchuk, B.; Zheludev, N.I.; Maier, S.A.; Halas, N.J.; Nordlander, P.; Giessen, H.; Chong, C.T. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 2010, 9, 707–715. [Google Scholar] [CrossRef] [PubMed]
- Rybin, M.V.; Khanikaev, A.B.; Inoue, M.; Samusev, K.B.; Steel, M.J.; Yushin, G.; Limonov, M.F. Fano resonance between Mie and Bragg scattering in photonic crystals. Phys. Rev. Lett. 2009, 103, 023901. [Google Scholar] [CrossRef]
- Guo, H.; Lin, J.; Qiu, M.; Tian, J.; Wang, Q.; Li, Y.; Sun, S.; He, Q.; Xiao, S.; Zhou, L. Flat optical transparent window: Mechanism and realization based on metasurfaces. J. Phys. D Appl. Phys. 2018, 51, 074001. [Google Scholar] [CrossRef]
- Hsu, C.W.; DeLacy, B.G.; Johnson, S.G.; Joannopoulos, J.D.; Soljacic, M. Theoretical criteria for scattering dark states in nanostructured particles. Nano Lett. 2014, 14, 2783–2788. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef]
- Huang, W.; Lin, J.; Qiu, M.; Liu, T.; He, Q.; Xiao, S.; Zhou, L. A complete phase diagram for dark-bright coupled plasmonic systems: Applicability of Fano’s formula. Nanophotonics 2020, 9, 3251–3262. [Google Scholar] [CrossRef]
- Yang, B.; Liu, T.; Guo, H.; Xiao, S.; Zhou, L. High-performance meta-devices based on multilayer meta-atoms: Interplay between the number of layers and phase coverage. Sci. Bull. 2019, 64, 823–835. [Google Scholar] [CrossRef]
- Koshelev, K.; Tang, Y.; Li, K.; Choi, D.-Y.; Li, G.; Kivshar, Y. Nonlinear Metasurfaces Governed by Bound States in the Continuum. ACS Photonics 2019, 6, 1639–1644. [Google Scholar] [CrossRef]
- Shi, T.; Deng, Z.-L.; Tu, Q.-A.; Cao, Y.; Li, X. Displacement-mediated bound states in the continuum in all-dielectric superlattice metasurfaces. PhotoniX 2021, 2, 7. [Google Scholar] [CrossRef]
- Wang, W.; Yan, H.; Xiong, L.; Zheng, L. Symmetry-protected bound state in the continuum in the metasurface of dielectric nanodisk with the inclined surface. J. Mod. Opt. 2021, 68, 699–706. [Google Scholar] [CrossRef]
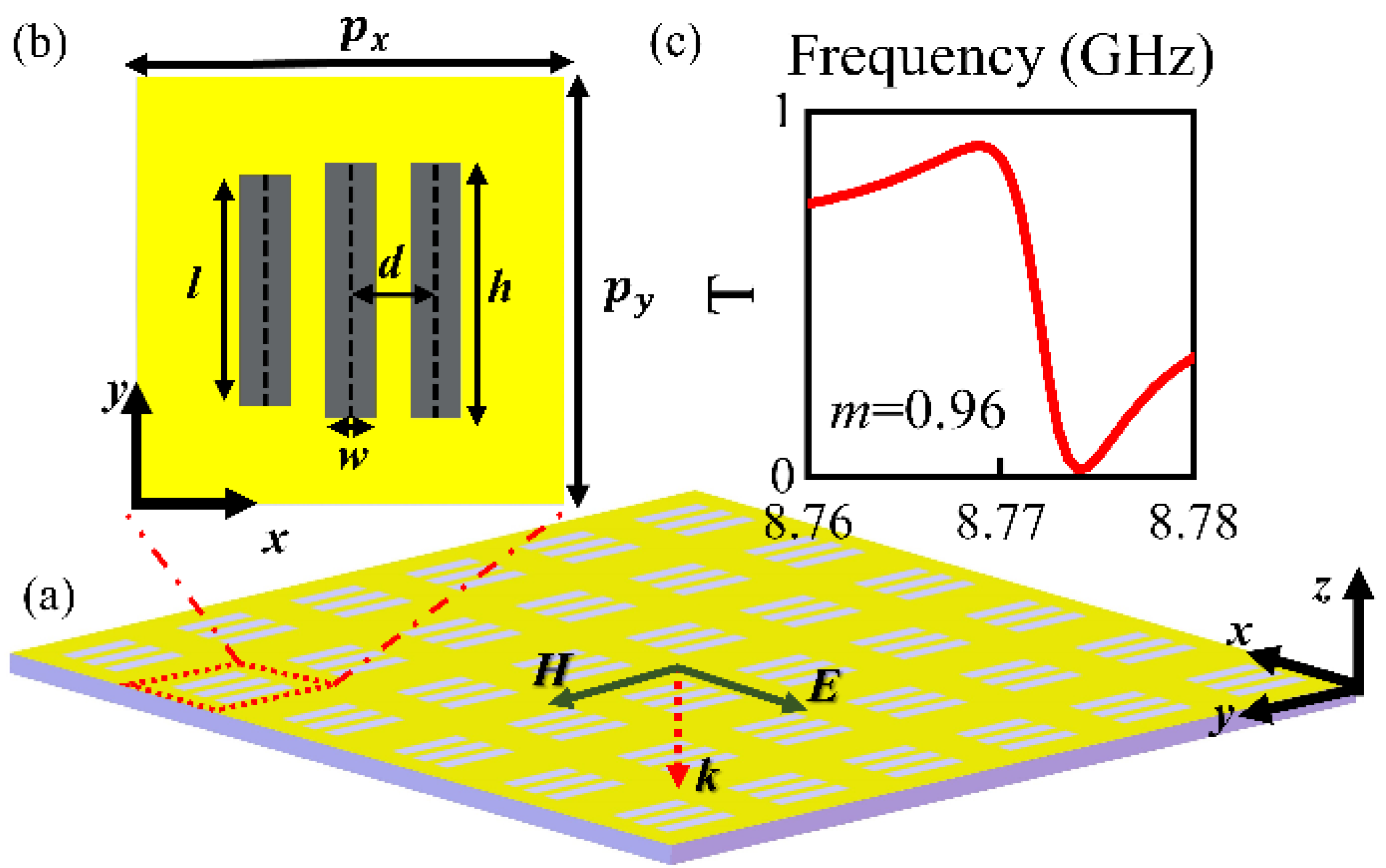
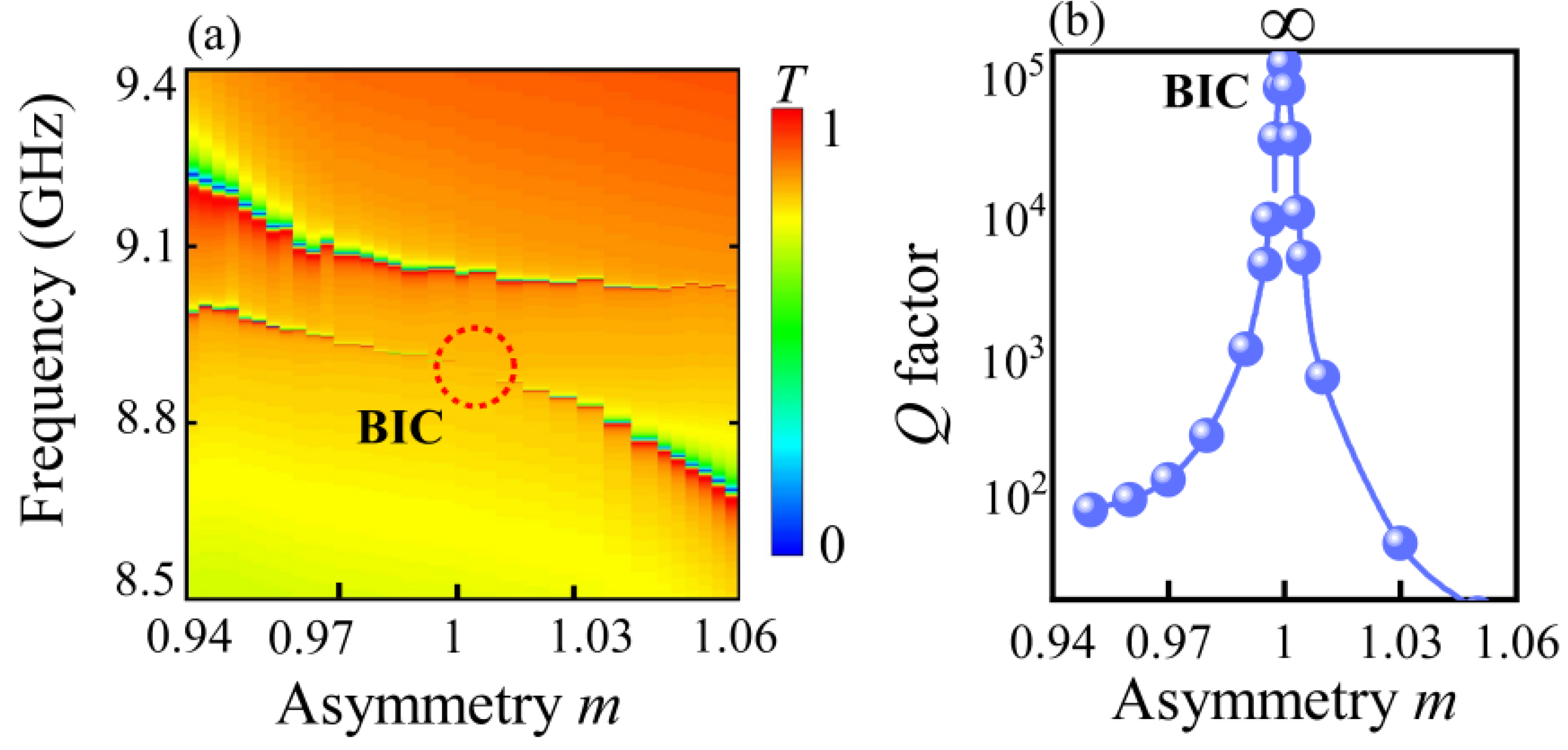
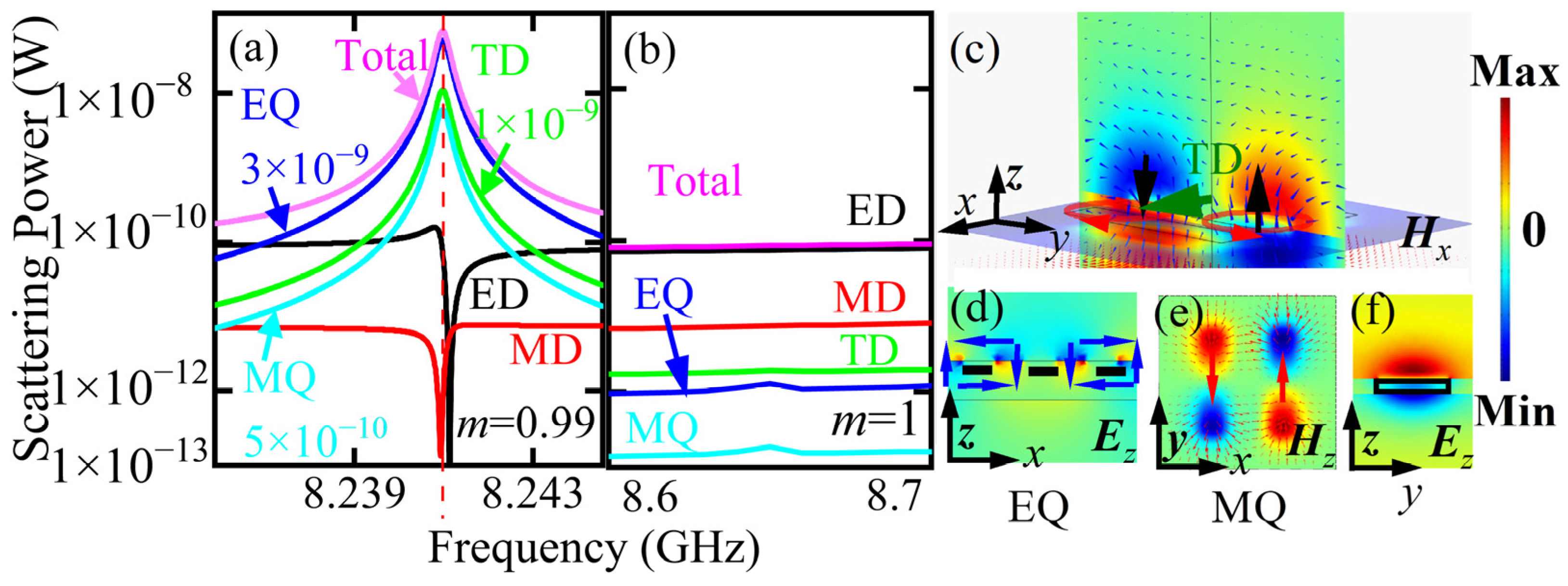
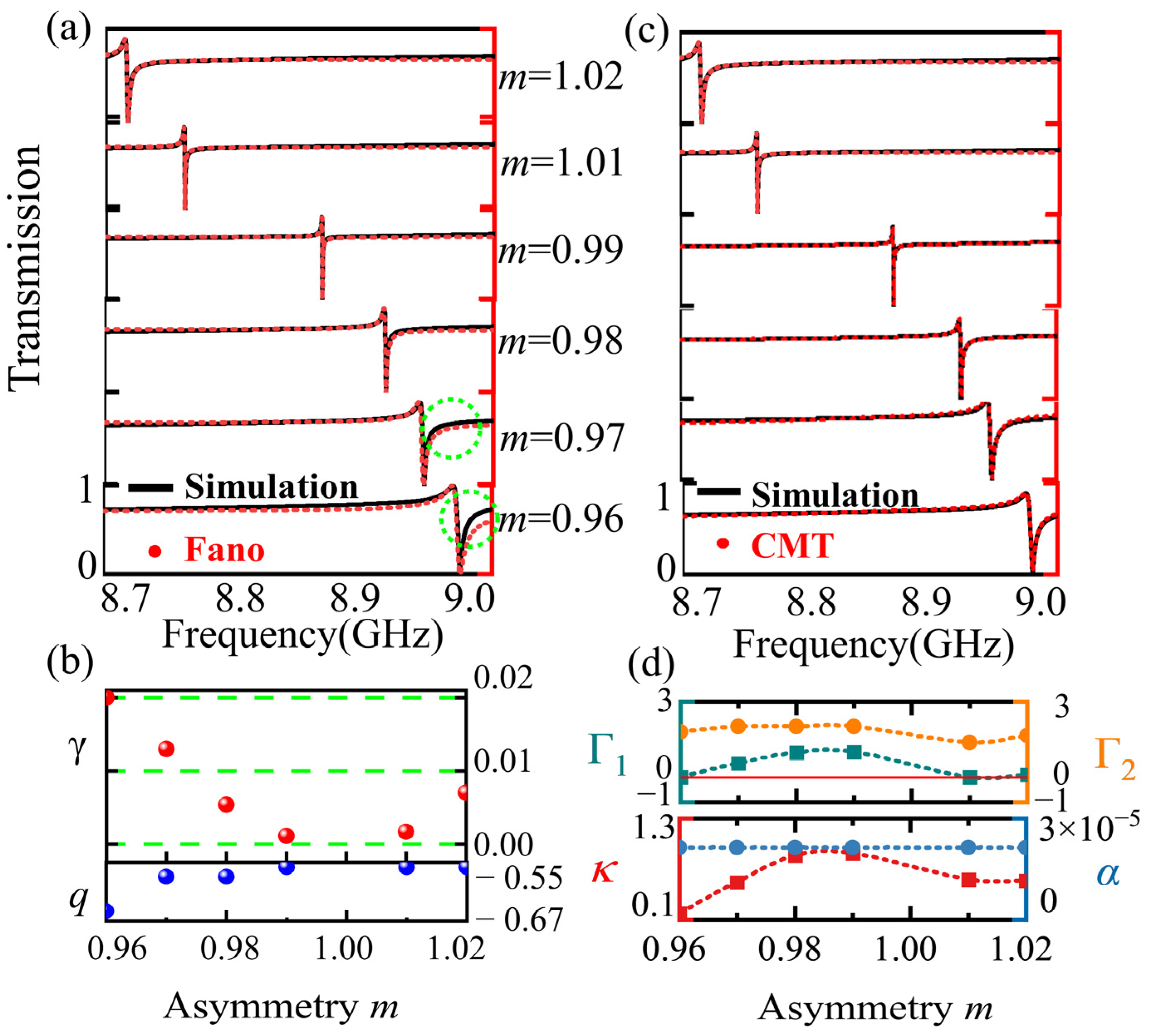
| Multipole | Multipole Expression | Scattering Power |
|---|---|---|
| Electric dipole (ED) | ||
| Magnetic dipole (MD) | ||
| Toroidal dipole (TD) | ||
| Electric quadrupole (EQ) | ||
| Magnetic quadrupole (MQ) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, T.; Wang, Z.; Chen, Y. A Bound State in the Continuum Supported by a Trimeric Metallic Metasurface. Photonics 2023, 10, 40. https://doi.org/10.3390/photonics10010040
Fu T, Wang Z, Chen Y. A Bound State in the Continuum Supported by a Trimeric Metallic Metasurface. Photonics. 2023; 10(1):40. https://doi.org/10.3390/photonics10010040
Chicago/Turabian StyleFu, Tao, Ziyan Wang, and Yonghe Chen. 2023. "A Bound State in the Continuum Supported by a Trimeric Metallic Metasurface" Photonics 10, no. 1: 40. https://doi.org/10.3390/photonics10010040
APA StyleFu, T., Wang, Z., & Chen, Y. (2023). A Bound State in the Continuum Supported by a Trimeric Metallic Metasurface. Photonics, 10(1), 40. https://doi.org/10.3390/photonics10010040




