Extracting Morphological and Sub-Resolution Features from Optical Coherence Tomography Images, a Review with Applications in Cancer Diagnosis
Abstract
:1. Introduction
Optical Coherence Tomography (OCT)
2. OCT Applications in Cancer Diagnosis
3. Intensity and Morphological Features for OCT Image Classification
3.1. Texture Features
3.2. Morphological Features
3.3. Fractal Features
4. Sub-Resolution Features for OCT Image Classification
4.1. Group Velocity Dispersion (GVD)
4.2. Index of Refraction (n)
4.3. Scatterer Size (SS)
4.4. Nanoscale OCT
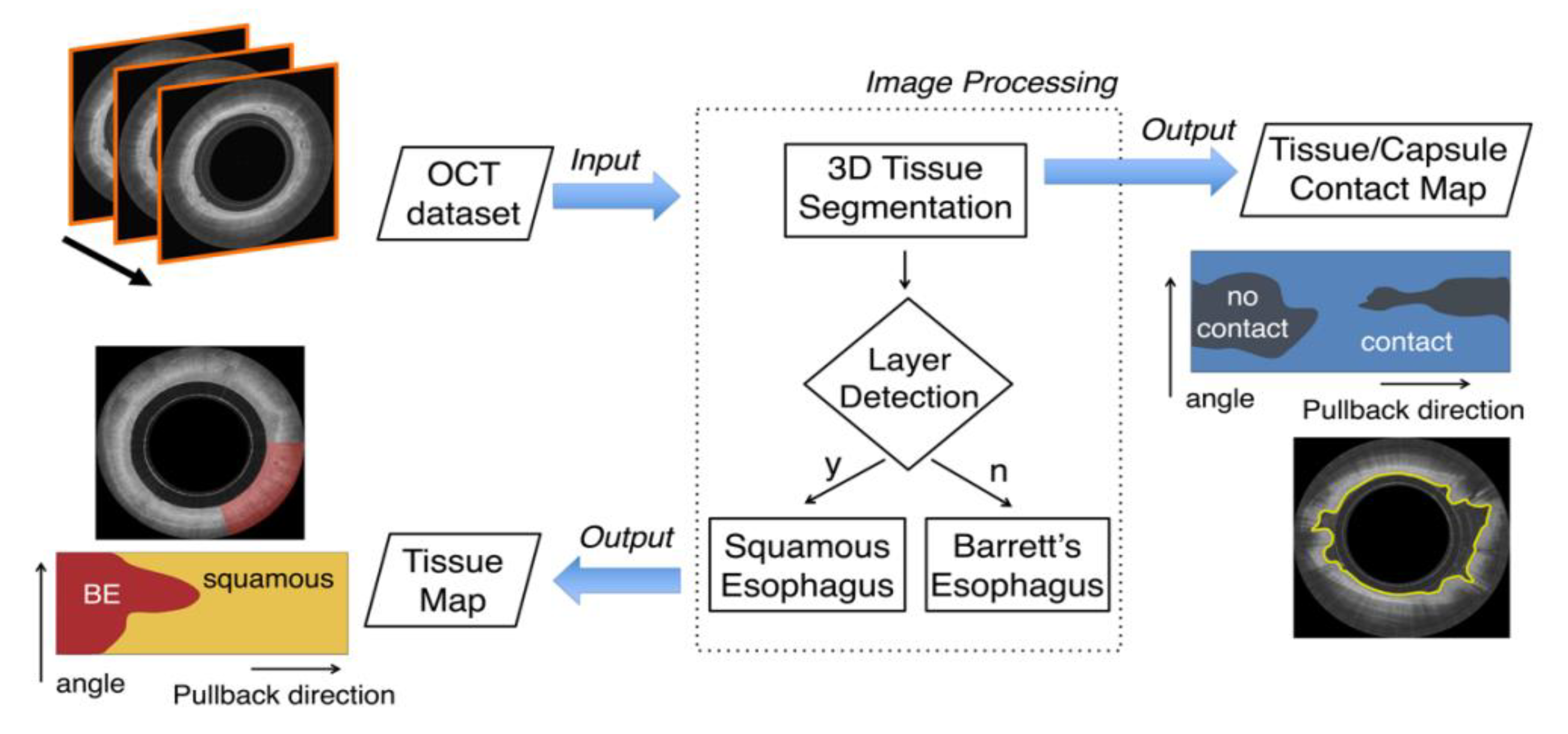
5. Segmentation and Classification of OCT Images for Cancer Diagnosis
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tomlins, P.H.; Wang, R.K. Simultaneous analysis of refractive index and physical thickness by Fourier domain optical coherence tomography. IEE Proc. Optoelectron. 2006, 153, 222–228. [Google Scholar] [CrossRef]
- Chang, S.; Cheng, Y.; Larin, K.V.; Mao, Y.; Sherif, S.; Flueraru, C. Optical coherence tomography used for security and fingerprint-sensing applications. IET Image Process. 2008, 2, 48–58. [Google Scholar] [CrossRef] [Green Version]
- Chang, S. Jade detection and analysis based on optical coherence tomography images. Opt. Eng. 2010, 49, 063602. [Google Scholar] [CrossRef] [Green Version]
- Rajabi-Estarabadi, A.; Bittar, J.M.; Zheng, C.; Nascimento, V.; Camacho, I.; Feun, L.G.; Nasiriavanaki, M.; Kunz, M.; Nouri, K. Optical coherence tomography imaging of melanoma skin cancer. Lasers Med. Sci. 2019, 34, 411–420. [Google Scholar] [CrossRef]
- Ferrante di Ruffano, L.; Dinnes, J.; Deeks, J.J.; Chuchu, N.; Bayliss, S.E.; Davenport, C.; Takwoingi, Y.; Godfrey, K.; O’sullivan, C.; Matin, R.N.; et al. Optical coherence tomography for diagnosing skin cancer in adults. Cochrane Database Syst. Rev. 2018, 2018, CD013189. [Google Scholar] [CrossRef]
- van Manen, L.; Dijkstra, J.; Boccara, C.; Benoit, E.; Vahrmeijer, A.L.; Gora, M.J.; Mieog, J.S.D. The clinical usefulness of optical coherence tomography during cancer interventions. J. Cancer Res. Clin. Oncol. 2018, 144, 1967–1990. [Google Scholar] [CrossRef] [Green Version]
- Acharya, N.; Melanthota, S.K.; Khokhar, M.; Chakrabarti, S.; Gopal, D.; Mallya, D.S.; Mazumder, N. Types of Optical Coherence Tomography for Cancer Diagnosis: A Systematic Review. J. Biomed. Photonics Eng. 2022, 8, 010201. [Google Scholar] [CrossRef]
- Fuchs, S.; Blinne, A.; Rödel, C.; Zastrau, U.; Hilbert, V.; Wünsche, M.; Bierbach, J.; Frumker, E.; Förster, E.; Paulus, G.G. Optical coherence tomography using broad-bandwidth XUV and soft X-ray radiation. Appl. Phys. B Lasers Opt. 2012, 106, 789–795. [Google Scholar] [CrossRef] [Green Version]
- Swanson, E.A.; Izatt, J.A.; Lin, C.P.; Fujimoto, J.G.; Schuman, J.S.; Hee, M.R.; Huang, D.; Puliafito, C.A. In vivo retinal imaging by optical coherence tomography. Opt. Lett. 1993, 18, 1864–1866. [Google Scholar] [CrossRef]
- Fercher, A.F.; Hitzenberger, C.K.; Kamp, G.; El-Zaiat, S.Y. Measurement of intraocular distances by backscattering spectral interferometry. Opt. Commun. 1995, 117, 43–48. [Google Scholar] [CrossRef]
- Seelamantula, C.S.; Villiger, M.L.; Leitgeb, R.A.; Unser, M. Exact and efficient signal reconstruction in frequency-domain optical-coherence tomography. J. Opt. Soc. Am. A 2008, 25, 1762–1771. [Google Scholar] [CrossRef] [Green Version]
- Leitgeb, R.A.; Hitzenberger, C.K.; Fercher, A.F.; Bajraszewski, T. Phase-shifting algorithm to achieve high-speed long-depth-range probing by frequency-domain optical coherence tomography. Opt. Lett. 2003, 28, 2201–2203. [Google Scholar] [CrossRef]
- Drexler, W.; Fujimoto, J.G. Optical Coherence Tomography: Technology and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Fercher, A.F.; Drexler, W.; Hitzenberger, C.K.; Lasser, T. Optical coherence tomography—Principles and applications. Rep. Prog. Phys. 2003, 66, 239–303. [Google Scholar] [CrossRef]
- Drexler, W.; Morgner, U.; Kärtner, F.X.; Pitris, C.; Boppart, S.A.; Li, X.D.; Ippen, E.P.; Fujimoto, J.G. In vivo ultrahigh-resolution optical coherence tomography. Opt. Lett. 1999, 24, 1221–1223. [Google Scholar] [CrossRef] [Green Version]
- Nam, H.S.; Yoo, H. Spectroscopic optical coherence tomography: A review of concepts and biomedical applications. Appl. Spectrosc. Rev. 2018, 53, 91–111. [Google Scholar] [CrossRef]
- Eladawi, N.; Elmogy, M.; Ghazal, M.; Helmy, O.; Aboelfetouh, A.; Riad, A.; Schaal, S.; El-Baz, A. Classification of retinal diseases based on OCT Images. Front. Biosci.—Landmark 2018, 23, 247–264. [Google Scholar] [CrossRef] [Green Version]
- Karst, S.G.; Salas, M.; Hafner, J.; Scholda, C.; Vogl, W.D.; Drexler, W.; Pircher, M.; Schmidt-Erfurth, U. Three-dimensional analysis of retinal microaneurysms with adaptive optics optical coherence tomography. Retina 2019, 39, 465–472. [Google Scholar] [CrossRef]
- Joner, M.; Koppara, T.; Byrne, R.A.; Castellanos, M.I.; Lewerich, J.; Novotny, J.; Guagliumi, G.; Xhepa, E.; Adriaenssens, T.; Godschalk, T.C. Neoatherosclerosis in Patients With Coronary Stent Thrombosis: Findings From Optical Coherence Tomography Imaging (A Report of the PRESTIGE Consortium). JACC Cardiovasc. Interv. 2018, 11, 1340–1350. [Google Scholar] [CrossRef]
- Samir, A.; ElGuindy, A. The role of intracoronary imaging in acute coronary syndromes: OCT in focus. Glob. Cardiol. Sci. Pract. 2016, 2016, e201636. [Google Scholar] [CrossRef] [Green Version]
- Podoleanu, A.G.; Rogers, J.A.; Jackson, D.A.; Dunne, S. Three dimensional OCT images from retina and skin. Opt. Express 2000, 7, 292–298. [Google Scholar] [CrossRef]
- Iftimia, N.V.; Maguluri, G.N.; Park, J.; Fox, W.J.; Rajadhyaksha, M. New advances in RCM-OCT imaging for non-melanoma skin cancer detection and therapy guidance (Conference Presentation). In Proceedings of the Optical Biopsy XVI: Toward Real-Time Spectroscopic Imaging and Diagnosis, San Francisco, CA, USA, 27 January–1 February 2018. [Google Scholar]
- Li, Y.; Liu, H.; Huang, H.; Zhu, Y.; Deng, H.; Yu, J.; Luo, S.; Huo, L.; Lin, L.; Xie, H.; et al. Progress of the application of optical coherence tomography in gastrointestinal tumor surgery. Zhonghua Wei Chang Wai Ke Za Zhi 2017, 20, 716–720. [Google Scholar]
- Lee, H.-C.; Ahsen, O.O.; Liu, J.J.; Tsai, T.-H.; Huang, Q.; Mashimo, H.; Fujimoto, J.G. Assessment of the radiofrequency ablation dynamics of esophageal tissue with optical coherence tomography. J. Biomed. Opt. 2017, 22, 076001. [Google Scholar] [CrossRef] [Green Version]
- Luo, S.; Liu, H.; Zhao, H.; An, X.; Xie, H.; Huo, L. Gastric and colon cancer imaging with swept source optical coherence tomography. In Proceedings of the 2017 Conference on Lasers and Electro-Optics Pacific Rim, CLEO-PR 2017, Singapore, 31 July–4 August 2017. [Google Scholar]
- Struk, P.; Billard, A.; Bargiel, S.; Tanguy, Q.; Gorecki, C.; Chutani, R.; Passilly, N.; Xie, H. The SS-OCT Endomicroscopy Probe Based on MOEMS Mirau Micro-Interferometer for Early Stomach Cancer Detection; SPIE: Bellingham, DC, USA, 2018. [Google Scholar]
- Boppart, S.A.; Luo, W.; Marks, D.L.; Singletary, K.W. Optical coherence tomography: Feasibility for basic research and image-guided surgery of breast cancer. Breast Cancer Res. Treat. 2004, 84, 85–97. [Google Scholar] [CrossRef] [Green Version]
- Erickson-Bhatt, S.J.; Mesa, K.J.; Marjanovic, M.; Chaney, E.J.; Ahmad, A.; Huang, P.C.; Liu, Z.G.; Cunningham, K.; Boppart, S.A. Intraoperative optical coherence tomography of the human thyroid: Feasibility for surgical assessment. Transl. Res. 2018, 195, 13–24. [Google Scholar] [CrossRef]
- Sommerey, S.; Al Arabi, N.; Ladurner, R.; Chiapponi, C.; Stepp, H.; Hallfeldt, K.K.J.; Gallwas, J.K.S. Intraoperative optical coherence tomography imaging to identify parathyroid glands. Surg. Endosc. 2015, 29, 2698–2704. [Google Scholar] [CrossRef]
- Lee, H.C.; Zhou, C.; Cohen, D.W.; Mondelblatt, A.E.; Wang, Y.; Aguirre, A.D.; Shen, D.; Sheikine, Y.; Fujimoto, J.G.; Connolly, J.L. Integrated optical coherence tomography and optical coherence microscopy imaging of ex vivo human renal tissues. J. Urol. 2012, 187, 691–699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Onozato, M.L.; Andrews, P.M.; Li, Q.; Jiang, J.; Cable, A.; Chen, Y. Optical Coherence Tomography of Human Kidney. J. Urol. 2010, 183, 2090–2094. [Google Scholar] [CrossRef]
- Xiong, Y.Q.; Tan, J.; Liu, Y.M.; Li, Y.Z.; You, F.F.; Zhang, M.Y.; Chen, Q.; Zou, K.; Sun, X. Diagnostic accuracy of optical coherence tomography for bladder cancer: A systematic review and meta-analysis. Photodiagn. Photodyn. Ther. 2019, 27, 298–304. [Google Scholar] [CrossRef]
- Gardecki, J.A.; Singh, K.; Wu, C.L.; Tearney, G.J. Imaging the human prostate gland using 1-lm-resolution optical coherence tomography. Arch. Pathol. Lab. Med. 2019, 143, 314–318. [Google Scholar] [CrossRef] [Green Version]
- Scolaro, L.; McLaughlin, R.A.; Kennedy, B.F.; Saunders, C.M.; Sampson, D.D. A review of optical coherence tomography in breast cancer. Photonics Lasers Med. 2014, 3, 225–240. [Google Scholar] [CrossRef]
- Men, J.; Huang, Y.; Solanki, J.; Zeng, X.; Alex, A.; Jerwick, J.; Zhang, Z.; Tanzi, R.E.; Li, A.; Zhou, C. Optical Coherence Tomography for Brain Imaging and Developmental Biology. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Malone, J.; Hohert, G.; Hoang, L.; Miller, D.M.; McAlpine, J.N.; MacAulay, C.E.; Lane, P.M. Endoscopic optical coherence tomography (OCT) and autofluorescence imaging (AFI) of ex vivo fallopian tubes. In Proceedings of the Multimodal Biomedical Imaging XV, San Francisco, CA, USA, 1–6 February 2020. [Google Scholar]
- Butola, A.; Ahmad, A.; Dubey, V.; Srivastava, V.; Qaiser, D.; Srivastava, A.; Senthilkumaran, P.; Mehta, D.S. Volumetric analysis of breast cancer tissues using machine learning and swept-source optical coherence tomography. Appl. Opt. 2019, 58, A135–A141. [Google Scholar] [CrossRef] [PubMed]
- Fujimoto, J.G.; Pitris, C.; Boppart, S.A.; Brezinski, M.E. Optical coherence tomography: An emerging technology for biomedical imaging and optical biopsy. Neoplasia 2000, 2, 9–25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jørgensen, T.M.; Tycho, A.; Mogensen, M.; Bjerring, P.; Jemec, G.B.E. Machine-learning classification of non-melanoma skin cancers from image features obtained by optical coherence tomography. Ski. Res. Technol. 2008, 14, 364–369. [Google Scholar] [CrossRef]
- Mogensen, M.; Joergensen, T.M.; NÜrnberg, B.M.; Morsy, H.A.; Thomsen, J.B.; Thrane, L.; Jemec, G.B.E. Assessment of optical coherence tomography imaging in the diagnosis of non-melanoma skin cancer and benign lesions versus normal skin: Observer-blinded evaluation by dermatologists and pathologists. Dermatol. Surg. 2009, 35, 965–972. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, M.; Von Braunmuehl, T.; Kurzen, H.; Dirschka, T.; Kellner, C.; Sattler, E.; Berking, C.; Welzel, J.; Reinhold, U. The sensitivity and specificity of optical coherence tomography for the assisted diagnosis of nonpigmented basal cell carcinoma: An observational study. Br. J. Dermatol. 2015, 173, 428–435. [Google Scholar] [CrossRef]
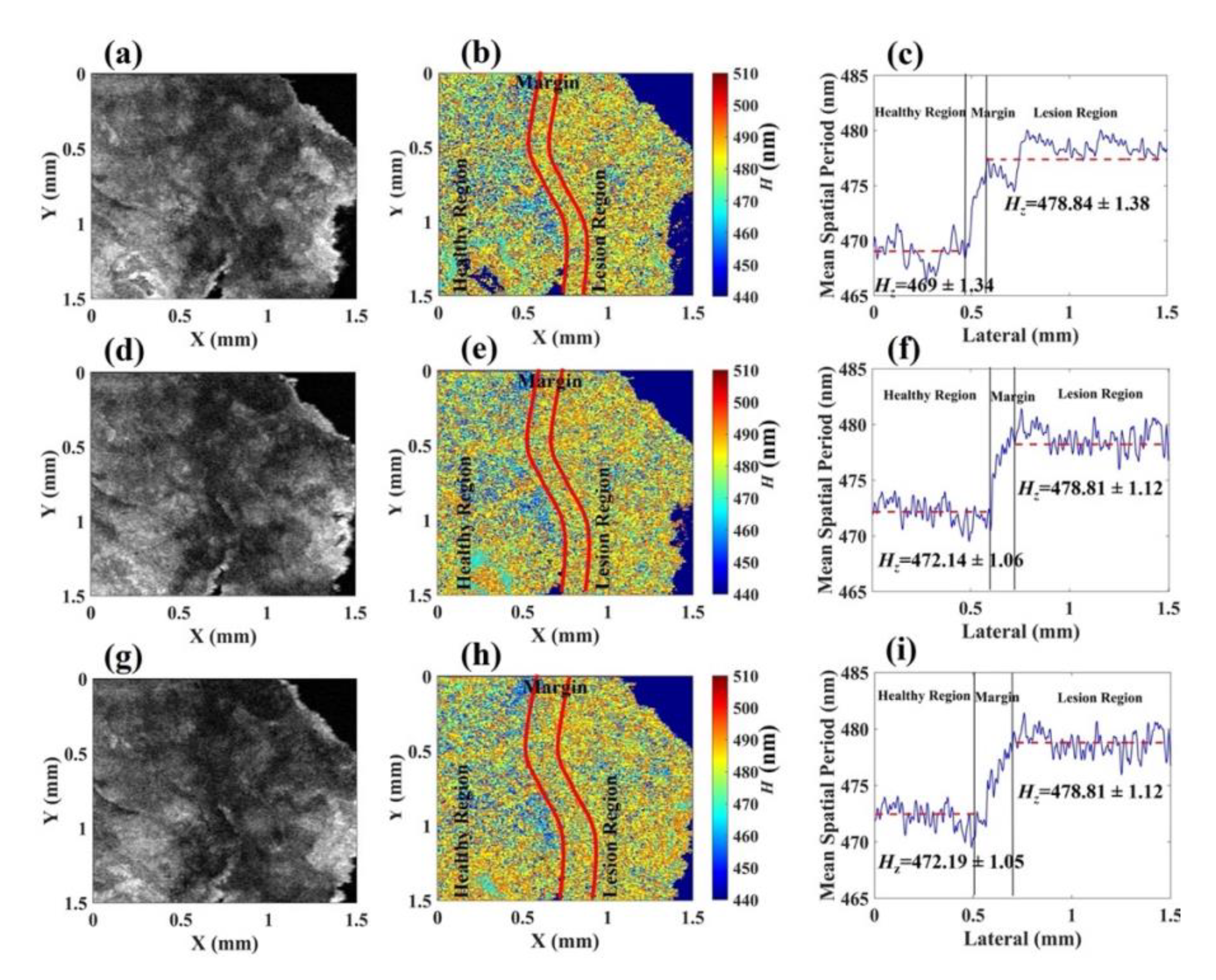
- Alexandrov, S.A.; Subhash, H.M.; Zam, A.; Leahy, M. Nano-sensitive optical coherence tomography. Nanoscale 2014, 6, 3545–3549. [Google Scholar] [CrossRef]
- Alexandrov, S.; Arangath, A.; Zhou, Y.; Murphy, M.; Duffy, N.; Neuhaus, K.; Shaw, G.; McAuley, R.; Leahy, M. Accessing depth-resolved high spatial frequency content from the optical coherence tomography signal. Sci. Rep. 2021, 11, 17123. [Google Scholar] [CrossRef]
- Dey, R.; Alexandrov, S.; Owens, P.; Kelly, J.; Phelan, S.; Leahy, M. Skin cancer margin detection using nanosensitive optical coherence tomography and a comparative study with confocal microscopy. Biomed. Opt. Express 2022, 13, 5654–5666. [Google Scholar] [CrossRef]
- Lal, C.; Alexandrov, S.; Rani, S.; Zhou, Y.; Ritter, T.; Leahy, M. Nanosensitive optical coherence tomography to assess wound healing within the cornea. Biomed. Opt. Express 2020, 11, 3407–3422. [Google Scholar] [CrossRef]
- Hamdoon, Z.; Jerjes, W.; McKenzie, G.; Jay, A.; Hopper, C. Optical coherence tomography in the assessment of oral squamous cell carcinoma resection margins. Photodiagn. Photodyn. Ther. 2016, 13, 211–217. [Google Scholar] [CrossRef] [PubMed]
- De Leeuw, F.; Casiraghi, O.; Ben Lakhdar, A.; Abbaci, M.; Laplace-Builhé, C. Full-field OCT for fast diagnostic of head and neck cancer. In Proceedings of the Photonic Therapeutics and Diagnostics XI, San Francisco, CA, USA, 7–12 February 2015; Volume 9303. [Google Scholar]
- Lam, S.; Standish, B.; Baldwin, C.; McWilliams, A.; LeRiche, J.; Gazdar, A.; Vitkin, A.I.; Yang, V.; Ikeda, N.; MacAulay, C. In vivo optical coherence tomography imaging of preinvasive bronchial lesions. Clin. Cancer Res. 2008, 14, 2006–2011. [Google Scholar] [CrossRef] [Green Version]
- Michel, R.G.; Kinasewitz, G.T.; Fung, K.M.; Keddissi, J.I. Optical coherence tomography as an adjunct to flexible bronchoscopy in the diagnosis of lung cancer: A pilot study. Chest 2010, 138, 984–988. [Google Scholar] [CrossRef] [Green Version]
- Whiteman, S.C.; Yang, Y.; Van Pittius, D.G.; Stephens, M.; Parmer, J.; Spiteri, M.A. Optical coherence tomography: Real-time imaging of bronchial airways microstructure and detection of inflammatory/neoplastic morphologic changes. Clin. Cancer Res. 2006, 12, 813–818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hariri, L.P.; Mino-Kenudson, M.; Lanuti, M.; Miller, A.J.; Mark, E.J.; Suter, M.J. Diagnosing lung carcinomas with optical coherence tomography. Ann. Am. Thorac. Soc. 2015, 12, 193–201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Assayag, O.; Antoine, M.; Sigal-Zafrani, B.; Riben, M.; Harms, F.; Burcheri, A.; Grieve, K.; Dalimier, E.; De Poly, B.L.C.; Boccara, C. Large field, high resolution full-field optical coherence tomography: A pre-clinical study of human breast tissue and cancer assessment. Technol. Cancer Res. Treat. 2014, 13, 455–468. [Google Scholar] [CrossRef] [Green Version]
- Nolan, R.M.; Adie, S.G.; Marjanovic, M.; Chaney, E.J.; South, F.A.; Monroy, G.L.; Shemonski, N.D.; Erickson-Bhatt, S.J.; Shelton, R.L.; Bower, A.J.; et al. Intraoperative optical coherence tomography for assessing human lymph nodes for metastatic cancer. BMC Cancer 2016, 16, 144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grieve, K.; Mouslim, K.; Assayag, O.; Dalimier, E.; Harms, F.; Bruhat, A.; Boccara, C.; Antoine, M. Assessment of Sentinel Node Biopsies With Full-Field Optical Coherence Tomography. Technol. Cancer Res. Treat. 2016, 15, 266–274. [Google Scholar] [CrossRef]
- Yao, X.; Gan, Y.; Chang, E.; Hibshoosh, H.; Feldman, S.; Hendon, C. Visualization and tissue classification of human breast cancer images using ultrahigh-resolution OCT. Lasers Surg. Med. 2017, 49, 258–269. [Google Scholar] [CrossRef] [Green Version]
- Peters, I.T.A.; Stegehuis, P.L.; Peek, R.; Boer, F.L.; Van Zwet, E.W.; Eggermont, J.; Westphal, J.R.; Kuppen, P.J.K.; Trimbos, J.B.; Hilders, C.G.J.M.; et al. Noninvasive detection of metastases and follicle density in ovarian tissue using full-field optical coherence tomography. Clin. Cancer Res. 2016, 22, 5506–5513. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Biswal, N.C.; Wang, T.; Kumavor, P.D.; Karimeddini, M.; Vento, J.; Sanders, M.; Brewer, M.; Zhu, Q. Potential role of a hybrid intraoperative probe based on OCT and positron detection for ovarian cancer detection and characterization. Biomed. Opt. Express 2011, 2, 5182–5187. [Google Scholar] [CrossRef] [PubMed]
- Nandy, S.; Sanders, M.; Zhu, Q. Classification and analysis of human ovarian tissue using full field optical coherence tomography. Biomed. Opt. Express 2016, 7, 5182–5187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- St-Pierre, C.; Madore, W.-J.; De Montigny, E.; Trudel, D. Dimension reduction technique using a multilayered descriptor for high-precision classification of ovarian cancer tissue using optical coherence tomography: A feasibility study. J. Med. Imaging 2017, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Testoni, P.A.; Mariani, A.; Mangiavillano, B.; Albarello, L.; Arcidiacono, P.G.; Masci, E.; Doglioni, C. Main pancreatic duct, common bile duct and sphincter of Oddi structure visualized by optical coherence tomography: An ex vivo study compared with histology. Dig. Liver Dis. 2006, 38, 409–414. [Google Scholar] [CrossRef]
- Testoni, P.A.; Mariani, A.; Mangiavillano, B.; Arcidiacono, P.G.; Di Pietro, S.; Masci, E. Intraductal optical coherence tomography for investigating main pancreatic duct strictures. Am. J. Gastroenterol. 2007, 102, 269–274. [Google Scholar] [CrossRef]
- Arvanitakis, M.; Hookey, L.; Tessier, G.; Demetter, P.; Nagy, N.; Stellke, A.; De Maertelaer, V.; Devière, J.; Le Moine, O. Intraductal optical coherence tomography during endoscopic retrograde cholangiopancreatography for investigation of biliary strictures. Endoscopy 2009, 41, 696–701. [Google Scholar] [CrossRef]
- Van Manen, L.; Stegehuis, P.L.; Fariña-Sarasqueta, A.; De Haan, L.M.; Eggermont, J.; Bonsing, B.A.; Morreau, H.; Lelieveldt, B.P.F.; Van De Velde, C.J.H.; Vahrmeijer, A.L.; et al. Validation of full-field optical coherence tomography in distinguishing malignant and benign tissue in resected pancreatic cancer specimens. PLoS ONE 2017, 12, e0175862. [Google Scholar] [CrossRef]
- Zhu, Y.; Gao, W.; Zhou, Y.; Guo, Y.; Guo, F.; He, Y. Rapid and high-resolution imaging of human liver specimens by full-field optical coherence tomography. J. Biomed. Opt. 2015, 20, 116010. [Google Scholar] [CrossRef]
- Bouma, B.E.; Tearney, G.J.; Compton, C.C.; Nishioka, N.S. High-resolution imaging of the human esophagus and stomach in vivo using optical coherence tomography. Gastrointest. Endosc. 2000, 51, 467–474. [Google Scholar] [CrossRef]
- Liang, K.; Ahsen, O.O.; Lee, H.C.; Wang, Z.; Potsaid, B.M.; Figueiredo, M.; Jayaraman, V.; Cable, A.E.; Huang, Q.; Mashimo, H.; et al. Volumetric mapping of Barrett’s esophagus and dysplasia with en face optical coherence tomography tethered capsule. Am. J. Gastroenterol. 2016, 111, 1664. [Google Scholar] [CrossRef] [Green Version]
- Swager, A.F.; Boerwinkel, D.F.; de Bruin, D.M.; Faber, D.J.; van Leeuwen, T.G.; Weusten, B.L.; Meijer, S.L.; Bergman, J.J.; Curvers, W.L. Detection of buried Barrett’s glands after radiofrequency ablation with volumetric laser endomicroscopy. Gastrointest. Endosc. 2016, 83, 80–88. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.A.; Poneros, J.M.; Bouma, B.E.; Bressner, J.; Halpern, E.F.; Shishkov, M.; Lauwers, G.Y.; Mino-Kenudson, M.; Nishioka, N.S.; Tearney, G.J. Optical coherence tomography to identify intramucosal carcinoma and high-grade dysplasia in Barrett’s esophagus. Clin. Gastroenterol. Hepatol. 2006, 4, 38–43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qi, X.; Sivak, M.V., Jr.; Wilson, D.L.; Rollins, A.M. Computer-aided diagnosis of dysplasia in Barrett"s esophagus using endoscopic optical coherence tomography. In Proceedings of the Coherence Domain Optical Methods and Optical Coherence Tomography in Biomedicine VIII, San Jose, CA, USA, 24–29 January 2004; Volume 5316. [Google Scholar]
- Qi, X.; Pan, Y.; Sivak, M.V.; Willis, J.E.; Isenberg, G.; Rollins, A.M. Image analysis for classification of dysplasia in Barrett’s esophagus using endoscopic optical coherence tomography. Biomed. Opt. Express 2010, 1, 825–847. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Isenberg, G.; Sivak, M.V.; Chak, A.; Wong, R.C.K.; Willis, J.E.; Wolf, B.; Rowland, D.Y.; Das, A.; Rollins, A. Accuracy of endoscopic optical coherence tomography in the detection of dysplasia in Barrett’s esophagus: A prospective, double-blinded study. Gastrointest. Endosc. 2005, 62, 825–831. [Google Scholar] [CrossRef]
- Chen, Y.; Aguirre, A.D.; Hsiung, P.L.; Desai, S.; Herz, P.R.; Pedrosa, M.; Huang, Q.; Figueiredo, M.; Huang, S.W.; Koski, A. Ultrahigh resolution optical coherence tomography of Barrett’s esophagus: Preliminary descriptive clinical study correlating images with histology. Endoscopy 2007, 39, 599–605. [Google Scholar] [CrossRef]
- Zuccaro, G.; Gladkova, N.; Vargo, J.; Feldchtein, F.; Zagaynova, E.; Conwell, D.; Falk, G.; Goldblum, J.; Dumot, J.; Ponsky, J. Optical coherence tomography of the esophagus and proximal stomach in health and disease. Am. J. Gastroenterol. 2001, 96, 2633–2639. [Google Scholar] [CrossRef]
- Hatta, W.; Uno, K.; Koike, T.; Yokosawa, S.; Iijima, K.; Imatani, A.; Shimosegawa, T. Optical coherence tomography for the staging of tumor infiltration in superficial esophageal squamous cell carcinoma. Gastrointest. Endosc. 2010, 71, 899–906. [Google Scholar] [CrossRef]
- Tearney, G.J.; Brezinski, M.E.; Southern, J.F.; Bouma, B.E.; Boppart, S.A.; Fujimoto, J.G. Optical biopsy in human gastrointestinal tissue using optical coherence tomography. Am. J. Gastroenterol. 1997, 92, 1800–1804. [Google Scholar]
- Westphal, V.; Rollins, A.M.; Willis, J.; Sivak, M.V.; Izatt, J.A. Correlation of endoscopic optical coherence tomography with histology in the lower-GI tract. Gastrointest. Endosc. 2005, 61, 537–546. [Google Scholar] [CrossRef]
- Ashok, P.C.; Praveen, B.B.; Bellini, N.; Riches, A.; Dholakia, K.; Herrington, C.S. Multi-modal approach using Raman spectroscopy and optical coherence tomography for the discrimination of colonic adenocarcinoma from normal colon. Biomed. Opt. Express 2013, 4, 2179–2186. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.Q.; Wu, X.J.; Tang, T.; Zhu, S.W.; Yao, Q.; Gao, B.Z.; Yuan, X.C. Quantitative analysis of rectal cancer by spectral domain optical coherence tomography. Phys. Med. Biol. 2012, 57, 5235–5244. [Google Scholar] [CrossRef] [PubMed]
- Gladkova, N.; Streltsova, O.; Zagaynova, E.; Kiseleva, E.; Gelikonov, V.; Gelikonov, G.; Karabut, M.; Yunusova, K.; Evdokimova, O. Cross-polarization optical coherence tomography for early bladder-cancer detection: Statistical study. J. Biophotonics 2011, 4, 519–532. [Google Scholar] [CrossRef] [PubMed]
- Goh, A.C.; Lerner, S.P. Application of new technology in bladder cancer diagnosis and treatment. World J. Urol. 2009, 27, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Manyak, M.J.; Gladkova, N.D.; Makari, J.H.; Schwartz, A.M.; Zagaynova, E.V.; Zolfaghari, L.; Zara, J.M.; Iksanov, R.; Feldchtein, F.I. Evaluation of superficial bladder transitional-cell carcinoma by optical coherence tomography. J. Endourol. 2005, 19, 570–574. [Google Scholar]
- Montagne, P.; Ducesne, I.; Anract, J.; Yang, C.; Sibony, M.; Beuvon, F.; Delongchamps, N.B.; Dalimier, E. Quality control and primo-diagnosis of transurethral bladder resections with full-field OCT. In Proceedings of the Therapeutics and Diagnostics in Urology: Lasers, Robotics, Minimally Invasive, and Advanced Biomedical Devices, San Francisco, CA, USA, 28 January–2 February 2017; Volume 10038. [Google Scholar]
- Rosenfeld, A. Picture Processing: 1981. Comput. Graph. Image Process. 1982, 19, 35–67. [Google Scholar] [CrossRef]
- Haralick, R.M. Statistical and structural approaches to texture. Proc. IEEE 1979, 67, 786–804. [Google Scholar] [CrossRef]
- Diggle, P.J.; Serra, J. Image Analysis and Mathematical Morphology. Biometrics 1983, 39, 536. [Google Scholar] [CrossRef]
- Chen, Y. Gray-scale morphological granulometric texture classification. Opt. Eng. 1994, 33, 2713–2722. [Google Scholar] [CrossRef]
- Weszka, J.S.; Dyer, C.R.; Rosenfeld, A. A Comparative Study of Texture Measures for Terrain Classification. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 269–285. [Google Scholar] [CrossRef]
- Julesz, B. Experiments in the visual perception of texture. Sci. Am. 1975, 232, 34–43. [Google Scholar] [CrossRef]
- Valkealahti, K.; Oja, E. Reduced multidimensional co-occurrence histograms in texture classification. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 90–94. [Google Scholar] [CrossRef]
- Szczypiński, P.M.; Strzelecki, M.; Materka, A.; Klepaczko, A. MaZda-A software package for image texture analysis. Comput. Methods Programs Biomed. 2009, 94, 66–76. [Google Scholar] [CrossRef] [PubMed]
- Cross, G.R.; Jain, A.K. Markov Random Field Texture Models. IEEE Trans. Pattern Anal. Mach. Intell. 1983, PAMI-5, 25–39. [Google Scholar] [CrossRef] [PubMed]
- Manjunath, B.S.; Chellappa, R. Unsupervised Texture Segmentation Using Markov Random Field Models. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 478–482. [Google Scholar] [CrossRef]
- Kaplan, L.M.; Kuo, C.C.J. Texture Roughness Analysis and Synthesis via Extended Self-Similar (ESS) Model. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 1043–1056. [Google Scholar] [CrossRef] [Green Version]
- Bovik, A.C. Properties of multichannel texture analysis filters. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Albuquerque, NM, USA, 3–6 April 1990; Volume 4. [Google Scholar]
- Lu, C.S.; Chung, P.C.; Chen, C.F. Unsupervised texture segmentation via wavelet transform. Pattern Recognit. 1997, 30, 729–742. [Google Scholar] [CrossRef]
- Lam, W.K.; Li, C.K. Rotated texture classification by improved iterative morphological decomposition. IEE Proc. Vis. Image Signal Process. 1997, 144, 171. [Google Scholar] [CrossRef]
- Gossage, K.W.; Smith, C.M.; Kanter, E.M.; Hariri, L.P.; Stone, A.L.; Rodriguez, J.J.; Williams, S.K.; Barton, J.K. Texture analysis of speckle in optical coherence tomography images of tissue phantoms. Phys. Med. Biol. 2006, 51, 1563–1575. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Zakharov, V.P.; Myakinin, O.O.; Bratchenko, I.A.; Artemyev, D.N.; Kornilin, D.V. Medical images classification for skin cancer using quantitative image features with optical coherence tomography. J. Innov. Opt. Health Sci. 2016, 9, 1650003. [Google Scholar] [CrossRef]
- Lingley-Papadopoulos, C.A.; Loew, M.H.; Manyak, M.J.; Zara, J.M. Computer recognition of cancer in the urinary bladder using optical coherence tomography and texture analysis. J. Biomed. Opt. 2008, 13, 024003. [Google Scholar] [CrossRef]
- Chen, Y.; Aguirre, A.D.; Hsiung, P.-L.; Huang, S.-W.; Mashimo, H.; Schmitt, J.M.; Fujimoto, J.G. Effects of axial resolution improvement on optical coherence tomography (OCT) imaging of gastrointestinal tissues. Opt. Express 2008, 16, 2469–2485. [Google Scholar] [CrossRef]
- Garcia-Allende, P.B.; Amygdalos, I.; Dhanapala, H.; Goldin, R.D.; Hanna, G.B.; Elson, D.S. Morphological analysis of optical coherence tomography images for automated classification of gastrointestinal tissues. Biomed. Opt. Express 2011, 2, 2821–2836. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, V.X.D.; Tang, S.J.; Gordon, M.L.; Qi, B.; Gardiner, G.; Cirocco, M.; Kortan, P.; Haber, G.B.; Kandel, G.; Vitkin, I.A.; et al. Endoscopic Doppler optical coherence tomography in the human GI tract: Initial experience. Gastrointest. Endosc. 2005, 61, 879–890. [Google Scholar] [CrossRef] [PubMed]
- Osiac, E.; Sǎftoiu, A.; Gheonea, D.I.; Mandrila, I.; Angelescu, R. Optical coherence tomography and Doppler optical coherence tomography in the gastrointestinal tract. World J. Gastroenterol. 2011, 17, 15–20. [Google Scholar] [CrossRef]
- Hufendiek, K.; Gamulescu, M.A.; Hufendiek, K.; Helbig, H.; Märker, D. Classification and characterization of acute macular neuroretinopathy with spectral domain optical coherence tomography. Int. Ophthalmol. 2018, 38, 2403–2416. [Google Scholar] [CrossRef] [PubMed]
- Konidaris, V.; Androudi, S.; Alexandridis, A.; Dastiridou, A.; Brazitikos, P. Optical coherence tomography-guided classification of epiretinal membranes. Int. Ophthalmol. 2014, 35, 495–501. [Google Scholar] [CrossRef] [PubMed]
- Apinyawasisuk, S.; McCannel, T.; Arnold, A.C. Clinical and Spectral-Domain Optical Coherence Tomography Appearance of Optic Disc Melanocytoma: A New Classification and Differentiation from Pigmented Choroidal Lesions. Ocul. Oncol. Pathol. 2017, 3, 142–148. [Google Scholar] [CrossRef] [PubMed]
- Jelvehgaran, P.; de Bruin, D.M.; Salguero, F.J.; Borst, G.R.; Song, J.-Y.; van Leeuwen, T.G.; de Boer, J.F.; Alderliesten, T.; van Herk, M. Feasibility of using optical coherence tomography to detect acute radiation-induced esophageal damage in small animal models. J. Biomed. Opt. 2018, 23, 046004. [Google Scholar] [CrossRef] [Green Version]
- Abdolmanafi, A.; Duong, L.; Dahdah, N.; Cheriet, F. Deep feature learning for automatic tissue classification of coronary artery using optical coherence tomography. Biomed. Opt. Express 2017, 8, 1203–1220. [Google Scholar] [CrossRef] [Green Version]
- Marvdashti, T.; Duan, L.; Aasi, S.Z.; Tang, J.Y.; Ellerbee Bowden, A.K. Classification of basal cell carcinoma in human skin using machine learning and quantitative features captured by polarization sensitive optical coherence tomography. Biomed. Opt. Express 2016, 7, 3721–3735. [Google Scholar] [CrossRef] [Green Version]
- Luo, S.; Fan, Y.; Chang, W.; Liao, H.; Kang, H.; Huo, L. Classification of human stomach cancer using morphological feature analysis from optical coherence tomography images. Laser Phys. Lett. 2019, 16, 095602. [Google Scholar] [CrossRef]
- Trindade, A.; George, B.; Berkowitz, J.; Sejpal, D.; McKinley, M. Volumetric laser endomicroscopy can target neoplasia not detected by conventional endoscopic measures in long segment Barrett’s esophagus. Endosc. Int. Open 2016, 4, E318–E322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Samel, N.S.; Mashimo, H. Application of OCT in the gastrointestinal tract. Appl. Sci. 2019, 9, 2991. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications. Biometrics 1990, 46, 886–887. [Google Scholar] [CrossRef]
- Long, M.; Peng, F. A Box-Counting Method with Adaptable Box Height for Measuring the Fractal Feature of Images. Radioengineering 2013, 22, 208–213. [Google Scholar]
- Flueraru, C.; Popescu, D.P.; Mao, Y.; Chang, S.; Sowa, M.G. Added soft tissue contrast using signal attenuation and the fractal dimension for optical coherence tomography images of porcine arterial tissue. Phys. Med. Biol. 2010, 55, 2317–2331. [Google Scholar] [CrossRef] [Green Version]
- Sullivan, A.C.; Hunt, J.P.; Oldenburg, A.L. Fractal analysis for classification of breast carcinoma in optical coherence tomography. J. Biomed. Opt. 2011, 16, 066010. [Google Scholar] [CrossRef]
- Raupov, D.; Myakinin, O.; Bratchenko, I.; Zakharov, V.; Khramov, A. Multimodal texture analysis of OCT images as a diagnostic application for skin tumors. J. Biomed. Photonics Eng. 2017, 3, 010307. [Google Scholar] [CrossRef] [Green Version]
- Matet, A.; Daruich, A.; Zografos, L. Radiation maculopathy after proton beam therapy for uveal melanoma: Optical coherence tomography angiography alterations influencing visual acuity. Investig. Ophthalmol. Vis. Sci. 2017, 58, 3851–3861. [Google Scholar] [CrossRef]
- Aharony, O.; Gal-Or, O.; Polat, A.; Nahum, Y.; Weinberger, D.; Zimmer, Y. Automatic characterization of retinal blood flow using oct angiograms. Transl. Vis. Sci. Technol. 2019, 8. [Google Scholar] [CrossRef] [Green Version]
- Zahid, S.; Dolz-Marco, R.; Freund, K.B.; Balaratnasingam, C.; Dansingani, K.; Gilani, F.; Mehta, N.; Young, E.; Klifto, M.R.; Chae, B.; et al. Fractal dimensional analysis of optical coherence tomography angiography in eyes with diabetic retinopathy. Investig. Ophthalmol. Vis. Sci. 2016, 57, 4940–4947. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, S.; Tsui, E.; Zahid, S.; Young, E.; Mehta, N.; Agemy, S.; Garcia, P.; Rosen, R.B.; Young, J.A. Value of fractal analysis of optical coherence tomography angiography in various stages of diabetic retinopathy. Retina 2017, 38, 1816–1823. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, A.; Aggarwal, K.; Akella, M.; Agrawal, R.; Khandelwal, N.; Bansal, R.; Singh, R.; Gupta, V. Fractal dimension and optical coherence tomography angiography features of the central macula after repair of rhegmatogenous retinal detachments. Retina 2019, 39, 2167–2177. [Google Scholar] [CrossRef] [PubMed]
- Schmoll, T.; Singh, A.S.G.; Blatter, C.; Schriefl, S.; Ahlers, C.; Schmidt-Erfurth, U.; Leitgeb, R.A. Imaging of the parafoveal capillary network and its integrity analysis using fractal dimension. Biomed. Opt. Express 2011, 2, 1159–1168. [Google Scholar] [CrossRef] [Green Version]
- Somfai, G.M.; Tátrai, E.; Laurik, L.; Varga, B.E.; Ölvedy, V.; Smiddy, W.E.; Tchitnga, R.; Somogyi, A.; DeBuc, D.C. Fractal-based analysis of optical coherence tomography data to quantify retinal tissue damage. BMC Bioinform. 2014, 15, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Shetty, G.; Kendall, C.; Shepherd, N.; Stone, N.; Barr, H. Raman spectroscopy: Elucidation of biochemical changes in carcinogenesis of oesophagus. Br. J. Cancer 2006, 94, 1460–1464. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.; Yamauchi, T.; Choi, W.; Dasari, R.; Feld, M.S. Spectroscopic phase microscopy for quantifying hemoglobin concentrations in intact red blood cells. Opt. Lett. 2009, 34, 3668–3670. [Google Scholar] [CrossRef] [Green Version]
- Fu, D.; Choi, W.; Sung, Y.; Yaqoob, Z.; Dasari, R.R.; Feld, M. Quantitative dispersion microscopy. Biomed. Opt. Express 2010, 1, 347–353. [Google Scholar] [CrossRef]
- Ding, H.; Lu, J.Q.; Wooden, W.A.; Kragel, P.J.; Hu, X.H. Refractive indices of human skin tissues at eight wavelengths and estimated dispersion relations between 300 and 1600 nm. Phys. Med. Biol. 2006, 51, 1479–1489. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, G. Applications of Nonlinear Fiber Optics; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Hee, M.R. Optical Coherence Tomography of the Eye. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1997. [Google Scholar]
- Lippok, N.; Murdoch, S.; Wu, K.L.; Nielsen, P.; Vanholsbeeck, F. Dispersion mapping at the micron scale using tri-band optical frequency domain imaging. In Proceedings of the European Conference on Biomedical Optics 2013, Munich, Germany, 12–16 May 2013. [Google Scholar]
- Kolenderska, S.M.; Bräuer, B.; Vanholsbeeck, F. Dispersion mapping as a simple postprocessing step for Fourier domain Optical Coherence Tomography data. Sci. Rep. 2018, 8, 9244. [Google Scholar] [CrossRef] [Green Version]
- Schlichting, S.; Willemsen, T.; Ehlers, H.; Morgner, U.; Ristau, D. Direct in situ GDD measurement in optical coating process. In Proceedings of the Optical Systems Design 2015: Advances in Optical Thin Films V, Jena, Germany, 7–10 September 2015; Volume 9627. [Google Scholar]
- Dorrer, C.; Belabas, N.; Likforman, J.-P.; Joffre, M. Spectral resolution and sampling issues in Fourier-transform spectral interferometry. J. Opt. Soc. Am. B 2000, 17, 1795–1802. [Google Scholar] [CrossRef]
- Photiou, C.; Bousi, E.; Zouvani, I.; Pitris, C. Using speckle to measure tissue dispersion in optical coherence tomography. Biomed. Opt. Express 2017, 8, 2528–2535. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Photiou, C.; Pitris, C. Comparison of tissue dispersion measurement techniques based on optical coherence tomography. J. Biomed. Opt. 2019, 24, 046003. [Google Scholar] [CrossRef] [PubMed]
- Photiou, C.; Bousi, E.; Zouvani, I.; Pitris, C. Measuring tissue dispersion using optical coherence tomography speckle. In Proceedings of the European Conference on Biomedical Optics 2017, Munich, Germany, 25–29 June 2017. [Google Scholar]
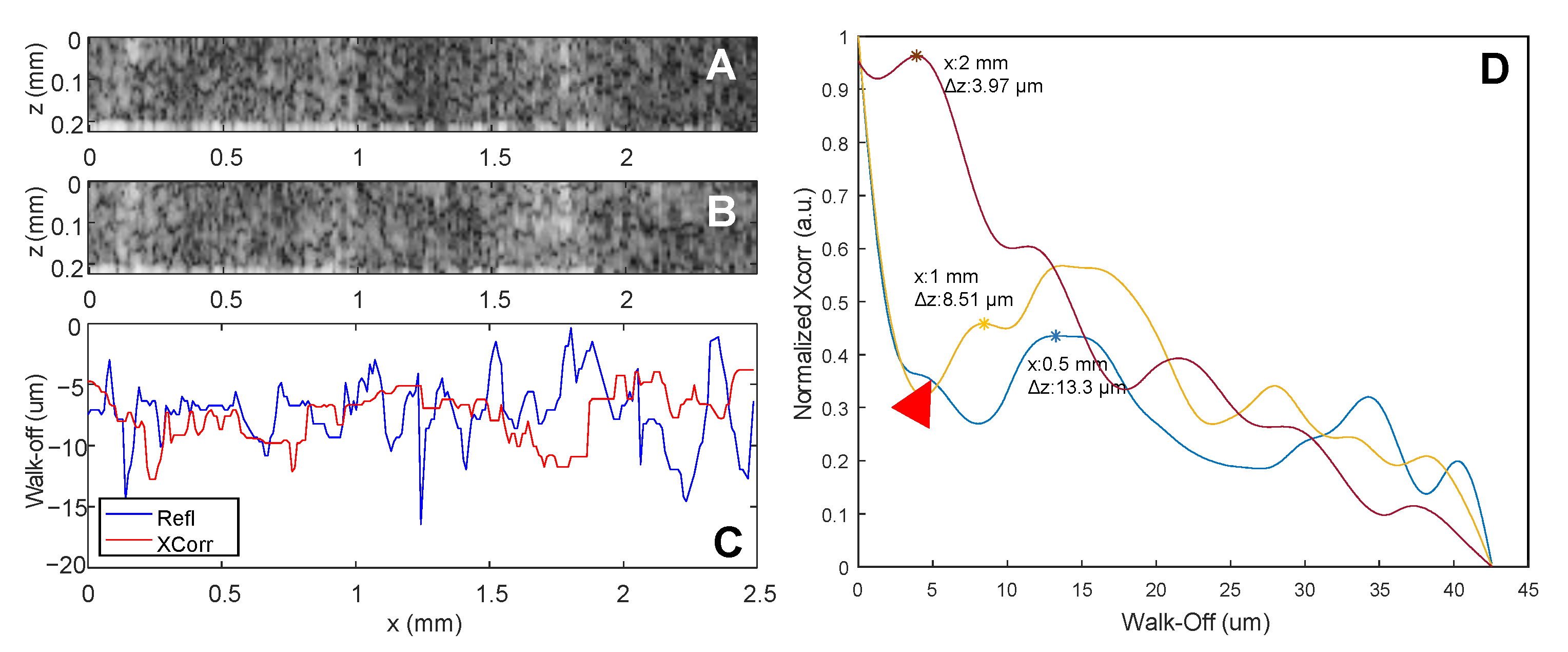
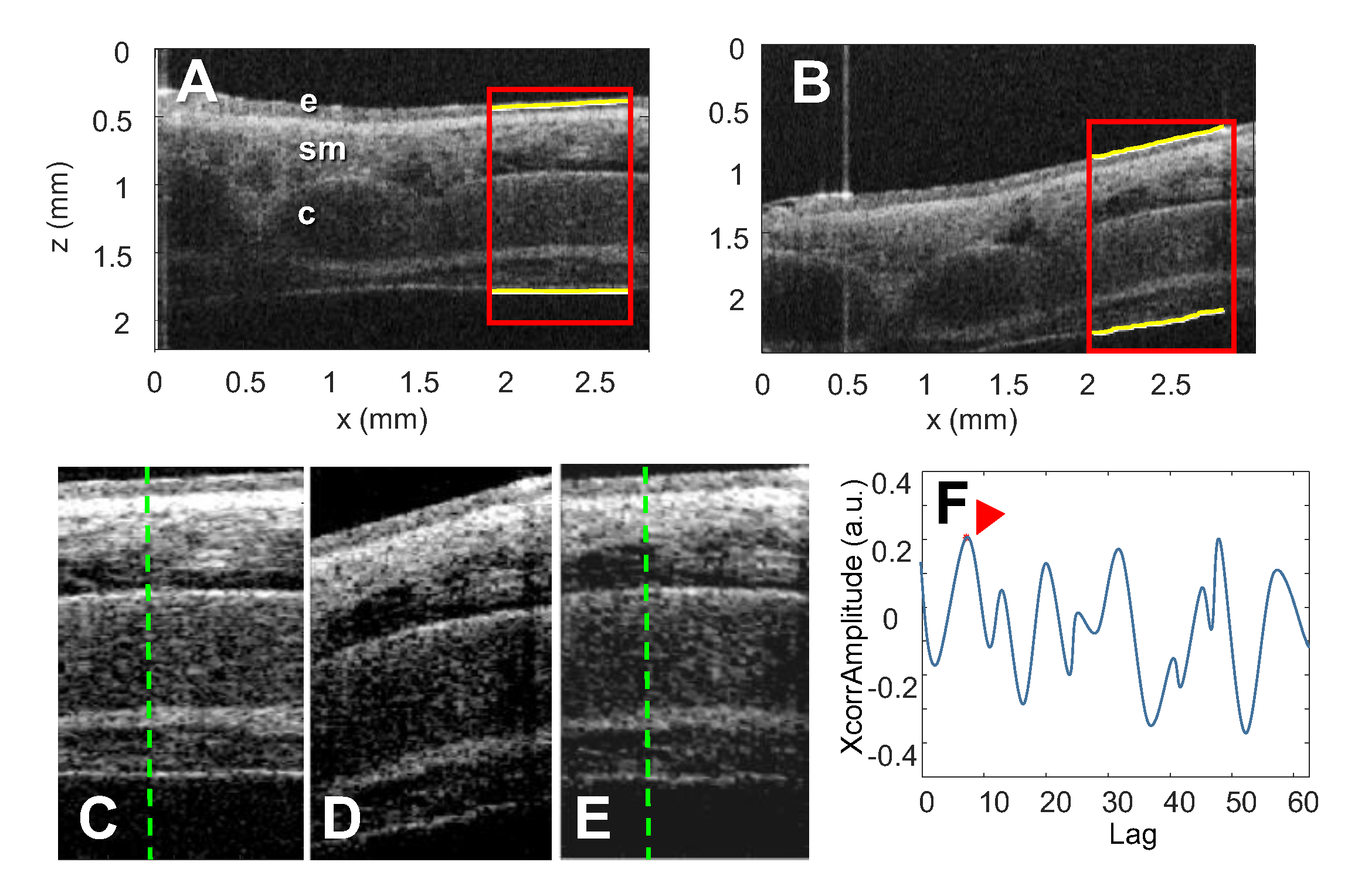
- Photiou, C.; Bousi, E.; Zouvani, I.; Pitris, C. Measuring tissue dispersion using the cross-correlation of half-spectrum optical coherence tomography images. In Proceedings of the Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XXIII, San Francisco, CA, USA, 2–7 February 2019. [Google Scholar]
- Rodrigues de Mercado, R.; van Hoorn, H.; de Valois, M.; Backendorf, C.; Eckert, J.; Schmidt, T. Characterization of cell-induced astigmatism in high-resolution imaging. Biomed. Opt. Express 2022, 13, 464. [Google Scholar] [CrossRef] [PubMed]
- Arakawa, E.T.; Tuminello, P.S.; Khare, B.N.; Milham, M.E. Optical properties of Erwinia herbicola bacteria at 0.190-2.50 μm. Biopolym.–Biospectroscopy Sect. 2003, 72, 391–398. [Google Scholar] [CrossRef]
- Cotte, Y.; Toy, F.; Jourdain, P.; Pavillon, N.; Boss, D.; Magistretti, P.; Marquet, P.; Depeursinge, C. Marker-free phase nanoscopy. Nat. Photonics 2013, 7, 113–117. [Google Scholar] [CrossRef]
- Kim, T.; Zhou, R.; Mir, M.; Babacan, S.D.; Carney, P.S.; Goddard, L.L.; Popescu, G. Supplementary Information: White-light diffraction tomography of unlabelled live cells. Nat. Photonics 2014, 8, 256–263. [Google Scholar] [CrossRef] [Green Version]
- Bennet, M.; Gur, D.; Yoon, J.; Park, Y.K.; Faivre, D. A Bacteria-Based Remotely Tunable Photonic Device. Adv. Opt. Mater. 2017, 5, 1600617. [Google Scholar] [CrossRef]
- Kim, K.; Yoon, H.; Diez-Silva, M.; Dao, M.; Dasari, R.R.; Park, Y. High-resolution three-dimensional imaging of red blood cells parasitized by Plasmodium falciparum and in situ hemozoin crystals using optical diffraction tomography. J. Biomed. Opt. 2013, 19, 011005. [Google Scholar] [CrossRef] [Green Version]
- Weatherall, D.J. Systems Biology and Red Cells. N. Engl. J. Med. 2011, 364, 376–377. [Google Scholar] [CrossRef]
- Jung, J.; Matemba, L.E.; Lee, K.; Kazyoba, P.E.; Yoon, J.; Massaga, J.J.; Kim, K.; Kim, D.J.; Park, Y. Optical characterization of red blood cells from individuals with sickle cell trait and disease in Tanzania using quantitative phase imaging. Sci. Rep. 2016, 6, 31698. [Google Scholar] [CrossRef] [PubMed]
- Welte, M.A. Fat on the move: Intracellular motion of lipid droplets. Biochem. Soc. Trans. 2009, 37, 991–996. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beuthan, J.; Minet, O.; Helfmann, J.; Herrig, M.; Müller, G. The spatial variation of the refractive index in biological cells. Phys. Med. Biol. 1996, 41, 369–382. [Google Scholar] [CrossRef] [PubMed]
- Sridharan, S.; Macias, V.; Tangella, K.; Kajdacsy-Balla, A.; Popescu, G. Prediction of prostate cancer recurrence using quantitative phase imaging. Sci. Rep. 2015, 5, 9976. [Google Scholar] [CrossRef] [Green Version]
- Majeed, H.; Kandel, M.E.; Han, K.; Luo, Z.; Macias, V.; Tangella, K.; Balla, A.; Popescu, G. Breast cancer diagnosis using spatial light interference microscopy. J. Biomed. Opt. 2015, 20, 111210. [Google Scholar] [CrossRef]
- Su, J.-W.; Lin, Y.-H.; Chiang, C.-P.; Lee, J.-M.; Hsieh, C.-M.; Hsieh, M.-S.; Yang, P.-W.; Wang, C.-P.; Tseng, P.-H.; Lee, Y.-C.; et al. Precancerous esophageal epithelia are associated with significantly increased scattering coefficients. Biomed. Opt. Express 2015, 6, 3795–3805. [Google Scholar] [CrossRef] [Green Version]
- Lee, M.; Lee, E.; Jung, J.; Yu, H.; Kim, K.; Yoon, J.; Lee, S.; Jeong, Y.; Park, Y. Label-free optical quantification of structural alterations in Alzheimer’s disease. Sci. Rep. 2016, 6, 31034. [Google Scholar] [CrossRef]
- Yang, S.A.; Yoon, J.; Kim, K.; Park, Y.K. Measurements of morphological and biophysical alterations in individual neuron cells associated with early neurotoxic effects in Parkinson’s disease. Cytom. Part A 2017, 91, 510–518. [Google Scholar] [CrossRef] [Green Version]
- Schnell, U.; Zimmermann, E.; Dandliker, R. Absolute distance measurement with synchronously sampled white-light channelled spectrum interferometry. Pure Appl. Opt. J. Eur. Opt. Soc. Part A 1995, 4, 643–651. [Google Scholar] [CrossRef]
- Tearney, G.J.; Brezinski, M.E.; Bouma, B.E.; Hee, M.R.; Southern, J.F.; Fujimoto, J.G. Determination of the refractive index of highly scattering human tissue by optical coherence tomography. Opt. Lett. 1995, 20, 2258–2260. [Google Scholar] [CrossRef]
- Ohmi, M.; Shiraishi, T.; Tajiri, H.; Haruna, M. Simultaneous Measurement of Refractive Index and Thickness of Transparent Plates by Low Coherence Interferometry. Opt. Rev. 1997, 4, 507–515. [Google Scholar] [CrossRef]
- Maruyama, H.; Mitsuyama, T.; Ohmi, M.; Haruna, M. Simultaneous measurement of refractive index and thickness by low coherence interferometry considering chromatic dispersion of index. Opt. Rev. 2000, 7, 468–472. [Google Scholar] [CrossRef]
- Zhou, Y.; Chan, K.K.H.; Lai, T.; Tang, S. Characterizing refractive index and thickness of biological tissues using combined multiphoton microscopy and optical coherence tomography. Biomed. Opt. Express 2013, 4, 38–50. [Google Scholar] [CrossRef]
- Fukano, T.; Yamaguchi, I. Simultaneous measurement of thicknesses and refractive indices of multiple layers by a low-coherence confocal interference microscope. Opt. Lett. 1996, 21, 1942–1944. [Google Scholar] [CrossRef] [PubMed]
- Abelès, F. La détermination de l’indice et de l’épaisseur des couches minces transparentes. J. Phys. Radium 1950, 11, 310–314. [Google Scholar] [CrossRef]
- Sorin, W.V.; Gray, D.F. Simultaneous Thickness and Group Index Measurement Using Optical Low-Coherence Reflectometry. IEEE Photonics Technol. Lett. 1992, 4, 105–107. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.P.; Wang, D.N.; Jin, W.; Chen, J.P.; Li, X.W.; Zhou, J.H. Reflectometry measuring refractive index and thickness of polymer samples simultaneously. J. Mod. Opt. 2006, 53, 1845–1851. [Google Scholar] [CrossRef]
- Ghim, Y.-S.; Kim, S.-W. Thin-film thickness profile and its refractive index measurements by dispersive white-light interferometry. Opt. Express 2006, 14, 11885–11891. [Google Scholar] [CrossRef]
- Matsumoto, H.; Sasaki, K.; Hirai, A. In situ measurement of group refractive index using tandem low-coherence interferometer. Opt. Commun. 2006, 266, 214–217. [Google Scholar] [CrossRef]
- Photiou, C.; Pitris, C. Dual-angle optical coherence tomography for index of refraction estimation using rigid registration and cross-correlation. J. Biomed. Opt. 2019, 24, 106001. [Google Scholar] [CrossRef]
- Backman, V. Erratum: Detection of preinvasive cancer cells (Nature (2000) 406 (35-36)). Nature 2000, 408, 428. [Google Scholar] [CrossRef] [Green Version]
- Mourant, J.R.; Bigio, I.J.; Boyer, J.; Conn, R.L.; Johnson, T.; Shimada, T. Spectroscopic diagnosis of bladder cancer with elastic light scattering. Lasers Surg. Med. 1995, 17, 350–357. [Google Scholar] [CrossRef] [PubMed]
- Pyhtila, J.W.; Wax, A. Rapid, depth-resolved light scattering measurements using Fourier domain, angle-resolved low coherence interferometry. Opt. Express 2004, 12, 6178–6183. [Google Scholar] [CrossRef] [PubMed]
- Wax, A.; Yang, C.; Izatt, J.A. Fourier-domain low-coherence interferometry for light-scattering spectroscopy. Opt. Lett. 2003, 28, 1230–1232. [Google Scholar] [CrossRef] [Green Version]
- Yi, J.; Radosevich, A.J.; Rogers, J.D.; Norris, S.C.P.; Çapoğlu, İ.R.; Taflove, A.; Backman, V. Can OCT be sensitive to nanoscale structural alterations in biological tissue? Opt. Express 2013, 21, 9043–9059. [Google Scholar] [CrossRef] [Green Version]
- Seck, H.L.; Zhang, Y.; Soh, Y.C. Contrast enhancement using Mie spectra representation for spectroscopic optical coherence tomography. Opt. Commun. 2015, 338, 328–335. [Google Scholar] [CrossRef]
- Robles, F.E.; Zhu, Y.; Lee, J.; Sharma, S.; Wax, A. Detection of early colorectal cancer development in the azoxymethane rat carcinogenesis model with Fourier domain low coherence interferometry. Biomed. Opt. Express 2010, 1, 736–745. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Carney, P.S.; Boppart, S.A. Wavelength-dependent scattering in spectroscopic optical coherence tomography. Opt. Express 2005, 13, 5450–5462. [Google Scholar] [CrossRef]
- Graf, R.N.; Robles, F.E.; Chen, X.; Wax, A. Detecting precancerous lesions in the hamster cheek pouch using spectroscopic white-light optical coherence tomography to assess nuclear morphology via spectral oscillations. J. Biomed. Opt. 2009, 14, 064030. [Google Scholar] [CrossRef] [Green Version]
- Oldenburg, A.L.; Xu, C.; Boppart, S.A. Spectroscopic optical coherence tomography and microscopy. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 1629–1640. [Google Scholar] [CrossRef]
- Adler, D.C.; Ko, T.H.; Herz, P.R.; Fujimoto, J.G. Optical coherence tomography contrast enhancement using spectroscopic analysis with spectral autocorrelation. Opt. Express 2004, 12, 5487–5501. [Google Scholar] [CrossRef] [PubMed]
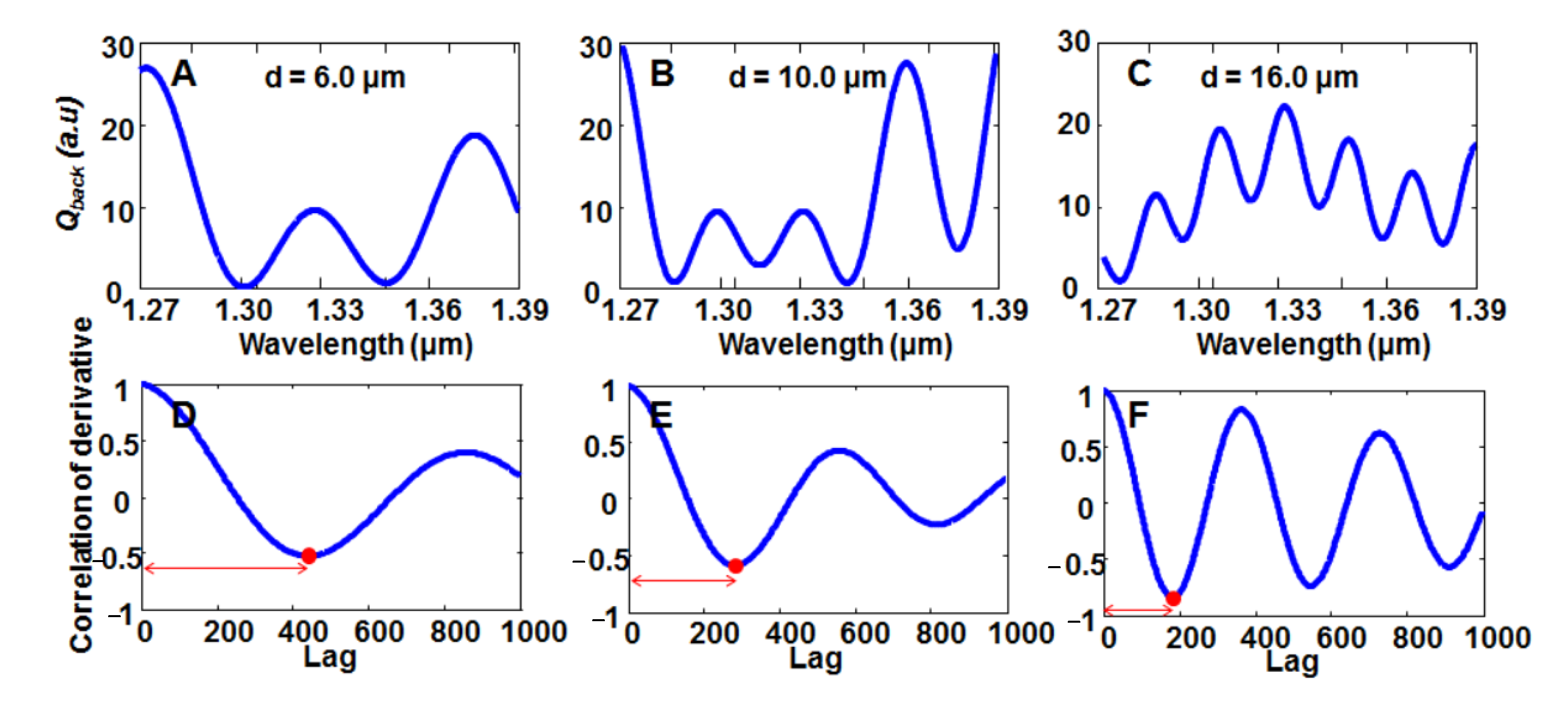
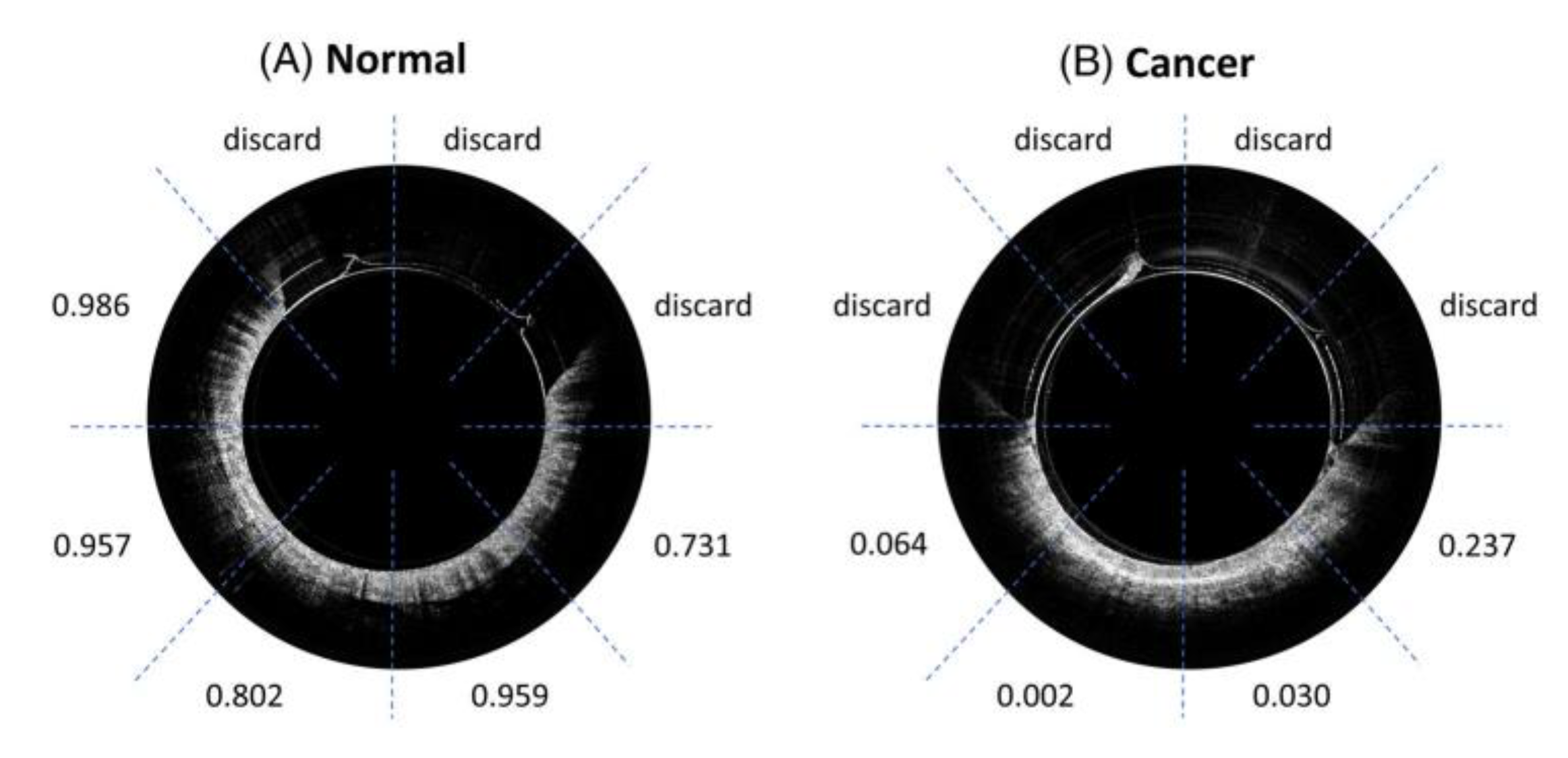
- Kartakoullis, A.; Bousi, E.; Pitris, C. Scatterer size-based analysis of optical coherence tomography images using spectral estimation techniques. Opt. Express 2010, 18, 9181–9191. [Google Scholar] [CrossRef] [PubMed]
- Jaedicke, V.; Agcaer, S.; Robles, F.E.; Steinert, M.; Jones, D.; Goebel, S.; Gerhardt, N.C.; Welp, H.; Hofmann, M.R. Comparison of different metrics for analysis and visualization in spectroscopic optical coherence tomography. Biomed. Opt. Express 2013, 4, 2945–2961. [Google Scholar] [CrossRef] [PubMed]
- Tay, B.C.M.; Chow, T.H.; Ng, B.K.; Loh, T.K.S. Dual-window dual-bandwidth spectroscopic optical coherence tomography metric for qualitative scatterer size differentiation in tissues. IEEE Trans. Biomed. Eng. 2012, 59, 2439–2448. [Google Scholar] [CrossRef] [PubMed]
- Kassinopoulos, M.; Bousi, E.; Zouvani, I.; Pitris, C. Correlation of the derivative as a robust estimator of scatterer size in optical coherence tomography (OCT) [Invited]. Biomed. Opt. Express 2017, 8, 1598–1606. [Google Scholar] [CrossRef] [Green Version]
- Photiou, C.; Plastiras, G.; Tearney, G.; Pitris, C. Comparison of classification methods of Barret’s and dysplasia in the esophagus from in vivo optical coherence tomography images. In Proceedings of the Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XXIV, San Francisco, CA, USA, 1–6 February 2020. [Google Scholar]
- Photiou, C.; Plastiras, G.; Tearney, G.; Pitris, C. Machine learning methods for Barret’s and dysplasia classification from in vivo optical coherence tomography images of human esophagus. In Proceedings of the Optical Coherence Tomography 2020, Washington, DC, USA, 20–23 April 2020. [Google Scholar]
- Alexandrov, S.; Subhash, H.; Leahy, M. Nanosensitive optical coherence tomography for the study of changes in static and dynamic structures. Quantum Electron. 2014, 44, 657–663. [Google Scholar] [CrossRef] [Green Version]
- Das, N.; Sergey, A.; Zhou, Y.; Gilligan, K.E.; Dwyer, R.M.; Leahy, M. Nanoscale structure detection and monitoring of tumour growth with optical coherence tomography. Nanoscale Adv. 2020, 2, 2853–2858. [Google Scholar] [CrossRef]
- Alexandrov, S.A.; Uttam, S.; Bista, R.K.; Liu, Y. Spectral contrast imaging microscopy. Opt. Lett. 2011, 36, 3323–3325. [Google Scholar] [CrossRef] [Green Version]
- Ladurner, R.; Hallfeldt, K.K.J.; Al Arabi, N.; Stepp, H.; Mueller, S.; Gallwas, J.K.S. Optical coherence tomography as a method to identify parathyroid glands. Lasers Surg. Med. 2013, 45, 654–659. [Google Scholar] [CrossRef]
- Macedo, M.M.G.; Takimura, C.K.; Lemos, P.A.; Gutierrez, M.A. A robust fully automatic lumen segmentation method for in vivo intracoronary optical coherence tomography. Rev. Bras. Eng. Biomed. 2016, 32, 35–43. [Google Scholar] [CrossRef] [Green Version]
- Heimann, T.; Meinzer, H.P. Statistical shape models for 3D medical image segmentation: A review. Med. Image Anal. 2009, 13, 543–563. [Google Scholar] [CrossRef] [PubMed]
- Cremers, D.; Rousson, M.; Deriche, R. A review of statistical approaches to level set segmentation: Integrating color, texture, motion and shape. Int. J. Comput. Vis. 2007, 72, 195–215. [Google Scholar] [CrossRef] [Green Version]
- Baghaie, A.; Yu, Z.; D’Souza, R.M. State-of-the-art in retinal optical coherence tomography image analysis. Quant. Imaging Med. Surg. 2015, 5, 603–617. [Google Scholar] [CrossRef] [PubMed]
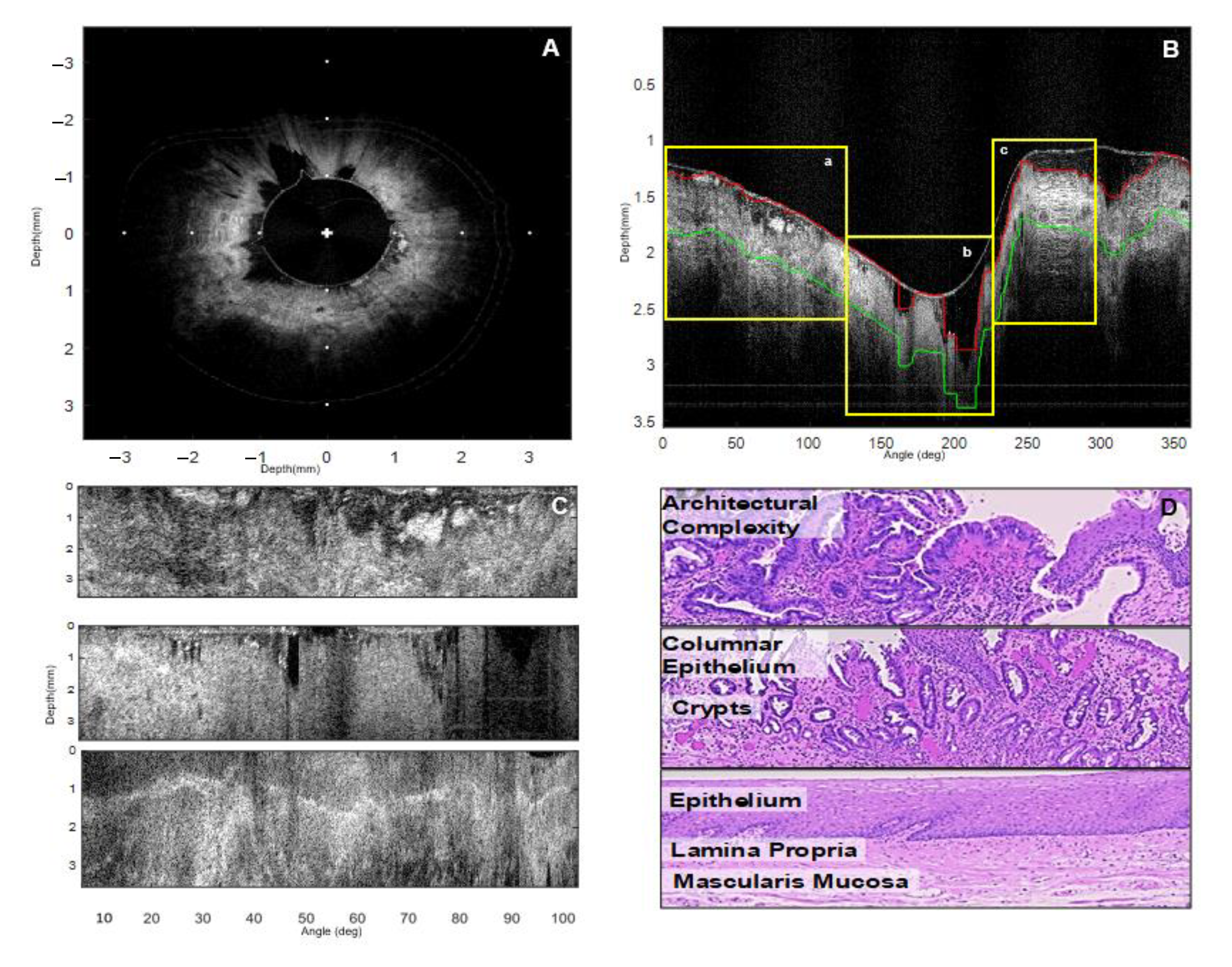
- Ughi, G.J.; Gora, M.J.; Swager, A.-F.; Soomro, A.; Grant, C.; Tiernan, A.; Rosenberg, M.; Sauk, J.S.; Nishioka, N.S.; Tearney, G.J. Automated segmentation and characterization of esophageal wall in vivo by tethered capsule optical coherence tomography endomicroscopy. Biomed. Opt. Express 2016, 7, 409–419. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Diaz, E.; Singh, S.K. Computer-Assisted Image Interpretation of Volumetric Laser Endomicroscopy in Barrett’s Esophagus. Gastroenterology 2015, 148, S-91. [Google Scholar] [CrossRef]
- Swager, A.F.; van der Sommen, F.; Klomp, S.R.; Zinger, S.; Meijer, S.L.; Schoon, E.J.; Bergman, J.J.G.H.M.; de With, P.H.; Curvers, L. Computer-aided detection of early Barrett’s neoplasia using volumetric laser endomicroscopy. Gastrointest. Endosc. 2017, 86, 839–846. [Google Scholar] [CrossRef] [Green Version]
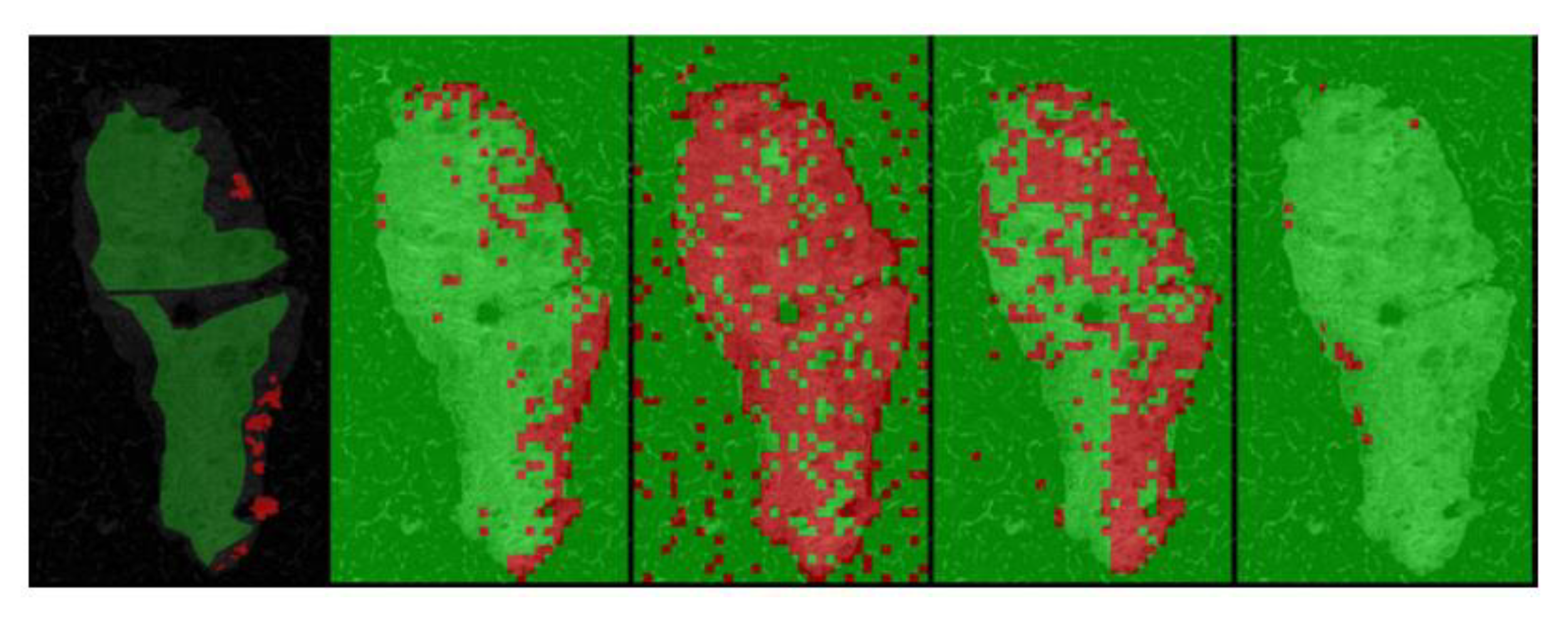
- Luo, S.; Ran, Y.; Liu, L.; Huang, H.; Tang, X.; Fan, Y. Classification of gastric cancerous tissues by a residual network based on optical coherence tomography images. Lasers Med. Sci. 2022, 37, 2727–2735. [Google Scholar] [CrossRef]
- Fonollà, R.; Scheeve, T.; Struyvenberg, M.R.; Curvers, W.L.; de Groof, A.J.; van der Sommen, F.; Schoon, E.J.; Bergman, J.J.G.H.M.; de With, P.H.N. Ensemble of deep convolutional neural networks for classification of early Barrett’s neoplasia using volumetric laser endomicroscopy. Appl. Sci. 2019, 9, 2183. [Google Scholar] [CrossRef] [Green Version]
- van der Putten, J.; Struyvenberg, M.; de Groof, J.; Scheeve, T.; Curvers, W.; Schoon, E.; Bergman, J.J.G.H.M.; de With, P.H.N.; van der Sommen, F. Deep principal dimension encoding for the classification of early neoplasia in Barrett’s Esophagus with volumetric laser endomicroscopy. Comput. Med. Imaging Graph. 2020, 80, 101701. [Google Scholar] [CrossRef]
- Gan, M.; Wang, C. Esophageal optical coherence tomography image synthesis using an adversarially learned variational autoencoder. Biomed. Opt. Express 2022, 13, 1188–1201. [Google Scholar] [CrossRef]
- Wang, C.; Gan, M.; Zhang, M.; Li, D. Adversarial convolutional network for esophageal tissue segmentation on OCT images. Biomed. Opt. Express 2020, 11, 3095–3110. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Li, S.; Zeng, Y.; Cheema, H.; Otegbeye, E.; Ahmed, S.; Chapman, W.C.; Mutch, M.; Zhou, C.; Zhu, Q. Human colorectal cancer tissue assessment using optical coherence tomography catheter and deep learning. J. Biophotonics 2022, 15, e202100349. [Google Scholar] [CrossRef] [PubMed]
- Lenz, M.; Krug, R.; Welp, H.; Schmieder, K.; Hofmann, M.R. Ex vivo brain tumor analysis using spectroscopic optical coherence tomography. In Proceedings of the Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XX, San Francisco, CA, USA, 13–18 February 2016; Volume 9697. [Google Scholar]
- Bareja, R.; Mojahed, D.; Hibshoosh, H.; Hendon, C. Classifying breast cancer in ultrahigh-resolution optical coherence tomography images using convolutional neural networks. Appl. Opt. 2022, 61, 4458–4462. [Google Scholar] [CrossRef] [PubMed]
- Foo, K.Y.; Newman, K.; Fang, Q.; Gong, P.; Ismail, H.M.; Lakhiani, D.D.; Zilkens, R.; Dessauvagie, B.F.; Latham, B.; Saunders, C.M.; et al. Multi-class classification of breast tissue using optical coherence tomography and attenuation imaging combined via deep learning. Biomed. Opt. Express 2022, 13, 3380–3400. [Google Scholar] [CrossRef] [PubMed]
- Boone, M.A.L.M.; Norrenberg, S.; Jemec, G.B.E.; Del Marmol, V. Imaging of basal cell carcinoma by high-definition optical coherence tomography: Histomorphological correlation. A pilot study. Br. J. Dermatol. 2012, 167, 856–864. [Google Scholar] [CrossRef]
- Markowitz, O.; Schwartz, M.; Feldman, E.; Bienenfeld, A.; Bieber, A.K.; Ellis, J.; Alapati, U.; Lebwohl, M.; Siegel, D.M. Evaluation of optical coherence tomography as a means of identifying earlier stage basal cell carcinomas while reducing the use of diagnostic biopsy. J. Clin. Aesthet. Dermatol. 2015, 8, 14–20. [Google Scholar]
- Schuh, S.; Kaestle, R.; Sattler, E.C.; Welzel, J. Optical coherence tomography of actinic keratoses and basal cell carcinomas—Differentiation by quantification of signal intensity and layer thickness. J. Eur. Acad. Dermatol. Venereol. 2016, 30, 1321–1326. [Google Scholar] [CrossRef]
- Mandache, D.; Dalimier, E.; Durkin, J.R.; Boceara, C.; Olivo-Marin, J.C.; Meas-Yedid, V. Basal cell carcinoma detection in full field OCT images using convolutional neural networks. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018. [Google Scholar]
- Taha, B.; Boley, D.; Sun, J.; Chen, C. Potential and limitations of radiomics in neuro-oncology. J. Clin. Neurosci. 2021, 90, 206–211. [Google Scholar] [CrossRef]



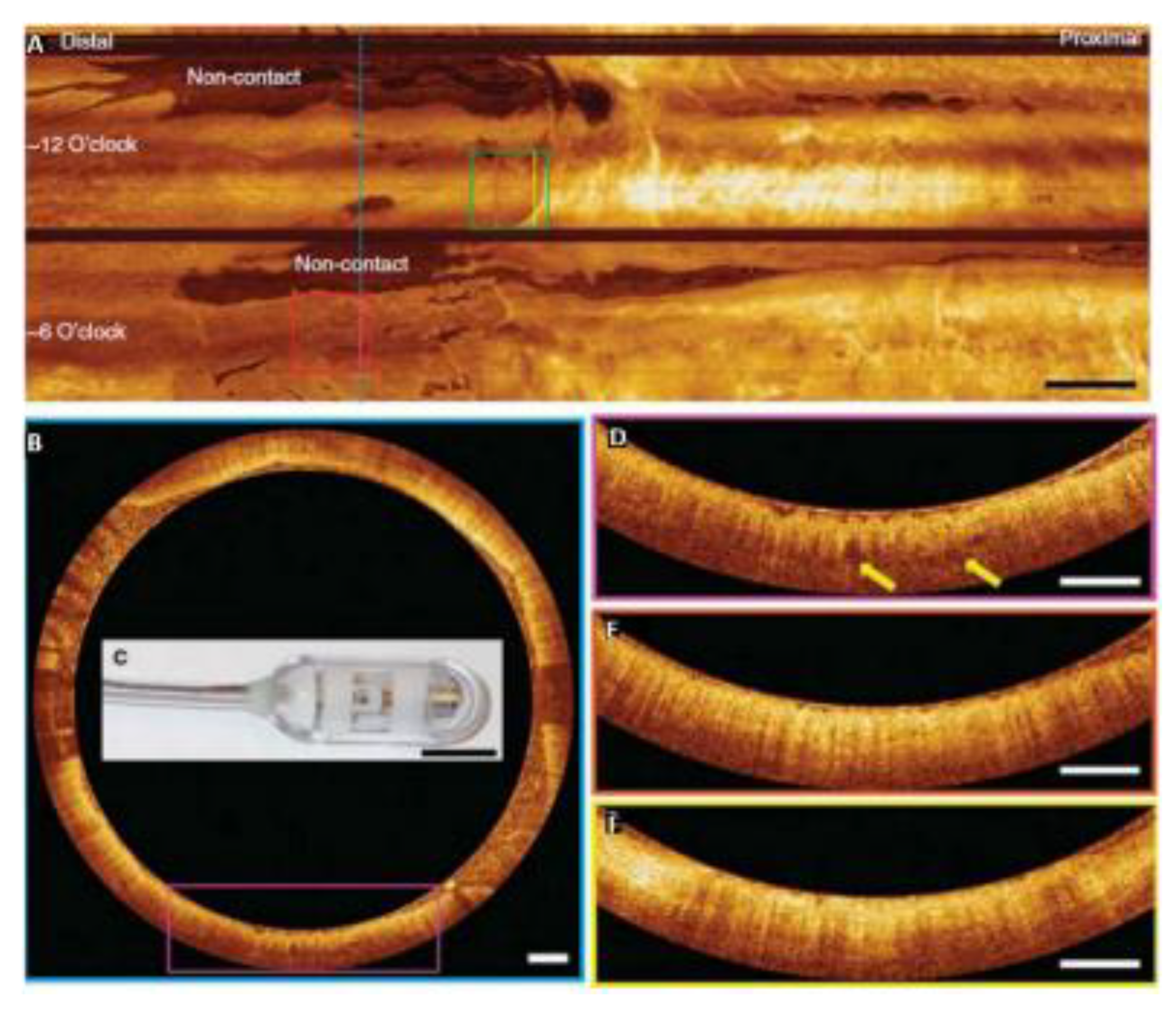

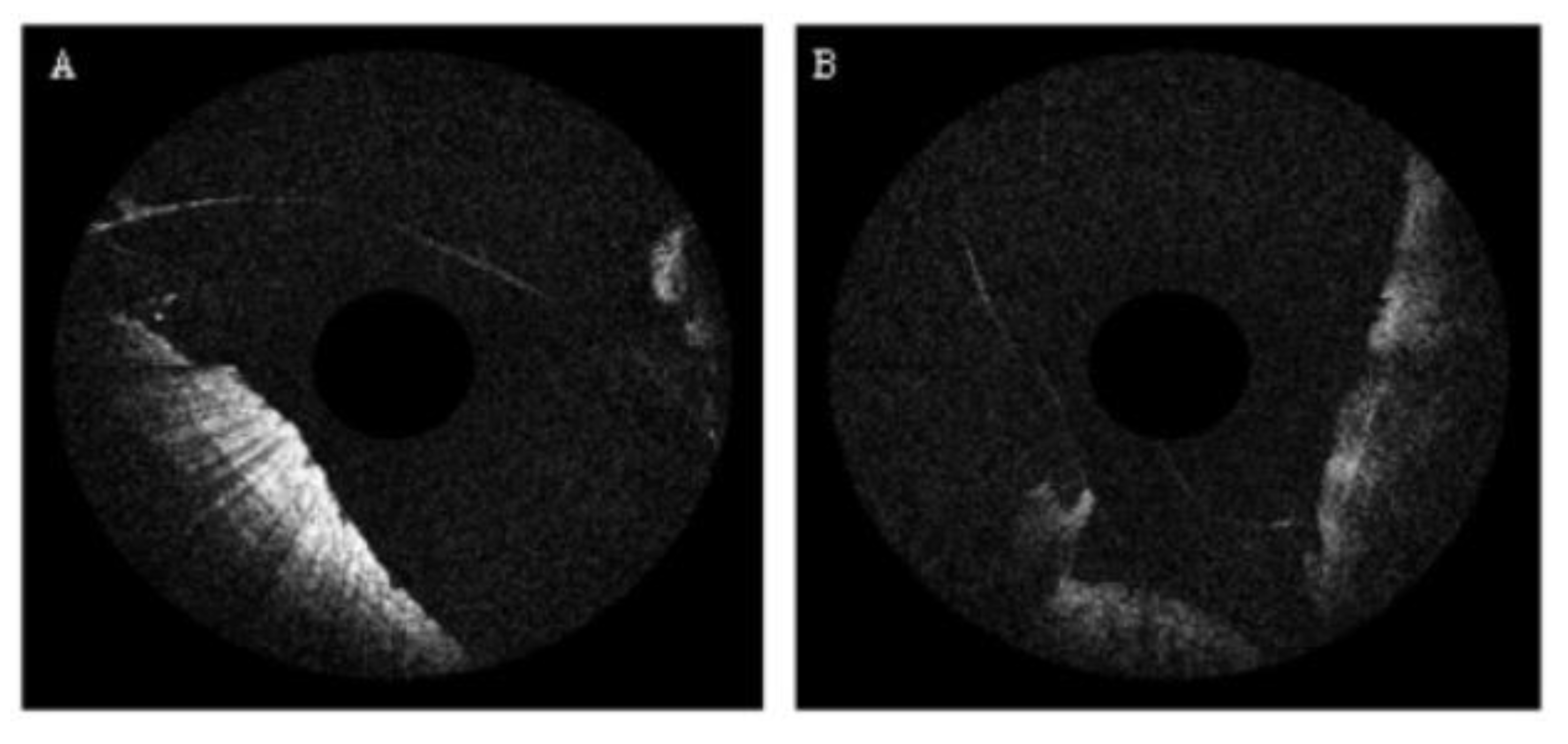
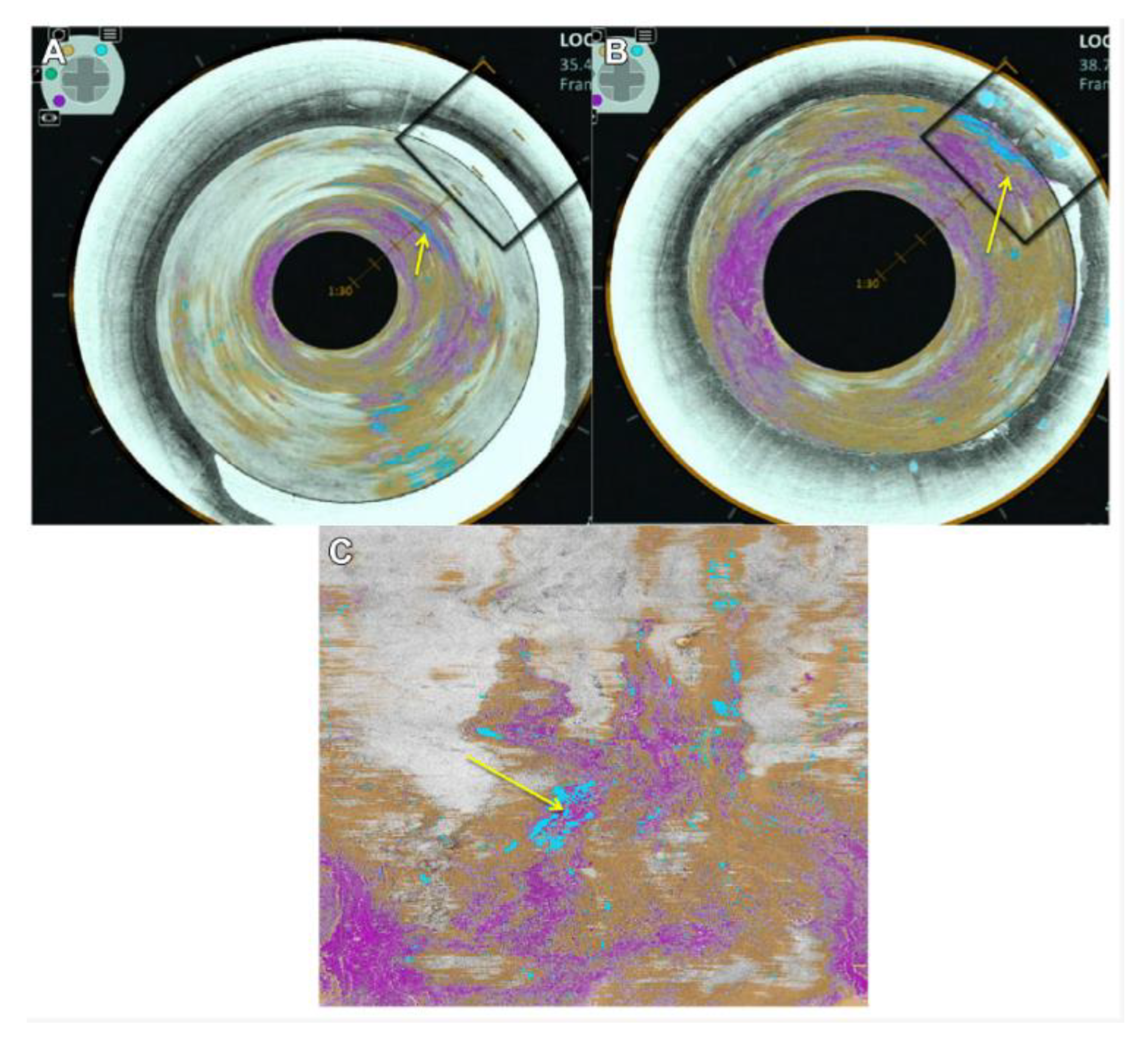
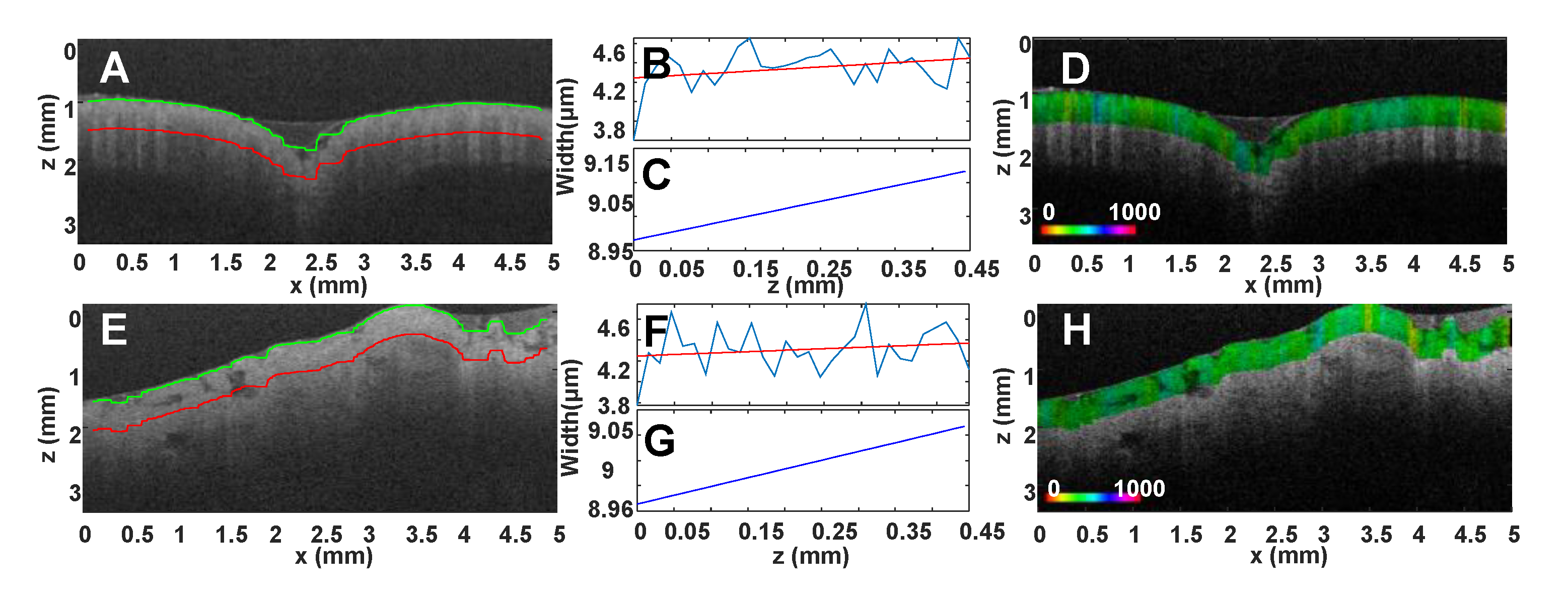

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Photiou, C.; Kassinopoulos, M.; Pitris, C. Extracting Morphological and Sub-Resolution Features from Optical Coherence Tomography Images, a Review with Applications in Cancer Diagnosis. Photonics 2023, 10, 51. https://doi.org/10.3390/photonics10010051
Photiou C, Kassinopoulos M, Pitris C. Extracting Morphological and Sub-Resolution Features from Optical Coherence Tomography Images, a Review with Applications in Cancer Diagnosis. Photonics. 2023; 10(1):51. https://doi.org/10.3390/photonics10010051
Chicago/Turabian StylePhotiou, Christos, Michalis Kassinopoulos, and Costas Pitris. 2023. "Extracting Morphological and Sub-Resolution Features from Optical Coherence Tomography Images, a Review with Applications in Cancer Diagnosis" Photonics 10, no. 1: 51. https://doi.org/10.3390/photonics10010051
APA StylePhotiou, C., Kassinopoulos, M., & Pitris, C. (2023). Extracting Morphological and Sub-Resolution Features from Optical Coherence Tomography Images, a Review with Applications in Cancer Diagnosis. Photonics, 10(1), 51. https://doi.org/10.3390/photonics10010051




