Coupled Strip-Array Waveguides for Integrated Mid-IR Gas Sensing
Abstract
:1. Introduction
2. Materials and Methods
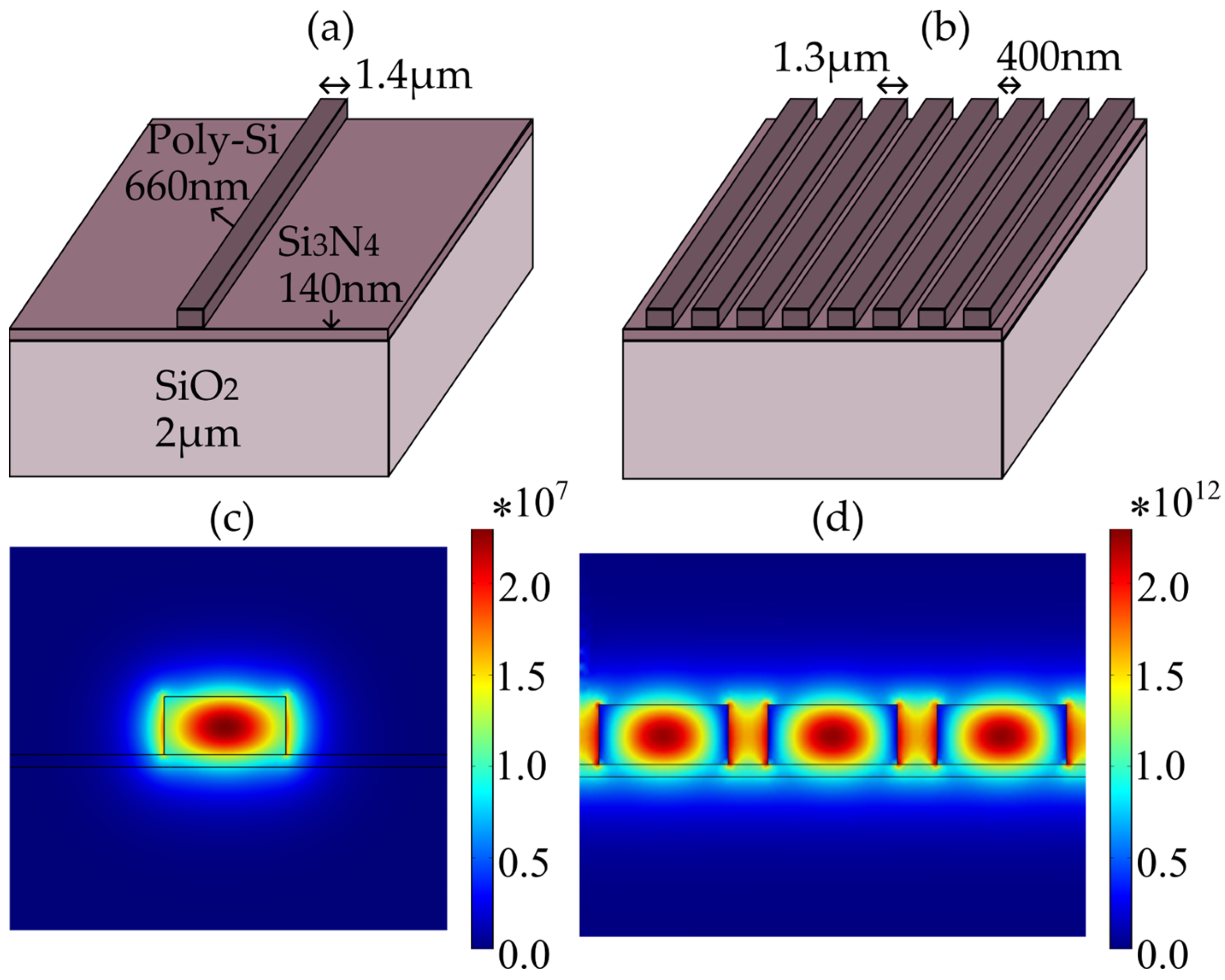
2.1. Simulations
| Waveguide | Width w [µm] | Gap g [nm] |
|---|---|---|
| Strip * | 1.4 | - |
| A | 1.0 | 300 |
| B | 1.2 | 300 |
| C | 1.3 | 300 |
| D | 1.3 | 400 |
2.2. Fabrication
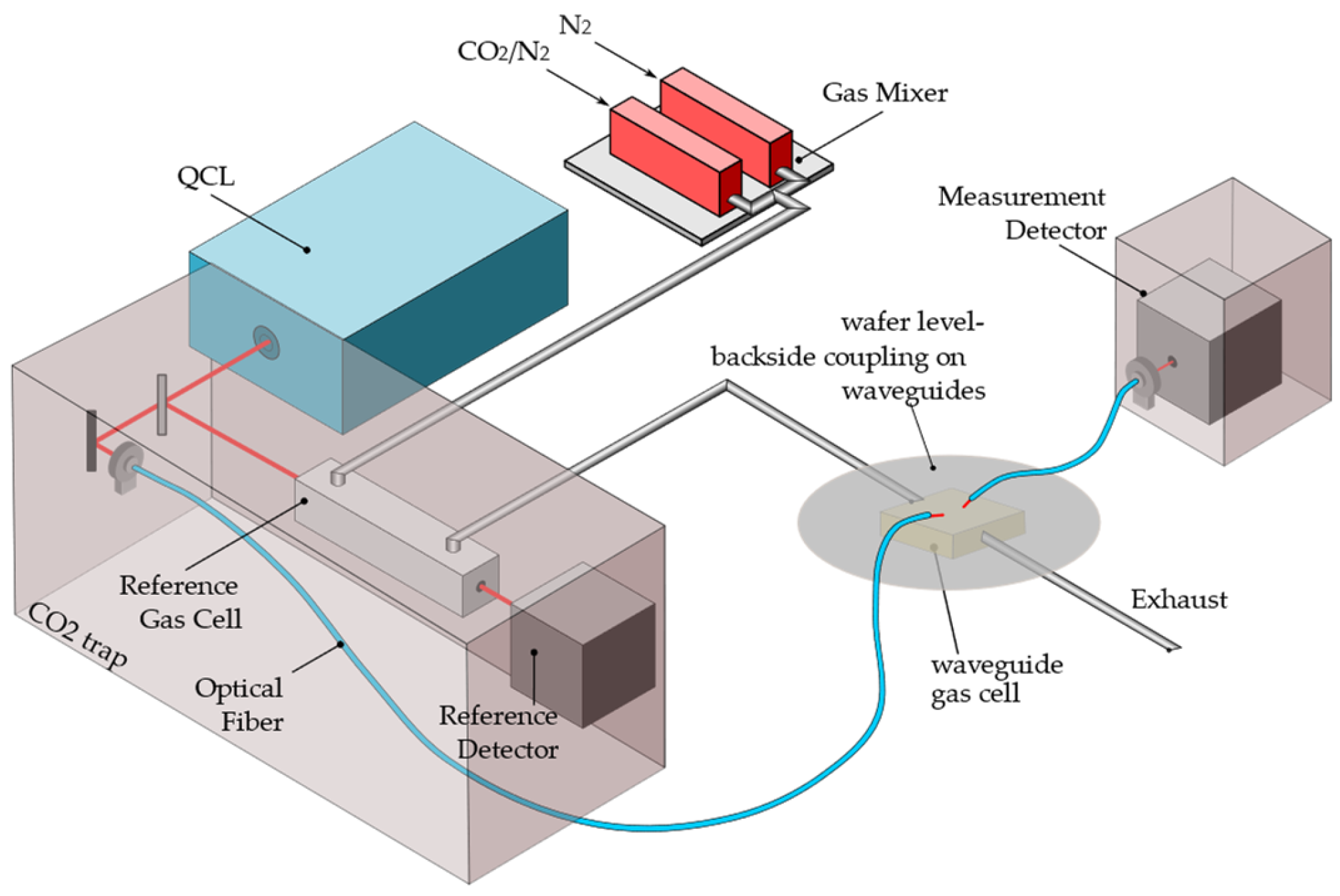
2.3. Experimental Setup
3. Results and Discussion
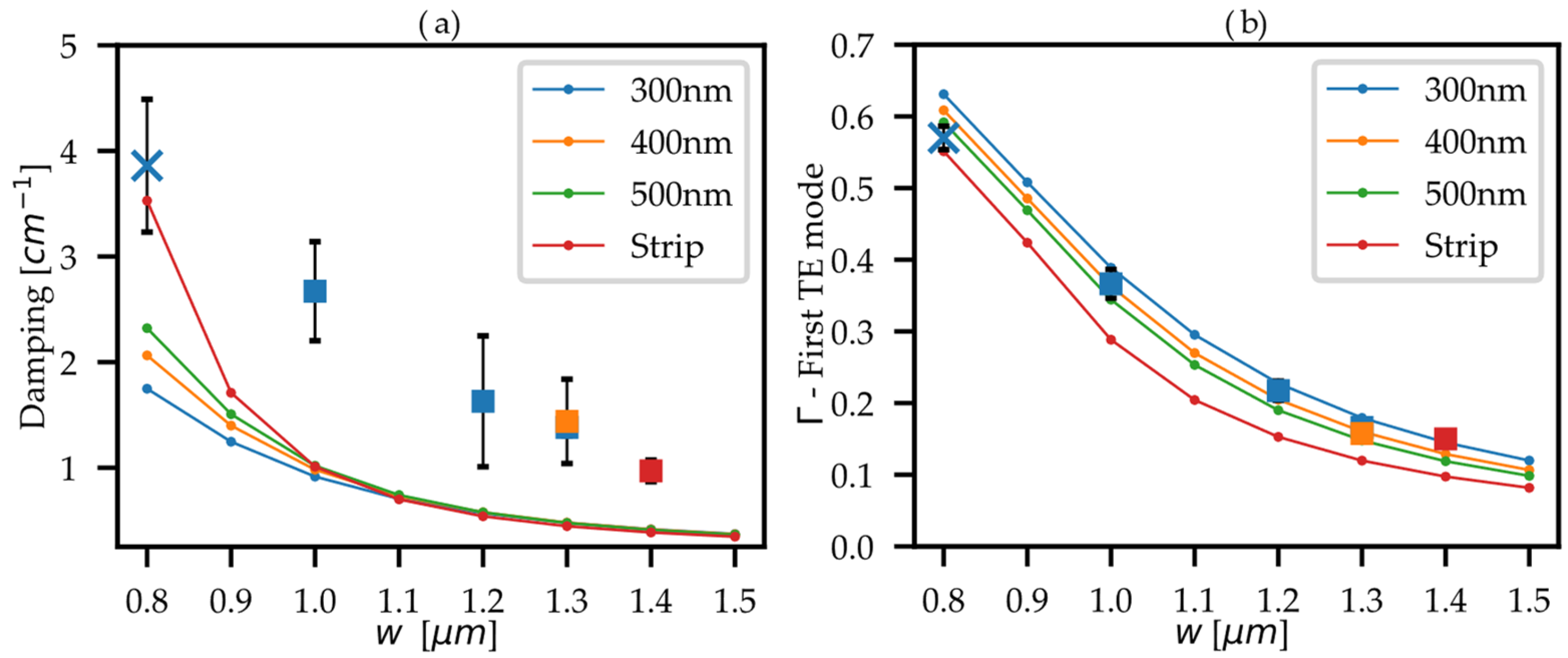
3.1. Simulations
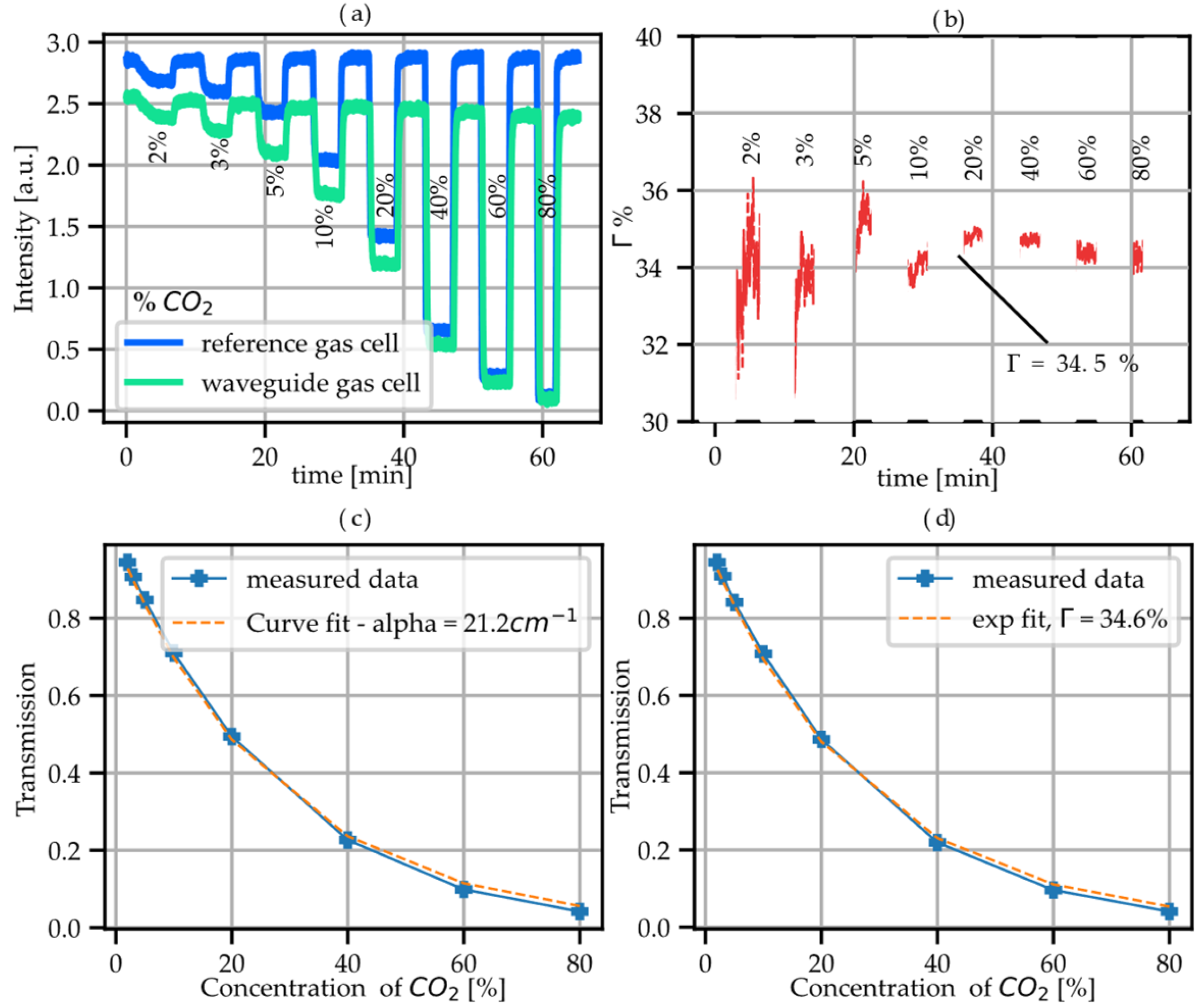
3.2. Experimental Determination of the Damping D
3.3. Experimental Determination of the Confinement Factor
3.4. Determination of the
- The capability of efficiently coupling thermal light into the waveguide. A recent paper [34] proposed a design for a Slab Tamm Plasmon Resonator coupled to a multistrip array for the efficient incoupling of thermal radiation in the mid-IR. While the study investigated only one geometry for the waveguide element, focusing instead on the dependence of the coupling on the slab thickness, it is very likely that the other CSA dimensions (g and w) might also have had an influence on the coupling efficiency and resonance damping.
- Final sensor size. The proposed CSA waveguides are “bulky” when compared to single-strip waveguides, which can be packed in compact meander structures. With the being similar for all structures, the structure with the shortest optimal length can be chosen to minimize the sensor size at a comparable performance.
- Fabrication capabilities. Depending on the available technologies and on the typical quality of the fabricated waveguides, a structure that is less demanding in terms of fabrication can be selected without loss in sensitivity.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lakkis, S.; Younes, R.; Alayli, Y.; Sawan, M. Review of Recent Trends in Gas Sensing Technologies and Their Miniaturization Potential. Sens. Rev. 2014, 34, 24–35. [Google Scholar] [CrossRef]
- Popa, D.; Udrea, F. Towards Integrated Mid-Infrared Gas Sensors. Sensors 2019, 19, 2076. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, M.F.; Hopper, R.; Ali, S.Z.; Gardner, J.W.; Udrea, F. MEMS Infrared Emitter and Detector for Capnography Applications. Procedia Eng. 2016, 168, 1204–1207. [Google Scholar] [CrossRef]
- Almeida, V.R.; Xu, Q.; Barrios, C.A.; Lipson, M. Guiding and Confining Light in Void Nanostructure. Opt. Lett. 2004, 29, 1209. [Google Scholar] [CrossRef]
- Lin, H.; Luo, Z.; Gu, T.; Kimerling, L.C.; Wada, K.; Agarwal, A.; Hu, J. Mid-Infrared Integrated Photonics on Silicon: A Perspective. Nanophotonics 2017, 7, 393–420. [Google Scholar] [CrossRef]
- Hu, T.; Dong, B.; Luo, X.; Liow, T.-Y.; Song, J.; Lee, C.; Lo, G.-Q. Silicon Photonic Platforms for Mid-Infrared Applications [Invited]. Photonics Res. 2017, 5, 417. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Yue, G.; Chen, W.; Xing, Z.; Wang, J.; Wong, W.R.; Cheng, Z.; Set, S.Y.; Senthil Murugan, G.; Wang, X.; et al. On-Chip Optical Gas Sensors Based on Group-IV Materials. ACS Photonics 2020, 7, 2923–2940. [Google Scholar] [CrossRef]
- Su, P.; Han, Z.; Kita, D.; Becla, P.; Lin, H.; Deckoff-Jones, S.; Richardson, K.; Kimerling, L.C.; Hu, J.; Agarwal, A. Monolithic On-Chip Mid-IR Methane Gas Sensor with Waveguide-Integrated Detector. Appl. Phys. Lett. 2019, 114, 051103. [Google Scholar] [CrossRef] [Green Version]
- Alberti, S.; Datta, A.; Jágerská, J. Integrated Nanophotonic Waveguide-Based Devices for IR and Raman Gas Spectroscopy. Sensors 2021, 21, 7224. [Google Scholar] [CrossRef]
- Vlk, M.; Datta, A.; Alberti, S.; Yallew, H.D.; Mittal, V.; Murugan, G.S.; Jágerská, J. Extraordinary Evanescent Field Confinement Waveguide Sensor for Mid-Infrared Trace Gas Spectroscopy. Light Sci. Appl. 2021, 10, 26. [Google Scholar] [CrossRef]
- Butt, M.A.; Degtyarev, S.A.; Khonina, S.N.; Kazanskiy, N.L. An Evanescent Field Absorption Gas Sensor at Mid-IR 3.39 Μm Wavelength. J. Mod. Opt. 2017, 64, 1892–1897. [Google Scholar] [CrossRef] [Green Version]
- Baehr-Jones, T.; Spott, A.; Ilic, R.; Spott, A.; Penkov, B.; Asher, W.; Hochberg, M. Silicon-on-Sapphire Integrated Waveguides for the Mid-Infrared. Opt. Express 2010, 18, 12127. [Google Scholar] [CrossRef] [Green Version]
- Ottonello-Briano, F.; Errando-Herranz, C.; Rödjegård, H.; Martin, H.; Sohlström, H.; Gylfason, K.B. Carbon Dioxide Absorption Spectroscopy with a Mid-Infrared Silicon Photonic Waveguide. Opt. Lett. 2020, 45, 109–112. [Google Scholar] [CrossRef] [Green Version]
- Ranacher, C.; Consani, C.; Vollert, N.; Tortschanoff, A.; Bergmeister, M.; Grille, T.; Jakoby, B. Characterization of Evanescent Field Gas Sensor Structures Based on Silicon Photonics. IEEE Photonics J. 2018, 10, 2700614. [Google Scholar] [CrossRef]
- Lim, J.; Shim, J.; Geum, D.-M.; Kim, S. Experimental Demonstration of Germanium-on-Silicon Slot Waveguides at Mid-Infrared Wavelength. IEEE Photonics J. 2022, 14, 582870. [Google Scholar] [CrossRef]
- Gutierrez-Arroyo, A.; Baudet, E.; Bodiou, L.; Nazabal, V.; Rinnert, E.; Michel, K.; Bureau, B.; Colas, F.; Charrier, J. Theoretical Study of an Evanescent Optical Integrated Sensor for Multipurpose Detection of Gases and Liquids in the Mid-Infrared. Sens. Actuators B Chem. 2017, 242, 842–848. [Google Scholar] [CrossRef]
- Kischkat, J.; Peters, S.; Gruska, B.; Semtsiv, M.; Chashnikova, M.; Klinkmüller, M.; Fedosenko, O.; Machulik, S.; Aleksandrova, A.; Monastyrskyi, G.; et al. Mid-Infrared Optical Properties of Thin Films of Aluminum Oxide, Titanium Dioxide, Silicon Dioxide, Aluminum Nitride, and Silicon Nitride. Appl. Opt. 2012, 51, 6789–6798. [Google Scholar] [CrossRef]
- Philipp, H.R. Optical Properties of Silicon Nitride. J. Electrochem. Soc. 1973, 120, 295. [Google Scholar] [CrossRef]
- Consani, C.; Dubois, F.; Auböck, G. Figures of Merit for Mid-IR Evanescent-Wave Absorption Sensors and Their Simulation by FEM Methods. Opt. Express 2021, 29, 9723. [Google Scholar] [CrossRef]
- Kita, D.M.; Michon, J.; Johnson, S.G.; Hu, J. Are Slot and Sub-Wavelength Grating Waveguides Better than Strip Waveguides for Sensing? Optica 2018, 5, 1046. [Google Scholar] [CrossRef]
- Zengzhi, H.; Zhang, Y.; Zeng, C.; Li, D.; Nisar, M.S.; Yu, J.; Xia, J. High Confinement Factor Ridge Slot Waveguide for Optical Sensing. IEEE Photonics Technol. Lett. 2015, 27, 2395–2398. [Google Scholar] [CrossRef]
- Steglich, P.; Villringer, C.; Dümecke, S.; Padilla Michel, Y.; Casalboni, M.; Schrader, S. Silicon-on-Insulator Slot-Waveguide Design Trade-Offs. In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology, Berlin, Germany, 13–15 March 2015; SCITEPRESS—Science and and Technology Publications: Berlin, Germany, 2015; pp. 47–52. [Google Scholar]
- Fohrmann, L.S.; Petrov, A.Y.; Lang, S.; Jalas, D.; Krauss, T.F.; Eich, M. Single Mode Thermal Emission. Opt. Express 2015, 23, 27672–27682. [Google Scholar] [CrossRef]
- Consani, C.; Dubois, F.; Thakkar, P.; Stocker, G.; Fleury, C.; Dao, T.D.; Zhai, Y.; Pühringer, G.; Jannesari, R.; Saeidi, P.; et al. A High Sensitivity Multi-Slot Silicon Waveguide for Mid-IR Evanescent-Field Sensing. Opt. Lett. 2022. submitted. [Google Scholar]
- Subramanian, A.Z.; Ryckeboer, E.; Dhakal, A.; Peyskens, F.; Malik, A.; Kuyken, B.; Zhao, H.; Pathak, S.; Ruocco, A.; De Groote, A.; et al. Silicon and Silicon Nitride Photonic Circuits for Spectroscopic Sensing On-a-Chip [Invited]. Photonics Res. 2015, 3, B47. [Google Scholar] [CrossRef] [Green Version]
- Pühringer, G.; Consani, C.; Jannesari, R.; Fleury, C.; Dubois, F.; Spettel, J.; Dao, T.D.; Stocker, G.; Grille, T.; Jakoby, B. Design of a Slab Tamm Plasmon Resonator Coupled to a Multistrip Array Waveguide for the Mid Infrared. Sensors 2022, 22, 2968. [Google Scholar] [CrossRef]
- Edwards, D.F.; Ochoa, E. Infrared Refractive Index of Silicon. Appl. Opt. 1980, 19, 4130–4131. [Google Scholar] [CrossRef]
- Luke, K.; Okawachi, Y.; Lamont, M.R.E.; Gaeta, A.L.; Lipson, M. Broadband Mid-Infrared Frequency Comb Generation in a Si3N4 Microresonator. Opt. Lett. 2015, 40, 4823–4826. [Google Scholar] [CrossRef]
- Ranacher, C.; Consani, C.; Tortschanoff, A.; Jannesari, R.; Bergmeister, M.; Grille, T.; Jakoby, B. Mid-Infrared Absorption Gas Sensing Using a Silicon Strip Waveguide. Sens. Actuators Phys. 2018, 277, 117–123. [Google Scholar] [CrossRef]
- Gao, F.; Ylinen, S.; Kainlauri, M.; Kapulainen, M. Smooth Silicon Sidewall Etching for Waveguide Structures Using a Modified Bosch Process. J. Micro/Nanolithography MEMS MOEMS 2014, 13, 013010. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Y.; Cao, G.; Jia, X.; Zhang, F. Reduction of Sidewall Roughness in Silicon-on-Insulator Rib Waveguides. Appl. Surf. Sci. 2006, 252, 5071–5075. [Google Scholar] [CrossRef]
- Lee, M.-C.M.; Wu, M.C. Thermal Annealing in Hydrogen for 3-D Profile Transformation on Silicon-on-Insulator and Sidewall Roughness Reduction. J. Microelectromech. Syst. 2006, 15, 338–343. [Google Scholar] [CrossRef]
- Lee, D.H.; Choo, S.J.; Jung, U.; Lee, K.W.; Kim, K.W.; Park, J.H. Low-Loss Silicon Waveguides with Sidewall Roughness Reduction Using a SiO2hard Mask and Fluorine-Based Dry Etching. J. Micromech. Microeng. 2014, 25, 015003. [Google Scholar] [CrossRef]
- Consani, C.; Ranacher, C.; Tortschanoff, A.; Grille, T.; Irsigler, P.; Jakoby, B. Mid-Infrared Photonic Gas Sensing Using a Silicon Waveguide and an Integrated Emitter. Sens. Actuators B Chem. 2018, 274, 60–65. [Google Scholar] [CrossRef]


| Simulation (First TE Mode) | Experiment | |||||
|---|---|---|---|---|---|---|
| Waveguide | (cm−1) | (cm−1) | ||||
| Strip | 0.09 | 0.38 | 3.97 | 0.15 ± 0.01 * | 0.97 ± 0.13 * | 6.5 ± 1.0 * |
| A | 0.39 | 0.92 | 2.36 | 0.37 ± 0.02 | 2.7 ± 0.5 | 7.3 ± 1.4 |
| B | 0.23 | 0.57 | 2.50 | 0.22 ± 0.01 | 1.6 ± 0.6 | 7.3 ± 2.7 |
| C | 0.18 | 0.48 | 2.67 | 0.17 ± 0.01 | 1.4 ± 0.1 | 8.2 ± 0.8 |
| D | 0.16 | 0.48 | 3.00 | 0.16 ± 0.01 | 1.4 ± 0.4 | 9.0 ± 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thakkar, P.; Fleury, C.; Stocker, G.; Dubois, F.; Dao, T.D.; Jannesari, R.; Saeidi, P.; Pühringer, G.; Ostermann, T.; Grille, T.; et al. Coupled Strip-Array Waveguides for Integrated Mid-IR Gas Sensing. Photonics 2023, 10, 55. https://doi.org/10.3390/photonics10010055
Thakkar P, Fleury C, Stocker G, Dubois F, Dao TD, Jannesari R, Saeidi P, Pühringer G, Ostermann T, Grille T, et al. Coupled Strip-Array Waveguides for Integrated Mid-IR Gas Sensing. Photonics. 2023; 10(1):55. https://doi.org/10.3390/photonics10010055
Chicago/Turabian StyleThakkar, Pooja, Clément Fleury, Gerald Stocker, Florian Dubois, Thang Duy Dao, Reyhaneh Jannesari, Parviz Saeidi, Gerald Pühringer, Thomas Ostermann, Thomas Grille, and et al. 2023. "Coupled Strip-Array Waveguides for Integrated Mid-IR Gas Sensing" Photonics 10, no. 1: 55. https://doi.org/10.3390/photonics10010055
APA StyleThakkar, P., Fleury, C., Stocker, G., Dubois, F., Dao, T. D., Jannesari, R., Saeidi, P., Pühringer, G., Ostermann, T., Grille, T., Jakoby, B., Tortschanoff, A., & Consani, C. (2023). Coupled Strip-Array Waveguides for Integrated Mid-IR Gas Sensing. Photonics, 10(1), 55. https://doi.org/10.3390/photonics10010055





