Broadband Second Harmonic Generation in a z-Cut Lithium Niobate on Insulator Waveguide Based on Type-I Modal Phase Matching
Abstract
:1. Introduction
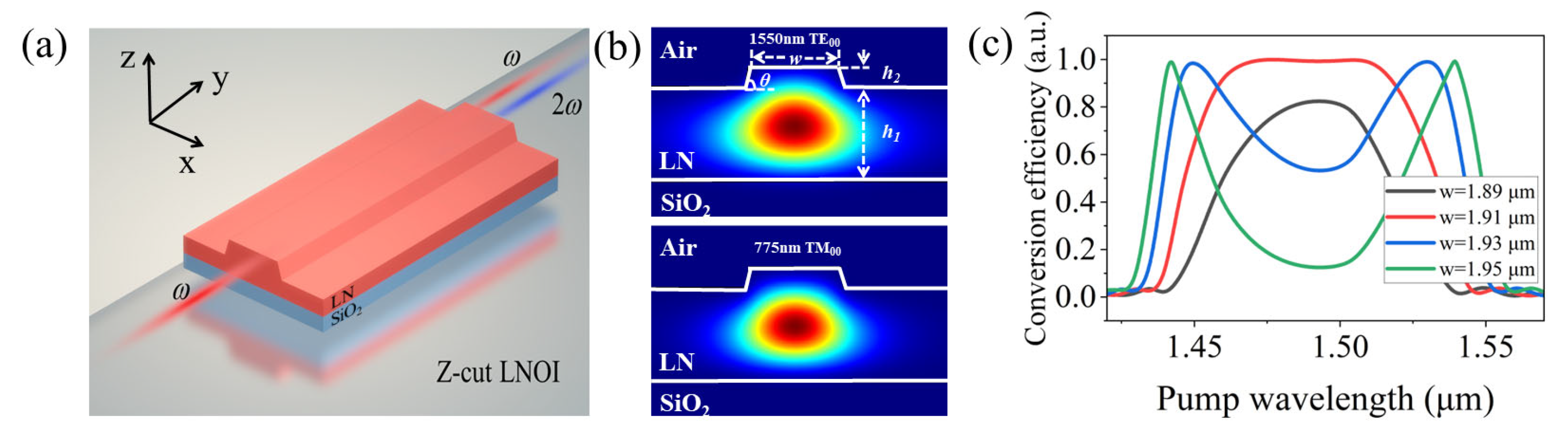
2. Theoretical Design
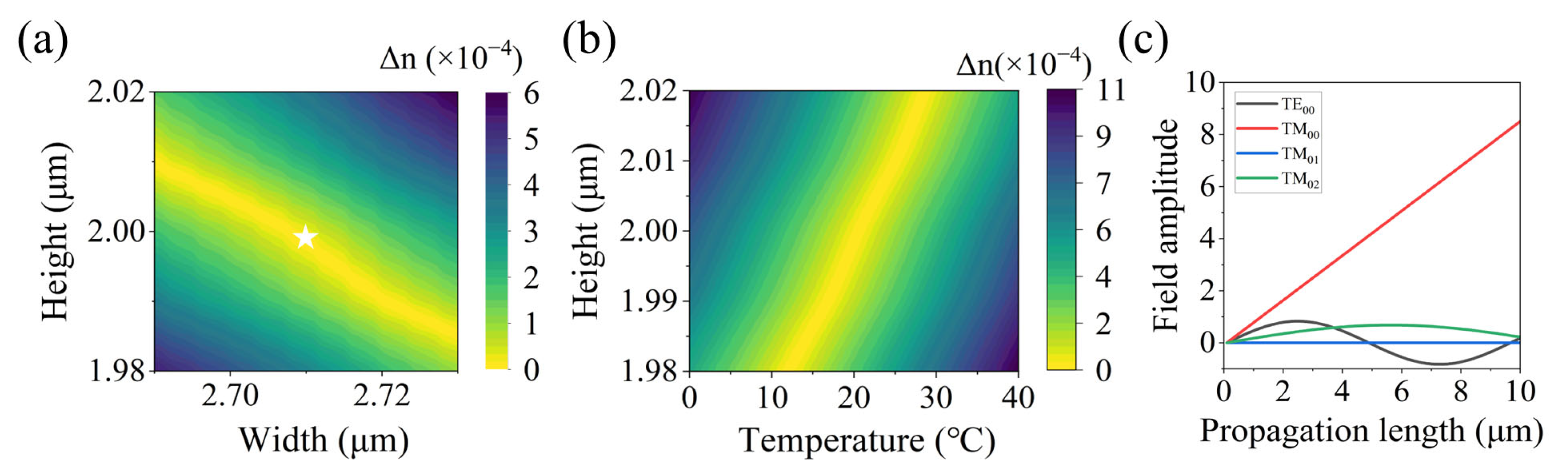
3. Broadband SHG Performance and the Spectral Tuning Capability
4. The Simulation Results of Ridge Waveguide
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, M.; Ling, J.; He, Y.; Javid, U.; Xue, S.; Lin, Q. Lithium niobate photonic-crystal electro-optic modulator. Nat. Commun. 2020, 11, 4123. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, H.; Liu, L.; Shang, J.; Yu, L.; Li, K.; Dong, J.; Qiu, W.; Guan, H.; Lu, H.; et al. An Optical Switch Based on Electro-Optic Mode Deflection in Lithium Niobate Waveguide. IEEE Photonics Technol. Lett. 2020, 20, 1295–1298. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, M.; Li, Y.; Shang, J.; Li, K.; Qiu, W.; Dong, J.; Guan, H.; Chen, Z.; Lu, H. Highly Efficient Second Harmonic Generation of Thin Film Lithium Niobate Nanograting near Bound States in the Continuum. Nanotechnology 2021, 32, 325207. [Google Scholar] [CrossRef] [PubMed]
- Weigand, H.; Vogler-Neuling, V.; Escalé, M.; Pohl, D.; Richter, F.; Karvounis, A.; Timpu, F.; Grange, R. Enhanced Electro-Optic Modulation in Resonant Metasurfaces of Lithium Niobate. ACS Photonics 2021, 8, 3004–3009. [Google Scholar] [CrossRef]
- Zaske, S.; Lenhard, A.; Keßler, C.; Kettler, J.; Hepp, C.; Arend, C.; Albrecht, R.; Schulz, W.; Jetter, M.; Michler, P.; et al. Visible-to-telecom quantum frequency conversion of light from a single quantum emitter. Phys. Rev. Lett. 2012, 109, 147404. [Google Scholar] [CrossRef] [Green Version]
- Lv, J.; Cheng, Y.; Aldana, J.; Hao, X.; Chen, F. Femtosecond Laser Writing of Optical-Lattice-Like Cladding Structures for Three-Dimensional Waveguide Beam Splitters in LiNbO3 Crystal. J. Light. Technol. 2016, 34, 3587–3591. [Google Scholar] [CrossRef]
- Lv, J.; Cheng, Y.; Yuan, W.; Hao, X.; Chen, F. Three-dimensional femtosecond laser fabrication of waveguide beam splitters in LiNbO3 crystal. Opt. Mater. Express 2015, 5, 1274–1280. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Stern, B.; Lipson, M.; Loncar, M. Nanophotonic lithium niobate electro-optic modulators. Opt. Express 2018, 26, 1547–1555. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Liang, Y.; Liu, Z.; Chu, W.; Zhang, H.; Yin, D. On-chip integrated waveguide amplifiers on Erbium-doped thin film lithium niobate on insulator. Laser Photonics Rev. 2021, 15, 21000308. [Google Scholar] [CrossRef]
- Beeck, C.; Mayor, F.M.; Cuyvers, S.; Poelman, S.; Herrmann, J.; Atalar, O.; McKenna, T.; Haq, B.; Jiang, W.; Witmer, J.; et al. III/V-on-lithium niobate amplifiers and lasers. Optica 2021, 8, 1288–1289. [Google Scholar] [CrossRef]
- Li, T.; Wua, K.; Cai, M.; Xiao, Z.; Zhang, H.; Li, C.; Xiang, J.; Huang, Y.; Chen, J. A single-frequency single-resonator laser on erbium-doped lithium niobate on insulator. APL Photonics 2021, 6, 101301. [Google Scholar] [CrossRef]
- Hu, Y.; Yu, M.; Buscaino, B.; Sinclair, N.; Zhu, D.; Shams-Ansari, A.; Shao, L.; Zhang, M.; Kahn, J.; Loncar, M. High-efficiency and broadband electro-optic frequency combs using coupled lithium-niobate microresonators. In Conference on Lasers and Electro-Optics; Optica Publishing Group: Washington, DC, USA, 2021. [Google Scholar]
- Hu, Y.; Yu, M.; Buscaino, B.; Sinclair, N.; Di Zhu, D.; Cheng, R.; Shams-Ansari, A.; Shao, L.; Zhang, M.; Kahn, J.M.; et al. High-efficiency and broadband on-chip electro-optic frequency comb generators. Nat. Photonics 2022, 16, 679–685. [Google Scholar] [CrossRef]
- Shams-Ansari, A.; Yu, M.; Chen, Z.; Reimer, C.; Zhang, M.; Picqué, N.; Lončar, M. Thin-film lithium-niobate electro-optic platform for spectrally tailored dual-comb spectroscopy. Commun. Phys. 2022, 5, 88. [Google Scholar] [CrossRef]
- Zhao, J.; Ma, C.; Rüsing, M.; Mookherjea, S. High Quality Entangled Photon Pair Generation in Periodically Poled Thin-Film Lithium Niobate Waveguides. Phys. Rev. Lett. 2020, 124, 163603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xue, G.; Niu, Y.; Liu, X.; Duan, J.; Chen, W.; Pan, Y.; Jia, K.; Wang, X.; Liu, H.; Liu, Y.; et al. Ultrabright Multiplexed Energy-Time-Entangled Photon Generation from Lithium Niobate on Insulator Chip. Phys. Rev. Appl. 2021, 15, 064059. [Google Scholar] [CrossRef]
- Lomonte, E.; Wolff, M.A.; Beutel, F.; Ferrari, S.; Schuck, C.; Pernice, W.H.; Lenzini, F. Single-photon detection and cryogenic reconfigurability in lithium niobate nanophotonic circuits. Nat. Commun. 2021, 12, 6847. [Google Scholar] [CrossRef]
- Fang, B.; Li, H.; Zhu, S.; Li, T. Second-harmonic generation and manipulation in lithium niobate slab waveguides by grating metasurfaces. Photonics Res. 2020, 8, 1296–1300. [Google Scholar] [CrossRef]
- Boes, A.; Chang, L.; Nguyen, T.; Ren, G.; Bowers, J.; Mitchell, A. Efficient second harmonic generation in lithium niobate on insulator waveguides and its pitfalls. J. Phys. Photonics 2021, 3, 012008. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Z.; Qiu, W.; Dong, J.; Guan, H.; Lu, H. Recent progress of second harmonic generation based on thin film lithium niobate [Invited]. Chin. Opt. Lett. 2021, 19, 060012. [Google Scholar] [CrossRef]
- Boyd, R. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Fang, B.; Gao, S.; Wang, Z.; Zhu, S.; Li, T. Efficient second harmonic generation in silicon covered lithium niobate waveguides. Chin. Opt. Lett. 2021, 19, 060004. [Google Scholar] [CrossRef]
- Peng, L.; Hong, L.; Chen, B.; He, P.; Li, Z. Robust modal phase matching in subwavelength x-cut and z-cut lithium niobate thin-film waveguides. Chin. Opt. Lett. 2021, 19, 071902. [Google Scholar] [CrossRef]
- Zhang, B.; Li, L.; Wang, L.; Chen, F. Second harmonic generation in femtosecond laser written lithium niobate waveguides based on birefringent phase matching. Opt. Mater. 2020, 107, 0925–3467. [Google Scholar] [CrossRef]
- Briggs, I.; Hou, S.; Cui, C.; Fan, L. Simultaneous type-I and type-II phase matching for second-order nonlinearity in integrated lithium niobate waveguide. Opt. Express 2021, 29, 26183–26190. [Google Scholar] [CrossRef]
- Masters, B.R.; Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Suntsov, S.; Rüter, C.; Brüske, D.; Kip, D. Watt-level 775 nm SHG with 70% conversion efficiency and 97% pump depletion in annealed/reverse proton exchanged diced PPLN ridge waveguides. Opt. Express 2021, 29, 11386–11393. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Zhou, W.; Ren, K.; Zhang, C.; Liu, X.; Xue, G.; Duan, J.; Cai, X.; Hu, X.; Gong, Y.; et al. Effect of dimension variation for second-harmonic generation in lithium niobate on insulator waveguide [Invited]. Chin. Opt. Lett. 2021, 19, 060015. [Google Scholar] [CrossRef]
- Niu, Y.; Yang, L.; Guo, D.; Chen, Y.; Li, X.; Zhao, G.; Hu, X. Efficient 671 nm red light generation in annealed proton-exchanged periodically poled LiNbO3 waveguides. Chin. Opt. Lett. 2020, 18, 111902. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, Y.; Qiu, J.; Tang, Y.; Ding, T.; Liu, S.; Zheng, Y.; Chen, X. Highly tunable birefringent phase-matched second-harmonic generation in an angle-cut lithium niobate-on-insulator ridge waveguide. Opt. Lett. 2022, 47, 1081–1084. [Google Scholar] [CrossRef]
- Chang, L.; Boes, A.; Guo, X.; Spencer, D.; Kennedy, M.; Peters, J.; Volet, N.; Chiles, J.; Kowligy, A.; Nader, N.; et al. Heterogeneously integrated GaAs waveguides on insulator for efficient frequency conversion. Laser Photonics Rev. 2018, 12, 1800149. [Google Scholar] [CrossRef] [Green Version]
- Bruch, A.; Liu, X.; Guo, X.; Surya, J.; Gong, Z.; Zhang, L.; Wang, J.; Yan, J.; Tang, H. 17,000%/W second-harmonic conversion efficiency in single-crystalline aluminum nitride ring resonators. Appl. Phys. Lett. 2018, 113, 131102. [Google Scholar] [CrossRef] [Green Version]
- Luo, R.; He, Y.; Liang, H.; Li, M.; Ling, J.; Lin, Q. Optical parametric generation in a lithium niobate microring with modal phase matching. Phys. Rev. Appl. 2019, 11, 034026. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Li, G.; Ge, L.; Zhu, B.; Hu, M.; Chen, X. Multiple-mode phase matching in a single-crystal lithium niobate waveguide for three-wave mixing. Chin. Opt. Lett. 2017, 15, 091901. [Google Scholar]
- Luo, R.; He, Y.; Liang, H.; Li, M.; Lin, Q. Highly tunable efficient second-harmonic generation in a lithium niobate nanophotonic waveguide. Optica 2018, 5, 1006–1011. [Google Scholar] [CrossRef]
- Luo, R.; He, Y.; Liang, H.; Li, M.; Lin, Q. Semi-nonlinear nanophotonic waveguides for highly efficient second-harmonic generation. Laser Photonics Rev. 2019, 13, 1800288. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Li, L.; Zhang, X.; Chen, F. Type I Phase Matching in Thin Film of Lithium Niobate on Insulator. Results Phys. 2020, 16, 103011. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhong, H.; Ning, M.; Fang, B.; Li, L.; Cheng, Y. Broadband Second Harmonic Generation in a z-Cut Lithium Niobate on Insulator Waveguide Based on Type-I Modal Phase Matching. Photonics 2023, 10, 80. https://doi.org/10.3390/photonics10010080
Wang C, Zhong H, Ning M, Fang B, Li L, Cheng Y. Broadband Second Harmonic Generation in a z-Cut Lithium Niobate on Insulator Waveguide Based on Type-I Modal Phase Matching. Photonics. 2023; 10(1):80. https://doi.org/10.3390/photonics10010080
Chicago/Turabian StyleWang, Changwen, Haozong Zhong, Minghao Ning, Bin Fang, Lin Li, and Ya Cheng. 2023. "Broadband Second Harmonic Generation in a z-Cut Lithium Niobate on Insulator Waveguide Based on Type-I Modal Phase Matching" Photonics 10, no. 1: 80. https://doi.org/10.3390/photonics10010080
APA StyleWang, C., Zhong, H., Ning, M., Fang, B., Li, L., & Cheng, Y. (2023). Broadband Second Harmonic Generation in a z-Cut Lithium Niobate on Insulator Waveguide Based on Type-I Modal Phase Matching. Photonics, 10(1), 80. https://doi.org/10.3390/photonics10010080





