Al2O3/GeO2/P2O5/F-Doped Silica Large-Mode-Area Optical Fibers for High-Power Single-Frequency Radiation Delivery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Acousto-Optical Properties of the Dopants
2.2. Calculation of the SBS Gain Spectrum
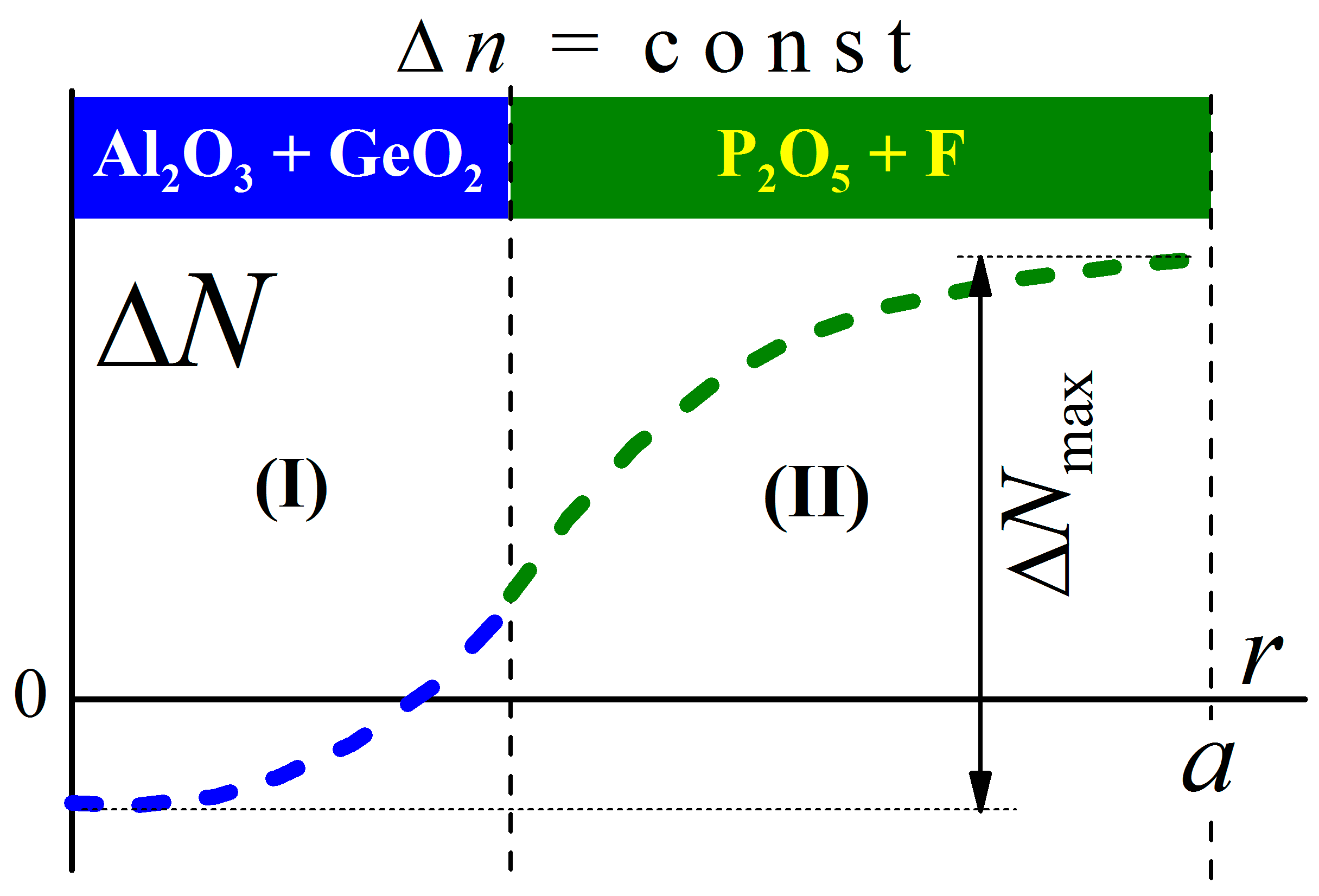
2.3. The Model of the SBS Suppressed LMA Fiber
3. Results
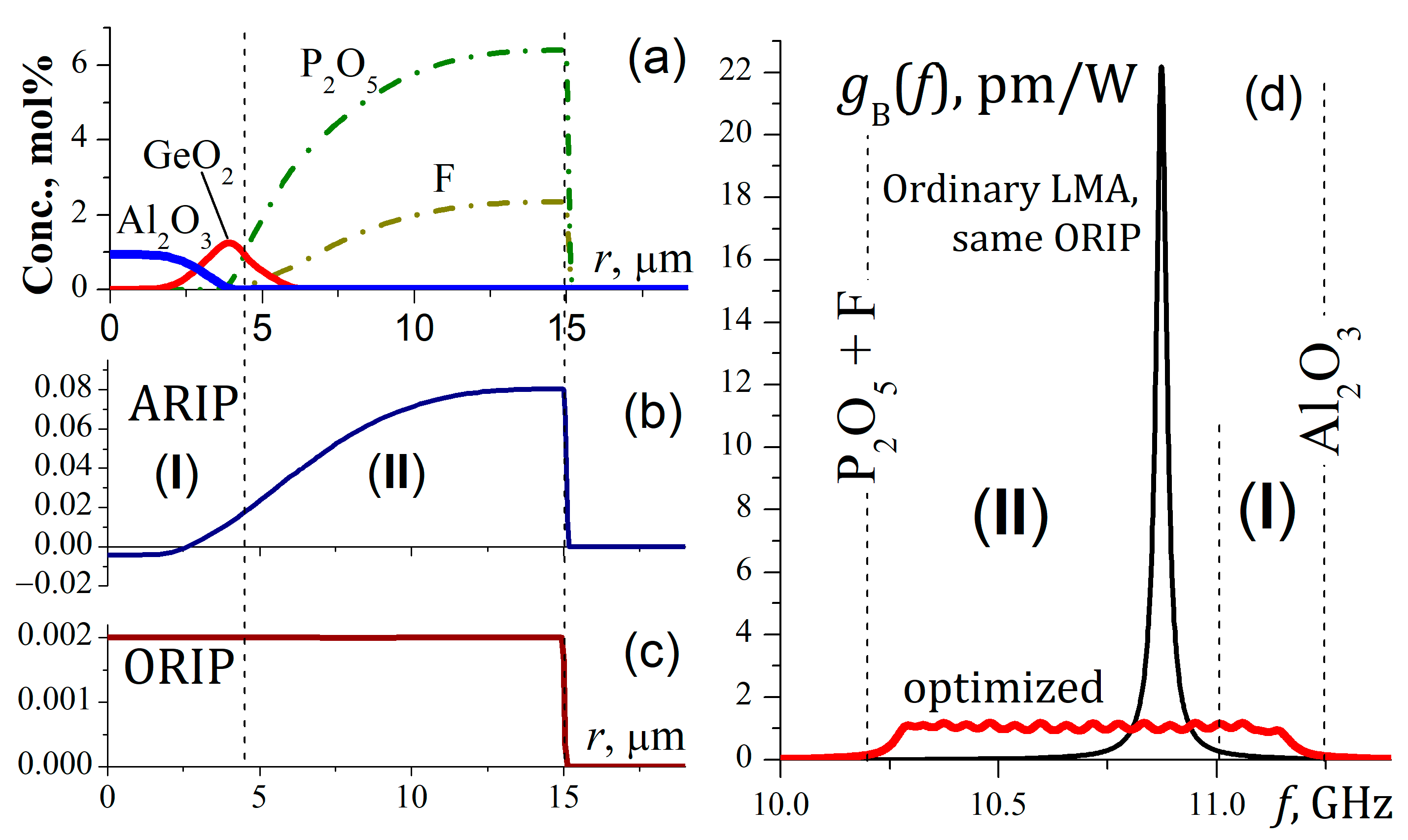
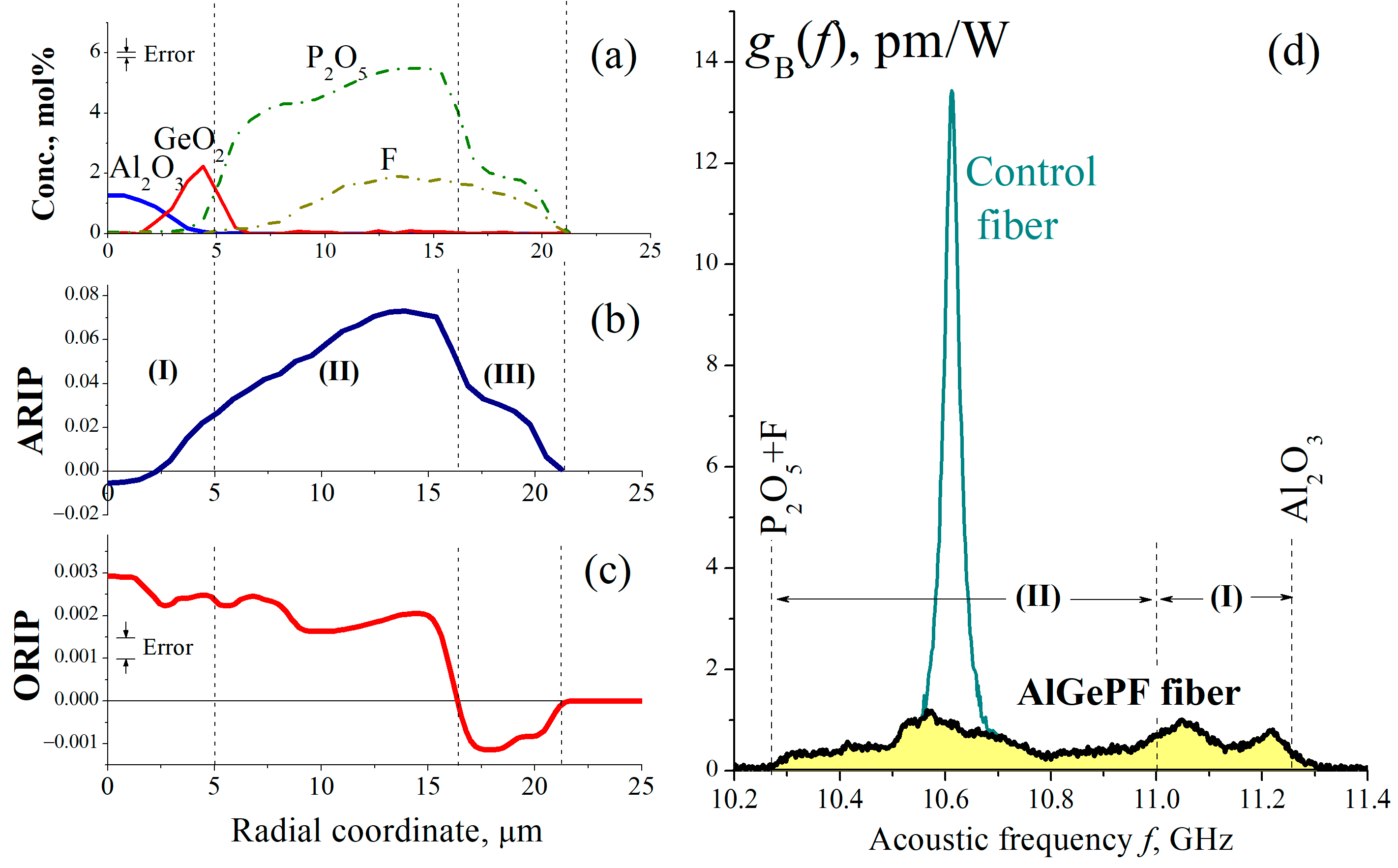
3.1. Fabricated Fiber
3.2. Measurements of the SBS Gain Spectrum
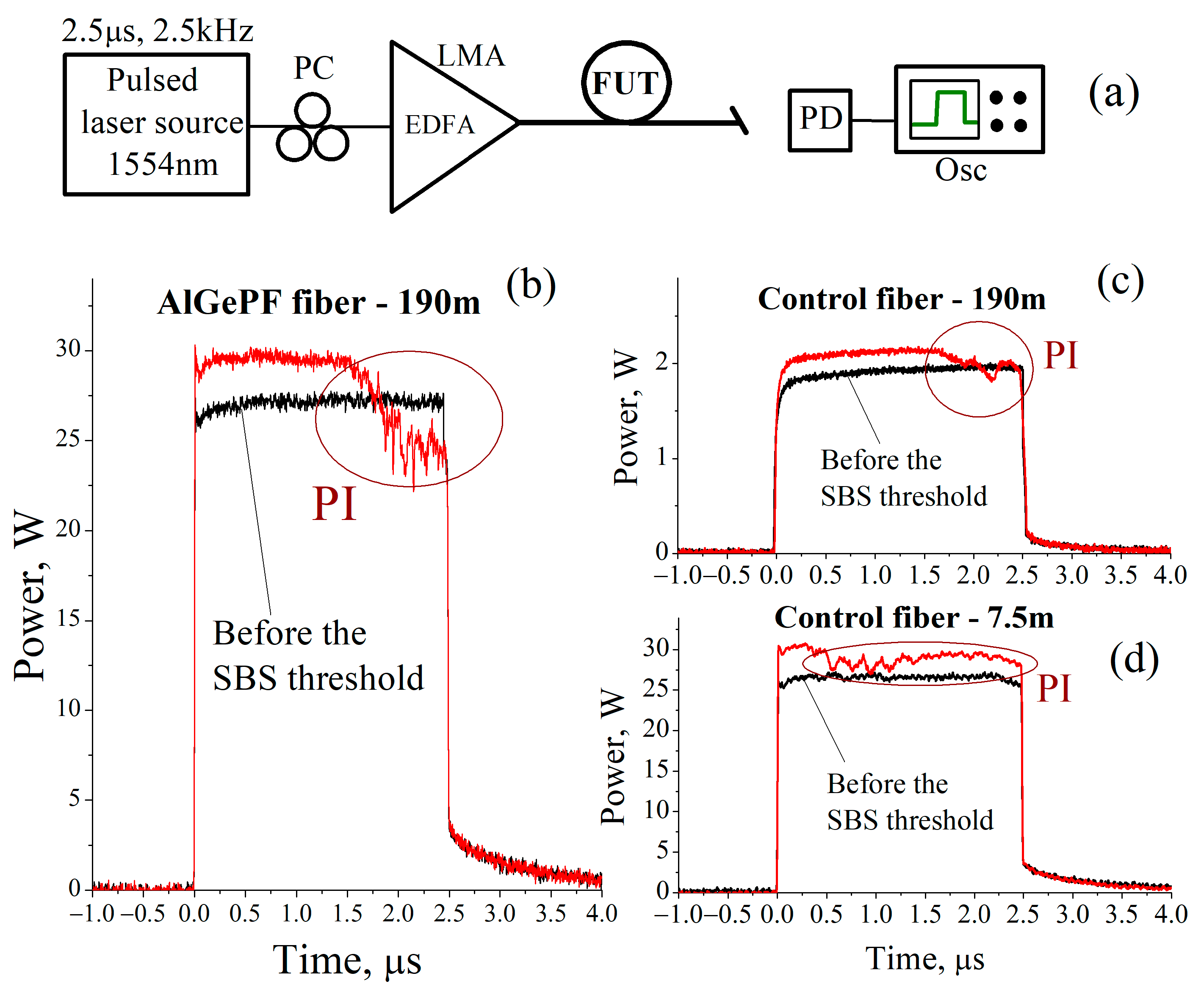
3.3. Measurements of the SBS Power Threshold
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Canat, G.; Lombard, L.; Le Gouët, J.; Dolfi-Bouteyre, A. Kilowatt level transform-limited 150 ns monolithic pulsed fiber laser emitting in the L band. In Proceedings of the Conference on Lasers and Electro-Optics—International Quantum Electronics Conference, Munich, Germany, 12–16 May 2013. paper CJ_5_6. [Google Scholar]
- Kotov, L.; Likhachev, M.; Bubnov, M.; Paramonov, V.; Belovolov, M.; Lipatov, D.; Guryanov, A. Record-peak-power all-fiber single-frequency 1550 nm laser. Laser Phys. Lett. 2014, 11, 095102–095107. [Google Scholar] [CrossRef]
- Huang, Y.; Pan, P.; Wang, Z.; Tian, J.; Li, D.; Gong, M. 2.19 kW narrow linewidth FBG-based MOPA configuration fiber laser. Opt. Expr. 2019, 27, 3136–3145. [Google Scholar] [CrossRef]
- Kerttula, J.; Filippov, V.; Chamorovskii, Y.; Ustimchik, V.; Golant, K.; Okhotnikov, O. Tapered fiber amplifier with high gain and output power. Laser Phys. 2012, 22, 1734–1738. [Google Scholar] [CrossRef]
- Mermelstein, M.; Andrejco, M.; Fini, J.; Yablon, A.; Headley, C.; DiGiovanni, D. 11.2 dB SBS gain suppression in a large mode area Yb-doped optical fiber. Proc. SPIE 2008, 6873, 68730N1–68730N7. [Google Scholar]
- Zhang, X.; Diao, W.; Liu, Y.; Liu, J.; Hou, X.; Chen, W. Single-frequency polarized eye-safe all-fiber laser with peak power over kilowatt. Appl. Phys. B 2014, 115, 123–127. [Google Scholar] [CrossRef]
- Lombard, L.; Dolfi-Bouteyre, A.; Besson, C.; Augère, B.; Bourdon, P.; Durécu, A.; Goular, D.; Le Gouët, J.; Planchat, C.; Renard, W.; et al. Long range wind lidars based on novel high spectral brilliance all-fibered sources. Proc. SPIE 2015, 9645, 96450B1–96450B12. [Google Scholar]
- Feng, Y.; Harish, A.; Feng, Y.; Zhao, N.; Nillson, J. Simulation on thermal load gradient mitigation with auxiliary multi-seeds amplification in fiber amplifier. In Proceedings of the 7th EPS-QEOD Europhoton Conference: Solid State, Fibre, and Waveguide Coherent Light Sources, Vienna, Austria, 21–26 August 2016. [Google Scholar]
- Dragic, P.; Liu, C.; Papen, G.; Galvanauskas, A. Optical fiber with an acoustic guiding layer for stimulated Brillouin scattering suppression. In Proceedings of the Conference on Lasers and Electro-Optics, Baltimore, MD, USA, 22–27 May 2005. paper CThZ3. [Google Scholar]
- Dragic, P. Acoustical-optical fibers for control of stimulated Brillouin scattering. In Proceedings of the 2006 Digest of the LEOS Summer Topical Meeting, Quebec City, QC, Canada, 17–19 July 2006; pp. 3–4. [Google Scholar]
- Li, M.; Chen, X.; Wang, J.; Gray, S.; Liu, A.; Demeritt, J.; Ruffin, A.; Crowley, A.; Walton, D.; Zenteno, L. Al/Ge co-doped large mode area fiber with high SBS threshold. Opt. Express 2007, 15, 8290–8299. [Google Scholar] [CrossRef] [PubMed]
- Thomas, P.; Lowell, N.; van Oriel, H.; Stegeman, G. Normal acoustic modes and Brillouin scattering in single-mode optical fibers. Phys. Rev. B 1979, 19, 4986–4998. [Google Scholar] [CrossRef]
- Jen, C.-K.; Safaai-Jazi, A.; Farnell, W. Leaky modes in weakly guiding fiber acoustic waveguides. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1986, 33, 634–643. [Google Scholar]
- Dong, L. Limits of stimulated Brillouin scattering suppression in optical fibers with transverse acoustic waveguide designs. J. Lightw. Technol. 2010, 28, 3156–3161. [Google Scholar]
- Yoo, S.; Codemard, C.; Jeong, Y.; Sahu, J.; Nilsson, J. Analysis and optimization of acoustic speed profiles with large transverse variations for mitigation of stimulated Brillouin scattering in optical fibers. Appl. Opt. 2010, 49, 1388–1399. [Google Scholar] [CrossRef] [PubMed]
- Tsvetkov, S.; Khudyakov, M.; Lobanov, A.; Lipatov, D.; Bubnov, M.; Guryanov, A.; Temyanko, V.; Likhachev, M. SBS gain suppression in a passive single-mode optical fiber by the multi-mode acoustic waveguide design. J. Lightw. Technol. 2021, 39, 592–599. [Google Scholar] [CrossRef]
- LMA-GDF-30_250-09M, LMA-GDF-30/250-09M, Matched Passive Double Clad, Optical Fiber. Available online: https://coherentinc.my.site.com/Coherent/specialty-optical-fibers/ (accessed on 1 January 2021).
- Lipatov, D.; Lobanov, A.; Guryanov, A.; Umnikov, A.; Abramov, A.; Khudyakov, M.; Likhachev, M.; Morozov, O. Fabrication and Characterization of Er/Yb Co-Doped Fluorophosphosilicate Glass Core Optical Fibers. Fibers 2021, 9, 15–25. [Google Scholar] [CrossRef]
- Jen, C.-K.; Neron, C.; Shang, A.; Abe, K.; Bonnell, L.; Kushibiki, J. Acoustic characterization of silica glasses. J. Am. Ceram. Soc. 1993, 76, 712–716. [Google Scholar] [CrossRef]
- Dragic, P.; Ballato, J.; Ballato, A.; Morris, S.; Hawkins, T.; Law, P.-C.; Ghosh, S.; Paul, M.C. Mass density and the Brillouin spectroscopy of aluminosilicate optical fibers. Opt. Mater. Express 2012, 2, 1641–1654. [Google Scholar] [CrossRef]
- Dragic, P.; Cavillon, M.; Ballato, J. The linear and nonlinear refractive index of amorphous Al2O3 deduced from aluminosilicate optical fibers. Int. J. Appl. Glass Sci. 2017, 9, 421–427. [Google Scholar] [CrossRef]
- Nakanishi, T.; Tanaka, M.; Hasegawa, T.; Hirano, M.; Okuno, T.; Onishi, M. Al2O3-SiO2 core highly nonlinear dispersion-shifted fiber with Brillouin gain suppression improved by 6.1 dB. Proc. ECOC 2006, 6, 17–18. [Google Scholar]
- Butov, O.V.; Golant, K.M.; Tomashuk, A.L.; van Stralen, M.J.N.; Breuls, A.H.E. Refractive index dispersion of doped silica for fiber optics. Opt. Comm. 2002, 213, 301–308. [Google Scholar] [CrossRef]
- Deroh, M.; Kibler, B.; Maillotte, H.; Sylvestre, T.; Beugnot, J. Large Brillouin gain in Germania-doped core optical fibers up to a 98 mol% doping level. Opt. Lett. 2018, 43, 4005–4008. [Google Scholar] [CrossRef]
- Koyamada, Y.; Sato, S.; Nakamura, S.; Sotobayashi, H.; Chujo, W. Simulating and designing Brillouin gain spectrum in singlemode fibers. J. Lightw. Technol. 2004, 22, 631–639. [Google Scholar] [CrossRef]
- Lagakos, N.; Bucaro, J.A.; Hughes, R. Acoustic sensitivity predictions of single-mode optical fibers using Brillouin scattering. Appl. Opt. 1980, 19, 3668–3670. [Google Scholar] [CrossRef] [PubMed]
- Yeniay, A.; Delavaux, J.-M.; Toulouse, J. Spontaneous and stimulated Brillouin scattering gain spectra in optical fibers. J. Lightw. Technol. 2002, 20, 1425–1432. [Google Scholar] [CrossRef]
- Dragic, P. Estimating the effect of Ge doping on the acoustic damping coefficient via a highly Ge-doped MCVD silica fiber. J. Opt. Soc. Am. B 2009, 26, 1614–1620. [Google Scholar] [CrossRef]
- Law, P.-C.; Liu, Y.-S.; Croteau, A.; Dragic, P.D. Acoustic coefficients of P2O5-doped silica fiber: Acoustic velocity, acoustic attenuation, and thermo-acoustic coefficient. Opt. Expr. 2011, 1, 686–699. [Google Scholar] [CrossRef]
- Bubnov, M.M.; Dianov, E.M.; Egorova, O.N.; Semjonov, S.L.; Guryanov, A.N.; Khopin, V.F.; DeLiso, E.M. Fabrication and investigation of single-mode highly Phosphorus-doped fibers for Raman lasers. Proc. SPIE Adv. Fiber Opt. 2000, 4083, 12–22. [Google Scholar]
- Fleming, J.W.; Wood, D.L. Refractive index dispersion and related properties in fluorine doped silica. Appl. Opt. 1983, 22, 3102–3104. [Google Scholar] [CrossRef]
- Guryanov, A.; Salganskii, M.; Khopin, V.; Kosolapov, A.; Semenov, S. High-aperture optical waveguides based on fluorine-doped silica glass. Inorg. Mater. 2009, 45, 823–826. [Google Scholar] [CrossRef]
- Agrawal, G. Nonlinear Fiber Optics, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 353–396. [Google Scholar]
- Kobyakov, A.; Kumar, S.; Chowdhury, D.Q.; Ruffin, A.B.; Sauer, M.; Bickham, S.R. Desing concept for optical fibers with enhanced SBS threshold. Opt. Expr. 2005, 13, 5338–5346. [Google Scholar] [CrossRef]
- Shibata, N.; Okamoto, K.; Azuma, Y. Longitudinal acoustic modes and Brillouin-gain spectra for GeO2-doped-core singlemode fibers. J. Opt. Soc. Am. B 1989, 6, 1167–1174. [Google Scholar] [CrossRef]
- DiGiovanni, D.; MacChesney, J.; Kometani, T. Structure and properties of silica containing aluminum and phosphorus near the AlPO4 join. J. Non-Crystal. Solids 1989, 113, 58–64. [Google Scholar] [CrossRef]
- Garus, D.; Krebber, K.; Schliep, F.; Gogolla, T. Distributed sensing technique based on Brillouin optical-fiber frequency-domain analysis. Opt. Lett. 1996, 21, 1402–1404. [Google Scholar] [CrossRef] [PubMed]
- Ippen, E.; Stolen, R. Stimulated Brillouin scattering in optical fibers. Appl. Phys. Lett. 1972, 21, 539–541. [Google Scholar] [CrossRef]
- Horiguchi, T.; Tateda, M.; Shibata, N.; Azuma, Y. Brillouin gain variation due to a polarization-state change of the pump or Stokes field in standard single-mode fibers. Opt. Lett. 1989, 14, 329–331. [Google Scholar] [CrossRef] [PubMed]


| Dopant, X | Rac,X, mol%−1 | Rop,X, mol%−1 | Kf, MHz/mol% at λ = 1.55 μm |
|---|---|---|---|
| Al2O3 | −4.5 × 10−3 [19,20,22] | 2.16 × 10−3 [20,21,22,23] | +50 |
| GeO2 | 7.9 × 10−3 [19,24,25,26,27,28] | 1.45 × 10−3 [23,24,26] | −87 |
| P2O5 | 9 × 10−3 [16,29] | 0.9 × 10−3 [29,30] | −99 |
| F | 9.4 × 10−3 [19,25] | −1.6 × 10−3 [31,32] | −107 |
| Fiber | ∆n | Core Radius, μm | Aeff, μm2 | λcutoff, μm | Losses@1.55 μm, dB/km |
|---|---|---|---|---|---|
| AlGePF | 0.002 | 15.5 | 370 | 3 | 2.7 (coiled on ∅11 cm) |
| Control | 0.0014 | 10 | 325 | 1.5 | 2 |
| Fiber | max gB, pm/W | L(Leff), m | ∆fB, MHz | Ppump, mW |
|---|---|---|---|---|
| AlGePF | 1.1 | 200 (187) | ~60 | 270 |
| Control | 13.4 | 52 (43.5) | 34 | 190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsvetkov, S.; Lobanov, A.; Lipatov, D.; Khudyakov, M.; Zaushitsyna, T.; Iskhakova, L.; Kotov, L.; Likhachev, M. Al2O3/GeO2/P2O5/F-Doped Silica Large-Mode-Area Optical Fibers for High-Power Single-Frequency Radiation Delivery. Photonics 2023, 10, 1150. https://doi.org/10.3390/photonics10101150
Tsvetkov S, Lobanov A, Lipatov D, Khudyakov M, Zaushitsyna T, Iskhakova L, Kotov L, Likhachev M. Al2O3/GeO2/P2O5/F-Doped Silica Large-Mode-Area Optical Fibers for High-Power Single-Frequency Radiation Delivery. Photonics. 2023; 10(10):1150. https://doi.org/10.3390/photonics10101150
Chicago/Turabian StyleTsvetkov, Sergey, Alexey Lobanov, Denis Lipatov, Maxim Khudyakov, Tatiana Zaushitsyna, Liudmila Iskhakova, Leonid Kotov, and Mikhail Likhachev. 2023. "Al2O3/GeO2/P2O5/F-Doped Silica Large-Mode-Area Optical Fibers for High-Power Single-Frequency Radiation Delivery" Photonics 10, no. 10: 1150. https://doi.org/10.3390/photonics10101150
APA StyleTsvetkov, S., Lobanov, A., Lipatov, D., Khudyakov, M., Zaushitsyna, T., Iskhakova, L., Kotov, L., & Likhachev, M. (2023). Al2O3/GeO2/P2O5/F-Doped Silica Large-Mode-Area Optical Fibers for High-Power Single-Frequency Radiation Delivery. Photonics, 10(10), 1150. https://doi.org/10.3390/photonics10101150





