1. Introduction
Recently, the optics and photonics community has been witnessing a renewed interest in multimode (MM) optical platforms [
1]. This has pushed researchers to take a broader look at systems like telecommunication links and mode-locked and Raman fiber lasers (RFL), for which single-mode fibers have been historically preferred. In particular, MM RFLs have attracted a great deal of interest owing to their extreme flexibility in terms of operating wavelengths [
2] and to the high efficiency in the conversion of multimode pump light into high-quality Stokes emission. As a matter of fact, recent studies have reported on the effect of brightness enhancement of the Stokes beam in graded-index (GRIN) MM RFLs [
3,
4]. Generally speaking, a proper investigation of the dynamics of optical beams in MM platforms has required the development of novel measurement techniques, like those of mode decomposition (MD). MD methods can be based on several approaches, like genetic algorithms [
5], phase modulation via spatial light modulators (SLM) [
6], and deep learning [
7,
8]. Remarkably, when applied to few-mode beams, the decomposing rate of the latter may be as high as a few hundred Hz, the speed-limiting factors being the camera performance and the computing resources. On the other hand, the SLM-based technique, which is known as the spatial correlation filtering (SCF) method, may require a much longer measurement time, during which the beam has to be stable. Still, SCF has a great advantage, i.e., its applicability is not limited by the number of modes. For this reason, SCF turned out to be extremely powerful in fundamental science. For instance, phase-only SLM devices were used for the MD of MM RFL beams, as well as for investigating the so-called Kerr beam self-cleaning effect [
9,
10,
11], and validating its description in the framework of optical thermodynamics [
12].
In spite of these successful examples, there is still room for improving MD methods in terms of speed, accuracy, and flexibility, e.g., using special mode bases. For instance, as it was used in [
11], the SCF method requires an acquisition time as long as several minutes, thus being unfit for the investigation of real-time mode distribution dynamics. As a matter of fact, real-time MD remains an urgent task, especially in the context of the investigation of transverse mode instability phenomena in high-power fiber lasers and amplifiers [
13,
14,
15,
16,
17]. In these cases, in fact, the correct interpretation of the mode distribution can only be achieved in an experimental way. In this regard, possible ways of MD multiplexing were proposed by different research groups. The general idea is to create a diffraction element that is able to split correlation signals for different modes in space; in this way, the amplitude and phase of more than one mode can be measured simultaneously. For example, it was shown that one can resolve eight modes at once by using specifically manufactured amplitude-phase mode analyzing elements [
18]. Since most SLMs are phase-only devices, the SCF method cannot be applied directly. However, it is well-known that by grouping pixels of SLM and forming so-called double-phase holograms (DPH), one can imitate amplitude modulation even with phase-only devices [
19]. In this regard, it has to be mentioned that a method developed directly for phase-only SLM was reported by Zhao et al. in 2019 [
20]. This is based on the encoding of a mode array into a hologram using a conjugate symmetric extension (CSE) method. In addition, the original SCF technique can also be multiplexed, as described in [
18]. Such a multiplexing method was successfully applied, for the first time, by Flamm et al. in 2012 to a beam composed of three modes [
6]. It should be noted that all aforementioned methods do not require larger computational resources and are limited only by the camera performance, so that, in principle, the decomposing rate can exceed 1 kHz for modern high-speed devices, regardless of the multiplexed mode number. But the more modes one would like to measure in parallel, the more complex a hologram should be encoded. To the best of our knowledge, limitations on the number of modes depending on the type of hologram have never been investigated.
In this work, we used numerical models to compare the above methods in terms of the accuracy of modal amplitude retrieval in a set of well-defined multimode beams. In order to make a representative sample of beams with a variety of modal content, a special algorithm of amplitude combination enumeration was developed. Compared to the case of a randomly generated set of amplitudes, which is used, for example, to prepare datasets in machine learning methods, our algorithm allows us to compare the accuracy of different MD methods in absolutely identical initial conditions and covers the space of all possible amplitude combinations uniformly. In particular, we considered the cases of three, six, and ten modes multiplexed in one hologram, allowing real-time measurements. These cases correspond to the previous investigations based on deep learning techniques [
7,
8] and to the number of modes for the firsts three principal quantum numbers for a GRIN fiber (namely, PQN
). Our results indicate that, among the SCF-based routines we tested, the most effective in terms of MD accuracy is the one based on a phase spatial correlation filter with the use of the Jacobi–Anger expansion.
2. Algorithm of Mode Combination Enumeration
First of all, we present an algorithm that allows us to obtain a reproducible set of mode amplitudes and cover the space of all possible combinations uniformly. Let us dub
the intensity of the
p-th mode with
, being
M the number of modes. Now, let us consider that each mode intensity may assume a value that belongs to a discrete set of values (levels of intensity). For the sake of simplicity, let us consider the following
n levels of intensity
:
Finally, let us neglect the phase associated with each mode, i.e., we suppose that all the modes have the same phase equal to zero. We make this assumption for several reasons: Not all methods considered here are able to retrieve phases, and to retrieve the phases it is necessary to retrieve the amplitudes first. To calculate inaccuracies we use the dot product between the initial and retrieved amplitude vectors, so that the phases do not contribute to the error in the result. With these conditions, we can define the set of admissible combinations of intensities
for the
M modes as
where the condition
must be fulfilled to ensure the intensity normalization to 1. The
components are considered intensities of modes forming the laser beam. The total number of combinations is derived through the permutation of balls and bars [
21]. The number of bars is taken as
(to obtain
M cells, which correspond to the number of modes to be considered). The number
p is taken as the number of balls in a cell (between two neighboring bars) and corresponds to the minimal portion of the mode intensity, defined by Equation (
1). At the same time, the total number of balls is constant and equal to
, since each ball corresponds to an addition to the intensity level of
. Consequently, to obtain the number of combinations of intensities, we need to divide the number of possible permutations of balls and bars by the number of permutations of identical elements. This gives
As a matter of fact, the set
consists of
equally spaced points located on the hyperplane described by the equation
. In order to sort (and thus enumerate) all those points, we consider a recursive algorithm. Let us consider the set
P of points from the set
projected along the vector
onto the plane formed by the other vectors. To determine the points of
lying on the hyperplane, we need to run through their projections and add another coordinate component to each point in the set
P in such a way that
, i.e.,
Hence, the set of projection points P for a given M is defined recursively. This allows a simple realization of the enumeration.
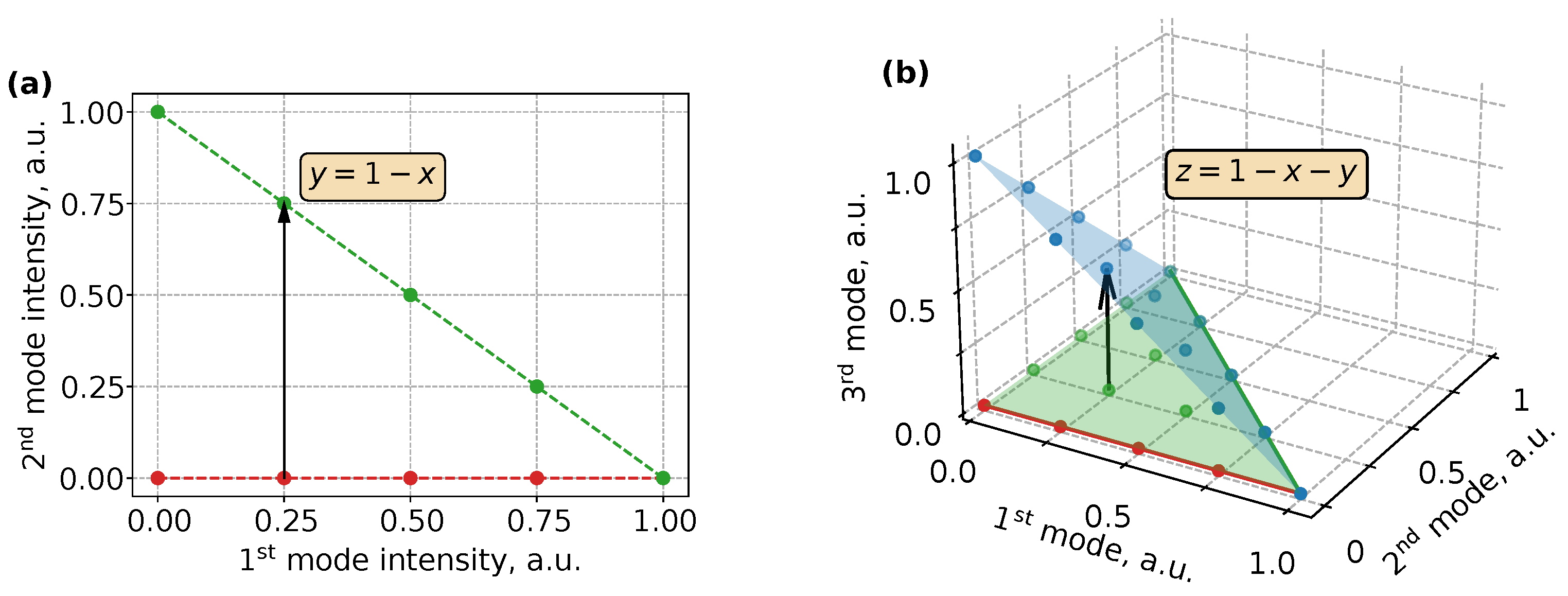
As an example of the working principle of the algorithm, we illustrate two simple cases where there are only
intensity levels. In the first case, which is depicted in
Figure 1a, we consider
modes. Here, the hyperplane with all possible combinations boils down to a straight line. However, in the second case, where we consider three modes (
), all combinations bounded by the line for
and marked by the green points (see
Figure 1b) have to be projected to the plane
to obtain the set of amplitudes that satisfies the condition
.
In the general case of
, the set
P is the points that have all coordinate components the same as the points in the set
P associated with
modes, but whose last coordinate component runs values from zero to maximal (as long as
is satisfied), i.e.,
In the following, this algorithm will be used further to compare different mode decomposition methods in absolutely equal initial conditions.
3. Parallel Mode Decomposition Methods Principle
The typical MD setup consists of an SLM, a lens that acts as a Fourier processor, and a CCD camera for recording the output transverse intensity distribution [
11]. Here, we simulate the beam from a set of amplitudes, multiply it to a phase transmission function, and compute the two-dimensional Fourier transform to take the intensity distribution in a camera plane. Next, we apply a retrieval procedure and compare the results and initial values.
The propagating laser beam
at the output of a multimode fiber can be represented as a sum of orthogonal normalized modes
with some complex coefficients
(complex amplitudes):
where
. Due to orthonormalization, the mode amplitude
is equal to a simple scalar product:
For a mode decomposition to be possible, it is crucial that this operation can be carried out in a fully optical way. Moreover, there are several algorithms to do this simultaneously for a set of modes using an SLM, which represent a diffraction optical element (DOE). The laser beam
falls on a DOE with a transmission function
recorded in it. In the general case, the field
E immediately after the DOE will have the following form:
The field
passes through the lens and is focused in the focal plane. It is a well-known fact that the field in the focal plane will be proportional to the Fourier image
of the original field
E:
where
is the coordinates in the frequency space (transverse component of wave vectors) and
is the coordinates in the focal plane. The coordinates in the focal plane
and the coordinates in the frequency space
are geometrically uniquely related, namely:
where
f is the focal distance of the lens and
is the modulus of the wave vector. Therefore, only the coordinates in the frequency space
are used below for convenience.
where
is a constant.
Thus, the objective of the mode decomposition method is to obtain the result of expression (
7) in a fully optical way by generating a hologram with an appropriate transmission function
. Next, we will briefly describe three different approaches.
3.1. Conjugate Symmetric Extension
The CSE method [
20] is based on the conjugate symmetric extension property [
22]. The method starts from a block mode matrix that is compiled for several modes
. For example, the symmetric conjugate extension
of a matrix
M, made of three elements
, i.e.,
is constructed by attaching to the matrix
M and its conjugate copy reflected along both axes, i.e.,
where ‘
’ means conjugation.
The elements of the discrete Fourier transform of a matrix of this form
are real numbers. The trick is that
F is written to the phase-only SLM, so that the transmission function in Equation (
24) takes the form
, where
H is
F scaled into the range
, as follows:
An example of such a phase mask is depicted in
Figure 2a.
Let us try to imagine the essence of the process of mode decomposition. The experimental setup consists of a 4f system with the SLM placed in the Fourier plane. When the initial field of a laser beam
U is focused by the Fourier lens onto the modulator, the field immediately after reflection from the SLM will have the form:
During further propagation, after passing through the Fourier lens, the field is expressed as follows:
where ‘∗’ means convolution. Thus, the intensity distribution in the camera plane (depicted in
Figure 3a) can be expressed in the following way:
This implies that the output field contains the convolutions of the original field with each block of the matrix
. One of them is enlarged and presented as an inset in
Figure 3a. Using the definition of convolution, it can be shown that at certain coordinates
x and
y the field
will be equal to the scalar product of
and the mode
. For other modes, the same will happen in other coordinates. Thus, by collecting the intensity in all those peculiar points, it is possible to obtain the amplitude of all modes simultaneously.
3.2. Double-Phase Hologram
As mentioned before, most of the MD tools rely on phase-only devices. Although these do not permit the direct modulation of the mode amplitude of a beam, it is possible to encode phase patterns to a multimode beam and still retrieve its amplitude-phase mode distribution [
19,
23]. To this goal, it is useful to define a macropixel as a 2 × 2 array of four real pixels of the SLM screen. In this case, the real transmittance function of a macropixel is the sum of the ideal amplitude-phase transmittance function
for this macropixel and a noise term, i.e.,
Note that here we are using a stepped form of the function
T, where the transmittance of the macropixel with index
is
. The basic idea of the method is to reduce the contribution of the noise term to the zeroth order of diffraction (near the optical axis of the lens) with a proper selection of additive phases at each of the four pixels. The transmission function
of a macropixel is expressed as:
The phase shifts
are chosen symmetrically here because this results in a symmetric noise distribution about the axis and, as a consequence, in a high signal-to-noise ratio (SNR) in the zero-order diffraction region:
From here, using the expression, one can obtain the final equations:
where
is the average phase of the macropixel with index
and
is the phase deviation inside it. It can be shown that the following modification of expression (22) leads to a higher SNR [
23]:
This happens because the sign of does not affect the signal component, but leads to the appearance of the phase multiplier in the noise term, which is equivalent to an additional high-periodic component of the hologram on which strong diffraction occurs.
The final hologram (see
Figure 2b) is obtained from the amplitude-phase function
by applying Equations (
20), (
21), and (
23). An example of a captured image is shown in
Figure 3b together with an enlarged area for one mode presented in the inset.
It should be mentioned that, despite the obvious advantage of the method in the form of simulation of amplitude-phase modulation, there is still a significant disadvantage associated with a decrease in resolution by a factor of four. This is due to the fact that four physical pixels of the modulator are equivalent to one pixel of the encoded amplitude-phase mask.
3.3. Spatial Correlation Filter Based on Jacobi–Anger Expansion
In this last method, the amplitude-phase transmission function from [
18] is written into a pure phase hologram, forming a phase correlation filter (PCF), as shown in [
24]. As a result, in the first-order diffraction after the Fourier lens, one obtains the convolutions of the laser beam with the Fourier images of the modes of interest, separated by distances that are defined by introducing an addition of carrier frequencies.
MD of a multimode light beam is possible using the SCF method, where a diffraction element with an amplitude-phase transmission function is used for decomposition [
18]. This function has the form:
Using the convolution theorem and relation (
8) we can rewrite Equation (
11) as follows:
Due to the fact that the modes have been written with slightly different carrier frequencies
in the transmission function (
24), the field
will contain terms of the form:
The convolutions (
26) at the correct choice of carrier frequencies
will not overlap with each other in the frequency space. In the center of each convolution (from the property of the Fourier transform) we obtain the following scalar product:
The transmission function
described above can be written in pure phase form through the Jacobi–Anger expansion [
24]. The function
is then treated as a signal to be recorded in the hologram (depicted in
Figure 2c). All convolutions defined by Equation (
26) will shift by another common carrier frequency into the first order of diffraction. Thus, by measuring the field intensity at the center of the correlation signals
in the focal plane, one can determine
, which is the square of the amplitude of the
m-th mode.
Then, in order to determine the mode phase
, i.e., the argument of the coefficient
, it is necessary to add specially defined terms to the sum in Equation (
24) [
18]. Note that the mode phases are defined with respect to a reference value. Usually, this is taken in such a way that the fundamental mode (
) has zero phase. To determine the cosine of the phase shift
of mode
we need a term of the form:
Whereas the following term is needed to determine the sine of the same phase shift:
The correlation signals corresponding to these terms will also be separated according to the selected carrier frequencies
and
(see
Figure 3c).
4. Results
All methods were applied to beams made of either
, 6, or 10 modes. We computed the correlation between the set and the retrieved amplitudes for all possible mode combinations, as described in
Section 2. In particular, for the case of three modes, we used
intensity levels. According to Equation (
3),
and
result in 45 combinations, henceforth frames. In contrast, in the cases of six and ten modes, we considered
intensity levels, which led to 4368 and 167,960 frames, respectively. For each frame, the correlation was calculated as the dot product of the initial amplitude vector and retrieved amplitude vector. The results are shown in
Figure 4,
Figure 5 and
Figure 6. As can be seen, the correlation values always stay on a relatively high level: the minimum value reached for the CSE method, is close to 96%, whereas PCF and DPH are associated with correlation values close to 100%. Interestingly, some outlier values of correlation arise in the CSE method when the beam consists primarily of one mode. In contrast, nearly monomode beams are not so critical for the other two methods.
One may notice that, because the initial mode amplitude is unknown, in real experiments there is no opportunity to verify the correctness of the MD as described above. Therefore, for the sake of completeness, here we mimic the test of an experimental MD validity by calculating the cross-correlation parameter [
25]. The latter, which allows us to compare two images (initial and reconstructed), is defined as
where
and
are the mean values of the matrices
A and
B, respectively, whose elements are
and
, respectively. Here, the matrices represent pixelated frames containing initial and reconstructed beams. The cross-correlation parameter was calculated for the CSE method in the case of three and six modes (red line in
Figure 4 and
Figure 5). As can be seen, we found a similar behavior to that of the amplitude correlation calculated via the dot product (green line). This agreement allowed us to conclude that the CSE method is less accurate than DPH and PCF. Still, it has to be underlined that the CSE’s accuracy remains comparable to that of methods based on neural networks [
26].
Finally, in order to make a graphical comparison of the three methods used in this work, in
Figure 7 we plot on a logarithmic scale the resulting mismatch for all cases reported in
Figure 4,
Figure 5 and
Figure 6. Specifically, on the horizontal axis of the figure we put the standard deviation, which characterizes the scatter of values in the target intensity set: the smaller the standard deviation, the smaller the error.
In addition to demonstrating once again that CSE is the least accurate of the three methods, the graphs allow us to conclude that, for all methods, the error increases as the number of modes grows larger. This is most noticeable for the DPH method, where the discrepancy increases by an order of magnitude when passing from to . As mentioned above, this effect may be ascribed to the four-fold decrease in the resolution of DPH in comparison with other methods.