Next Article in Journal
The Role of Collision Ionization of K-Shell Ions in Nonequilibrium Plasmas Produced by the Action of Super Strong, Ultrashort PW-Class Laser Pulses on Micron-Scale Argon Clusters with Intensity up to 5 × 1021 W/cm2
Next Article in Special Issue
Analysis of the Influence of Fabrication Errors on the Far-Field Performance of Si and Si3N4 Antennas
Previous Article in Journal
Vector Light Field Immediately behind an Ideal Spherical Lens: Spin–Orbital Conversion, Additional Optical Vortices, Spin Hall Effect, Magnetization
Previous Article in Special Issue
Photonic Hook Initiated Using an Air–Liquid Interface
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 10
Issue 11
10.3390/photonics10111248
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Collective Modes in the Luminescent Response of Si Nanodisk Chains with Embedded GeSi Quantum Dots

by
Vladimir A. Zinovyev
1,
Zhanna V. Smagina
1,
Aigul F. Zinovieva
1,2,
Ekaterina E. Rodyakina
1,2,
Aleksey V. Kacyuba
1,
Ksenya N. Astankova
1,
Vladimir A. Volodin
1,2,*,
Kseniia V. Baryshnikova
3,
Mihail I. Petrov
3,
Mikhail S. Mikhailovskii
3,
Valery A. Verbus
4,5,
Margarita V. Stepikhova
5 and
Alexey V. Novikov
5
1
Rzhanov Institute of Semiconductor Physics, Siberian Branch of Russian Academy of Sciences, 630090 Novosibirsk, Russia
2
Department of Physics, Novosibirsk State University, 630090 Novosibirsk, Russia
3
Department of Physics and Engineering, ITMO University, 197101 St. Petersburg, Russia
4
Department of Economics, National Research University Higher School of Economics, 603155 Nizhny Novgorod, Russia
5
Institute for Physics of Microstructures of Russian Academy of Sciences, 603950 Nizhny Novgorod, Russia
*
Author to whom correspondence should be addressed.
Photonics 2023, 10(11), 1248; https://doi.org/10.3390/photonics10111248
Submission received: 1 October 2023 / Revised: 23 October 2023 / Accepted: 29 October 2023 / Published: 10 November 2023
(This article belongs to the Special Issue Sciences and Applications of Nano-Photonics)
Browse Figures
Review Reports Versions Notes

Abstract

:
In this paper, we study the effects of GeSi quantum dot emission coupling with the collective modes in the linear chains of Si disk resonators positioned on an SiO2 layer. The emission spectra as a function of the chain period and disk radius were investigated using micro-photoluminescence (micro-PL) spectroscopy. At optimal parameters of the disk chains, two narrow PL peaks, with quality factors of around 190 and 340, were observed in the range of the quantum dot emission. A numerical analysis of the mode composition allowed us to associate the observed peaks with two collective modes with different electric field polarization relative to the chain line. The theoretical study demonstrates the change of the far-field radiation pattern with increasing length of the disk chain. The intensive out-of-plane emission was explained by the appearance of the dipole mode contribution. The obtained results can be used for the development of Si-based near-infrared light sources.

1. Introduction

Many results have now been obtained indicating that the modification of the optical properties of materials by using various types of micro- and nano-resonators can be successfully applied to create efficient photon radiation sources, lasers with low threshold powers and narrow generation lines, optical filters with controlled bandwidth, and others [1,2,3,4,5,6,7,8,9,10,11]. This approach is already being used for solving the urgent problem of creating compact, efficient light sources compatible with Si technology. The solution of this problem can lead to great progress in the development of silicon photonics. One of the promising variants is tunable structures with dielectric Mie resonators, allowing control of the light–matter interaction [6,7,8,9,10,11,12]. Emission enhancement can be achieved due to an increase in the probability of optical transitions, when some kinds of emitters, which can be quantum dots, are placed at the maximum of the electric field inside the Mie resonator (Purcell effect [12,13]). In the frame of Si-based technology, GeSi quantum dots (QDs) can be considered a suitable variant of radiation sources with emission bandwidth coinciding with the highly demanded near-infrared range [14,15,16,17,18]. The choice of GeSi QDs as an emitting medium is determined by several factors. The localization of the charge carriers on GeSi QDs weakens the influence of surface defects on the emitting properties of the structures. The possibility of the growth of structures with GeSi quantum dots on silicon-on-insulator (SOI) substrates allows limiting the propagation of light in one of the directions and simplifies the preparation of dielectric resonators. The luminescence signal of GeSi QDs is characterized by a large width, which allows us to use it for studies of the interaction with different modes of resonators. In addition, for this type of heterostructure, there are well-developed methods of spatial ordering of QDs [19,20,21,22,23,24,25,26,27], which can be used for the development of devices with high efficiency of interaction of a small number of emitters (down to single emitter [1,2,3]) with the modes of micro- and nano-resonators. GeSi QDs formed on silicon emit at room temperature in the wavelength range of 1.3–1.55 μm, which makes them promising for the creation of light sources for silicon photonics. The best results in QD emission enhancement were achieved by creating structures supporting high quality states [28,29,30,31,32,33,34,35,36]. The high quality factor is an inherent property of a special type of states, bound states in continuum (BIC) [37]. There are two types of BICs: the first type is the symmetry-protected BIC arising inthe center of the Brillouin zone (in the Γ-point) of some periodical photonic structure and completely decoupled from the radiation continuum due to the high symmetry [38,39,40]; the second type is off-Γ BIC, which can be obtained by tuning the parameters of the photonic system [41,42,43,44]. This latter BIC is also called the accidental BIC or Friedrich–Wintgen state (FW–BIC) [45]. The most intensive studies of BICs have been conducted for PhC structures [18,42,46]; however, there are many works dealing with dielectric Mie resonators. A large amount of theoretical and experimental material has been accumulated in this direction, both on single resonators [8,9,47] and on chains of resonators [5,7,10,11,44,48,49,50,51]. The possibility of creating experimental systems on the basis of disk resonator chains supporting high quality states, such as symmetry-protected and accidental BICs, was demonstrated [44,50]. Recently, a new approach for achieving the giant Q-factors in finite-length periodic arrays of subwavelength optical Si resonators was proposed [7]. It is based on the interference between the band-edge mode and a standing mode in the resonator chain, which leads to the suppression of radiative losses and the formation of high Q localized state. The collective band-edge modes were studied also in linear chains of Si nanopillars with embedded GeSi quantum dots [10], where the effective coupling of GeSi QDs to the Mie resonance modes of the nanopillars was demonstrated. The 10-fold enhancement of the luminescent signal due to the excitation of resonant antisymmetric magnetic and electric dipole modes was obtained for the nanopillar trimer. In the next paper by the same authors [11], a Q-factor of around 500 was experimentally measured for an array of 11 pillars, which demonstrates the potential of engineering optical nanopillar cavities for active photonic devices on an Si platform. The high quality factor was provided by the formation of the collective dipolar mode in a nanopillar array.
Until now, as far as we know, experimental structures with chains of Si disk resonators supporting BIC states (symmetry-protected or accidental) have not yet been realized and investigated. There are papers with impressive results on anapole-based energy transfer along Si disk chains [52,53], but unfortunately no BIC states were detected there [53]. The main results on the realization of BIC states in disk resonator chains are obtained on systems with ceramic microwave resonators [44,50], which cannot be directly incorporated into the existing Si technology. In the present paper, we have investigated structures with linear chains of Si disk resonators on a SiO2 layer, depending on the period and radius of disks in order to verify the possibility of the formation of high quality states in this system. At optimal parameters, we have demonstrated the enhancement of the emission of GeSi quantum dots. The micro-PL study demonstrates the appearance of two narrow PL peaks even for short chains with the number of disks N ≥ 2. By analysis of the mode composition, the correspondence between the observed PL peaks and two high quality collective modes were found. The change of radiation pattern from in-plane to out-of-plane was detected at the transition from the case of a single disk resonator to a linear chain of disks. The obtained results can be used for the development of near-infrared light sources compatible with Si-based technology.

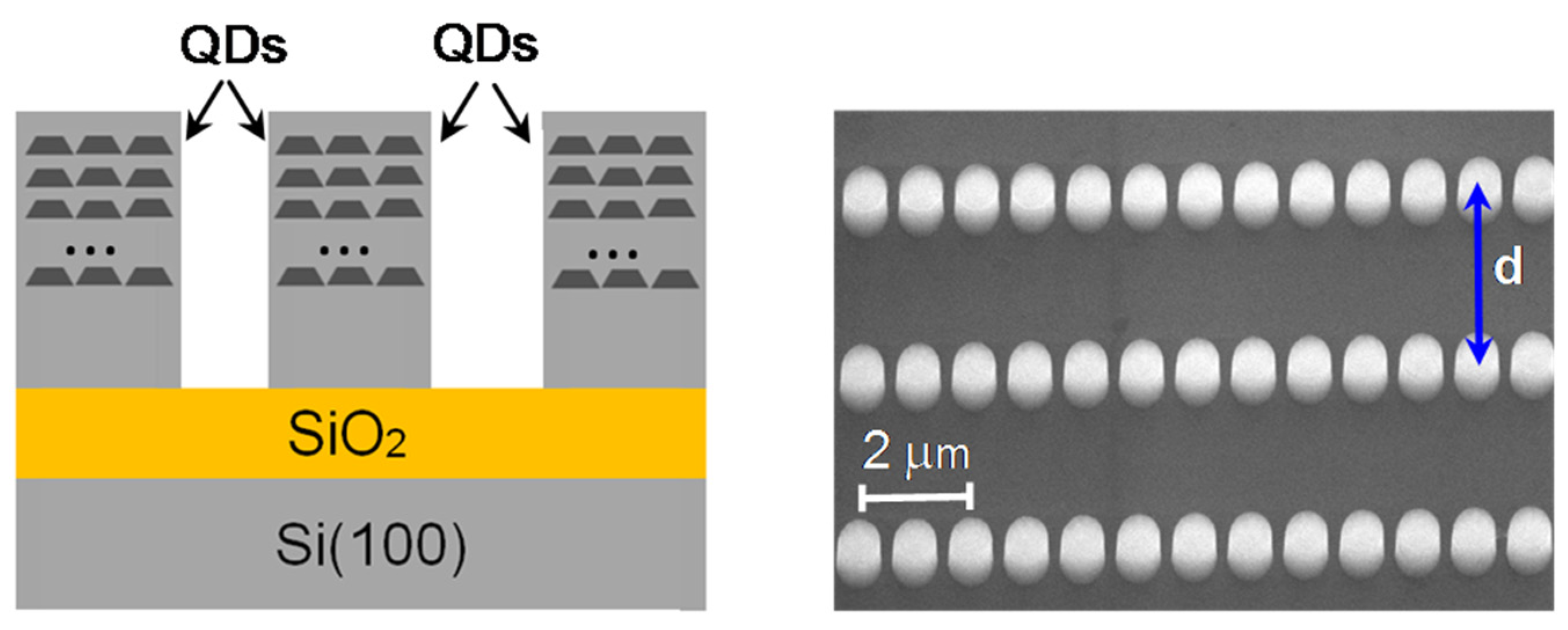
2. Materials and Methods

To fabricate the linear chains of disk resonators with embedded GeSi QDs, a silicon-on-insulator (SOI) substrate with a 180 nm-thick top Si layer and a 3 μm-thick SiO2 layer was used. At the first step, a 110 nm-thick Si buffer layer was grown by molecular beam epitaxy at 500 °C ata rate of 0.6 Å/s. At the next step, ten layers of GeSi QDs separated by 15 nm-thick silicon spacer layers were grown at 600 °C. Each QD layer was formed by the deposition of 7 monolayers of Ge at a growing rate of 0.05 Å/s. At the final stage, the structure was covered with a 15 nm-thick Si layer. Si spacers and cap-layer were grown at a rate of 1 Å/s. The total thickness of the multilayer structure was 440 nm. Then, using e-beam lithography and plasma-etching, linear chains of disk resonators with different diameters and periods were formed on the surface of the SiO2 layer. In the first step, by means of e-beam lithography, the chains of holes were created in positive resist PMMA-950K with a thickness of 200 nm. The radius of the holes in the resist layer varied from 330 ± 10 nm to 385 ± 10 nm with a step of 15 nm. The distance between the linear chains d was chosen to avoid the coupling of different chain resonators. It was varied depending on the period of the chain a. In our experimental implementation, for a = 1 µm, d = 3 µm; for a = 2 µm, d = 4 µm; for a = 3 µm, d = 6 µm; for a = 10 µm, d = 10 µm; for a = 15 µm, d = 15 µm were chosen. Then, a thin layer of chromium (20 nm) was deposited by magnetron sputtering on top of the resist layer with holes. After lift-off lithography, the periodic arrays of Cr disks were obtained, which served as a mask for the fabrication of the resonators. In the next step, anisotropic plasma chemical etching of the top Si layer with GeSi QDs was carried out in SF6/CHF3 gas mixture through a Cr mask down to the SiO2 layer. The etching rate was ~10 nm/s. According to scanning electron microscopy (SEM) measurements, the linear chains of disk resonators with radii 330 ± 10 nm, 345 ± 10 nm, 365 ± 10 nm, 385 ± 10 nm were obtained for each value of period. A schematic representation and scanning electron microscopy image of the obtained 1D arrays of disks with embedded GeSi QDs are shown in Figure 1. As well as the full-length chains, we investigated chains with different lengths. Such structures were fabricated by ultrasonic treatment, which resulted in removing some parts of the chains and the formation of chains with different lengths.
The luminescent properties of the structures were studied by the micro-photoluminescence (micro-PL) method with high spatial and spectral resolutions. The micro-PL signal was excited by a continuous laser at the wavelength of 532 nm. The laser radiation was focused in a spot of ~2 μm with a Mitutoyo M Plan APO 50× objective (numerical aperture NA = 0.42). The excitation power was 5 mW. Measurements were carried out in the normal incidence geometry of the exciting and detected beams. The PL signal collection angle was 2ϑ = 48°.The micro-PL signal was detected by a cooled Ge detector using a Bruker IFS 125HR high-resolution Fourier spectrometer. The spectra were recorded with resolution 4 cm−1. The measurements were carried out at a temperature of 77 K. To analyze the obtained experimental results, we have simulated the emission spectra of the studied structures with resonator chains. The near-field components distributions and dispersion dependences of the eigenmodes are numerically calculated using COMSOL Multiphysics software.

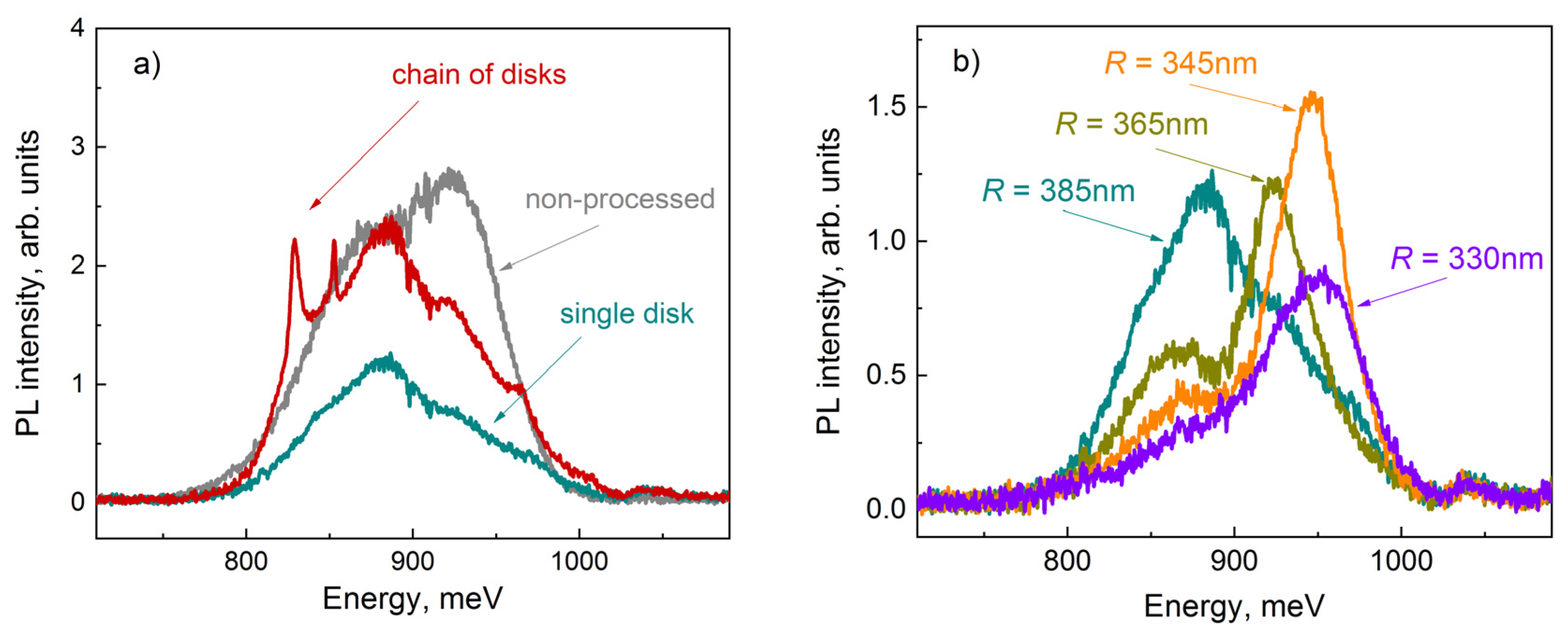
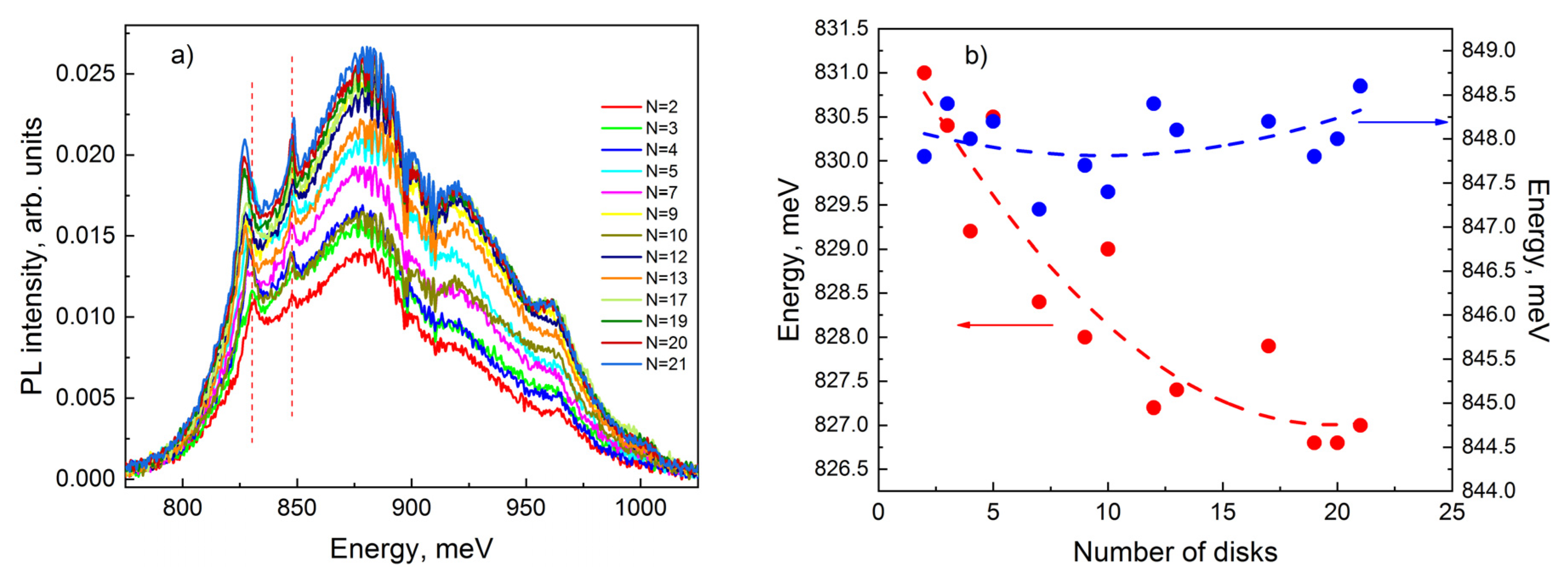
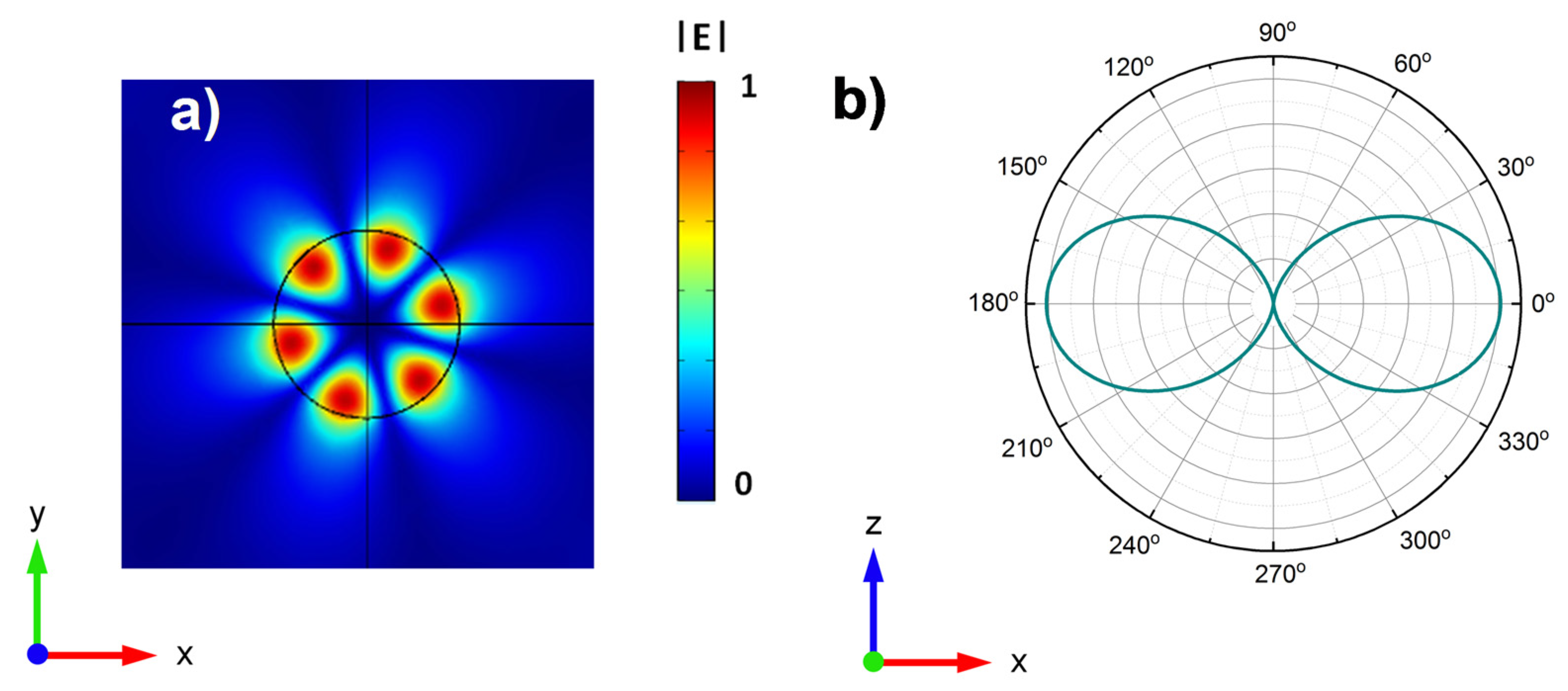
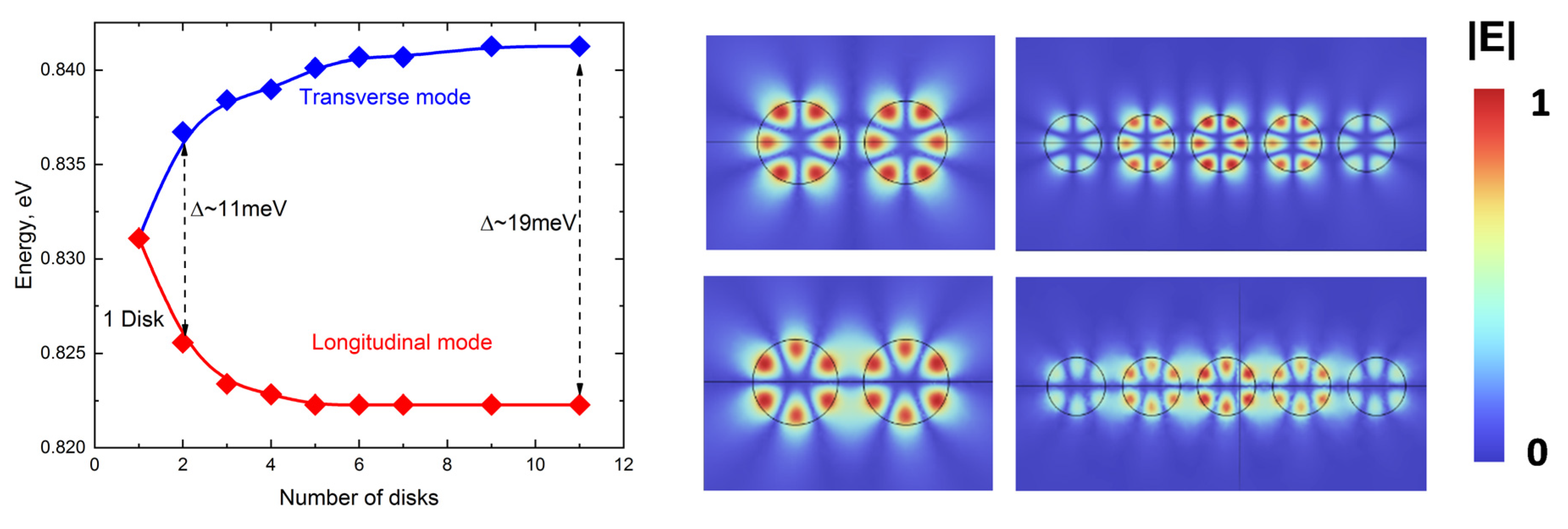
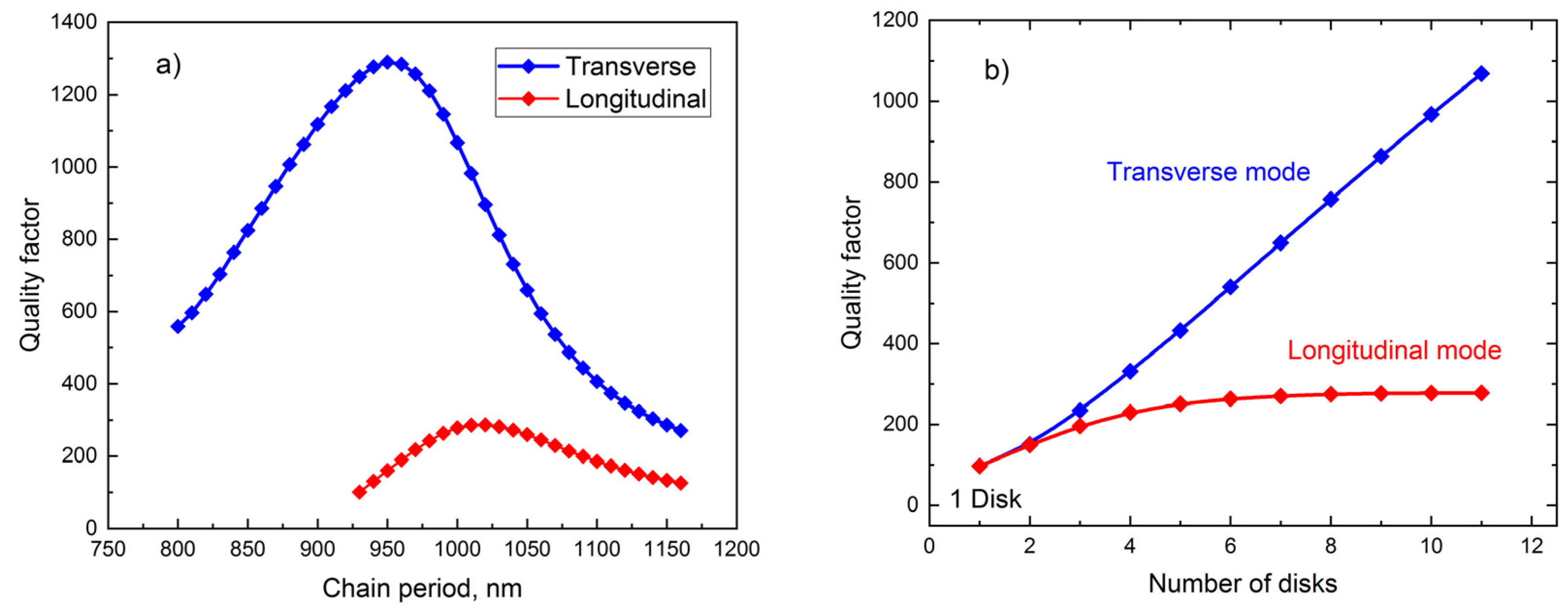
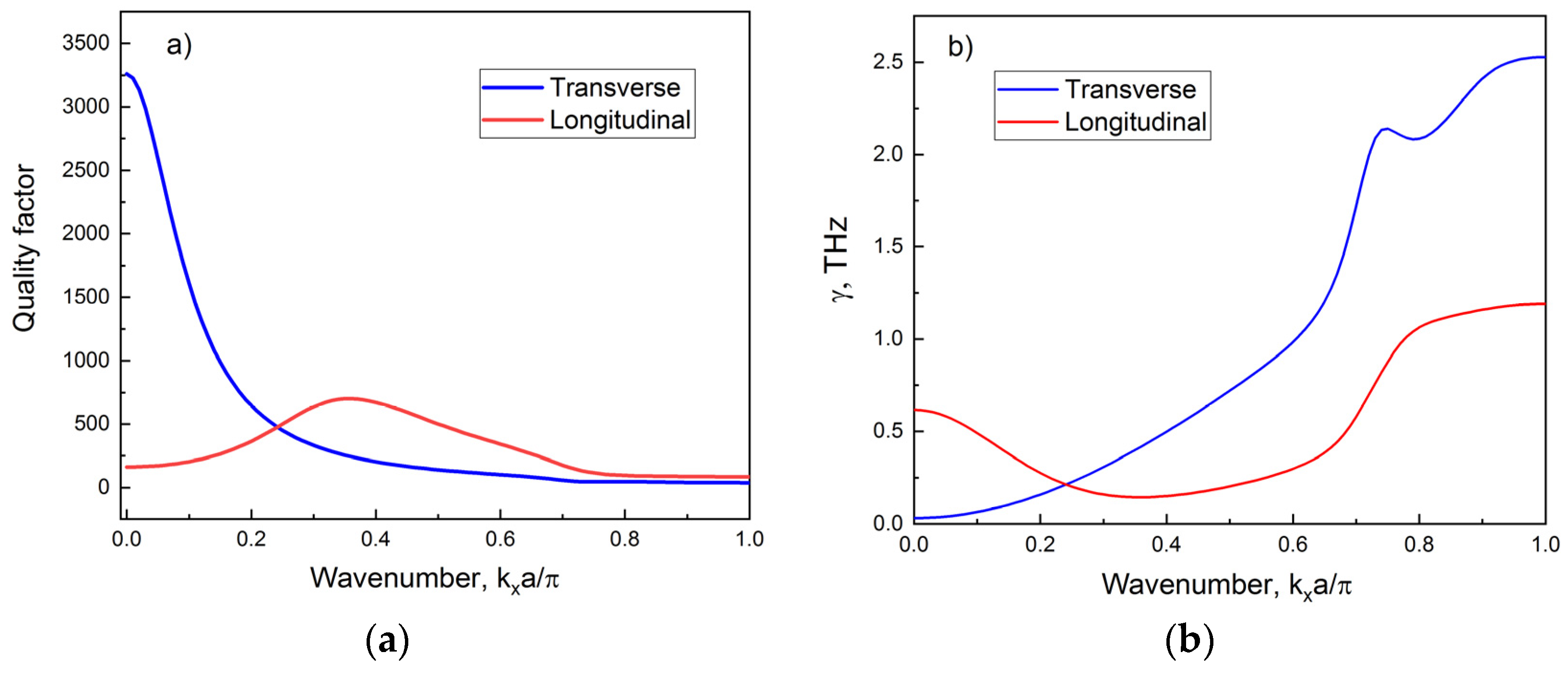
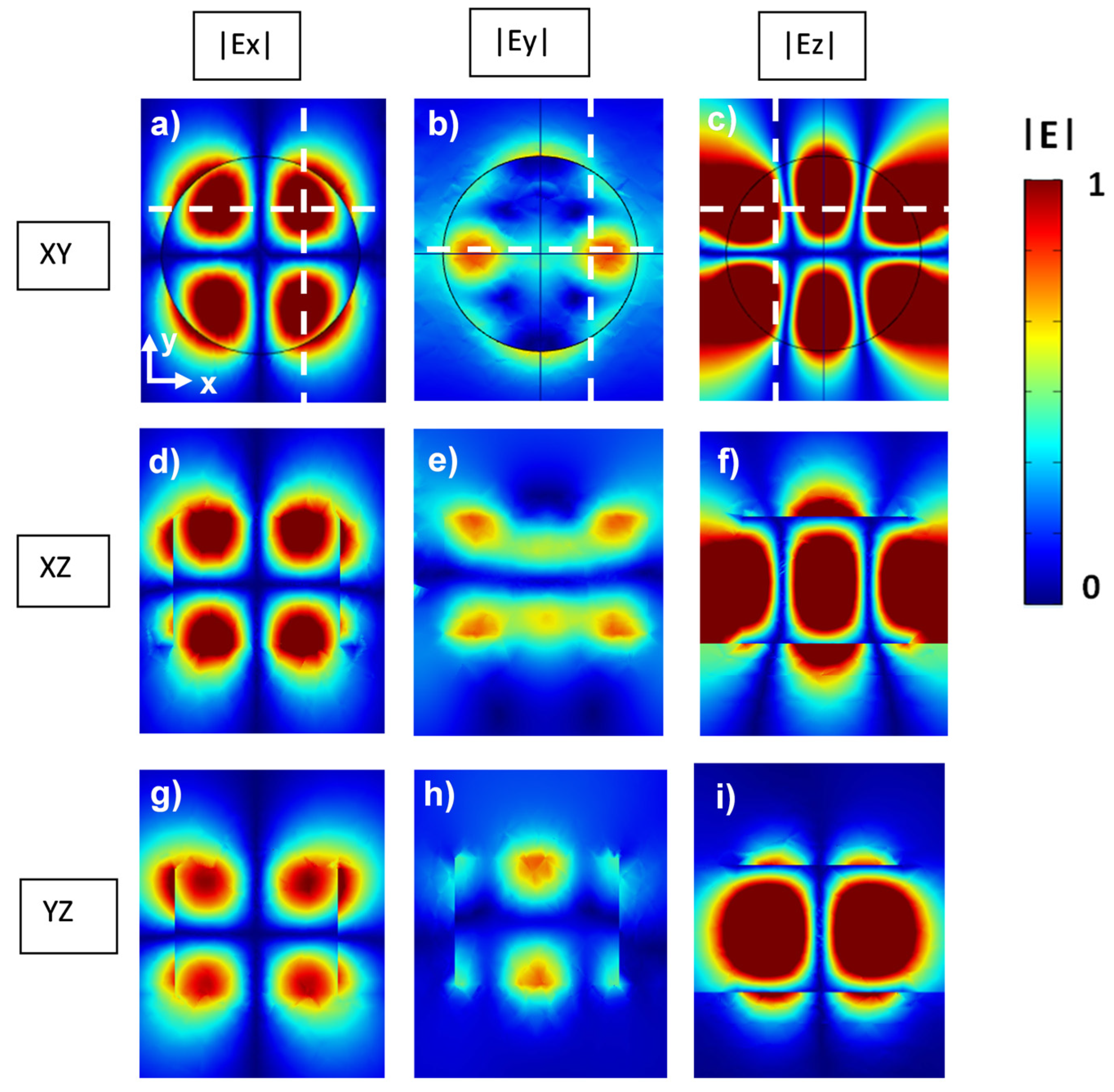
3. Results and Discussion

The micro-PL study shows that the formation of linear chains of Si disks with embedded GeSi QDs led to PL spectra modification as compared with the original, unprocessed area (Figure 2). The most significant changes were observed for chains with period 1 μm (Figure 3). In contrast, at periods ≥ 2 µm, the spectra are very similar to the spectrum of a single disk and represent broad PL peaks with a maximum position depending on the disk radius (Figure 2b). At period 1 μm and disk radius ≈ 385 nm, two narrow peaks at E1 ≈ 827 meV and E2 ≈ 849 meV appear in the PL spectra (Figure 2a, red curve, the data are given for maximum chain length N = 51). These peaks are present in the spectra of even very short chains, for example, when the number of resonators in the chain N = 2. With increasing N, these peaks became narrower and more intensive. At N = 51, the quality factors of the peaks were 190 (peak at 827 meV) and 340 (peak at 849 meV). These values were obtained on the basis of PL spectrum fitting by a set of Lorentz functions (Figure S1 in Supplementary Materials).
The gap between the narrow peaks depended on the number of disks in the chain, it increased with N (Figure 4). At N = 2, the gap between peaks is smallest and consists of ≈17 meV (E1 ≈ 831 meV and E2 ≈ 848 meV). By increasing the number of disks, the narrower peak was practically unchanged in its position, while the broader peak slightly shifted (by ~4 meV) to longer wavelengths. Also, the dependence of the PL peak position on the radius of the disks was observed. The PL spectra at the period of the chain a = 1 µm (Figure 3a) showed the blueshift of narrow peaks with decreasing radius.
To understand the nature of the observed narrow peaks, we performed simulations for model structures that represented the linear chains of disk resonators with parameters corresponding to experimental ones. First, we studied the eigenmodes of the single disk resonator with radius 385 nm and height 440 nm. In the range 790–870 meV, we have found many eigenmodes (~60) and made a selection by the value of the quality factor. We have chosen a two-fold degenerate mode with energy of 831 meV and a quality factor of 97, an order of magnitude higher than the others. The near-field configuration shown in Figure 5a indicates that this is the Mie mode with orbital angular momentum m = 3 (magnetic octupole, MO mode). The far-field pattern demonstrated the predominantly in-plane emission (Figure 5b).
At the second step, we studied the modes of linear chains with different numbers of resonators. Special attention is paid to the evolution of the MO mode. Already at N = 2 the mode splitting occurs and two collective modes were formed (Figure 6). One of the modes, with larger electric field amplitude in the gap between disks, shifted downward in energy scale, while the other shifted upward. In the following, we will refer to the former as the “longitudinal” mode (with a spread electric field along the chain) and the latter as the “transverse” mode. By increasing N, the splitting between modes increased and after N = 10 practically did not change. According to the calculation results, with enough long chains (N ≥ 10) the “longitudinal” mode had energy ≈ 822 meV, while the “transverse” mode achieved energy ≈ 841 meV, which is in good agreement with the experiment. The “transverse” mode is characterized by a higher field concentration inside disk than the “longitudinal” one. This corresponds well to the experimentally revealed difference in the quality factor of low- and high-energy peaks (Figure 2a). We would like to point out that the near field configurations of the considered modes (see the wave field pattern in Figure S3) are very similar to configurations of the true BICs found for infinitely long rods and cylinders [56,57,58], namely, the field pattern of our “transverse” mode is similar to one of the symmetry-protected BIC, while the field pattern of the “longitudinal” mode is close to one of the accidental BIC studied in these works.
Figure 7 demonstrates the results of calculations of quality factors for “transverse” and “longitudinal” modes depending on the chain period and on the number of disks in the chain.
The dependence of the quality factor on the chain period a (calculated at N = 11) showed that for the “transverse” mode the optimal period is slightly smaller than experimental value (a = 1 μm) and consisted of 950 nm, while for the “longitudinal” mode it is equal to 1020 nm. So, the chosen experimental period is very close to optimal one. The Q dependence on the period calculated for infinite chain is presented in Supplementary Materials (Figure S4). This dependence demonstrates that the quality factor can reach the value Q = 7500 at a = 1400 μm, if we turn off the material losses in the SiO2 substrate.
The Q dependence on N (calculated at a = 1 μm) shows that the quality factor of the “transverse” mode increased with chain length, while the quality factor of the “longitudinal” mode tended to stabilize at 200 after an initial growth. For the “transverse” mode, the quality factor reached the value of ~1100 at N = 11, demonstrating an almost linear dependence. Such dependence is preserved up to N = 20, and then the increase in the quality factor slows down, reaching saturation (Figure S5) near the value ~3000. The existing studies of the dependence Q(N) carried out on chains of dielectric resonators [44,50] show the dependence Q~N2 for BIC at Γ-point and Q~N for accidental BIC. However, it is also shown there that the presence of radiation losses can lead to a weaker dependence on N [50].
The theoretical consideration of infinite chains can give more detailed physical insights into the nature of the observed modes, so we have calculated the dependence of Q on the wave vector kx (along the chain line) and dispersion dependence of radiation losses γ = Im[ω(kx)] for the “transverse” and the “longitudinal” modes in the infinite chain of Si disks (Figure 8a,b). These dependences demonstrated the growth of Q near the Γ-point for the “transverse” mode and the presence of Q maximum out of the Γ-point (at kx =0.36π/a) for the “longitudinal” mode. This behavior indicated that these modes can be considered as candidates for BICs, but the non-zero radiation losses at maximum Q points do not allow them to be so classified.
We think that the main reason of finite Q values is that the dispersion branches are located in regions with one and two open diffraction channels (Figure 9). The leakage into the 2nd diffraction continuum can leads to a significant decrease of Q factors [50,59].
In the experiments we have obtained a lower value Q = 340 than predicted theoretically, which could be for several reasons. The first possible reason was of some imperfections in the experimental structures, which could have led to additional radiation losses. However, we think that this is not the main reason. The second, main reason in our opinion, is the absorption on free charge carriers excited by laser pumping during the micro-PL measurements. At given sizes of disks the excitation, already at low pump powers, could have led to a significant concentration of charge carriers in the disk, since the “diffusive escaping” is problematic. In general, this could even have caused the overheating of the sample. In our experiments, we controlled the power of pumping to avoid the displacement of PL peaks to the long-wavelength region due to overheating of the sample.
The most interesting result of our theoretical study is the change of the far-field pattern with increasing length of the disk chain. The typical far-field distribution for magnetic octupole mode is shown in Figure 5b. Such a far-field pattern is very suitable for use in planar device structures, but for up-emission light sources it is major disadvantage. However, in our structures, as the number of disks in the chain increased, the far-field distribution changed (Figure 10). For both modes, it is clearly seen that the probability of up-emission increased even for a two-disk chain (Figure 10b,d). For the “transverse” mode, at N = 3, the angle distribution of emission is broader than that for the “longitudinal” mode (Figure 10f).
To explain the obtained result, one can assume that at the formation of the collective state another mode with high out-of-plane emission was mixed with the main octupole mode. This assumption can be verified by analysis of the mode composition for the case of the infinite disk chain. To make the calculations as close as possible to our experiment, we placed inside each disk a point dipole, and considered all possible orientations of this dipole (the X-dipole is oriented along the chain, the Y-dipole is transverse to the chain line orientation, and the Z-dipole is oriented along the vertical axis of the disk).
It turned out that Z-dipole predominantly excited the “longitudinal” collective mode in the chain. The up-emission intensity spectrum of Z-dipole is shown in Figure S7. There is only one intensive peak at λ ≈ 1.506 μm (E ≈ 823 meV), which corresponds to our “longitudinal” mode. In Figure 11, the near-field distribution for this mode is shown. We have plotted separately the Ex, Ey, Ez components distribution in XY, XZ, YZ-sections. It is clearly seen that the collective “longitudinal” mode is a superposition of the TM mode (magnetic octupole) and the two TE modes (dipole and quadrupole modes).
The X-dipole predominantly excited the “transverse” collective mode in the chain. The up-emission spectra of the X-dipole is shown in Figure S7. These spectra were richer in peaks than the Z-dipole spectra, but there was only one intensive peak in the range of interest to us, at λ ≈ 1.488 μm (E ≈ 833 meV), which corresponded to our “transverse” mode. In Figure 12, the near-field distribution for this mode is shown. It is clearly seen that the collective “transverse” mode is also a superposition of TM mode (magnetic octupole) and two TE modes (dipole and quadrupole modes). The principal difference of the “transverse” collective mode case is another orientation of admixed dipole mode relative to the chain line. For the “transverse” collective mode, the admixed dipole mode was oriented along Y-axis, while for “longitudinal” collective mode the dipole mode was oriented along the chain line.
It should be noted that the analysis of the mode composition in the case of a single disk resonator demonstrates the presence of an admixture of the quadrupole mode (Figure S8). But the dipole mode is added only in the case of the linear chain of disks. Thus, one can conclude that the intensive up-emission is provided by an appearance of the dipole mode admixture.

4. Conclusions

As a result of this study, it was obtained that for structures with linear chains of Si disks on a SiO2 substrate it is possible to select such parameters (disk radius, period, and length of the chain), which ensure the existence of high-quality collective modes. These modes are distant relatives of the BIC states found for infinitely long rods in [56,57,58]. Embedding quantum dots in such disk chains led to multiple amplification of the QD emission due to interaction with these collective modes. The change of the far-field radiation pattern from in-plane to out-of-plane emission is found with increasing length of the disk chain. The result is explained by the appearance of the dipole mode admixture.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/photonics10111248/s1, Figure S1: The fitting of micro-PL spectra by a set of Lorentz functions; Figure S2: The dependence of PL peak intensity on the number of Si disks in the chain; Figure S3: The wave field pattern calculated for the “longitudinal” and “transverse” modes; Figure S4: The dependences of quality factors of “transverse” mode on the period of the infinite chain; Figure S5: The dependences of quality factors on the number of disks calculated for “transverse” and “longitudinal” modes in the chains of Si disks positioned on SiO2. Figure S6: The dependences of losses γ = Im[ω(kx)] on the wave vector kx (along the chain line) calculated for “transverse” and “longitudinal” modes in the infinite chains of Si disks. Figure S7: The calculated up−emission intensity spectra for infinite linear chains of silicon disk resonators with embedded point dipoles. Figure S8: The near field distributions for eigenmode at λ = 1.493 µm (≈830 meV) for an isolated Si disk.

Author Contributions

Conceptualization, V.A.Z., Z.V.S., A.V.N. and M.I.P.; Structure fabrication, A.V.K.; Diagnostic of fabricated structures, Z.V.S. and E.E.R.; Lithography, Z.V.S. and E.E.R.; Micro-PL studies, M.V.S.; Simulation, K.V.B., M.S.M., V.A.Z., K.N.A. and V.A.V. (Valery A. Verbus); Supervision, V.A.Z.; Writing—original draft, A.F.Z., V.A.Z., V.A.V. (Vladimir A. Volodin), M.S.M. and M.I.P. All authors have read and agreed to the published version of the manuscript.

Funding

This work is funded by Russian Science Foundation (grant # 21-72-20184) in the part of development of the structures with linear chains of Si disk resonators with embedded GeSi QDs and experimental PL study of the effects of GeSi quantum dot emission coupling with collective modes as well as theoretical calculation of emission spectra. The analysis of the eigenmodes of the single disk resonator and linear chains of disk resonators was done in the Center of Excellence «Center of Photonics» funded by the Ministry of Science and Higher Education of the Russian Federation, contract No. 075-15-2022-316. The calculations of dispersion dependences for the “transverse” and the “longitudinal” modes and their quality factors were supported by the Federal Academic Leadership Program Priority 2030.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Acknowledgments

Authors thank the NSU Multiple-access Center “VTAN” and ISP SB RAS Multiple-access Center “Nanostructures” for the provision of measurement equipment. The authors gratefully acknowledge A. V. Armbrister for the growth of experimental structures.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zeng, C.; Ma, Y.; Zhang, Y.; Li, D.; Huang, Z.; Wang, Y.; Huang, Q.; Li, J.; Zhong, Z.; Yu, J.; et al. Single germanium quantum dot embedded in photonic crystal nanocavity for light emitter on silicon chip. Opt. Express 2015, 23, 22250–22261. [Google Scholar] [CrossRef] [PubMed]
  2. Schatzl, M.; Hackl, F.; Glaser, M.; Rauter, P.; Brehm, M.; Spindlberger, L.; Simbula, A.; Galli, M.; Fromherz, T.; Schaffler, F. Enhanced telecom emission from single group iv quantum dots by precise CMOS-compatible positioning in photonic crystal cavities. ACS Photonics 2017, 4, 665–673. [Google Scholar] [CrossRef]
  3. Poempool, T.; Aberl, J.; Clementi, M.; Spindlberger, L.; Vukušić, L.; Galli, M.; Gerace, D.; Fournel, F.; Hartmann, J.-M.; Schäffler, F.; et al. Single SiGe Quantum Dot Emission Deterministically Enhanced in a High-Q Photonic Crystal Resonator. Opt. Express 2023, 31, 15564. [Google Scholar] [CrossRef] [PubMed]
  4. Kalinic, B.; Cesca, T.; Balasa, I.G.; Trevisani, M.; Jacassi, A.; Maier, S.A.; Sapienza, R.; Mattei, G. Quasi-BIC Modes in All-Dielectric Slotted Nanoantennas for Enhanced Er3+ Emission. ACS Photonics 2023, 10, 534–543. [Google Scholar] [CrossRef] [PubMed]
  5. Hoang, T.X.; Ha, S.T.; Pan, Z.; Phua, W.K.; Paniagua-Domínguez, R.; Png, C.E.; Chu, H.-S.; Kuznetsov, A.I. Collective Mie Resonances for Directional On-Chip Nanolasers. Nano Lett. 2020, 20, 5655–5661. [Google Scholar] [CrossRef] [PubMed]
  6. Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef]
  7. Kornovan, D.F.; Savelev, R.S.; Kivshar, Y.; Petrov, M.I. High-Q localized states in finite arrays of subwavelength resonators. ACS Photonics 2017, 8, 3627–3632. [Google Scholar] [CrossRef]
  8. Rybin, M.V.; Koshelev, K.L.; Sadrieva, Z.F.; Samusev, K.B.; Bogdanov, A.A.; Limonov, M.F.; Kivshar, Y.S. High-Q supercavity modes in subwavelength dielectric resonators. Phys. Rev. Lett. 2017, 119, 243901. [Google Scholar] [CrossRef]
  9. Koshelev, K.; Kruk, S.; Melik-Gaykazyan, E.; Choi, J.H.; Bogdanov, A.; Park, H.G.; Kivshar, Y. Subwavelength dielectric resonators for nonlinear nanophotonics. Science 2020, 367, 288–292. [Google Scholar] [CrossRef]
  10. Rutckaia, V.; Heyroth, F.; Novikov, A.; Shaleev, M.; Petrov, M.; Schilling, J. Quantum Dot Emission Driven by Mie Resonances in Silicon Nanostructures. Nano Lett. 2017, 17, 6886–6892. [Google Scholar] [CrossRef]
  11. Rutckaia, V.; Heyroth, F.; Schmidt, G.; Novikov, A.; Shaleev, M.; Savelev, R.S.; Schilling, J.; Petrov, M. Coupling of Germanium Quantum Dots with Collective Sub-radiant Modes of Silicon Nanopillar Arrays. ACS Photonics 2021, 8, 209–217. [Google Scholar] [CrossRef] [PubMed]
  12. Purcell, E.M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar]
  13. Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef]
  14. Brehm, M.; Grydlik, M.; Hackl, F.; Lausecker, E.; Fromherz, T.; Bauer, G. Excitation Intensity Driven PL Shifts of SiGe Islands on Patterned and Planar Si(001) Substrates: Evidence for Ge-rich Dots in Islands. Nanoscale Res. Lett. 2010, 5, 1868–1872. [Google Scholar] [CrossRef] [PubMed]
  15. Zinovyev, V.A.; Zinovieva, A.F.; Kuchinskaya, P.A.; Smagina, Z.V.; Armbrister, V.A.; Dvurechenskii, A.V.; Borodavchenko, O.M.; Zhivulko, V.D.; Mudryi, A.V. Strain-induced improvement of photoluminescence from the groups of laterally ordered SiGe quantum dots. Appl. Phys. Lett. 2017, 110, 102101. [Google Scholar] [CrossRef]
  16. Stepikhova, M.V.; Novikov, A.V.; Yablonskiy, A.N.; Shaleev, M.V.; Utkin, D.E.; Rutckaia, V.V.; Skorokhodov, E.V.; Sergeev, S.M.; Yurasov, D.V.; Krasilnik, Z.F. Light emission from Ge(Si)/SOI self-assembled nanoislands embedded in photonic crystal slabs of various periods with and without cavities. Semicond. Sci. Technol. 2019, 34, 024003–024009. [Google Scholar] [CrossRef]
  17. Jannesari, R.; Schatzl, M.; Hackl, F.; Glaser, M.; Hinger, K.; Fromherz, T.; Schaffler, F. Commensurate germanium light emitters in silicon-on-insulator photonic crystal slabs. Opt. Express 2014, 22, 25426–25435. [Google Scholar] [CrossRef]
  18. Dyakov, S.A.; Stepikhova, M.V.; Bogdanov, A.A.; Novikov, A.V.; Yurasov, D.V.; Shaleev, M.V.; Krasilnik, Z.F.; Tikhodeev, S.G.; Gippius, N.A. Photonic bound states in the continuum in Si structures with the self-assembled Ge nanoislands. Laser Photonics Rev. 2021, 15, 2000242. [Google Scholar] [CrossRef]
  19. Zhong, Z.; Bauer, G. Site-controlled and size-homogeneous Ge islands on prepatterned Si(001) substrates. Appl. Phys. Lett. 2004, 84, 1922–1923. [Google Scholar] [CrossRef]
  20. Stangl, J.; Holý, V.; Bauer, G. Structural properties of self-organized semiconductor nanostructures. Rev. Mod. Phys. 2004, 76, 725–783. [Google Scholar] [CrossRef]
  21. Grützmacher, D.; Fromherz, T.; Dais, C.; Stangl, J.; Müller, E.; Ekinci, Y.; Solak, H.H.; Sigg, H.; Lechner, R.T.; Wintersberger, E.; et al. Three-Dimensional Si/Ge Quantum Dot Crystals. Nano Lett. 2007, 7, 3150–3156. [Google Scholar] [CrossRef] [PubMed]
  22. Grydlik, M.; Langer, G.; Fromherz, T.; Schäffler, F.; Brehm, M. Recipes for the fabrication of strictly ordered Ge islands on pit-patterned Si(001) substrates. Nanotechnology 2013, 24, 105601. [Google Scholar] [CrossRef] [PubMed]
  23. Ma, Y.J.; Zeng, C.; Zhou, T.; Huang, S.F.; Fan, Y.L.; Zhong, Z.; Yang, X.J.; Xia, J.S.; Jiang, Z.M. Ordering of low-density Ge quantum dot on patterned Si substrate. J. Phys. D Appl. Phys. 2014, 47, 485303. [Google Scholar] [CrossRef]
  24. Wang, S.; Zhang, N.; Chen, P.; Wang, L.; Yang, X.; Jiang, Z.; Zhong, Z. Toward precise site–controlling of self–assembled Ge quantum dots on Si microdisks. Nanotechnology 2018, 29, 345606. [Google Scholar] [CrossRef]
  25. Brehm, M.; Grydlik, M.; Tayagaki, T.; Langer, G.; Schäffler, F.; Schmidt, O.G. Photoluminescence investigation of strictly ordered Ge dots grown on pit-patterned Si substrates. Nanotechnology 2015, 26, 225202. [Google Scholar] [CrossRef]
  26. Brehm, M.; Grydlik, M. Site-controlled and advanced epitaxial Ge/Si quantum dots: Fabrication, properties, and applications. Nanotechnology 2017, 28, 392001. [Google Scholar] [CrossRef]
  27. Yan, J.; Zhang, Z.; Zhang, N.; Huang, Q.; Zhan, Y.; Jiang, Z.; Zhong, Z. Competitive Growth of Ge Quantum Dots on a Si Micropillar with Pits for a Precisely Site-Controlled QDs/Microdisk System. Nanomaterials 2023, 13, 2323. [Google Scholar] [CrossRef]
  28. Li, Y.; Cui, C.; Song, J.; Liu, Q.; Yuan, S.; Zeng, C.; Xia, J. Precisely ordered Ge quantum dots on a patterned Si microring for enhanced light-emission. Nanotechnology 2020, 31, 385603. [Google Scholar] [CrossRef]
  29. Zhang, N.; Wang, S.; Chen, P.; Zhang, L.; Peng, K.; Jiang, Z.; Zhong, Z. An array of SiGe nanodisks with Ge quantum dots on bulk Si substrates demonstrating a unique light–matter interaction associated with dual coupling. Nanoscale 2019, 11, 15487–15496. [Google Scholar] [CrossRef]
  30. Zhang, N.; Chen, P.; Yan, J.; Peng, K.; Wang, L.; Hu, H.; Jiang, Z.; Zhong, Z. Sensitively Site-Dependent Enhancement of Emissions from Ge Quantum Dots in SiGe Microdisks. Adv. Photonics Res. 2022, 3, 2200100. [Google Scholar] [CrossRef]
  31. Zhang, N.; Hao, Y.; Yao, Y.; Gao, L.; Miao, T.; Hu, H.; Wang, L.; Zhong, Z. Enhancing emission in a QD–nanodisk system via the alignment of the orientation of excitons with the polarization of Mie modes. Appl. Phys. Lett. 2023, 122, 261104. [Google Scholar] [CrossRef]
  32. Zhang, Z.; Yan, J.; Dong, Z.; Zhang, N.; Chen, P.; Peng, K.; Zhu, Y.; Zhong, Z.; Jiang, Z. Unique Enhancement of the Whispering Gallery Mode in Hexagonal Microdisk Resonator Array with Embedded Ge Quantum Dots on Si. Nanomaterials 2023, 13, 2553. [Google Scholar] [CrossRef] [PubMed]
  33. Yuan, S.; Qiu, X.; Cui, C.; Zhu, L.; Wang, Y.; Li, Y.; Song, J.; Huang, Q.; Xia, J. Strong Photoluminescence Enhancement in All-Dielectric Fano Metasurface with High Quality Factor. ACS Nano 2017, 11, 10704–10711. [Google Scholar] [CrossRef] [PubMed]
  34. Cui, C.; Zhou, C.; Yuan, S.; Qiu, X.; Zhu, L.; Wang, Y.; Li, Y.; Song, J.; Huang, Q.; Wang, Y.; et al. Multiple Fano Resonances in Symmetry Breaking Silicon Metasurface for Manipulating Light Emission. ACS Photonics 2018, 5, 4074–4080. [Google Scholar] [CrossRef]
  35. Cui, C.; Yuan, S.; Qiu, X.; Zhu, L.; Wang, Y.; Li, Y.; Song, J.; Huang, Q.; Zeng, C.; Xia, J. Light emission driven by magnetic and electric toroidal dipole resonances in silicon metasurface. Nanoscale 2019, 11, 14446–14454. [Google Scholar] [CrossRef]
  36. Gladyshev, S.A.; Bogdanov, A.A.; Kapitanova, P.V.; Rybin, M.V.; Koshelev, K.L.; Sadrieva, Z.F.; Samusev, K.B.; Kivshar, Y.S.; Limonov, M.F. High-Q states and Strong mode coupling in high-index dielectric resonators. J. Phys. Conf. Ser. 2018, 1124, 051058. [Google Scholar] [CrossRef]
  37. Joseph, S.; Pandey, S.; Sarkar, S.; Joseph, J. Bound states in the continuum in resonant nanostructures: An overview of engineered materials for tailored applications. Nanophotonics 2021, 10, 4175–4207. [Google Scholar] [CrossRef]
  38. Lee, J.; Zhen, B.; Chua, S.-L.; Qiu, W.; Joannopoulos, J.D.; Soljačić, M.; Shapira, O. Observation and Differentiation of Unique High-Q Optical Resonances Near Zero Wave Vector in Macroscopic Photonic Crystal Slabs. Phys. Rev. Lett. 2012, 109, 067401. [Google Scholar] [CrossRef]
  39. Moiseyev, N. Suppression of Feshbach Resonance Widths in Two-Dimensional Waveguides and Quantum Dots: A Lower Bound for the Number of Bound States in the Continuum. Phys. Rev. Lett. 2009, 102, 167404. [Google Scholar] [CrossRef]
  40. Plotnik, Y.; Peleg, O.; Dreisow, F.; Heinrich, M.; Nolte, S.; Szameit, A.; Segev, M. Experimental Observation of Optical Bound States in the Continuum. Phys. Rev. Lett. 2011, 107, 183901. [Google Scholar] [CrossRef]
  41. Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Observation of trapped light within the radiation continuum. Nature 2013, 499, 188–191. [Google Scholar] [CrossRef] [PubMed]
  42. Yang, Y.; Peng, C.; Liang, Y.; Li, Z.; Noda, S. Analytical Perspective for Bound States in the Continuum in Photonic Crystal Slabs. Phys. Rev. Lett. 2014, 113, 037401. [Google Scholar] [CrossRef] [PubMed]
  43. Azzam, S.I.; Shalaev, V.M.; Boltasseva, A.; Kildishev, A.V. Formation of Bound States in the Continuum in Hybrid Plasmonic-Photonic Systems. Phys. Rev. Lett. 2018, 121, 253901. [Google Scholar] [CrossRef]
  44. Sidorenko, M.S.; Sergaeva, O.N.; Sadrieva, Z.F.; Roques-Carmes, C.; Muraev, P.S.; Maksimov, D.N.; Bogdanov, A.A. Observation of an Accidental Bound State in the Continuum in a Chain of Dielectric Disks. Phys. Rev. Appl. 2021, 15, 034041. [Google Scholar] [CrossRef]
  45. Friedrich, H.; Wintgen, D. Interfering resonances and bound states in the continuum. Phys. Rev. A 1985, 32, 3231–3242. [Google Scholar] [CrossRef]
  46. Azzam, S.I.; Kildishev, A.V. Photonic Bound States in the Continuum: From Basics to Applications. Adv. Optical Mater. 2021, 9, 2001469. [Google Scholar] [CrossRef]
  47. Odit, M.; Koshelev, K.; Gladyshev, S.; Ladutenko, K.; Kivshar, Y.; Bogdanov, A. Observation of Supercavity Modes in Subwavelength Dielectric Resonators. Adv. Mater. 2021, 33, 2003804. [Google Scholar] [CrossRef]
  48. Krasnok, A.; Glybovski, S.; Petrov, M.; Makarov, S.; Savelev, R.; Belov, P.; Simovski, C.; Kivshar, Y. Demonstration of the enhanced Purcell factor in all-dielectric structures. Appl. Phys. Lett. 2016, 108, 211105. [Google Scholar] [CrossRef]
  49. Bulgakov, E.N.; Sadreev, A.F. High-Q resonant modes in a finite array of dielectric particles. Phys. Rev. A 2019, 99, 033851. [Google Scholar] [CrossRef]
  50. Sadrieva, Z.F.; Belyakov, M.A.; Balezin, M.A.; Kapitanova, P.V.; Nenasheva, E.A.; Sadreev, A.F.; Bogdanov, A.A. Experimental observation of a symmetry-protected bound state in the continuum in a chain of dielectric disks. Phys. Rev. A 2019, 99, 053804. [Google Scholar] [CrossRef]
  51. Mikhailovskii, M.S.; Savelev, R.S.; Sidorenko, M.S.; Sadrieva, Z.F.; Bogdanov, A.A.; Petrov, M.I. Collective states with high quality factors in chains of dielectric resonators. St. Petersburg Polytech. Univ. J. Phys. Math. 2022, 15, 213–218. [Google Scholar]
  52. Huang, T.; Wang, B.; Zhang, W.; Zhao, C. Ultracompact Energy Transfer in Anapole-based Metachains. Nano Lett. 2021, 21, 6102–6110. [Google Scholar] [CrossRef] [PubMed]
  53. Díaz-Escobar, E.; Barreda, A.I.; Mercadé, L.; Griol, A.; Pitanti, A.; Martínez, A. Light Guidance Aided by the Toroidal Dipole and the Magnetic Quadrupole in Silicon Slotted-Disk Chains. ACS Photonics 2023, 10, 707–714. [Google Scholar] [CrossRef] [PubMed]
  54. Schinke, C.; Peest, P.C.; Schmidt, J.; Brendel, R.; Bothe, K.; Vogt, M.R.; Kröger, I.; Winter, S.; Schirmacher, A.; Lim, S.; et al. Uncertainty analysis for the coefficient of band-to-band absorption of crystalline silicon. AIP Adv. 2015, 5, 67168. [Google Scholar] [CrossRef]
  55. Rodríguez-de Marcos, L.V.; Larruquert, J.I.; Méndez, J.A.; Aznárez, J.A. Self-consistent optical constants of SiO2 and Ta2O5 films. Opt. Mater. Express 2016, 6, 3622–3637. [Google Scholar] [CrossRef]
  56. Bulgakov, E.N.; Sadreev, A.F. Nearly bound states in the radiation continuum in a circular array of dielectric rods. Phys. Rev. A 2018, 97, 033834. [Google Scholar] [CrossRef]
  57. Bulgakov, E.N.; Sadreev, A.F. Bloch bound states in the radiation continuum in a periodic array of dielectric rods. Phys. Rev. A 2014, 90, 053801. [Google Scholar] [CrossRef]
  58. Yuan, L.; Lu, Y.Y. Propagating Bloch modes above the light line on a periodic array of cylinders. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 05LT01. [Google Scholar] [CrossRef]
  59. Bulgakov, E.N.; Sadreev, A.F. Bound states in the continuum with high orbital angular momentum in a dielectric rod with periodically modulated permittivity. Phys. Rev. A 2017, 96, 013841. [Google Scholar] [CrossRef]
Photonics 10 01248 g001
Figure 1. Left—a schematic view of the structure under study. Right—a scanning electron microscopy image of the sample with linear chains of disk resonators. The disk diameter is 770 nm, the period is 1 μm, and the distance d between chains is 3 μm.
Figure 1. Left—a schematic view of the structure under study. Right—a scanning electron microscopy image of the sample with linear chains of disk resonators. The disk diameter is 770 nm, the period is 1 μm, and the distance d between chains is 3 μm.
Photonics 10 01248 g001
Photonics 10 01248 g002
Figure 2. (a) Micro-PL spectra measured at 77 K on the samples with linear chains of Si disks with embedded GeSi QDs (red curve, disk radius ≈ 385 nm and period ≈ 1 μm, the number of disks in the chain N = 51). For comparison, the PL spectra of the non-processed area (gray spectrum) and the single disk (dark cyan spectrum) are presented. The laser radiation was focused in a spot of ~2 μm. In the case of the non-processed area, all QDs under the laser beam were excited, while in the case of a disk chain, only QDs in two disks in the central part of chain were excited. Therefore, the number of excited QDs in the disk chain is about 3 times less than in the non-processed area. Taking this fact into account, it was possible to estimate the true ratio (~6 times for the low-energy narrow peak) of PL signal intensities of the disk chain (red spectrum) and the non-processed area (gray spectrum). (b) The PL spectra in dependence on the disk radiusat fixed period of a chain, a = 2 µm (at this period the disks can be considered as isolated).
Figure 2. (a) Micro-PL spectra measured at 77 K on the samples with linear chains of Si disks with embedded GeSi QDs (red curve, disk radius ≈ 385 nm and period ≈ 1 μm, the number of disks in the chain N = 51). For comparison, the PL spectra of the non-processed area (gray spectrum) and the single disk (dark cyan spectrum) are presented. The laser radiation was focused in a spot of ~2 μm. In the case of the non-processed area, all QDs under the laser beam were excited, while in the case of a disk chain, only QDs in two disks in the central part of chain were excited. Therefore, the number of excited QDs in the disk chain is about 3 times less than in the non-processed area. Taking this fact into account, it was possible to estimate the true ratio (~6 times for the low-energy narrow peak) of PL signal intensities of the disk chain (red spectrum) and the non-processed area (gray spectrum). (b) The PL spectra in dependence on the disk radiusat fixed period of a chain, a = 2 µm (at this period the disks can be considered as isolated).
Photonics 10 01248 g002
Photonics 10 01248 g003
Figure 3. (a) Micro-PL spectra in dependence on the disk radius R at fixed period of a chain, a = 1 µm. The arrows indicate the positions of narrow peaks. (b) Micro-PL spectra depending on the period of the chain at fixed radius R = 385 nm. The number of disks in the chain N = 51.
Figure 3. (a) Micro-PL spectra in dependence on the disk radius R at fixed period of a chain, a = 1 µm. The arrows indicate the positions of narrow peaks. (b) Micro-PL spectra depending on the period of the chain at fixed radius R = 385 nm. The number of disks in the chain N = 51.
Photonics 10 01248 g003
Photonics 10 01248 g004
Figure 4. (a) The dependence of the micro-PL spectra on the number of the disks in the chain N at fixed period and radius, a = 1 µm and R = 385 nm. (b) The dependence of the gap between the narrow PL peaks on the number of disks in the chain at fixed radius R = 385 nm. The red symbols correspond to the positions of the low-energy peak, and the blue symbols correspond to the positions of the high-energy peak. The dashed lines are guides to the eye. We have processed the spectra and plotted the dependence of peak intensity on the number of resonators in the chain (the results are presented in Supplementary Materials, Figure S2).
Figure 4. (a) The dependence of the micro-PL spectra on the number of the disks in the chain N at fixed period and radius, a = 1 µm and R = 385 nm. (b) The dependence of the gap between the narrow PL peaks on the number of disks in the chain at fixed radius R = 385 nm. The red symbols correspond to the positions of the low-energy peak, and the blue symbols correspond to the positions of the high-energy peak. The dashed lines are guides to the eye. We have processed the spectra and plotted the dependence of peak intensity on the number of resonators in the chain (the results are presented in Supplementary Materials, Figure S2).
Photonics 10 01248 g004
Photonics 10 01248 g005
Figure 5. (a) The near field distribution, calculated for the Mie mode with an orbital angular momentum m = 3 in a single Si resonator positioned on the SiO2 layer. (b) The cross-section of the far field radiation pattern for this mode, calculated without SiO2 layer, in the homogeneous medium approximation. The radius of disks was 385 nm. The refractive index and the extinction coefficient of silicon and SiO2 were taken according to [54,55].
Figure 5. (a) The near field distribution, calculated for the Mie mode with an orbital angular momentum m = 3 in a single Si resonator positioned on the SiO2 layer. (b) The cross-section of the far field radiation pattern for this mode, calculated without SiO2 layer, in the homogeneous medium approximation. The radius of disks was 385 nm. The refractive index and the extinction coefficient of silicon and SiO2 were taken according to [54,55].
Photonics 10 01248 g005
Photonics 10 01248 g006
Figure 6. The left panel shows the calculated spectral positions of “longitudinal” (red symbols) and “transverse”(blue symbols) modes depending on the number of Si disks in the chain positioned on SiO2 layer. The right panels demonstrate the near-field distributions for “transverse” (top panels) and “longitudinal” (bottom panels) modes in the chains of 2 and 5 disks. We show |E| as in Figure 5. The radius of the disks is 385 nm, and the period is 1 µm. The refractive index and extinction coefficient of silicon and SiO2 were taken according to [54,55].
Figure 6. The left panel shows the calculated spectral positions of “longitudinal” (red symbols) and “transverse”(blue symbols) modes depending on the number of Si disks in the chain positioned on SiO2 layer. The right panels demonstrate the near-field distributions for “transverse” (top panels) and “longitudinal” (bottom panels) modes in the chains of 2 and 5 disks. We show |E| as in Figure 5. The radius of the disks is 385 nm, and the period is 1 µm. The refractive index and extinction coefficient of silicon and SiO2 were taken according to [54,55].
Photonics 10 01248 g006
Photonics 10 01248 g007
Figure 7. The dependences of quality factors of “transverse” and “longitudinal” modes (a) on the chain period and (b) on the number of Si disks in the chain with period 1 µm. The dependence on the chain period is calculated for N = 11. The radius of disks is 385 nm. The refractive index and extinction coefficient of silicon and SiO2 were taken according to [54,55].
Figure 7. The dependences of quality factors of “transverse” and “longitudinal” modes (a) on the chain period and (b) on the number of Si disks in the chain with period 1 µm. The dependence on the chain period is calculated for N = 11. The radius of disks is 385 nm. The refractive index and extinction coefficient of silicon and SiO2 were taken according to [54,55].
Photonics 10 01248 g007
Photonics 10 01248 g008
Figure 8. The dependences of quality factors (a) and radiation losses γ = Im[ω(kx)] (b) on the wave vector kx (along the chain line) calculated for the “transverse” and the “longitudinal” modes in the infinite chains of Si disks. The radius of the disks was 385 nm, and the period was 1 µm. Calculations were done without substrate, and the refractive index of the surroundings was taken as n = 1. The refractive index and extinction coefficient of silicon were taken according to [54]. The results of calculations performed for the disk chains positioned on SiO2 substrate are presented in the Supplementary Materials (Figure S6).
Figure 8. The dependences of quality factors (a) and radiation losses γ = Im[ω(kx)] (b) on the wave vector kx (along the chain line) calculated for the “transverse” and the “longitudinal” modes in the infinite chains of Si disks. The radius of the disks was 385 nm, and the period was 1 µm. Calculations were done without substrate, and the refractive index of the surroundings was taken as n = 1. The refractive index and extinction coefficient of silicon were taken according to [54]. The results of calculations performed for the disk chains positioned on SiO2 substrate are presented in the Supplementary Materials (Figure S6).
Photonics 10 01248 g008
Photonics 10 01248 g009
Figure 9. Diagram showing the number of open diffraction channels, Λ, depending on the frequency ω and the wave vector kx. Blue and red curves show the dispersion dependences for the “transverse” and the “longitudinal” modes, respectively, in infinite chains of Si disks. The radius of disks is 385 nm, and the period is 1 µm. The calculations were done without substrate, the refractive index of surroundings was taken as n = 1. The refractive index and extinction coefficient of silicon are taken according to [54].
Figure 9. Diagram showing the number of open diffraction channels, Λ, depending on the frequency ω and the wave vector kx. Blue and red curves show the dispersion dependences for the “transverse” and the “longitudinal” modes, respectively, in infinite chains of Si disks. The radius of disks is 385 nm, and the period is 1 µm. The calculations were done without substrate, the refractive index of surroundings was taken as n = 1. The refractive index and extinction coefficient of silicon are taken according to [54].
Photonics 10 01248 g009
Photonics 10 01248 g010
Figure 10. The left panels (a,c,e,g) show the near-field distributions calculated for the “longitudinal” (a,e)” and transverse” (c,g) modes in the model structures corresponding to the experimental chains of resonators with N = 2, 3 positioned on SiO2 layer. The right panels (b,d,f,h) show the corresponding cross-sections of the far-field radiation pattern, calculated without SiO2 layer, in the homogeneous medium approximation. The radius of the disks is 385 nm, and the period of the chains is 1 µm. The refractive index and extinction coefficient of silicon and SiO2 were taken according to [54,55].
Figure 10. The left panels (a,c,e,g) show the near-field distributions calculated for the “longitudinal” (a,e)” and transverse” (c,g) modes in the model structures corresponding to the experimental chains of resonators with N = 2, 3 positioned on SiO2 layer. The right panels (b,d,f,h) show the corresponding cross-sections of the far-field radiation pattern, calculated without SiO2 layer, in the homogeneous medium approximation. The radius of the disks is 385 nm, and the period of the chains is 1 µm. The refractive index and extinction coefficient of silicon and SiO2 were taken according to [54,55].
Photonics 10 01248 g010
Photonics 10 01248 g011
Figure 11. The near-field distributions calculated at λ = 1.506 (E ≈ 823 meV) µm for the infinite chain of resonators with embedded Z-dipoles. The radius of disks was 385 nm, the period of the chain is 1 µm, and the height H = 440 nm. The Z-dipole was placed at a depth of 150 nm from the top plane of the disk. In XY-plane, this dipole was positioned on the Y-axis at a distance 2R/3 from the symmetry axis of the disk. The dashed lines show the positions of the XY- and XZ-sections. The panels (a,d,g) are related to the Ex component. The panels (b,e,h)—Ey component. The panels (c,f,i)—the Ez component. The refractive index and extinction coefficient of silicon and SiO2 were taken according to [54,55].
Figure 11. The near-field distributions calculated at λ = 1.506 (E ≈ 823 meV) µm for the infinite chain of resonators with embedded Z-dipoles. The radius of disks was 385 nm, the period of the chain is 1 µm, and the height H = 440 nm. The Z-dipole was placed at a depth of 150 nm from the top plane of the disk. In XY-plane, this dipole was positioned on the Y-axis at a distance 2R/3 from the symmetry axis of the disk. The dashed lines show the positions of the XY- and XZ-sections. The panels (a,d,g) are related to the Ex component. The panels (b,e,h)—Ey component. The panels (c,f,i)—the Ez component. The refractive index and extinction coefficient of silicon and SiO2 were taken according to [54,55].
Photonics 10 01248 g011
Photonics 10 01248 g012
Figure 12. The near-field distributions calculated at λ = 1.488 µm (E ≈ 833 meV) for the infinite chain of resonators with embedded X-dipoles. The radius of the disks is 385 nm, the period of the chain is 1 µm, and the height H = 440 nm. The X-dipole is placed at a depth of 150 nm from the top plane of the disk. In XY-plane, this dipole is positioned on the Y-axis at a distance of 2R/3 from the symmetry axis of the disk. The dashed lines show the positions of the XY- and XZ-sections. The panels (a,d,g) are related to the Ex component. The panels (b,e,h)—Ey component. The panels (c,f,i)—Ez component.
Figure 12. The near-field distributions calculated at λ = 1.488 µm (E ≈ 833 meV) for the infinite chain of resonators with embedded X-dipoles. The radius of the disks is 385 nm, the period of the chain is 1 µm, and the height H = 440 nm. The X-dipole is placed at a depth of 150 nm from the top plane of the disk. In XY-plane, this dipole is positioned on the Y-axis at a distance of 2R/3 from the symmetry axis of the disk. The dashed lines show the positions of the XY- and XZ-sections. The panels (a,d,g) are related to the Ex component. The panels (b,e,h)—Ey component. The panels (c,f,i)—Ez component.
Photonics 10 01248 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zinovyev, V.A.; Smagina, Z.V.; Zinovieva, A.F.; Rodyakina, E.E.; Kacyuba, A.V.; Astankova, K.N.; Volodin, V.A.; Baryshnikova, K.V.; Petrov, M.I.; Mikhailovskii, M.S.; et al. Collective Modes in the Luminescent Response of Si Nanodisk Chains with Embedded GeSi Quantum Dots. Photonics 2023, 10, 1248. https://doi.org/10.3390/photonics10111248

AMA Style

Zinovyev VA, Smagina ZV, Zinovieva AF, Rodyakina EE, Kacyuba AV, Astankova KN, Volodin VA, Baryshnikova KV, Petrov MI, Mikhailovskii MS, et al. Collective Modes in the Luminescent Response of Si Nanodisk Chains with Embedded GeSi Quantum Dots. Photonics. 2023; 10(11):1248. https://doi.org/10.3390/photonics10111248

Chicago/Turabian Style

Zinovyev, Vladimir A., Zhanna V. Smagina, Aigul F. Zinovieva, Ekaterina E. Rodyakina, Aleksey V. Kacyuba, Ksenya N. Astankova, Vladimir A. Volodin, Kseniia V. Baryshnikova, Mihail I. Petrov, Mikhail S. Mikhailovskii, and et al. 2023. "Collective Modes in the Luminescent Response of Si Nanodisk Chains with Embedded GeSi Quantum Dots" Photonics 10, no. 11: 1248. https://doi.org/10.3390/photonics10111248

APA Style

Zinovyev, V. A., Smagina, Z. V., Zinovieva, A. F., Rodyakina, E. E., Kacyuba, A. V., Astankova, K. N., Volodin, V. A., Baryshnikova, K. V., Petrov, M. I., Mikhailovskii, M. S., Verbus, V. A., Stepikhova, M. V., & Novikov, A. V. (2023). Collective Modes in the Luminescent Response of Si Nanodisk Chains with Embedded GeSi Quantum Dots. Photonics, 10(11), 1248. https://doi.org/10.3390/photonics10111248

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop