Tunable Vernier Series-Coupled Microring Resonator Filters Based on InGaAs/InAlAs Multiple Quantum-Well Waveguide
Abstract
:1. Introduction
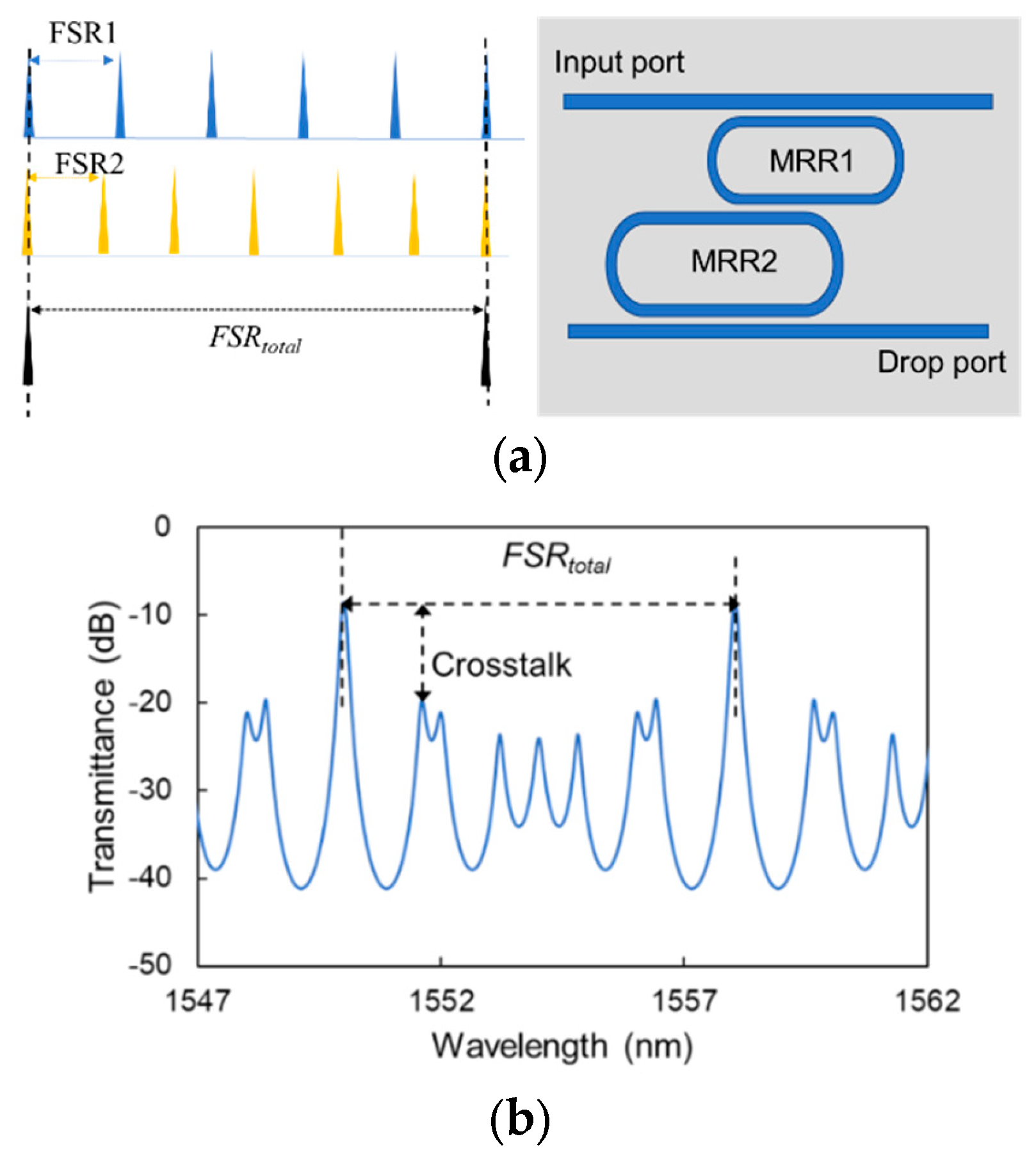
2. Working Principle and Transfer function
3. Fourth-Order Vernier MRR Filter Design and Fabrication
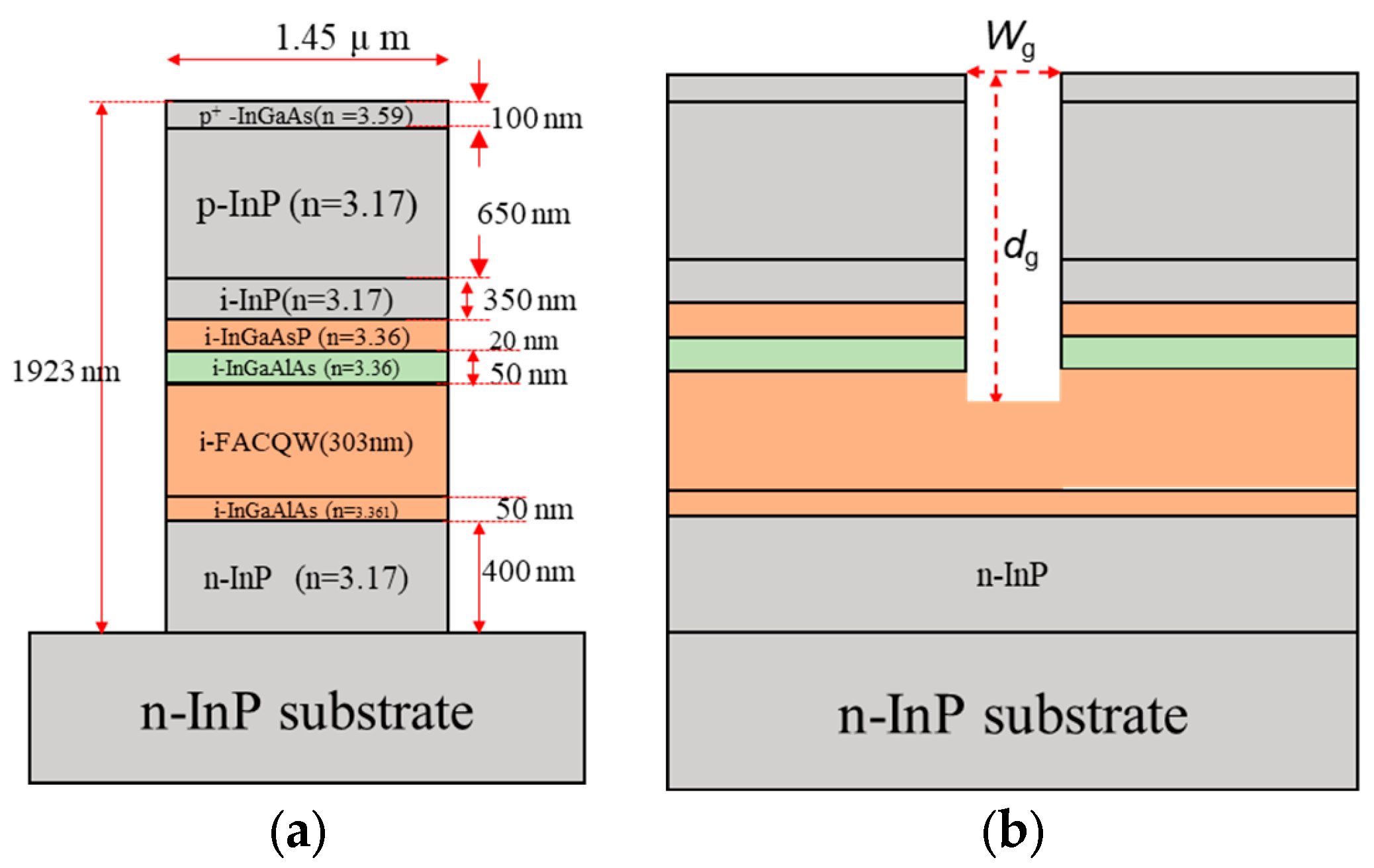
3.1. MRR Filter Design
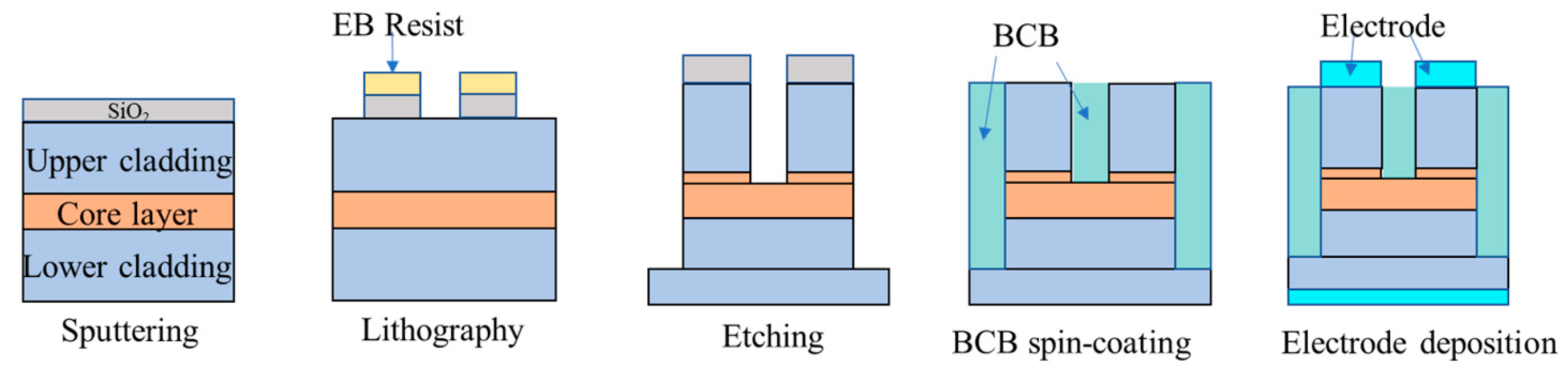
3.2. Fabrication
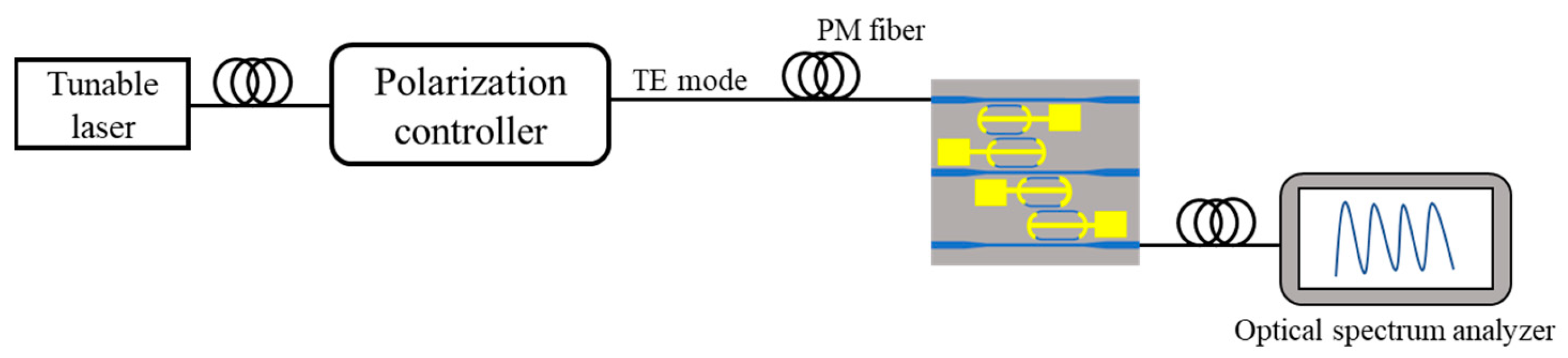
4. Result and Discussion
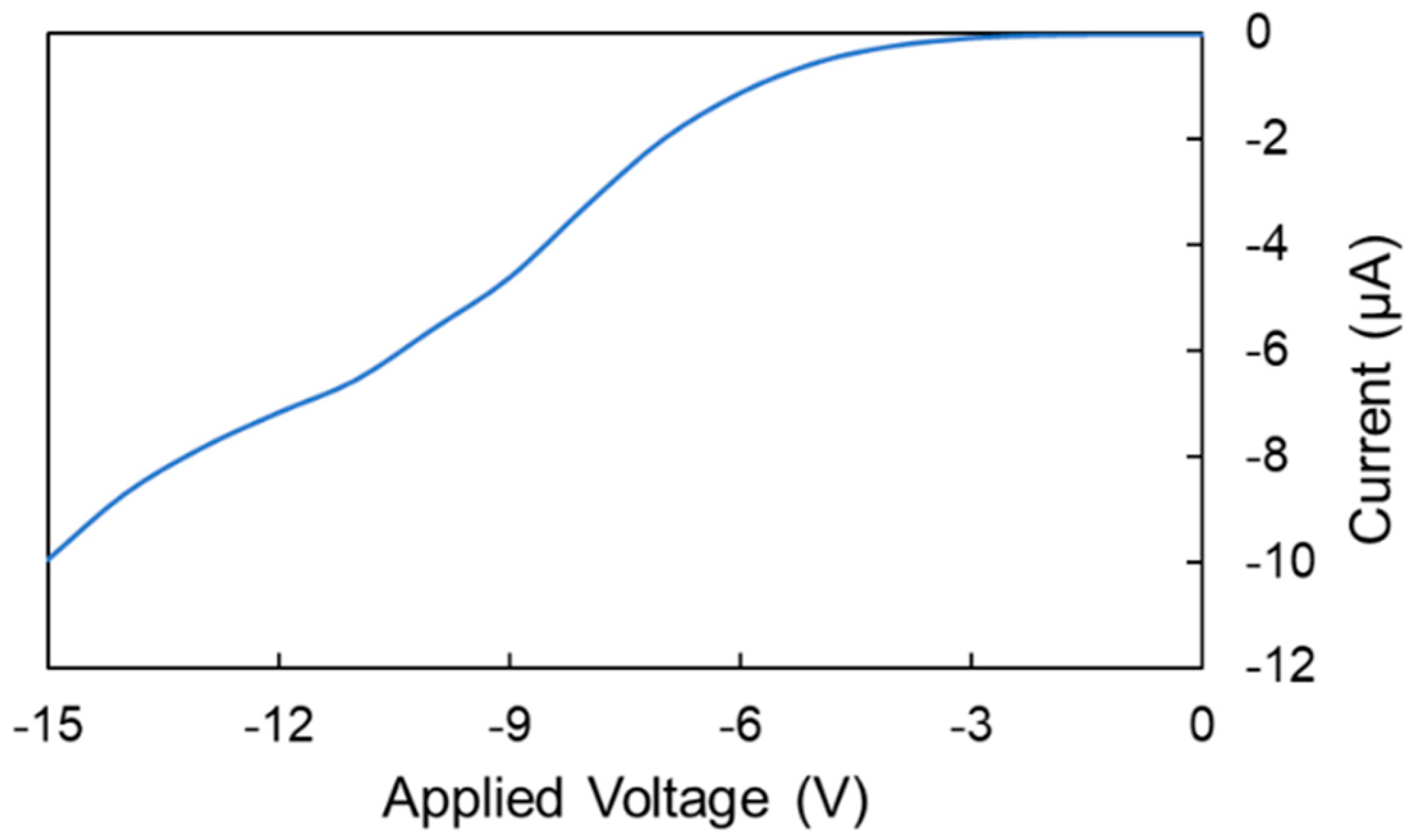
4.1. MRR Filter Characteristic
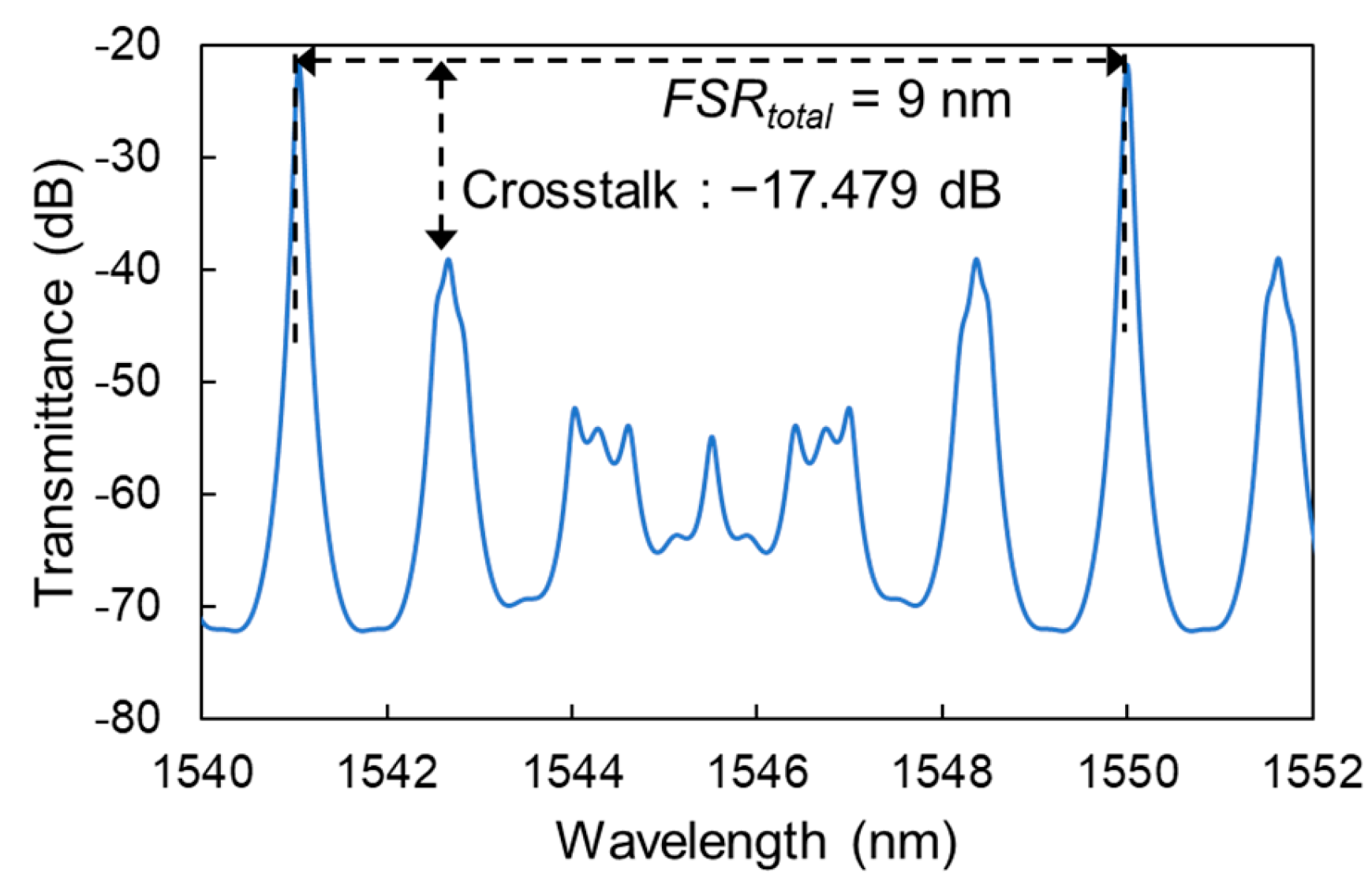
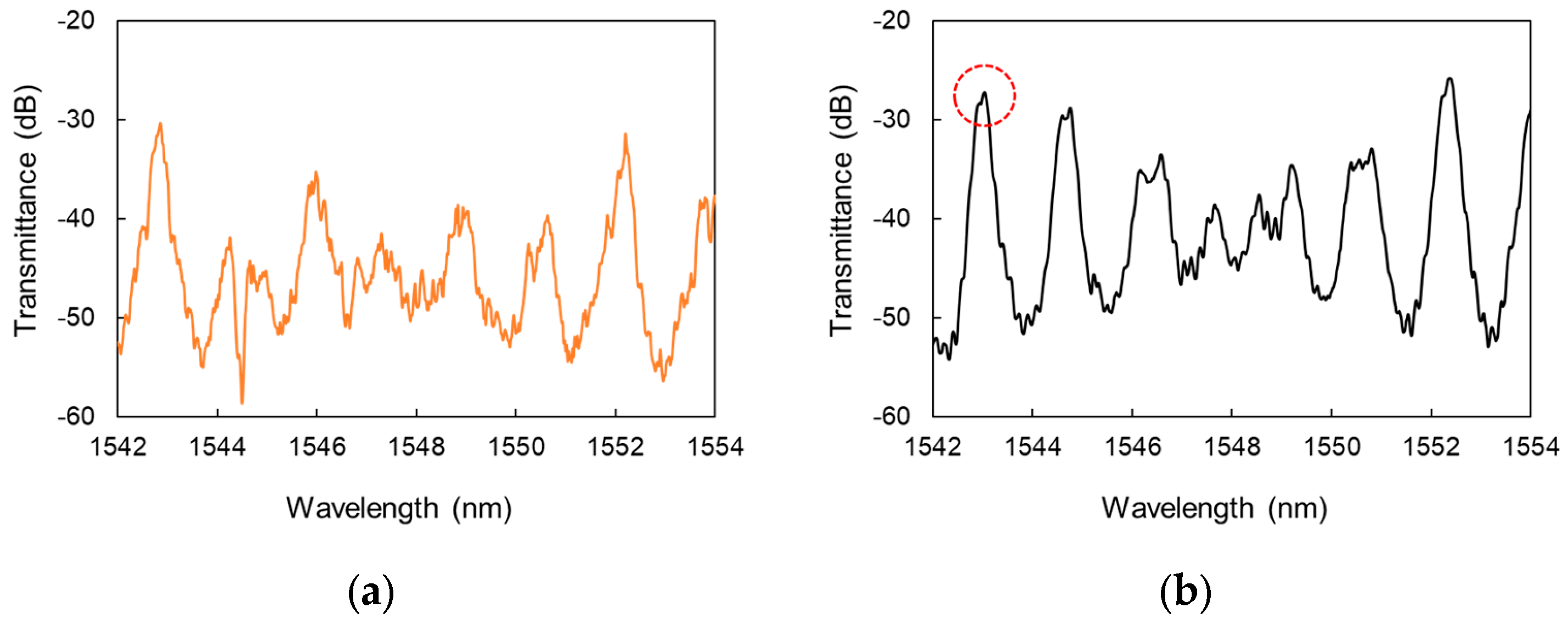
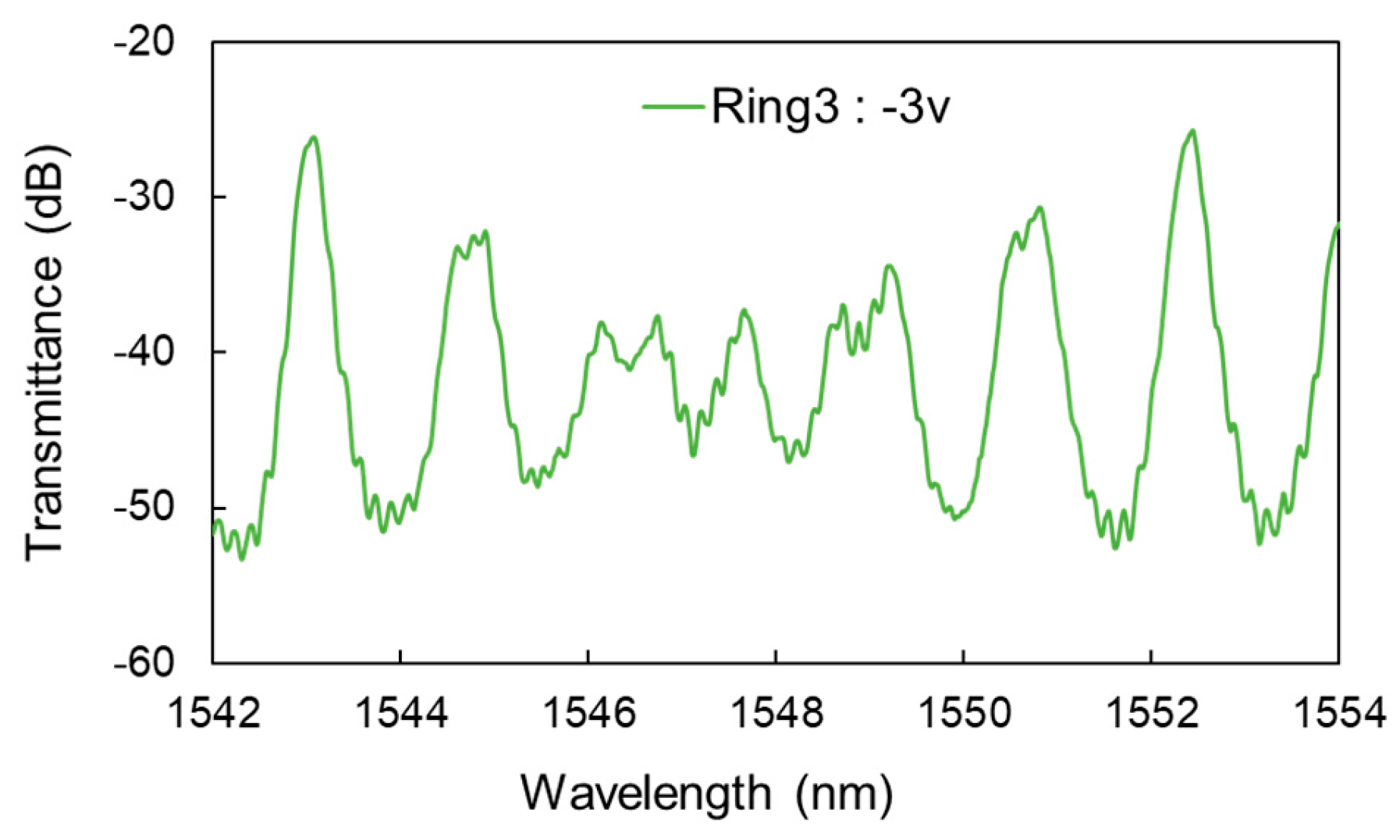
4.2. Vernier Effect Characteristic
4.3. Discussion
5. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Madsen, C.K.; Lenz, G.; Bruce, A.J.; Capuzzo, M.A.; Gomez, L.T.; Nielsen, T.N.; Brener, I. Multistage dispersion compensator using ring resonators. Opt. Lett. 1999, 24, 1555–1557. [Google Scholar] [CrossRef]
- Fan, Y.; Epping, J.P.; Oldenbeuving, R.M.; Roeloffzen, C.G.; Hoekman, M.; Dekker, R.; Heideman, R.G.; van der Slot, P.J.; Boller, K.J. Optically Integrated InP–Si3N4 Hybrid Laser. IEEE Photon. J. 2016, 8, 1505111. [Google Scholar] [CrossRef]
- Wei, H.; Krishnaswamy, S. Polymer micro-ring resonator integrated with a fiber ring laser for ultrasound detection. Opt. Lett. 2017, 42, 2655–2658. [Google Scholar] [CrossRef] [PubMed]
- Sakai, K.; Kato, S.; Yoshikawa, N.; Kokubun, Y.; Arakawa, T. Proposal of ultra-low voltage quantum well optical modulator for optical interconnection in superconducting integrated circuit systems. J. Appl. Phys. 2020, 59, SOOB01. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, Y.; Zhang, T.; Shao, Z.; Wen, Y.; Xu, P.; Zhang, Y.; Yu, S. Design and optimization of optical modulators based on graphene-on-silicon nitride microring resonators. J. Opt. 2017, 19, 045801. [Google Scholar] [CrossRef]
- Waldow, M.; Plötzing, T.; Gottheil, M.; Först, M.; Bolten, J.; Wahlbrink, T.; Kurz, H. 25ps all-optical switching in oxygen implanted silicon-on-insulator microring resonator. Opt. Express 2008, 16, 7693–7702. [Google Scholar] [CrossRef] [PubMed]
- Pelc, J.S.; Rivoire, K.; Vo, S.; Santori, C.; Fattal, D.A.; Beausoleil, R.G. Picosecond all-optical switching in hydrogenated amorphous silicon microring resonators. Opt. Express 2014, 22, 3797–3810. [Google Scholar] [CrossRef]
- Katti, R.; Prince, S. Photonic delay lines based on silicon coupled resonator optical waveguide structures. Silicon 2018, 10, 2793–2800. [Google Scholar] [CrossRef]
- Dey, S. Optical hextuple ring resonator-based delay line architecture. J. Opt. 2022, 51, 106–114. [Google Scholar] [CrossRef]
- Liu, S.; Shoji, Y.; Mizumoto, T. TE-mode magneto-optical isolator based on an asymmetric microring resonator under a unidirectional magnetic field. Opt. Express 2022, 30, 9934–9943. [Google Scholar] [CrossRef]
- Pintus, P.; Huang, D.; Zhang, C.; Shoji, Y.; Mizumoto, T.; Bowers, J.E. Microring-based optical isolator and circulator with integrated electromagnet for silicon photonics. J. Light. Technol. 2017, 35, 1429–1437. [Google Scholar] [CrossRef]
- Saharia, A.; Mudgal, N.; Choure, K.K.; Maddila, R.; Tiwari, M.; Singh, G. Proposed all-optical read-only memory element employing Si3N4 based optical microring resonator. Optik 2022, 25, 168493. [Google Scholar] [CrossRef]
- Gu, J.; Feng, C.; Zhao, Z.; Ying, Z.; Liu, M.; Chen, R.T.; Pan, D.Z. SqueezeLight: Towards scalable optical neural networks with multi-operand ring resonators. In Proceedings of the Design, Automation Test in Europe Conference Exhibition (DATE), Grenoble, France, 1–5 February 2021; pp. 238–243. [Google Scholar]
- Matsuura, S.; Yamasaku, N.; Nishijima, Y.; Okazaki, S.; Arakawa, T. Characteristics of highly sensitive hydrogen sensor based on Pt-WO3/Si microring resonator. Sensors 2019, 20, 96. [Google Scholar] [CrossRef] [PubMed]
- Yamasaku, N.; Matsuura, S.; Nishijima, Y.; Arakawa, T.; Okazaki, S. Response Characteristics of Silicon Microring Resonator Hydrogen Sensor. Proceedings 2018, 2, 795. [Google Scholar]
- Barwicz, T.; Popovic, M.A.; Rakich, P.T.; Watts, M.R.; Haus, H.A.; Ippen, E.P.; Smith, H.I. Microring-resonator-based add-drop filters in SiN: Fabrication and analysis. Opt. Express 2004, 12, 1437–1442. [Google Scholar] [CrossRef]
- Ding, Y.; Tao, S.; Wang, X.; Shang, C.; Pan, A.; Zeng, C.; Xia, J. Thermo-optic tunable optical filters with GHz-bandwidth and flat-top passband on thin film lithium niobate platform. Opt. Express 2022, 30, 22135–22142. [Google Scholar] [CrossRef] [PubMed]
- Samanta, S.; Dey, P.K.; Banerji, P.; Ganguly, P. Development of micro-ring resonator-based optical bandpass filter using SU-8 polymer and optical lithography. Opt. Mater. 2018, 77, 122–126. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, C.; Liang, D.; Dai, D. Submicron-resonator-based add-drop optical filter with an ultra-large free spectral range. Opt. Express 2019, 27, 416–422. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Wang, W.; Qiu, C.; Yu, P.; Qiu, H.; Zhao, Y.; Jiang, X.; Yang, J. Thermally tunable filters based on third-order microring resonators for WDM applications. IEEE Photon. Technol. Lett. 2012, 24, 524–526. [Google Scholar] [CrossRef]
- Liu, L.; Xue, W.; Jin, X.; Yue, J.; Yu, Z.; Zhou, L. Bandwidth and wavelength tunable all-optical filter based on cascaded opto-mechanical microring resonators. IEEE Photon. J. 2019, 11, 7800210. [Google Scholar] [CrossRef]
- Arakawa, T.; Toya, T.; Ushigome, M.; Yamaguchi, K.; Ide, T.; Tada, K. InGaAs/InAlAs five-layer asymmetric coupled quantum well exhibiting giant electrorefractive index change. Jpn. J. Appl. Phys. 2011, 50, 032204. [Google Scholar] [CrossRef]
- Ikehara, H.; Goto, T.; Kamiya, H.; Arakawa, T.; Kokubun, Y. Hitless wavelength-selective switch based on quantum well second-order series-coupled microring resonators. Opt. Express 2013, 21, 6377–6390. [Google Scholar] [CrossRef] [PubMed]
- Arakawa, T.; Hariki, T.; Amma, Y.; Fukuoka, M.; Ushigome, M.; Tada, K. Low-voltage Mach–Zehnder modulator with InGaAs/InAlAs five-layer asymmetric coupled quantum well. Jpn. J. Appl. Phys. 2012, 51, 042203. [Google Scholar] [CrossRef]
- Makino, T.; Gotoh, T.; Hasegawa, R.; Arakawa, T.; Kokubun, Y. Microring resonator wavelength tunable filter using five-layer asymmetric coupled quantum well. J. Light. Technol. 2011, 29, 2387–2393. [Google Scholar] [CrossRef]
- Kamiya, H.; Goto, T.; Ikehara, H.; Katouf, R. Arakawa, and Y. Kokubun. Hitless wavelength-selective switch with quadruple series-coupled microring resonators using multiple-quantum-well waveguides. Opt. Express 2013, 21, 20837–20850. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, X.; Lu, L.; Chen, J. Tunable Vernier Microring Optical Filters With p-i-p-Type Microheaters. IEEE Photon. J. 2013, 5, 6601211. [Google Scholar] [CrossRef]
- Boeck, R.; Jaeger, N.A.; Rouger, N.; Chrostowski, L. Series-coupled silicon racetrack resonators and the Vernier effect: Theory and measurement. Opt. Express 2010, 18, 25151–25157. [Google Scholar] [CrossRef]
- Goebuchi, Y.; Kato, T.; Kokubun, Y. Optimum arrangement of high-order series-coupled microring resonator for crosstalk reduction. J. Appl. Phys. 2006, 45, 5769. [Google Scholar] [CrossRef]
- Peng, Z.; Komatsubara, T.; Yamauchi, M.; Arakawa, T. Design of a series-coupled microring resonator wavelength filter using the digital filter design method. J. Opt. Soc. B. 2021, 38, 2837–2846. [Google Scholar] [CrossRef]
- Chaichuay, C.; Yupapin, P.P.; Saeung, P. The serially coupled multiple ring resonator filters and Vernier effect. Opt. Appl. 2009, 39, 174. [Google Scholar]







| Parameters | Designed Values |
|---|---|
| FSRtotal (nm) | 9 |
| Coupling efficiencies, K0–K5 | 0.178, 0.01, 0.179, 0.179, 0.01, 0.181 |
| Coupling lengths, L0–L5 (μm) | 37.87, 8.70, 37.99, 37.99, 8.70, 38.20 |
| Round-trip lengths of Ring 1 and Ring 2 (μm) | 351.19, 421.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Arakawa, T. Tunable Vernier Series-Coupled Microring Resonator Filters Based on InGaAs/InAlAs Multiple Quantum-Well Waveguide. Photonics 2023, 10, 1256. https://doi.org/10.3390/photonics10111256
Peng Z, Arakawa T. Tunable Vernier Series-Coupled Microring Resonator Filters Based on InGaAs/InAlAs Multiple Quantum-Well Waveguide. Photonics. 2023; 10(11):1256. https://doi.org/10.3390/photonics10111256
Chicago/Turabian StylePeng, Zhifeng, and Taro Arakawa. 2023. "Tunable Vernier Series-Coupled Microring Resonator Filters Based on InGaAs/InAlAs Multiple Quantum-Well Waveguide" Photonics 10, no. 11: 1256. https://doi.org/10.3390/photonics10111256
APA StylePeng, Z., & Arakawa, T. (2023). Tunable Vernier Series-Coupled Microring Resonator Filters Based on InGaAs/InAlAs Multiple Quantum-Well Waveguide. Photonics, 10(11), 1256. https://doi.org/10.3390/photonics10111256





