Theoretical Substantiation of the Possibility of Performing Non-Damaging UV Diagnostics of Biological Tissues In Vivo
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Outline
2.2. Experimental
2.3. Monte Carlo Modeling
3. Results and Discussion
3.1. Determination of Diffuse Reflectance from Skin
3.2. Selection of the Optical Parameters of Skin
3.3. Calculation of Distribution of Radiation Energy Absorption in Skin
3.4. Experimental Validation of Theoretical Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moseley, H.; Allan, D.; Amatiello, H.; Coleman, A.; du Peloux Menagé, H.; Edwards, C.; Exton, L.S.; Ferguson, J.; Garibaldinos, T.; Martin, C.; et al. Guidelines on the measurement of ultraviolet radiation levels in ultraviolet phototherapy: Report issued by the British Association of Dermatologists and British Photodermatology Group 2015. Br. J. Dermatol. 2015, 173, 333–350. [Google Scholar] [CrossRef]
- Herzinger, T.; Berneburg, M.; Ghoreschi, K.; Gollnick, H.; Hölzle, E.; Hönigsmann, P.; Lehmann, P.; Peters, T.; Röcken, M.; Scharffetter-Kochanek, K.; et al. S1-Guidelines on UV phototherapy and photochemotherapy. J. Dtsch. Dermatol. Ges. 2016, 14, 853–876. [Google Scholar] [CrossRef]
- Makmatov-Rys, M.B.; Kulikov, D.A.; Kaznacheeva, E.V.; Khlebnikova, A.N. Pathogenic features of acute ultraviolet-induced skin damage. Russ. J. Clinic. Dermatol. Venereol. 2019, 18, 412–417. (In Russian) [Google Scholar] [CrossRef]
- IAEA. Absorbed Dose Determination in External Beam Radiotherapy. In Technical Reports Series No. 398; IAEA: Vienna, Austria, 2000; p. 229. [Google Scholar]
- Almond, P.R.; Biggs, P.J.; Coursey, B.M.; Hanson, W.F.; Huq, M.S.; Nath, R.; Rogers, D.W. AAPM’s TG-51 protocol for clinical reference dosimetry of high-energy photon and electron beams. Med. Phys. 1999, 26, 1847–1870. [Google Scholar] [CrossRef]
- Lehnen, M.; Koppermann, M.; Korber, A.; Grabbe, S.; Dissemond, J. Vergleich der minimalen Erythemdosis von Schmalspektrum-UV-B-und Breitspektrum-UV-B-Strahlern mit einem neuen UV-Handgerät. Hautarzt 2005, 56, 258–264. [Google Scholar] [CrossRef]
- Gambichler, T.; Majert, J.; Pljakic, A.; Rooms, I.; Wolf, P. Determination of the minimal erythema dose for ultraviolet A1 radiation. Br. J. Dermatol. 2017, 177, 238–244. [Google Scholar] [CrossRef]
- Yun, S.; Kwok, S. Light in diagnosis, therapy and surgery. Nat. Biomed. Eng. 2017, 1, 0008. [Google Scholar] [CrossRef]
- Tuchin, V.V.; Utz, S.R.; Yaroslavsky, I.V. Tissue optics, light distribution, and spectroscopy. Opt. Eng. 1994, 33, 3178–3188. [Google Scholar] [CrossRef]
- Yurii, P.; Sinichkin, Y.P.; Utz, S.R.; Mavliutov, A.H.; Pilipenko, H.A. In vivo fluorescence spectroscopy of the human skin: Experiments and models. J. Biomed. Opt. 1998, 3, 201–211. [Google Scholar] [CrossRef]
- Throm, C.M.; Wiora, G.; Reble, C.; Schleusener, J.; Schanzer, S.; Karrer, H.; Kolbe, L.; Khazaka, G.; Meinke, M.C.; Lademann, J. In vivo sun protection factor and UVA protection factor determination using (hybrid) diffuse reflectance spectroscopy and a multi-lambda-LED light source. J. Biophotonics 2020, 14, e202000348. [Google Scholar] [CrossRef]
- Utzinger, U.; Richards-Kortum, R.R. Fiber optic probes for biomedical optical spectroscopy. J. Biomed. Opt. 2003, 8, 121–147. [Google Scholar] [CrossRef]
- Kulikov, D.; Makmatov-Rys, M.; Raznitsyna, I.; Glazkova, P.; Gerzhik, A.; Glazkov, A.; Andreeva, V.; Kassina, D.; Rogatkin, D. Methods of Non-Invasive In Vivo Optical Diagnostics in the Assessment of Structural Changes in the Skin Induced by Ultraviolet Exposure in an Experimental Model. Diagnostics 2021, 11, 1464. [Google Scholar] [CrossRef]
- Parrish, J.A.; Jaenicke, K.F.; Anderson, R.R. Erythema and melanogenesis action spectra of normal human skin. Photochem. Photobiol. 1982, 36, 187–191. [Google Scholar] [CrossRef]
- Raznitsyna, I.A.; Tarasov, A.P.; Rogatkin, D.A. An improved system for in vivo fluorescent analysis in medicine. Instrum. Exp. Tech. 2020, 63, 267–272. [Google Scholar] [CrossRef]
- Tarasov, A.P.; Raznitsyna, I.A.; Shtyflyuk, M.E.; Rogatkin, D.A. Is the Minimal Erythema Dose Achievable at Optical Spectroscopy of Skin in Vivo? In Proceedings of the 2023 IEEE Radiation and Scattering of Electromagnetic Waves, Divnomorskoe, Russia, 26–30 June 2023; pp. 340–343. [Google Scholar] [CrossRef]
- Prahl, S.A.; Keijzer, M.; Jacques, S.L.; Welch, A.J. A Monte Carlo model of light propagation in tissue. Dosim. Laser Radiat. Med. Biol. 1989, 10305, 105–114. [Google Scholar]
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Meth. Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Bruls, W.A.; Slaper, H.; van Der Leun, J.C.; Berrens, L. Transmission of human epidermis and stratum corneum as a function of thickness in the ultraviolet and visible wavelengths. Photochem. Photobiol. 1984, 40, 485–494. [Google Scholar] [CrossRef]
- Patwardhan, S.V.; Dhawan, A.P.; Relue, P.A. Monte Carlo simulation of light-tissue interaction: Three-dimensional simulation for trans-illumination-based imaging of skin lesions. IEEE Trans. Biomed. Eng. 2005, 52, 1227–1236. [Google Scholar] [CrossRef]
- Nielsen, K.P.; Zhao, L.; Juzenas, P.; Stamnes, J.J.; Stamnes, K.; Moan, J. Reflectance Spectra of Pigmented and Nonpigmented Skin in the UV Spectral Region. Photochem. Photobiol. 2004, 80, 450–455. [Google Scholar] [CrossRef]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef]
- Friebel, M.; Roggan, A.; Müller, G.J.; Meinke, M.C. Determination of optical properties of human blood in the spectral range 250 to 1100 nm using Monte Carlo simulations with hematocrit-dependent effective scattering phase functions. J. Biomed. Opt. 2006, 11, 034021. [Google Scholar] [CrossRef]
- Bosschaart, N.; Edelman, G.J.; Aalders, M.C.; van Leeuwen, T.G.; Faber, D.J. A literature review and novel theoretical approach on the optical properties of whole blood. Lasers Med. Sci. 2014, 29, 453–479. [Google Scholar] [CrossRef]


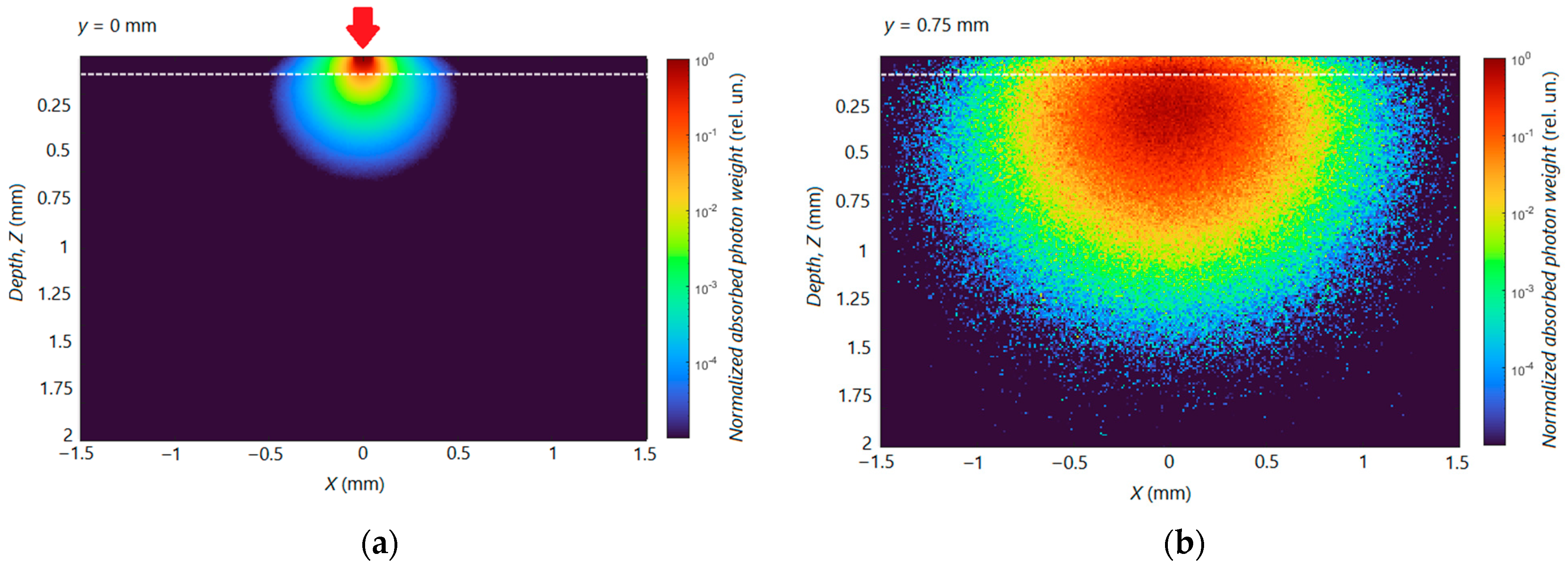
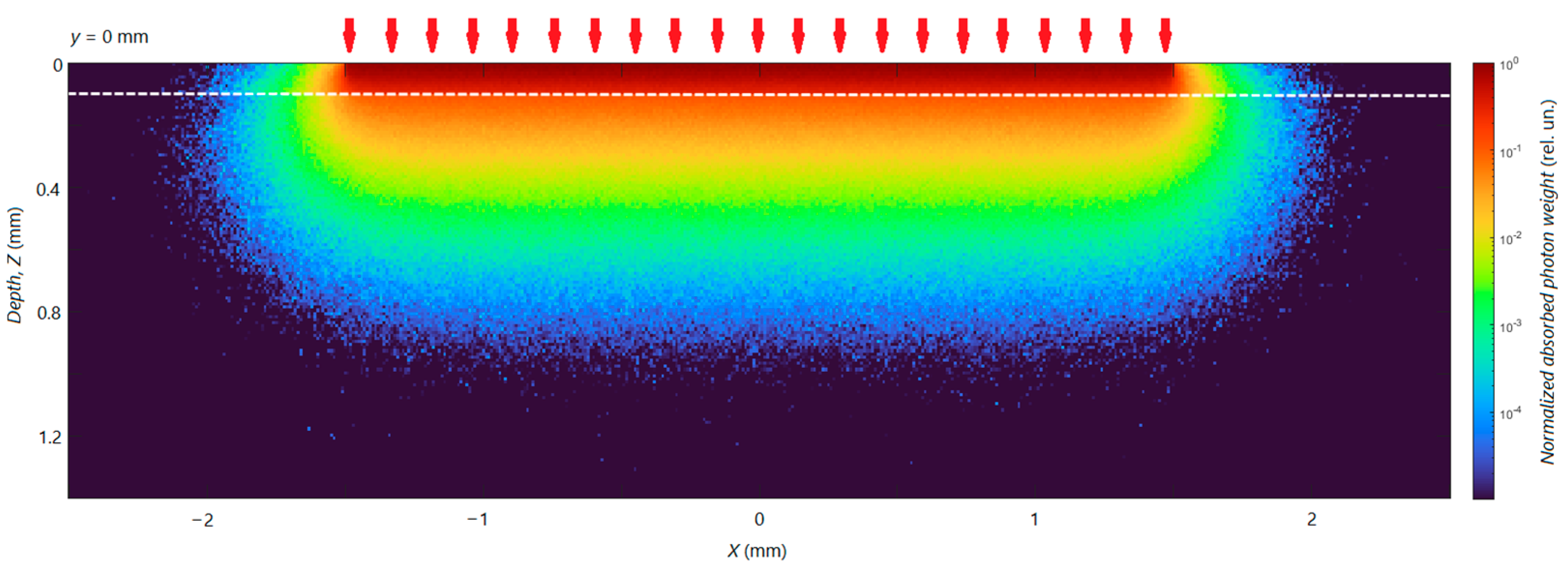


| Layer | µa (cm−1)/µs’ (cm−1) | |
|---|---|---|
| λ = 337 nm | λ = 315 nm | |
| Epidermis | 80/120 | 100/125 |
| Dermis | 30/115 | 35/120 |
| Time (sec) | λ = 337 nm | λ = 315 nm | ||
|---|---|---|---|---|
| DS (J/cm2) | DV (J/cm3) | DS (J/cm2) | DV (J/cm3) | |
| 5 | 7.7 | 11.2 | 0.2 | 0.6 |
| 20 | 31.0 | 44.7 | 0.9 | 2.4 |
| 100 | 154.8 | 223.3 | 4.7 | 12.0 |
| 200 | 309.6 | 446.6 | 9.4 | 24.0 |
| 400 | 619.2 | 893.2 | 18.8 | 48.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarasov, A.P.; Shtyflyuk, M.E.; Rogatkin, D.A. Theoretical Substantiation of the Possibility of Performing Non-Damaging UV Diagnostics of Biological Tissues In Vivo. Photonics 2023, 10, 1289. https://doi.org/10.3390/photonics10121289
Tarasov AP, Shtyflyuk ME, Rogatkin DA. Theoretical Substantiation of the Possibility of Performing Non-Damaging UV Diagnostics of Biological Tissues In Vivo. Photonics. 2023; 10(12):1289. https://doi.org/10.3390/photonics10121289
Chicago/Turabian StyleTarasov, Andrey P., Maria E. Shtyflyuk, and Dmitry A. Rogatkin. 2023. "Theoretical Substantiation of the Possibility of Performing Non-Damaging UV Diagnostics of Biological Tissues In Vivo" Photonics 10, no. 12: 1289. https://doi.org/10.3390/photonics10121289
APA StyleTarasov, A. P., Shtyflyuk, M. E., & Rogatkin, D. A. (2023). Theoretical Substantiation of the Possibility of Performing Non-Damaging UV Diagnostics of Biological Tissues In Vivo. Photonics, 10(12), 1289. https://doi.org/10.3390/photonics10121289





