Density Functional Study of Structural and Vibrational Properties of α-Moganite
Abstract
:1. Introduction
2. Theoretical Approach
3. Results and Discussion
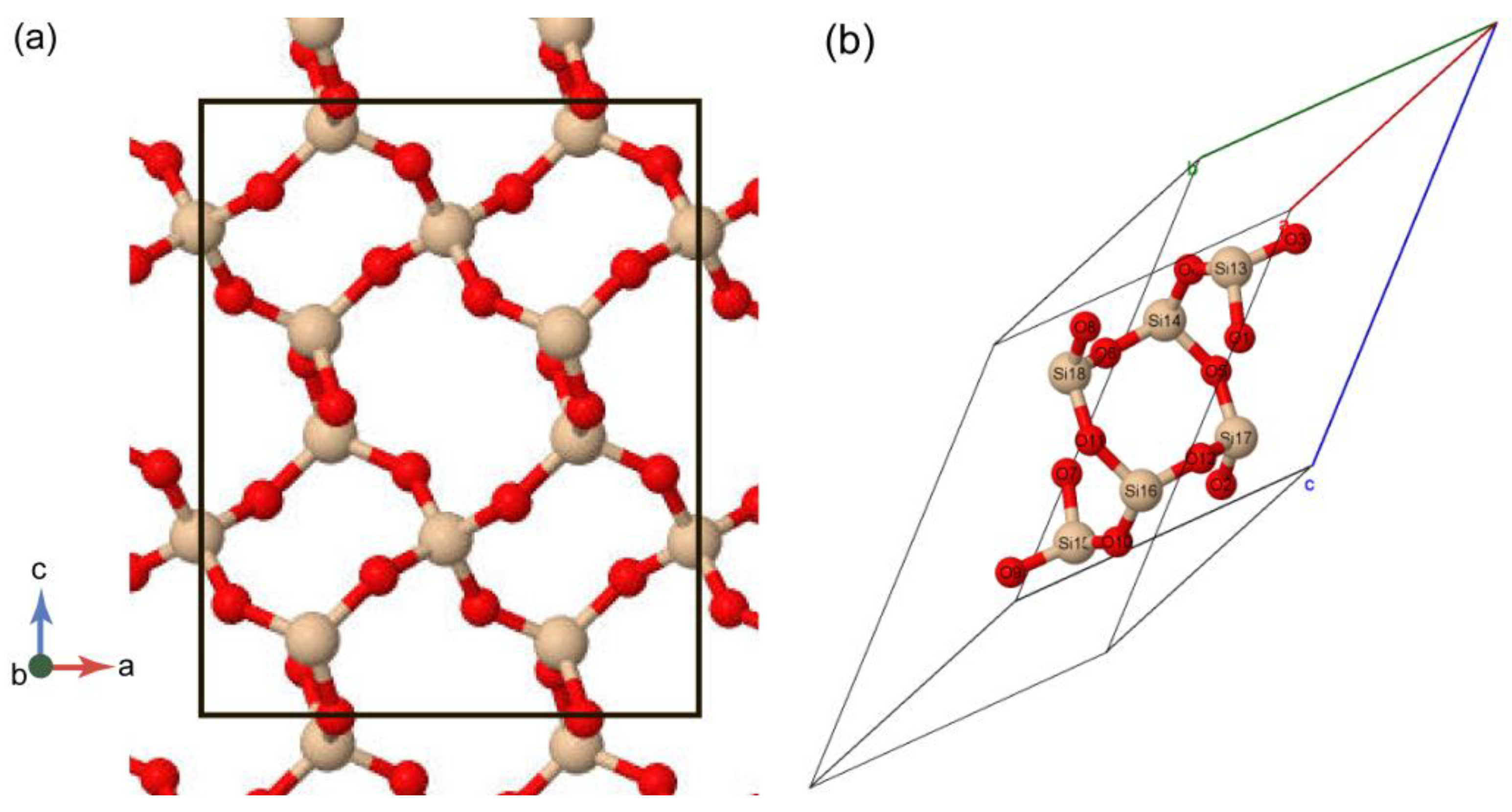
3.1. Structural Parameters
3.2. Vibrational Properties at Ambient Pressure
3.2.1. Group Theoretic Approach
3.2.2. Interpretation of Raman Spectra
3.2.3. Interpretation of the IR Absorption Spectra
3.3. Comparison of Quartz and Moganite Vibrational Spectra
3.3.1. Comparison of Raman Spectra
3.3.2. Comparison of IR Absorbance Spectra
3.4. Vibrational Properties of Moganite under Pressure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Borowicz, P.; Taube, A.; Rzodkiewicz, W.; Latek, M.; Gierałtowska, S. Raman Spectra of High-k Dielectric Layers Investigated with Micro-Raman Spectroscopy Comparison with Silicon Dioxide. Sci. World J. 2013, 2013, 208081. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, M.; Roginskii, E.; Savin, A.; Mazhenov, N.; Pankin, D. Density-Functional Study of the Si/SiO2 Interfaces in Short-Period Superlattices: Structures and Energies. Coatings 2023, 13, 1231. [Google Scholar] [CrossRef]
- Lee, S.; Xu, H.; Xu, H.; Neuefeind, J. Crystal Structure of Moganite and Its Anisotropic Atomic Displacement Parameters Determined by Synchrotron X-Ray Diffraction and X-Ray/Neutron Pair Distribution Function Analyses. Minerals 2021, 11, 272. [Google Scholar] [CrossRef]
- Flörke, O.W.; Jones, J.B.; Schmincke, H.-U. A New Microcrystalline Silica from Gran Canaria. Z. Krist. Cryst. Mater. 1976, 143, 156–165. [Google Scholar] [CrossRef]
- Miehe, G.; Graetsch, H. Crystal Structure of Moganite: A New Structure Type for Silica. Eur. J. Mineral. 1992, 4, 693–706. [Google Scholar] [CrossRef]
- Miehe, G.; Graetsch, H.; Florke, O.W. Crystal Structure and Growth Fabric of Length-Fast Chalcedony. Phys. Chem. Miner. 1984, 10, 197–199. [Google Scholar] [CrossRef]
- Kingma, K.J.; Hemley, R.J. Raman Spectroscopic Study of Microcrystalline Silica. Am. Mineral. 1994, 79, 269–273. [Google Scholar]
- Heaney, P.J.; McKeown, D.A.; Post, J.E. Anomalous Behavior at the I2/a to Imab Phase Transition in SiO2-Moganite: An Analysis Using Hard-Mode Raman Spectroscopy. Am. Mineral. 2007, 92, 631–639. [Google Scholar] [CrossRef]
- Hardgrove, C.; Rogers, A.D. Thermal Infrared and Raman Microspectroscopy of Moganite-Bearing Rocks. Am. Mineral. 2013, 98, 78–84. [Google Scholar] [CrossRef]
- Hatipoğlu, M. Moganite and Quartz Inclusions in the Nano-Structured Anatolian Fire Opals from Turkey. J. Afr. Earth Sci. 2009, 54, 1–21. [Google Scholar] [CrossRef]
- Casadio, F.; Daher, C.; Bellot-Gurlet, L. Raman Spectroscopy of Cultural Heritage Materials: Overview of Applications and New Frontiers in Instrumentation, Sampling Modalities, and Data Processing. Top. Curr. Chem. 2016, 374, 62. [Google Scholar] [CrossRef] [PubMed]
- Bersani, D.; Madariaga, J.M. Applications of Raman Spectroscopy in Art and Archaeology. J. Raman Spectrosc. 2012, 43, 1523–1528. [Google Scholar] [CrossRef]
- Povolotckaia, A.; Pankin, D.; Kurganov, N.; Borisov, E.; Grigorieva, I.; Kurochkin, A. Xiongnu Ancient Nomad Inlaid Buckles (2nd-1st Centuries BC): Multi-Analytical Research. J. Archaeol. Sci. Rep. 2023, 52, 104253. [Google Scholar] [CrossRef]
- Prado Figueroa, M.; Flores, L.; Sanchez, J.; Cesaretti, N. Biosilicification (chalcedony) in human cerebral cortex, hippocampus and cerebellum from aged patients. Micron 2008, 39, 859–867. [Google Scholar] [CrossRef] [PubMed]
- Çetin, A.; Okutan, M.; İçelli, O.; Yalçın, Z.; San, S.E.; Kibar, R.; Pesen, E. Electrical and optical properties of chalcedony and striped chalcedony. Vacuum 2013, 97, 75–80. [Google Scholar] [CrossRef]
- Kayama, M.; Nagaoka, H.; Niihara, T. Lunar and Martian Silica. Minerals 2018, 8, 267. [Google Scholar] [CrossRef]
- Moxon, T.; Ríos, S. Moganite and Water Content as a Function of Age in Agate: An XRD and Thermogravimetric Study. Eur. J. Mineral. 2004, 16, 269–278. [Google Scholar] [CrossRef]
- Zhang, M.; Moxon, T. Infrared Absorption Spectroscopy of SiO2-Moganite. Am. Mineral. 2014, 99, 671–680. [Google Scholar] [CrossRef]
- Sitarz, M.; Wyszomirski, P.; Handke, B.; Jeleń, P. Moganite in Selected Polish Chert Samples: The Evidence from MIR, Raman and X-Ray Studies. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014, 122, 55–58. [Google Scholar] [CrossRef]
- Schmidt, P.; Bellot-Gurlet, L.; Leá, V.; Sciau, P. Moganite Detection in Silica Rocks Using Raman and Infrared Spectroscopy. Eur. J. Mineral. 2014, 25, 797–805. [Google Scholar] [CrossRef]
- Rodgers, K.A.; Cressey, G. The Occurrence, Detection and Significance of Moganite (SiO2) among Some Silica Sinters. Mineral. Mag. 2001, 65, 157–167. [Google Scholar] [CrossRef]
- Parthasarathy, G.; Kunwar, A.C.; Srinivasan, R. Occurrence of Moganite-Rich Chalcedony in Deccan Flood Basalts, Killari, Maharashtra, India. Eur. J. Mineral. 2001, 13, 127–134. [Google Scholar] [CrossRef]
- Zhang, M.; Moxon, T. In Situ Infrared Spectroscopic Studies of OH, H2O and CO2 in Moganite at High Temperatures. Eur. J. Mineral. 2012, 24, 123–131. [Google Scholar] [CrossRef]
- Götze, J.; Nasdala, L.; Kleeberg, R.; Wenzel, M. Occurrence and Distribution of “Moganite” in Agate/Chalcedony: A Combined Micro-Raman, Rietveld, and Cathodoluminescence Study. Contrib. Mineral. Petrol. 1998, 133, 96–105. [Google Scholar] [CrossRef]
- Squyres, S.W.; Arvidson, R.E.; Ruff, S.; Gellert, R.; Morris, R.V.; Ming, D.W.; Crumpler, L.; Farmer, J.D.; Des Marais, D.J.; Yen, A.; et al. Detection of Silica-Rich Deposits on Mars. Science 2008, 320, 1063–1067. [Google Scholar] [CrossRef] [PubMed]
- Hantsch, U.; Winkler, B.; Pickard, C.J.; Gale, J.D.; Warren, M.C.; Milman, V.; Mauri, F. Theoretical Investigation of Moganite. Eur. J. Mineral. 2005, 17, 21–30. [Google Scholar] [CrossRef]
- Güler, E.; Uğur, G.; Uğur, Ş.; Güler, M. A Theoretical Study for the Band Gap Energies of the Most Common Silica Polymorphs. Chin. J. Phys. 2020, 65, 472–480. [Google Scholar] [CrossRef]
- Mehmood, S.; Ali, Z.; Altuijri, R.; El Maati, L.A.; Khan, S.R.; Trukhanov, S.V.; Zubar, T.I.; Sayyed, M.I.; Tishkevich, D.I.; Trukhanov, A.V. First-principles study of the rare earth anti-TH3P4 type zintles for opto-electronic and thermoelectric applications. Phys. B Condens. Matter 2023, 670, 415353. [Google Scholar] [CrossRef]
- Alharbi, F.F.; Mehmood, S.; Ali, Z.; Aman, S.; Khosa, R.Y.; Kostishyn, V.G.; Trukhanov, S.V.; Sayyed, M.I.; Tishkevich, D.I.; Trukhanov, A.V. First principles calculation to investigate the effect of Mn substitution on Cu site in CeCu 3− x Mn x V 4 O 12 (x = 0, 1, 2 and 3) system. RSC Adv. 2023, 13, 12973–12981. [Google Scholar] [CrossRef]
- Guo, Z.A.; Xian, J.Y.; Rong, L.R.; Qin, H.; Jie, Z. Theoretical study of metal ion impact on geometric and electronic properties of terbutaline compounds. Monatshefte Für Chem.-Chem. Mon. 2019, 150, 1355–1364. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, S.; Rong, C.; Zhong, A.; Liu, S. Toward Understanding the Isomeric Stability of Fullerenes with Density Functional Theory and the Information-Theoretic Approach. ACS Omega 2018, 3, 17986–17990. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; He, X.; Rong, C.; Zhong, A.; Liu, S.; Zhao, D. On the origin and nature of internal methyl rotation barriers: An information-theoretic approach study. Theor. Chem. Acc. 2022, 141, 68. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Perdew, J.P. Jacob’s Ladder of Density Functional Approximations for the Exchange-Correlation Energy. AIP Conf. Proc. 2001, 577, 1–20. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. Kristallogr. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Refson, K.; Tulip, P.R.; Clark, S.J. Variational Density-Functional Perturbation Theory for Dielectrics and Lattice Dynamics. Phys. Rev. B 2006, 73, 155114. [Google Scholar] [CrossRef]
- Aarons, J. A New CASTEP and Onetep Geometry Optimiser, 2011. Available online: http://www.hector.ac.uk/cse/distributedcse/reports/castep-geom/castep-geom/HTML/dCSE_project.html (accessed on 29 October 2023).
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Gonze, X.; Lee, C. Dynamical Matrices, Born Effective Charges, Dielectric Permittivity Tensors, and Interatomic Force Constants from Density-Functional Perturbation Theory. Phys. Rev. B 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Baroni, S.; Giannozzi, P.; Testa, A. Green’s-Function Approach to Linear Response in Solids. Phys. Rev. Lett. 1987, 58, 1861–1864. [Google Scholar] [CrossRef]
- Binggeli, N.; Chelikowsky, J.R. Elastic instability in α-quartz under pressure. Phys. Rev. Lett. 1992, 69, 2220–2223. [Google Scholar] [CrossRef]
- Hu, Q.Y.; Shu, J.-F.; Yang, W.G.; Park, C.; Chen, M.W.; Fujita, T.; Sheng, H.W. Stability limits and transformation pathways of α -quartz under high pressure. Phys. Rev. B 2017, 95, 104112. [Google Scholar] [CrossRef]
- Jmol: An Open-Source Java Viewer for Chemical Structures in 3D. Available online: https://Jmol.Sourceforge.Net/ (accessed on 29 October 2023).
- Heaney, P.J.; Post, J.E. Evidence for an I2/a Phase Transition in the Silica Polymorph Moganite at ~570 K. Am. Mineral. 2001, 86, 1358–1366. [Google Scholar] [CrossRef]
- Scott, J.F.; Porto, S.P.S. Longitudinal and Transverse Optical Lattice Vibrations in Quartz. Phys. Rev. 1967, 161, 903–910. [Google Scholar] [CrossRef]
- Shi, Y.; Neuefeind, J.; Ma, D.; Page, K.; Lamberson, L.A.; Smith, N.J.; Tandia, A.; Song, A.P. Ring Size Distribution in Silicate Glasses Revealed by Neutron Scattering First Sharp Diffraction Peak Analysis. J. Non Cryst. Solids 2019, 516, 71–81. [Google Scholar] [CrossRef]
- Salh, R. Defect Related Luminescence in Silicon Dioxide Network: A Review. In Crystalline Silicon-Properties and Uses; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Long, D.A. The Raman Effect; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Kolesov, B.A.; Geiger, C.A. Molecules in the SiO2-Clathrate Melanophlogite: A Single-Crystal Raman Study. Am. Mineral. 2004, 88, 1364–1368. [Google Scholar] [CrossRef]
- Etchepare, J.; Merian, M.; Smetankine, L. Vibrational Normal Modes of SiO2. I. α and β Quartz. J. Chem. Phys. 1974, 60, 1873–1876. [Google Scholar] [CrossRef]
- Etchepare, J.; Merian, M.; Kaplan, P. Vibrational Normal Modes of SiO2. II. Cristobalite and Tridymite. J. Chem. Phys. 1978, 68, 1531–1537. [Google Scholar] [CrossRef]
- Bustillo, M.Á.; Pérez-Jiménez, J.L.; Alonso-Zarza, A.M.; Furio, M. Moganite in the Chalcedony Varieties of Continental Cherts (Miocene, Madrid Basin, Spain). Spectrosc. Lett. 2012, 45, 109–113. [Google Scholar] [CrossRef]
- Lider, M.C.; Yurtseven, H. Temperature Dependence of the Raman Frequency of an Internal Mode for SiO2-Moganite Close to the α-β Transition. J. Thermodyn. 2012, 2012, 892696. [Google Scholar] [CrossRef]
- He, M.; Yan, W.; Chang, Y.; Liu, K.; Liu, X. Fundamental infrared absorption features of α-quartz: An unpolarized single-crystal absorption infrared spectroscopic study. Vib. Spectrosc. 2019, 101, 52–63. [Google Scholar] [CrossRef]








| Parameters | Calculations | Experiment 1 [44] | Experiment 2 [5] |
|---|---|---|---|
| a (Å) | 8.5222 | 8.797 | 8.758 |
| b (Å) | 4.7675 | 4.869 | 4.876 |
| c (Å) | 10.5895 | 10.722 | 10.715 |
| β (°) | 90.12 | 90.19 | 90.08 |
| Atom | Calculations | Experiment 1 [44] | Experiment 2 [5] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Si1 * | 1/4 | 0.96574 | 0 | 1/4 | 0.9726 | 0 | 1/4 | 0.9908 | 0 |
| Si2 * | 0.01534 | 0.29534 | 0.16564 | 0.0103 | 0.2486 | 0.1682 | 0.0115 | 0.25330 | 0.1678 |
| O1 | 0.97829 | 0.11483 | 0.29169 | 0.9781 | 0.0644 | 0.2878 | 0.9686 | 0.0680 | 0.2860 |
| O2 | 0.17034 | 0.16721 | 0.10384 | 0.1678 | 0.1708 | 0.1002 | 0.1711 | 0.1770 | 0.1050 |
| O3 | 0.87842 | 0.22505 | 0.06816 | 0.8703 | 0.2296 | 0.0675 | 0.8657 | 0.2148 | 0.0739 |
| Experimental Phonon Frequency, cm−1 | Theoretical Phonon Frequency, cm−1 | ||
|---|---|---|---|
| Reference [20] | Reference [7] | Ag Modes | Bg Modes |
| 67 | |||
| 82 | |||
| 130 | 129 | 131 | |
| 140 | 141 | 143 | 140 |
| 207 | 220 | 230 | |
| 270 | 265 | 262 | 279 |
| 317 | 310 | ||
| 356 | |||
| 375 | 370 | 361 | |
| 377 | 381 | ||
| 398 | |||
| 432 | 421 | ||
| 449 | 449 | 442 | |
| 464 | 463 | 489 | |
| 500 | 501 | 494 | |
| 710 | 693 | 693 | 699 |
| 790 | 792 | 791 | |
| 804 | |||
| 820 | 833 | 842 | |
| 1060 | 1058 | 1059 | 1067 |
| 1080 | 1084 | 1087 | 1084 |
| 1171 | 1161 | ||
| 1180 | 1177 | 1163 | |
| Au Modes | Bu Modes | ||||||
|---|---|---|---|---|---|---|---|
| Experiment | Theory, This Work | Experiment | Theory, This Work | ||||
| [18] | [5] | [22] | [18] | [5] | [22] | ||
| 207 | 201 | 165 | 162 | ||||
| 264 | 263 | 276 | |||||
| 284 | 343 | 341 | 324 | ||||
| 296 | 295 | 292 | 398 | ||||
| 369 | 448 | 447 | 447 | 432 | |||
| 421 | 420 | 418 | 409 | 483 | 480 | 473 | |
| 576 | 572 | 570 | 544 | 696 | 700 | 695 | |
| 612 | 600 | 606 | 780 | 800 | 772 | ||
| 798 | 800 | 808 | 802 | 798 | 800 | 808 | 801 |
| 1058 | 1082 | 1100 | 1105 | 1070 | |||
| 1167 | 1164 | 1080 | |||||
| 1191 | 1191 | 1193 | 1145 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pankin, D.; Smirnov, M.; Roginskii, E.; Savin, A.; Kolesnikov, I.; Povolotckaia, A. Density Functional Study of Structural and Vibrational Properties of α-Moganite. Photonics 2023, 10, 1346. https://doi.org/10.3390/photonics10121346
Pankin D, Smirnov M, Roginskii E, Savin A, Kolesnikov I, Povolotckaia A. Density Functional Study of Structural and Vibrational Properties of α-Moganite. Photonics. 2023; 10(12):1346. https://doi.org/10.3390/photonics10121346
Chicago/Turabian StylePankin, Dmitrii, Mikhail Smirnov, Evgenii Roginskii, Aleksandr Savin, Ilya Kolesnikov, and Anastasia Povolotckaia. 2023. "Density Functional Study of Structural and Vibrational Properties of α-Moganite" Photonics 10, no. 12: 1346. https://doi.org/10.3390/photonics10121346
APA StylePankin, D., Smirnov, M., Roginskii, E., Savin, A., Kolesnikov, I., & Povolotckaia, A. (2023). Density Functional Study of Structural and Vibrational Properties of α-Moganite. Photonics, 10(12), 1346. https://doi.org/10.3390/photonics10121346





