Structural Optimization and Temperature Compensation of GMM-FBG Fiber Current Transducer
Abstract
:1. Introduction
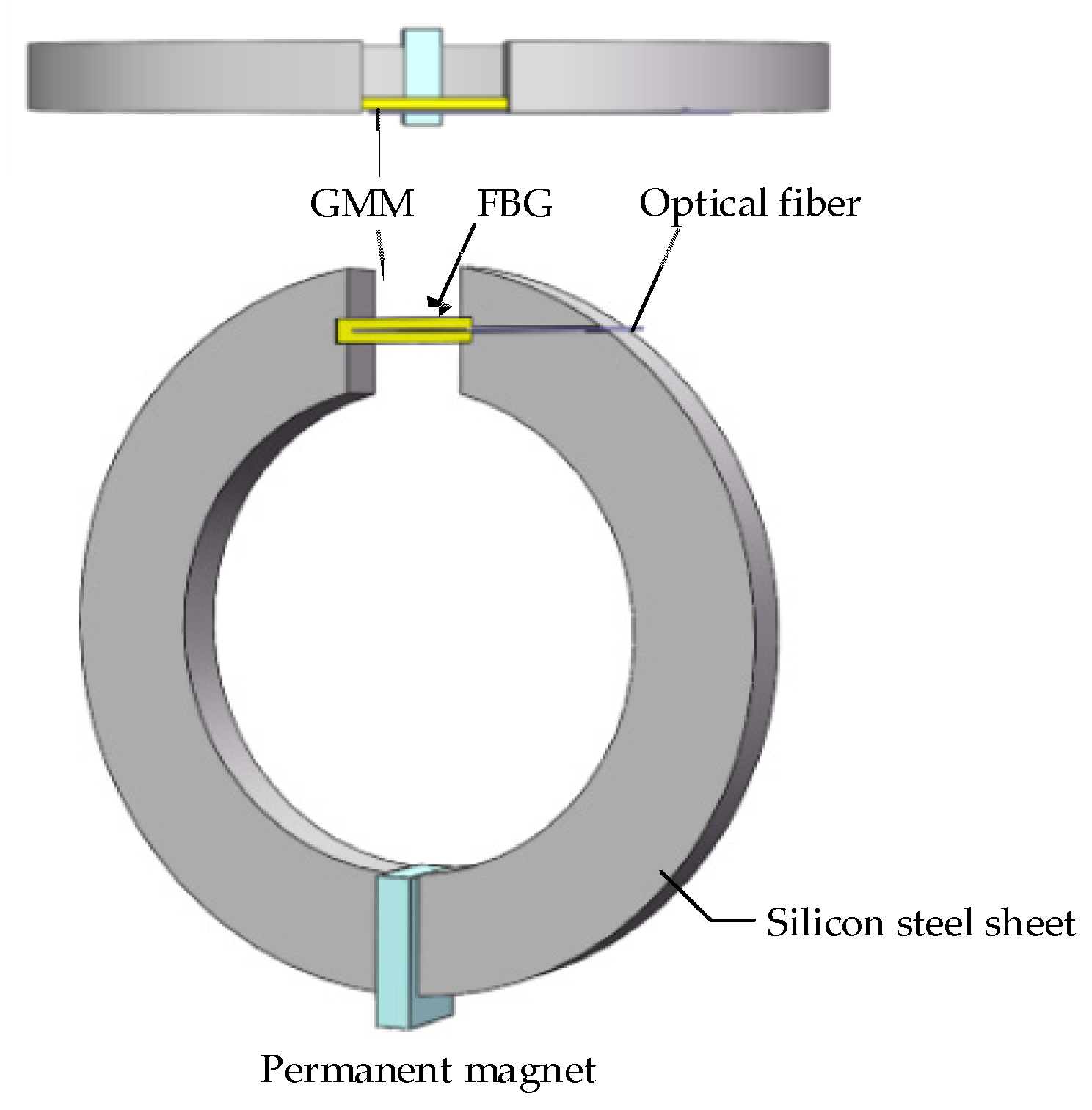
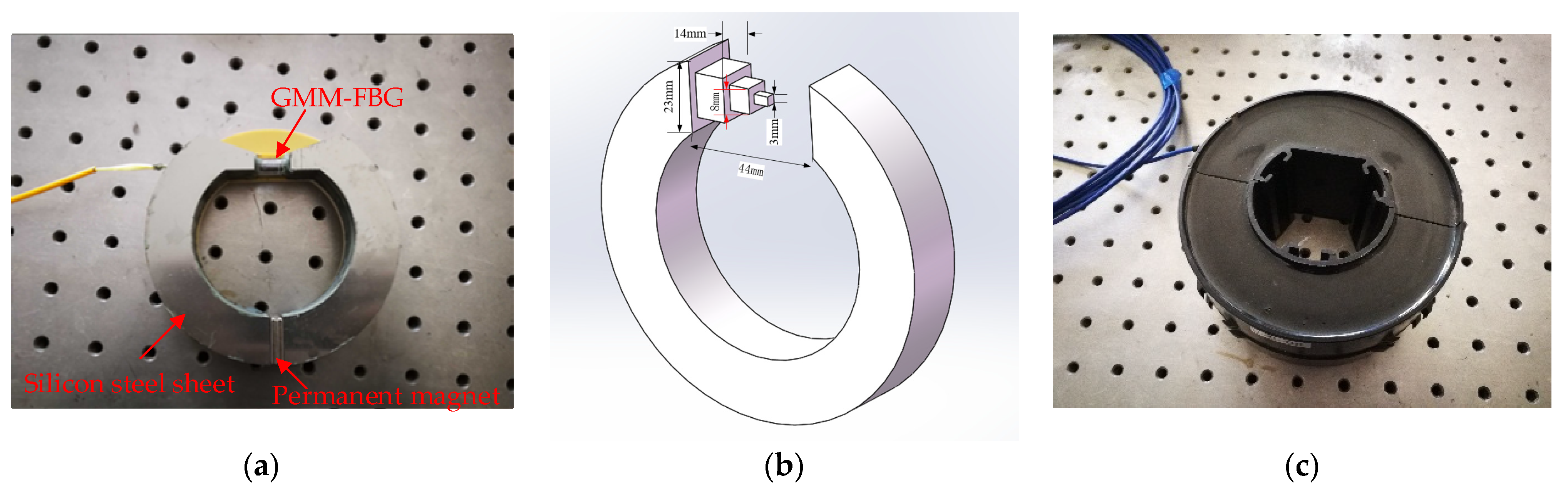
2. Fundamental Structure and Principle of GMM-FBG Sensor
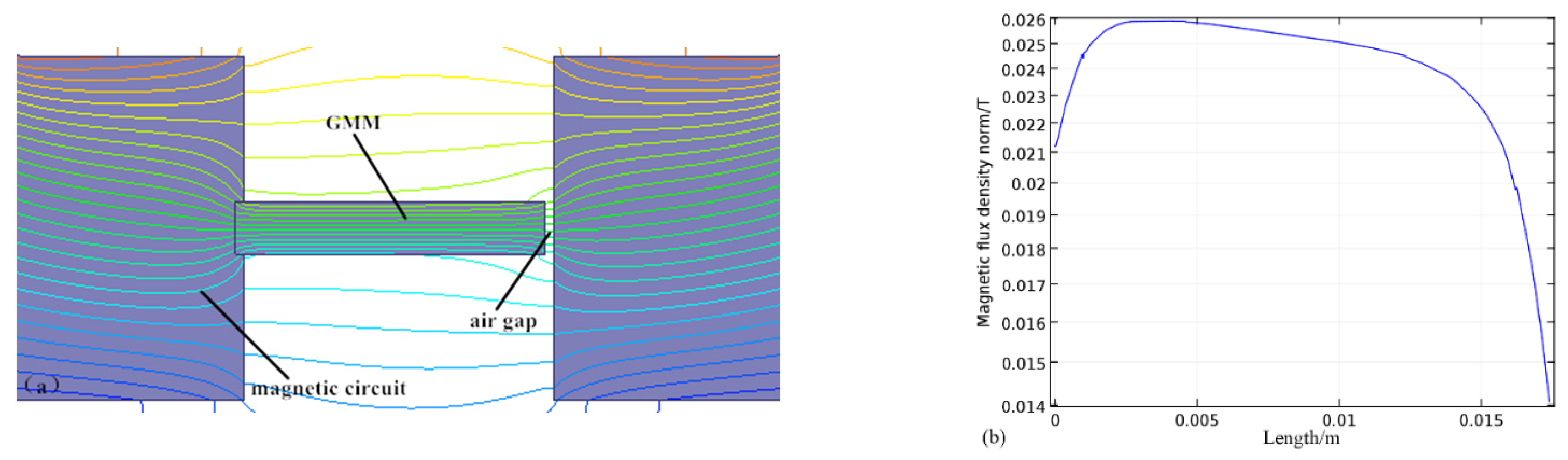
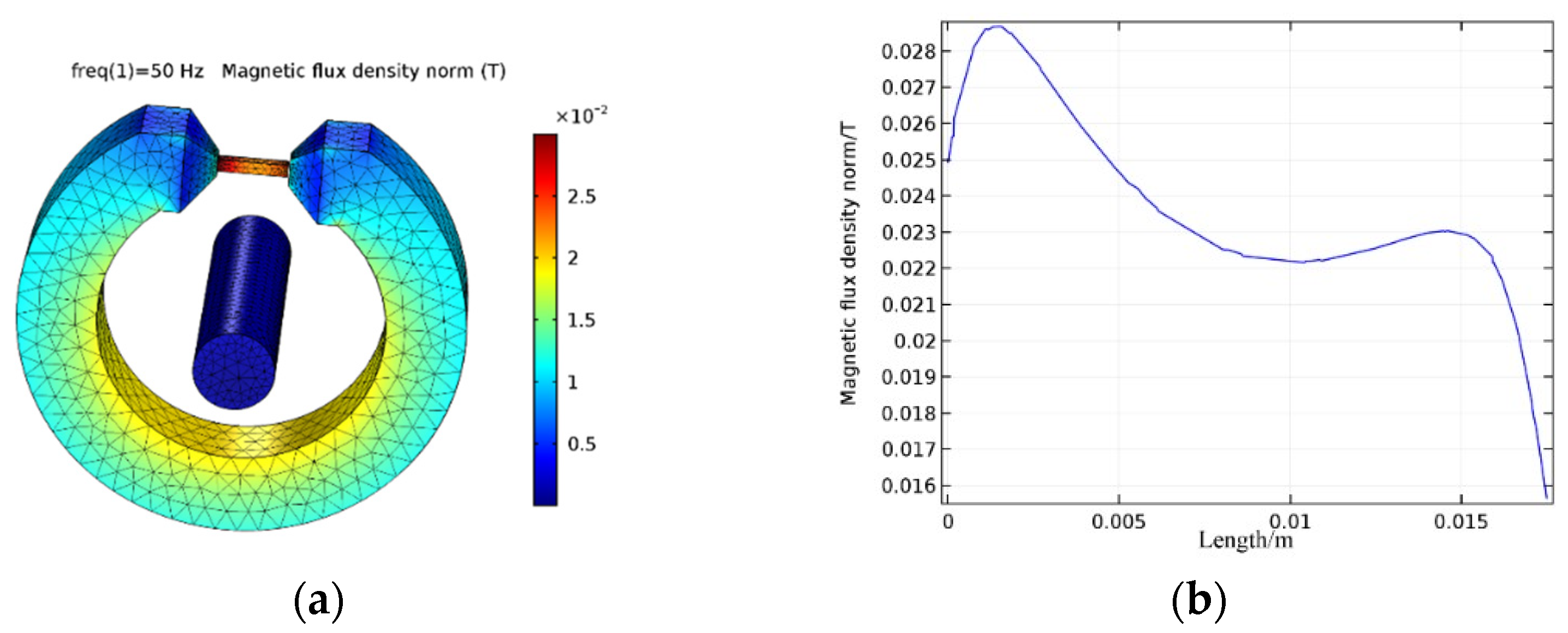
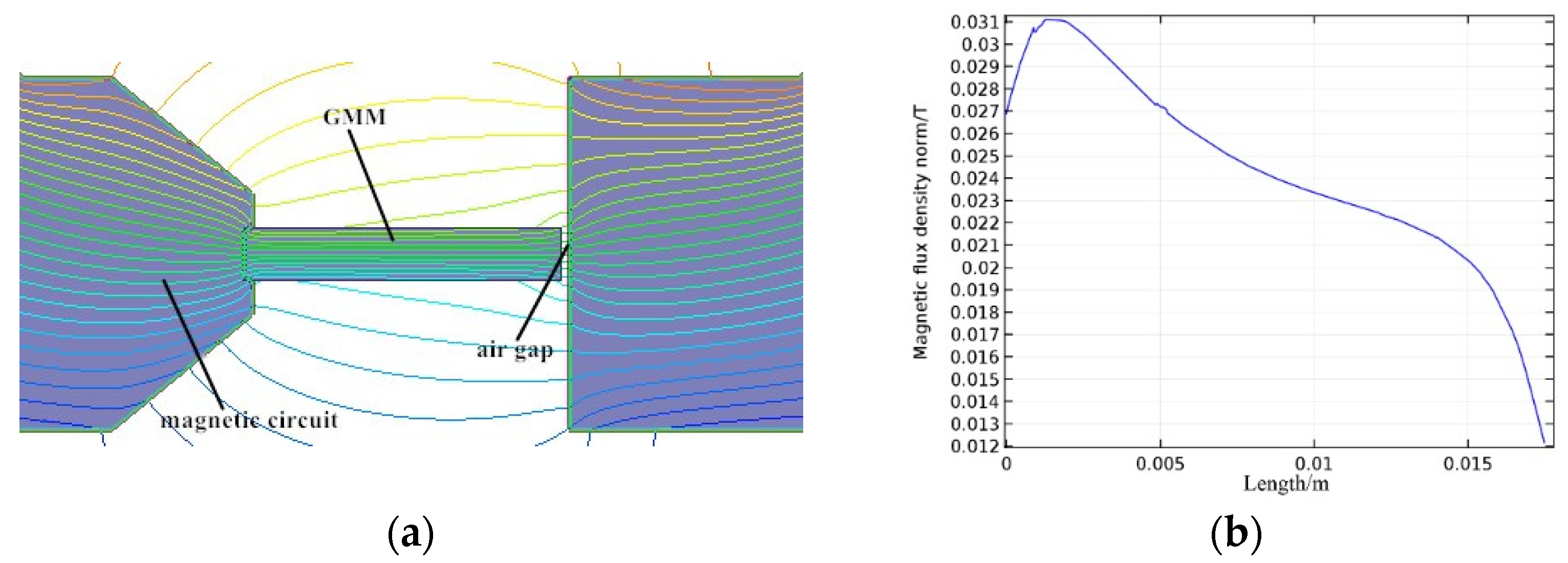
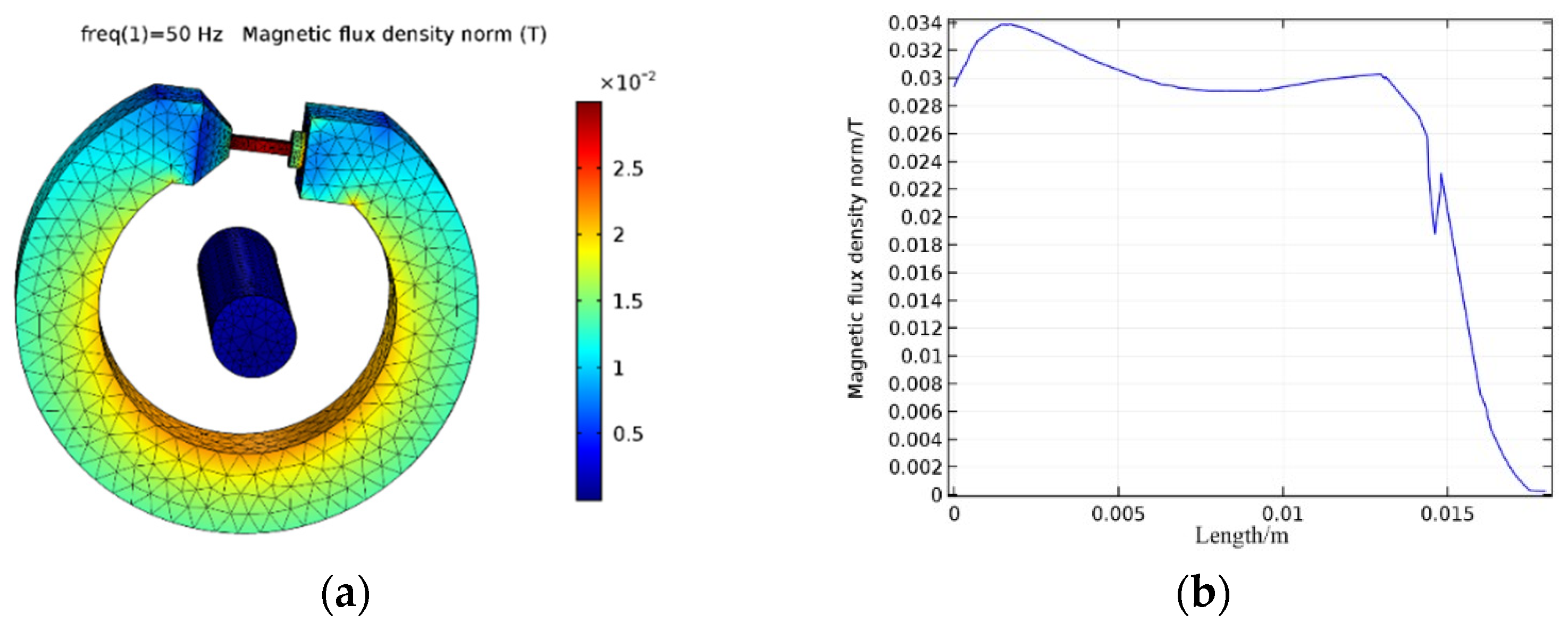
3. Simulation and Design of Magnetic Circuit System
4. Temperature Characteristics and Analysis
4.1. GMM-FBG Sensor Experiment System
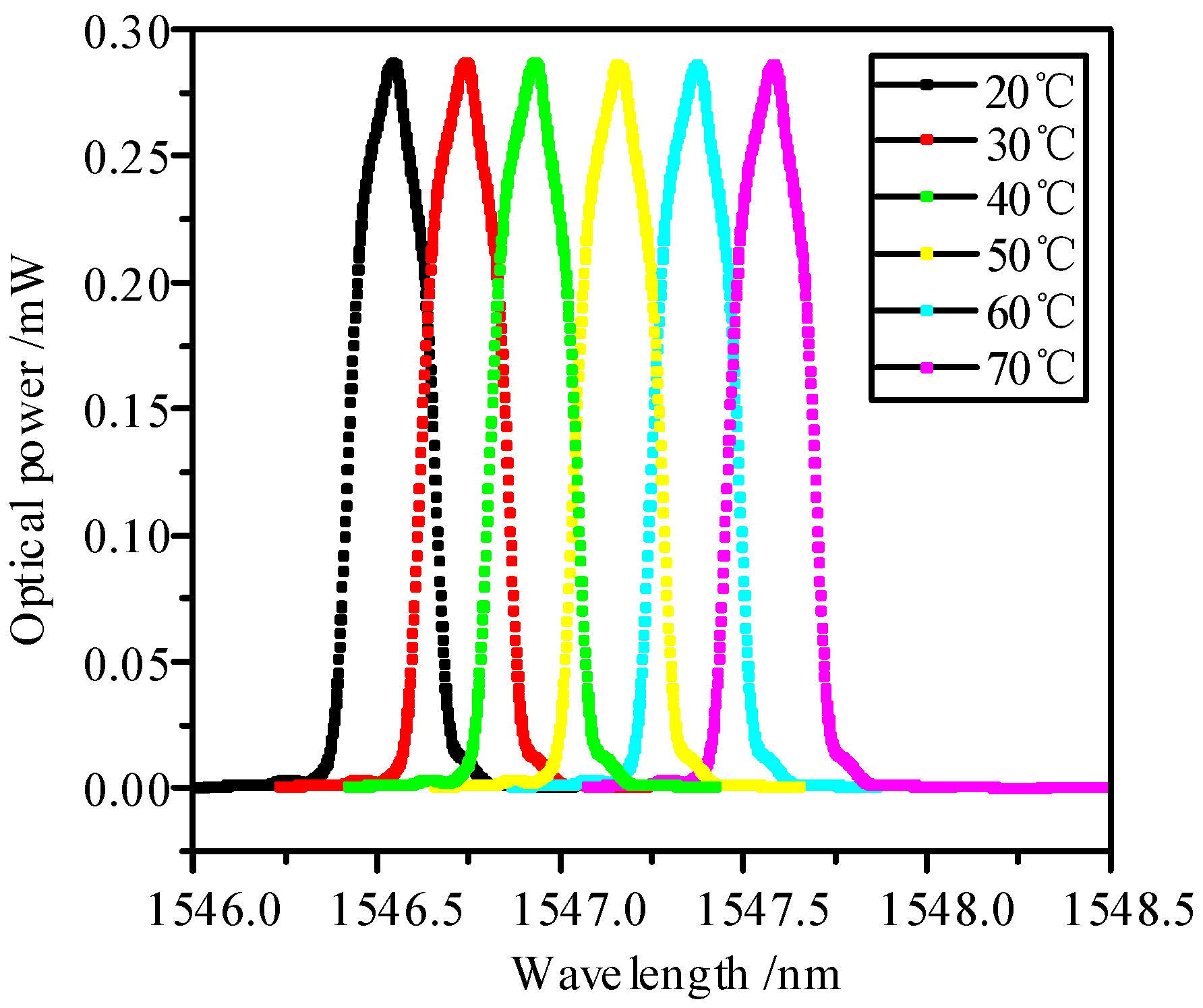
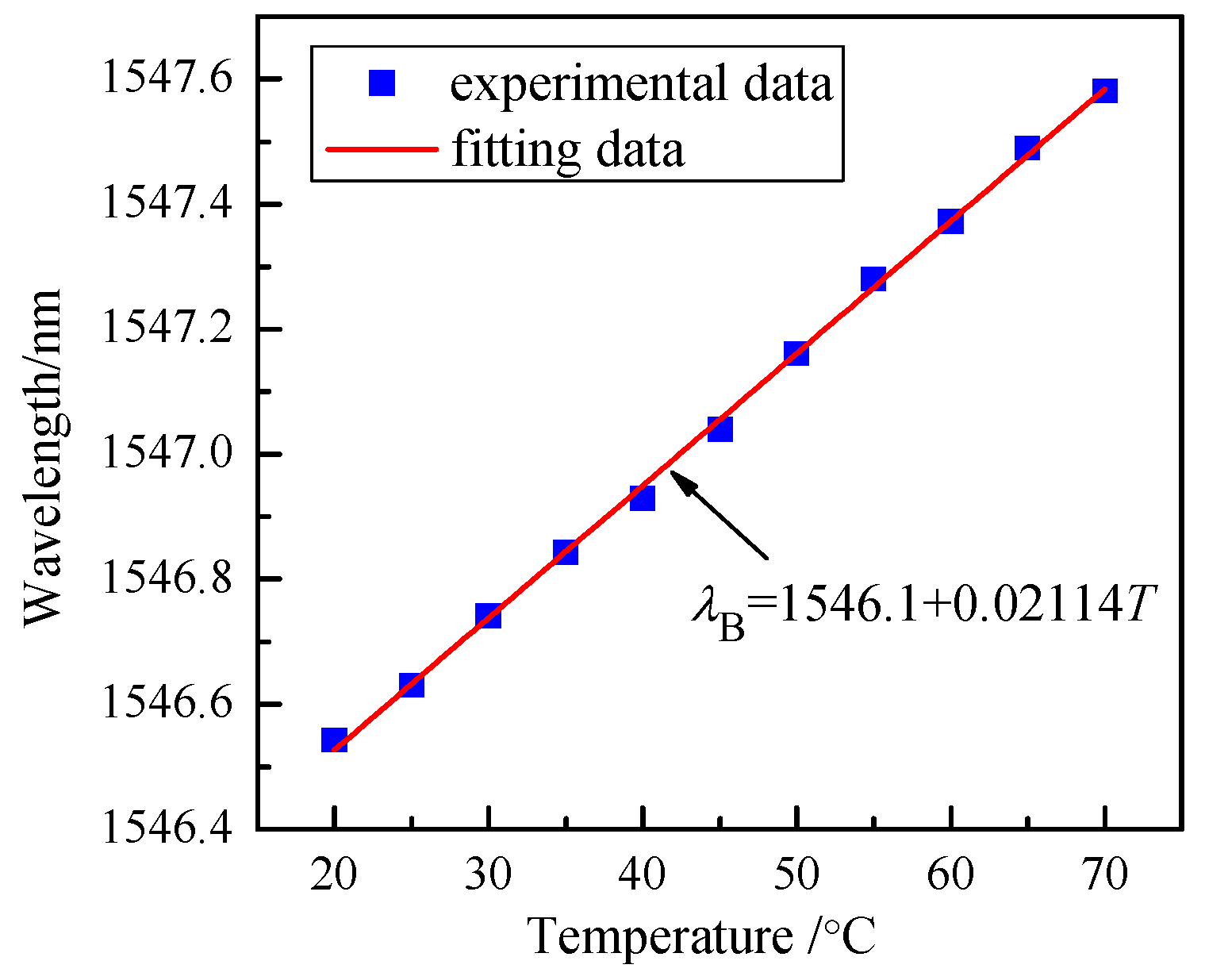
4.2. Packaged FBG Temperature Sensitivity Experiment
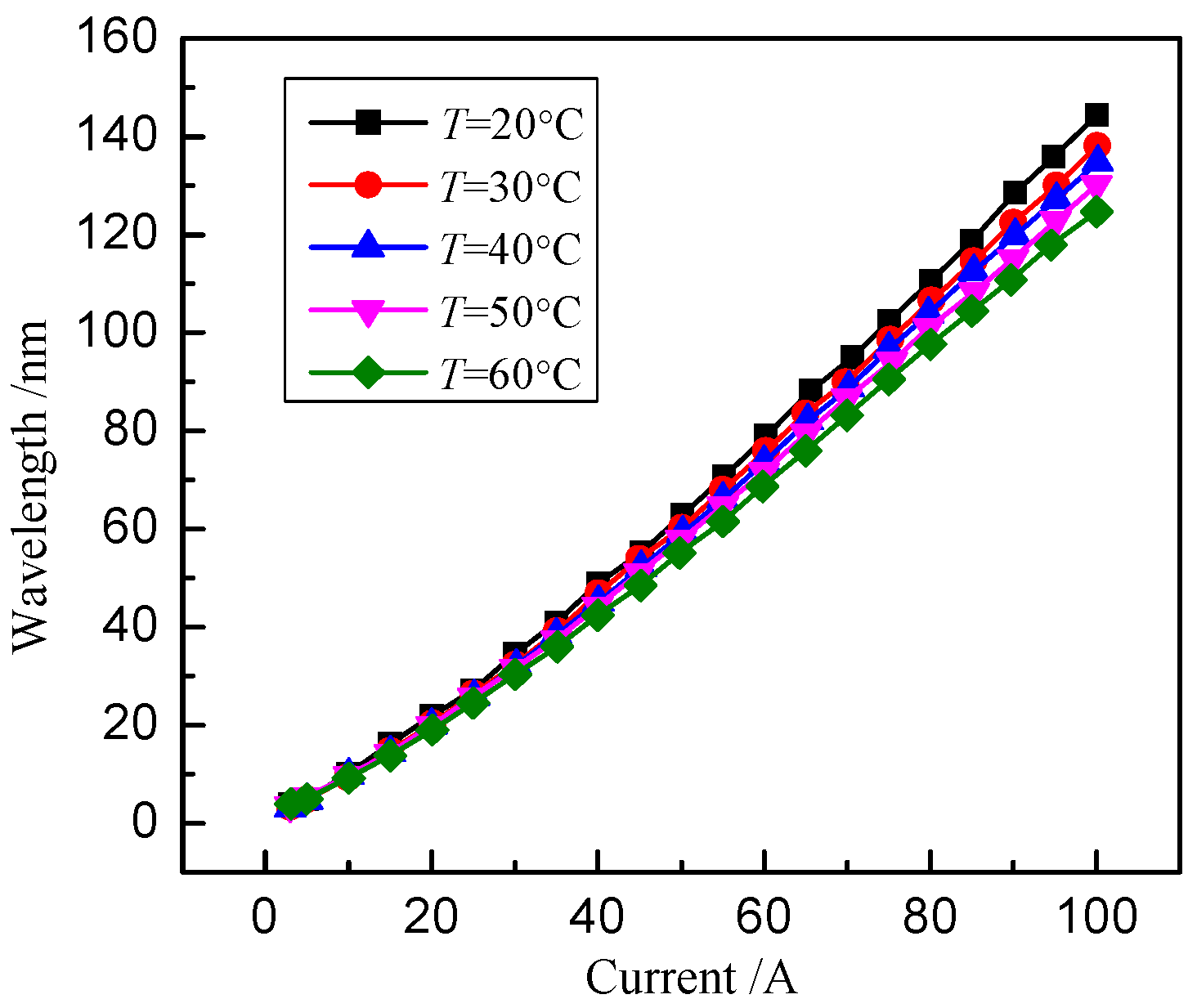
4.3. Current Response Comparison at Different Temperatures
4.4. Current Calibration Scheme
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Villalobos, R.J.; Moran, L.A.; Huenupan, F.; Vallejos, F.; Moncada, R.; Pesce, C. A new current transducer for on-line monitoring of leakage current on HV insulator strings. IEEE Access 2022, 10, 78818–78826. [Google Scholar] [CrossRef]
- Vieira, F.; de Nazaré, B.; Werneck, M.M. Compact optomagnetic bragg-grating-based current sensor for transmission lines. IEEE Sens. J. 2015, 15, 100–109. [Google Scholar]
- Kurosawa, K. Development of fiber-optic current sensing technique and its applications in electric power systems. Photonic Sens. 2014, 4, 12–20. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, G.; Sheng, Q.; Jing, Z.; Han, M.; Peng, W. Fiber-Optic Current Sensor Based on Ohmic Heating of Tin Sphere with Embedded Silicon Fabry–Perot Interferometer. J. Light. Technol. 2019, 37, 2165–2171. [Google Scholar] [CrossRef]
- Li, S.; Huang, S.; Su, Q.; Wu, T.; Zhang, D.; Guo, P.; Cai, Y. Anti-crosstalk magnetic field method for straight-light path type optical current transducer based on the background of gas-insulated substation. Opt. Eng. 2023, 62, 044104. [Google Scholar] [CrossRef]
- Huang, Y.; Xu, Q.; Xie, N.; Liu, L. A linear optical current transducer implemented with a strip aluminum polarization grating. IEEE Sens. J. 2021, 21, 7532–7540. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, N.; Huang, X.; Yin, B.; Mu, H.; Han, M.; Chen, D. High sensitivity demodulation of a reflective interferometer-based optical current sensor using an optoelectronic oscillator. Opt. Lett. 2020, 45, 4519–4522. [Google Scholar] [CrossRef] [PubMed]
- Kumari, S.; Chakraborty, S. Study of different magneto-optic materials for current sensing applications. J. Sens. Sens. Syst. 2018, 7, 421–431. [Google Scholar] [CrossRef]
- Ye, W.; Dong, Z.; Ren, R.; Liu, J.; Huang, K.; Zhang, C. Application research on fiber-optic current sensor in large pulse current measurement. J. Phys. Conf. Ser. 2020, 1507, 072015. [Google Scholar] [CrossRef]
- Jia, D.P.; Wu, W. Fiber Bragg grating current sensor based on giant magnetostrictive material. J. Electron. Meas. Instrum. 2015, 29, 1806–1812. [Google Scholar]
- Chun, H.; Kim, B.; Park, J. Analysis and Design of a Magnetostrictive Current Sensor Based on the Sensitivity Dependence of the Quality Factor. IEEE Trans. Magn. 2018, 54, 7001005. [Google Scholar]
- Zhao, J.; Zhao, K.; Li, Y.; Wang, Q.; Chen, K.P. Long-term stabilities fiber Bragg grating (FBG) arrays inscribed by femtosecond lasers at 910C. In Proceedings of the 2021 Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 9–14 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–2. [Google Scholar]
- Badar, M.; Lu, P.; Wang, Q.; Boyer, T.; Chen, K.P.; Ohodnicki, P.R. Real-time optical fiber-based distributed temperature monitoring of insulation oil-immersed commercial distribution power transformer. IEEE Sens. J. 2020, 21, 3013–3019. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Zhao, K.; Wang, Q.; Swinehart, P.; Jewart, C.; Petrie, C.; Chen, K.P. High-speed interrogation of embedded fiber Bragg grating (FBG) sensors fabricated by ultrasonic additive manufacturing. In Proceedings of the 27th International Conference on Optical Fiber Sensors, Alexandria, VA, USA, 29 August–2 September 2022; Optica Publishing Group: Washington, DC, USA, 2022; Volume W4, p. 40. [Google Scholar]
- Sah, R.K.; Kumar, A.; Gautam, A.; Rajak, V.K. Temperature independent FBG based displacement sensor for crack detection in civil structures. Opt. Fiber Technol. 2022, 74, 103137. [Google Scholar]
- Cremonezi, A.O.; Ferreira, E.C.; Filho, A.J.B.; Dias, J.A.S. A fiber Bragg grating RMS current transducer based on the magnetostriction effect using a Terfenol-D Toroidal-shaped modulator. IEEE Sens. J. 2013, 13, 683–690. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, M.; Zhou, X. A Novel FBG Temperature-Decoupling Method for Structural Health Monitoring of Bridges. Sensors 2020, 20, 6708. [Google Scholar]
- Guan, B.O.; Tam, H.Y.; Liu, S.Y. Temperature-independent fiber Bragg grating tilt sensor. IEEE Photonics Technol. Lett. 2004, 16, 224–226. [Google Scholar] [CrossRef]
- Dante, A.; Lopez, J.D.; Carvalho, C.C.; Allil, R.C.; Werneck, M.M. A compact FBG-Based magnetostrictive optical current sensor with reduced mass of Terfenol-D. IEEE Photonics Technol. Lett. 2019, 31, 1461–1464. [Google Scholar] [CrossRef]
- Yin, J.; Shu, D.H.; Jiang, M.S.; Sai, Y.Z.; Sui, Q.M. Conductor Temperature Monitoring under different current using FBG Sensor. In Proceedings of the International Industrial Informatics and Computer Engineering Conference, Xi’an, China, 10–11 January 2015; Atlantis Press: Amsterdam, The Netherlands, 2015; pp. 2029–2032. [Google Scholar]







| Property | Value |
|---|---|
| Magnetostrictive coefficient (1/m) | 2 × 10−3 |
| Toughness index | 2.5 |
| Relative permeability | 8 |
| Saturated magnetic field strength (kA/m) | 200 |
| Property | Value |
|---|---|
| Relative permeability | 2 × 103 |
| Saturation magnetic induction (T) | 1.8 |
| Resistivity (μΩ·m) | 100 |
| Magnetostrictive coefficient (1/m) | 2 × 10−8 |
| Double Large Section Structure | Optimized Structure | |
|---|---|---|
| x1 | 0.249 | 0.0330 |
| x2 | 0.258 | 0.0332 |
| x3 | 0.259 | 0.0305 |
| x4 | 0.258 | 0.0290 |
| x5 | 0.254 | 0.0288 |
| x6 | 0.250 | 0.0290 |
| x7 | 0.249 | 0.0300 |
| x8 | 0.244 | 0.0301 |
| x9 | 0.237 | 0.0282 |
| x10 | 0.226 | 0.0210 |
| S2 | 0.0786 | 0.0093 |
| Physical Quantity | Values | ||||
| Temperature/°C | 30 | ||||
| Current/A | 20 | 30 | 40 | 50 | 60 |
| Amplitude/pm | 20.586 | 32.952 | 46.372 | 60.485 | 75.429 |
| Temperature/°C | Fitted Function |
|---|---|
| 20 | P = 0.003806i2(t) + 1.085i(t) − 0.9263 |
| 30 | P = 0.003437i2(t) + 1.076i(t) − 1.6030 |
| 40 | P = 0.003317i2(t) + 1.042i(t) − 1.4080 |
| 50 | P = 0.003093i2(t) + 1.024i(t) − 0.8944 |
| 60 | P = 0.002991i2(t) + 0.967i(t) − 0.7307 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.-C.; Li, L.-H.; Zhang, T. Structural Optimization and Temperature Compensation of GMM-FBG Fiber Current Transducer. Photonics 2023, 10, 1376. https://doi.org/10.3390/photonics10121376
Zhang W-C, Li L-H, Zhang T. Structural Optimization and Temperature Compensation of GMM-FBG Fiber Current Transducer. Photonics. 2023; 10(12):1376. https://doi.org/10.3390/photonics10121376
Chicago/Turabian StyleZhang, Wei-Chao, Lin-Heng Li, and Tao Zhang. 2023. "Structural Optimization and Temperature Compensation of GMM-FBG Fiber Current Transducer" Photonics 10, no. 12: 1376. https://doi.org/10.3390/photonics10121376
APA StyleZhang, W.-C., Li, L.-H., & Zhang, T. (2023). Structural Optimization and Temperature Compensation of GMM-FBG Fiber Current Transducer. Photonics, 10(12), 1376. https://doi.org/10.3390/photonics10121376





