Propagation Properties of Generalized Schell-Model Pulse Sources in Dispersive Media
Abstract
:1. Introduction
2. Theoretical Model
3. Propagation of the Generalized Schell-Model Pulses in Dispersive Media
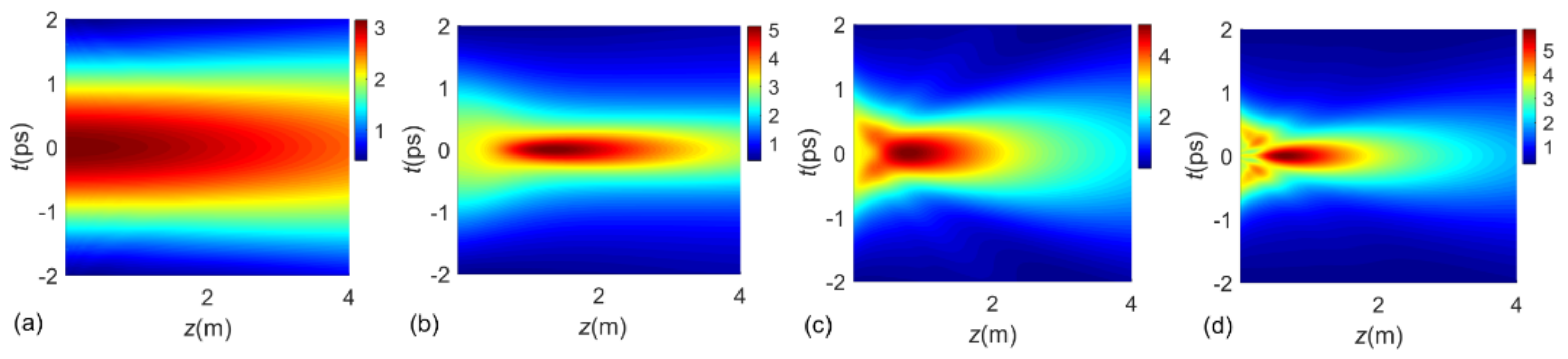
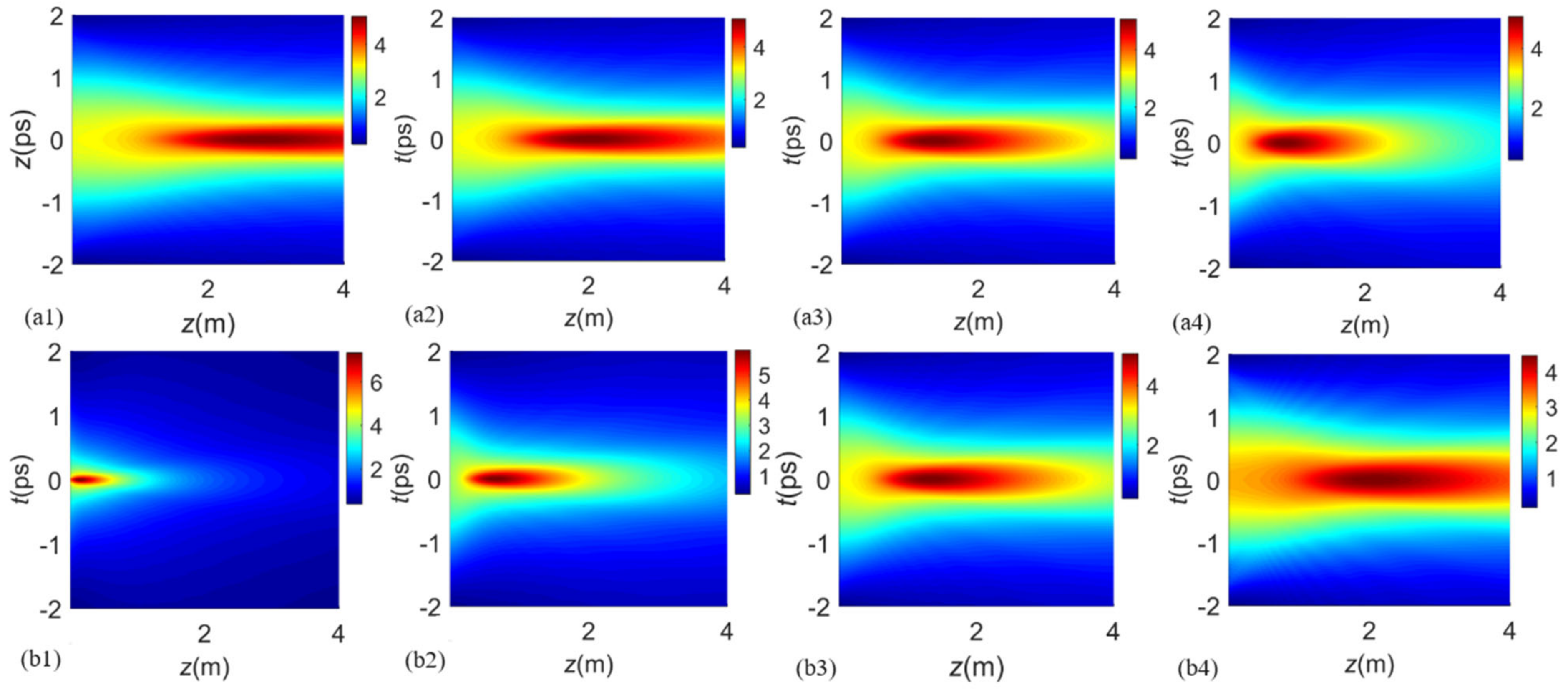
3.1. Generalized Gaussian Schell-Model Pulse
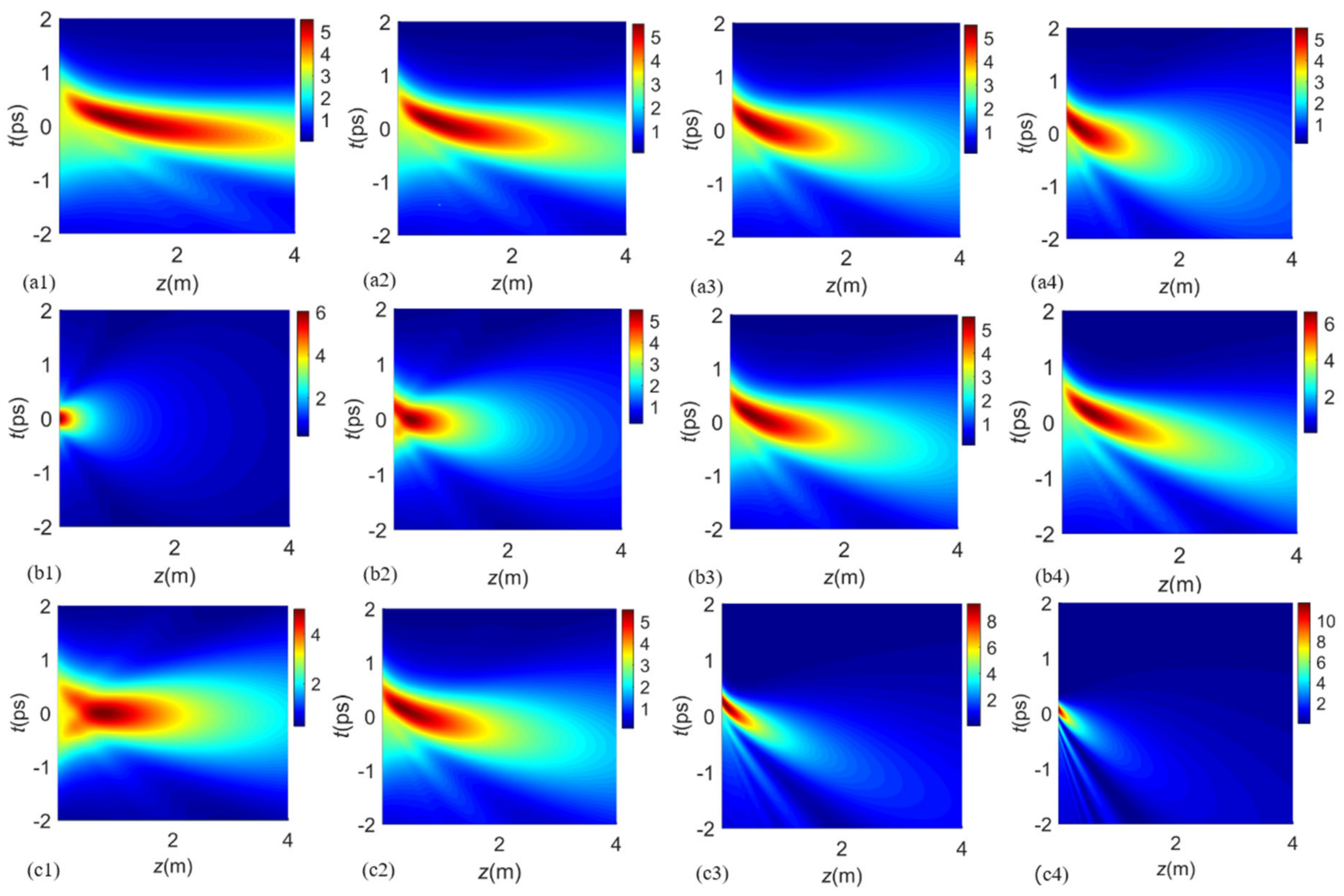
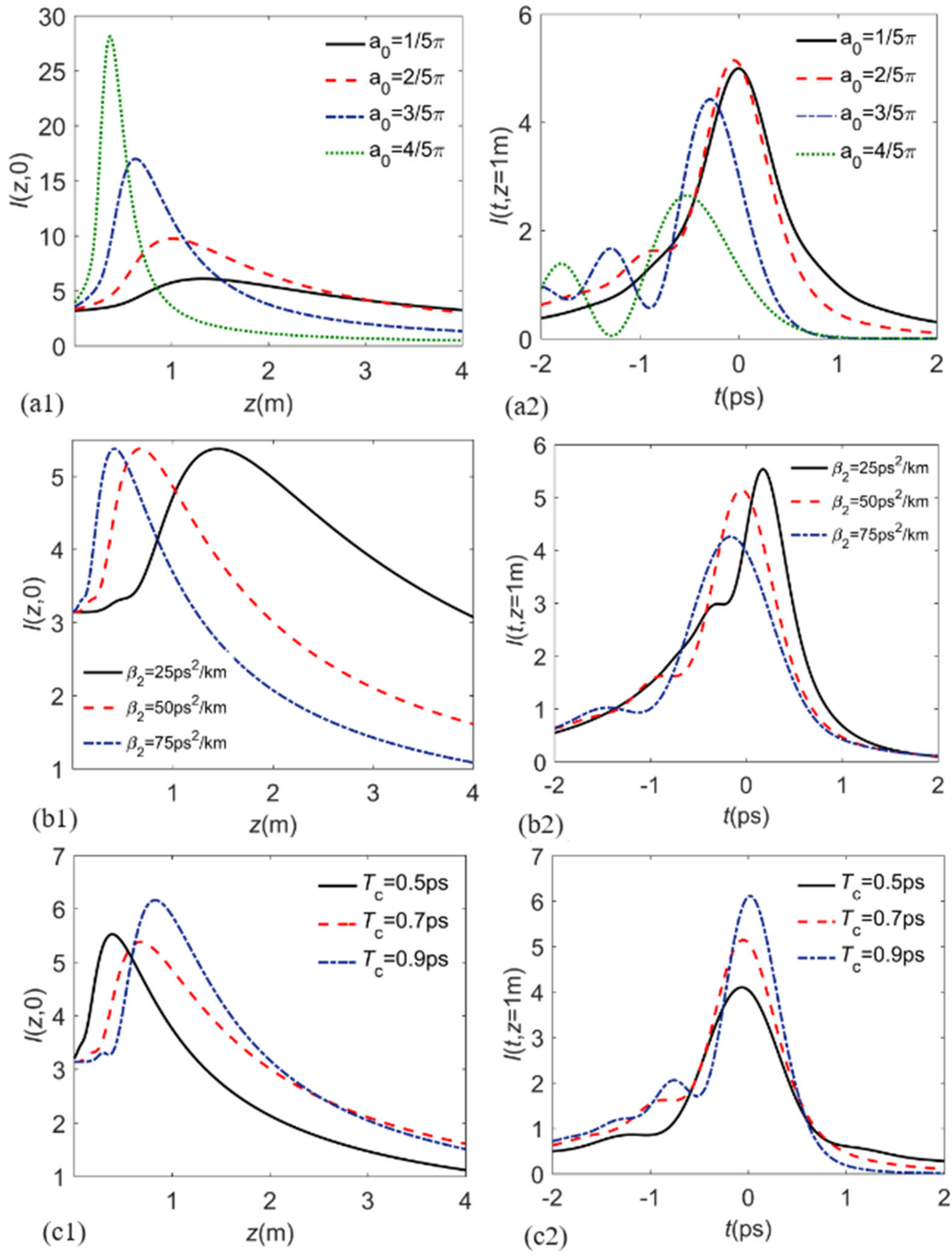
3.2. Generalized Multi-Gaussian Schell-Model Pulse
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation function. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef] [PubMed]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef] [PubMed]
- Sahin, S.; Korotkova, O. Light sources generating far fields with tunable flat profiles. Opt. Lett. 2012, 37, 2970–2972. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O. Random sources for rectangular far fields. Opt. Lett. 2014, 39, 64–67. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.R.; Mao, Y.H. Multi-sinc Schell-model beams and the interaction with a linear random medium. Laser Phys. Lett. 2015, 12, 095002. [Google Scholar] [CrossRef]
- Mei, Z.R.; Korotkova, O. Cosine-Gaussian Schell-model sources. Opt. Lett. 2013, 38, 2578–2580. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.H.; Gu, J.X.; Wang, F.; Cai, Y.J. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam. Phys. Rev. A 2015, 91, 013823. [Google Scholar] [CrossRef]
- Bogatyryova, G.V.; Fel’ de, C.V.; Polyanskii, P.V.; Ponomarenko, S.A.; Soskin, M.S.; Wolf, E. Partially coherent vortex beams with a separable phase. Opt. Lett. 2003, 28, 878–880. [Google Scholar] [CrossRef]
- Palacios, D.M.; Maleev, I.D.; Marathay, A.S.; Swartzlander, G. Spatial correlation singularity of a vortex field. Phys. Rev. Lett. 2004, 92, 143905. [Google Scholar] [CrossRef]
- Liu, X.L.; Shen, Y.; Liu, L.; Wang, F.; Cai, Y.J. Experimental demonstration of vortex phase-induced reduction in scintillation of a partially coherent beam. Opt. Lett. 2013, 38, 5323–5326. [Google Scholar] [CrossRef]
- Borghi, R. Twisting partially coherent light. Opt. Lett. 2018, 43, 1627–1630. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Cai, Y.J.; Eyyuboglu, H.T.; Baykal, Y. Twist phase-induced reduction in scintillation of a partially coherent beam in turbulent atmosphere. Opt. Lett. 2012, 37, 184–186. [Google Scholar] [CrossRef]
- Wan, L.P.; Zhao, D.M. Controllable rotating Gaussian Schell-model beams. Opt. Lett. 2019, 44, 735–737. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O.; Chen, X. Phase structuring of the complex degree of coherence. Opt. Lett. 2018, 43, 4727–4730. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Korotkova, O. Phase structuring of the 2D complex coherence states. Opt. Lett. 2019, 44, 2470–2473. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.R.; Korotkova, O. Cross-spectral densities with helical-Cartesian phase. Opt. Express 2020, 28, 20438–20488. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.R. Generalized Schell-model sources. Opt. Express 2020, 28, 39058–39066. [Google Scholar] [CrossRef] [PubMed]
- Ata, Y.; Korotkova, O. Electromagnetic phase coherence grating for atmospheric applications. Opt. Lett. 2021, 46, 5240–5243. [Google Scholar] [CrossRef] [PubMed]
- Mei, Z.R. Special correlation model sources producing a self-focusing field. Opt. Express 2021, 29, 25337–25343. [Google Scholar] [CrossRef]
- Mei, Z.R.; Korotkova, O.; Zhao, D.; Mao, Y. Self-focusing vortex beams. Opt. Lett. 2021, 46, 2384–2387. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Non-uniformly correlated partially coherent pulses. Opt. Express 2013, 21, 190–195. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.L.; Korotkova, O.; Pan, L.Z. The control of pulse profiles with tunable temporal coherence. Phys. Lett. A 2014, 378, 1687–1690. [Google Scholar] [CrossRef]
- Liu, H.L.; Hu, Z.H.; Du, Z.H.; Xia, J.; He, A.; Lü, Y.F. Temporal pulse source generating far fields with sharp optical pulse. Phys. Lett. A 2021, 390, 127102. [Google Scholar] [CrossRef]
- Ding, C.L.; Korotkova, O.; Zhang, Y.T.; Pan, L.Z. Cosine-Gaussian correlated Schell-model pulsed beams. Opt. Express 2014, 22, 931–942. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.H.; Tang, J.H.; Wang, Y.H.; Liu, X.; Liang, C.H.; Zhao, L.N.; Hoenders, B.J.; Cai, Y.J.; Ma, P.J. Complex and phase screen methods for studying arbitrary genuine Schell-model partially coherent pulses in nonlinear media. Opt. Express 2022, 30, 24222–24231. [Google Scholar] [CrossRef]
- Liu, H.L.; Du, Z.H.; Li, Y.Z.; Chen, H.; Lü, Y.F. Self-focusing and self-splitting properties of partially coherent temporal pulses propagating in dispersive media. Opt. Express 2023, 31, 7336–7350. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.L.; Koivurova, M.; Turunen, J.; Pan, L.Z. Temporal self-splitting of optical pulses. Phys. Rev. A 2018, 97, 053838. [Google Scholar] [CrossRef]
- Bliokh, K.Y. Spatiotemporal vortex pulses: Angular momenta and spin-orbit interaction. Phys. Rev. L 2021, 126, 243601. [Google Scholar] [CrossRef]
- Hyde, M.W. Twisted space-frequency and space-time partially coherence beam. Sci. Rep. 2020, 10, 12443. [Google Scholar] [CrossRef]
- Huang, S.L.; Wang, p.; Shen, X.; Liu, J. Properties of the generation and propagation of spatiotemporal optical vortices. Opt. Express 2021, 29, 26995–27003. [Google Scholar] [CrossRef]
- Mirando, A.; Zang, Y.M.; Zhan, Q.W.; Chong, A. Generation of spatiotemporal optical vortices with partial temporal coherence. Opt. Express 2021, 29, 30426–30435. [Google Scholar] [CrossRef] [PubMed]
- Cao, Q.; Chen, J.; Lu, K.Y.; Wan, C.H.; Chong, A.D.; Zhan, Q.W. Sculpturing spatiotemporal wavepackets with chirped pulses. Photonics Res. 2021, 9, 11002261. [Google Scholar] [CrossRef]
- Ding, C.L.; Horoshko, D.; Kotorkova, O.; Jian, C.; Qi, X.X.; Pan, L.Z. Source coherence-induced control of spatiotemporal coherency vortices. Opt. Express 2022, 30, 19871–19888. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Koivurova, M.; Turunen, J.; Setälä, T.; Friberg, A. Coherence control of pulse trains by spectral phase modulation. J. Opt. 2017, 19, 095501. [Google Scholar] [CrossRef]
- Zhang, Y.T.; Ding, C.L.; Hyde, W., IV; Korotkova, O. Non-stationary pulses with complex-valued temporal degree of coherence. J. Opt. 2020, 22, 105607. [Google Scholar] [CrossRef]
- Talukder, R.; Halder, A.; Koivurova, M.; Ding, C.L.; Setälä, T.; Turunen, J.; Friberg, A. Generation of pulse trains with nonconventional temporal correlation properties. J. Opt. 2022, 24, 055502. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Cai, Z.; Wang, X.; Xu, B. Propagation Properties of Generalized Schell-Model Pulse Sources in Dispersive Media. Photonics 2023, 10, 1378. https://doi.org/10.3390/photonics10121378
Liu X, Cai Z, Wang X, Xu B. Propagation Properties of Generalized Schell-Model Pulse Sources in Dispersive Media. Photonics. 2023; 10(12):1378. https://doi.org/10.3390/photonics10121378
Chicago/Turabian StyleLiu, Xiayin, Zhiyu Cai, Xiaogang Wang, and Bijun Xu. 2023. "Propagation Properties of Generalized Schell-Model Pulse Sources in Dispersive Media" Photonics 10, no. 12: 1378. https://doi.org/10.3390/photonics10121378
APA StyleLiu, X., Cai, Z., Wang, X., & Xu, B. (2023). Propagation Properties of Generalized Schell-Model Pulse Sources in Dispersive Media. Photonics, 10(12), 1378. https://doi.org/10.3390/photonics10121378




