Generation of Perfect Vortex Beams with Complete Control over the Ring Radius and Ring Width
Abstract
:1. Introduction
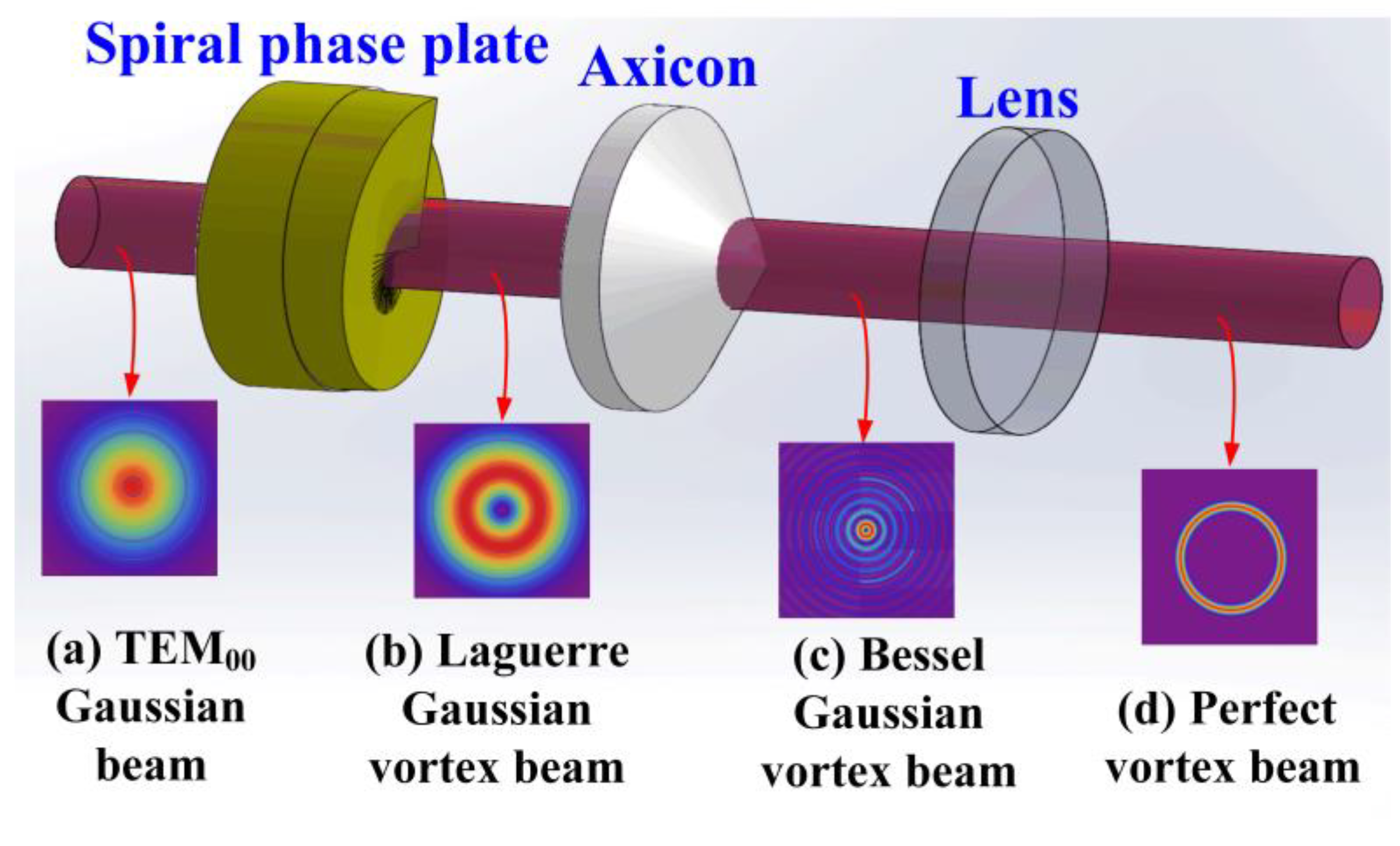
2. Theoretical Analysis
3. Experimental Setup
4. Results and Discussion
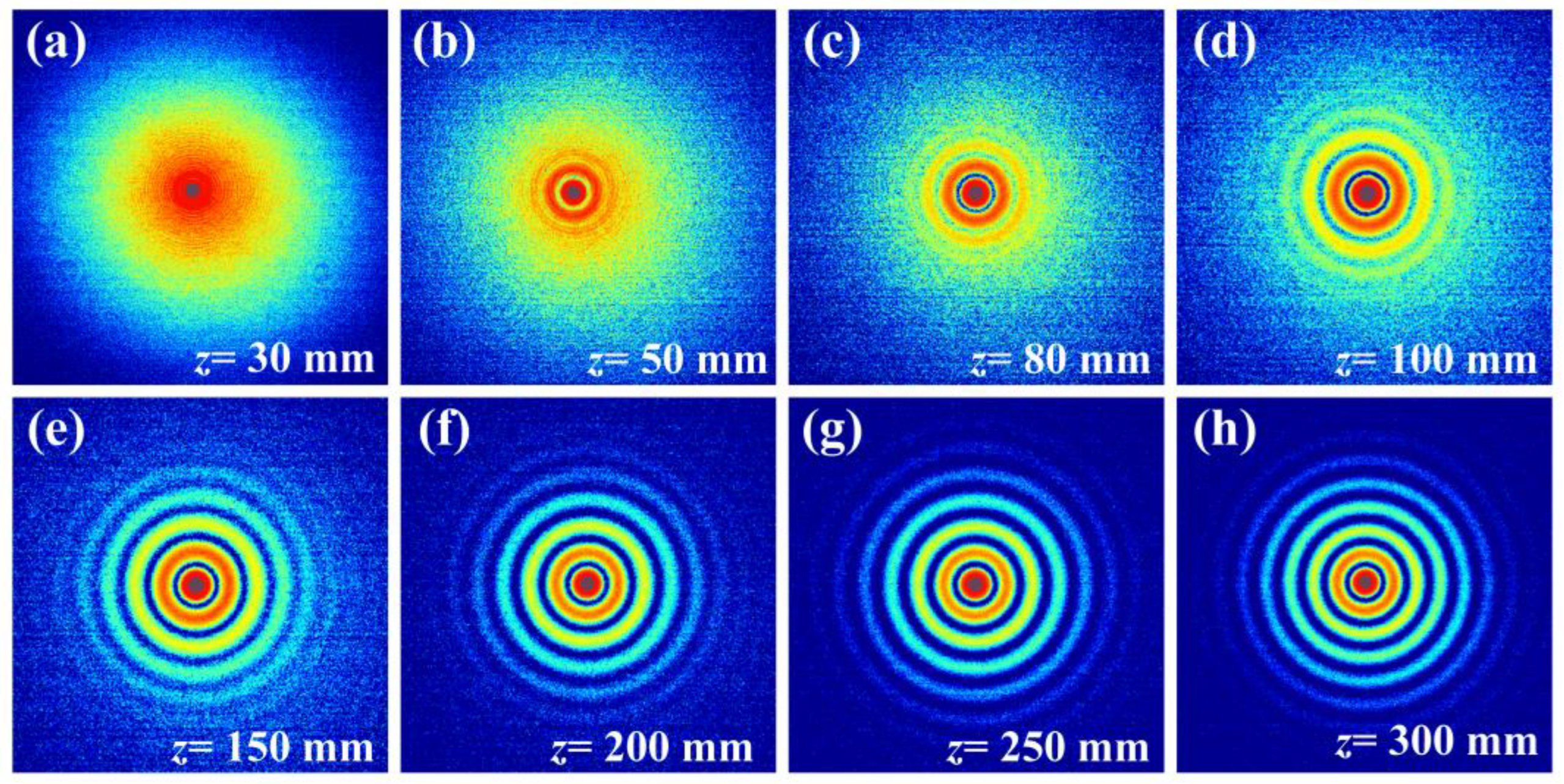
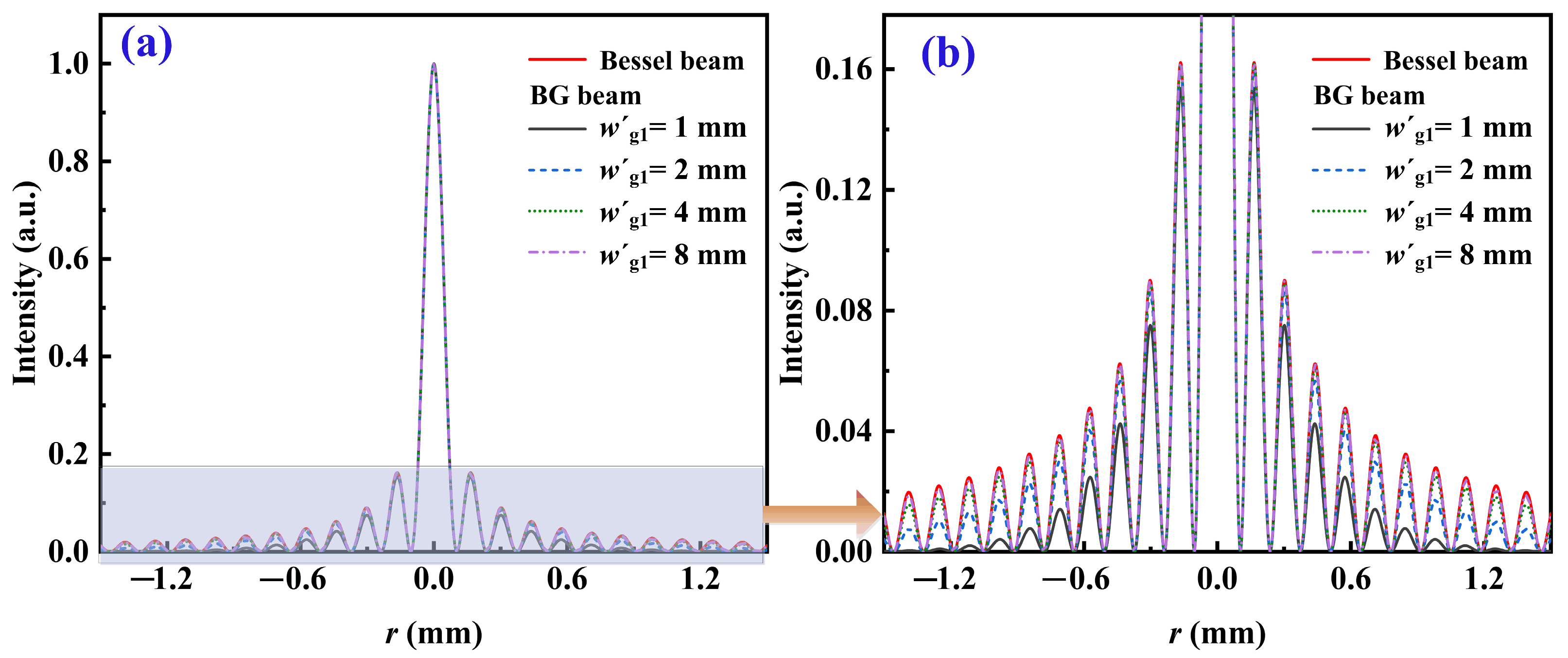
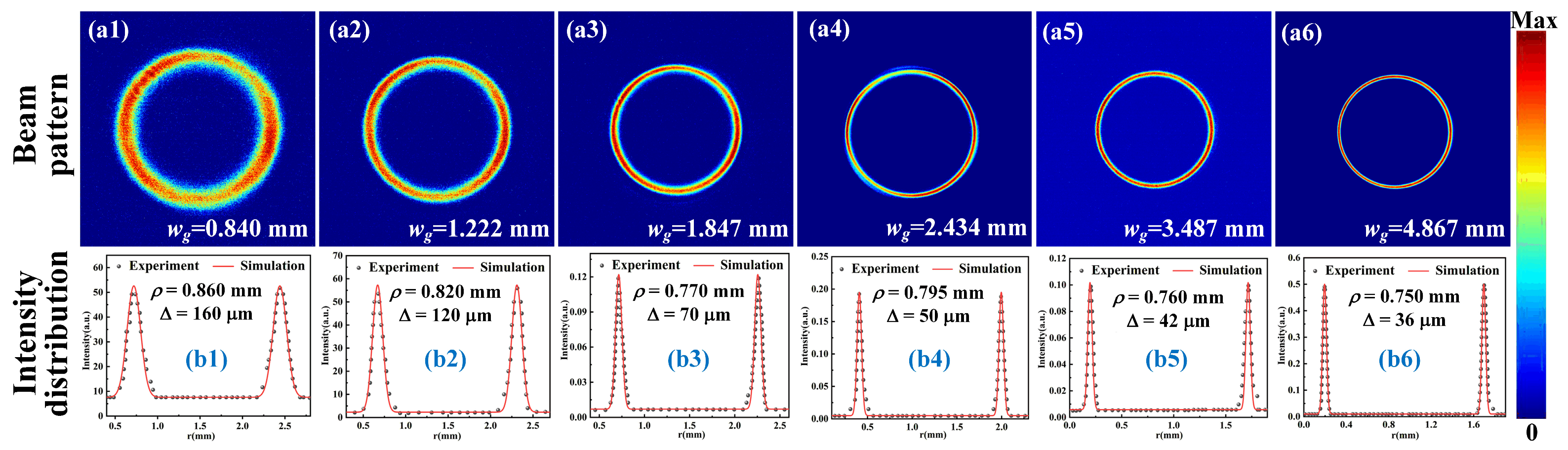
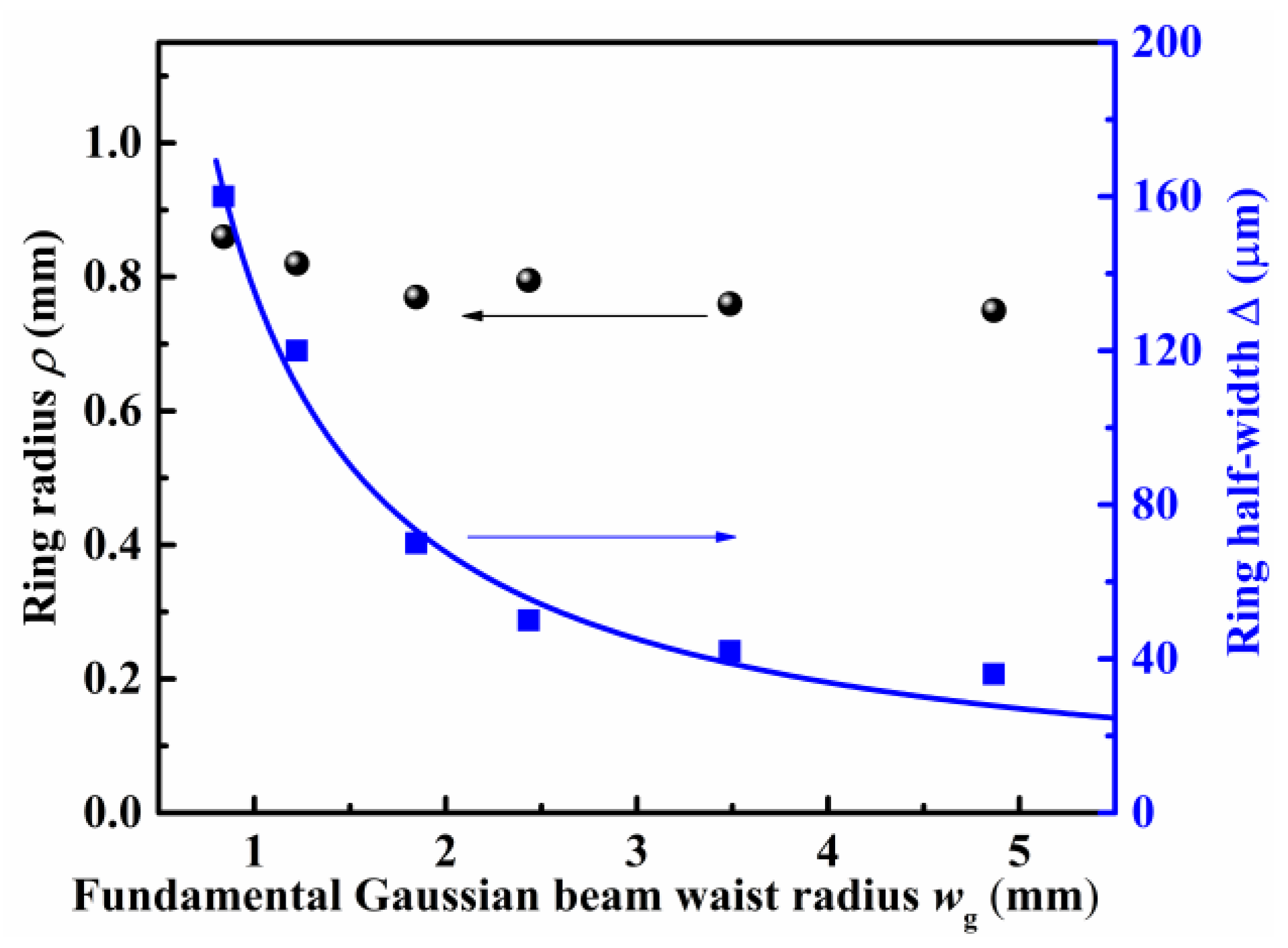
4.1. Characteristics of the Generated BG Beam for Different Propagation Distance z behind the Axicon and the Input Fundamental Beam with Waist Radius wg
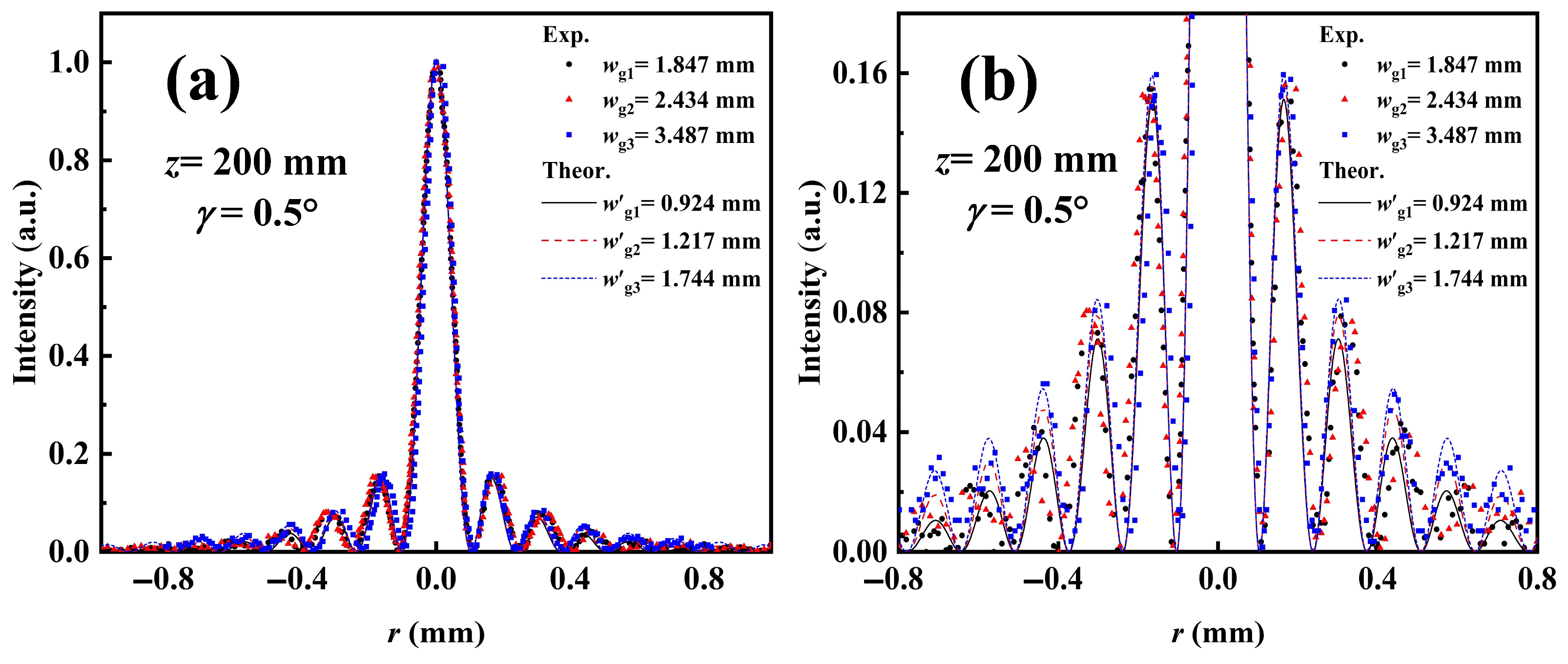
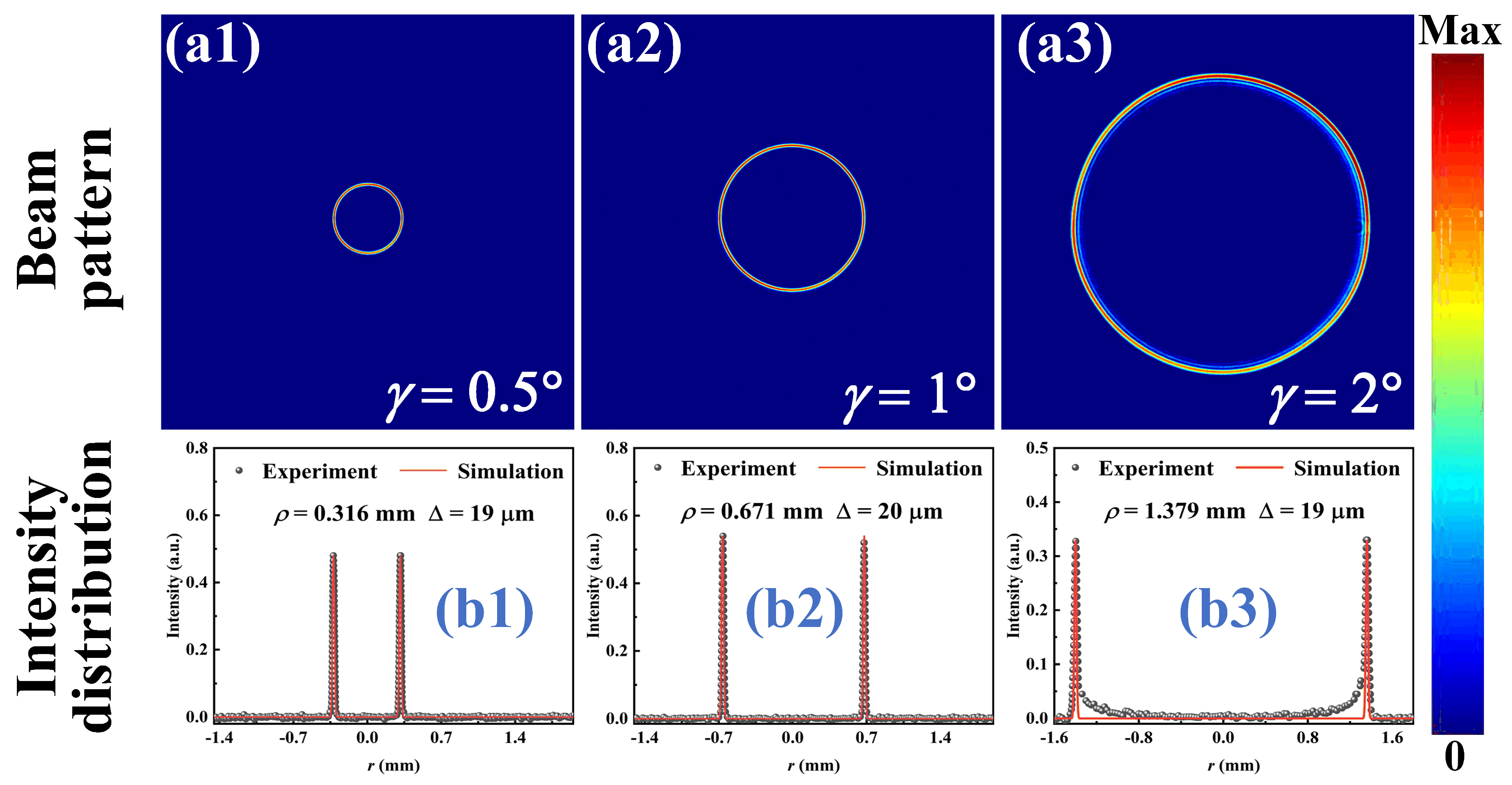
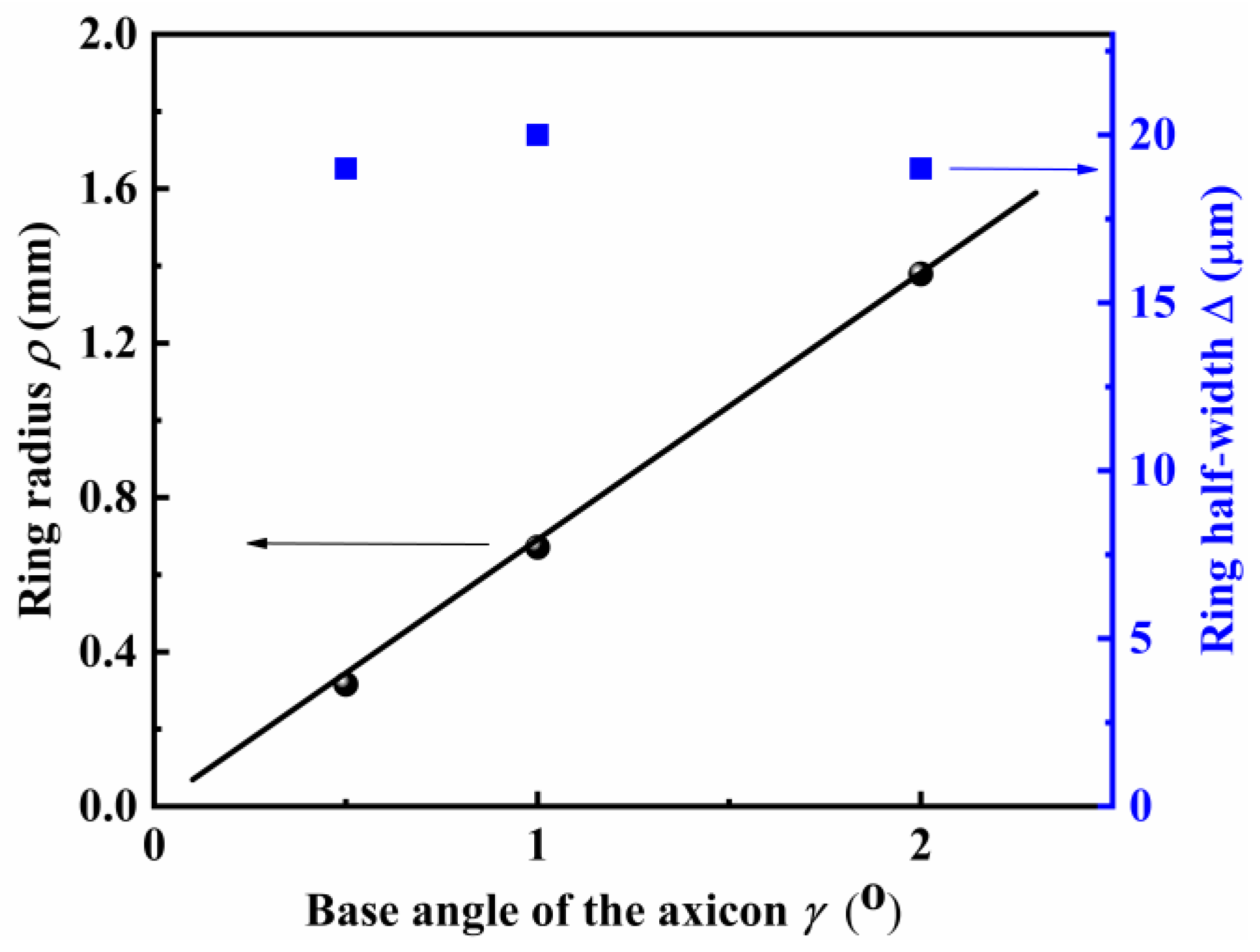
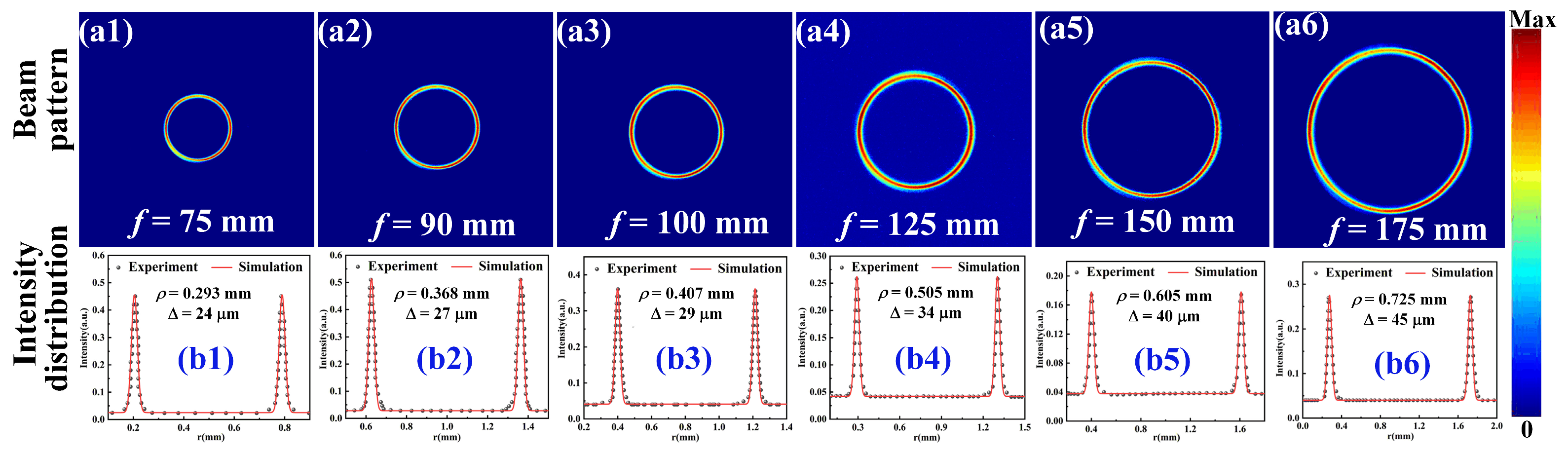
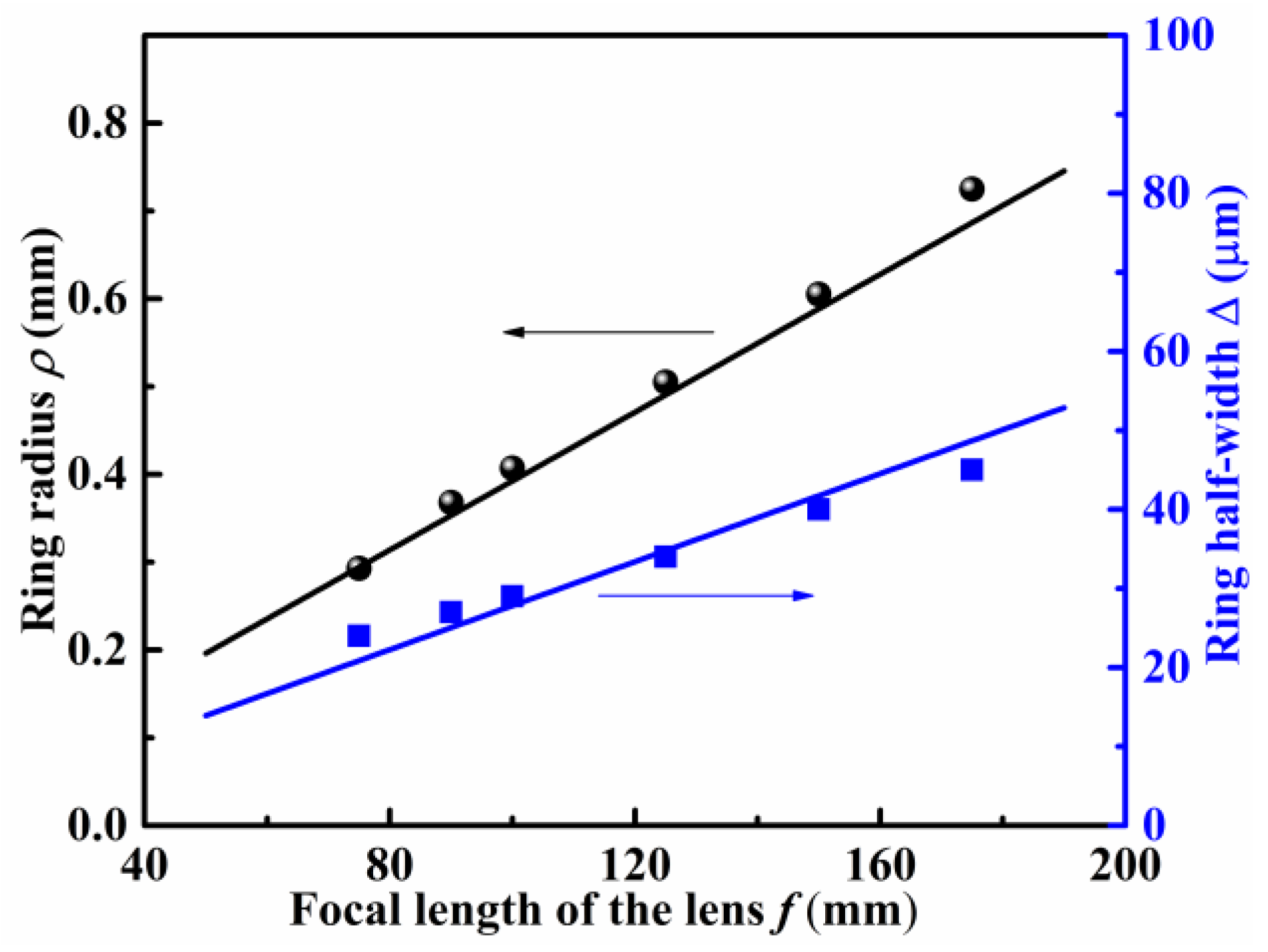
4.2. Effects of Waist Radius wg, Base Angle γ and Focal Length f on the Spot Parameters of the PVB for TC = 0
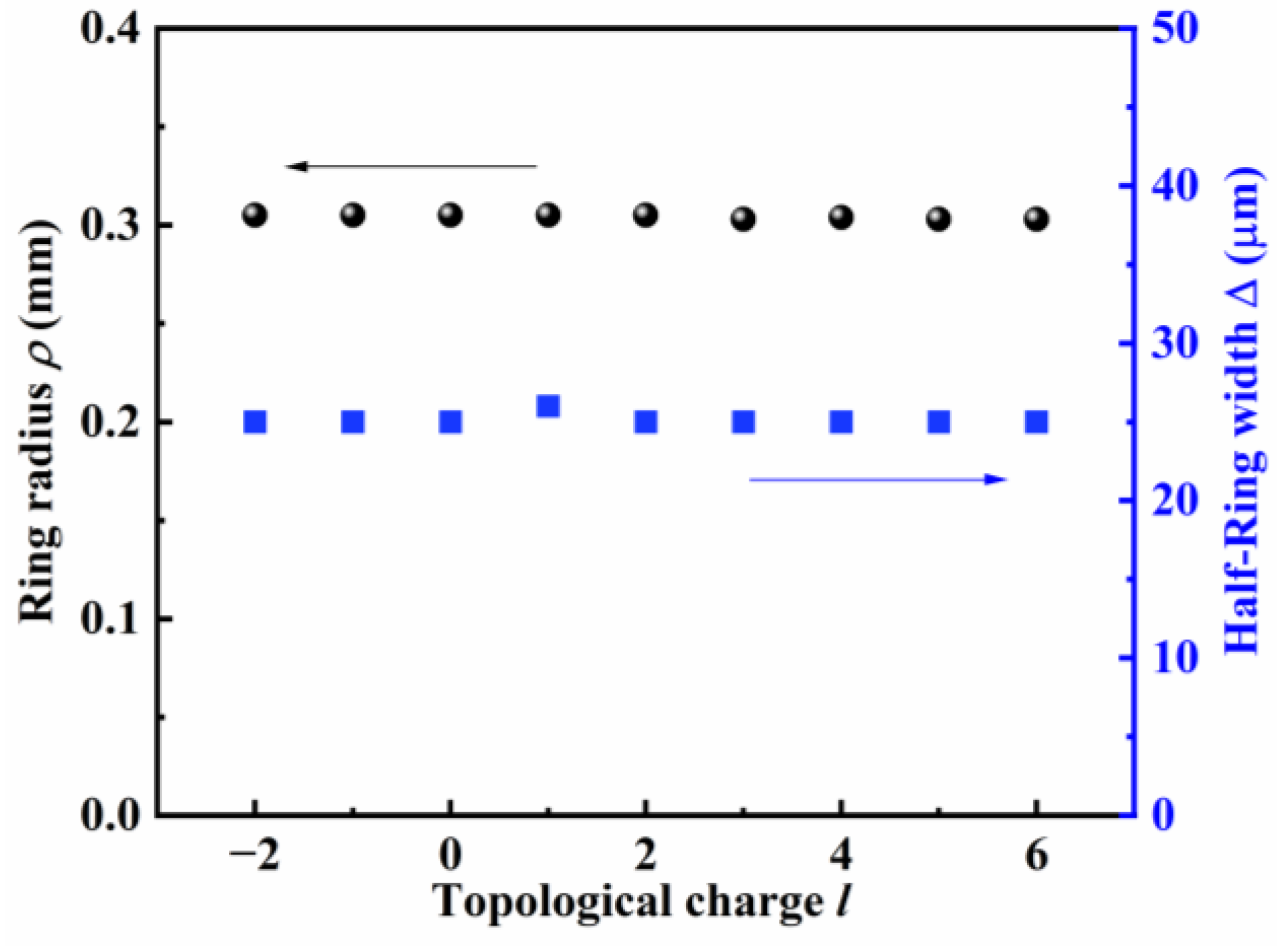
4.3. Characteristics of PVBs with Different TCs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Fürhapter, S.; Jesacher, A.; Bernet, S.; Ritsch-Marte, M. Spiral phase contrast imaging in microscopy. Opt. Expr. 2005, 13, 689–694. [Google Scholar] [CrossRef]
- Spektor, B.; Normatov, A.; Shamir, J. Singular beam microscopy. Appl. Opt. 2008, 47, A78–A87. [Google Scholar] [CrossRef]
- Wang, B.; Shi, J.; Zhang, T.; Xu, X.; Cao, Y.; Li, X. Improved lateral resolution with an annular vortex depletion in STED microscopy. Opt. Lett. 2017, 42, 4885–4888. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.M.; Ihn, Y.S.; Kim, Y.H. Direct generation of narrow-band hyperentangled photons. Phys. Rev. Lett. 2019, 122, 123607. [Google Scholar] [CrossRef]
- Graffitti, F.; D’Ambrosio, V.; Proietti, M.; Ho, J.; Piccirillo, B.; De Lisio, C.; Marrucci, L.; Fedrizzi, A. Hyperentanglement in structured quantum light. Phys. Rev. Res. 2020, 2, 043350. [Google Scholar] [CrossRef]
- Rahmani, A.; Colas, D.; Voronova, N.; Jamshidi-Ghaleh, K.; Dominici, L.; Laussy, F.P. Topologically driven Rabi-oscillating interference dislocation. Nanophotonics 2022, 11, 2909–2919. [Google Scholar] [CrossRef]
- Grier, D.G. A resolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Paterson, L.; MacDonald, M.P.; Arlt, J.; Sibbett, W.; Bryant, P.E.; Dholakia, K. Controlled rotation of optically trapped microscopic particles. Science 2001, 292, 912–914. [Google Scholar] [CrossRef]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343–348. [Google Scholar] [CrossRef]
- Lavery, M.P.J.; Speirits, F.C.; Barnett, S.M.; Padagett, M.J. Detection of a spinning object using light’s orbital angular momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef]
- Vallone, G.; D’Ambrosio, V.; Sponselli, A.; Slussarenko, S.; Marrucci, L.; Sciarrino, F.; Villoresi, P. Free-space quantum key distribution by rotation-invariant twisted photons. Phys. Rev. Lett. 2014, 113, 060503. [Google Scholar] [CrossRef] [PubMed]
- Bae, J.Y.; Jeon, C.; Pae, K.H.; Kim, C.M.; Kim, H.S.; Han, I.; Yeo, W.J.; Jeong, B.; Jeon, M.; Lee, D.H.; et al. Generation of low-order Laguerre-Gaussian beams using hybrid-machined reflective spiral phase plates for intense laser-plasma interactions. Results Phys. 2020, 19, 103499. [Google Scholar] [CrossRef]
- Yu, T.; Xia, H.; Xie, W.K.; Xiao, G.Z.; Li, H.J. The generation and verification of Bessel-Gaussian beam based on coherent beam combining. Results Phys. 2020, 16, 102872. [Google Scholar] [CrossRef]
- Lyu, C.; Belić, M.R.; Li, Y.; Zhang, Y. Generation of diffraction-free Bessel beams based on combined axicons. Opt. Laser. Technol. 2023, 164, 109548. [Google Scholar] [CrossRef]
- Li, X.Z.; Ma, H.X.; Yin, C.L.; Tang, J.; Li, H.H.; Tang, M.M.; Wang, J.G.; Tai, Y.P.; Li, X.F.; Wang, Y.S. Controllable mode transformation in perfect optical vortices. Opt. Expr. 2018, 26, 651–662. [Google Scholar] [CrossRef]
- Yan, H.W.; Zhang, E.T.; Zhao, B.Y.; Duan, K.L. Free-space propagation of guided optical vortices excited in an annular core fiber. Opt. Expr. 2012, 20, 17904–17915. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Mazilu, M.; Arita, Y.; Wright, E.M.; Dholakia, K. Dynamics of microparticles trapped in a perfect vortex Beam. Opt. Lett. 2013, 38, 4919–4922. [Google Scholar] [CrossRef]
- Ostrovsky, S.; Rickenstorff-Parrao, C.; Arrizón, V. Generation of the “perfect” optical vortex using a liquid-crystal spatial light modulator. Opt. Lett. 2013, 38, 534–536. [Google Scholar] [CrossRef] [PubMed]
- García-García, J.; Rickenstorff-Parrao, C.; Ramos-García, R.; Arrizon, V.; Ostrovsky, A.S. Simple technique for generating the perfect optical vortex. Opt. Lett. 2014, 39, 5305–5308. [Google Scholar] [CrossRef] [PubMed]
- Vaity, P.; Rusch, L. Perfect vortex beam: Fourier transformation of a Bessel beam. Opt. Lett. 2015, 40, 597–600. [Google Scholar] [CrossRef]
- Li, L.; Chang, C.; Yuan, C.; Feng, S.; Nie, S.; Ren, Z.C.; Wang, H.T.; Ding, J. High efficiency generation of tunable ellipse perfect vector beams. Photonics Res. 2018, 6, 1116–1123. [Google Scholar] [CrossRef]
- Gu, F.; Li, L.; Chang, C.; Yuan, C.; Feng, S.; Nie, S.; Ding, J. Generation of fractional ellipse perfect vector beams. Opt. Commun. 2019, 443, 44–47. [Google Scholar] [CrossRef]
- Pradhan, P.; Sharma, M.; Ung, B. Generation of perfect cylindrical vector beams with complete control over the ring width and ring diameter. IEEE Photon. J. 2018, 10, 6500310. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Optimal phase element for generating a perfect optical vortex. JOSAA 2016, 33, 2376–2384. [Google Scholar] [CrossRef] [PubMed]
- Carvajal, N.A.; Acevedo, C.H.; Moreno, Y.T. Generation of perfect optical vortices by using a transmission liquid crystal spatial light modulator. Int. J. Opt. 2017, 2017, 6852019. [Google Scholar] [CrossRef]
- Li, X.; Wei, H.; Visser, T.D.; Cai, Y.J.; Liu, X.L. Partially coherent perfect vortex beam generated by an axicon phase. Appl. Phys. Lett. 2021, 119, 171108. [Google Scholar] [CrossRef]
- Wang, T.; Fu, S.; He, F.; Gao, C. Generation of perfect polarization vortices using combined gratings in a single spatial light modulator. Appl. Opt. 2017, 56, 7567–7571. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Mazilu, M.; Arita, Y.; Wright, E.M.; Dholakia, K. Creating and probing of a perfect vortex in situ with an optically trapped particle. Opt. Rev. 2015, 22, 162–165. [Google Scholar] [CrossRef]
- Zhu, F.; Huang, S.; Shao, W.; Zhang, J.; Chen, M.; Zhang, W.; Zeng, J. Free-space optical communication link using perfect vortex beams carrying orbital angular momentum (OAM). Opt. Commun. 2017, 396, 50–57. [Google Scholar] [CrossRef]
- Li, X.; Meng, Y.; Li, H.; Wang, J.; Yin, C.; Tai, Y.; Wang, H.; Zhang, L. Generation of Perfect Vortex Beams and Space Free-Control Technology. Acta Opt. Sin. 2016, 36, 1026018. [Google Scholar]
- Reddy, S.G.; Chithrabhanu, P.; Vaity, P.; Aadhi, A.; Prabhakar, S.; Singh, R.P. Non-diffracting speckles of a perfect vortex beam. J. Opt. 2016, 18, 055602. [Google Scholar] [CrossRef]
- Wang, C.; Ren, Y.; Liu, T.; Liu, Z.; Qiu, S.; Li, Z.; Ding, Y.; Wu, H. Generating a new type of polygonal perfect optical vortex. Opt. Expr. 2021, 29, 14126–14134. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Han, Y.; Deng, D.; Zhu, D. High order perfect optical vortex shaping. Opt. Commun. 2019, 435, 93–96. [Google Scholar] [CrossRef]
- Zhang, C.; Min, C.; Yuan, X.C. Shaping perfect optical vortex with amplitude modulated using a digital micro-mirror device. Opt. Commun. 2016, 381, 292–295. [Google Scholar] [CrossRef]
- Deng, D.; Li, Y.; Han, Y.; Su, X.; Ye, J.; Gao, J.; Sun, Q.; Qu, S. Perfect vortex in three-dimensional multifocal array. Opt. Expr. 2016, 24, 28270–28278. [Google Scholar] [CrossRef]
- García-García, J.; García-de-Blas, M.; Geday, M.A.; Quintana, X.; Caño-Grcía, M. Flat variable liquid crystal diffractive spiral axicon enabling perfect vortex beams generation. Sci. Rep. 2023, 13, 2385. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, H.; Xiang, L.; Chen, L.; Yang, J.; Wen, J.; Shang, Y.; Wang, T.; Pang, F. Generation of perfect vortex beams with polymer-based phase plate. IEEE Photon. Technol. Lett. 2020, 32, 565–568. [Google Scholar] [CrossRef]
- Mandal, A.; Maji, S.; Brundavanam, M.M. Common-path generation of stable cylindrical perfect vector vortex beams with arbitrary order. Opt. Commun. 2020, 469, 125807. [Google Scholar] [CrossRef]
- Ke, Y.; Chen, S.; Shu, W.; Luo, H. Generation of perfect vector beams based on the combined modulation of dynamic and geometric phases. Opt. Commun. 2019, 446, 191–195. [Google Scholar] [CrossRef]
- Wang, G.X.; Weng, X.Y.; Kang, X.Y.; Li, Z.Y.; Chen, K.Y.; Gao, X.M.; Zhuang, S.L. Free-space creation of a perfect vortex beam with fractional topological charge. Opt. Expr. 2023, 31, 5757–5766. [Google Scholar] [CrossRef] [PubMed]
- Jabir, M.V.; Apurv Chaitanya, N.; Aadhi, A.; Samanta, G.K. Generation of “perfect” vortex of variable size and its effect in angular spectrum of the down-converted photons. Sci. Rep. 2016, 6, 21877. [Google Scholar]
- Knyazev, B.; Cherkassky, V.; Kameshkov, O. “Perfect” terahertz vortex beams formed using diffractive axicons and prospects for excitation of vortex surface plasmon polaritons. Appl. Sci. 2021, 11, 717. [Google Scholar] [CrossRef]
- Karahroudi, M.K.; Parmoon, B.; Qasemi, M.; Mobashery, A.; Saghafifar, H. Generation of perfect optical vortices using a Bessel-Gaussian beam diffracted by curved fork grating. Appl. Opt. 2017, 56, 5817–5823. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Zhang, Y.; Liu, S.; Ma, C.J.; Han, L.; Cheng, H.C.; Zhao, J.L. Generation of perfect vectorial vortex beams. Opt. Lett. 2016, 41, 2205–2208. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Khorasaninejad, M.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Zaidi, A.; Capasso, F. Generation of wavelength-independent subwavelength Bessel beams using metasurfaces. Light Sci. Appl. 2017, 6, e16259. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Liang, Y.; Yun, X.; Wang, Z.; Zhao, T.; Wang, S.; Bianco, P.R.; Lei, M. Generalized perfect optical vortices with free lens modulation. Photonics Res. 2023, 11, 27–34. [Google Scholar] [CrossRef]
- Pinnell, J.; Rodríguez-Fajardo, V.; Forbes, A. How perfect are perfect vortex beams? Opt. Lett. 2019, 44, 5614–5617. [Google Scholar] [CrossRef]
- Chen, Y.; Fang, Z.X.; Ren, Y.X.; Gong, L.; Lu, R.D. Generation and characterization of a perfect vortex beam with a large topological charge through a digital micromirror device. Appl. Opt. 2015, 54, 8030–8035. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, T.; Ren, Y.; Fang, Z.; Ding, G.; He, L.; Lu, R.; Huang, K. Generalized perfect optical vortices along arbitrary trajectories. J. Phys. D Appl. Phys. 2021, 54, 214001. [Google Scholar] [CrossRef]
- Huang, Y.; Qin, Y.; Tu, P.; Zhu, H.; Zhang, Q.; Lin, R.; Xia, J.; Zhao, M.; Yang, Z. Radial phase shift spiral zone plate fabrication using direct laser writing for generating a perfect vortex beam. In Proceedings of the Twelfth International Conference on Information Optics and Photonics, Xi’an, China, 1 November 2021. [Google Scholar]
- Sabatyan, A.; Behjat, Z. Radial phase modulated spiral zone plate for generation and manipulation of optical perfect vortex. Opt. Quant. Electron. 2017, 49, 371. [Google Scholar] [CrossRef]
- Liu, Y.; Ke, Y.; Zhou, J.; Liu, Y.; Luo, H.; Wen, S.; Fan, D. Generation of perfect vortex and vector beams based on Pancharatnam-Berry phase elements. Sci. Rep. 2017, 7, 44096. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.; Gao, J.; Yang, X. Generating focused 3D perfect vortex beams by plasmonic metasurfaces. Adv. Opt. Mater. 2018, 6, 1701228. [Google Scholar] [CrossRef]
- Ahmed, H.; Ansari, M.A.; Li, Y.; Zentgraf, T.; Mehmood, M.Q.; Chen, X. Dynamic control of hybrid grafted perfect vector vortex beams. Nat. Commun. 2023, 14, 3915. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Wan, M.; Zhang, X.; Yuan, S.; Zhang, L.; Wang, J. Generating ultraviolet perfect vortex beams using a high-efficiency broadband dielectric metasurface. Opt. Expr. 2022, 30, 4806–4816. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wu, J.; Ren, B.; Yao, J.; Tang, S.; Lü, C.; Jiang, Y. High-performance polarization-controlled perfect optical vortex generation via all-dielectric metasurfaces in the visible region. Phys. Scr. 2023, 98, 085931. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, C.; Guo, K.; Wei, Z.; Liu, H. Generation and measurement of irregular polygonal perfect vortex optical beam based on all-dielectric geometric metasurface. Opt. Expr. 2023, 31, 16192–16204. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhou, C.; Guo, K.; Wei, Z.; Liu, H. Generation of multi-channel perfect vortex beams with the controllable ring radius and the topological charge based on an all-dielectric transmission metasurface. Opt. Expr. 2022, 30, 30881–30893. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Huang, H.; Geng, D.; Wang, Y.; Ma, K.; Guo, H.; Ma, A.N. Generation and polarization analysis of vector perfect optical vortex. J. Opt. 2023, 50, 1–8. [Google Scholar] [CrossRef]
- Zhou, Q.W.; Liu, M.Z.; Zhu, W.Q.; Chen, L.; Ren, Y.Z.; Lezec, H.J.; Lu, Y.Q.; Agrawal, A.; Xu, T. Generation of perfect vortex beams by dielectric geometric metasurface for visible light. Laser Photonics Rev. 2021, 15, 2100390. [Google Scholar] [CrossRef]
- Zhang, B.L.; Hu, Z.D.; Wu, J.J.; Wang, J.C.; Nie, Y.G.; Zhang, F.; Li, M.M.; Khakhomov, S. Metasurface-based perfect vortex beams with trigonometric-function topological charge for OAM manipulation. Opt. Lett. 2023, 48, 2409–2412. [Google Scholar] [CrossRef]
- Ju, P.; Fan, W.; Gao, W.; Li, Z.; Gao, Q.; Jiang, X.; Zhang, T. Phase control scheme of the coherent beam combining system for generating perfect vectorial vortex beams assisted by a Dammann vortex grating. Opt. Expr. 2023, 31, 22372–22384. [Google Scholar] [CrossRef]
- Ju, P.; Fan, W.; Gao, W.; Li, Z.; Gao, Q.; Li, G.; Jiang, X.; Zhang, T. Generation of perfect vectorial vortex beams by employing coherent beam combining. Opt. Expr. 2023, 31, 11885–11898. [Google Scholar] [CrossRef]
- Sueda, K.; Miyaji, G.; Miyanaga, N.; Nakatsuka, M. Laguerre-Gaussian beam generated with a multilevel spiral phase plate for high intensity laser pulses. Opt. Expr. 2004, 12, 3548–3553. [Google Scholar] [CrossRef]
- Longman, A.; Fedosejevs, R. Mode conversion efficiency to Laguerre-Gaussian OAM modes using spiral phase optics. Opt. Expr. 2017, 25, 17382–17392. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Li, P.; Ma, J.; Zhang, S.; Gu, Y. Generation and Detection of Optical Vortices with Multiple Cascaded Spiral Phase Plates. Photonics 2022, 9, 354. [Google Scholar] [CrossRef]
- Ruffato, G.; Massari, M.; Romanato, F. Generation of high-order Laguerre-Gaussian modes by means of spiral phase plates. Opt. Lett. 2014, 39, 5094–5097. [Google Scholar] [CrossRef]
- Jarutis, V.; Paška, R.; Stabinis, A. Focusing of Laguerre-Gaussian beams by axicon. Opt. Commun. 2000, 184, 105–112. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K. Generation of high-order Bessel beams by use of an axicon. Opt. Commun. 2000, 177, 297–301. [Google Scholar] [CrossRef]
- Parsa, S.; Fallah, H.R.; Ramezani, M.; Soltanolkotabi, S. Generation of pulsed Bessel-Gaussian beams using passive axicon-theoretical and experimental studies. Appl. Opt. 2012, 51, 7339–7344. [Google Scholar] [CrossRef]
- Zhang, S.; Hou, W.; Tao, X.; Guo, M.; Li, Y.; Li, P. Second-Harmonic Generation of the Vortex Beams with Integer and Fractional Topological Charges. Photonics 2023, 10, 867. [Google Scholar] [CrossRef]
- Ma, J.; Li, P.; Gu, Y. Characteristics of Spiral Patterns Formed by Coaxial Interference between Two Vortex Beams with Different Radii of Wavefront Curvatures. Photonics 2021, 8, 393. [Google Scholar] [CrossRef]
- Ma, J.; Li, P.; Zhou, Z.H.; Gu, Y. Characteristics of fork-shaped fringes formed by off-axis interference of two vortex beams. JOSA A 2021, 38, 115–123. [Google Scholar] [CrossRef] [PubMed]
- Vaity, P.; Brunet, C.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Exciting OAM modes in annular-core fibers via perfect OAM beams. In Proceedings of the 2014 European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014. [Google Scholar]
- Ma, Y.Y.; Lee, A.J.; Pask, H.M.; Miyamoto, K.; Omatsu, T. Direct generation of 1108 nm and 1173 nm Laguerre-Gaussian modes from a self-Raman Nd: GdVO4 laser. Opt. Expr. 2020, 28, 24095–24103. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, X.; Liang, Y.; Zhang, S.; Li, Y.; Guo, M.; Li, P. Generation of Perfect Vortex Beams with Complete Control over the Ring Radius and Ring Width. Photonics 2023, 10, 1382. https://doi.org/10.3390/photonics10121382
Tao X, Liang Y, Zhang S, Li Y, Guo M, Li P. Generation of Perfect Vortex Beams with Complete Control over the Ring Radius and Ring Width. Photonics. 2023; 10(12):1382. https://doi.org/10.3390/photonics10121382
Chicago/Turabian StyleTao, Xin, Yong Liang, Shirui Zhang, Yueqing Li, Minghao Guo, and Peng Li. 2023. "Generation of Perfect Vortex Beams with Complete Control over the Ring Radius and Ring Width" Photonics 10, no. 12: 1382. https://doi.org/10.3390/photonics10121382
APA StyleTao, X., Liang, Y., Zhang, S., Li, Y., Guo, M., & Li, P. (2023). Generation of Perfect Vortex Beams with Complete Control over the Ring Radius and Ring Width. Photonics, 10(12), 1382. https://doi.org/10.3390/photonics10121382




