Asymptotic Capacity Maximization for MISO Visible Light Communication Systems with a Liquid Crystal RIS-Based Receiver
Abstract
:1. Introduction
- An LC RIS-aided MISO-VLC system is proposed with an LC RIS in the VLC receiver to steer the incident light dynamically; meanwhile, the corresponding asymptotic capacity in the MISO-VLC system is enhanced after applying the LC RIS;
- For the LC RIS-aided MISO-VLC system, the asymptotic capacity in high SNR with peak-constrained inputs is derived. Additionally, we formulate an optimization problem with the asymptotic capacity derived by us as the objective function and the refractive index of LC RIS as the independent variable. For this nonconvex optimization problem, we propose a metaheuristic optimization algorithm (particle swarm optimization algorithm) to determine the optimal refractive index of the LC RIS according to the environmental changes;
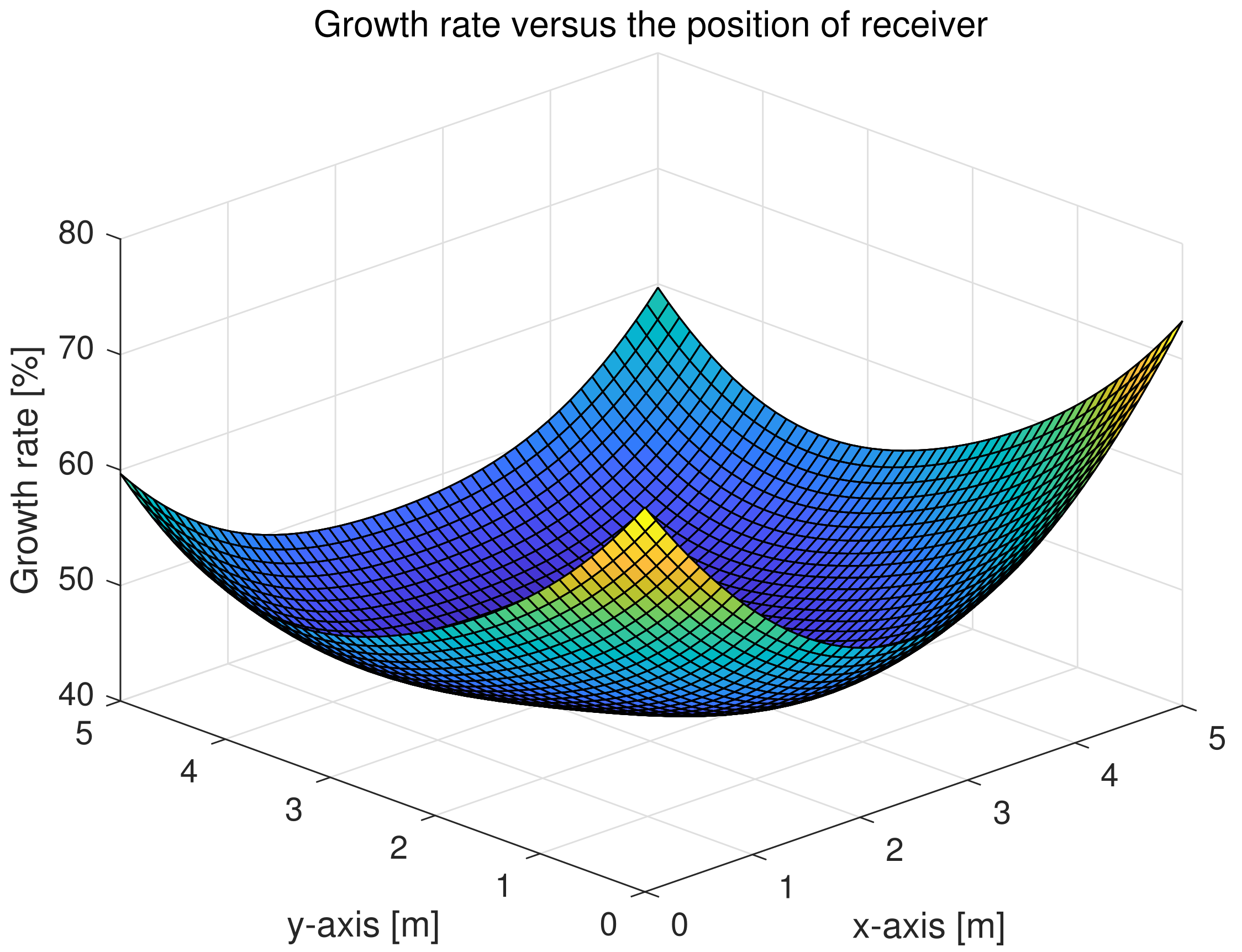
- The simulation results demonstrate that the employment of an LC RIS in VLC receivers can raise the communication performance of MISO-VLC systems to a greater degree. Simultaneously, compared with the exhaustive search method, the PSO algorithm is an effective method to deal with the optimization problems for LC RIS-based MISO-VLC systems. Meanwhile, we found that there was a significant performance gain compared with a benchmark scheme (BSch) (randomly selecting a refractive index of LC RIS) or the MISO-VLC systems with receivers without the LC RIS. In addition, the LC RIS is expected to solve the dead zone problem in traditional VLC systems by analyzing the growth rate of communication performance for each location on the floor.
2. System Model
2.1. Channel Gain
2.1.1. Channel Gain through the Air
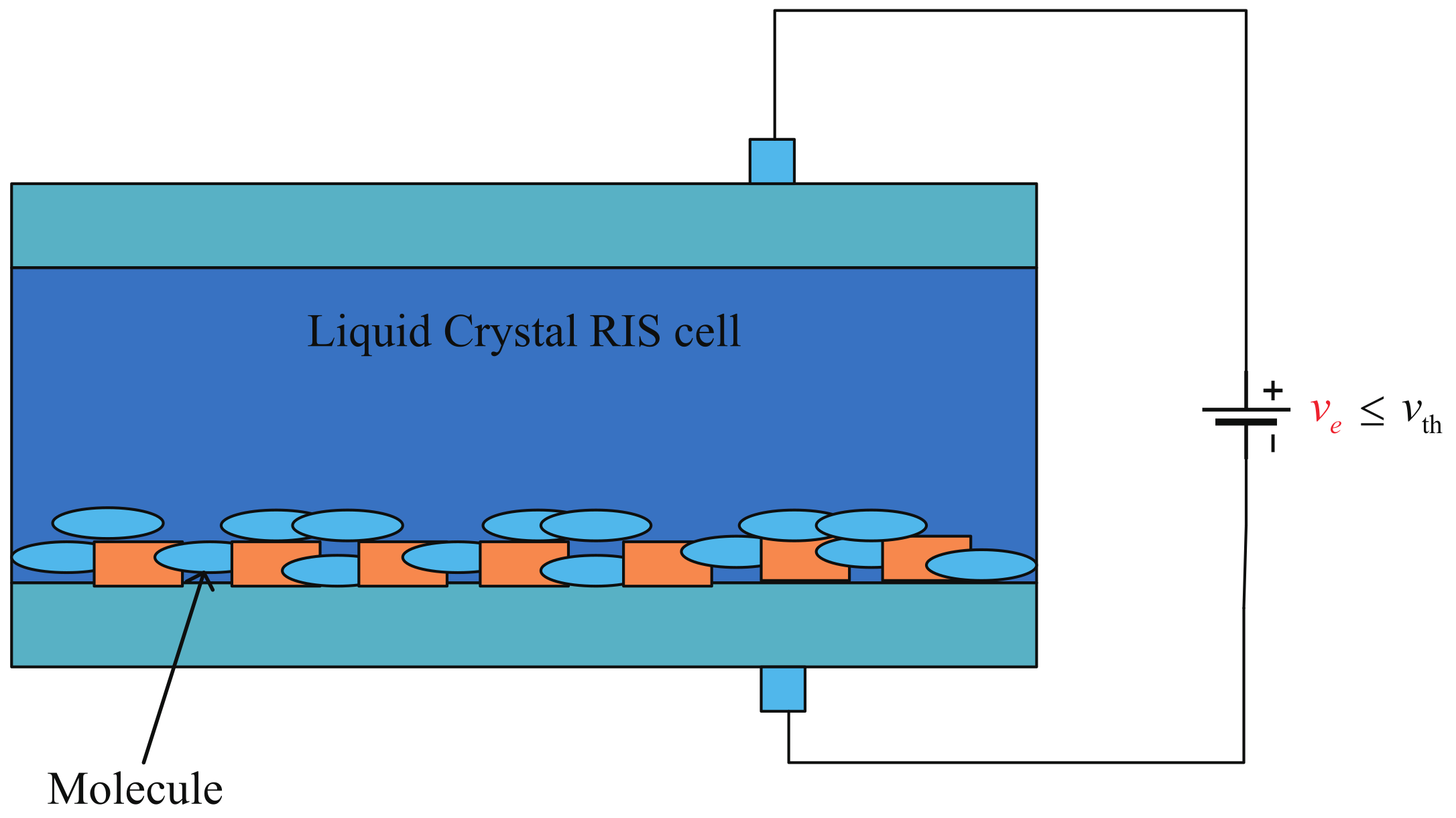
2.1.2. The Transition Coefficient through the LC RIS
2.2. Amplification Coefficient
3. Asymptotic Capacity Optimization
3.1. Asymptotic Capacity Maximization Problem
3.2. Proposed Solution Algorithm
| Algorithm 1 The PSO Algorithm for Asymptotic Capacity Maximization |
|
3.3. Complexity Analysis
4. Simulation Results and Analysis
4.1. Simulation Parameters
4.2. Simulation Results
4.2.1. Convergence Analysis for the Proposed Algorithm
4.2.2. Asymptotic Capacity Performance Gain for the Optimal Design of LC RIS versus a Baseline Scheme
4.2.3. Growth Rate of the Performance versus the Position of the Receiver
5. Conclusions and Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Samsung Research. 6G: The Next Hyper Connected Experience for All. 2020. Available online: https://research.samsung.com/next-generation-communications (accessed on 24 July 2022).
- Karunatilaka, D.; Zafar, F.; Kalavally, V.; Parthiban, R. LED based indoor visible light communications: State of the art. IEEE Commun. Surv. Tutorials 2015, 17, 1649–1678. [Google Scholar] [CrossRef]
- Luo, S.; Hao, J.; Ye, F.; Li, J.; Ruan, Y.; Cui, H.; Liu, W.; Chen, L. Evolution of the electromagnetic manipulation: From tunable to programmable and intelligent metasurfaces. Micromachines 2021, 12, 988. [Google Scholar] [CrossRef] [PubMed]
- ElMossallamy, M.A.; Zhang, H.; Song, L.; Seddik, K.G.; Han, Z.; Li, G.Y. Reconfigurable intelligent surfaces for wireless communications: Principles, challenges, and opportunities. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 990–1002. [Google Scholar] [CrossRef]
- Basar, E.; Di Renzo, M.; De Rosny, J.; Debbah, M.; Alouini, M.S.; Zhang, R. Wireless communications through reconfigurable intelligent surfaces. IEEE Access 2019, 7, 116753–116773. [Google Scholar] [CrossRef]
- Guo, H.; Liang, Y.C.; Chen, J.; Larsson, E.G. Weighted sum-rate maximization for reconfigurable intelligent surface aided wireless networks. IEEE Trans. Wirel. Commun. 2020, 19, 3064–3076. [Google Scholar] [CrossRef] [Green Version]
- Ma, Q.; Bai, G.D.; Jing, H.B.; Yang, C.; Li, L.; Cui, T.J. Smart metasurface with self-adaptively reprogrammable functions. Light Sci. Appl. 2019, 8, 98. [Google Scholar] [CrossRef] [Green Version]
- Renzo, M.D.; Debbah, M.; Phan-Huy, D.T.; Zappone, A.; Alouini, M.S.; Yuen, C.; Sciancalepore, V.; Alexandropoulos, G.C.; Hoydis, J.; Gacanin, H.; et al. Smart radio environments empowered by reconfigurable AI meta-surfaces: An idea whose time has come. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 129. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Yang, H.; Hu, R.Q.; Wang, J. MmWave and VLC-based indoor channel models in 5G wireless networks. IEEE Wirel. Commun. 2018, 25, 70–77. [Google Scholar] [CrossRef]
- Aboagye, S.; Ngatched, T.M.; Dobre, O.A.; Ndjiongue, A.R. Intelligent reflecting surface-aided indoor visible light communication systems. IEEE Commun. Lett. 2021, 25, 3913–3917. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, J.; Guo, J.N. Position Design for Reconfigurable Intelligent-Surface-Aided Indoor Visible Light Communication Systems. Electronics 2022, 11, 3076. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, J.; Guo, J. Capacity Maximization for Reconfigurable Intelligent Surface-Aided MISO Visible Light Communications. Photonics 2022, 9, 487. [Google Scholar] [CrossRef]
- Qian, L.; Chi, X.; Zhao, L.; Chaaban, A. Secure visible light communications via intelligent reflecting surfaces. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Sun, S.; Yang, F.; Song, J.; Han, Z. Joint resource management for intelligent reflecting surface–aided visible light communications. IEEE Trans. Wirel. Commun. 2022, 21, 6508–6522. [Google Scholar] [CrossRef]
- Sun, S.; Yang, F.; Song, J.; Zhang, R. Intelligent Reflecting Surface for MIMO VLC: Joint Design of Surface Configuration and Transceiver Signal Processing. arXiv 2022, arXiv:2206.14465. [Google Scholar] [CrossRef]
- Han, Y.; Xiao, Y.; Zhang, X.; Gao, Y.; Zhu, Q.; Dong, B. Design of dynamic active-passive beamforming for reconfigurable intelligent surfaces assisted hybrid VLC/RF communications. IET Commun. 2022, 16, 1531–1544. [Google Scholar] [CrossRef]
- Abdelhady, A.M.; Salem, A.K.S.; Amin, O.; Shihada, B.; Alouini, M.S. Visible light communications via intelligent reflecting surfaces: Metasurfaces vs. mirror arrays. IEEE Open J. Commun. Soc. 2020, 2, 1–20. [Google Scholar] [CrossRef]
- Aboagye, S.; Ndjiongue, A.R.; Ngatched, T.; Dobre, O.; Poor, H.V. RIS-Assisted Visible Light Communication Systems: A Tutorial. arXiv 2022, arXiv:2204.07198. [Google Scholar] [CrossRef]
- Ndjiongue, A.R.; Ngatched, T.M.; Dobre, O.A.; Haas, H. Re-configurable intelligent surface-based VLC receivers using tunable liquid-crystals: The concept. J. Light. Technol. 2021, 39, 3193–3200. [Google Scholar] [CrossRef]
- Ndjiongue, A.R.; Ngatched, T.M.; Dobre, O.A.; Haas, H. Toward the use of re-configurable intelligent surfaces in VLC systems: Beam steering. IEEE Wirel. Commun. 2021, 28, 156–162. [Google Scholar] [CrossRef]
- Forkel, G.J.; Krohn, A.; Hoeher, P.A. Optical interference suppression based on LCD-filtering. Appl. Sci. 2019, 9, 3134. [Google Scholar] [CrossRef] [Green Version]
- Krohn, A.; Forkel, G.J.; Hoeher, P.A.; Pachnicke, S. LCD-based optical filtering suitable for non-imaging channel decorrelation in VLC applications. J. Light. Technol. 2019, 37, 5892–5898. [Google Scholar] [CrossRef]
- Zhang, X.G.; Sun, Y.L.; Zhu, B.; Jiang, W.X.; Yu, Q.; Tian, H.W.; Qiu, C.W.; Zhang, Z.; Cui, T.J. A metasurface-based light-to-microwave transmitter for hybrid wireless communications. Light Sci. Appl. 2022, 11, 126. [Google Scholar] [CrossRef]
- Krohn, A.; Pachnicke, S.; Hoeher, P.A. Genetic optimization of liquid crystal matrix based interference suppression for VLC MIMO transmissions. IEEE Photonics J. 2021, 14, 1–5. [Google Scholar] [CrossRef]
- Aboagye, S.; Ndjiongue, A.R.; Ngatched, T.M.; Dobre, O.A. Design and Optimization of Liquid Crystal RIS-Based Visible Light Communication Receivers. IEEE Photonics J. 2022, 14, 1–7. [Google Scholar] [CrossRef]
- Lee, K.; Park, H.; Barry, J.R. Indoor channel characteristics for visible light communications. IEEE Commun. Lett. 2011, 15, 217–219. [Google Scholar] [CrossRef]
- Komine, T.; Nakagawa, M. Fundamental analysis for visible-light communication system using LED lights. IEEE Trans. Consum. Electron. 2004, 50, 100–107. [Google Scholar] [CrossRef]
- Hébert, M.; Hersch, R.D.; Emmel, P. Fundamentals of optics and radiometry for color reproduction. In Handbook of Digital Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 1–57. [Google Scholar]
- Saleh, B.E.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Moser, S.M.; Wang, L.; Wigger, M. Capacity results on multiple-input single-output wireless optical channels. IEEE Trans. Inf. Theory 2018, 64, 6954–6966. [Google Scholar] [CrossRef] [Green Version]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]





| Name of Parameter | Value |
|---|---|
| 1 | |
| a | |
| 12 | |
| 0.8 V | |
| 1.2 V | |
| d | |
| (m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Zhang, J.; Zhang, Y.; Xin, G.; Guo, D. Asymptotic Capacity Maximization for MISO Visible Light Communication Systems with a Liquid Crystal RIS-Based Receiver. Photonics 2023, 10, 128. https://doi.org/10.3390/photonics10020128
Wu Q, Zhang J, Zhang Y, Xin G, Guo D. Asymptotic Capacity Maximization for MISO Visible Light Communication Systems with a Liquid Crystal RIS-Based Receiver. Photonics. 2023; 10(2):128. https://doi.org/10.3390/photonics10020128
Chicago/Turabian StyleWu, Qi, Jian Zhang, Yanyu Zhang, Gang Xin, and Dongqin Guo. 2023. "Asymptotic Capacity Maximization for MISO Visible Light Communication Systems with a Liquid Crystal RIS-Based Receiver" Photonics 10, no. 2: 128. https://doi.org/10.3390/photonics10020128
APA StyleWu, Q., Zhang, J., Zhang, Y., Xin, G., & Guo, D. (2023). Asymptotic Capacity Maximization for MISO Visible Light Communication Systems with a Liquid Crystal RIS-Based Receiver. Photonics, 10(2), 128. https://doi.org/10.3390/photonics10020128





