Enhancing the Self-Healing Ability of a Partially Coherent Airy Beam via Fourier Processing: Numerical Investigation
Abstract
1. Introduction
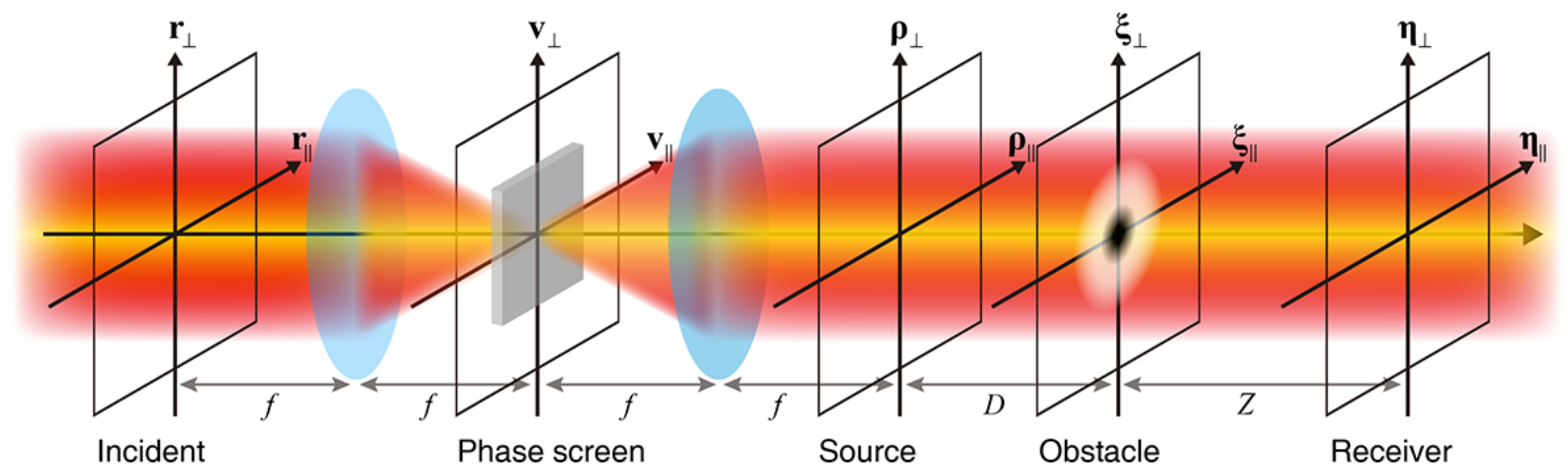
2. Theory
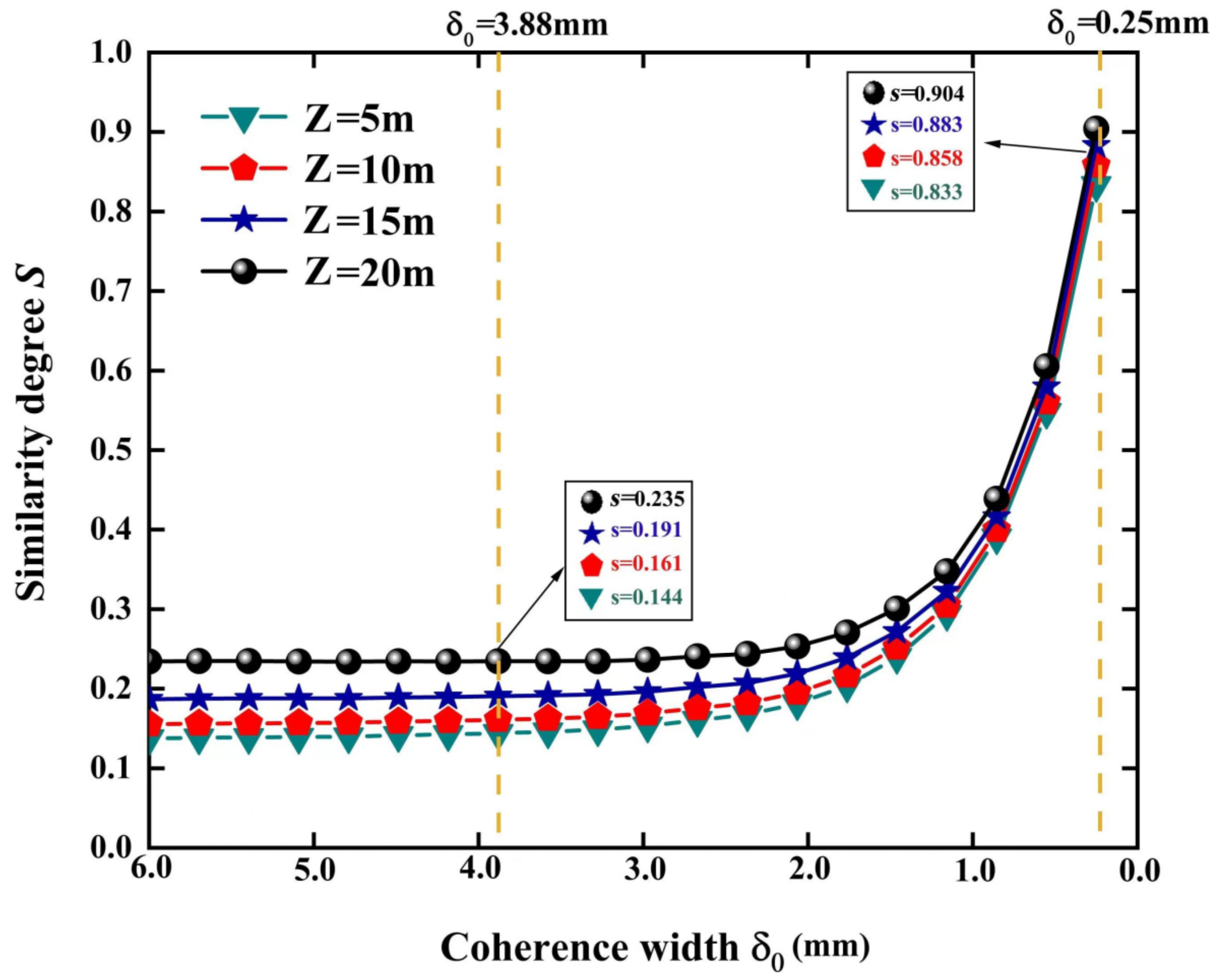
3. Numerical Results
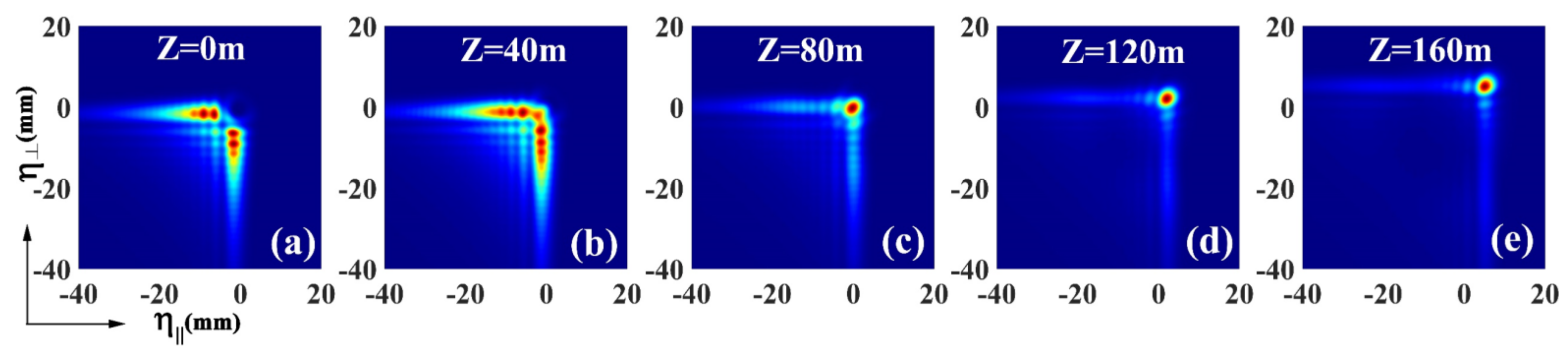
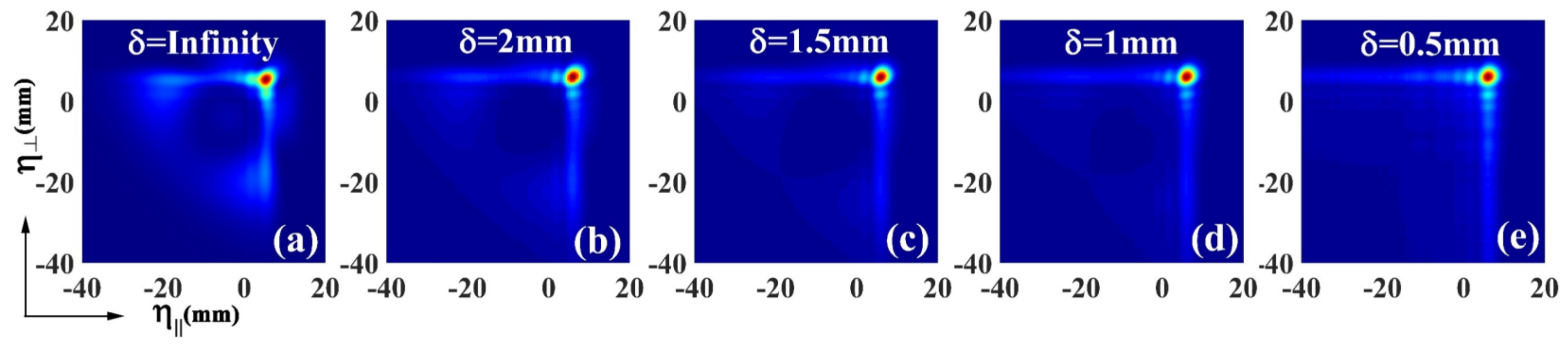
- Case 1:
- The Obstacle Is Located in the Source Plane
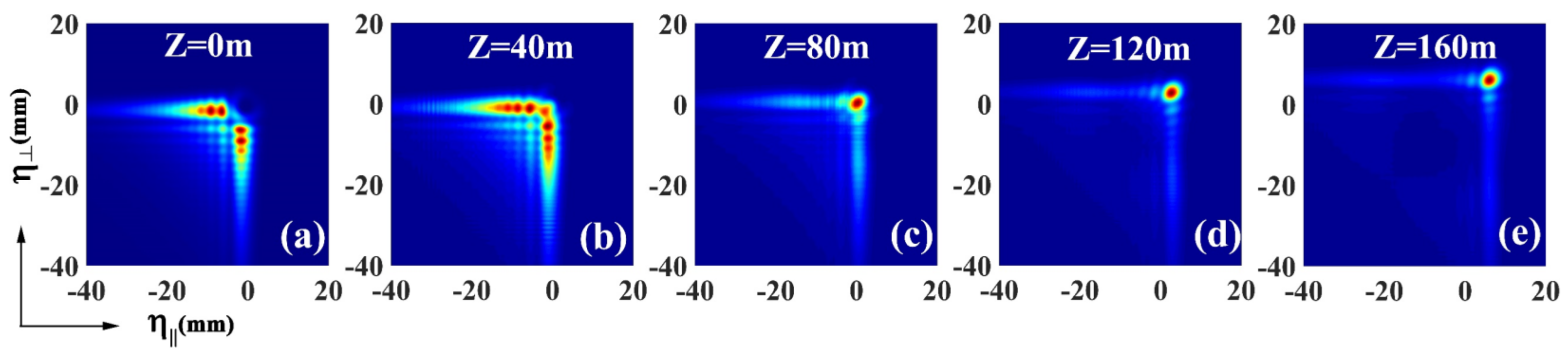
- Case 2:
- The Obstacle Is Located in the Propagation Path at D = 10 m
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef] [PubMed]
- Gori, F.; Ramírez-Sánchez, V.; Santarsiero, M.; Shirai, T. On genuine cross-spectral density matrices. J. Opt. A Pure Appl. Opt. 2009, 11, 085706. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Liu, X.; Cai, Y.; Korotkova, O. Experimental generation of cosine-Gaussian-correlated Schell-model beams with rectangular symmetry. Opt. Lett. 2014, 39, 769–772. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Liu, X.; Xu, Z.; Wang, F.; Wen, W.; Ponomarenko, S.A.; Cai, Y.; Ma, P. Perfect optical coherence lattices. Appl. Phys. Lett. 2021, 119, 131109. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Cai, Y. Propagation of partially coherent beam in turbulent atmosphere: A review (invited review). Prog. Electromagn. Res. 2015, 150, 123–143. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, X.; Cai, Y.; Ponomarenko, S.A.; Liang, C. Structurally stable beams in the turbulent atmosphere: Dark and antidark beams on incoherent background. J. Opt. Soc. Am. A 2022, 39, C51–C57. [Google Scholar] [CrossRef]
- Wang, H.; Ji, X.-L.; Deng, Y.; Li, X.-Q.; Yu, H. Theory of the quasi-steady-state self-focusing of partially coherent light pulses in nonlinear media. Opt. Lett. 2020, 45, 710–713. [Google Scholar] [CrossRef]
- Wang, X.; Tang, J.; Wang, Y.; Liu, X.; Liang, C.; Zhao, L.; Hoenders, B.J.; Cai, Y.; Ma, P. Complex and phase screen methods for studying arbitrary genuine Schell-model partially coherent pulses in nonlinear media. Opt. Express 2022, 30, 24222–24231. [Google Scholar] [CrossRef]
- Dong, Y.; Guo, L.; Liang, C.; Wang, F.; Cai, Y. Statistical properties of a partially coherent cylindrical vector beam in oceanic turbulence. J. Opt. Soc. Am. A 2015, 32, 894–901. [Google Scholar] [CrossRef]
- Duan, M.; Du, J.; Zhao, H.; Zhang, X.; Gao, Y. The singularity of the partially coherent beam in biological tissue. Results Phys. 2022, 43, 106097. [Google Scholar]
- Van Dijk, T.; Fischer, D.G.; Visser, T.D.; Wolf, E. Effects of spatial coherence on the angular distribution of radiant intensity generated by scattering on a sphere. Phys. Rev. Lett. 2010, 104, 173902. [Google Scholar] [CrossRef]
- Lu, X.; Shao, Y.; Zhao, C.; Konijnenberg, S.; Zhu, X.; Tang, Y.; Cai, Y.; Urbach, H.P. Noniterative spatially partially coherent diffractive imaging using pinhole array mask. Adv. Photon. 2019, 1, 016005. [Google Scholar] [CrossRef]
- Xu, Z.; Li, X.; Liu, X.; Ponomarenko, S.A.; Cai, Y.; Liang, C. Vortex preserving statistical optical beams. Opt. Express 2020, 28, 8475–8483. [Google Scholar] [CrossRef]
- Redding, B.; Choma, M.A.; Cao, H. Speckle-free laser imaging using random laser illumination. Nat. Photonics 2012, 6, 355–359. [Google Scholar] [CrossRef]
- Liang, C.; Wu, G.; Wang, F.; Li, W.; Cai, Y.; Ponomarenko, S.A. Overcoming the classical Rayleigh diffraction limit by controlling two-point correlations of partially coherent light sources. Opt. Express 2017, 25, 28352–28362. [Google Scholar] [CrossRef]
- Liang, C.; Monfared, Y.E.; Liu, X.; Qi, B.; Wang, F.; Korotkova, O.; Cai, Y. Optimizing illumination’s complex coherence state for overcoming Rayleigh’s resolution limit. Chin. Opt. Lett. 2021, 19, 052601. [Google Scholar] [CrossRef]
- Peng, D.; Huang, Z.; Liu, Y.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Optical coherence encryption with structured random light. PhotoniX 2021, 2, 6. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Wang, F.; Cai, Y.; Liang, C.; Korotkova, O. Robust far-field imaging by spatial coherence engineering. Opto-Electron. Adv. 2021, 4, 210027. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Dong, Z.; Peng, D.; Chen, Y.; Wang, F.; Cai, Y. Robust far-field optical image transmission with structured random light beams. Phys. Rev. Appl. 2022, 17, 024043. [Google Scholar] [CrossRef]
- Pan, R.; Liu, X.; Tang, J.; Ye, H.; Liu, Z.; Ma, P.; Wen, W.; Hoenders, B.J.; Cai, Y.; Liang, C. Enhancing the self-reconstruction ability of the degree of coherence of a light beam via manipulating the cross-phase structure. Appl. Phys. Lett. 2021, 119, 111105. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, X.; Chen, Y.; Wang, F.; Liu, L.; Monfared, Y.E.; Ponomarenko, S.A.; Cai, Y.; Liang, C. Self-healing properties of Hermite-Gaussian correlated Schell-model beams. Opt. Express 2020, 28, 2828–2837. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Chen, Y.; Liu, X.; Cai, Y.; Ponomarenko, S.A. Self-reconstruction of partially coherent light beams scattered by opaque obstacles. Opt. Express 2016, 24, 23735–23746. [Google Scholar] [CrossRef] [PubMed]
- Broky, J.; Siviloglou, G.A.; Dogariu, A.; Christodoulides, D.N. Self-healing properties of optical Airy beams. Opt. Express 2008, 16, 12880–12891. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.; Zhou, G.; Chen, R. Analytical study of the self-healing property of Airy beams. Phys. Rev. A 2012, 85, 013815. [Google Scholar] [CrossRef]
- Vetter, C.; Steinkopf, R.; Bergner, K.; Ornigotti, M.; Nolte, S.; Gross, H.; Szameit, A. Realization of Free-Space Long-Distance Self-Healing Bessel Beams. Laser Photonics Rev. 2019, 13, 1900103. [Google Scholar] [CrossRef]
- Rasouli, S.; Khazaei, A.M.; Hebri, D. Radial carpet beams: A class of nondiffracting, accelerating, and self-healing beams. Phys. Rev. A 2018, 97, 033844. [Google Scholar] [CrossRef]
- Ring, J.D.; Lindberg, J.; Mourka, A.; Mazilu, M.; Dholakia, K.; Dennis, M.R. Auto-focusing and self-healing of Pearcey beams. Opt. Express 2012, 20, 18955–18966. [Google Scholar] [CrossRef]
- Wu, G.; Wang, F.; Cai, Y. Generation and self-healing of a radially polarized Bessel-Gauss beam. Phys. Rev. A 2014, 89, 043807. [Google Scholar] [CrossRef]
- Bouchal, Z.; Wagner, J.; Chlup, M. Self-reconstruction of a distorted nondiffracting beam. Opt. Commun. 1998, 151, 207–211. [Google Scholar] [CrossRef]
- Kaganovsky, Y.; Heyman, E. Wave analysis of Airy beams. Opt. Express 2010, 18, 8440–8452. [Google Scholar] [CrossRef]
- Fahrbach, F.O.; Simon, P.; Rohrbach, A. Microscopy with self-reconstructing beams. Nat. Photonics 2010, 4, 780–785. [Google Scholar] [CrossRef]
- Li, S.; Wang, J. Adaptive free-space optical communications through turbulence using self-healing Bessel beams. Sci. Rep. 2017, 7, 43233. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, G.; Cai, Y.; Wang, F.; Hoenders, B.J. Application of self-healing property of partially coherent beams to ghost imaging. Appl. Phys. Lett. 2020, 117, 171104. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of accelerating Airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef]
- Greenberger, D.M. Comment on “Nonspreading wave packets”. Am. J. Phys. 1980, 48, 256. [Google Scholar] [CrossRef]
- Zhu, Y.; Dong, Z.; Wang, F.; Chen, Y.; Cai, Y. Compact generation of robust Airy beam pattern with spatial coherence engineering. Opt. Lett. 2022, 47, 2846–2849. [Google Scholar] [CrossRef]
- Hajati, M.; Sieben, V.; Ponomarenko, S.A. Airy beams on incoherent background. Opt. Lett. 2021, 46, 3961–3964. [Google Scholar] [CrossRef]
- Liu, X.; Xia, D.; Monfared, Y.E.; Liang, C.; Wang, F.; Cai, Y.; Ma, P. Generation of novel partially coherent truncated Airy beams via Fourier phase processing. Opt. Express 2020, 28, 9777–9785. [Google Scholar] [CrossRef]
- Sun, B.; Huang, Z.; Zhu, X.; Wu, D.; Chen, Y.; Wang, F.; Cai, Y.; Korotkova, O. Random source for generating Airy-like spectral density in the far field. Opt. Express 2020, 28, 7182–7196. [Google Scholar] [CrossRef]
- Wen, W.; Mi, X.; Xiang, S. Quality factor of partially coherent Airy beams in a turbulent atmosphere. J. Opt. Soc. Am. A 2021, 38, 1612–1618. [Google Scholar] [CrossRef] [PubMed]
- Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photonics 2008, 2, 675–678. [Google Scholar] [CrossRef]
- Jia, S.; Vaughan, J.C.; Zhuang, X. Isotropic three-dimensional super-resolution imaging with a self-bending point spread function. Nat. Photonics 2014, 8, 302–306. [Google Scholar] [CrossRef] [PubMed]
- Vettenburg, T.; Dalgarno, H.I.; Nylk, J.; Coll-Lladó, C.; Ferrier, D.E.; Čižmár, T.; Gunn-Moore, F.J.; Dholakia, K. Light-sheet microscopy using an Airy beam. Nat. Methods 2014, 11, 541–544. [Google Scholar] [CrossRef]
- Wang, J.; Hua, X.; Guo, C.; Liu, W.; Jia, S. Airy-beam tomographic microscopy. Optica 2020, 7, 790–793. [Google Scholar] [CrossRef]
- Liang, Y.; Hu, Y.; Song, D.; Lou, C.; Zhang, X.; Chen, Z.; Xu, J. Image signal transmission with Airy beams. Opt. Lett. 2015, 40, 5686–5689. [Google Scholar] [CrossRef]
- Zhu, G.; Wen, Y.; Wu, X.; Chen, Y.; Liu, J.; Yu, S. Obstacle evasion in free-space optical communications utilizing Airy beams. Opt. Lett. 2018, 43, 1203–1206. [Google Scholar] [CrossRef]
- Ma, P.; Kacerovská, B.; Khosravi, R.; Liang, C.; Zeng, J.; Peng, X.; Mi, C.; Monfared, Y.E.; Zhang, Y.; Wang, F.; et al. Numerical approach for studying the evolution of the degrees of coherence of partially coherent beams propagation through an ABCD optical system. Appl. Sci. 2019, 9, 2084. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wang, Y.; Chen, Q.; Ma, P.; Cai, Y.; Liang, C. Enhancing the Self-Healing Ability of a Partially Coherent Airy Beam via Fourier Processing: Numerical Investigation. Photonics 2023, 10, 143. https://doi.org/10.3390/photonics10020143
Zhao Y, Wang Y, Chen Q, Ma P, Cai Y, Liang C. Enhancing the Self-Healing Ability of a Partially Coherent Airy Beam via Fourier Processing: Numerical Investigation. Photonics. 2023; 10(2):143. https://doi.org/10.3390/photonics10020143
Chicago/Turabian StyleZhao, Yuefeng, Yinghe Wang, Qian Chen, Pujuan Ma, Yangjian Cai, and Chunhao Liang. 2023. "Enhancing the Self-Healing Ability of a Partially Coherent Airy Beam via Fourier Processing: Numerical Investigation" Photonics 10, no. 2: 143. https://doi.org/10.3390/photonics10020143
APA StyleZhao, Y., Wang, Y., Chen, Q., Ma, P., Cai, Y., & Liang, C. (2023). Enhancing the Self-Healing Ability of a Partially Coherent Airy Beam via Fourier Processing: Numerical Investigation. Photonics, 10(2), 143. https://doi.org/10.3390/photonics10020143





