Deep Sub–Wavelength Focusing Metalens at Terahertz Frequency
Abstract
:1. Introduction
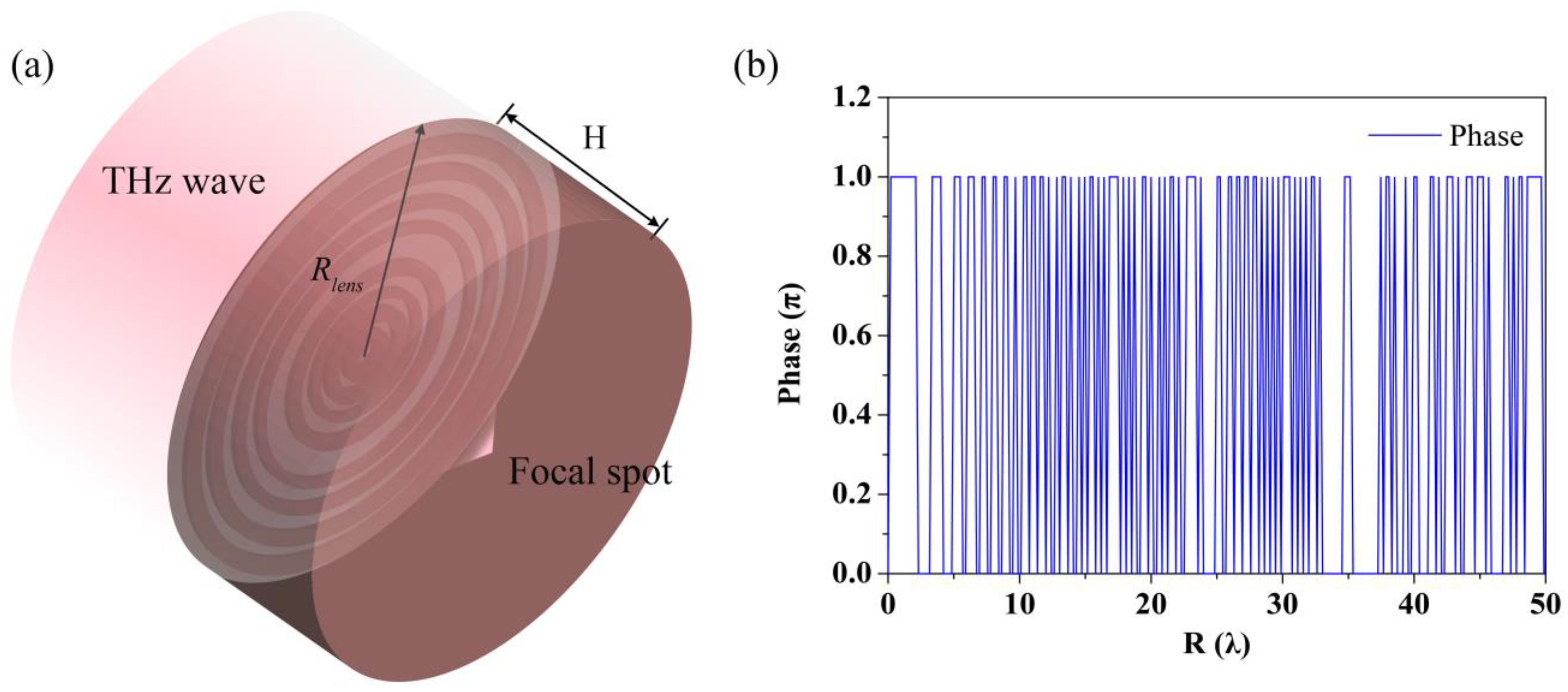
2. Design and Theoretical Analysis
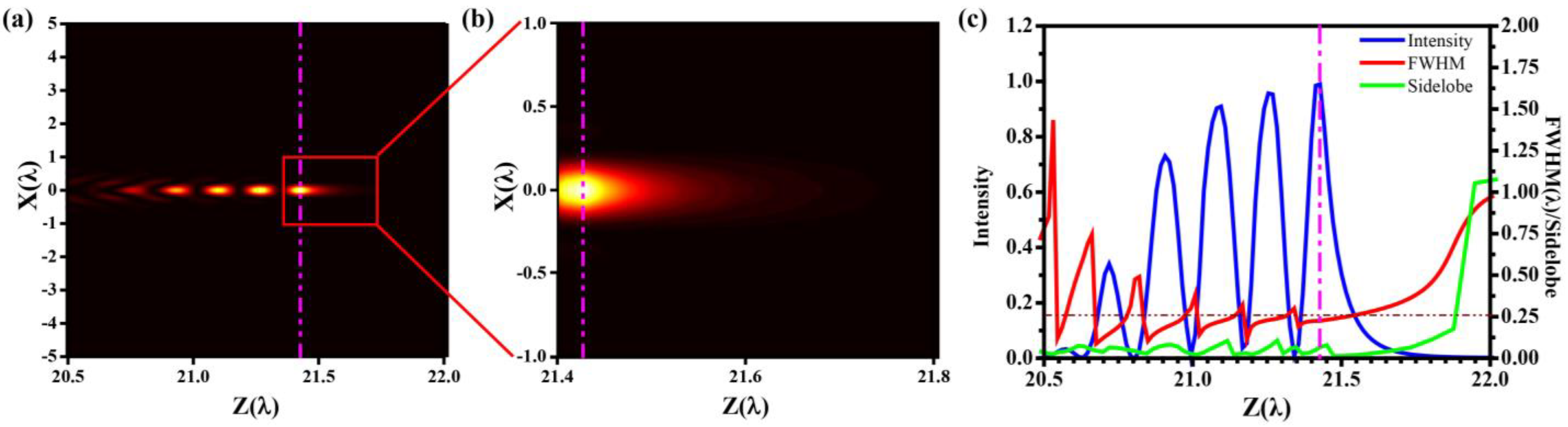
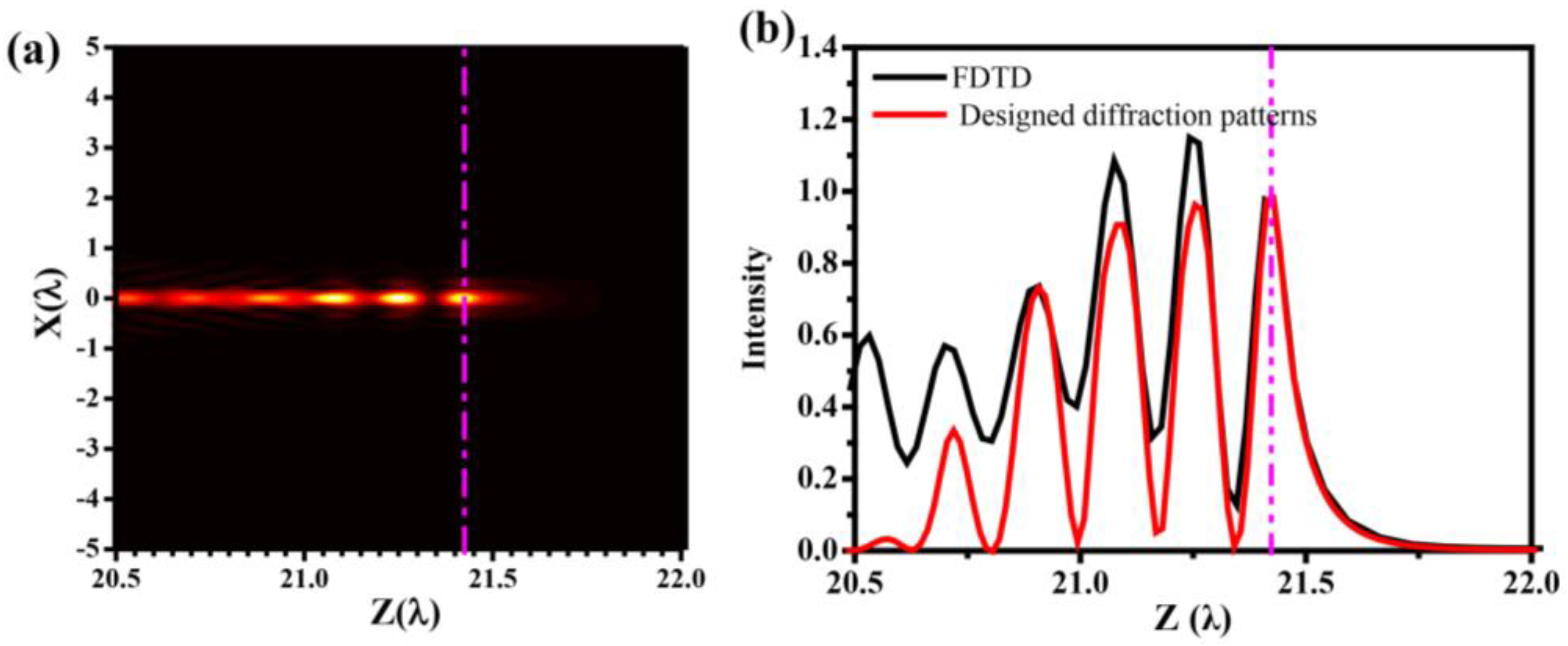
3. Simulation Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ako, R.T.; Upadhyay, A.; Withayachumnankul, W.; Bhaskaran, M.; Sriram, S. Dielectrics for Terahertz Metasurfaces: Material Selection and Fabrication Techniques. Adv. Opt. Mater. 2019, 8, 1900750. [Google Scholar] [CrossRef]
- Woodward, R.M.; Cole, B.E.; Wallace, V.P.; Pye, R.J.; Arnone, D.D.; Linfield, E.H.; Pepper, M. Terahertz pulse imaging in reflection geometry of human skin cancer and skin tissue. Phys. Med. Biol. 2002, 47, 3853–3863. [Google Scholar] [CrossRef]
- Pickwell, E.; Wallace, V.P. Biomedical applications of terahertz technology. J. Phys. D Appl. Phys. 2006, 39, R301–R310. [Google Scholar] [CrossRef]
- Yu, C.; Fan, S.; Sun, Y. Pickwell-Macpherson, E. The potential of terahertz imaging for cancer diagnosis: A review of investigations to date. Quant. Imaging Med. Surg. 2012, 2, 33–45. [Google Scholar]
- Nikitkina, A.I.; Bikmulina, P.Y.; Gafarova, E.R.; Kosheleva, N.V.; Efremov, Y.M.; Bezrukov, E.A.; Butnaru, D.V.; Dolganova, I.N.; Chernomyrdin, N.V.; Cherkasova, O.P.; et al. Terahertz radiation and the skin: A review. J. Biomed. Opt. 2021, 26, 043005. [Google Scholar] [CrossRef]
- Peralta, X.G.; Lipscomb, D.; Wilmink, G.J.; Echchgadda, I. Terahertz spectroscopy of human skin tissue models with different melanin content. Biomed. Opt. Express 2019, 10, 2942. [Google Scholar] [CrossRef]
- Chernomyrdin, N.V.; Schadko, A.O.; Lebedev, S.P.; Tolstoguzov, V.L.; Kurlov, V.N.; Reshetov, I.V.; Spektor, I.E.; Skorobogatiy, M.; Yurchenko, S.O.; Zaytsev, K.I. Solid immersion terahertz imaging with sub–wavelength resolution. Appl. Phys. Lett. 2017, 110, 221109. [Google Scholar]
- Kurvits, J.A.; Jiang, M.; Zia, R. Comparative analysis of imaging configurations and objectives for Fourier microscopy. J. Opt. Soc. Am. A 2015, 32, 2082–2092. [Google Scholar] [CrossRef] [Green Version]
- Huo, P.; Zhang, S.; Liang, Y.; Lu, Y.; Xu, T. Hyperbolic Metamaterials and Metasurfaces: Fundamentals and Applications. Adv. Opt. Mater. 2019, 7, 1801616. [Google Scholar] [CrossRef]
- Jiang, X.; Chen, H.; Li, Z.; Yuan, H.; Cao, L.; Luo, Z.; Zhang, K.; Zhang, Z.; Wen, Z.; Zhu, L.; et al. All–dielectric metalens for terahertz wave imaging. Opt. Express 2018, 26, 14132. [Google Scholar] [CrossRef] [PubMed]
- Hong, X.; Feng, S.; Guo, H.; Li, C. A small–spot–size and polarization–insensitive flat lens employing dielectric metasurface in the terahertz region. Opt. Commun. 2020, 459, 125083. [Google Scholar] [CrossRef]
- Chen, H.; Wu, Z.; Li, Z.; Luo, Z.; Jiang, X.; Wen, Z.; Zhu, L.; Zhou, X.; Li, H.; Shang, Z.; et al. Sub–wavelength tight–focusing of terahertz waves by polarization–independent high–numerical–aperture dielectric metalens. Opt. Express 2018, 26, 29817–29825. [Google Scholar] [CrossRef] [PubMed]
- Danila, O. Polyvinylidene Fluoride–Based Metasurface for High–Quality Active Switching and Spectrum Shaping in the Terahertz G–Band. Polymers 2021, 13, 1860. [Google Scholar] [CrossRef]
- Liang, Y.; Wei, Z.; Guo, J.; Wang, F.; Meng, H.; Liu, H. Metalenses Based on Symmetric Slab Waveguide and c–TiO2: Efficient Polarization–Insensitive Focusing at Visible Wavelengths. Nanomaterials 2018, 8, 699. [Google Scholar] [CrossRef] [Green Version]
- Dănilă, O.; Mănăilă-Maximean, D.; Bărar, A.; Loiko, V.A. Non–Layered Gold–Silicon and All–Silicon Frequency–Selective Metasurfaces for Potential Mid–Infrared Sensing Applications. Sensors 2021, 21, 5600. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, J.; Shu, Y.; Wu, L.; Lu, L.; Qi, K.; Che, Y.; Li, L.; Yin, H. High numerical aperture and large focusing efficiency metalens based on multilayer transmitarray elements. Opt. Laser. Eng. 2021, 147, 106734. [Google Scholar] [CrossRef]
- Liang, Y.; Liu, H.; Wang, F.; Meng, H.; Guo, J.; Li, J.; Wei, Z. High–Efficiency, Near–Diffraction Limited, Dielectric Metasurface Lenses Based on Crystalline Titanium Dioxide at Visible Wavelengths. Nanomaterials 2018, 8, 288. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.T.; Zhu, A.Y.; Khorasaninejad, M.; Shi, Z.; Sanjeev, V.; Capasso, F. Immersion Meta–Lenses at Visible Wavelengths for Nanoscale Imaging. Nano Lett. 2017, 17, 3188–3194. [Google Scholar] [CrossRef]
- Liang, H.; Lin, Q.; Xie, X.; Sun, Q.; Wang, Y.; Zhou, L.; Liu, L.; Yu, X.; Zhou, J.; Krauss, T.F.; et al. Ultrahigh Numerical Aperture Metalens at Visible Wavelengths. Nano Lett. 2018, 18, 4460–4466. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Ruan, D.; Du, L.; Qin, C.; Li, Z.; Lin, C.; Chen, G.; Wen, Z. Subdiffraction focusing of total electric fields of terahertz wave. Opt. Commun. 2020, 458, 124764. [Google Scholar] [CrossRef]
- Ruan, D.; Li, Z.; Du, L.; Zhou, X.; Zhu, L.; Lin, C.; Yang, M.; Chen, G.; Yuan, W.; Liang, G.; et al. Realizing a terahertz far–field sub–diffraction optical needle with sub–wavelength concentric ring structure array. Appl. Optics. 2018, 57, 7905–7909. [Google Scholar] [CrossRef]
- Yuan, G.H.; Lin, Y.H.; Tsai, D.P.; Zheludev, N.I. Superoscillatory quartz lens with effective numerical aperture greater than one. Appl. Phys. Lett. 2020, 117, 021106. [Google Scholar] [CrossRef]
- Huang, K.; Liu, H.; Garcia-Vidal, F.J.; Hong, M.; Luk Yanchuk, B.; Teng, J.; Qiu, C. Ultrahigh–capacity non–periodic photon sieves operating in visible light. Nat. Commun. 2015, 6, 7059. [Google Scholar] [CrossRef] [Green Version]
- Rogers, E.T.F.; Lindberg, J.; Roy, T.; Savo, S.; Chad, J.E.; Dennis, M.R.; Zheludev, N.I. A super–oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 2012, 11, 432–435. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Li, H.; Zhu, Y.; Yu, Y. Controllable design of super–oscillatory lenses with multiple sub–diffraction–limit foci. Sci. Rep. 2017, 7, 1335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mansfield, S.M.; Kino, G.S. Solid Immersion Microscopy. Appl. Phys. Lett. 1990, 57, 2615–2616. [Google Scholar] [CrossRef]
- Liu, T.; Tan, J.; Liu, J.; Wang, H. Vectorial design of super–oscillatory lens. Opt. Express 2013, 21, 15090. [Google Scholar] [CrossRef]


| x Linearly Polarized Light | y Linearly Polarized Light | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Z(λ) | Intensity | FWHMx | FWHMy | SLRx (%) | SLRy (%) | Intensity | FWHMx | FWHMy | SLRx (%) | SLRy (%) |
| 21.43 | 2701.09 | 0.24 λ | 0.2 λ | 20.57 | 6.70 | 2701.38 | 0.2 λ | 0.238 λ | 6.75 | 20.14 |
| 21.46 | 1893.29 | 0.25 λ | 0.23 λ | 22 | 7.87 | 1893.5 | 0.21 λ | 0.24 λ | 7.87 | 22 |
| 21.47 | 1293.78 | 0.25 λ | 0.232 λ | 24.19 | 9.50 | 1293.9 | 0.23 λ | 0.24 λ | 9.51 | 24.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Shen, X.; Wen, Z. Deep Sub–Wavelength Focusing Metalens at Terahertz Frequency. Photonics 2023, 10, 222. https://doi.org/10.3390/photonics10020222
Yang M, Shen X, Wen Z. Deep Sub–Wavelength Focusing Metalens at Terahertz Frequency. Photonics. 2023; 10(2):222. https://doi.org/10.3390/photonics10020222
Chicago/Turabian StyleYang, Mengyu, Xin Shen, and Zhongquan Wen. 2023. "Deep Sub–Wavelength Focusing Metalens at Terahertz Frequency" Photonics 10, no. 2: 222. https://doi.org/10.3390/photonics10020222
APA StyleYang, M., Shen, X., & Wen, Z. (2023). Deep Sub–Wavelength Focusing Metalens at Terahertz Frequency. Photonics, 10(2), 222. https://doi.org/10.3390/photonics10020222





