Single-Pixel Hyperspectral Imaging via an Untrained Convolutional Neural Network
Abstract
1. Introduction
2. Principle and Method
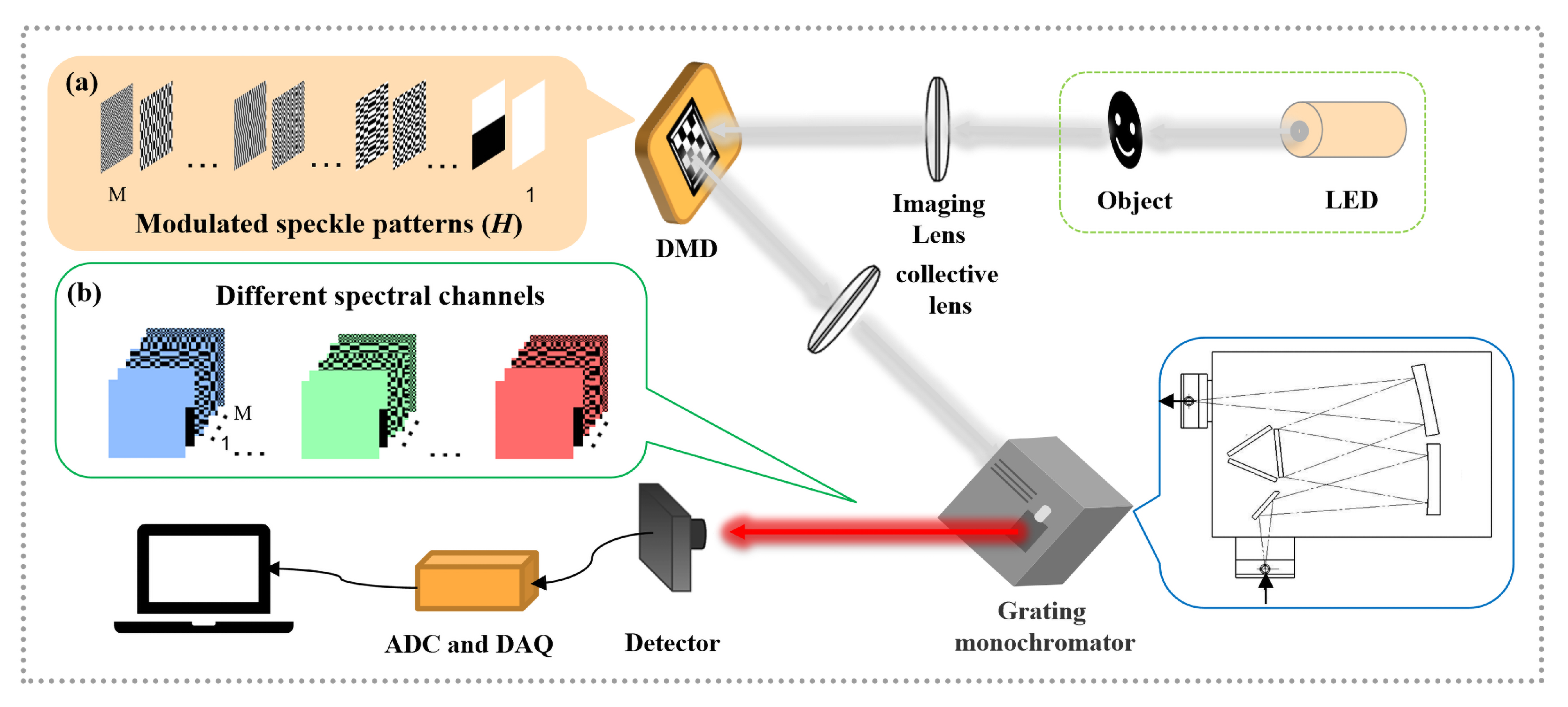
2.1. Experimental Setup
2.2. Data Collection and Processing
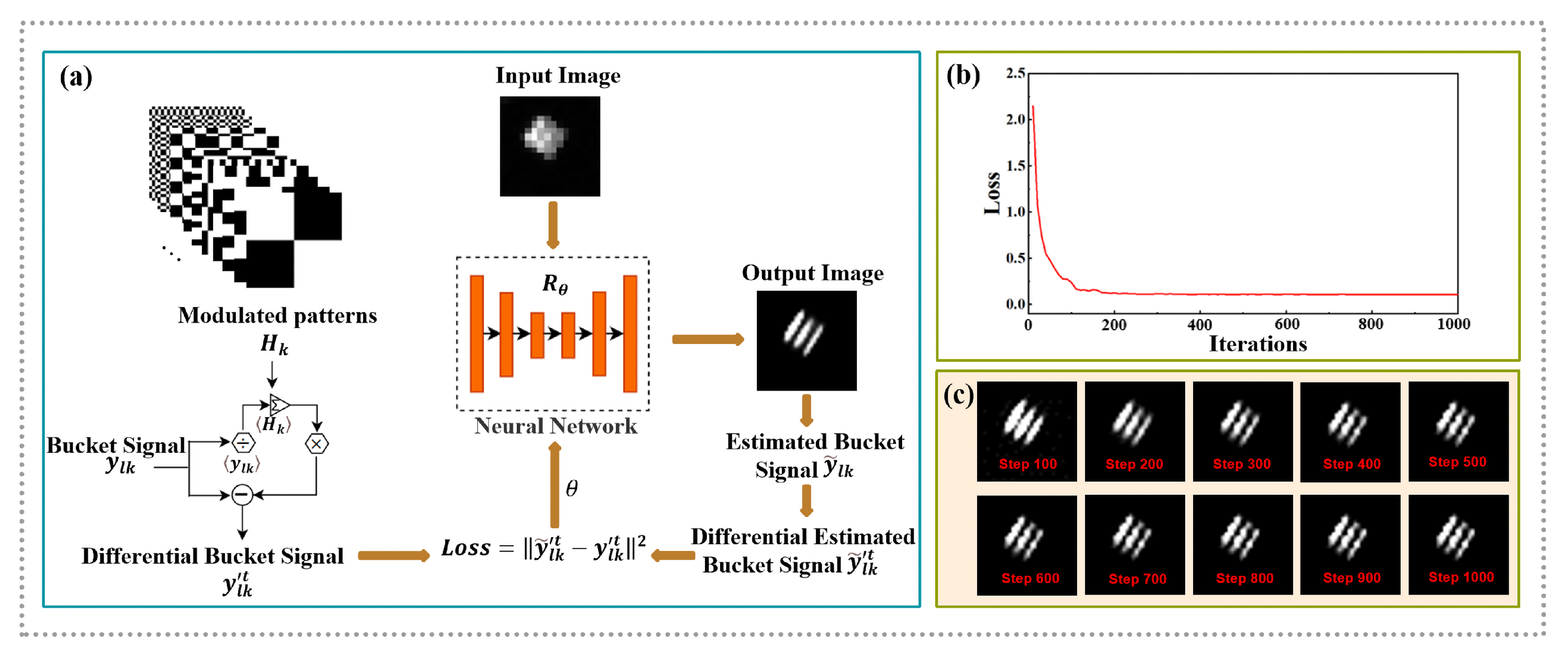
2.3. Image Reconstruction by Untrained Neural Network
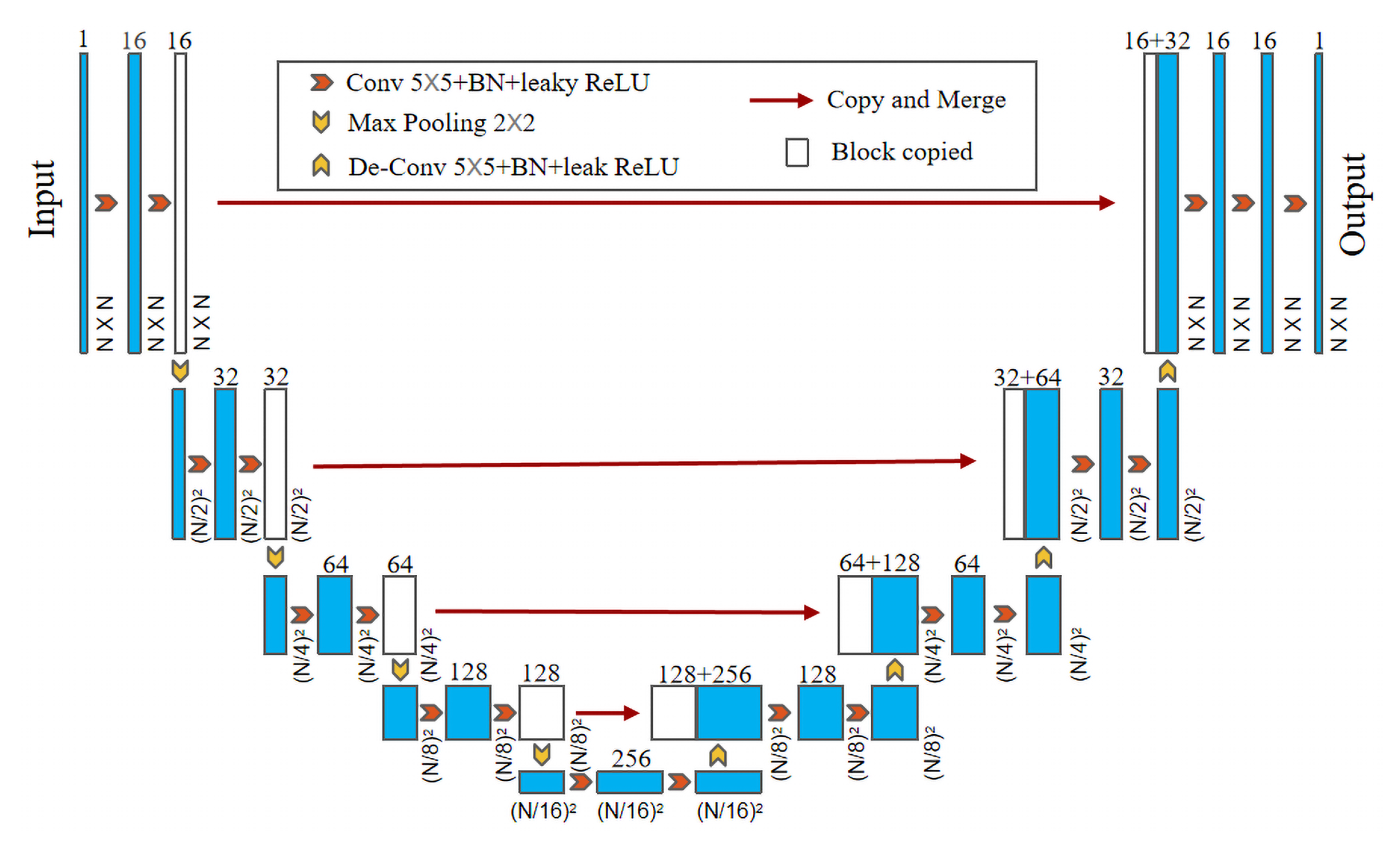
2.4. Network Architecture
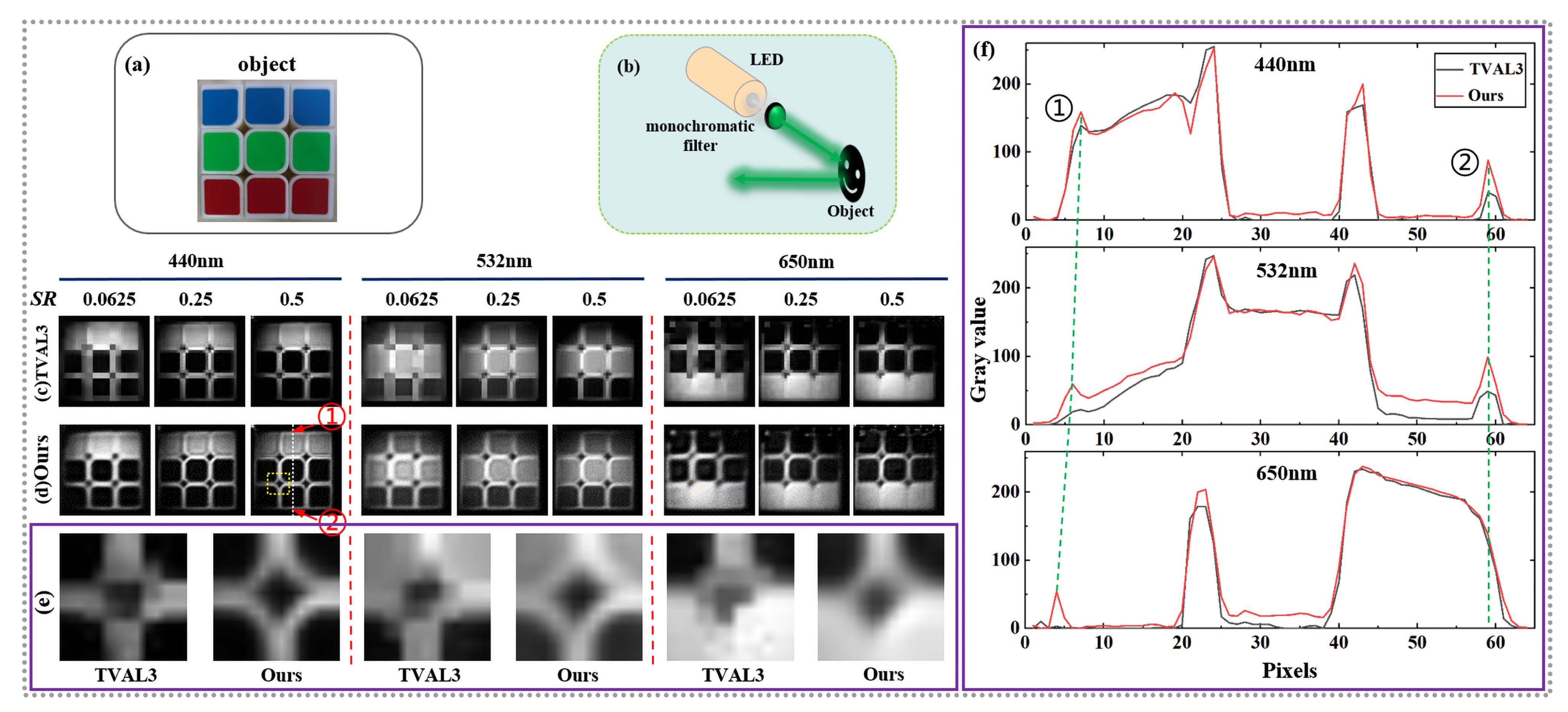
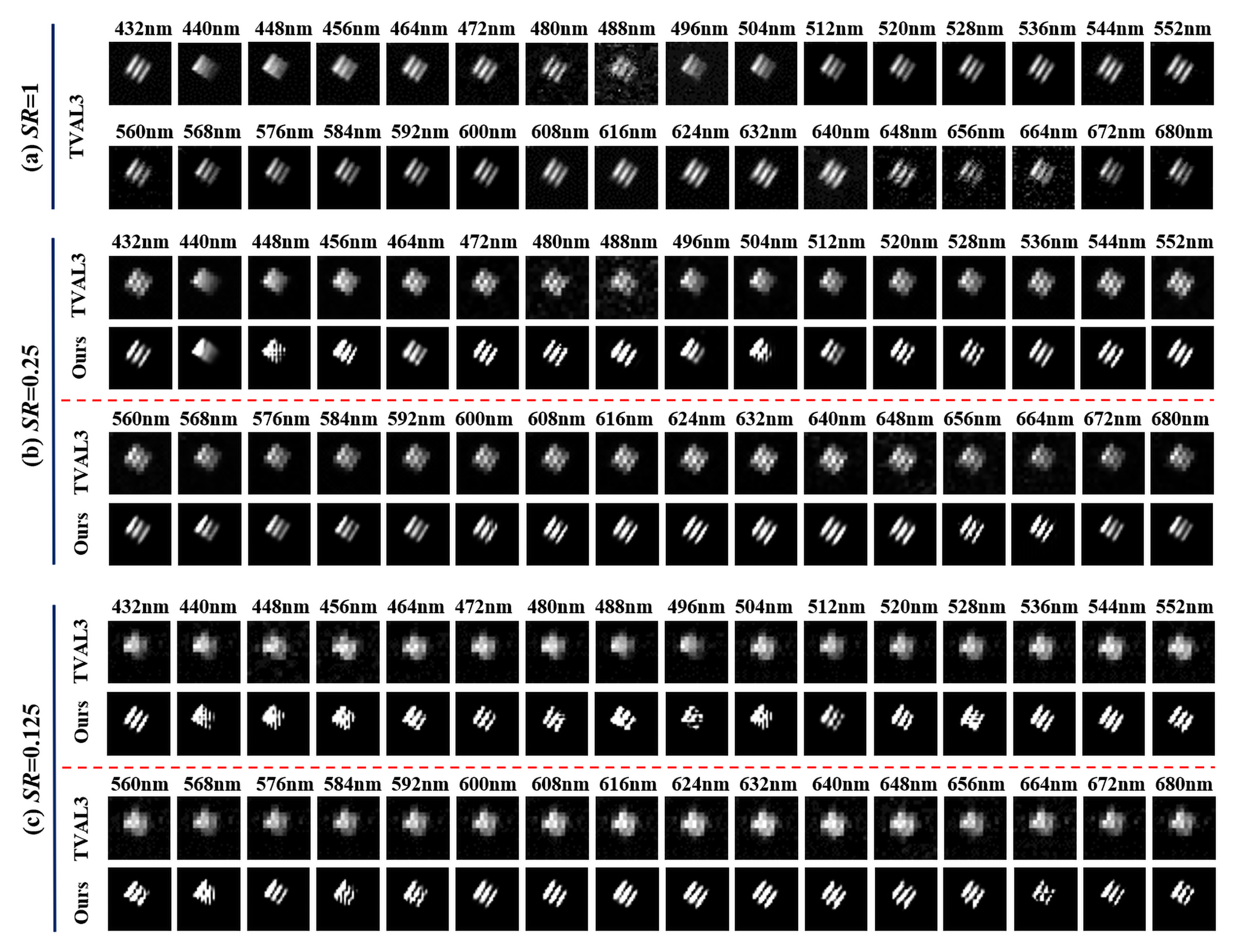
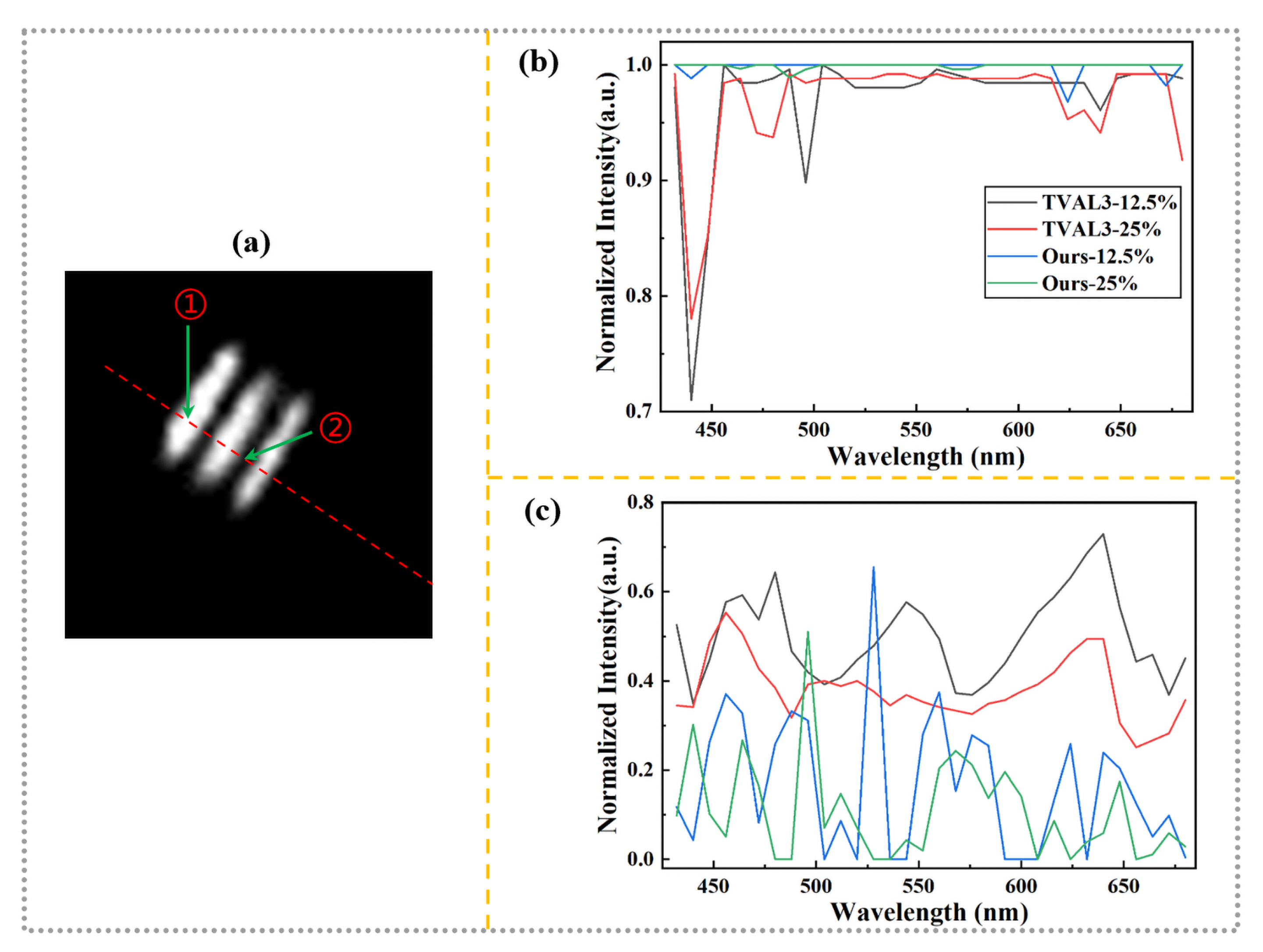
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Garini, Y.; Young, I.T.; McNamara, G. Spectral imaging: Principles and applications. Cytom. Part A J. Int. Soc. Anal. Cytol. 2006, 69, 735–747. [Google Scholar] [CrossRef] [PubMed]
- Govender, M.; Chetty, K.; Bulcock, H. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water SA 2007, 33, 145–151. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Carrasco, O.; Gomez, R.B.; Chainani, A.; Roper, W.E. Hyperspectral imaging applied to medical diagnoses and food safety. In Proceedings of the Geo-Spatial and Temporal Image and Data Exploitation III, Orlando, FL, USA, 24 April 2003; SPIE: Bellingham, WA, USA, 2003; Volume 5097, pp. 215–221. [Google Scholar] [CrossRef]
- Afromowitz, M.A.; Callis, J.B.; Heimbach, D.M.; DeSoto, L.A.; Norton, M.K. Multispectral imaging of burn wounds: A new clinical instrument for evaluating burn depth. IEEE Trans. Biomed. Eng. 1988, 35, 842–850. [Google Scholar] [CrossRef] [PubMed]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The contribution of outdoor air pollution sources to premature mortality on a global scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef]
- Bian, L.; Suo, J.; Situ, G.; Li, Z.; Fan, J.; Chen, F.; Dai, Q. Multispectral imaging using a single bucket detector. Sci. Rep. 2016, 6, 24752. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Kutyniok, G. Compressed Sensing: Theory and Applications; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Arce, G.R.; Brady, D.J.; Carin, L.; Arguello, H.; Kittle, D.S. Compressive coded aperture spectral imaging: An introduction. IEEE Signal Process. Mag. 2013, 31, 105–115. [Google Scholar] [CrossRef]
- Lin, X.; Liu, Y.; Wu, J.; Dai, Q. Spatial-spectral encoded compressive hyperspectral imaging. ACM Trans. Graph. 2014, 33, 1–11. [Google Scholar] [CrossRef]
- Wagadarikar, A.; John, R.; Willett, R.; Brady, D. Single disperser design for coded aperture snapshot spectral imaging. Appl. Opt. 2008, 47, B44–B51. [Google Scholar] [CrossRef]
- Yuan, X.; Brady, D.J.; Katsaggelos, A.K. Snapshot compressive imaging: Theory, algorithms, and applications. IEEE Signal Process. Mag. 2021, 38, 65–88. [Google Scholar] [CrossRef]
- Lin, X.; Wetzstein, G.; Liu, Y.; Dai, Q. Dual-coded compressive hyperspectral imaging. Opt. Lett. 2014, 39, 2044–2047. [Google Scholar] [CrossRef]
- Garcia, H.; Correa, C.V.; Villarreal, O.; Pinilla, S.; Arguello, H. Multi-resolution reconstruction algorithm for compressive single pixel spectral imaging. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 468–472. [Google Scholar] [CrossRef]
- Duarte, M.F.; Davenport, M.A.; Takhar, D.; Laska, J.N.; Sun, T.; Kelly, K.F.; Baraniuk, R.G. Single-pixel imaging via compressive sampling. IEEE Signal Process. Mag. 2008, 25, 83–91. [Google Scholar] [CrossRef]
- Shapiro, J.H. Computational ghost imaging. Phys. Rev. A 2008, 78, 061802. [Google Scholar] [CrossRef]
- Edgar, M.; Gibson, G.M.; Bowman, R.W.; Sun, B.; Radwell, N.; Mitchell, K.J.; Welsh, S.S.; Padgett, M.J. Simultaneous real-time visible and infrared video with single-pixel detectors. Sci. Rep. 2015, 5, 10669. [Google Scholar] [CrossRef]
- Schechner, Y.Y.; Nayar, S.K.; Belhumeur, P.N. Multiplexing for optimal lighting. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1339–1354. [Google Scholar] [CrossRef]
- Morris, P.A.; Aspden, R.S.; Bell, J.E.; Boyd, R.W.; Padgett, M.J. Imaging with a small number of photons. Nat. Commun. 2015, 6, 5913. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X.; Zhong, J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat. Commun. 2015, 6, 6225. [Google Scholar] [CrossRef]
- Sun, B.; Edgar, M.P.; Bowman, R.; Vittert, L.E.; Welsh, S.; Bowman, A.; Padgett, M.J. 3D computational imaging with single-pixel detectors. Science 2013, 340, 844–847. [Google Scholar] [CrossRef]
- Tian, N.; Guo, Q.; Wang, A.; Xu, D.; Fu, L. Fluorescence ghost imaging with pseudothermal light. Opt. Lett. 2011, 36, 3302–3304. [Google Scholar] [CrossRef]
- Clemente, P.; Durán, V.; Torres-Company, V.; Tajahuerce, E.; Lancis, J. Optical encryption based on computational ghost imaging. Opt. Lett. 2010, 35, 2391–2393. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Gong, W.; Chen, M.; Li, E.; Wang, H.; Xu, W.; Han, S. Ghost imaging lidar via sparsity constraints. Appl. Phys. Lett. 2012, 101, 141123. [Google Scholar] [CrossRef]
- Magana-Loaiza, O.S.; Howland, G.A.; Malik, M.; Howell, J.C.; Boyd, R.W. Compressive object tracking using entangled photons. Appl. Phys. Lett. 2013, 102, 231104. [Google Scholar] [CrossRef]
- Li, C.; Sun, T.; Kelly, K.F.; Zhang, Y. A compressive sensing and unmixing scheme for hyperspectral data processing. IEEE Trans. Image Process. 2011, 21, 1200–1210. [Google Scholar] [CrossRef]
- Magalhães, F.; Araújo, F.M.; Correia, M.; Abolbashari, M.; Farahi, F. High-resolution hyperspectral single-pixel imaging system based on compressive sensing. Opt. Eng. 2012, 51, 071406. [Google Scholar] [CrossRef]
- Welsh, S.S.; Edgar, M.P.; Bowman, R.; Jonathan, P.; Sun, B.; Padgett, M.J. Fast full-color computational imaging with single-pixel detectors. Opt. Express 2013, 21, 23068–23074. [Google Scholar] [CrossRef]
- Radwell, N.; Mitchell, K.J.; Gibson, G.M.; Edgar, M.P.; Bowman, R.; Padgett, M.J. Single-pixel infrared and visible microscope. Optica 2014, 1, 285–289. [Google Scholar] [CrossRef]
- August, Y.; Vachman, C.; Rivenson, Y.; Stern, A. Compressive hyperspectral imaging by random separable projections in both the spatial and the spectral domains. Appl. Opt. 2013, 52, D46–D54. [Google Scholar] [CrossRef]
- Hahn, J.; Debes, C.; Leigsnering, M.; Zoubir, A.M. Compressive sensing and adaptive direct sampling in hyperspectral imaging. Digit. Signal Process. 2014, 26, 113–126. [Google Scholar] [CrossRef]
- Tao, C.; Zhu, H.; Wang, X.; Zheng, S.; Xie, Q.; Wang, C.; Wu, R.; Zheng, Z. Compressive single-pixel hyperspectral imaging using RGB sensors. Opt. Express 2021, 29, 11207–11220. [Google Scholar] [CrossRef]
- Yi, Q.; Heng, L.Z.; Liang, L.; Guangcan, Z.; Siong, C.F.; Guangya, Z. Hadamard transform-based hyperspectral imaging using a single-pixel detector. Opt. Express 2020, 28, 16126–16139. [Google Scholar] [CrossRef]
- Jin, S.; Hui, W.; Wang, Y.; Huang, K.; Shi, Q.; Ying, C.; Liu, D.; Ye, Q.; Zhou, W.; Tian, J. Hyperspectral imaging using the single-pixel Fourier transform technique. Sci. Rep. 2017, 7, 45209. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, S.; Peng, J.; Yao, M.; Zheng, G.; Zhong, J. Simultaneous spatial, spectral, and 3D compressive imaging via efficient Fourier single-pixel measurements. Optica 2018, 5, 315–319. [Google Scholar] [CrossRef]
- Moshtaghpour, A.; Bioucas-Dias, J.M.; Jacques, L. Compressive hyperspectral imaging: Fourier transform interferometry meets single pixel camera. arXiv 2018, arXiv:1809.00950. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Arias, F.; Sierra, H.; Arzuaga, E. A Framework For An Artificial Neural Network Enabled Single Pixel Hyperspectral Imager. In Proceedings of the 2019 10th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 24–26 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Xiong, Z.; Shi, Z.; Li, H.; Wang, L.; Liu, D.; Wu, F. HSCNN: CNN-Based Hyperspectral Image Recovery From Spectrally Undersampled Projections. In Proceedings of the IEEE International Conference on Computer Vision (ICCV) Workshops, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Barbastathis, G.; Ozcan, A.; Situ, G. On the use of deep learning for computational imaging. Optica 2019, 6, 921–943. [Google Scholar] [CrossRef]
- Lyu, M.; Wang, W.; Wang, H.; Wang, H.; Li, G.; Chen, N.; Situ, G. Deep-learning-based ghost imaging. Sci. Rep. 2017, 7, 17865. [Google Scholar] [CrossRef]
- He, Y.; Wang, G.; Dong, G.; Zhu, S.; Chen, H.; Zhang, A.; Xu, Z. Ghost imaging based on deep learning. Sci. Rep. 2018, 8, 6469. [Google Scholar] [CrossRef]
- Higham, C.F.; Murray-Smith, R.; Padgett, M.J.; Edgar, M.P. Deep learning for real-time single-pixel video. Sci. Rep. 2018, 8, 2369. [Google Scholar] [CrossRef]
- Wang, F.; Wang, H.; Wang, H.; Li, G.; Situ, G. Learning from simulation: An end-to-end deep-learning approach for computational ghost imaging. Opt. Express 2019, 27, 25560–25572. [Google Scholar] [CrossRef]
- Shang, R.; Hoffer-Hawlik, K.; Wang, F.; Situ, G.; Luke, G.P. Two-step training deep learning framework for computational imaging without physics priors. Opt. Express 2021, 29, 15239–15254. [Google Scholar] [CrossRef] [PubMed]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef] [PubMed]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep image prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 9446–9454. [Google Scholar]
- Wang, F.; Bian, Y.; Wang, H.; Lyu, M.; Pedrini, G.; Osten, W.; Barbastathis, G.; Situ, G. Phase imaging with an untrained neural network. Light Sci. Appl. 2020, 9, 77. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wang, C.; Chen, M.; Gong, W.; Zhang, Y.; Han, S.; Situ, G. Far-field super-resolution ghost imaging with a deep neural network constraint. Light Sci. Appl. 2022, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Wang, C.; Deng, C.; Han, S.; Situ, G. Single-pixel imaging using physics enhanced deep learning. Photonics Res. 2022, 10, 104–110. [Google Scholar] [CrossRef]
- Meng, Z.; Yu, Z.; Xu, K.; Yuan, X. Self-Supervised Neural Networks for Spectral Snapshot Compressive Imaging. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021; pp. 2622–2631. [Google Scholar]
- Lin, S.; Wang, X.; Zhu, A.; Xue, J.; Xu, B. Steganographic optical image encryption based on single-pixel imaging and an untrained neural network. Opt. Express 2022, 30, 36144–36154. [Google Scholar] [CrossRef]
- Lin, J.; Yan, Q.; Lu, S.; Zheng, Y.; Sun, S.; Wei, Z. A Compressed Reconstruction Network Combining Deep Image Prior and Autoencoding Priors for Single-Pixel Imaging. Photonics 2022, 9, 343. [Google Scholar] [CrossRef]
- Li, M.; Yan, L.; Yang, R.; Liu, Y. Fast single-pixel imaging based on optimized reordering Hadamard basis. Acta Phys. Sin. 2019, 68, 064202. [Google Scholar] [CrossRef]
- Gibson, G.M.; Johnson, S.D.; Padgett, M.J. Single-pixel imaging 12 years on: A review. Opt. Express 2020, 28, 28190–28208. [Google Scholar] [CrossRef]
- Yang, S.; Qin, H.; Yan, X.; Yuan, S.; Yang, T. Deep spatial-spectral prior with an adaptive dual attention network for single-pixel hyperspectral reconstruction. Opt. Express 2022, 30, 29621–29638. [Google Scholar] [CrossRef]
- Ferri, F.; Magatti, D.; Lugiato, L.A.; Gatti, A. Differential Ghost Imaging. Phys. Rev. Lett. 2010, 104, 253603. [Google Scholar] [CrossRef]
- Wang, C.H.; Bie, S.H.; Lv, R.B.; Li, H.Z.; Fu, Q.; Bao, Q.Q.; Meng, S.Y.; Chen, X.H. High-quality single-pixel imaging in a diffraction-limited system using a deep image prior-based network. Opt. Express, 2022; submitted. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Springer International Publishing: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.H.; Yu, Y.J.; Wu, L.A.; Song, M.Y.; Zhao, Z.H. Chromatic-Aberration-Corrected Hyperspectral Single-Pixel Imaging. Photonics 2023, 10, 7. [Google Scholar] [CrossRef]
- Li, Z.; Suo, J.; Hu, X.; Deng, C.; Fan, J.; Dai, Q. Efficient single-pixel multispectral imaging via non-mechanical spatio-spectral modulation. Sci. Rep. 2017, 7, 41435. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-H.; Li, H.-Z.; Bie, S.-H.; Lv, R.-B.; Chen, X.-H. Single-Pixel Hyperspectral Imaging via an Untrained Convolutional Neural Network. Photonics 2023, 10, 224. https://doi.org/10.3390/photonics10020224
Wang C-H, Li H-Z, Bie S-H, Lv R-B, Chen X-H. Single-Pixel Hyperspectral Imaging via an Untrained Convolutional Neural Network. Photonics. 2023; 10(2):224. https://doi.org/10.3390/photonics10020224
Chicago/Turabian StyleWang, Chen-Hui, Hong-Ze Li, Shu-Hang Bie, Rui-Bing Lv, and Xi-Hao Chen. 2023. "Single-Pixel Hyperspectral Imaging via an Untrained Convolutional Neural Network" Photonics 10, no. 2: 224. https://doi.org/10.3390/photonics10020224
APA StyleWang, C.-H., Li, H.-Z., Bie, S.-H., Lv, R.-B., & Chen, X.-H. (2023). Single-Pixel Hyperspectral Imaging via an Untrained Convolutional Neural Network. Photonics, 10(2), 224. https://doi.org/10.3390/photonics10020224



