SCAPS Empowered Machine Learning Modelling of Perovskite Solar Cells: Predictive Design of Active Layer and Hole Transport Materials
Abstract
1. Introduction
2. Materials and Methods
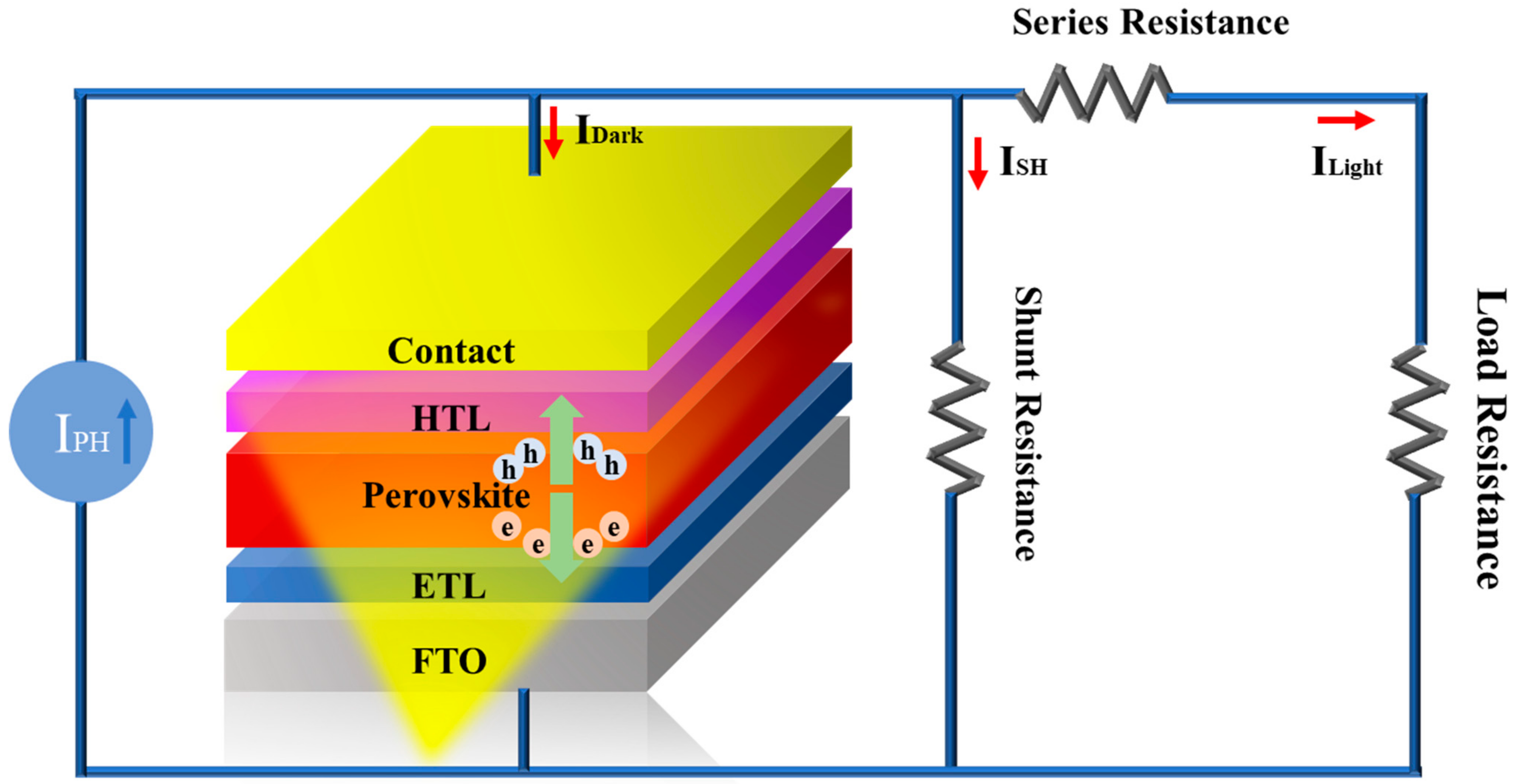
2.1. SCAPS 1-D
2.2. Machine Learning
3. Results and Discussion
3.1. Type of Hole Transport Layer
3.2. Effect of CsSnI3
3.2.1. Thickness
3.2.2. Doping Density
3.2.3. Defect Density
3.3. Active Layer
3.3.1. Effect of Thickness
3.3.2. Effect of Defect Density
3.4. Machine Learning
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Verduci, R.; Romano, V.; Brunetti, G.; Nia, N.Y.; Di Carlo, A.; Angelo, G.D.; Ciminelli, C. Solar Energy in Space Applications: Review and Technology Perspectives. Adv. Energy Mater. 2022, 19, 2200125. [Google Scholar] [CrossRef]
- Esiner, S.; Wang, J.; Janssen, R.A.J. Light-Driven Electrochemical Carbon Dioxide Reduction to Carbon Monoxide and Methane Using Perovskite Photovoltaics. Cell Rep. Phys. Sci. 2020, 1, 100058. [Google Scholar] [CrossRef]
- Liang, J.; Han, X.; Qiu, Y.; Fang, Q.; Zhang, B.; Wang, W.; Zhang, J.; Ajayan, P.M.; Lou, J. A Low-Cost and High-Efficiency Integrated Device toward Solar-Driven Water Splitting. ACS Nano 2020, 14, 5426–5434. [Google Scholar] [CrossRef] [PubMed]
- Pascaris, A.S.; Schelly, C.; Burnham, L.; Pearce, J.M. Integrating Solar Energy with Agriculture: Industry Perspectives on the Market, Community, and Socio-Political Dimensions of Agrivoltaics. Energy Res. Soc. Sci. 2021, 75, 102023. [Google Scholar] [CrossRef]
- Al-Ezzi, A.S.; Ansari, M.N.M. Photovoltaic Solar Cells: A Review. Appl. Syst. Innov. 2022, 5, 67. [Google Scholar] [CrossRef]
- Pastuszak, J.; Węgierek, P. Photovoltaic Cell Generations and Current Research Directions for Their Development. Materials 2022, 15, 5542. [Google Scholar] [CrossRef]
- Dhonde, M.; Sahu, K.; Das, M.; Yadav, A.; Ghosh, P.; Murty, V.V.S. Review—Recent Advancements in Dye-Sensitized Solar Cells; From Photoelectrode to Counter Electrode. J. Electrochem. Soc. 2022, 169, 066507. [Google Scholar] [CrossRef]
- Jun, H.K.; Tung, H.T. A Short Overview on Recent Progress in Semiconductor Quantum Dot-Sensitized Solar Cells. J. Nanomater. 2022, 2022, 1382580. [Google Scholar] [CrossRef]
- Shen, H.; Wan, L.; Fu, Z.; Xue, L.; Liu, J.; Han, S.; Du, S.; Lu, F.; Li, J. Simultaneously Enhancing the Performance and Mobility of Organic Solar Classical Systems by a Novel Additive. Opt. Mater. 2023, 135, 113219. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X.; Chen, C.; Wang, Q.; Li, H.; Ren, Y.; Shen, H.; Lu, X.; Yang, C.; Tong, J.; et al. Self-Doping n-Type Polymer as Cathode Interface Layer Enables Efficient Organic Solar Cells. Opt. Mater. 2023, 135, 113288. [Google Scholar] [CrossRef]
- Yang, M.; Fu, S.; Wang, L.; Ren, M.; Li, H.; Han, S.; Lu, X.; Lu, F.; Tong, J.; Li, J. Efficient Organic Solar Cells by Modulating Photoactive Layer Morphology with Halogen-Free Additives. Opt. Mater. 2023, 137, 113503. [Google Scholar] [CrossRef]
- Shen, H.; Ren, Y.; Li, J.; Xu, Y.; Han, C.; Zou, W.; Xu, H.; Sun, Y.; Kan, Y.; Gao, K. Enhanced Performance via π-Bridge Alteration of Porphyrin-Based Donors for All-Small-Molecule Organic Solar Cells. Chin. J. Chem. 2023, 41, 644–650. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, J.-W.; Jung, H.S.; Shin, H.; Park, N.-G. High-Efficiency Perovskite Solar Cells. Chem. Rev. 2020, 120, 7867–7918. [Google Scholar] [CrossRef]
- Bati, A.S.R.; Zhong, Y.L.; Burn, P.L.; Nazeeruddin, M.K.; Shaw, P.E.; Batmunkh, M. Next-Generation Applications for Integrated Perovskite Solar Cells. Commun. Mater. 2023, 4, 2. [Google Scholar] [CrossRef]
- Aynehband, S.; Mohammadi, M.; Poushimin, R.; Azar, M.H.; Nunzi, J.-M.; Simchi, A. Self-Assembly, Stability, and Photoresponse of PbS Quantum Dot Films Capped with Mixed Halide Perovskite Ligands. Mater. Res. Bull. 2022, 147, 111648. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, T.; Liang, C.; Xia, J.; Li, D.; Zhang, H.; Amini, A.; Xing, G.; Cheng, C. Towards Simplifying the Device Structure of High-Performance Perovskite Solar Cells. Adv. Funct. Mater. 2020, 30, 2000863. [Google Scholar] [CrossRef]
- Pei, Y.; Zou, X.; Qi, X.; Teng, G.; Li, Q.; Guo, D.; Zeng, S. Effect of Perovskite Film Preparation on Performance of Solar Cells. J. Chem. 2016, 2016, 1975763. [Google Scholar] [CrossRef]
- Ghosh, S.; Mishra, S.; Singh, T. Antisolvents in Perovskite Solar Cells: Importance, Issues, and Alternatives. Adv. Mater. Interfaces 2020, 7, 2000950. [Google Scholar] [CrossRef]
- Albero, J.; Asiri, A.M.; García, H. Influence of the Composition of Hybrid Perovskites on Their Performance in Solar Cells. J. Mater. Chem. A 2016, 4, 4353–4364. [Google Scholar] [CrossRef]
- Cai, F.; Yan, Y.; Yao, J.; Wang, P.; Wang, H.; Gurney, R.S.; Liu, D.; Wang, T. Ionic Additive Engineering Toward High-Efficiency Perovskite Solar Cells with Reduced Grain Boundaries and Trap Density. Adv. Funct. Mater. 2018, 28, 1801985. [Google Scholar] [CrossRef]
- Tara, A.; Bharti, V.; Sharma, S.; Gupta, R. Device Simulation of FASnI3 Based Perovskite Solar Cell with Zn(O0.3,S0.7) as Electron Transport Layer Using SCAPS-1D. Opt. Mater. 2021, 119, 111362. [Google Scholar] [CrossRef]
- Husainat, A.; Ali, W.; Cofie, P.; Attia, J.; Fuller, J. Simulation and Analysis of Methylammonium Lead Iodide (CH3NH3PbI3) Perovskite Solar Cell with Au Contact Using SCAPS 1D Simulator. Am. J. Opt. Photonics 2019, 7, 33. [Google Scholar] [CrossRef]
- Yan, W.; Liu, Y.; Zang, Y.; Cheng, J.; Wang, Y.; Chu, L.; Tan, X.; Liu, L.; Zhou, P.; Li, W.; et al. Machine Learning Enabled Development of Unexplored Perovskite Solar Cells with High Efficiency. Nano Energy 2022, 99, 107394. [Google Scholar] [CrossRef]
- Mahmood, A.; Wang, J.-L. Machine Learning for High Performance Organic Solar Cells: Current Scenario and Future Prospects. Energy Environ. Sci. 2021, 14, 90–105. [Google Scholar] [CrossRef]
- Workman, M.; Zhi Chen, D.; Musa, S.M. Machine Learning for Predicting Perovskite Solar Cell Opto-Electronic Properties. In Proceedings of the 2020 International Conference on Data Analytics for Business and Industry: Way Towards a Sustainable Economy (ICDABI), Sakheer, Bahrain, 26 October 2020; pp. 1–5. [Google Scholar]
- Rono, N.; Merad, A.E.; Kibet, J.K.; Martincigh, B.S.; Nyamori, V.O. A Theoretical Investigation of the Effect of the Hole and Electron Transport Materials on the Performance of a Lead-Free Perovskite Solar Cell Based on CH3NH3SnI3. J. Comput. Electron. 2021, 20, 993–1005. [Google Scholar] [CrossRef]
- Haider, S.Z.; Anwar, H.; Wang, M. A Comprehensive Device Modelling of Perovskite Solar Cell with Inorganic Copper Iodide as Hole Transport Material. Semicond. Sci. Technol. 2018, 33, 035001. [Google Scholar] [CrossRef]
- Ahn, N.; Son, D.-Y.; Jang, I.-H.; Kang, S.M.; Choi, M.; Park, N.-G. Highly Reproducible Perovskite Solar Cells with Average Efficiency of 18.3% and Best Efficiency of 19.7% Fabricated via Lewis Base Adduct of Lead(II) Iodide. J. Am. Chem. Soc. 2015, 137, 8696–8699. [Google Scholar] [CrossRef]
- Habisreutinger, S.N.; Leijtens, T.; Eperon, G.E.; Stranks, S.D.; Nicholas, R.J.; Snaith, H.J. Carbon Nanotube/Polymer Composites as a Highly Stable Hole Collection Layer in Perovskite Solar Cells. Nano Lett. 2014, 14, 5561–5568. [Google Scholar] [CrossRef]
- Hosseini, S.; Delibaş, N.; Bahramgour, M.; Tabatabaei Mashayekh, A.; Niaie, A. Performance Comparison of Different Hole Transport Layer Configurations in a Perovskite-Based Solar Cell Using SCAPS-1D Simulation. Eur. J. Sci. Technol. 2021, 31, 121–126. [Google Scholar] [CrossRef]
- Srivastava, S.; Singh, A.K.; Kumar, P.; Pradhan, B. Comparative Performance Analysis of Lead-Free Perovskites Solar Cells by Numerical Simulation. J. Appl. Phys. 2021, 131, 175001. [Google Scholar] [CrossRef]
- Teimouri, R.; Mohammadpour, R. Potential Application of CuSbS2 as the Hole Transport Material in Perovskite Solar Cell: A Simulation Study. Superlattices Microstruct. 2018, 118, 116–122. [Google Scholar] [CrossRef]
- Sawicka-Chudy, P.; Starowicz, Z.; Wisz, G.; Yavorskyi, R.; Zapukhlyak, Z.; Bester, M.; GŁowa; Sibiński, M.; Cholewa, M. Simulation of TiO2/CuO Solar Cells with SCAPS-1D Software. Mater. Res. Express 2019, 6, 085918. [Google Scholar] [CrossRef]
- Lin, L.; Jiang, L.; Li, P.; Xiong, H.; Kang, Z.; Fan, B.; Qiu, Y. Simulated Development and Optimized Performance of CsPbI3 Based All-Inorganic Perovskite Solar Cells. Sol. Energy 2020, 198, 454–460. [Google Scholar] [CrossRef]
- Ouslimane, T.; Et-taya, L.; Elmaimouni, L.; Benami, A. Impact of Absorber Layer Thickness, Defect Density, and Operating Temperature on the Performance of MAPbI3 Solar Cells Based on ZnO Electron Transporting Material. Heliyon 2021, 7, e06379. [Google Scholar] [CrossRef] [PubMed]
- Hasanzadeh Azar, M.; Mohammadi, M.; Rezaei, N.T.; Aynehband, S.; Shooshtari, L.; Mohammadpour, R.; Simchi, A. Stable Photodetectors Based on Formamidinium Lead Iodide Quantum Well Perovskite Nanoparticles Fabricated with Excess Organic Cations. ACS Appl. Nano Mater. 2021, 4, 7788–7799. [Google Scholar] [CrossRef]
- Azar, M.H.; Mohammadi, M.; Rezaei, N.T.; Aynehband, S.; Simchi, A. Effect of Silica Encapsulation on the Stability and Photoluminescence Emission of FAPbI3 Nanocrystals for White-Light-Emitting Perovskite Diodes. J. Alloys Compd. 2022, 907, 164465. [Google Scholar] [CrossRef]
- Karthick, S.; Velumani, S.; Bouclé, J. Experimental and SCAPS Simulated Formamidinium Perovskite Solar Cells: A Comparison of Device Performance. Sol. Energy 2020, 205, 349–357. [Google Scholar] [CrossRef]
- Slami, A.; Bouchaour, M.; Merad, L. Numerical Study of Based Perovskite Solar Cells by SCAPS-1D. Int. J. Energy Environ. 2019, 13, 17–21. [Google Scholar]
- DuPindolia, G.; Shinde, S.M.; Jha, P.K. Optimization of an Inorganic Lead Free RbGeI3 Based Perovskite Solar Cell by SCAPS-1D Simulation. Sol. Energy 2022, 236, 802–821. [Google Scholar] [CrossRef]
- Raoui, Y.; Ez-Zahraouy, H.; Tahiri, N.; El Bounagui, O.; Ahmad, S.; Kazim, S. Performance Analysis of MAPbI3 Based Perovskite Solar Cells Employing Diverse Charge Selective Contacts: Simulation Study. Sol. Energy 2019, 193, 948–955. [Google Scholar] [CrossRef]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (Pymatgen): A Robust, Open-Source Python Library for Materials Analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef]
- Ward, L.; Dunn, A.; Faghaninia, A.; Zimmermann, N.E.R.; Bajaj, S.; Wang, Q.; Montoya, J.; Chen, J.; Bystrom, K.; Dylla, M.; et al. Matminer: An Open Source Toolkit for Materials Data Mining. Comput. Mater. Sci. 2018, 152, 60–69. [Google Scholar] [CrossRef]
- Barupal, D.K.; Fiehn, O. Generating the Blood Exposome Database Using a Comprehensive Text Mining and Database Fusion Approach. Environ. Health Perspect. 2019, 127, 2825–2830. [Google Scholar] [CrossRef] [PubMed]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 445, pp. 56–61. [Google Scholar] [CrossRef]
- Jin, Z.; Shang, J.; Zhu, Q.; Ling, C.; Xie, W.; Qiang, B. RFRSF: Employee Turnover Prediction Based on Random Forests and Survival Analysis. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2020; Volume 12343, pp. 503–515. ISBN 9783030620073. [Google Scholar]
- Bendib, T.; Bencherif, H.; Abdi, M.A.; Meddour, F.; Dehimi, L.; Chahdi, M. Combined Optical-Electrical Modeling of Perovskite Solar Cell with an Optimized Design. Opt. Mater. 2020, 109, 110259. [Google Scholar] [CrossRef]
- Zhang, Y.; Seo, S.; Lim, S.Y.; Kim, Y.; Kim, S.-G.; Lee, D.-K.; Lee, S.-H.; Shin, H.; Cheong, H.; Park, N.-G. Achieving Reproducible and High-Efficiency (>21%) Perovskite Solar Cells with a Presynthesized FAPbI3 Powder. ACS Energy Lett. 2020, 5, 360–366. [Google Scholar] [CrossRef]
- Jiang, Q.; Zhang, X.; You, J. SnO2: A Wonderful Electron Transport Layer for Perovskite Solar Cells. Small 2018, 14, 1801154. [Google Scholar] [CrossRef]
- Rombach, F.M.; Haque, S.A.; Macdonald, T.J. Lessons Learned from Spiro-OMeTAD and PTAA in Perovskite Solar Cells. Energy Environ. Sci. 2021, 14, 5161–5190. [Google Scholar] [CrossRef]
- Ye, T.; Wang, K.; Hou, Y.; Yang, D.; Smith, N.; Magill, B.; Yoon, J.; Mudiyanselage, R.R.H.H.; Khodaparast, G.A.; Wang, K.; et al. Ambient-Air-Stable Lead-Free CsSnI3 Solar Cells with Greater than 7.5% Efficiency. J. Am. Chem. Soc. 2021, 143, 4319–4328. [Google Scholar] [CrossRef]
- Byranvand, M.M.; Saliba, M. Defect Passivation of Perovskite Films for Highly Efficient and Stable Solar Cells. Sol. RRL 2021, 5, 2100295. [Google Scholar] [CrossRef]
- Song, X.; Zhang, Y.; Zhang, H.; Yu, Y.; Cao, M.; Che, Y.; Dai, H.; Yang, J.; Ding, X.; Yao, J. Graphene and PbS Quantum Dot Hybrid Vertical Phototransistor. Nanotechnology 2017, 28, 145201. [Google Scholar] [CrossRef]
- Jeng, J.Y.; Chiang, Y.F.; Lee, M.H.; Peng, S.R.; Guo, T.F.; Chen, P.; Wen, T.C. CH3NH3PbI3 Perovskite/Fullerene Planar-Heterojunction Hybrid Solar Cells. Adv. Mater. 2013, 25, 3727–3732. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.; Lin, P.; Wang, G.; Liu, Y.; Xu, Z.; Lin, Y. Controllable Design of Solid-State Perovskite Solar Cells by SCAPS Device Simulation. Solid State Electron. 2016, 126, 75–80. [Google Scholar] [CrossRef]
- Duan, Q.; Ji, J.; Hong, X.; Fu, Y.; Wang, C.; Zhou, K.; Liu, X.; Yang, H.; Wang, Z.-Y. Design of Hole-Transport-Material Free CH3NH3PbI3/CsSnI3 All-Perovskite Heterojunction Efficient Solar Cells by Device Simulation. Sol. Energy 2020, 201, 555–560. [Google Scholar] [CrossRef]
- Teimouri, R.; Heydari, Z.; Ghaziani, M.P.; Madani, M.; Abdy, H.; Kolahdouz, M.; Asl-Soleimani, E. Synthesizing Li Doped TiO2 Electron Transport Layers for Highly Efficient Planar Perovskite Solar Cell. Superlattices Microstruct. 2020, 145, 106627. [Google Scholar] [CrossRef]
- Salah, M.M.; Abouelatta, M.; Shaker, A.; Hassan, K.M.; Saeed, A. A Comprehensive Simulation Study of Hybrid Halide Perovskite Solar Cell with Copper Oxide as HTM. Semicond. Sci. Technol. 2019, 34, 115009. [Google Scholar] [CrossRef]
- Marinova, N.; Tress, W.; Humphry-Baker, R.; Dar, M.I.; Bojinov, V.; Zakeeruddin, S.M.; Nazeeruddin, M.K.; Grätzel, M. Light Harvesting and Charge Recombination in CH3NH3PbI3 Perovskite Solar Cells Studied by Hole Transport Layer Thickness Variation. ACS Nano 2015, 9, 4200–4209. [Google Scholar] [CrossRef]
- Jamal, S.; Khan, A.D.; Khan, A.D. High Performance Perovskite Solar Cell Based on Efficient Materials for Electron and Hole Transport Layers. Optik 2020, 218, 164787. [Google Scholar] [CrossRef]
- Azri, F.; Meftah, A.; Sengouga, N.; Meftah, A. Electron and Hole Transport Layers Optimization by Numerical Simulation of a Perovskite Solar Cell. Sol. Energy 2019, 181, 372–378. [Google Scholar] [CrossRef]
- Wang, T.; Chen, J.; Wu, G.; Li, M. Optimal Design of Efficient Hole Transporting Layer Free Planar Perovskite Solar Cell. Sci. China Mater. 2016, 59, 703–709. [Google Scholar] [CrossRef]
- Dzikri, I.; Hariadi, M.; Purnamaningsih, R.W.; Poespawati, N.R. Analysis of the Role of Hole Transport Layer Materials to the Performance of Perovskite Solar Cell. E3S Web Conf. 2018, 67, 01021. [Google Scholar] [CrossRef]
- Paquin, F.; Rivnay, J.; Salleo, A.; Stingelin, N.; Silva, C. Multi-Phase Semicrystalline Microstructures Drive Exciton Dissociation in Neat Plastic Semiconductors. J. Mater. Chem. C 2015, 3, 10715–10722. [Google Scholar] [CrossRef]
- Abdelaziz, S.; Zekry, A.; Shaker, A.; Abouelatta, M. Investigating the Performance of Formamidinium Tin-Based Perovskite Solar Cell by SCAPS Device Simulation. Opt. Mater. 2020, 101, 109738. [Google Scholar] [CrossRef]
- Yoo, J.J.; Seo, G.; Chua, M.R.; Park, T.G.; Lu, Y.; Rotermund, F.; Kim, Y.-K.; Moon, C.S.; Jeon, N.J.; Correa-Baena, J.-P.; et al. Efficient Perovskite Solar Cells via Improved Carrier Management. Nature 2021, 590, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Anwar, F.; Mahbub, R.; Satter, S.S.; Ullah, S.M. Effect of Different HTM Layers and Electrical Parameters on ZnO Nanorod-Based Lead-Free Perovskite Solar Cell for High-Efficiency Performance. Int. J. Photoenergy 2017, 2017, 9846310. [Google Scholar] [CrossRef]
- Dumin, N.A.; Dickerson, K.J.; Dumin, D.J.; Moore, B.T. Correlation of the Decay of Tunneling Currents with Trap Generation inside Thin Oxides. Solid State Electron. 1996, 39, 655–660. [Google Scholar] [CrossRef]
- Wu, F.; Bahrami, B.; Chen, K.; Mabrouk, S.; Pathak, R.; Tong, Y.; Li, X.; Zhang, T.; Jian, R.; Qiao, Q. Bias-Dependent Normal and Inverted J–V Hysteresis in Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2018, 10, 25604–25613. [Google Scholar] [CrossRef]
- Ghebouli, M.A.; Ghebouli, B.; Larbi, R.; Chihi, T.; Fatmi, M. Effect of Buffer Nature, Absorber Layer Thickness and Temperature on the Performance of CISSe Based Solar Cells, Using SCAPS-1D Simulation Program. Optik 2021, 241, 166203. [Google Scholar] [CrossRef]
- Mehlig, B. Machine Learning with Neural Networks; Cambridge University Press: Cambridge, UK, 2021; ISBN 9781108860604. [Google Scholar]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Kabir, H.; Garg, N. Machine Learning Enabled Orthogonal Camera Goniometry for Accurate and Robust Contact Angle Measurements. Sci. Rep. 2023, 13, 1497. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Remeseiro, B. Feature Selection in Image Analysis: A Survey. Artif. Intell. Rev. 2020, 53, 2905–2931. [Google Scholar] [CrossRef]









| Parameter | FAPbI3 | MAPbI3 | CsPbI3 |
|---|---|---|---|
| Thickness (nm) | 550 | 550 | 550 |
| Eg (eV) | 1.51 | 1.55 | 1.73 |
| χ (eV) | 4 | 3.9 | 3.95 |
| εr | 6.6 | 6.6 | 6.6 |
| NC (1/cm3) | 1.2 × 1019 | 1.2 × 1019 | 1.2 × 1019 |
| NV (1/cm3) | 2.9 × 1018 | 2.9 × 1018 | 2.9 × 1018 |
| μn (cm2/Vs) | 2.7 | 0.5 | 16 |
| μp (cm2/Vs) | 1.8 | 0.5 | 16 |
| ND (1/cm3) | 1.3 × 1016 | 1.3 × 1016 | 1.3 × 1016 |
| NA (1/cm3) | 1.3 × 1016 | 1.3 × 1016 | 1.3 × 1016 |
| Nt (1/cm3) | 1.5× 1014 | 1.5× 1014 | 1.5× 1014 |
| Reference | [38] | [39] | [34] |
| Parameter | SnO2 | Spiro-OMeTAD | CIS | CsSnI3 |
|---|---|---|---|---|
| Thickness (nm) | 90 | 200 | 200 | 200 |
| Eg (eV) | 3.5 | 2.9 | 1.5 | 1.3 |
| χ (eV) | 4 | 2.2 | 3.55 | 3.95 |
| εr | 9 | 3 | 13.6 | 9.93 |
| NC (1/cm3) | 2.2 × 1017 | 2.2 × 1018 | 1 × 1019 | 1 × 1019 |
| NV (1/cm3) | 2.2 × 1017 | 2.2 × 1018 | 1 × 1018 | 1 × 1018 |
| μn (cm2/Vs) | 20 | 1 × 10−4 | 25 | 1500 |
| μp (cm2/Vs) | 10 | 1 × 10−4 | 25 | 585 |
| ND (1/cm3) | 1015 | 0 | 0 | 0 |
| NA (1/cm3) | 0 | 1.3 × 1018 | 1.3 × 1018 | 1.3 × 1018 |
| Nt (1/cm3) | 1018 | 1015 | 1015 | 1015 |
| Reference | [38] | [38] | [32] | [40] |
| Interface | Defect Type | Ae (cm2) | Ah (cm2) | Energetic Distribution | Et | Ef (eV) |
|---|---|---|---|---|---|---|
| ETM/FAPbI3 | Acceptor | 1 × 10−17 | 1 × 10−18 | Single | Above the highest EV | 0.32 |
| FAPbI3/HTL | Acceptor | 1 × 10−18 | 1 × 10−19 | Single | Above the highest EV | 0.07 |
| HTL | VOC (V) | JSC (mA/cm2) | FF (%) | Efficiency (%) |
|---|---|---|---|---|
| Spiro-OMeTAD | 1.123 | 25.59 | 73.26 | 21.07 |
| CIS | 1.1051 | 26.50 | 73.94 | 21.65 |
| CsSnI3 | 0.935 | 29.5 | 79.86 | 22.02 |
| Perovskite | VOC (V) | JSC (mA/cm2) | FF (%) | Efficiency (%) |
|---|---|---|---|---|
| FAPbI3 | 1.010 | 29.02 | 82.11 | 23.94 |
| MAPbI3 | 1.102 | 24.05 | 83.54 | 22.15 |
| CsPbI3 | 1.015 | 23.02 | 75.33 | 17.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasanzadeh Azar, M.; Aynehband, S.; Abdollahi, H.; Alimohammadi, H.; Rajabi, N.; Angizi, S.; Kamraninejad, V.; Teimouri, R.; Mohammadpour, R.; Simchi, A. SCAPS Empowered Machine Learning Modelling of Perovskite Solar Cells: Predictive Design of Active Layer and Hole Transport Materials. Photonics 2023, 10, 271. https://doi.org/10.3390/photonics10030271
Hasanzadeh Azar M, Aynehband S, Abdollahi H, Alimohammadi H, Rajabi N, Angizi S, Kamraninejad V, Teimouri R, Mohammadpour R, Simchi A. SCAPS Empowered Machine Learning Modelling of Perovskite Solar Cells: Predictive Design of Active Layer and Hole Transport Materials. Photonics. 2023; 10(3):271. https://doi.org/10.3390/photonics10030271
Chicago/Turabian StyleHasanzadeh Azar, Mahdi, Samaneh Aynehband, Habib Abdollahi, Homayoon Alimohammadi, Nooshin Rajabi, Shayan Angizi, Vahid Kamraninejad, Razieh Teimouri, Raheleh Mohammadpour, and Abdolreza Simchi. 2023. "SCAPS Empowered Machine Learning Modelling of Perovskite Solar Cells: Predictive Design of Active Layer and Hole Transport Materials" Photonics 10, no. 3: 271. https://doi.org/10.3390/photonics10030271
APA StyleHasanzadeh Azar, M., Aynehband, S., Abdollahi, H., Alimohammadi, H., Rajabi, N., Angizi, S., Kamraninejad, V., Teimouri, R., Mohammadpour, R., & Simchi, A. (2023). SCAPS Empowered Machine Learning Modelling of Perovskite Solar Cells: Predictive Design of Active Layer and Hole Transport Materials. Photonics, 10(3), 271. https://doi.org/10.3390/photonics10030271






