Research on the Linear Demodulation Range and Background Noise of Fiber-Optic Interferometer System
Abstract
1. Introduction
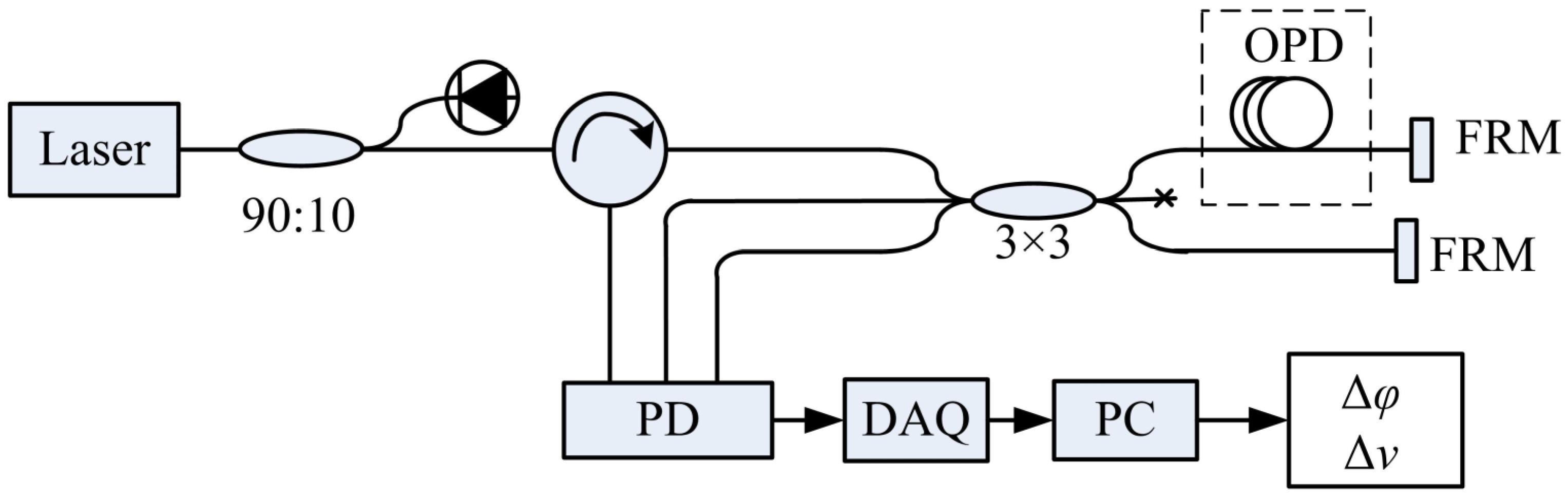
2. Experimental Setup and Methods
3. Experimental Results and Discussions
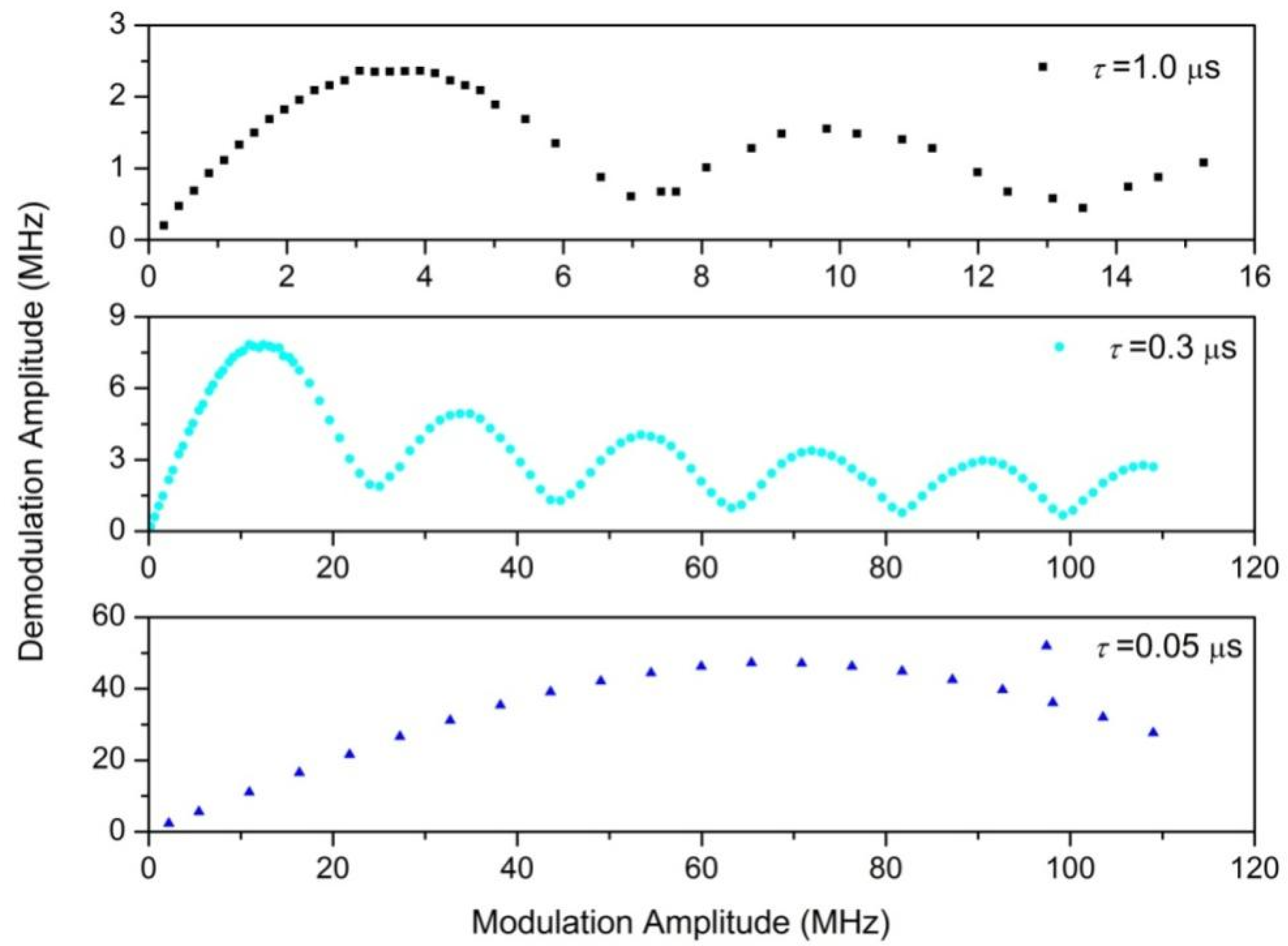
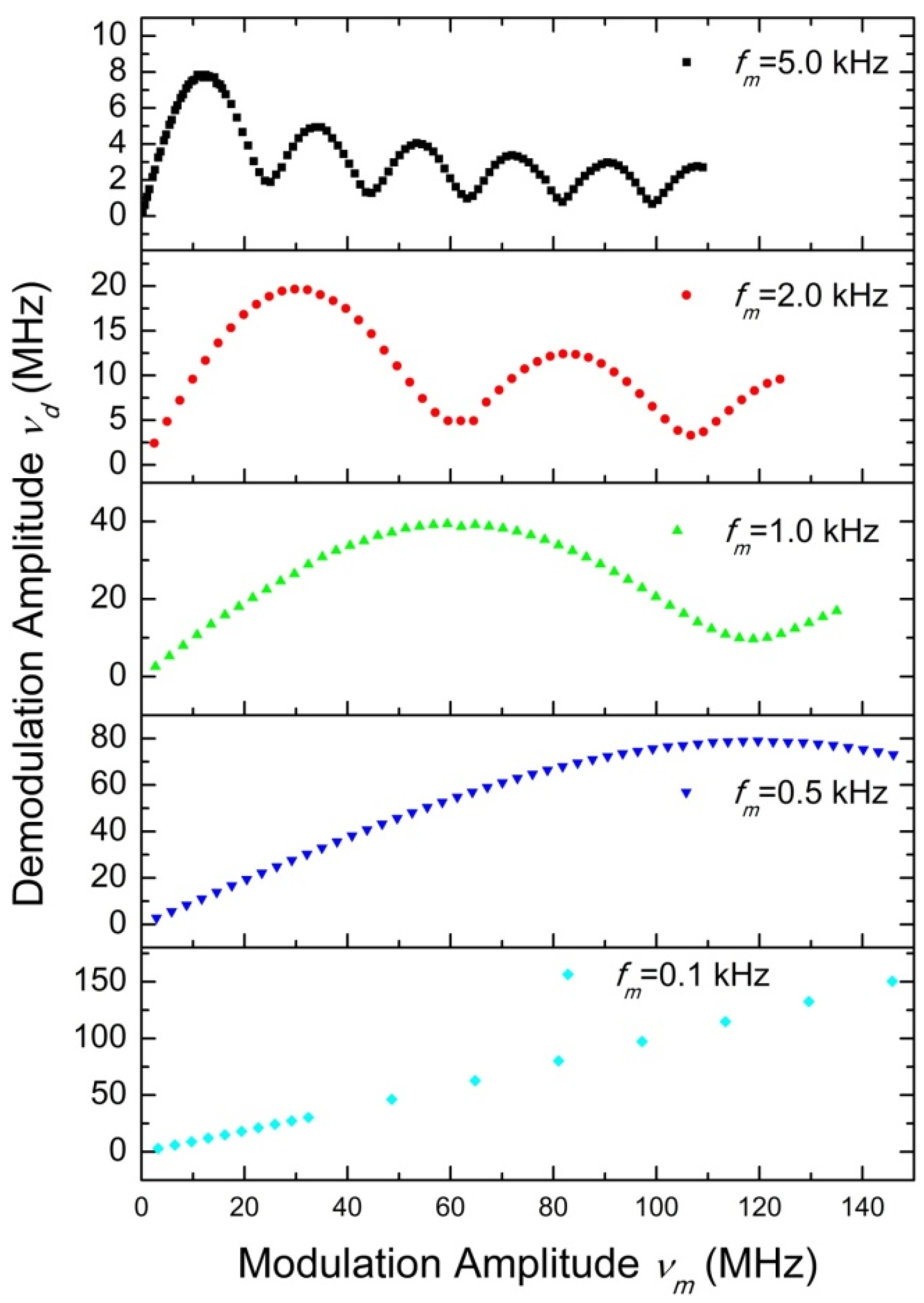
3.1. Linear Demodulation Range of the Interferometer System
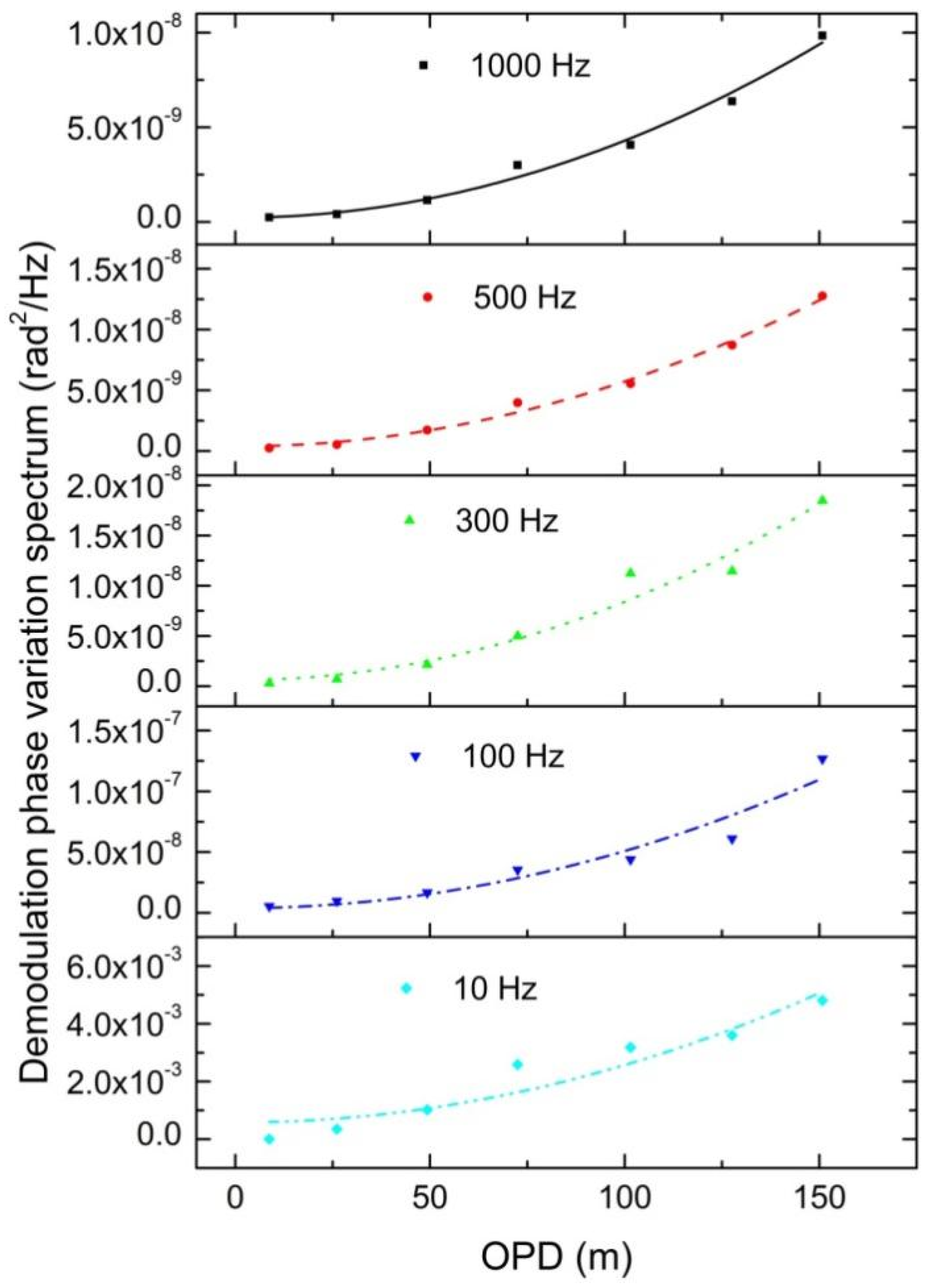
3.2. Background Noise of the Demodulation System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Lee, B.; Kim, Y.; Park, K.; Eom, J.; Kim, M.; Rho, B.; Choi, H. Interferometric Fiber Optic Sensors. Sensors 2012, 12, 2467–2486. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Zhou, P.; Peng, H.; Hu, Y.; Xiao, Q.; Wu, H.; Jia, B. Improved localization algorithm for distributed fiber-optic sensor based on merged Michelson-Sagnac interferometer. Opt. Express 2020, 28, 7207–7220. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Yang, F.; Chen, D.; Wei, F.; Cai, H.; Fang, Z.; Qu, R. Laser phase and frequency noise measurement by Michelson interferometer composed of a 3 × 3 optical fiber coupler. Opt. Express 2015, 23, 22386–22393. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Shang, Y.; Wang, C.; Song, Z.; Qi, H.; Sun, Z.; Zhang, X.; Ni, J.; Guo, J.; Zhang, F.; et al. Phase and frequency noise measurement using passive self-homodyne technique. Opt. Eng. 2017, 56, 066106. [Google Scholar] [CrossRef]
- Wang, C.; Shang, Y.; Liu, X.H.; Wang, C.; Yu, H.H.; Jiang, D.S.; Peng, G.D. Distributed OTDR-interferometric sensing network with identical ultra-weak fiber Bragg gratings. Opt. Express 2015, 23, 29038–29046. [Google Scholar] [CrossRef] [PubMed]
- Masoudi, A.; Belal, M.; Newson, T. A distributed optical fibre dynamic strain sensor based on phase-OTDR. Meas. Sci. Technol. 2013, 24, 085204. [Google Scholar] [CrossRef]
- Chen, M.; Masoudi, A.; Parmigiani, F.; Brambilla, G. Distributed acoustic sensor based on a two-mode fiber. Opt. Express 2018, 26, 25399–25407. [Google Scholar] [CrossRef] [PubMed]
- Dandridge, A.; Tveten, A.B.; Thomas, G.G. Homodyne demodulation scheme for fiber optic sensors using phase generated carrier. IEEE Trans. Microw. Theory 1982, 30, 1635–1641. [Google Scholar] [CrossRef]
- Alan, D.; Dandridge, A.; Tveten, A.B. Time-division multiplexing of interferometric fiber sensors using passive phase-generated carrier interrogation. Opt. Lett. 1987, 12, 775–777. [Google Scholar]
- Huynh, T.N.; Nguyen, L.; Barry, L.P. Delayed self-heterodyne phase noise measurements with coherent phase modulation detection. IEEE Photonic Technol. Lett. 2012, 24, 249–251. [Google Scholar] [CrossRef]
- Wang, C.; Wang, C.; Shang, Y.; Liu, X.; Peng, G. Distributed acoustic mapping based on interferometry of phase optical time-domain reflectometry. Opt. Commun. 2015, 346, 172–177. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Ashry, I.; Mao, Y.; Wang, B.; Hveding, F.; Bukhmisn, A.; Ng, T.; Ooi, B. A Review of Distributed Fiber–Optic Sensing in the Oil and Gas Industry. J. Light. Technol. 2022, 40, 1407–1431. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Dawe, T.C.; Ajo-Franklin, J.B. Illuminating seafloor faults and ocean dynamics with dark fiber distributed acoustic sensing. Science 2019, 366, 1103–1107. [Google Scholar] [CrossRef] [PubMed]
- Gallion, P.; Guy, D. Quantum phase noise and field correlation in single frequency semiconductor laser systems. IEEE J. Quantum Electron. 1984, 20, 343–349. [Google Scholar] [CrossRef]
- Piazzolla, S.; Spano, P.; Tamburrini, M. Characterization of phase noise in semiconductor lasers. Appl. Phys. Lett. 1982, 41, 695–696. [Google Scholar] [CrossRef]
- Michael, J.C.; Galeti, J.H.; Kitano, C. Michelson interferometer vibrometer using self-correcting synthetic-heterodyne demodulation. Appl. Opt. 2015, 54, 5734–5738. [Google Scholar]
| τ(μs) = 0.05 | τ(μs) = 0.30 | τ(μs) = 1.00 | ||||
|---|---|---|---|---|---|---|
| fm(kHz) | νM (MHz) | 4πνMτfm (kHz) | νM (MHz) | 4πνMτfm (kHz) | νM (MHz) | 4πνMτfm (kHz) |
| 0.1 | - | - | - | - | - | - |
| 0.5 | - | - | 125.6 | 236.75 | 37.8 | 237.5 |
| 1.0 | - | - | 62.1 | 234.11 | 18.8 | 236.25 |
| 2.0 | - | - | 31.1 | 234.49 | 9.9 | 236.25 |
| 5.0 | 75.2 | 236.25 | 12.4 | 233.73 | 3.7 | 232.48 |
| Modulation Frequency fm (Hz) | System Noise δ(f) (rad/√Hz) | True Phase Fluctuation Normalized to OPD = 1 m Δφ@1m(f) (rad/√Hz) |
|---|---|---|
| 10 | 2.41 × 10−2 | 4.46 × 10−4 |
| 100 | 6.20 × 10−5 | 2.17 × 10−6 |
| 300 | 2.47 × 10−5 | 8.83 × 10−7 |
| 500 | 1.95 × 10−5 | 7.31 × 10−7 |
| 1000 | 1.50 × 10−5 | 6.38 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wang, C.; Qu, S.; Qi, H.; Song, Z.; Jiang, P.; Guo, J.; Shang, Y.; Ni, J.; Peng, G. Research on the Linear Demodulation Range and Background Noise of Fiber-Optic Interferometer System. Photonics 2023, 10, 283. https://doi.org/10.3390/photonics10030283
Wang W, Wang C, Qu S, Qi H, Song Z, Jiang P, Guo J, Shang Y, Ni J, Peng G. Research on the Linear Demodulation Range and Background Noise of Fiber-Optic Interferometer System. Photonics. 2023; 10(3):283. https://doi.org/10.3390/photonics10030283
Chicago/Turabian StyleWang, Weitao, Chen Wang, Shuai Qu, Haifeng Qi, Zhiqiang Song, Pengbo Jiang, Jian Guo, Ying Shang, Jiasheng Ni, and Gangding Peng. 2023. "Research on the Linear Demodulation Range and Background Noise of Fiber-Optic Interferometer System" Photonics 10, no. 3: 283. https://doi.org/10.3390/photonics10030283
APA StyleWang, W., Wang, C., Qu, S., Qi, H., Song, Z., Jiang, P., Guo, J., Shang, Y., Ni, J., & Peng, G. (2023). Research on the Linear Demodulation Range and Background Noise of Fiber-Optic Interferometer System. Photonics, 10(3), 283. https://doi.org/10.3390/photonics10030283






