Abstract
Measuring resident space objects (RSOs) by star trackers has become a research hotspot in space situational awareness. However, the arc length measured by star trackers is too short to complete the high-precision orbit determination of the RSO. In this paper, a staring–tracking measurement (STM) method is proposed to obtain a sufficiently long arc. Firstly, the three-axis attitude calculation model of the satellite is established for tracking RSOs during the staring process. Secondly, an observation method of the RSO location is proposed based on the principle of the angular distance invariance and the imaging mapping function of the star tracker. Finally, the numerical simulations and the ground experiment were conducted to verify the proposed algorithm. Simulation results show that the acquisition time of the measurable arcs is longer than 6 min, and the accuracy of the declination and the ascension can meet the standard for RSO orbit determination. The physical experiment shows that the acquisition time is consistent with that in the simulation. Our work provides a new idea for the realization of high-precision space-based optical measurement.
1. Introduction
With an increasing number of resident space objects (RSOs), the space beyond Earth is becoming more and more crowded. This greatly threatens the safety of on-orbit spacecraft operations [1,2,3]. For protecting spacecraft from potential collisions, it is critical to accurately determine the RSO position in a timely manner [4,5,6]. Compared with conventional ground-based observations, space-based optical observations have unique advantages in measuring the RSO position for eliminating the restrictions on weather and terrain [7,8,9,10]. Among space-based optical devices, dedicated measurement payloads such as telescopes are expensive and difficult to manufacture [11]. Therefore, this paper adopted star trackers as the payloads for observing RSOs, because of their advantages in terms of compact structure, low cost, and high precision [12]. The precondition of star tracker imaging is collecting sufficient energy from RSOs [13]. When the star tracker receives enough sunlight radiation reflected from the RSO, the image would have a high signal-to-noise ratio (SNR) and the RSO can be detected [14].
However, this kind of optical observation belongs to the bearings-only passive positioning, which can only directly obtain the angle information of RSOs [15]. Additionally, the measurement arcs are usually less than 20 s through one observation because of the limitations of the star tracker, namely the relative dynamics and the small field of view (FOV). In general, a measurement arc is defined as an excessively short arc (TSA) whose measurement arc is less than 60 s [16]. Under TSA conditions, there are some works which consider the orbit determination (OD) of RSO as an optimization problem. Ansalone et al. proposed a genetic algorithm (GA) to yield a good estimation of the orbital parameters through genetic operators [17]. Hu et al. proposed a solution group optimization method to consider the error of the estimated orbits on the projection plane for a well-optimized solution [18]. Xie et al. proposed a differential evolution algorithm (EA) with multimodal properties to solve the OD problem from the perspective of multimodal optimization [19]. However, it is still challenging to obtain the accurate orbit determination of RSOs directly from original TSA, because the limited solution constraints can lead to unrealistic and multiple optimal results. Therefore, the researchers prefer to use long measurement arcs to solve the TSA problem and obtain accurate RSOs positions.
The main idea of getting sufficiently long measurement arcs is the correlation of short measurement arcs [20,21]. There have been many studies about the correlation of the arcs obtained from multiple star trackers. Huang et al. proposed a TSA correlation method based on the principle of epiploic geometry, which has a correlation accuracy of more than 90% [22]. Huang et al. calculated the initial orbit parameters by improving the Laplacian method and the fuzzy correlation principle to realize the correlation between the orbits [23]. Huang et al. proposed a space target correlation method based on sine fitting, which distinguishes the space targets from different orbits [24]. These long-arc-based OD methods combine short arcs from the multiple measurements of the same object into one long arc. However, the orbital elements’ solutions using multiple short-arc observations will be affected by the specific contingency of the correlation algorithms and the orbital perturbation [25]. Therefore, we need find a way to directly obtain the long measurement arc of the RSO in one observation, which not only increases the arc data, but also reduces the error generated by the correlation algorithms.
Satellites are commonly used as a platform in space-based observation missions. Recently, a new dynamic imaging mode based on the high agility of satellites [26,27], called staring imaging, was proposed for Earth observation in remote sensing [28]. The satellite stares at the same target by adjusting the attitude when performing staring imaging, which increases the observation time compared with traditional push-broom imaging [29]. Obviously, this staring imaging model can significantly extend the measurement arc length of RSOs in one observation, which is very suitable for solving the TSA problem in accurate RSO position determination. Therefore, a staring–tracking measurement (STM) method is proposed in this paper to obtain a sufficiently long arc RSO observation by star trackers. The proposed STM method completes both the tracking and the observation of the RSO. Firstly, the expected attitude of the satellite is calculated for staring at the RSO and collecting long-arc measurement data. Additionally, a position vector measurement method based on the principle of angular distance invariance and the imaging mapping function of the star tracker is then proposed in the process of staring–tracking for RSOs.
This paper is organized as follows: the attitude planning model of the satellite for staring–tracking, and the measurement method of the RSO position vector are introduced in Section 2. The simulations and experiments of the proposed method were carried out in Section 3. The discussions based on the results in Section 3 are given in Section 4, and the conclusions are given in Section 5.
2. Materials and Methods
2.1. Three-Axis Attitude Model of the Satellite for RSOs Staring–Tracking Imaging
The star tracker is a device that determines the satellite attitude in the celestial navigation system by taking pictures of stars in space. This paper presents the STM method based on the star tracker for achieving a long measurement arc of RSOs. Figure 1 shows the staring process of the proposed STM method for RSOs. Where the dotted line represents the initial orbit of the RSO estimated from the original TSA data, the blue point represents the estimated RSO position. The red line is the real RSO orbit, and the red point represents the actual position of the RSO. During the tracking process from time to , the optical axis of the star tracker keeps tracking and staring at the real RSO, which effectively extends the measurement arcs. The staring–tracking law is the star tracker and should always keep the real RSO in the center of the FOV. However, due to the estimated initial orbit elements being inaccurate, the optical axis cannot keep pointing at the real RSO. Therefore, we first analyze the visibility conditions of RSOs to ensure that the proposed STM method could always observe the real RSOs during staring–tracking imaging.
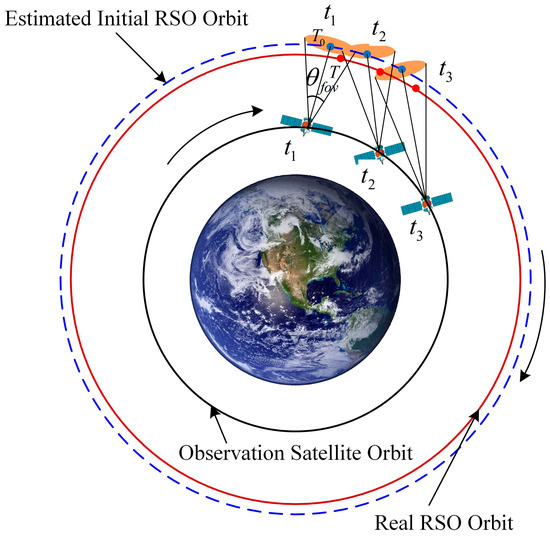
Figure 1.
Schematic diagram of tacking imaging in the star tracker.
Figure 2 shows the observation area of the star tracker on the RSO orbital plane, since the FOV of the star tracker is assumed to be a circle, it is an ellipse. The blue and red points represent the estimated RSO and the actual RSO positions, respectively. This paper considers the estimated RSO orbital plane to be the same as the actual orbital plane to simplify the analysis of the visibility conditions. According to the geometric relationship in the observation area, the lengths of the major and minor semi-axes of the ellipse can be separately determined as:
where is the semi-major axis of the observable region; is the semi-minor axis; denotes the half FOV of the star tracker; denotes the angle between the optical axis of the star tracker and the direction vector of the RSO; is the distance between the RSO and the observation satellite. Additionally, is defined as the angle between the orbital plane and the optical axis, and is the complement of .
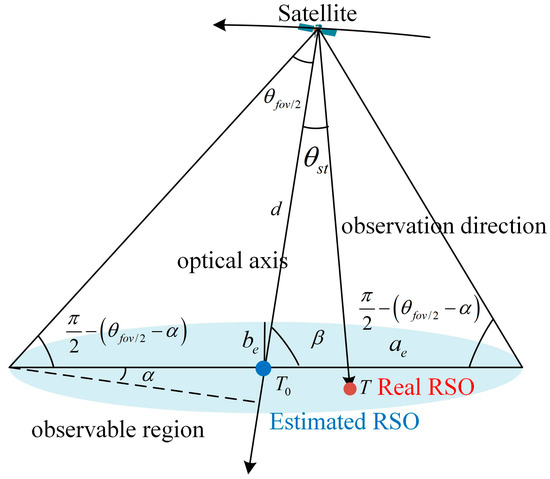
Figure 2.
Schematic diagram of the observable region of the star tracker on the RSO orbit plane.
When is smaller than , the real RSO is in the observable region that can be captured by the star tracker. Moreover, the observable region can be expressed as:
Obviously, due to the inaccurately estimated RSO, the optical axis is not identical to the real observation direction. We defined the current optical axis direction of the estimated RSO in the center of the FOV as the initial observation direction (the star tracker is fixed on the satellite), and the observation direction that the real RSO is in the center of the FOV as the expected observation direction. To track and stare at the real RSO, the satellite should adjust its three-axis attitude to make the initial observation direction consistent with the expected observation direction, as shown in Figure 3.
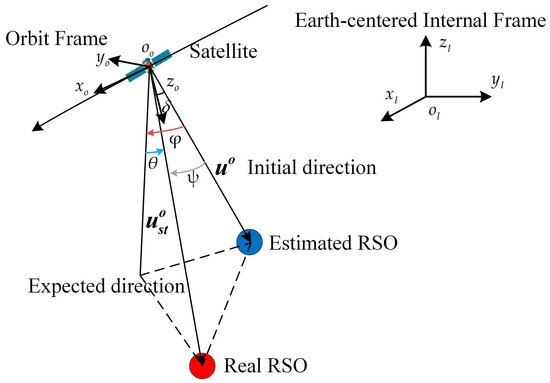
Figure 3.
The process of satellite attitude maneuver in staring–tracking imaging mode.
Figure 3 shows the satellite maneuvering process from the initial direction to the expected direction. Before we calculate the expected satellite attitude, then two frames should be defined first. The Earth-centered (ECI) internal frame: the original point is the Earth center, the z axis points to the north pole, the x axis points to the spring equinox in the equator plane, and the y axis obeys the right-hand rule in the equator plane. The orbit frame: the original point is the satellite center, the z axis points to the Earth center in the orbit plane, the x axis is the same as the satellite moving direction in the orbit plane, and the y-axis obeys the right-hand rule. In the orbit frame, the satellite changes the yaw , roll , pitch angel around the z, x, and y axes, which meets the requirements of staring–tracking. Additionally, the expected three-axis attitude can be expressed as the expected quaternion [30]:
where is the included angle between the optical axis unit vector and the expected observation unit vector in the orbit frame, the vector is perpendicular to and at the same time, expressed separately as:
The unit vector could be determined by the satellite position and the installation angle of the star tracker. Additionally, the unit vector can be expressed as:
where is the transformation matrix from the ECI frame to the orbital frame, represents the unit observation vector of the real RSO in the ECI frame, and represents the unit position vector of satellites in the ECI frame, represents the unit observation vector in the ECI frame. Figure 4 shows the positions of the observation satellite and the RSO in the ECI frame during staring–tracking imaging.
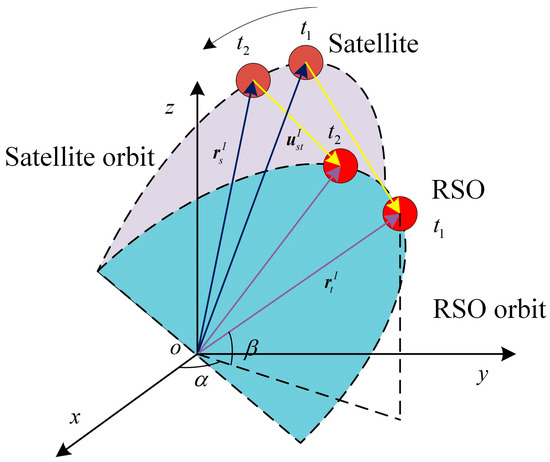
Figure 4.
Schematic of staring–tracking to the RSO.
can be expressed by the right ascension and the declination of the real RSO is ECI frame as:
where can be determined through the measurement method based on the principle of angular distance invariance proposed in Section 2.2.
The specific observation satellite position can be determined by Keplerian elements. Where can be defined as: is the semi-major axis of the orbit, is the eccentricity of the orbit, is the orbit inclination, is the true anomaly, is the argument of periapsis, and is the longitude of the ascending node. Therefore, the observation satellite position in the ECI frame can be expressed as
where is the near-point angle, is the matrix of the unit vector along the semi-major axis, and represents the matrix of the unit vector along the semi-minor axis of the orbit in the ECI system:
Additionally, the unit vector can be expressed as:
where denotes the distance between the Earth center and the satellite center. In summary, the expected quaternion of the satellite can be obtained through Equation (3). Because the rotation sequence affects the attitude angle and the quaternion, when the satellite rotates in a 3–1–2 order, the expected three-axis attitude angle of the satellite in the orbit frame can be obtained as follows:
where represents the yaw angle, represents the pitch angle, and represents the roll angle. The satellite tracks and observes the RSO by adjusting the attitude. In this proposed STM, the star tracker will obtain the continuous measurement arcs of the RSO.
2.2. Observation Measurement Method Based on the Principle of Angular Distance Invariance
As mentioned in Section 2.1, the proposed STM method could image RSO during the staring–tracking process. According to Equation (6), the measurement of the real RSO vector in the ECI frame is important for the STM method. To directly obtain in the ECI frame from the star image without calculating the complex transaction matrixes between a few of frames, an observation method is proposed in this paper. The method is based on the principle of angular distance invariance (ADI), which means that the angle distance between two vectors does not change under different frames. In addition to the RSO, there are stars in the star image captured by the star tracker. The unit observation vector of the RSO is defined as , and the unit vector of the star is defined as . When the reference frame is the star tracker frame, these two vectors can be expressed as and , respectively. When the reference frame is ECI frame, these two vectors can be expressed as and , respectively. Based on the ADI principle, the angle distance between and is the same as the angle between and .
The angle distance in the star tracker frame can be calculated as:
Figure 5 shows the imaging process of the star tracker, and the position of the star or the RSO in the star tracker body coordinate system can be converted into the image plane position through pinhole imaging model. Thus, and can be calculated by the positions of the RSO and the star on the star image:
where are the image positions of the star or the RSO, are the principal point positions of the image plane, and is the focal length of the star tracker. The angular distance can be calculated based on Equations (13) and (14).
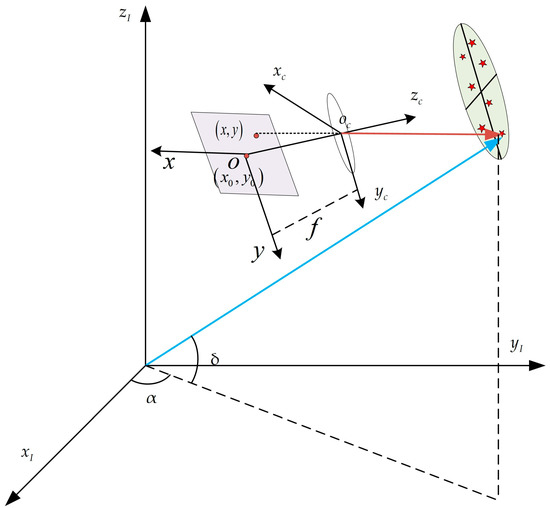
Figure 5.
Schematic diagram of the star tracker imaging process.
Additionally, the angle distance in the ECI frame can be calculated as:
where and can be calculated by positions of the RSO and the star in the ECI frame:
where are the angles of the star or the RSO in the ECI frame. We define , as the right ascension and the declination of the i-th star, and the RSO, respectively. Additionally, can be obtained from the star catalogue by star identification [31]. Thus, can be expressed as:
According to the ADI principle, is equal to . Therefore, the solution of should meet the following conditions:
where is the loss function. The optimal solution of occurs when the loss function is minimized. Additionally, when the partial derivative of the loss function is equal to zero, the loss function has the minimum value.
The partial derivative of the loss function is shown as follows:
When the partial derivative is equal to zero, it can be expressed as:
Therefore, the optimal solution of can be obtained by:
Therefore, can be expressed as:
Additionally, of the RSO in the ECI frame can be expressed as:
After completing the coordinate measurement of the RSO, it is necessary to remove the aberration of light. This method in [32] is used to complete the correction of the aberration.
3. Results
In this section, numerical simulations and physical experiments were performed to validate the proposed STM method. Simulation settings were firstly introduced, and simulations and physical experiments were performed to analyze the length and accuracy of the observation arcs obtained in the staring–tracking imaging process.
3.1. Simulation Settings of the Proposed STM Method
As demonstrated in Section 2.1, there are three orbits in the staring–tracking process: the observation satellite orbit, the estimated initial RSO orbit from original TSA measurements, and the real RSO orbit. In Section 2.2, the observation measurement method of the star tracker based on the ADI principle was analyzed. We analyze the orbit elements and the star tracker parameters to design appropriate simulation parameters for the STM method.
3.1.1. Orbit Parameters Settings of the Proposed STM Method
When the star tracker performs staring–tracking, its optical axis should always point at the real RSO, and keeps the projection locations of RSOs in the center on the image plane. However, the estimated initial RSO orbit elements from original TSA measurements are not accurate. In the ECI frame, the RSO position error caused by orbit elements is defined as displacement . To design reasonable orbits for the STM method, we specifically analyzed the relationship between the displacement and orbital elements. The actual RSO orbit elements and the errors of the orbit elements in the simulation are listed in Table 1, respectively.

Table 1.
Orbital elements of RSO in simulation.
The estimated RSO positions are calculated according to the parameters in Table 1. The results of displacement between the true RSO orbit and the estimated inaccurate RSO orbit are shown in Figure 6. The true and inaccurate RSO positions in 3D space are shown in Figure 6a. Meanwhile, the tendency curves of with at different times are shown in Figure 6b based on Equation (6), respectively. The simulation results show that changes periodically in one period of the orbit and the maximum displacement error is caused by the semi-major, followed by the eccentricity. Additionally, the error caused by other orbital elements are much smaller.
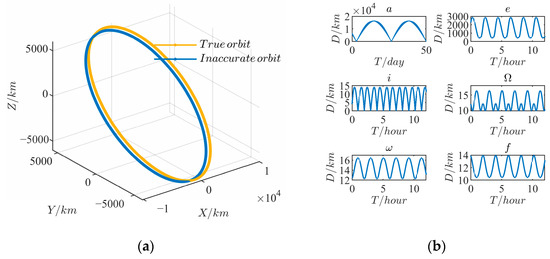
Figure 6.
Simulation results of the displacement : (a) positions of the true and inaccurate RSO orbits in 3D space; (b) curves of with different orbit elements in one period of the RSO orbit.
Therefore, the reasonable orbital elements of the three orbits simulated in the STM method are listed in Table 2. Apart from the semi-major axis and eccentricity, the other elements of the real and estimated RSO orbits are essentially the same. The high-performance of satellite attitude control is reflected in the optimal attitude pointing technology with a satellite attitude accuracy of 8’’/s and adaptive line-frequency matching technology for attitude motion estimation with a matching time of 3 μs. Furthermore, the planned attitude of the observation satellite in the STM method can be calculated according to Equation (12). In the orbit frame, the calculated satellite attitude angle and angular velocity are shown in Figure 7 while the satellite rotates in the 3–1–2 order.

Table 2.
Orbital elements of the observation satellite and the RSO.
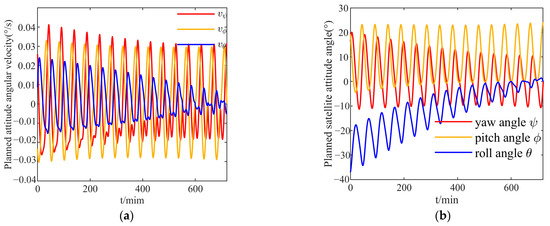
Figure 7.
Planned satellite attitude angle and angular velocity: (a) three-axis satellite attitude angle; and (b) three-axis satellite angular velocity.
3.1.2. Star Tracker Parameters Settings
The main purpose of the proposed STM method is RSO measurement, which means that the RSO should always be within the observation area. Because of the difference between the observation orbit plane and the RSO orbit plane, the observable region of the star tracker on the RSO orbit plane is an ellipse area. According to Equation (1), the semi-major and the semi-minor axis of the observable region are simulated and analyzed, respectively. There are three factors that affect the length of the major axis: the distance , the half FOV , and the angle between the orbital plane and the observation plane. The curves of and under different conditions are shown in Figure 8.
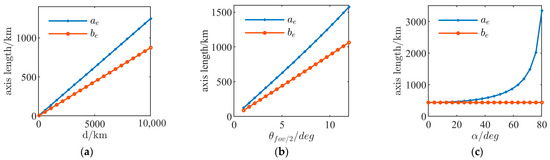
Figure 8.
The curves of the major axes and : (a) curves with the increase in the detection distance ; (b) curves with the increase in half FOV ; and (c) curves with the increase in angle .
Apparently, the curves of and both increase linearly with the increase in and , as shown in Figure 8a,b, respectively. The curve of is independent with the increase in as shown in Figure 8c. Meanwhile, increases nonlinearly when is in the range of 30°–70°, and increases rapidly when is greater than 70°. Among the three factors, is determined by the relative position of the RSO and the star tracker, which should be larger than 70° to enlarge the observation area. As for the distance and the half FOV , these are determined by the parameters of the star tracker. For a considerable observation area under consideration with the star tracker performance, the parameters of the star tracker in the STM method are listed in Table 3.

Table 3.
Parameters of star tracker.
In contrast with static star images, the energy of star images captured in the staring–tracking method are distrusted as streaks. The planned satellite attitude angle and angular velocity in Section 3.1.1 are used to generate star images. A more detailed discussion of the simulation for simulating dynamic star images can be found in [33]. The magnitudes of stars are added with Gaussian noise to test the accuracy of the proposed observation method. The standard deviation of 0.05 pixels and 5000 dynamic star images are generated for the simulation of measurement accuracy, as shown in Figure 9.

Figure 9.
A dynamic smearing star image simulated in the staring–tracking imaging.
3.2. Numerical Simulation of the Proposed STM Method
The main purpose of the proposed STM method was long-precision measurement arcs acquisition. Then, the numerical simulations of the STM method in one period orbit were conducted to evaluate the observation arcs’ length and accuracy, respectively.
3.2.1. Simulation of the Observation Arcs in One Orbit Period of Staring–Tracking Imaging
The acquisition time of the arc measured by traditional methods is usually less than 20 s in one observation. The observation arc obtained by the STM method is much longer than that of traditional methods. In the process of staring–tracking, the observation satellite adjusts the optical axis direction of the star tracker according to the planned attitude in Section 3.1.1. However, the star tracker cannot always observe the RSO because of the orbital elements error. The RSO can only be observed when the observation angle is smaller than the half FOV of the star tracker . The simulation results of the relationship between and in the STM method are shown in Figure 10. Where the blue line represents , the three straight lines represent at 0.5°, 5°, and 10°, respectively. Therefore, the RSO can be measured several times during the orbit period when the blue line is under the straight line. During the first 30 min of the observation period, the measurable arcs at , are approximately 6 min, respectively. The RSO cannot be observed at , because the FOV is too small to catch RSOs.
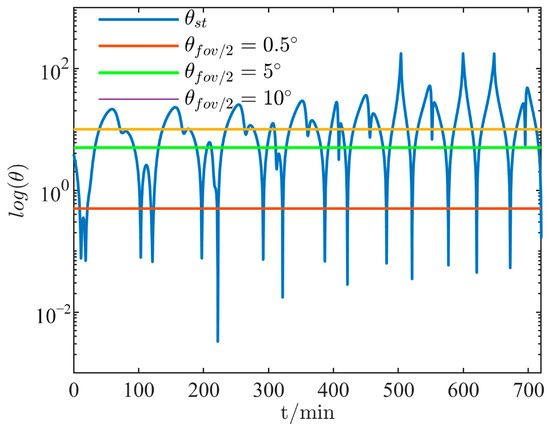
Figure 10.
The simulated observation arcs of the RSO in the STM method.
3.2.2. Simulation of the Measurement Accuracy
The following simulation was carried out to evaluate the accuracy of the RSO observation arc. The measurement accuracy of the proposed method was verified by the 5000 dynamic star images. In simulated images, the measured RSO is randomly selected from star points in the simulated star image to avoid accidental errors. The true position vector of the measured RSO in the ECI frame can be obtained by adding the position vector to the selected star and the star tracker position vector. The centroid coordinates of stars and the RSO are calculated by the centroid extraction algorithm described in [34] to determine their unit observation vectors in the camera frame. The position vector of the RSO can be determined according to the method proposed in Section 2.2. The errors of right ascensions and declinations and are shown in Figure 11. The maximum absolute value of is , and the maximum absolute value of is .
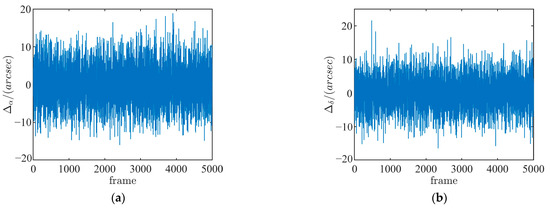
Figure 11.
Errors of the RSO locations: (a) ascension direction; and (b) declination direction.
The root-mean-square error (RMSE) of the results are calculated through Equation (24) to evaluate the effectiveness of the proposed STM method. The simulation results show that the RMSE of the ascension is , and that the RMSE of declination is .
3.3. Physical Experiment
To verify the effectiveness of the STM method, the ground physical experiment was carried out in this section. As shown in Figure 12a, the smallest observable region is a circular area wherein the optical axis of the star tracker is perpendicular to the orbital plane. Thus, the ground physical experiment was carried out under this vertical condition. Figure 12b shows the schematic of the ground experiment system. The LED panel, used as an RSO generation device, displays the actual and estimated RSO locations. The CMOS (complementary metal oxide semiconductor) camera was used for taking pictures of the LED panel, which plays the role of the star tracker.
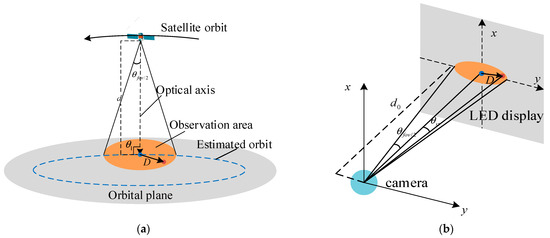
Figure 12.
Experimental schematic diagram of the observable region search range: (a) observable region; and (b) schematic of the ground experiment system.
The principle of the physical experiment system for the STM method validation is geometric scaling. This means that the parameters on the ground experiment system and the on-orbit parameters are scaled at 1:107. The parameters of the experimental system are listed in Table 4. The object distance between the camera and the LED panel is 60 cm, which means that the actual distance between the star tracker and the RSO is 6000 km according to the scale bar. Additionally, the ground experiment system is shown in Figure 13. To achieve sub-pixel centroid algorithm accuracy, the 3 × 3 pixel-matrix is used to complete the display of the RSO, as shown in Figure 13. The two centroids of the pixel-matrix represent the actual and estimated RSO positions.

Table 4.
Ground experiment parameters.

Figure 13.
Ground physics simulation experiment system.
To simplify the experimental process, the estimated RSO locations are set to the center of the LED panel. When a specific real RSO is in the scope of the camera, the location can be measured through the proposed observation method. The estimated and the real RSO locations in each image are generated by the orbital elements listed in Table 2. To improve the reliability of the experiment, Gaussian noise with a mean of 3 pixels is added to the actual and estimated RSO locations. When the image frequency is set to 5 Hz in ground experiment, 9000 images containing the actual and estimated RSO locations are shown on the LED panel within 30 min, and the CMOS camera is used to take pictures. Due to the limited distance on the ground and the pixel size of CMOS, it is impossible to obtain the same measurement accuracy of the RSO as that in numerical simulation. However, the length of the observable arc can be verified in the ground experiment. The observable arc in the experiment is a set of all observable positions, which is shown as Figure 14. The acquisition time of the measurable arc in the experiment is approximately 5.8 min. According to the results in Section 3.2.1, the theoretical acquisition time is approximately 6 min, which is like the acquisition time obtained in the experiment.
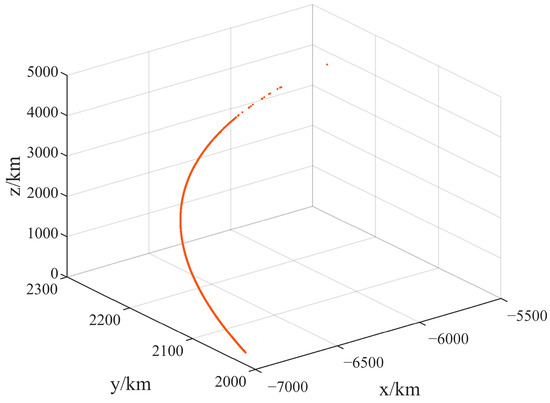
Figure 14.
Experimental results of measurable arc.
4. Discussion
The simulations in Section 3.1 show that the orbit elements’ errors have a huge impact on the RSO positions. We can see that the changes in the displacement between the real and estimated positions is higher with the semi-major axis and more eccentric than the other four elements. The real RSO will also be found thanks to the planned satellite attitude. In summary, even a small orbital element error can also lead to massive displacement, which means that the staring–tracking observation requires a considerable observable region. Moreover, from the results in ta 8, it can be found that the FOV of the star tracker has a significantly high impact on the measurement arcs. With the increment of the half FOV, the probability of catching real RSO is improved in staring–tacking imaging. Therefore, enlarging the FOV of the star tracker is very helpful for achieving the long arcs. The appropriate design of orbits and the star tracker parameters makes the proposed STM method improve the length and accuracy of measurement arcs.
From the results in Figure 10, it can be found that measurement arcs in staring–tracking imaging is obviously extended with more reasonable imaging parameters. In one orbit period, the continuous staring and tracking of RSO increases the observation change. Figure 11 shows the RSO measurement errors of the right ascensions and declinations, respectively. It can also be found that both the accuracy of the declination and the ascension can meet the standard for RSO orbit determination. In the ground experiment, the results validate that the proposed STM method could be implemented on experimental devices and achieve the measured arcs which are close to the simulation results. Based on these analyses, the proposed STM method could achieve long arcs and maintain the accuracy.
5. Conclusions
To solve the low-precision problem of TSA measurement data for RSO orbit determination, the staring–tracking measurement method based on the star tracker is proposed in this paper. The proposed method significantly enlarges the acquisition time of the measured arc and maintains the observation accuracy of RSOs. The simulation results show that the acquisition time of the arc obtained by staring–tracking method is extended, while the accuracy of the right ascension and declination did not exceed , which meets the requirement for accurate orbit determination. Within the range of allowable error, the physical experiment show that the acquisition time of the measurement arc is in good agreement with the simulation results. This method provides technical support for the precise orbital determination of RSOs and lays the foundation for real-time situational awareness. In this study, only the orbit elements error is considered in the observation process, which is not completely reasonable in the actual situation. In the future, we will intensively study the influence of the Earth occlusion and the equivalent magnitude of the RSO on the staring–tracking method.
Author Contributions
Conceptualization, T.X. and X.Y.; methodology, T.X. and Z.F.; software, M.W. and Z.F.; validation, T.X., Z.F. and S.G.; formal analysis, T.X.; investigation, T.X.; resources, Z.F.; data curation, Z.F.; writing—original draft preparation, T.X. and Z.F.; writing—review and editing, X.Y. and S.G.; visualization, M.W.; supervision, X.Y.; project administration, X.Y.; funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jilin Province, grant number 20210101099JC.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Y.; Li, B.; Liu, H.K.; Sang, J.Z. An analysis of close approaches and probability of collisions between LEO resident space objects and mega constellations. Geo-Spat. Inf. Sci. 2022, 25, 104–120. [Google Scholar] [CrossRef]
- Rodriguez-Villamizar, J.; Cordelli, E.; Schildknecht, T. The stare and chase observation strategy at the Swiss Optical Ground Station and Geodynamics Observatory Zimmerwald: From concept to implementation. Acta Astronaut. 2021, 189, 352–367. [Google Scholar] [CrossRef]
- Lagona, E.; Hilton, S.; Afful, A.; Gardi, A.; Sabatini, R. Autonomous Trajectory Optimisation for Intelligent Satellite Systems and Space Traffic Management. Acta Astronaut. 2022, 194, 185–201. [Google Scholar] [CrossRef]
- Pastor, A.; Sanjurjo-Rivo, M.; Escobar, D. Initial orbit determination methods for track-to-track association. Adv. Space Res. 2021, 68, 2677–2694. [Google Scholar] [CrossRef]
- AlDahoul, N.; Karim, H.A.; Momo, M.A. RGB-D based multi-modal deep learning for spacecraft and debris recognition. Sci. Rep. 2022, 12, 3924. [Google Scholar] [CrossRef] [PubMed]
- Schwab, D.; Singla, P.; O’Rourke, S. Angles-Only Initial Orbit Determination via Multivariate Gaussian Process Regression. Electronics 2022, 11, 588. [Google Scholar] [CrossRef]
- Feng, G.H.; Li, W.H.; Zhang, H. Geomagnetic Energy Approach to Space Debris Deorbiting in a Low Earth Orbit. Int. J. Aerosp. Eng. 2019, 2019, 5876861. [Google Scholar] [CrossRef]
- Du, J.L.; Chen, J.Y.; Li, B.; Sang, J.Z. Tentative design of SBSS constellations for LEO debris catalog maintenance. Acta Astronaut. 2019, 155, 379–388. [Google Scholar] [CrossRef]
- Yates, J.M.; Spanbauer, B.W.; Black, J.T. Geostationary orbit development and evaluation for space situational awareness. Acta Astronaut. 2012, 81, 256–272. [Google Scholar] [CrossRef]
- Utzmann, J.; Ferreira, L.; Strasser, N.; Vives, G.; Probst, D.; Lievre, N. Optical In-Situ Monitor a Breadboard System to Enable Space-Based Optical Observation of Space Debris. In Proceedings of the 7th European Conference on Space Debris, Darmstadt, Germany, 18–21 April 2017. [Google Scholar]
- Hu, Y.P.; Li, K.B.; Liang, Y.G.; Chen, L. Review on strategies of space-based optical space situational awareness. J. Syst. Eng. Electron. 2021, 32, 1152–1166. [Google Scholar] [CrossRef]
- Spiller, D.; Magionami, E.; Schiattarella, V.; Curti, F.; Facchinetti, C.; Ansalone, L.; Tuozzi, A. On-orbit recognition of resident space objects by using star trackers. Acta Astronaut. 2020, 177, 478–496. [Google Scholar] [CrossRef]
- Liebe, C.C. Accuracy performance of star trackers—A tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Liu, M.Y.; Wang, H.; Yi, H.W.; Xue, Y.K.; Wen, D.S.; Wang, F.; Shen, Y.; Pan, Y. Space Debris Detection and Positioning Technology Based on Multiple Star Trackers. Appl. Sci. 2022, 12, 3593. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Xiang, J.H.; Zhang, Y.L. Error analysis of line-of-sight measurement for video satellite. Adv. Mech. Eng. 2017, 9, 1687814017742823. [Google Scholar] [CrossRef]
- Lei, X.X.; Wang, K.P.; Zhang, P.; Pan, T.; Li, H.F.; Sang, J.Z.; He, D.L. A geometrical approach to association of space-based very short-arc LEO tracks. Adv. Space Res. 2018, 62, 542–553. [Google Scholar] [CrossRef]
- Ansalone, L.; Curti, F. A genetic algorithm for Initial Orbit Determination from a too short arc optical observation. Adv. Space Res. 2013, 52, 477–489. [Google Scholar] [CrossRef]
- Hu, J.; Li, B.; Li, J. Initial orbit determination utilizing solution group optimization. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 897–911. [Google Scholar] [CrossRef]
- Xie, H.; Sun, S.; Xue, T.; Xu, W.; Liu, H.; Lei, L.; Zhang, Y. A Multimodal Differential Evolution Algorithm in Initial Orbit Determination for a Space-Based Too Short Arc. Remote Sens. 2022, 14, 5140. [Google Scholar] [CrossRef]
- Shang, H.T.; Chen, D.F.; Cao, H.W.; Fu, T.; Gao, M.C. Initial Orbit Determination Using Very Short Arc Data Based on Double-Station Observation. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1596–1611. [Google Scholar] [CrossRef]
- Zhang, S.; Fu, T.; Chen, D.; Ding, S.; Gao, M. An Initial Orbit Determination Method Using Single-Site Very Short Arc Radar Observations. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1856–1872. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, Y.; Feng, F. Space target synchronization association method under distributed star sensor. Chin. J. Sci. Instrum. 2019, 40, 106–113. [Google Scholar]
- Huang, Q.; Zhang, Y.; Feng, F. Algorithm of space track segment association under distributed star sensor. Syst. Eng. Electron. 2020, 42, 1007–1013. [Google Scholar]
- Huang, Q.; Zhang, Y.; Feng, F. Short-arc association algorithm for space target based on sine fitting. Chin. Space Sci. Technol. 2020, 40, 111–118. [Google Scholar] [CrossRef]
- Qian, Y.-J.; Zong, K.; Yang, X.-D.; Si, Z.; Gao, F. Forced resonance orbit analysis of binary asteroid system with consideration of solar radiation pressure. Nonlinear Dyn. 2022, 109, 1399–1422. [Google Scholar] [CrossRef]
- Xiao, Y.; de Ruiter, A.; Ye, D.; Sun, Z. Attitude Coordination Control for Flexible Spacecraft Formation Flying with Guaranteed Performance Bounds. IEEE Trans. Aerosp. Electron. Syst. 2022. [Google Scholar] [CrossRef]
- Zhang, H.Z.; Ye, D.; Xiao, Y.; Sun, Z.W. Adaptive Control on SE (3) for Spacecraft Pose Tracking with Harmonic Disturbance and Input Saturation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4578–4594. [Google Scholar] [CrossRef]
- d’Angelo, P.; Kuschk, G.; Reinartz, P. Evaluation of Skybox Video and Still Image Products. In Proceedings of the ISPRS Technical Commission I Symposium, Denver, CO, USA, 17–20 November 2014; pp. 95–99. [Google Scholar]
- Jiang, L.; Yang, X.B. Study on Enlarging the Searching Scope of Staring Area and Tracking Imaging of Dynamic Targets by Optical Satellites. IEEE Sens. J. 2021, 21, 5349–5358. [Google Scholar] [CrossRef]
- Wang, J.; Yu, P.; Ya, C.; Ren, J.; He, B. Space Optical Remote Sensor Image Motion Velocity Vector Computational Modeling. Acta Opt. Sin. 2004, 24, 1585–1589. [Google Scholar]
- Lu, K.L.; Liu, E.H.; Zhao, R.J.; Tian, H.; Zhang, H. A Fast Star Identification Algorithm of Star Sensors in the LIS Mode. Remote Sens. 2022, 14, 1739. [Google Scholar] [CrossRef]
- Chen, X.D.; Xing, F.; You, Z.; Zhong, X.; Qi, K.H. On-Orbit High-Accuracy Geometric Calibration for Remote Sensing Camera Based on Star Sources Observation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5608211. [Google Scholar] [CrossRef]
- Haibo, L.I.U.; Dezhi, S.U.; Jichun, T.A.N.; Jiankun, Y.; Xiujian, L.I. An Approach to Star Image Simulation for Star Sensor Considering Satellite Orbit Motion and Effect of Image Shift. J. Chin. Soc. Astronaut. 2011, 32, 1190–1194. [Google Scholar]
- Wan, X.; Wang, G.; Wei, X.; Li, J.; Zhang, G. ODCC: A Dynamic Star Spots Extraction Method for Star Sensors. IEEE Trans. Instrum. Meas. 2021, 70, 3073716. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).