Dispersion-Oriented Inverse Design of Photonic-Crystal Fiber for Four-Wave Mixing Application
Abstract
1. Introduction
2. Principle of DNN-Based Inverse PCF Design for FWM
2.1. Principle of Phase-Matching in FWM
2.2. Empirical Formula of PCF Dispersion
2.3. The Calculation of Effective Modal Area
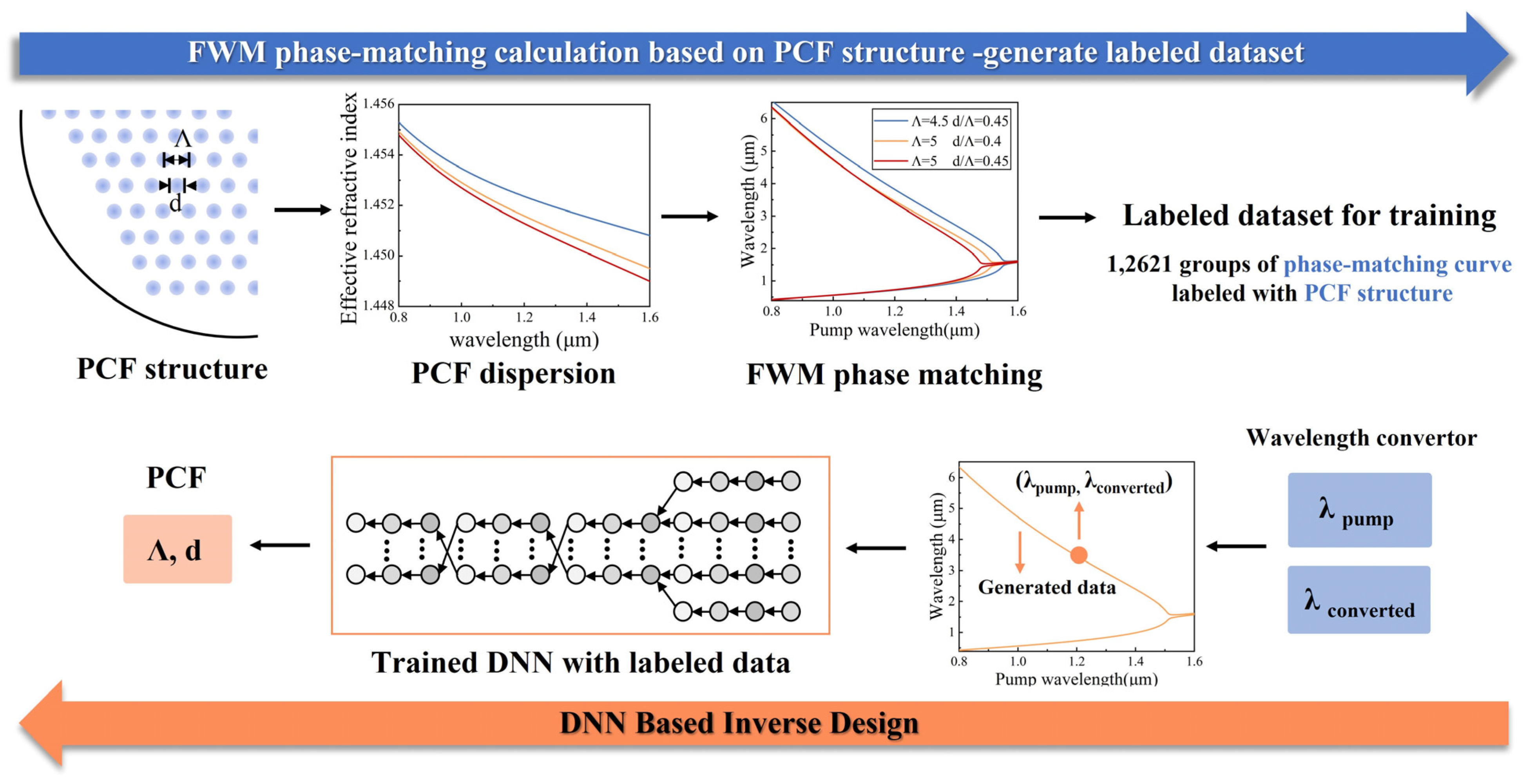
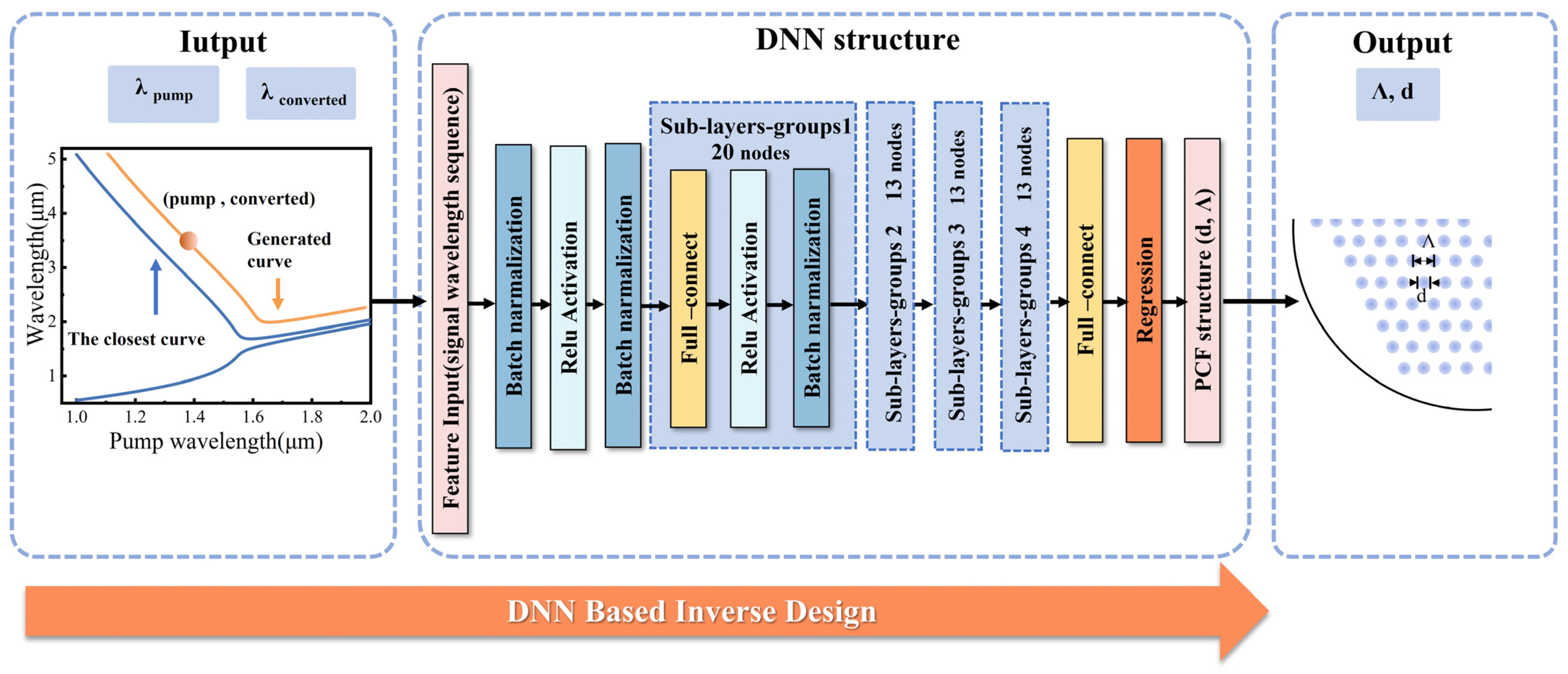
2.4. Inverse Design Based on Deep Learning Neural Network
2.4.1. Data Preparation for the DNN Model
2.4.2. Implementation of the DNN Algorithm
3. Results
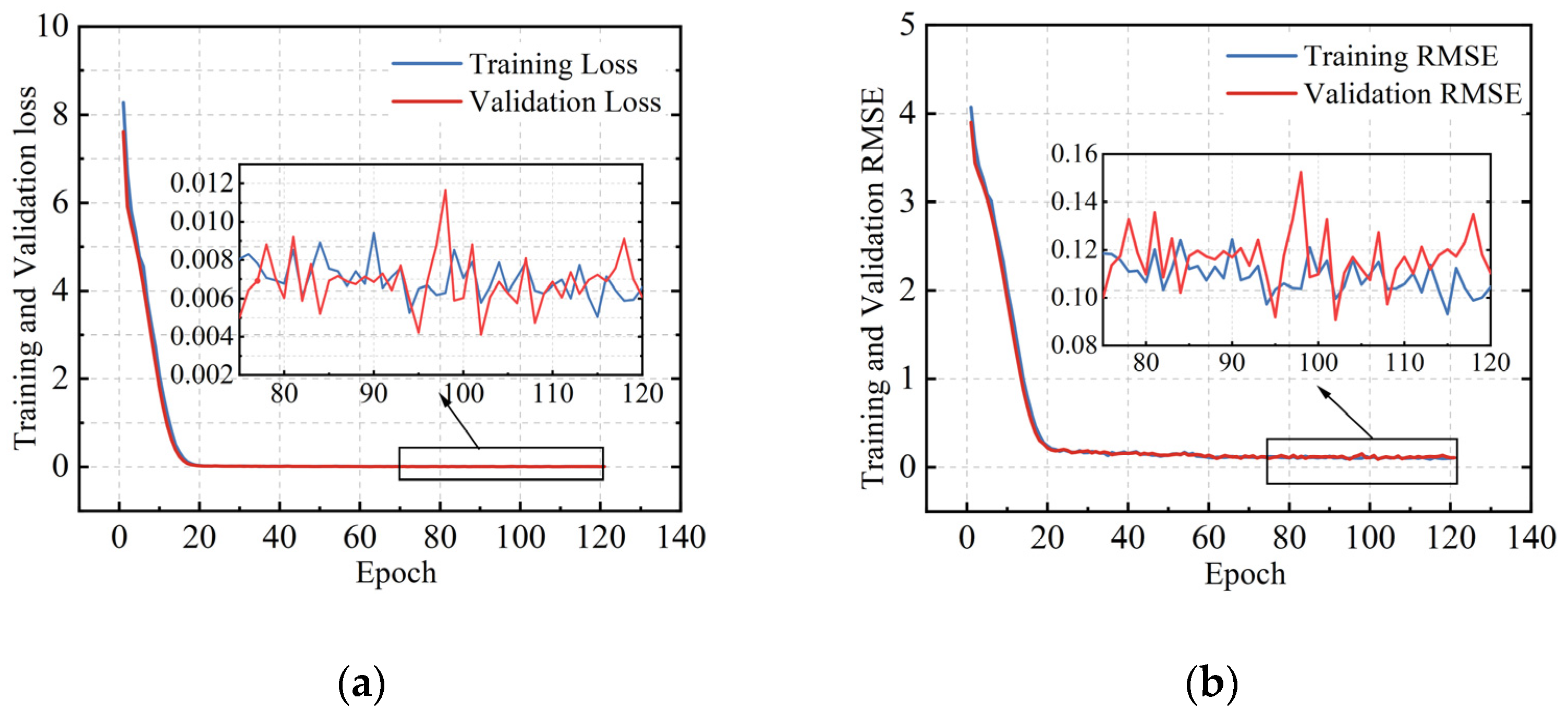
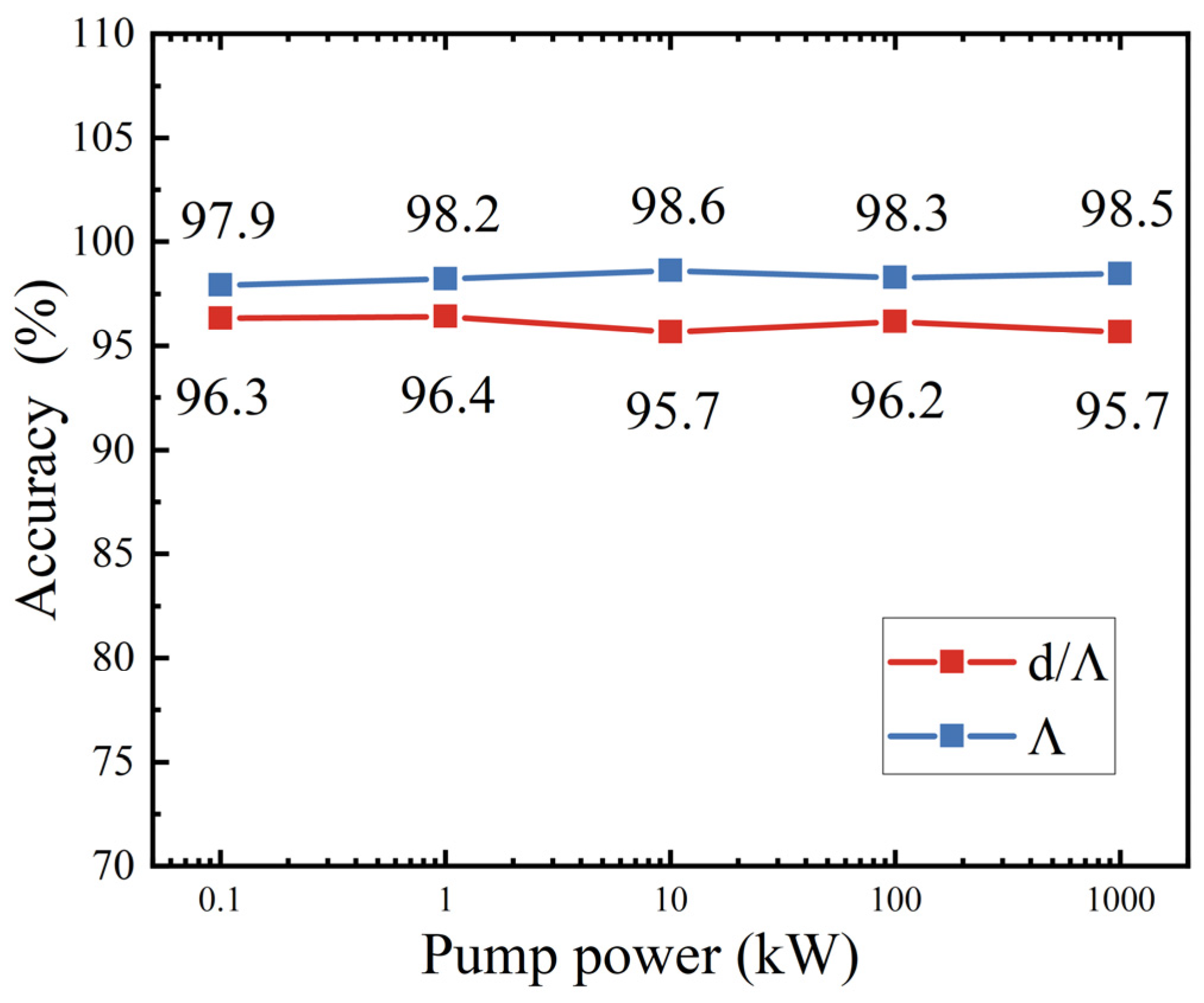
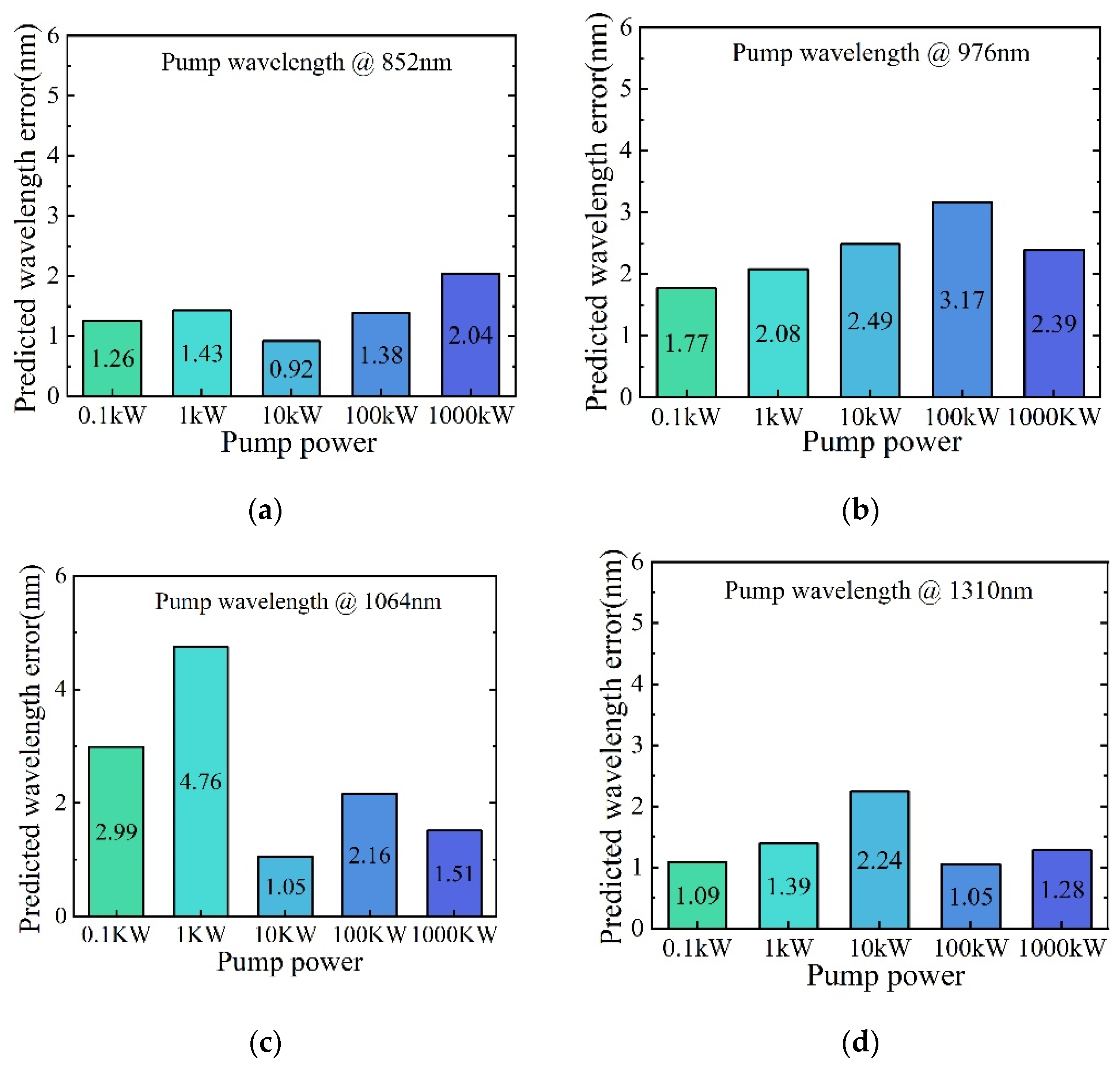
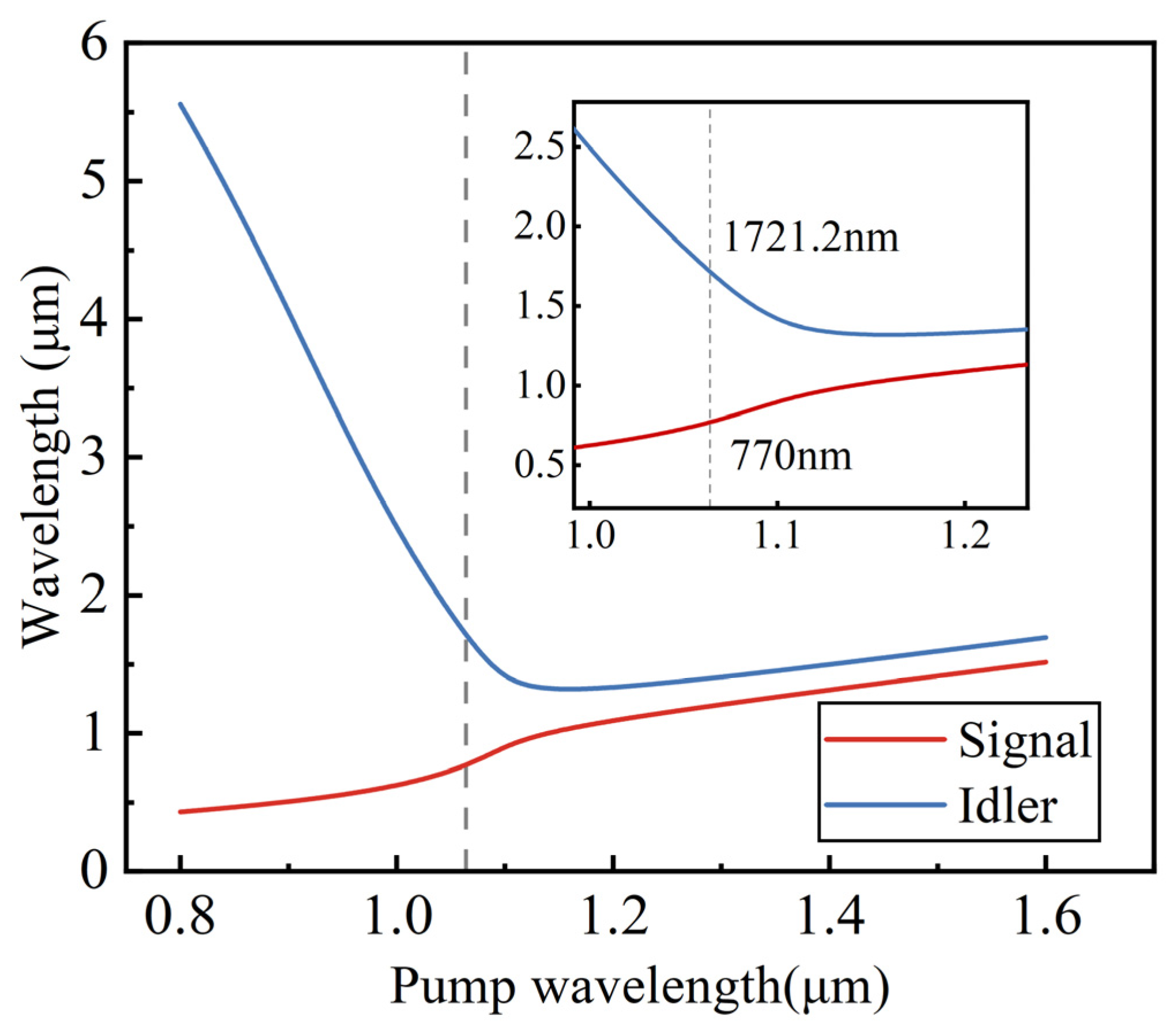
3.1. Evaluation of Trained DNN for FWM
3.2. Experimental Demonstration
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wadsworth, W.J.; Joly, N.; Knight, J.C.; Birks, T.A.; Biancalana, F.; Russell, P.S.J. Supercontinuum and Four-Wave Mixing with Q-Switched Pulses in Endlessly Single-Mode Photonic Crystal Fibres. Opt. Express 2004, 12, 299. [Google Scholar] [CrossRef] [PubMed]
- Saitoh, K.; Koshiba, M. Empirical Relations for Simple Design of Photonic Crystal Fibers. Opt. Express 2005, 13, 267. [Google Scholar] [CrossRef] [PubMed]
- Abdelaziz, I.; AbdelMalek, F.; Haxha, S.; Ademgil, H.; Bouchriha, H. Photonic Crystal Fiber With an Ultrahigh Birefringence and Flattened Dispersion by Using Genetic Algorithms. J. Light. Technol. 2013, 31, 343–348. [Google Scholar] [CrossRef]
- Knight, J.C.; Arriaga, J.; Birks, T.A.; Ortigosa-Blanch, A.; Wadsworth, W.J.; Russell, P.S.J. Anomalous Dispersion in Photonic Crystal Fiber. IEEE Photonics Technol. Lett. 2000, 12, 807–809. [Google Scholar] [CrossRef]
- Wang, D.; Yi, Z.; Ma, G.; Dai, B.; Yang, J.; Zhang, J.; Yu, Y.; Liu, C.; Wu, X.; Bian, Q. Two-Channel Photonic Crystal Fiber Based on Surface Plasmon Resonance for Magnetic Field and Temperature Dual-Parameter Sensing. Phys. Chem. Chem. Phys. 2022, 24, 21233–21241. [Google Scholar] [CrossRef]
- Wang, D.; Zhu, W.; Yi, Z.; Ma, G.; Gao, X.; Dai, B.; Yu, Y.; Zhou, G.; Wu, P.; Liu, C. Highly Sensitive Sensing of a Magnetic Field and Temperature Based on Two Open Ring Channels SPR-PCF. Opt. Express 2022, 30, 39055–39067. [Google Scholar] [CrossRef]
- Garay-Palmett, K.; McGuinness, H.J.; Cohen, O.; Lundeen, J.S.; Rangel-Rojo, R.; U’Ren, A.B.; Raymer, M.G.; McKinstrie, C.J.; Radic, S.; Walmsley, I.A. Photon Pair-State Preparation with Tailored Spectral Properties by Spontaneous Four-Wave Mixing in Photonic-Crystal Fiber. Opt. Express 2007, 15, 14870–14886. [Google Scholar] [CrossRef]
- Reeves, W.H.; Skryabin, D.V.; Biancalana, F.; Knight, J.C.; Russell, P.S.J.; Omenetto, F.G.; Efimov, A.; Taylor, A.J. Transformation and Control of Ultra-Short Pulses in Dispersion-Engineered Photonic Crystal Fibres. Nature 2003, 424, 511–515. [Google Scholar] [CrossRef]
- Chen, Y.; Wadsworth, W.J.; Birks, T.A. Ultraviolet Four-Wave Mixing in the LP_02 Fiber Mode. Opt. Lett. 2013, 38, 3747. [Google Scholar] [CrossRef]
- Ahmedou, S.-E.; Dauliat, R.; Février, S.; Walter, G.; Delagnes, J.-C.; Labonte, L.; Tanzilli, S.; Gérôme, F.; Debord, B.; Benabid, F.; et al. Dispersion Engineered Tapered Photonic Crystal Fiber for Broadband and Tuned 2 Μm Emission Using Degenerate Four-Wave Mixing. In Proceedings of the Optica Advanced Photonics Congress 2022 (2022), Maastricht, The Netherlands, 24 July 2022; Optica Publishing Group: Washington, DC, USA, 2022; p. SoW5G.5. [Google Scholar]
- Jiang, R.; Saperstein, R.; Alic, N.; Nezhad, M.; McKinstrie, C.; Ford, J.; Fainman, Y.; Radic, S. 375 THz Parametric Translation of Modulated Signal from 1550 nm to Visible Band. In Proceedings of the 2006 Optical Fiber Communication Conference, and the 2006 National Fiber Optic Engineers Conference, Anaheim, CA, USA, 5–10 March 2006. [Google Scholar] [CrossRef]
- Andrekson, P.A.; Hansryd, J. Fiber-Based Optical Parametric Amplifiers and Their Applications. Eur. Conf. Opt. Commun. 2002, 2, 506–520. [Google Scholar]
- Yuan, J.; Zhou, G.; Xia, C.; Sang, X.; Li, F.; Yu, C.; Wang, K.; Yan, B.; Tam, H.Y.; Wai, P.K.A. Degenerate Four-Wave Mixing-Based Light Source for CARS Microspectroscopy. IEEE Photonics Technol. Lett. 2016, 28, 763–766. [Google Scholar] [CrossRef]
- Hameed, M.F.O.; Hassan, A.S.O.; Elqenawy, A.E.; Obayya, S.S.A. Modified Trust Region Algorithm for Dispersion Optimization of Photonic Crystal Fibers. J. Light. Technol. 2017, 35, 3810–3818. [Google Scholar] [CrossRef]
- Wang, N.; Yan, W.; Qu, Y.; Ma, S.; Li, S.Z.; Qiu, M. Intelligent Designs in Nanophotonics: From Optimization towards Inverse Creation. PhotoniX 2021, 2, 22. [Google Scholar] [CrossRef]
- Liu, C.; Maier, S.; Li, G. Genetic-Algorithm-Aided Meta-Atom Multiplication for Improved Absorption and Coloration in Nanophotonics. ACS Photonics 2020, 7, 1716–1722. [Google Scholar] [CrossRef]
- Mirjalili, S.M.; Abedi, K.; Mirjalili, S. Optical Buffer Performance Enhancement Using Particle Swarm Optimization in Ring-Shape-Hole Photonic Crystal Waveguide. Optik 2013, 124, 5989–5993. [Google Scholar] [CrossRef]
- Zhao, R.; Wei, Y.; Xu, H.; He, X. Process optimization of contact hole patterns via a simulated annealing algorithm in extreme ultraviolet lithography. Appl. Opt. 2023, 62, 927–932. [Google Scholar] [CrossRef]
- Poletti, F.; Finazzi, V.; Monro, T.M.; Broderick, N.G.R.; Tse, V.; Richardson, D.J. Inverse design and fabrication tolerances of ultra-flattened dispersion holey fibers. Opt. Express 2005, 13, 3728–3736. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, F.; Hu, L. Inverse Design of Equivalent-Graded-Index Photonic-Crystal Fiber Based on Empirical Dispersion Formula. J. Light. Technol. 2021, 39, 5598–5603. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, H.; Dong, S.; Wang, F.; Situ, G. Incoherent Imaging through Highly Nonstatic and Optically Thick Turbid Media Based on Neural Network. Photonics Res. 2021, 9, B220. [Google Scholar] [CrossRef]
- Information, E. Multi-Task Deep Neural Network (MT-DNN) Enabled Optical Performance Monitoring from Directly Detected PDM-QAM Signals. Opt. Express 2019, 27, 19062–19074. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Milam, D.; Weber, M.J.; Glass, A.J. Nonlinear refractive index of fluoride crystals. Appl. Phys. Lett. 1977, 31, 822–825. [Google Scholar] [CrossRef]
- Fletcher, R.; Reeves, C.M. Function Minimization by Conjugate Gradients. Comput. J. 1964, 7, 149–154. [Google Scholar] [CrossRef]
- Gan, L. Dispersion-Oriented Inverse Design of Photonic-Crystal Fiber for Four-Wave Mixing Application. Sci. Data Bank 2023. [Google Scholar] [CrossRef]
- Karanov, B.; Chagnon, M.; Thouin, F.; Eriksson, T.A.; Bulow, H.; Lavery, D.; Bayvel, P.; Schmalen, L. End-to-End Deep Learning of Optical Fiber Communications. J. Light. Technol. 2018, 36, 4843–4855. [Google Scholar] [CrossRef]
- Juvekar, V.; Su Lim, C.; Joon Lee, D.; Jun Park, S.; Ok Song, G.; Kang, H.; Myung Kim, H. An Azo Dye for Photodynamic Therapy That Is Activated Selectively by Two-Photon Excitation. Chem. Sci. 2021, 12, 427–434. [Google Scholar] [CrossRef]
- Xu, H.; Wu, J.; Dai, Y.; Xu, C.; Lin, J. Design Procedure for Photonic Crystal Fibers with Ultra-Flattened Chromatic Dispersion. Chin. Opt. Lett. 2011, 9, 050603. [Google Scholar] [CrossRef]
- Stepniewski, G.; Kasztelanic, R.; Pysz, D.; Stepien, R.; Klimczak, M.; Buczynski, R. Temperature Sensitivity of Chromatic Dispersion in Nonlinear Silica and Heavy Metal Oxide Glass Photonic Crystal Fibers. Opt. Mater. Express 2016, 6, 2689. [Google Scholar] [CrossRef]


| i = 1 | i = 2 | i = 3 | i = 4 | i = 1 | i = 2 | i = 3 | i = 4 | ||
|---|---|---|---|---|---|---|---|---|---|
| −0.4783 | −0.0511 | −0.0192 | 2.6930 | 0.0259 | 1.6916 | −0.0082 | 1.4322 | ||
| 1.3702 | −0.53310 | 0.1690 | 7.2702 | −4.0257 | −0.0675 | 0.0101 | −3.0778 | ||
| 2.9490 | 0.3114 | 0.4532 | 6.1010 | −1.1083 | 1.8010 | −1.0497 | −0.5835 | ||
| 0.6149 | 2.0477 | 0.7288 | −0.2080 | 1.4085 | −0.2888 | −4.7 × 10−5 | −1.2964 | ||
| −0.3761 | −1.1588 | −4.1604 | 3.2312 | −1.2357 | 1.0219 | −0.0242 | 1.7864 | ||
| 1.4081 | 1.5846 | 0.6462 | −2.4868 | 0.6089 | −1.7010 | 51.7550 | 0.8151 | ||
| 1.1698 | −2.3328 | 2.8651 | 0.6660 | −0.8973 | 0.8085 | 4.3971 | 0.5550 |
| PTEST | PDNN | PTEST | PDNN | |||||
|---|---|---|---|---|---|---|---|---|
| d/Λ | Λ (μm) | d/Λ | Λ (μm) | d/Λ | Λ (μm) | d/Λ | Λ (μm) | |
| 0.1 kW | 0.33 | 3.095 | 0.33 | 3.071 | 0.26 | 2.875 | 0.26 | 2.812 |
| 0.28 | 3.655 | 0.29 | 3.589 | 0.39 | 4.51 | 0.39 | 4.459 | |
| 0.27 | 4.110 | 0.28 | 4.041 | 0.38 | 2.400 | 0.381 | 2.411 | |
| 1 kW | 0.37 | 2.545 | 0.37 | 2.553 | 0.32 | 3.870 | 0.33 | 3.908 |
| 0.33 | 3.095 | 0.34 | 3.109 | 0.36 | 3.855 | 0.36 | 3.891 | |
| 0.32 | 4.475 | 0.33 | 4.516 | 0.27 | 4.335 | 0.27 | 4.375 | |
| 10 kW | 0.27 | 4.335 | 0.27 | 4.360 | 0.40 | 4.535 | 0.41 | 4.529 |
| 0.33 | 3.095 | 0.33 | 3.076 | 0.29 | 3.680 | 0.29 | 3.695 | |
| 0.29 | 4.780 | 0.29 | 4.767 | 0.32 | 3.730 | 0.32 | 3.791 | |
| 100 kW | 0.32 | 3.870 | 0.328 | 3.871 | 0.320 | 4.475 | 0.322 | 4.491 |
| 0.36 | 3.855 | 0.361 | 3.878 | 0.400 | 4.535 | 0.402 | 4.594 | |
| 0.37 | 2.545 | 0.33 | 3.095 | 0.371 | 2.595 | 0.333 | 3.105 | |
| 1000 kW | 0.28 | 3.63 | 0.28 | 3.646 | 0.36 | 3.855 | 0.36 | 3.967 |
| 0.34 | 4.705 | 0.35 | 4.772 | 0.32 | 4.475 | 0.33 | 4.586 | |
| 0.39 | 4.125 | 0.39 | 4.156 | 0.3 | 2.095 | 0.31 | 2.105 | |
| ZDW (nm) | PCF Λ (μm) | PCF d/Λ | Signal (nm) | Idler (nm) | ||||
|---|---|---|---|---|---|---|---|---|
| 1140 | DNN | Fab. | DNN | Fab. | Tar. | Exp. | Tar. | Exp. |
| 3.93 | 3.82 | 0.37 | 0.41 | 770 | 770.2 | 1721.2 | 1724.9 | |
| Signal (nm) | Idler (nm) | Signal (nm) | Idler (nm) | ||
|---|---|---|---|---|---|
| 30 °C | 770.9 | 1725.0 | 70 °C | 767.3 | 1734.2 |
| 40 °C | 769.3 | 1728.1 | 80 °C | 765.6 | 1738.7 |
| 50 °C | 768.1 | 1725.5 | 90 °C | 765.8 | 1741.5 |
| 60 °C | 767.4 | 1733.2 | 100 °C | 762.2 | 1737.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, L.; Yu, F.; Wang, Y.; Wang, N.; Zhu, X.; Hu, L.; Yu, C. Dispersion-Oriented Inverse Design of Photonic-Crystal Fiber for Four-Wave Mixing Application. Photonics 2023, 10, 294. https://doi.org/10.3390/photonics10030294
Gan L, Yu F, Wang Y, Wang N, Zhu X, Hu L, Yu C. Dispersion-Oriented Inverse Design of Photonic-Crystal Fiber for Four-Wave Mixing Application. Photonics. 2023; 10(3):294. https://doi.org/10.3390/photonics10030294
Chicago/Turabian StyleGan, Linqiao, Fei Yu, Yazhou Wang, Ning Wang, Xinyue Zhu, Lili Hu, and Chunlei Yu. 2023. "Dispersion-Oriented Inverse Design of Photonic-Crystal Fiber for Four-Wave Mixing Application" Photonics 10, no. 3: 294. https://doi.org/10.3390/photonics10030294
APA StyleGan, L., Yu, F., Wang, Y., Wang, N., Zhu, X., Hu, L., & Yu, C. (2023). Dispersion-Oriented Inverse Design of Photonic-Crystal Fiber for Four-Wave Mixing Application. Photonics, 10(3), 294. https://doi.org/10.3390/photonics10030294






