Simulation and Design of a PIC-Based Heterodyne Optical Phase Locked Loop
Abstract
:1. Introduction
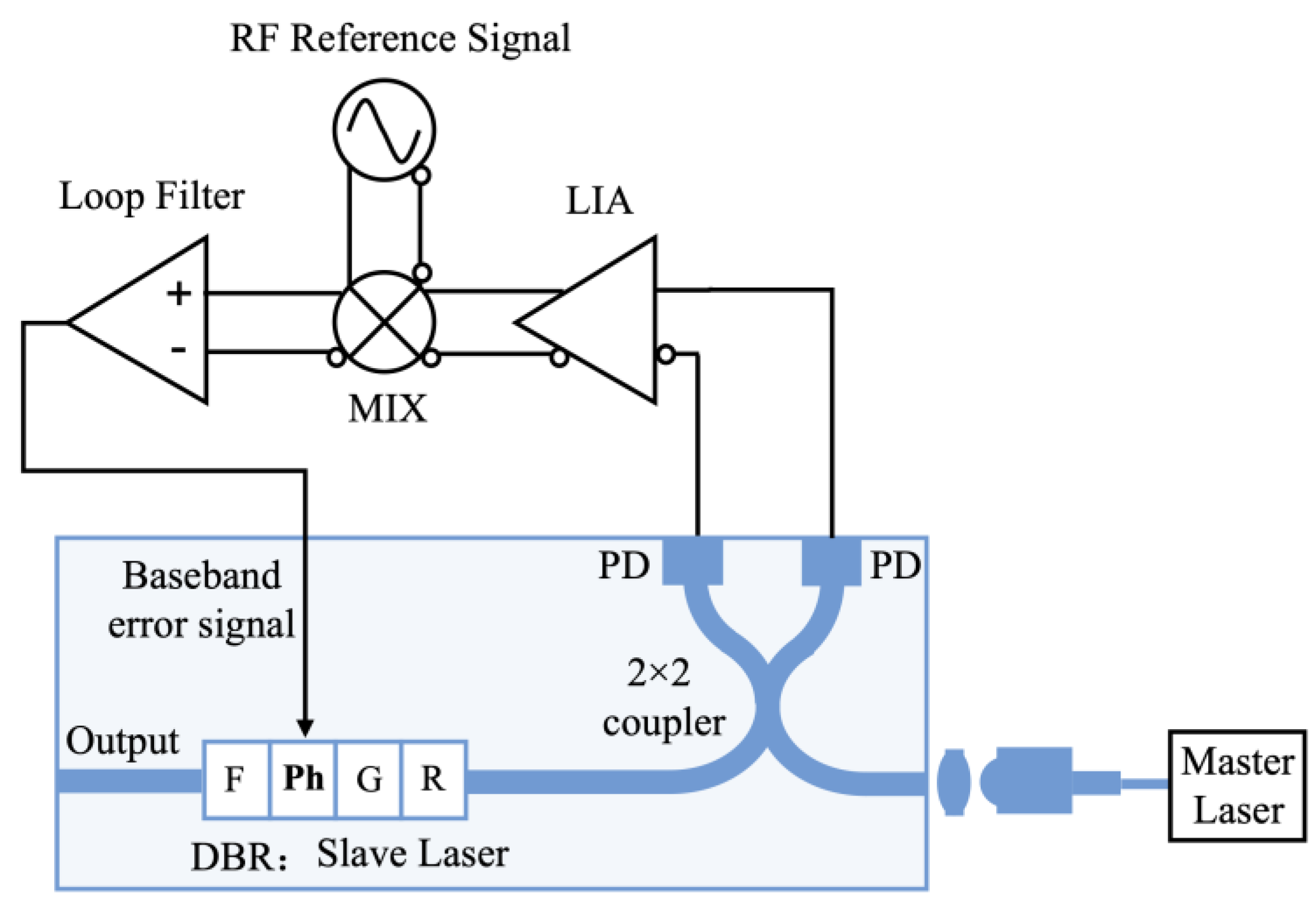
2. Models and Simulations
2.1. Loop Frequency-Domain Model
2.2. Loop Maximum Load Capacity Model
2.3. Loop Phase Noise Model
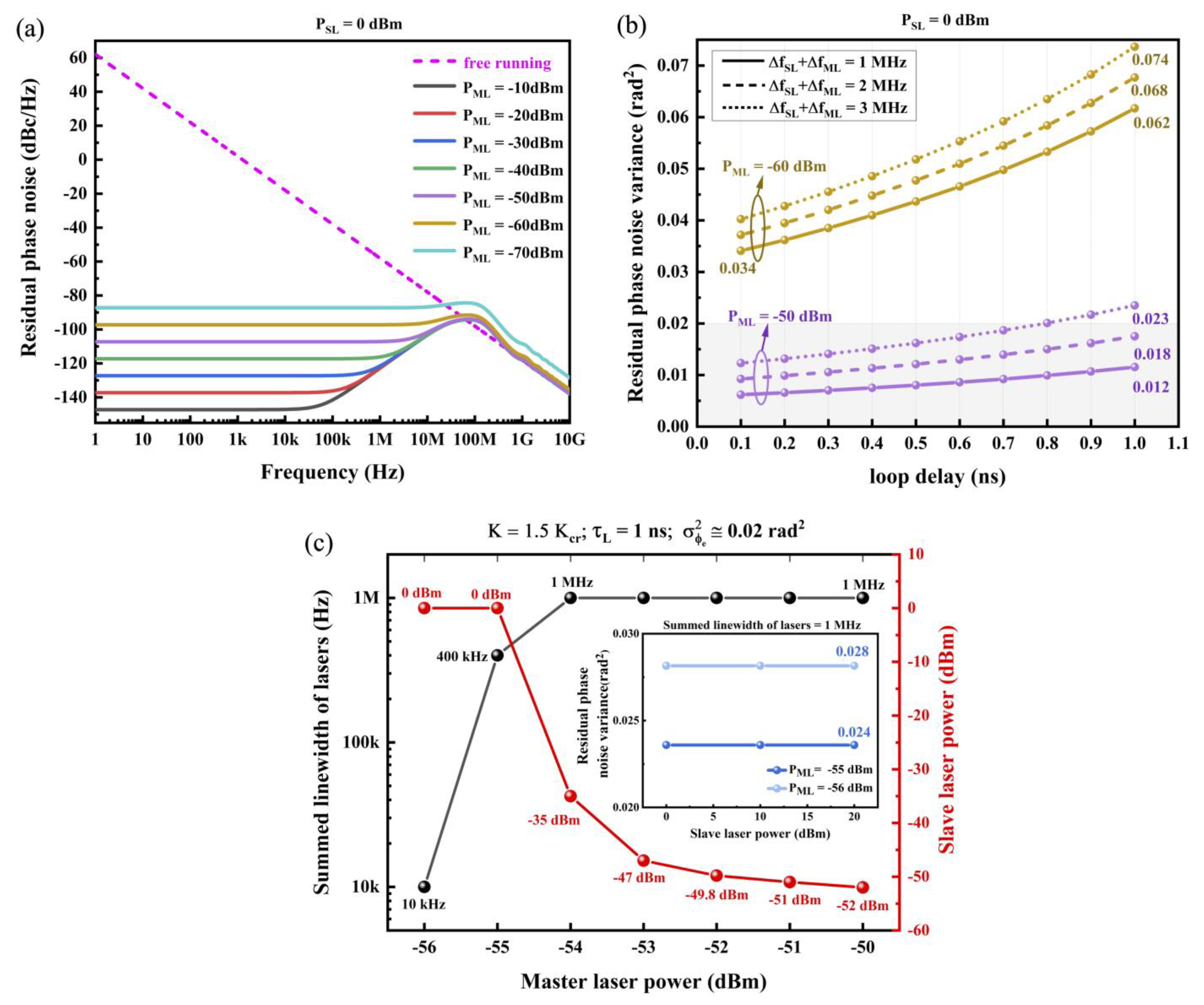
3. Results and Discussion
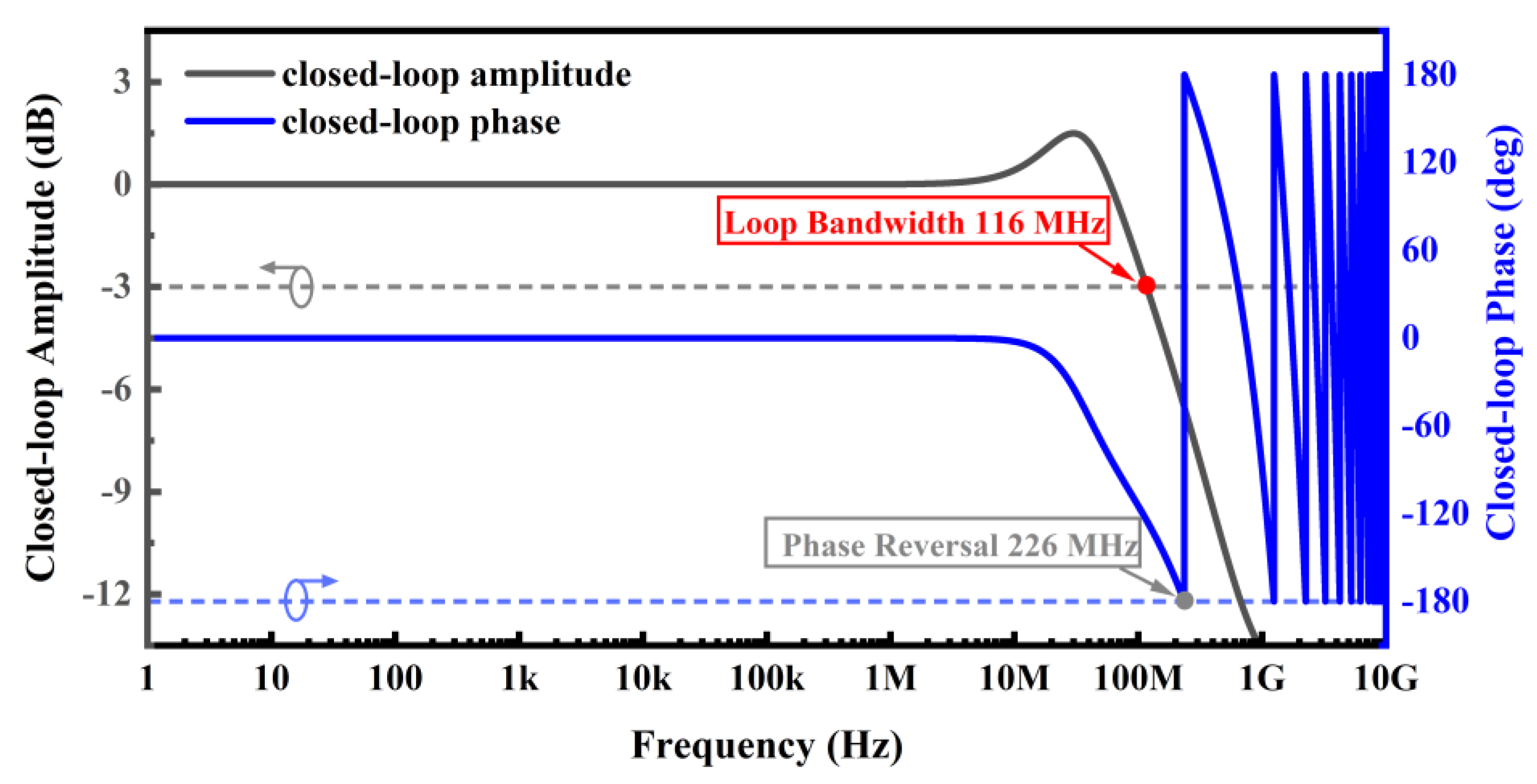
3.1. Loop Stability Analysis
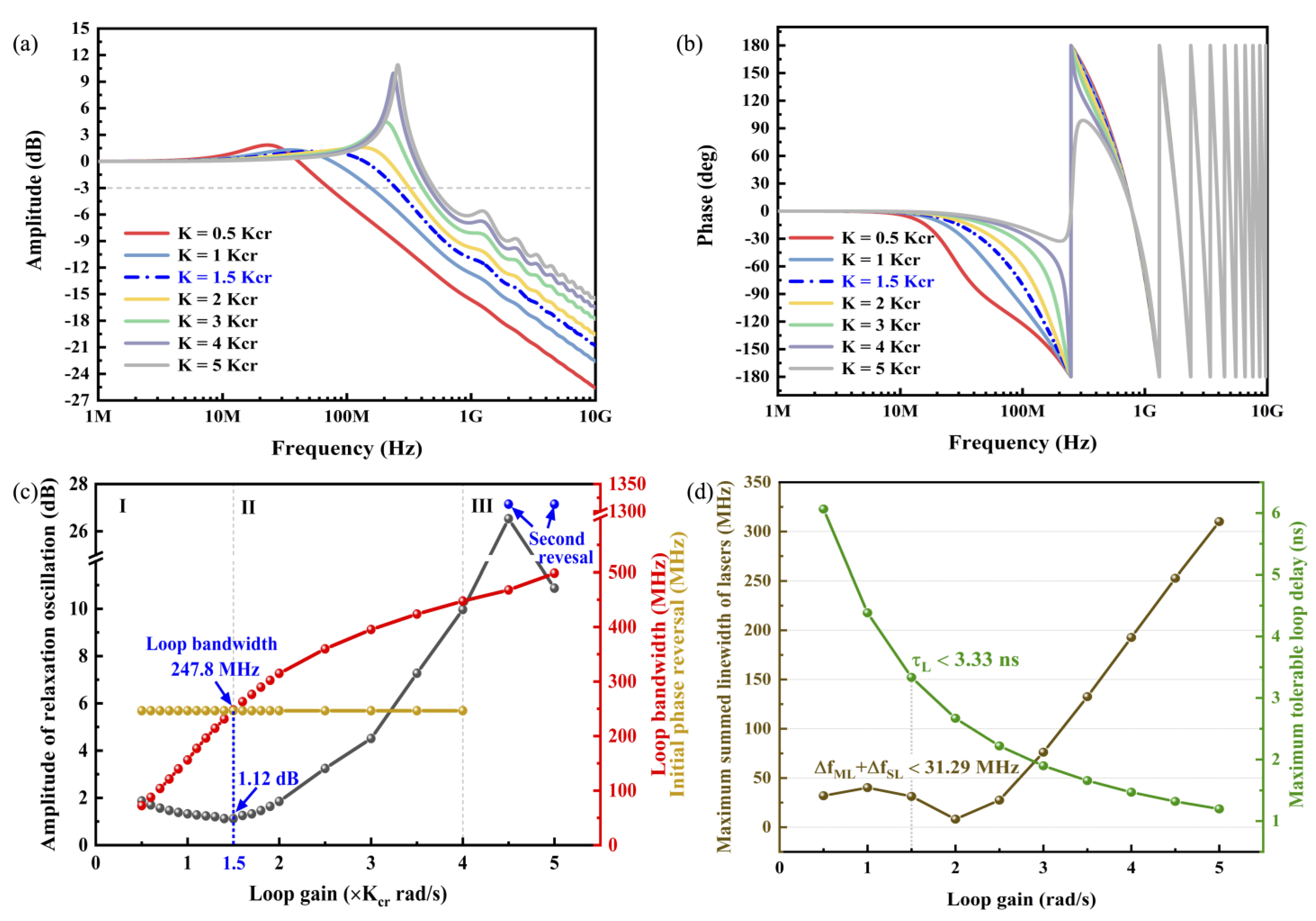
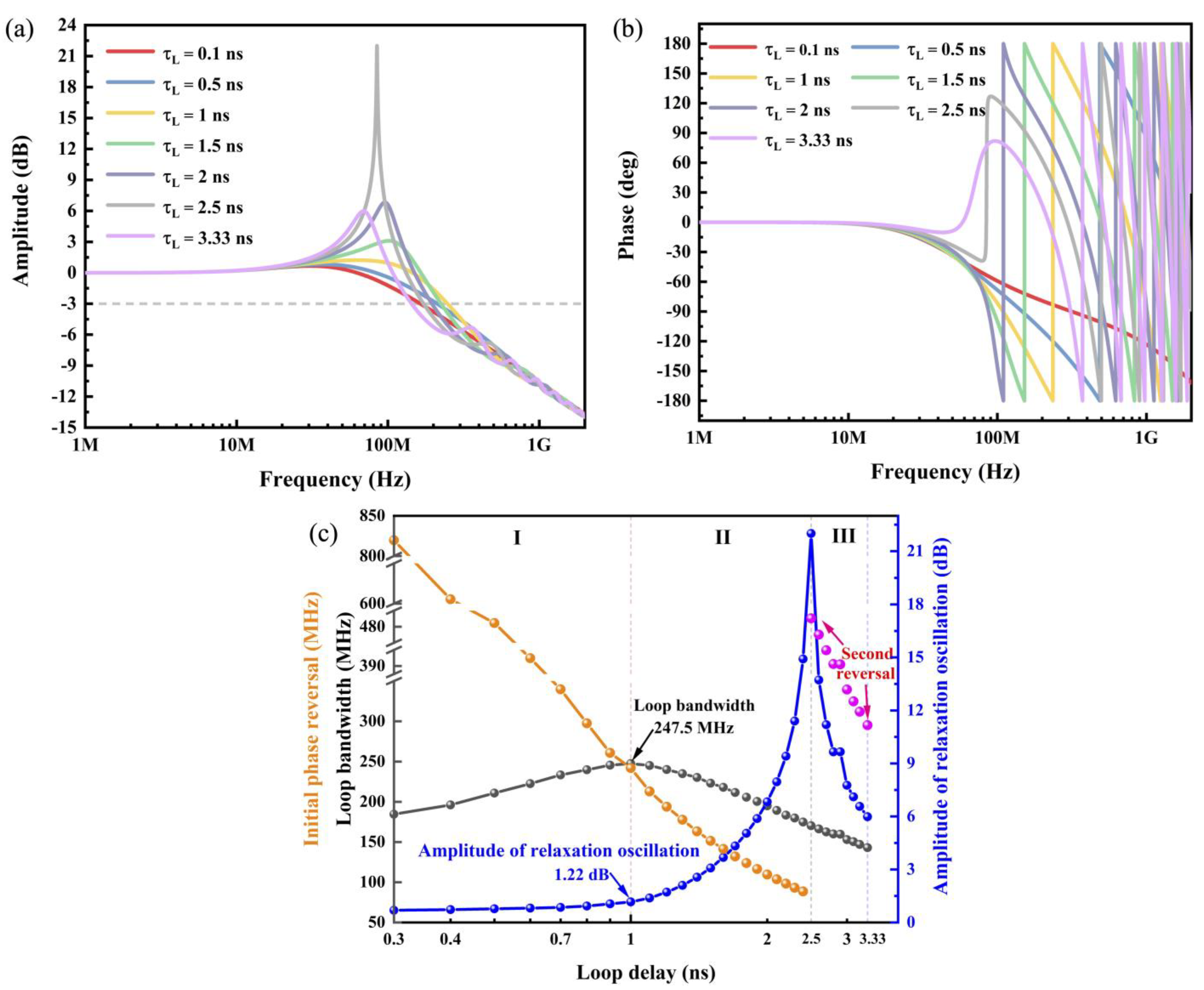
3.2. Loop Bandwidth Characteristics
3.3. Loop Phase Noise Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lezius, M.; Wilken, T.; Deutsch, C.; Giunta, M.; Mandel, O.; Thaller, A.; Schkolnik, V.; Schiemangk, M.; Dinkelaker, A.; Kohfeldt, A.; et al. Space-Borne Frequency Comb Metrology. Optica 2016, 3, 1381. [Google Scholar] [CrossRef]
- Capmany, J.; Munoz, P. Integrated Microwave Photonics for Radio Access Networks. J. Light. Technol. 2014, 32, 2849–2861. [Google Scholar] [CrossRef]
- Cygan, A.; Lisak, D.; Morzyński, P.; Bober, M.; Zawada, M.; Pazderski, E.; Ciuryło, R. Cavity Mode-Width Spectroscopy with Widely Tunable Ultra Narrow Laser. Opt. Express 2013, 21, 29744. [Google Scholar] [CrossRef] [PubMed]
- Capmany, J.; Novak, D. Microwave Photonics Combines Two Worlds. Nat. Photon 2007, 1, 319–330. [Google Scholar] [CrossRef]
- Wang, G.; Jang, Y.-S.; Hyun, S.; Chun, B.J.; Kang, H.J.; Yan, S.; Kim, S.-W.; Kim, Y.-J. Absolute Positioning by Multi-Wavelength Interferometry Referenced to the Frequency Comb of a Femtosecond Laser. Opt. Express 2015, 23, 9121. [Google Scholar] [CrossRef] [Green Version]
- Schnatz, H.; Terra, O.; Predehl, K.; Feldmann, T.; Legero, T.; Lipphardt, B.; Sterr, U.; Grosche, G.; Holzwarth, R.; Hansch, T.W.; et al. Phase-Coherent Frequency Comparison of Optical Clocks Using a Telecommunication Fiber Link. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2010, 57, 175–181. [Google Scholar] [CrossRef]
- Langley, L.N.; Elkin, M.D.; Edge, C.; Wale, M.J.; Gliese, U.; Huang, X.; Seeds, A.J. Packaged Semiconductor Laser Optical Phase-Locked Loop (OPLL) for Photonic Generation, Processing and Transmission of Microwave Signals. IEEE Trans. Microw. Theory Techn. 1999, 47, 1257–1264. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Jin, S.; Ding, D.; Li, Y. Monolithically Integrated Virtual Balanced ACP-OPLL for PM RF Photonic Links. J. Light. Technol. 2018, 36, 789–796. [Google Scholar] [CrossRef]
- Steed, R.J.; Ponnampalam, L.; Fice, M.J.; Renaud, C.C.; Rogers, D.C.; Moodie, D.G.; Maxwell, G.D.; Lealman, I.F.; Robertson, M.J.; Pavlovic, L.; et al. Hybrid Integrated Optical Phase-Lock Loops for Photonic Terahertz Sources. IEEE J. Select. Top. Quantum Electron. 2011, 17, 210–217. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Jin, S.; Rodriguez, J.; Sun, T.; Herczfeld, P. Wideband OPLL Photonic Integrated Circuit Enabling Ultrahigh Dynamic Range PM RF/Photonic Link. Optica 2019, 6, 1078. [Google Scholar] [CrossRef]
- Ristic, S.; Bhardwaj, A.; Rodwell, M.J.; Coldren, L.A.; Johansson, L.A. An Optical Phase-Locked Loop Photonic Integrated Circuit. J. Light. Technol. 2010, 28, 526–538. [Google Scholar] [CrossRef]
- Satyan, N.; Liang, W.; Kewitsch, A.; Rakuljic, G.; Yariv, A. Coherent Power Combination of Semiconductor Lasers Using Optical Phase-Lock Loops. IEEE J. Select. Top. Quantum Electron. 2009, 15, 240–247. [Google Scholar] [CrossRef] [Green Version]
- Bałakier, K.; Fice, M.J.; Ponnampalam, L.; Graham, C.S.; Wonfor, A.; Seeds, A.J.; Renaud, C.C. Foundry Fabricated Photonic Integrated Circuit Optical Phase Lock Loop. Opt. Express 2017, 25, 16888. [Google Scholar] [CrossRef] [PubMed]
- Steed, R.J.; Pozzi, F.; Fice, M.J.; Renaud, C.C.; Rogers, D.C.; Lealman, I.F.; Moodie, D.G.; Cannard, P.J.; Lynch, C.; Johnston, L.; et al. Monolithically Integrated Heterodyne Optical Phase-Lock Loop with RF XOR Phase Detector. Opt. Express 2011, 19, 20048. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Satyan, N. Phase Noise Reduction of a Semiconductor Laser in a Composite Optical Phase-Locked Loop. Opt. Eng 2010, 49, 124301. [Google Scholar] [CrossRef] [Green Version]
- Imajuku, W.; Takada, A. In-Line Optical Phase-Sensitive Amplifier with Pump Light Source Controlled by Optical Phase-Lock Loop. J. Light. Technol. 1999, 17, 637–646. [Google Scholar] [CrossRef]
- Lu, M.; Park, H.; Bloch, E.; Sivananthan, A.; Bhardwaj, A.; Griffith, Z.; Johansson, L.A.; Rodwell, M.J.; Coldren, L.A. Highly Integrated Optical Heterodyne Phase-Locked Loop with Phase/Frequency Detection. Opt. Express 2012, 20, 9736. [Google Scholar] [CrossRef]
- Ponnampalam, L.; Fice, M.J.; Pozzi, F.; Renaud, C.C.; Rogers, D.C.; Lealman, I.F.; Moodie, D.G.; Cannard, P.J.; Lynch, C.; Johnston, L.; et al. Monolithically Integrated Photonic Heterodyne System. J. Light. Technol. 2011, 29, 2229–2234. [Google Scholar] [CrossRef]
- Arafin, S.; Simsek, A.; Kim, S.-K.; Dwivedi, S.; Liang, W.; Eliyahu, D.; Klamkin, J.; Matsko, A.; Johansson, L.; Maleki, L.; et al. Towards Chip-Scale Optical Frequency Synthesis Based on Optical Heterodyne Phase-Locked Loop. Opt. Express 2017, 25, 681. [Google Scholar] [CrossRef]
- Balakier, K.; Fice, M.J.; Ponnampalam, L.; Seeds, A.J.; Renaud, C.C. Monolithically Integrated Optical Phase Lock Loop for Microwave Photonics. J. Light. Technol. 2014, 32, 3893–3900. [Google Scholar] [CrossRef]
- Gliese, U.; Nielsen, T.N.; Bruun, M.; Lintz Christensen, E.; Stubkjaer, K.E.; Lindgren, S.; Broberg, B. A Wideband Heterodyne Optical Phase-Locked Loop for Generation of 3-18 GHz Microwave Carriers. IEEE Photon. Technol. Lett. 1992, 4, 936–938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grant, M.; Michie, W.; Fletcher, M. The Performance of Optical Phase-Locked Loops in the Presence of Nonnegligible Loop Propagation Delay. J. Light. Technol. 1987, 5, 592–597. [Google Scholar] [CrossRef]
- Tang, L.; Yang, S.; Chen, H.; Chen, M. Hybrid Integrated Low Noise Optical Phase-Locked Loop Based on Self-Injection Locked Semiconductor Laser. J. Light. Technol. 2022, 40, 2033–2039. [Google Scholar] [CrossRef]
- Herzog, F.; Kudielka, K.; Erni, D.; Bachtold, W. Optical Phase Locking by Local Oscillator Phase Dithering. IEEE J. Quantum Electron. 2006, 42, 973–985. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, X.; Wu, R.; Sun, Y.; Wei, F.; Yang, F.; Gui, Y.; Cai, H. High-Gain Optical Injection Locking Amplifier in Phase-Coherent Optical Frequency Transmission. IEEE Photonics J. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- Ramos, R.T.; Seeds, A.J. Delay, Linewidth and Bandwidth Limitations in Optical Phase-Locked Loop Design. Electron. Lett. 1990, 26, 389. [Google Scholar] [CrossRef]
- Ramos, R.T.; Seeds, A.J. Comparison between First-Order and Second-Order Optical Phase-Lock Loops. IEEE Microw. Guid. Wave Lett. 1994, 4, 6–8. [Google Scholar] [CrossRef]
- Balakier, K.; Ponnampalam, L.; Fice, M.J.; Renaud, C.C.; Seeds, A.J. Integrated Semiconductor Laser Optical Phase Lock Loops. IEEE J. Select. Top. Quantum Electron. 2018, 24, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Gardner, F.M. Phaselock Techniques; Wiley: Hoboken, NJ, USA, 2005; pp. 282–335. [Google Scholar]
- Bordonalli, A.C.; Walton, C.; Seeds, A.J. High-Performance Phase Locking of Wide Linewidth Semiconductor Lasers by Combined Use of Optical Injection Locking and Optical Phase-Lock Loop. J. Light. Technol. 1999, 17, 328–342. [Google Scholar] [CrossRef] [Green Version]
- Best, R.E. Phase-Locked Loops: Design, Simulation, and Applications; McGraw-Hill Education: New York, NY, USA, 2007; pp. 67–70. [Google Scholar]
- Arafin, S.; Simsek, A.; Lu, M.; Rodwell, M.J.; Coldren, L.A. Heterodyne Locking of a Fully Integrated Optical Phase-Locked Loop with on-Chip Modulators. Opt. Lett. 2017, 42, 3745. [Google Scholar] [CrossRef]



| OPLL | Parameters | Symbol | Value | Units |
|---|---|---|---|---|
| optical path | ML linewidth | 100 | kHz | |
| ML initial power | −10 | dBm | ||
| SL initial linewidth | 10 | MHz | ||
| SL phase tuning sensitivity | 2.496 | GHz/A | ||
| SL initial power | 0 | dBm | ||
| RF reference signal power | 6.98 | dBm | ||
| PD responsivity | 0.85 | A/W | ||
| electrical path | LIA gain | 100 | - | |
| MIX gain | 10 | - | ||
| loop filter gain | 10 | - | ||
| loop filter time constant | 7.49 | s | ||
| 7.49 | s | |||
| overall OPLL | cycle slip time | 1000 | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Luo, C.; Zhang, B.; Qiu, B.; Zhang, R. Simulation and Design of a PIC-Based Heterodyne Optical Phase Locked Loop. Photonics 2023, 10, 336. https://doi.org/10.3390/photonics10030336
Yang X, Luo C, Zhang B, Qiu B, Zhang R. Simulation and Design of a PIC-Based Heterodyne Optical Phase Locked Loop. Photonics. 2023; 10(3):336. https://doi.org/10.3390/photonics10030336
Chicago/Turabian StyleYang, Xiu, Chanchan Luo, Ben Zhang, Bocang Qiu, and Ruiying Zhang. 2023. "Simulation and Design of a PIC-Based Heterodyne Optical Phase Locked Loop" Photonics 10, no. 3: 336. https://doi.org/10.3390/photonics10030336
APA StyleYang, X., Luo, C., Zhang, B., Qiu, B., & Zhang, R. (2023). Simulation and Design of a PIC-Based Heterodyne Optical Phase Locked Loop. Photonics, 10(3), 336. https://doi.org/10.3390/photonics10030336





