A Hybrid Cladding Ring-Core Photonic Crystal Fibers for OAM Transmission with Weak Spin–Orbit Coupling and Strong Bending Resistance
Abstract
:1. Introduction
2. Fiber Design
3. Fiber Characteristics
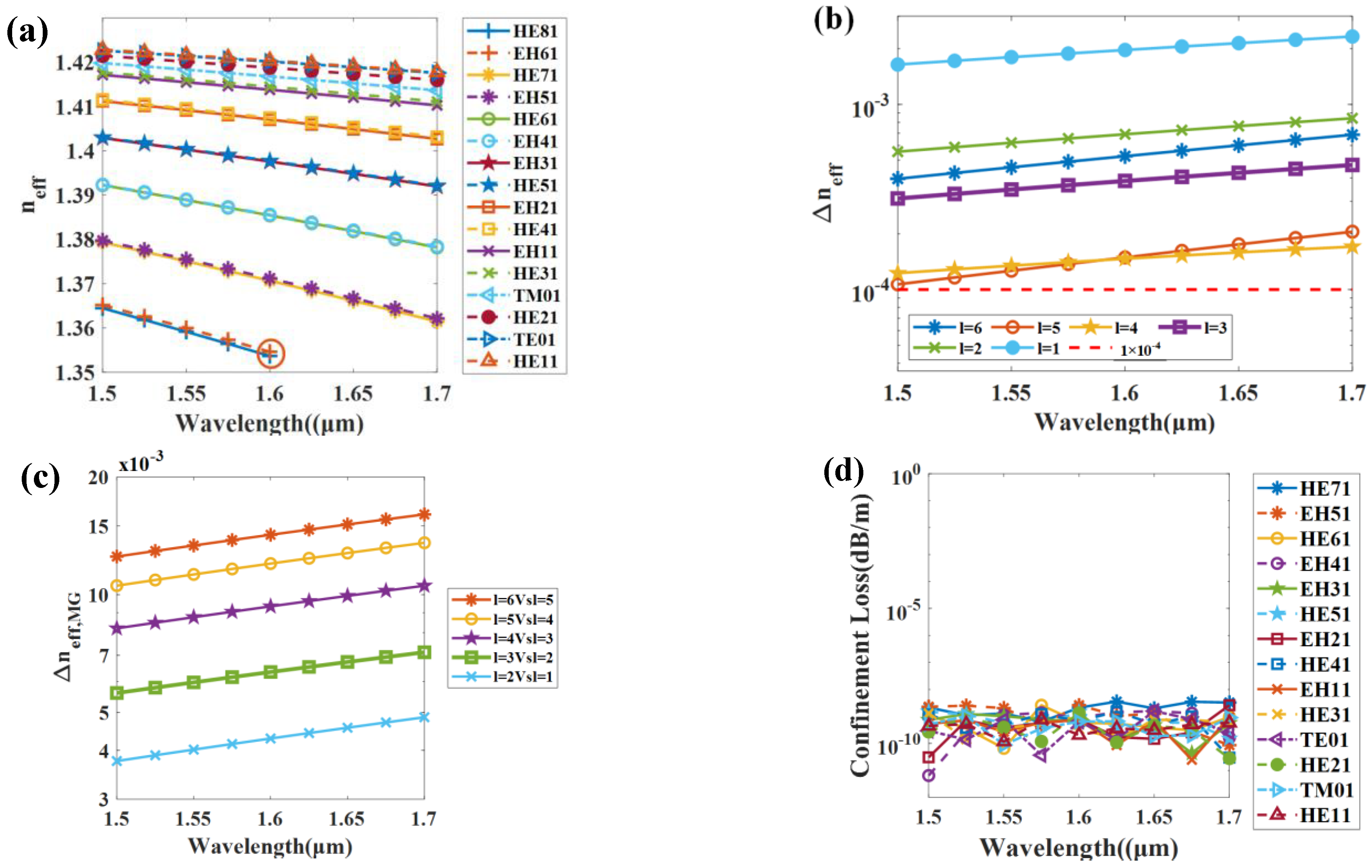
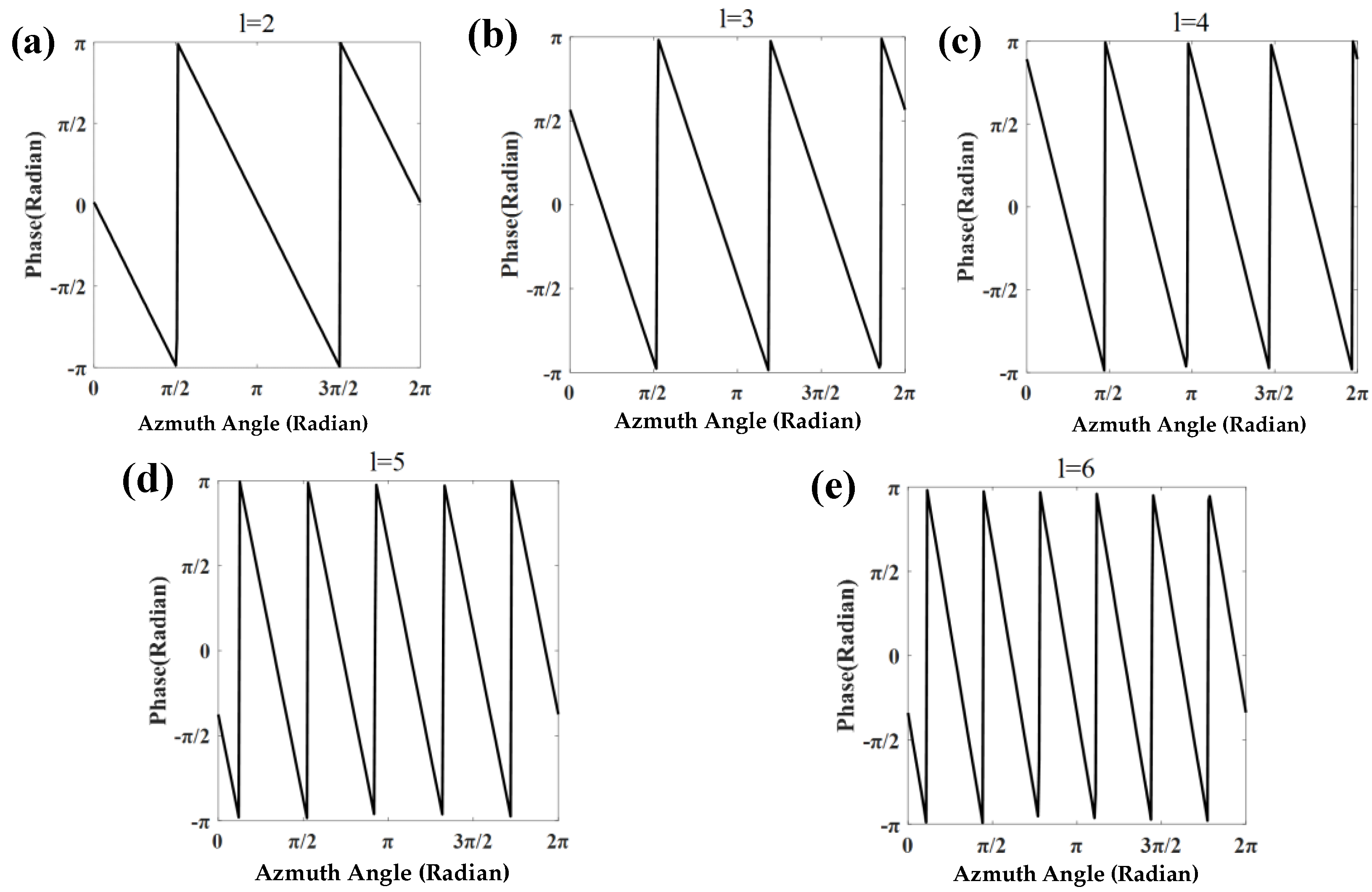
3.1. Number and Stability of OAM Modes
3.2. Weak Spin–Orbit Coupling
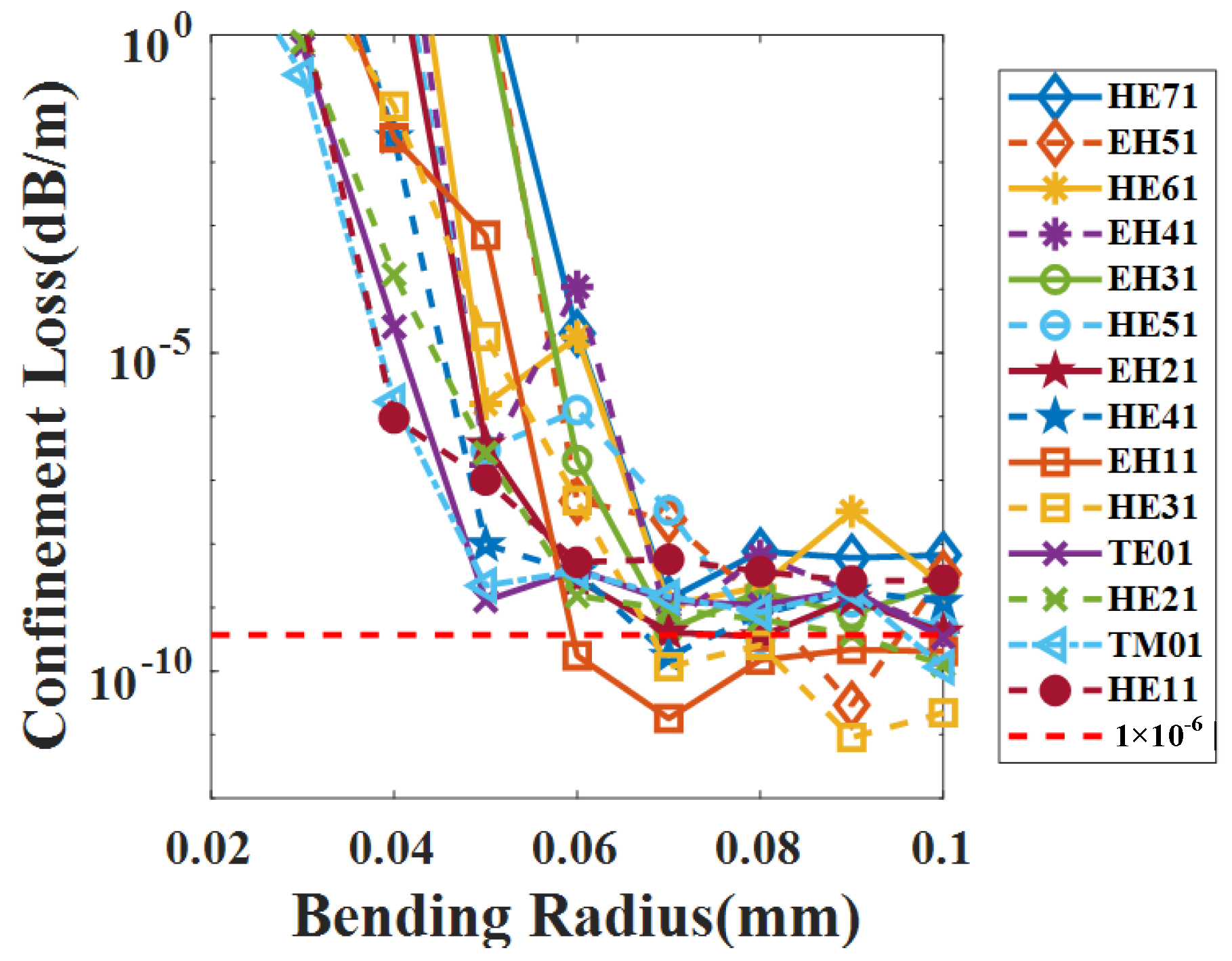
3.3. Strong Bending Resistance
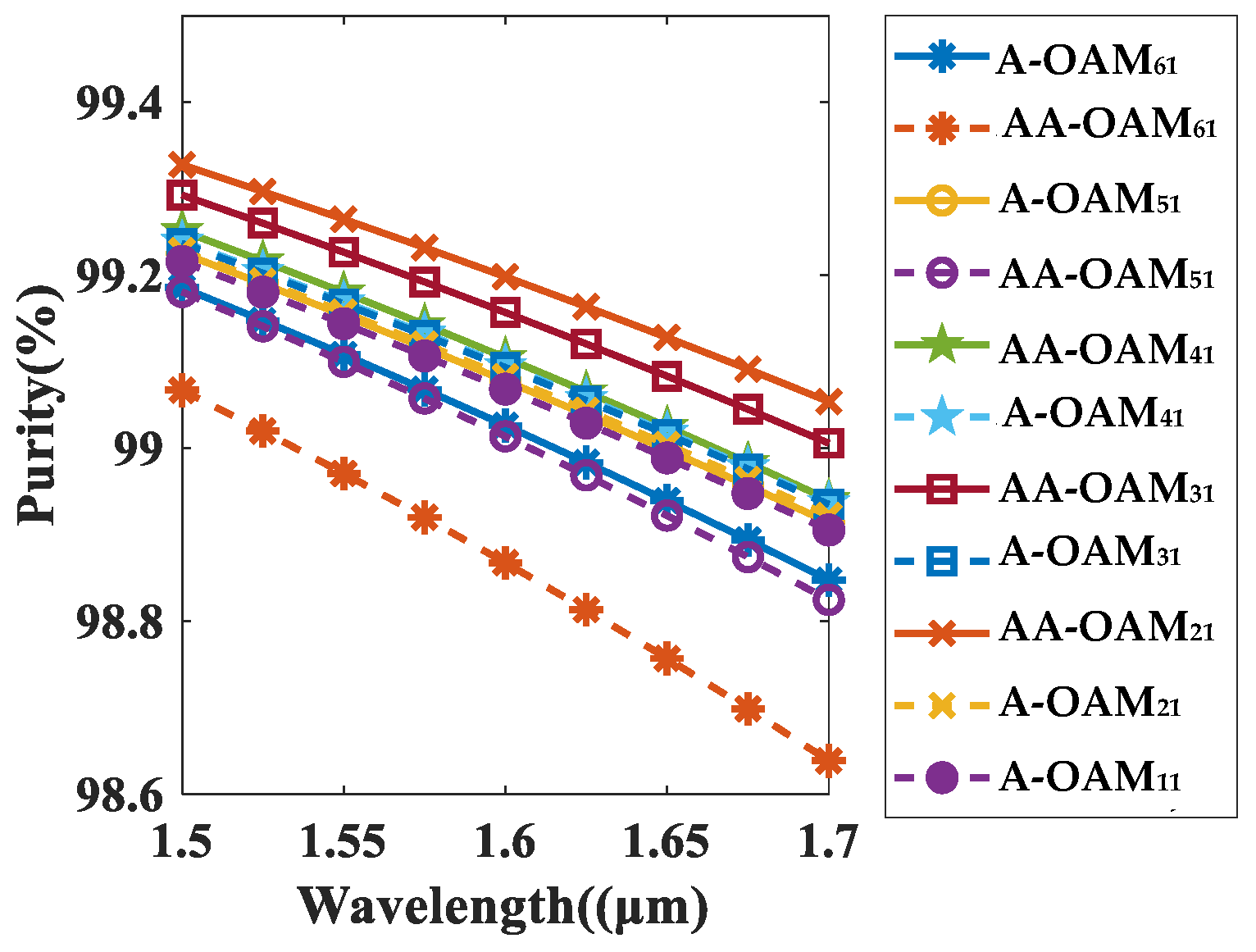
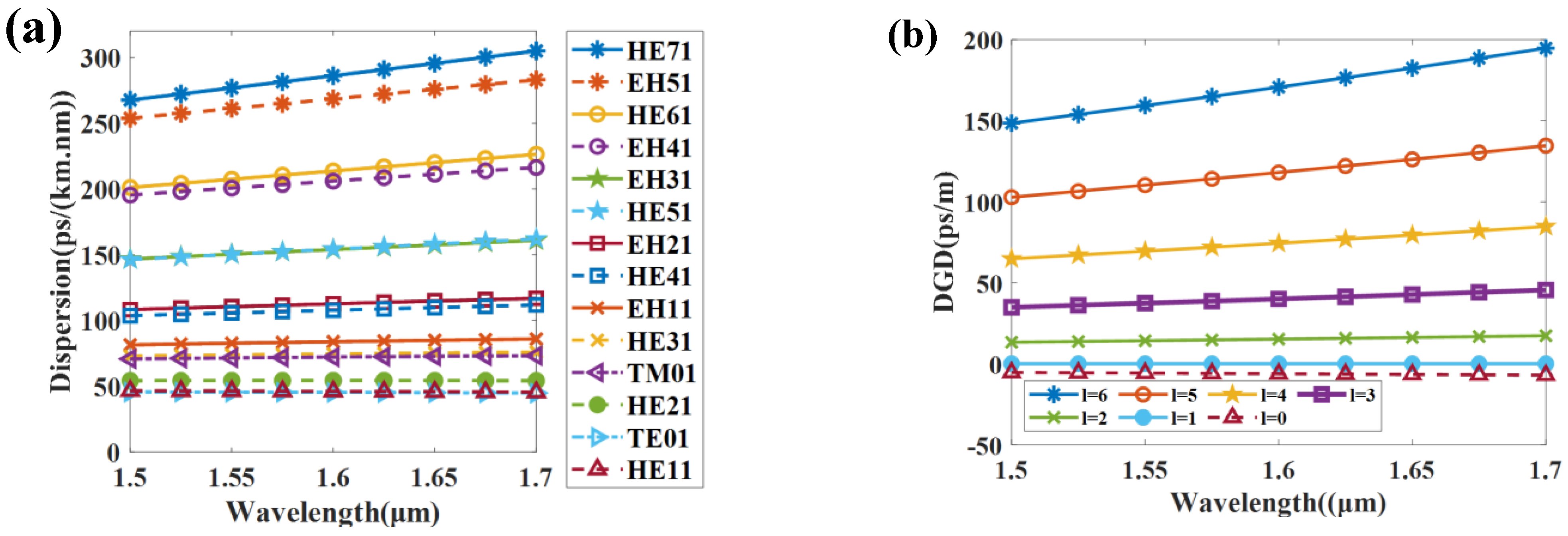
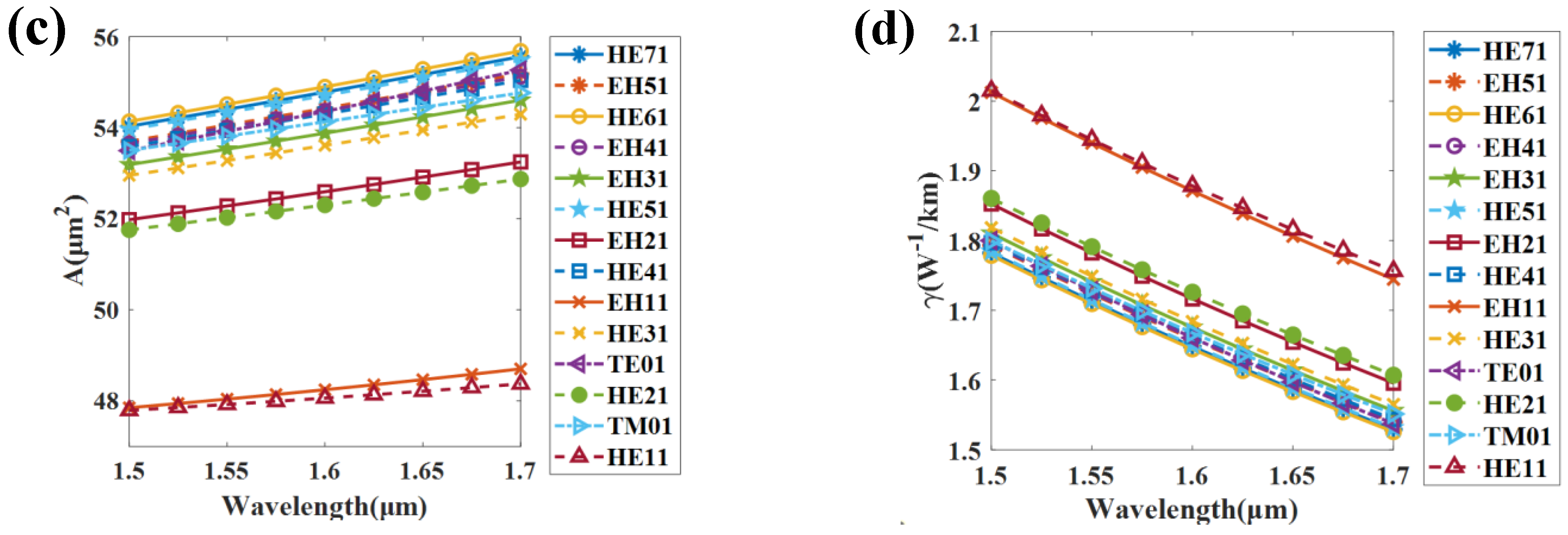
3.4. Transmission of OAM Modes
4. Discussion on Mode Number and Fiber Fabrication
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Bai, N.; Zhao, N.; Xia, C. Space-division multiplexing: The next frontier in optical communication. Adv. Opt. Photonics 2014, 6, 5041–5046. [Google Scholar] [CrossRef] [Green Version]
- Willner, A.E.; Huang, H.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; Wang, J.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef] [Green Version]
- Svetislav, S.; Alexandar, D. Mode coupling and its influence on space division multiplexing in step-index plastic-clad silica fibers. Opt. Fiber Technol. 2018, 46, 192–197. [Google Scholar]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-sscale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.E.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Nejad, R.M.; Allahverdyan, K.; Vaity, P.; Amiralizadeh, S.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Mode division multiplexing using orbital angular momentum modes over 1.4-km ring core fiber. J. Light. Technol. 2016, 34, 4252–4258. [Google Scholar] [CrossRef] [Green Version]
- Zhu, G.; Hu, Z.; Wu, X.; Du, C.; Luo, W.; Chen, Y.; Cai, X.; Liu, J.; Zhu, J.; Yu, S. Scalable mode division multiplexed transmission over a 10-km ring-core fiber using high-order orbital angular momentum modes. Opt. Express 2018, 26, 594–604. [Google Scholar] [CrossRef]
- Ren, Y.; Li, L.; Wang, Z.; Kamali, S.M.; Arbabi, E.; Arbabi, A.; Zhao, Z.; Xie, G.; Cao, Y.; Ahmed, N.; et al. Orbital angular momentum-based space division multiplexing for high-capacity underwater optical communications. Sci. Rep. 2016, 6, 33306. [Google Scholar] [CrossRef] [Green Version]
- Feng, F.; Jin, X.; O’Brien, D.; Payne, F.P.; Wilkinson, T.D. Mode group multiplexed transmission using OAM modes over 1 km ring-core fiber without MIMO processing. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 19–23 March 2017. [Google Scholar]
- Zhang, J.; Zhu, G.; Liu, J.; Wu, X.; Zhu, J.; Du, C.; Luo, W.; Chen, Y.; Yu, S. Orbital-angular-momentum mode-group multiplexed transmission over a graded-index ring-core fiber based on receive diversity and maximal ratio combining. Opt. Express 2018, 26, 4243–4257. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, A.; Chen, S.; Liu, J.; Mo, Q.; Du, C.; Wang, J. Orbital angular momentum mode groups multiplexing transmission over 26-km conventional multi-mode fiber. Opt. Express 2017, 25, 25637–25645. [Google Scholar] [CrossRef] [PubMed]
- Ingerslev, K.; Patrick, G.; Da Ros, F.; Hu, H.; Bao, F.; Castaneda, M.A.U.; Kristensen, P.; Rubano, A.; Marrucci, L.; Rottwitt, K.; et al. 12 mode, WDM, MIMO-free orbital angular momentum transmission. Opt. Express 2018, 26, 20225–20232. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liang, Y.; Zhang, X.; Chen, S.; Shen, L.; Zhang, L.; Luo, J.; Wang, J. Low-loss orbital angular momentum ring-core fiber: Design, fabrication and characterization. J. Light. Technol. 2020, 38, 6327–6333. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Liu, J.; Lin, Z.; Li, Z.; Lin, Z.; Zhang, J.; Huang, C.; Mo, S.; Shen, L.; et al. 1-Pbps orbital angular momentum fibre-optic transmission. Light Sci. Appl. 2022, 11, 202. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.; Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Ramachandran, S.; Kristensen, P. Optical vortices in fiber. Nanophotonics 2013, 2, 455–474. [Google Scholar] [CrossRef]
- Brunet, C.; Rusch, L.A. Optical fibers for the transmission of orbital angular momentum modes. Opt. Fiber Technol. 2016, 31, 172–177. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Zhu, G.; Zhang, J.; Wen, Y.; Wu, X.; Zhang, Y.; Chen, Y.; Cai, X.; Li, Z.; Hu, Z.; et al. Mode division multiplexing based on ring core optical fibers. IEEE J. Quantum Elect. 2018, 54, 0700118–0700135. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, X.; Li, H.; Deng, Y.; Zhang, X.; Xi, L.; Tang, X.; Zhang, W. A design strategy of the circular photonic crystal fiber supporting good quality orbital angular momentum mode transmission. Opt. Commun. 2017, 397, 59–66. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Li, H.; Deng, Y.; Xi, L.; Tang, X.; Zhang, W. The orbital angular momentum modes supporting fibers based on the photonic crystal fiber structure. Crystals 2017, 7, 286. [Google Scholar] [CrossRef] [Green Version]
- Yue, Y.; Yan, Y.; Ahmed, N.; Yang, J.; Erkmen, B.I.; Dolinar, S.; Tur, M.; Willner, A.E. Mode properties and propagation effects of optical orbital angular momentum (OAM) modes in a ring fiber. IEEE Photonics J. 2012, 4, 535–543. [Google Scholar]
- Brunet, C.; Vaity, P.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Design, fabrication and validation of an OAM fiber supporting 36 states. Opt. Express 2014, 22, 26117–26127. [Google Scholar] [CrossRef]
- Brunet, C.; Ung, B.; Bélanger, P.A.; Messaddeq, Y.; LaRochelleand, S.; Rusch, L.A. Vector mode analysis of ring-core fibers: Design tools for spatial division multiplexing. J. Light. Technol. 2014, 32, 4046–4057. [Google Scholar] [CrossRef] [Green Version]
- Brunet, C.; Ung, B.; Vaity, P.; Wang, L.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Design of a family of ring-core fibers for OAM transmission studies. Opt. Express 2015, 23, 10553–10563. [Google Scholar] [CrossRef] [PubMed]
- Yue, Y.; Zhang, L.; Yan, Y.; Ahmed, N.; Yang, J.; Huang, H.; Ren, Y.; Dolinar, S.; Tur, M.; Willner, A.E. Octave-spanning supercontinuum generation of vortices in an As2S3 ring photonic crystal fiber. Opt. Lett. 2012, 37, 1889–1891. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W.; Xi, L.; Tang, X.; Zhang, X.; Zhang, X. A new type circular photonic crystal fiber for orbital angular momentum mode transmission. IEEE Photonics Technol. Lett. 2016, 28, 1426–1429. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, Y.; Luo, A.; Cui, H.; Luo, Z.; Xu, W. Photonic crystal fiber for supporting 26 orbital angular momentum modes. Opt. Express 2016, 24, 17285–17291. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Zhou, G.; Chen, C.; Xu, M.; Xia, C.; Hou, Z. Design and analysis of a microstructure ring fiber for orbital angular momentum transmission. IEEE Photonics J. 2016, 8, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H.; Zhang, X.; Zhang, Z.; Xi, L.; Tang, X.; Zhang, W.; Zhang, X. Design tool for circular photonic crystal fibers supporting orbital angular momentum modes. Appl. Opt. 2018, 57, 2474–2481. [Google Scholar] [CrossRef]
- Fu, C.; Liu, S.; Wang, Y.; Bai, Z.; He, J.; Liao, C.; Zhang, Y.; Zhang, F.; Yu, B.; Gao, S.; et al. High-order orbital angular momentum mode generator based on twisted photonic crystal fiber. Opt. Lett. 2018, 43, 1786–1789. [Google Scholar] [CrossRef] [Green Version]
- Jia, C.; Jia, H.; Wang, N.; Chai, J.; Xu, X.; Lei, Y.; Liu, G.; Peng, Y.; Xie, J. Theoretical analysis of a 750-nm bandwidth hollow-core ring photonic crystal fiber with a graded structure for transporting 38 orbital angular momentum modes. IEEE Access 2018, 6, 20291–20297. [Google Scholar] [CrossRef]
- Sharma, M.; Amirkhan, F.; Mishra, S.K.; Sengupta, D.; Messaddeq, Y.; Blanchard, F.; Ung, B. Annular core photonic crystal fiber for propagation of optical vortices. In Proceedings of the Conference on Lasers and Electro-Optics, Washington, DC, USA, 10–15 May 2020. [Google Scholar]
- Hong, S.; Lee, Y.; Choi, H.; Chai, Q.; Li, Y.; Kim, S.; Oh, K. Hollow silica photonic crystal fiber guiding 101 orbital angular momentum modes without phase distortion in C+L band. J. Light. Technol. 2020, 38, 1010–1018. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Y.; Bao, C.; Geng, W.; Fang, Y.; Mao, B.; Wang, Z.; Liu, Y.; Huang, H.; Ren, Y.; et al. Hollow ring-core photonic crystal fiber with >500 OAM modes over 360-nm communications bandwidth. IEEE Access 2021, 9, 66999–67005. [Google Scholar] [CrossRef]
- Amezcua-Correa, R.; Broderick, N.G.; Petrovich, M.N.; Poletti, F.; Richardson, D.J. Design of 7 and 19 cells core air-guiding photonic crystal fibers for low-loss, wide bandwidth and dispersion controlled operation. Opt. Express 2007, 15, 17577–17586. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Rodriguez-Fortuno, J.; Nori, F.; Zayats, A.V. Spin-orbit interactions of light. Nat. Photonics 2015, 9, 156–163. [Google Scholar] [CrossRef] [Green Version]
- Golowich, S. Asymptotic theory of strong spin-orbit coupling in optical fiber. Opt. Lett. 2014, 39, 92–95. [Google Scholar] [CrossRef] [PubMed]
- Guerra, G.; Lonardi, M.; Galtarossa, A.; Rusch, L.A.; Bononi, A.; Palmieri, L. Analysis of modal coupling due to birefringence and ellipticity in strongly guiding ring-core OAM fibers. Opt. Express 2019, 27, 8308–8326. [Google Scholar] [CrossRef] [Green Version]
- Gregg, P.; Kristensen, P.; Rubano, A.; Golowich, S.; Marrucci, L.; Ramachandran, S. Spin-orbit coupled, non-integer OAM fibers: Unlocking a new eigenbasis for transmitting 24 uncoupled modes. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 5–10 June 2016. [Google Scholar]
- Zhang, Z.; Gan, J.; Heng, X.; Wu, Y.; Li, Q.; Qian, Q.; Chen, D.; Yang, Z. Optical fiber design with orbital angular momentum light purity higher than 99.9%. Opt. Express 2015, 23, 29331–29341. [Google Scholar] [CrossRef]
- Han, J.; Gao, J.; Zhao, Y.; Hou, S. Bend performance analysis of few-mode fibers with high modal multiplicity factors. J. Light. Technol. 2017, 35, 2526–2534. [Google Scholar] [CrossRef]
- Tandjè, A.; Yammine, J.; Dossou, M.; Bouwmans, G.; Baudelle, K.; Vianou, A.; Andresen, E.R.; Bigot, L. Ring-core photonic crystal fiber for propagation of oam modes. Opt. Lett. 2019, 44, 1611–1614. [Google Scholar] [CrossRef]
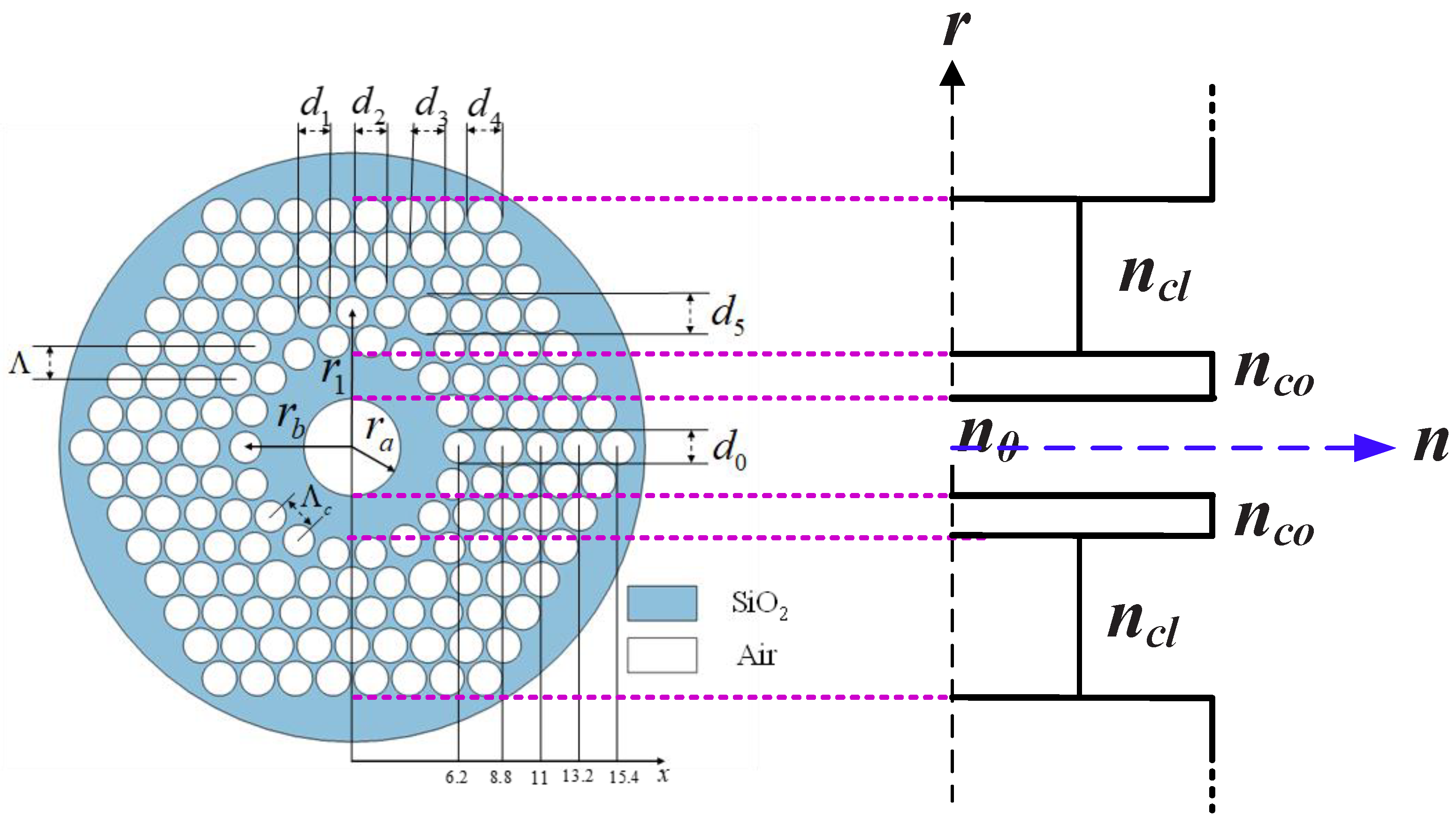
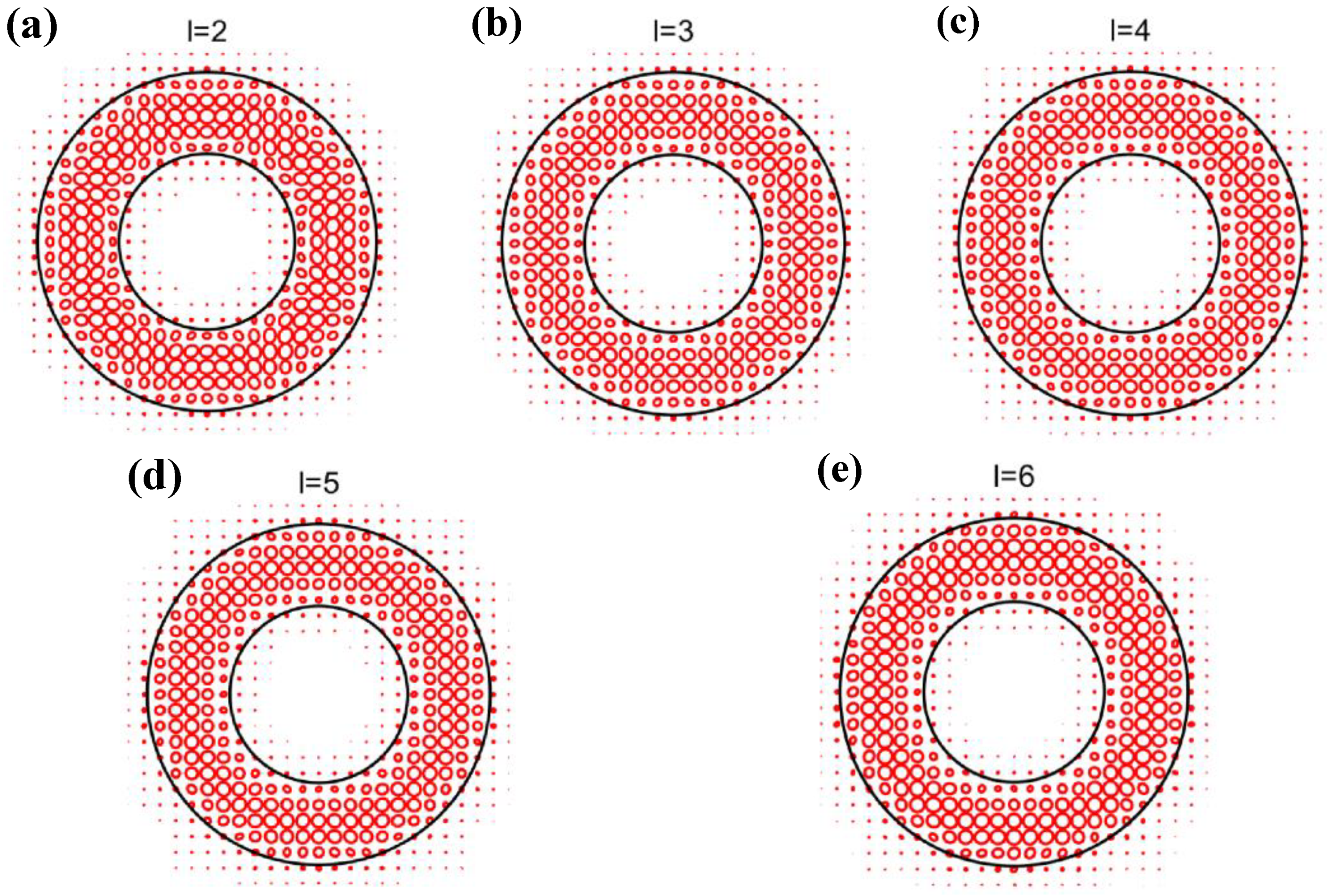
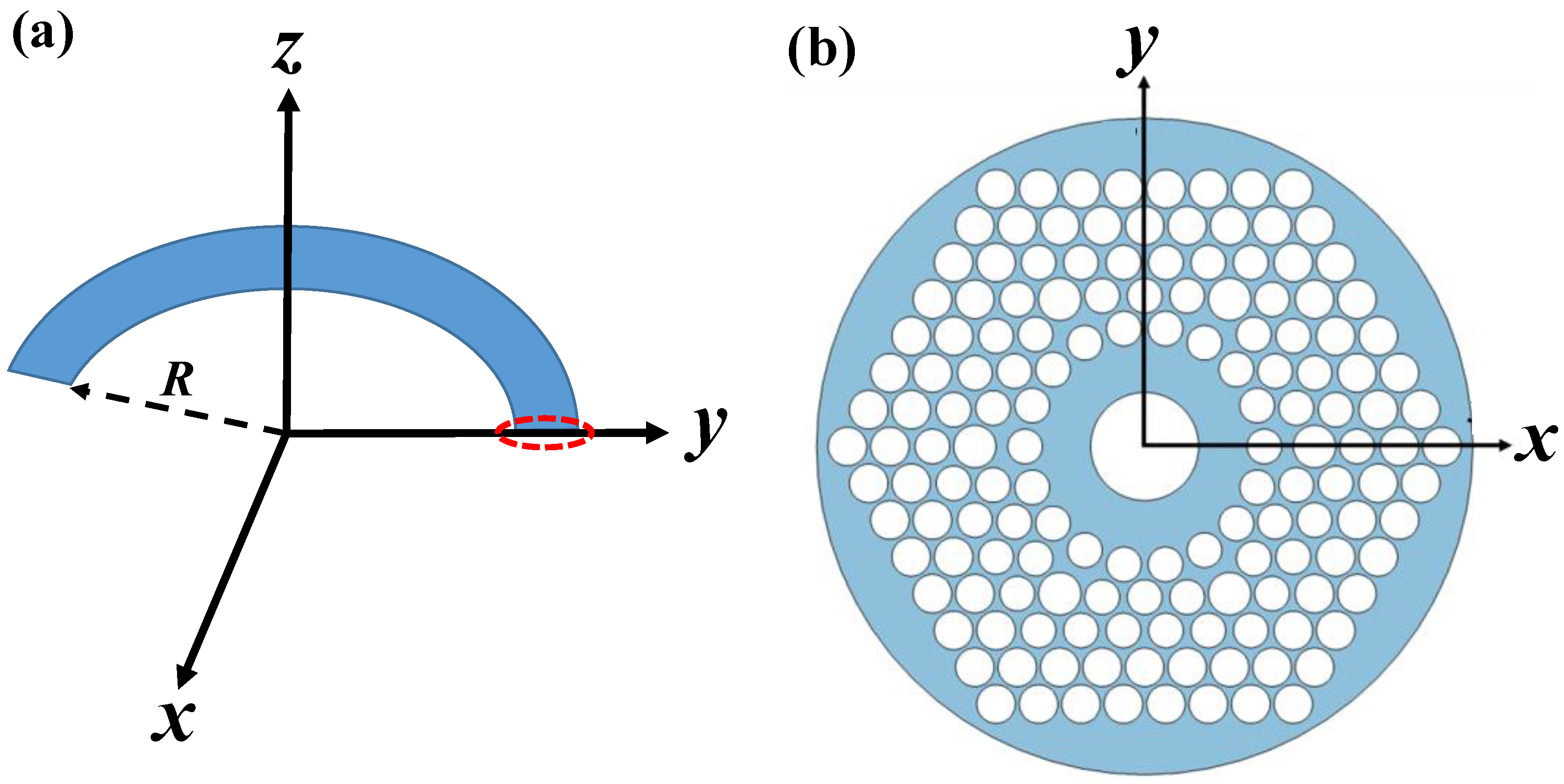
| Parameter | d0 | d1 | d2 | d3 | d4 | d5 | ra | rb | r1 | Λ | Λc |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value(μm) | 1.8 | 1.8 | 1.8 | 2 | 2 | 2.2 | 2.8 | 6.2 | 8.8 | 2.2 | 2.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Fang, S.; Wang, J.; Feng, H.; Li, H.; Wan, D.; Zhang, X.; Xi, L. A Hybrid Cladding Ring-Core Photonic Crystal Fibers for OAM Transmission with Weak Spin–Orbit Coupling and Strong Bending Resistance. Photonics 2023, 10, 352. https://doi.org/10.3390/photonics10040352
Zhang H, Fang S, Wang J, Feng H, Li H, Wan D, Zhang X, Xi L. A Hybrid Cladding Ring-Core Photonic Crystal Fibers for OAM Transmission with Weak Spin–Orbit Coupling and Strong Bending Resistance. Photonics. 2023; 10(4):352. https://doi.org/10.3390/photonics10040352
Chicago/Turabian StyleZhang, Hu, Songke Fang, Jiaqi Wang, Haixia Feng, Hui Li, Dong Wan, Xiaoguang Zhang, and Lixia Xi. 2023. "A Hybrid Cladding Ring-Core Photonic Crystal Fibers for OAM Transmission with Weak Spin–Orbit Coupling and Strong Bending Resistance" Photonics 10, no. 4: 352. https://doi.org/10.3390/photonics10040352
APA StyleZhang, H., Fang, S., Wang, J., Feng, H., Li, H., Wan, D., Zhang, X., & Xi, L. (2023). A Hybrid Cladding Ring-Core Photonic Crystal Fibers for OAM Transmission with Weak Spin–Orbit Coupling and Strong Bending Resistance. Photonics, 10(4), 352. https://doi.org/10.3390/photonics10040352





