Wafer Eccentricity Deviation Measurement Method Based on Line-Scanning Chromatic Confocal 3D Profiler
Abstract
1. Introduction
2. Principle of Wafer Defect Inspection and Error Measurement
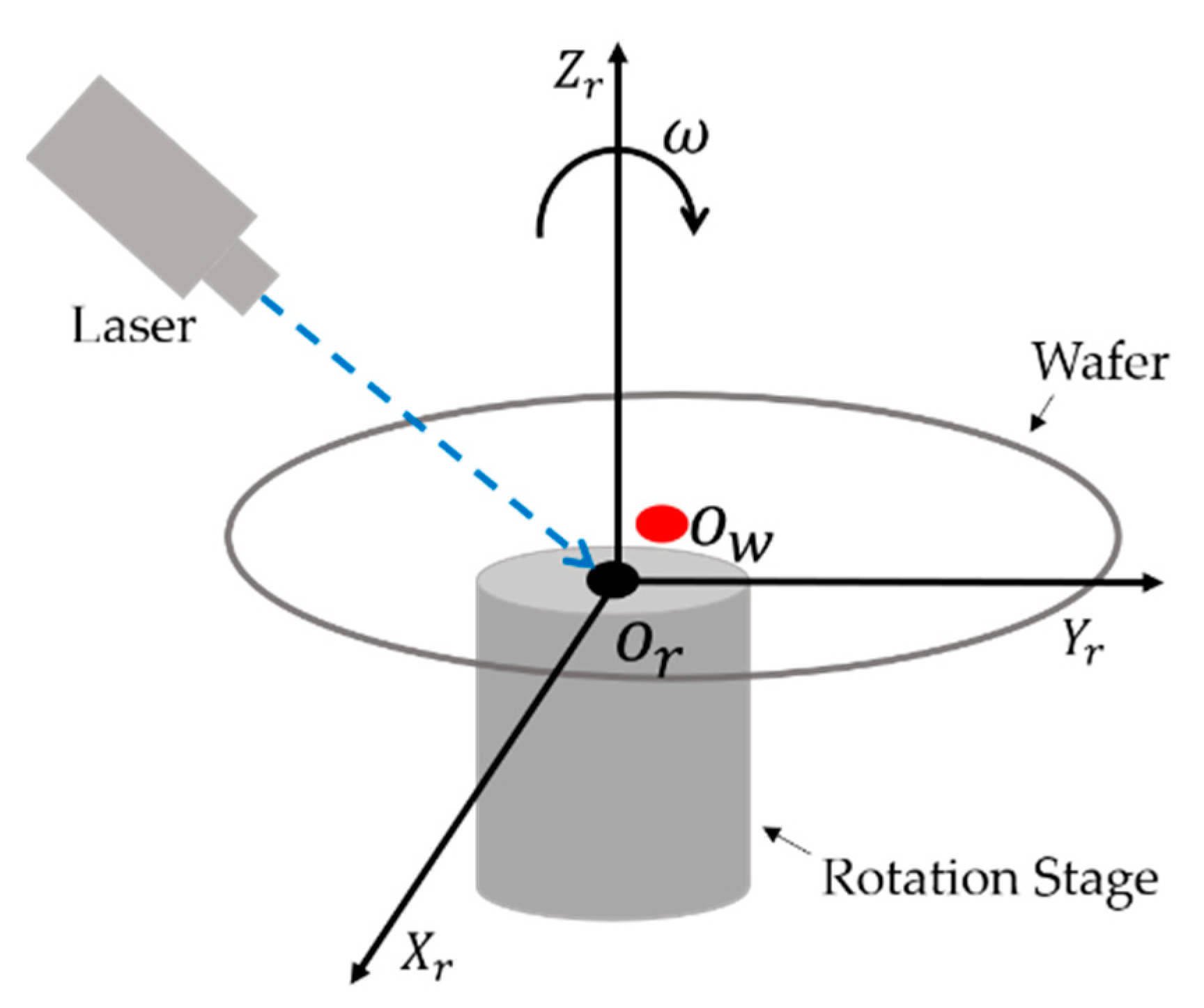
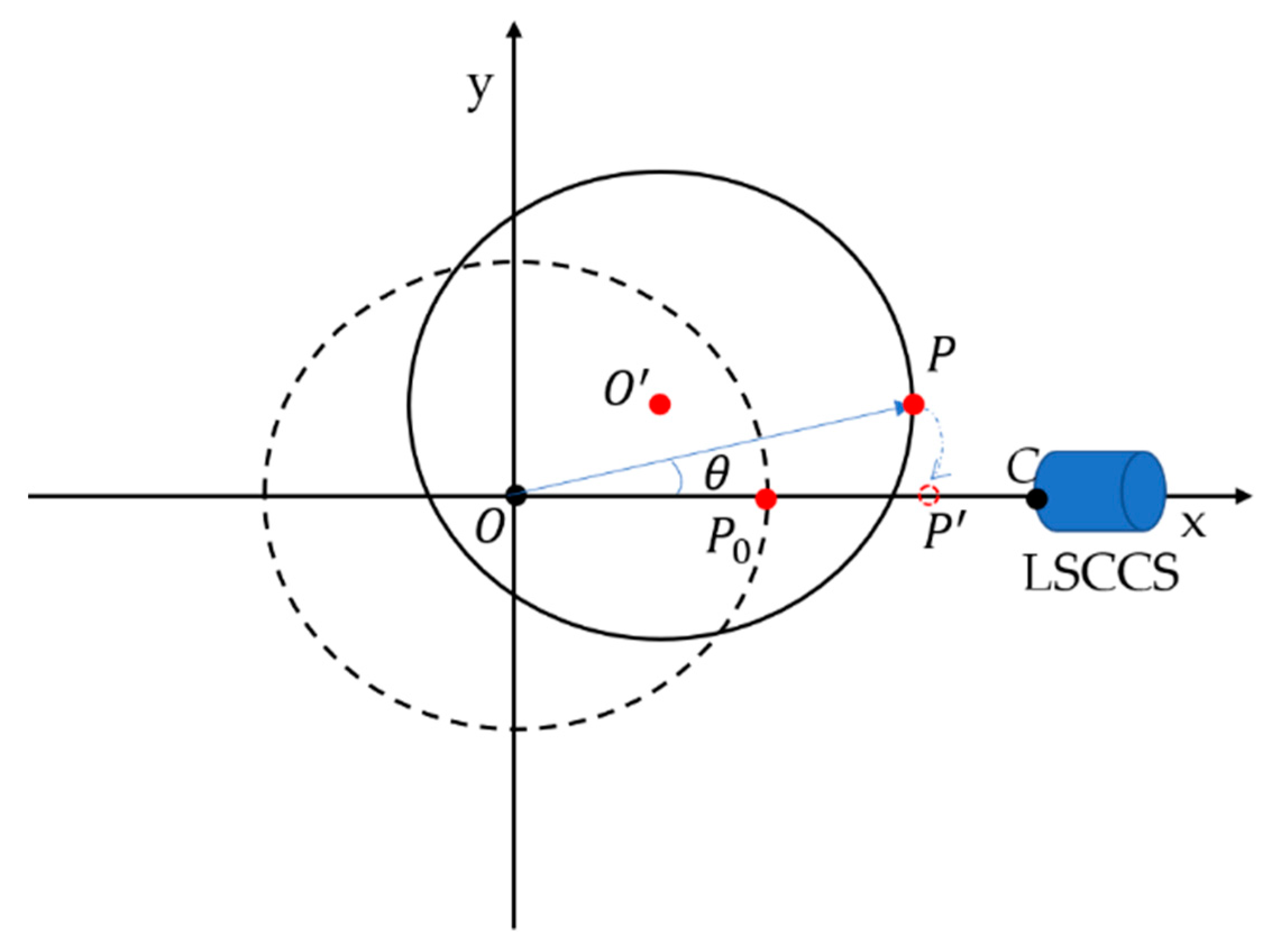
2.1. Spot Scanning Wafer Surface Defect Inspection and Wafer Eccentricity Deviation Error
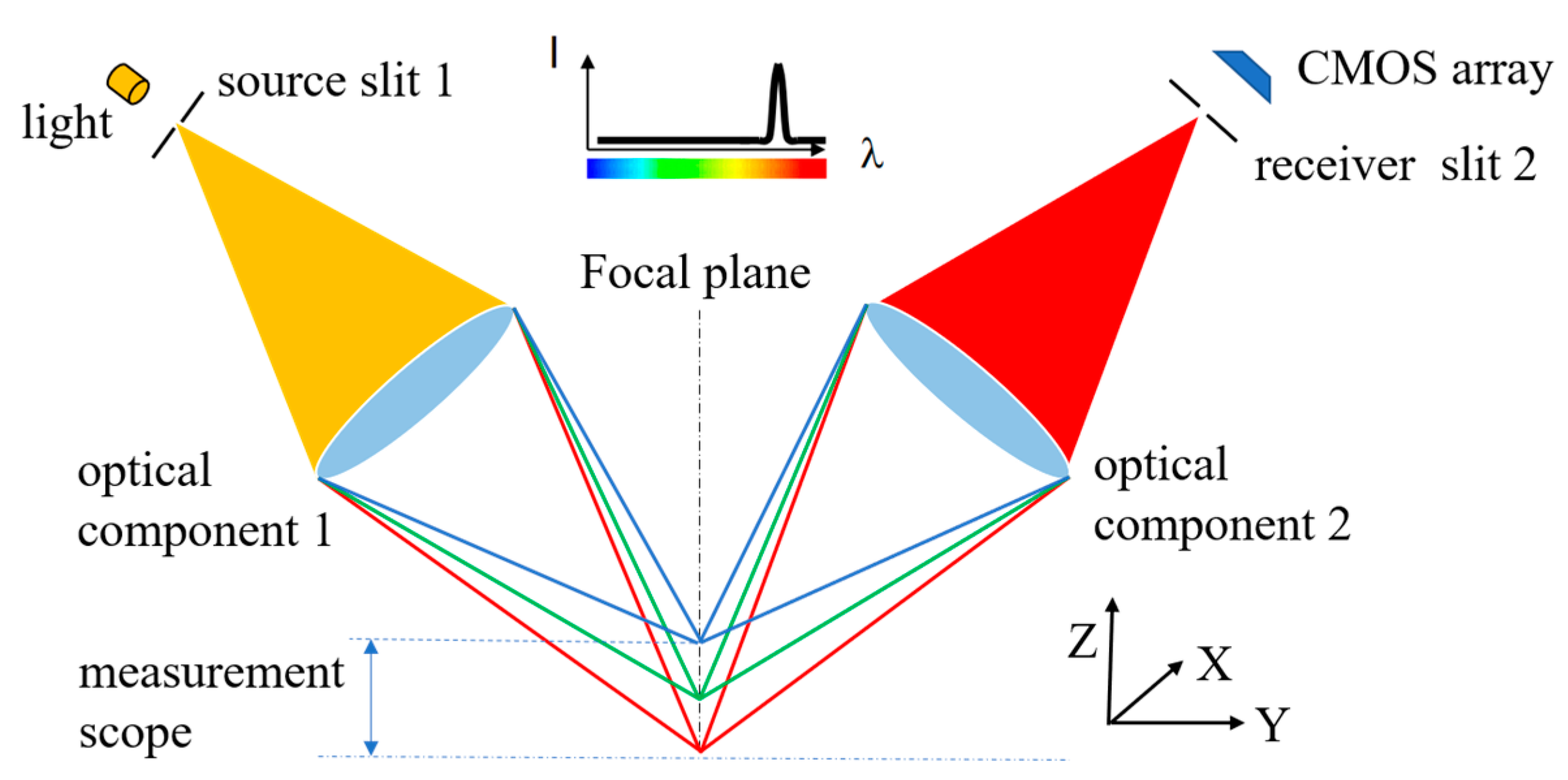
2.2. Line-Scanning Chromatic Confocal Sensor
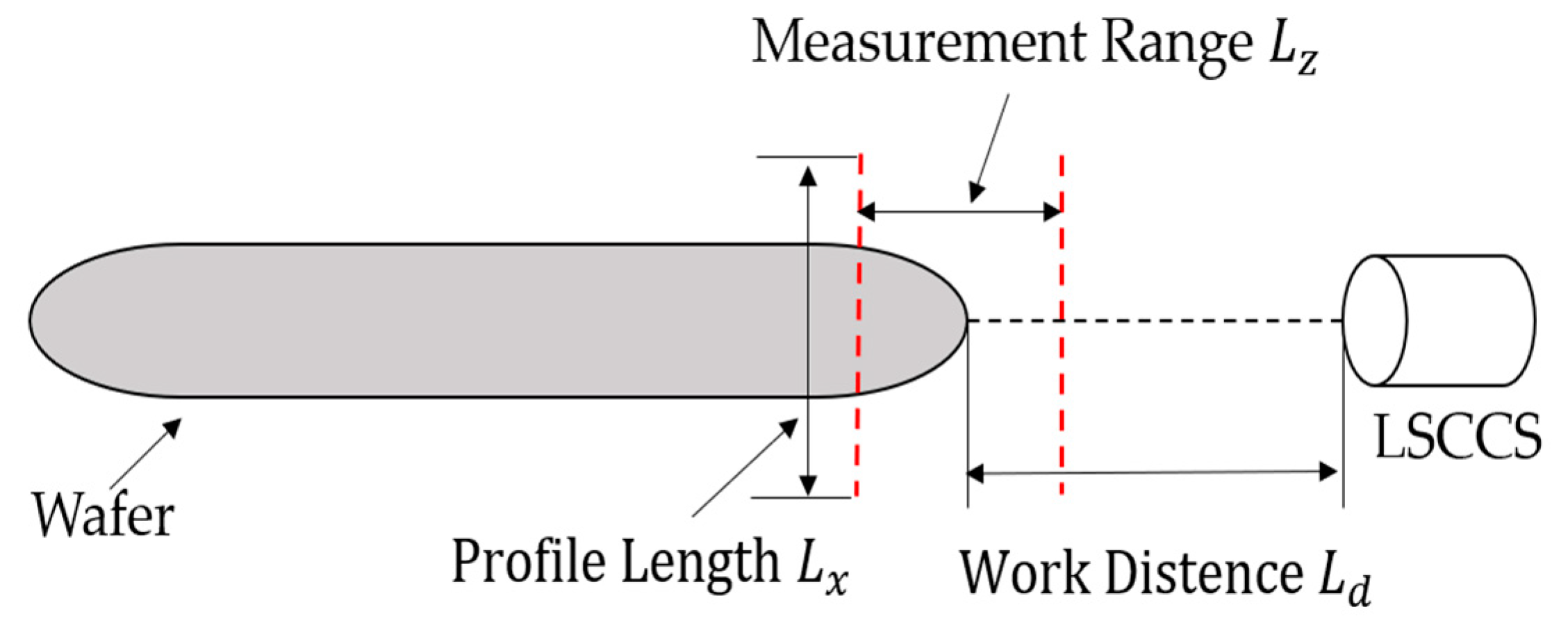
2.3. Wafer Eccentricity Deviation Measurement System Setup
3. Results
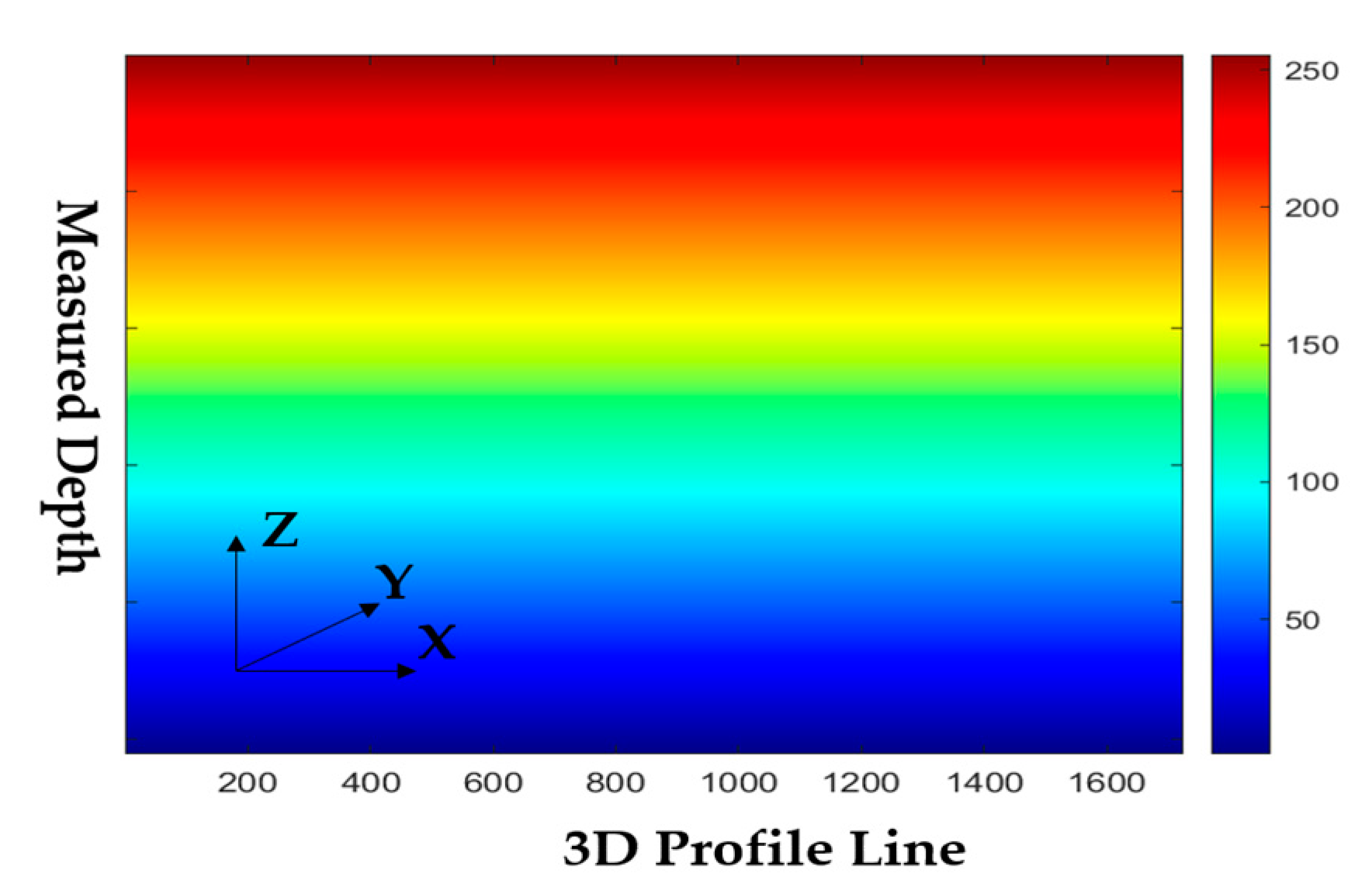
3.1. Signal Processing and Edge Distance Acquisition
3.2. Wafer Eccentricity Deviation Calculation
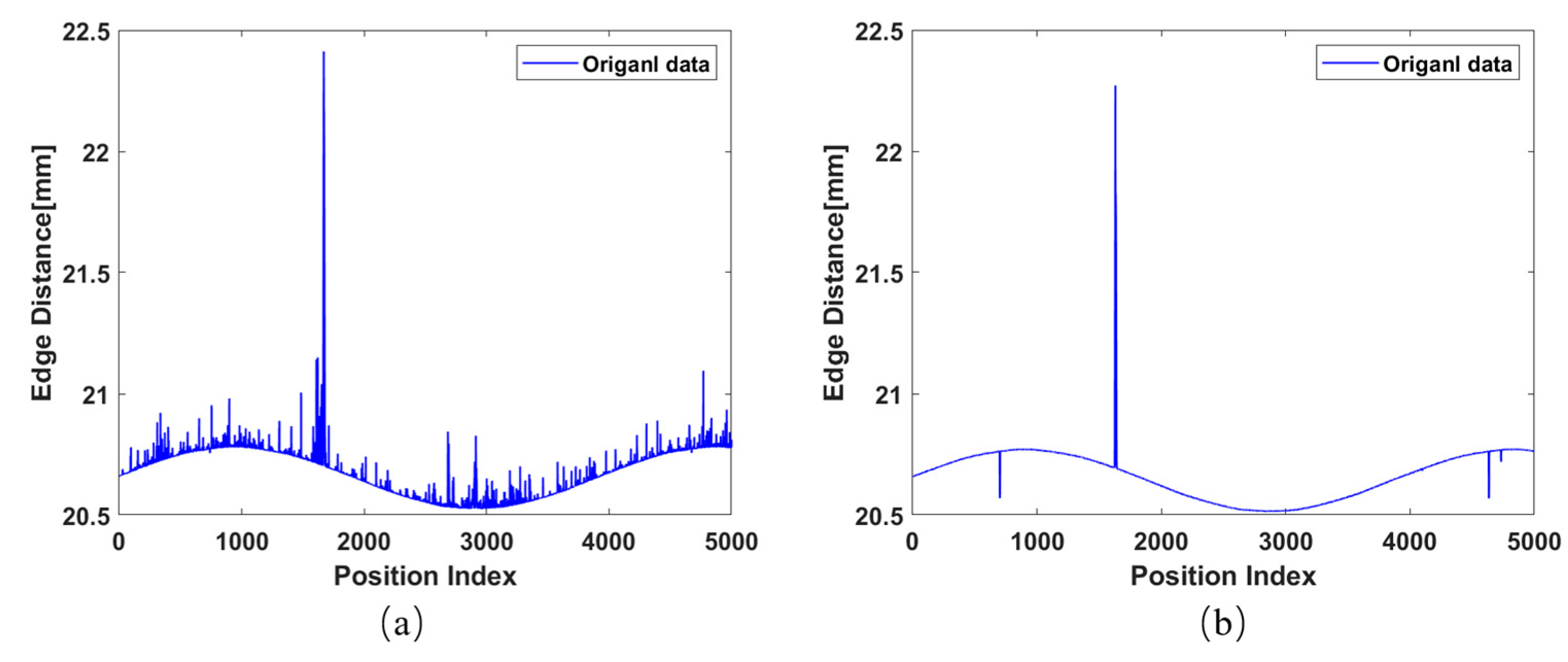
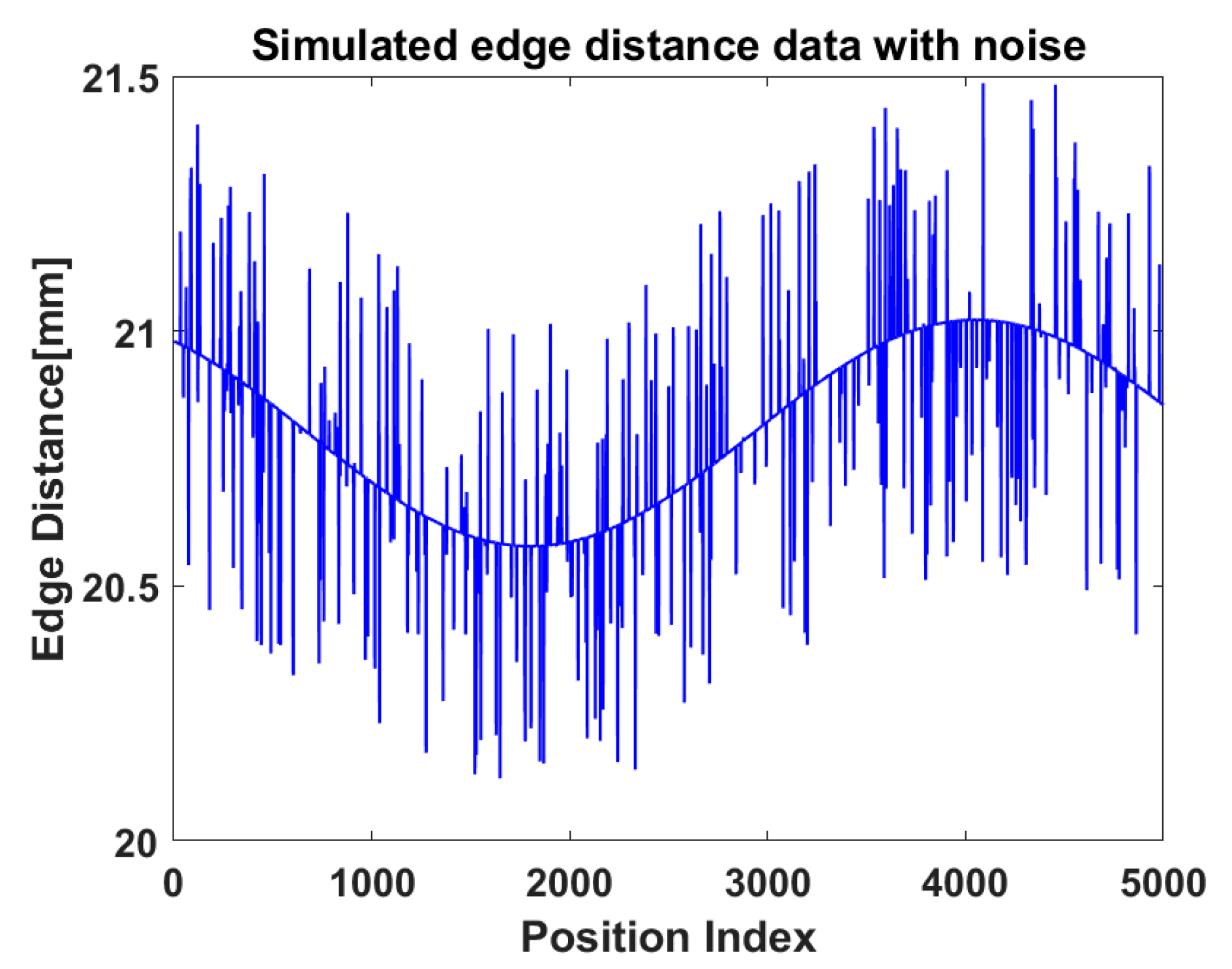
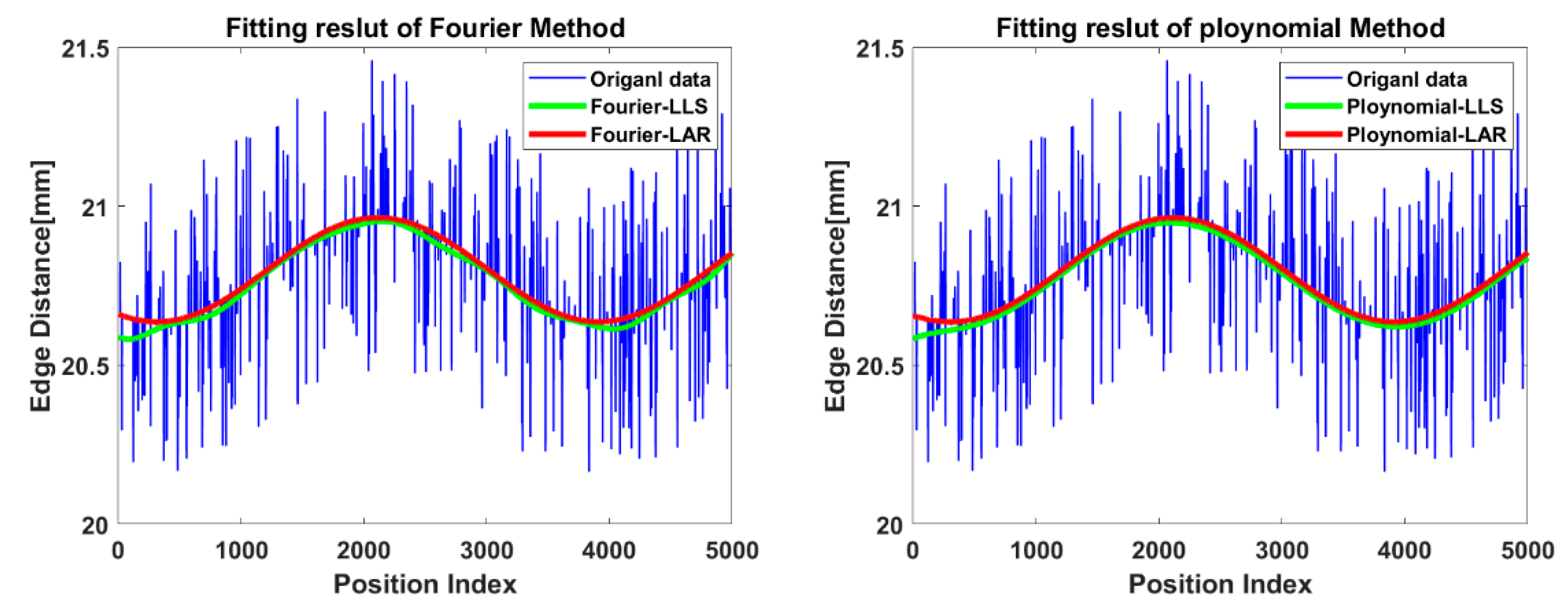
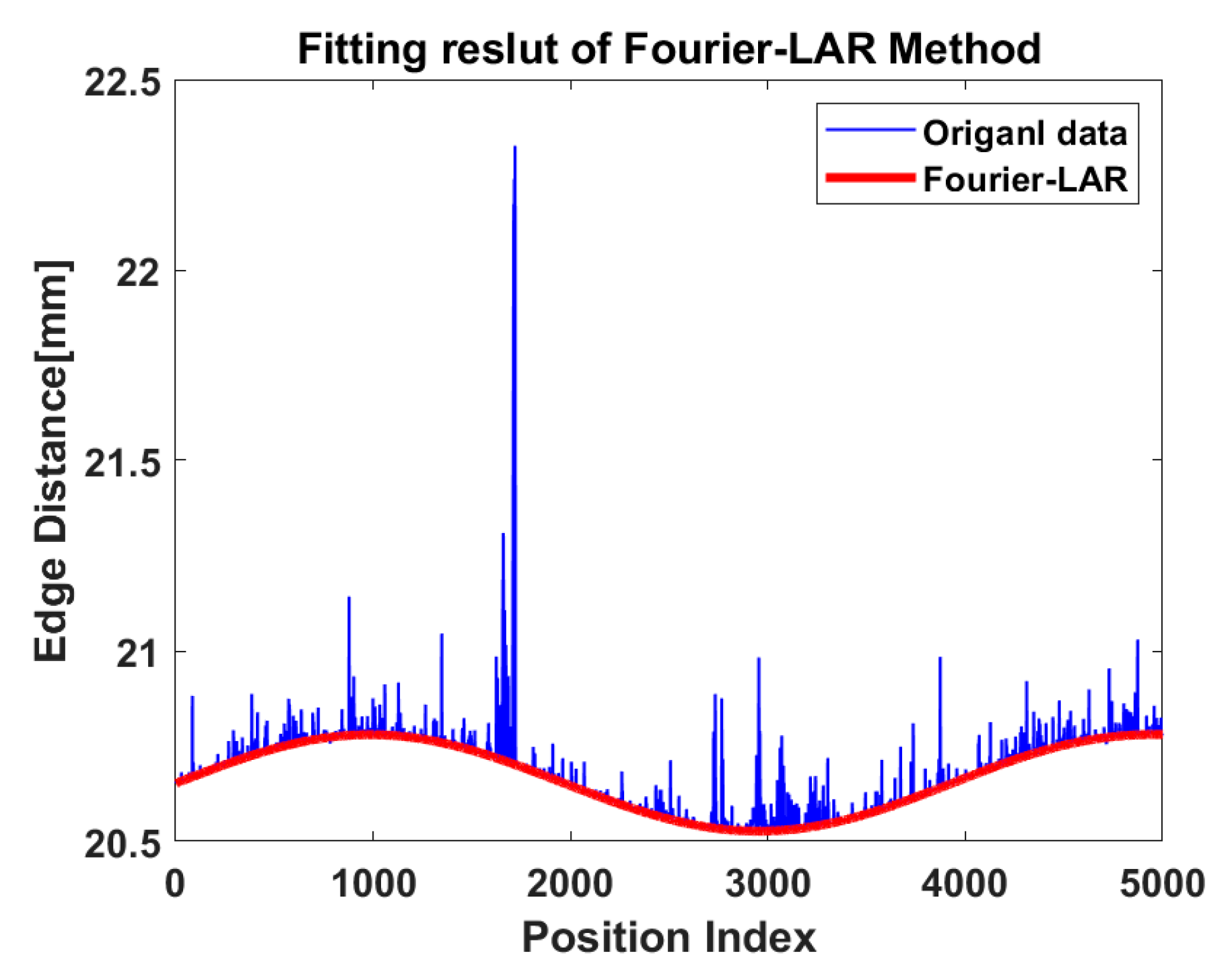
3.3. Simulation Analysis for Dealing with Outliers of Edge Distance
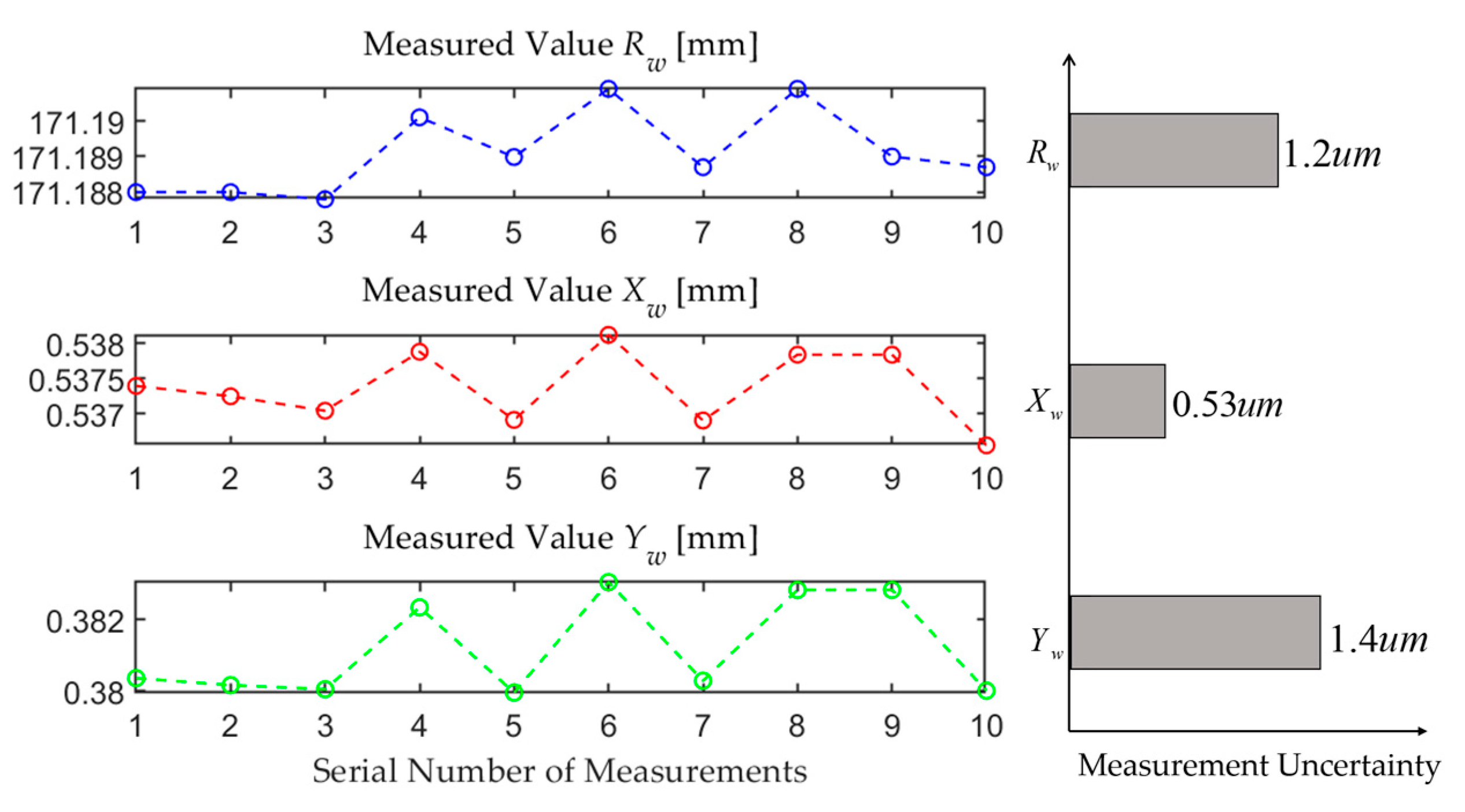
3.4. Uncertainty Estimation of Measurement System
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sah, K.; Cross, A.; Plihal, M.; Anantha, V.; Babulnath, R.; Fung, D.; De Bisschop, P.; Halder, S. EUV stochastic defect monitoring with advanced broadband optical wafer inspection and e-beam review systems. In Proceedings of the International Conference on Extreme Ultraviolet Lithography (EUVLS), Monterey, CA, USA, 17–20 September 2018. [Google Scholar]
- Shkalim, A.; Crider, P.; Bal, E.; Madmon, R.; Chereshnya, A.; Cohen, O.; Dassa, O.; Petel, O.; Cohen, B. 193nm Mask Inspection Challenges and Approaches for 7nm/5nm Technology and Beyond. In Proceedings of the Photomask Technology Conference, Monterey, CA, USA, 15–19 September 2019. [Google Scholar]
- Wen, G.; Gao, Z.; Cai, Q.; Wang, Y.; Mei, S. A Novel Method Based on Deep Convolutional Neural Networks for Wafer Semiconductor Surface Defect Inspection. IEEE Trans. Instrum. Meas. 2020, 69, 9668–9680. [Google Scholar] [CrossRef]
- Knapek, A.; Drozd, M.; Matejka, M.; Chlumska, J.; Kral, S.; Kolarik, V. Automated System for Optical Inspection of Defects in Resist-coated Non-patterned Wafer. Jordan J. Phys. 2020, 13, 93–100. [Google Scholar] [CrossRef]
- Xiaoyan, C.; Chundong, Z.; Jianyong, C.; Dongyang, Z.; Kuifeng, Z.; Yanjie, S. A compact Robot-based defect detection device design for silicon wafer. J. Phys. Conf. Ser. 2020, 1449, 012111. [Google Scholar] [CrossRef]
- Robinson, C.; Bright, J.; Corliss, D.; Guse, M.; Lang, B.; Mack, G. Monitoring defects at wafer’s edge for improved immersion lithography performance. In Optical Microlithography XXI, Pts 1-3; Levinson, H.J., Dusa, M.V., Eds.; SPIE: Bellingham, WA, USA, 2008; Volume 6924, pp. 1528–1537. [Google Scholar]
- Pishkenari, H.N.; Meghdari, A. Surface defects characterization with frequency and force modulation atomic force microscopy using molecular dynamics simulations. Curr. Appl. Phys. 2010, 10, 583–591. [Google Scholar] [CrossRef]
- Abraham, Z. SEM defect review and classification for semiconductors devices manufacturing. In Proceedings of the Conference on Metrology-Based Control for Micro-Manufacturing, San Jose, CA, USA, 24–25 January 2001; pp. 99–106. [Google Scholar]
- Tuung, L.; Rong, L.; Chimin, C.; Hsiang-Chou, L.; Ling-Wu, Y.; Tahone, Y.; Kuang-Chao, C.; Chih-Yuan, L. Smart Review Sampling Methodology in Huge Inspection Results. ECS Trans. 2014, 60, 881–885. [Google Scholar] [CrossRef]
- Choi, W.J.; Ryu, S.Y.; Kim, J.K.; Kim, J.Y.; Kim, D.U.; Chang, K.S. Fast mapping of absorbing defects in optical materials by full-field photothermal reflectance microscopy. Opt. Lett. 2013, 38, 4907–4910. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Liu, D.; Cao, P.; Xie, S.; Li, Y.; Chen, Y.; Yang, Y. Automated discrimination between digs and dust particles on optical surfaces with dark-field scattering microscopy. Appl. Opt. 2014, 53, 5131–5140. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Cao, P.; Du, Y.B.; Hu, H.T.; Yang, Y.Y. Calibration and Image Reconstruction in a Spot Scanning Detection System for Surface Defects. Appl. Sci. 2020, 10, 2503. [Google Scholar] [CrossRef]
- Steven, W.M.; Rusmin, K.; William, W.; Hung, P.N. Wafer Edge Inspection. U.S. Patent 7161667B2, 9 January 2007. [Google Scholar]
- Meng, C.; Shi, J.F.; Hao, F.; Zhang, Z.S.; Dai, M. A novel circle center location method for a large-scale wafer. Meas. Sci. Technol. 2021, 32, abfc85. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Y.; Yan, Z.; Huang, X.; Duan, Y.; Ren, L. OmniFusion: 360 Monocular Depth Estimation via Geometry-Aware Fusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 2791–2800. [Google Scholar]
- Liu, J.; Ji, P.; Bansal, N.; Cai, C.; Yan, Q.; Huang, X.; Xu, Y. PlaneMVS: 3D Plane Reconstruction from Multi-View Stereo. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 8655–8665. [Google Scholar]
- Liu, Y.; Ju, Y.; Jian, M.; Gao, F.; Rao, Y.; Hu, Y.; Dong, J. A deep-shallow and global-local multi-feature fusion network for photometric stereo. Image Vis. Comput. 2022, 118, 104368. [Google Scholar] [CrossRef]
- Ju, Y.; Jian, M.; Guo, S.; Wang, Y.; Zhou, H.; Dong, J. Incorporating Lambertian Priors Into Surface Normals Measurement. IEEE Trans. Instrum. Meas. 2021, 70, 3096282. [Google Scholar] [CrossRef]
- Hu, H.; Mei, S.; Fan, L.; Wang, H. A line-scanning chromatic confocal sensor for three-dimensional profile measurement on highly reflective materials. Rev. Sci. Instrum. 2021, 92, 053707. [Google Scholar] [CrossRef] [PubMed]
- Miks, A.; Novak, J.; Novak, P. Analysis of method for measuring thickness of plane-parallel plates and lenses using chromatic confocal sensor. Appl. Opt. 2010, 49, 3259–3264. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.W.; Cai, J.X.; Zhang, D.S.; Chen, X.C.; Wang, Y.J. Nonlinear Correction for Fringe Projection Profilometry With Shifted-Phase Histogram Equalization. IEEE Trans. Instrum. Meas. 2022, 71, 3145361. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Y.L.; Shang, W.J.; Dong, S.C.; Wang, C.; Wang, Y.; Liu, T.; Cheng, F. Thickness Measurement for Glass Slides Based on Chromatic Confocal Microscopy with Inclined Illumination. Photonics 2021, 8, 170. [Google Scholar] [CrossRef]
- Xi, M.; Wang, Y.; Liu, H.; Xiao, H.; Li, X.; Li, H.; Ding, Z.; Jia, Z. Calibration of beam vector deviation for four-axis precision on-machine measurement using chromatic confocal probe. Measurement 2022, 194, 111011. [Google Scholar] [CrossRef]



| Fitting Method | (µm) | (µm) | (µm) |
|---|---|---|---|
| Fourier-LLS | 8.03 | 8.03 | 7.81 |
| Fourier-LAR | 0.62 | 0.73 | 0.572 |
| Polynomial-LLS | 18.36 | 6.84 | 6.7 |
| Polynomial-LAR | 0.57 | 0.78 | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, D.; Zhou, Z.; Li, Z.; Ding, R.; Jin, W.; Luo, H.; Xiong, W. Wafer Eccentricity Deviation Measurement Method Based on Line-Scanning Chromatic Confocal 3D Profiler. Photonics 2023, 10, 398. https://doi.org/10.3390/photonics10040398
Qu D, Zhou Z, Li Z, Ding R, Jin W, Luo H, Xiong W. Wafer Eccentricity Deviation Measurement Method Based on Line-Scanning Chromatic Confocal 3D Profiler. Photonics. 2023; 10(4):398. https://doi.org/10.3390/photonics10040398
Chicago/Turabian StyleQu, Dingjun, Zuoda Zhou, Zhiwei Li, Ruizhe Ding, Wei Jin, Haiyan Luo, and Wei Xiong. 2023. "Wafer Eccentricity Deviation Measurement Method Based on Line-Scanning Chromatic Confocal 3D Profiler" Photonics 10, no. 4: 398. https://doi.org/10.3390/photonics10040398
APA StyleQu, D., Zhou, Z., Li, Z., Ding, R., Jin, W., Luo, H., & Xiong, W. (2023). Wafer Eccentricity Deviation Measurement Method Based on Line-Scanning Chromatic Confocal 3D Profiler. Photonics, 10(4), 398. https://doi.org/10.3390/photonics10040398






