All-Solid Single-Polarization Anti-Resonant Fiber Base on Anisotropic Glass
Abstract
1. Introduction
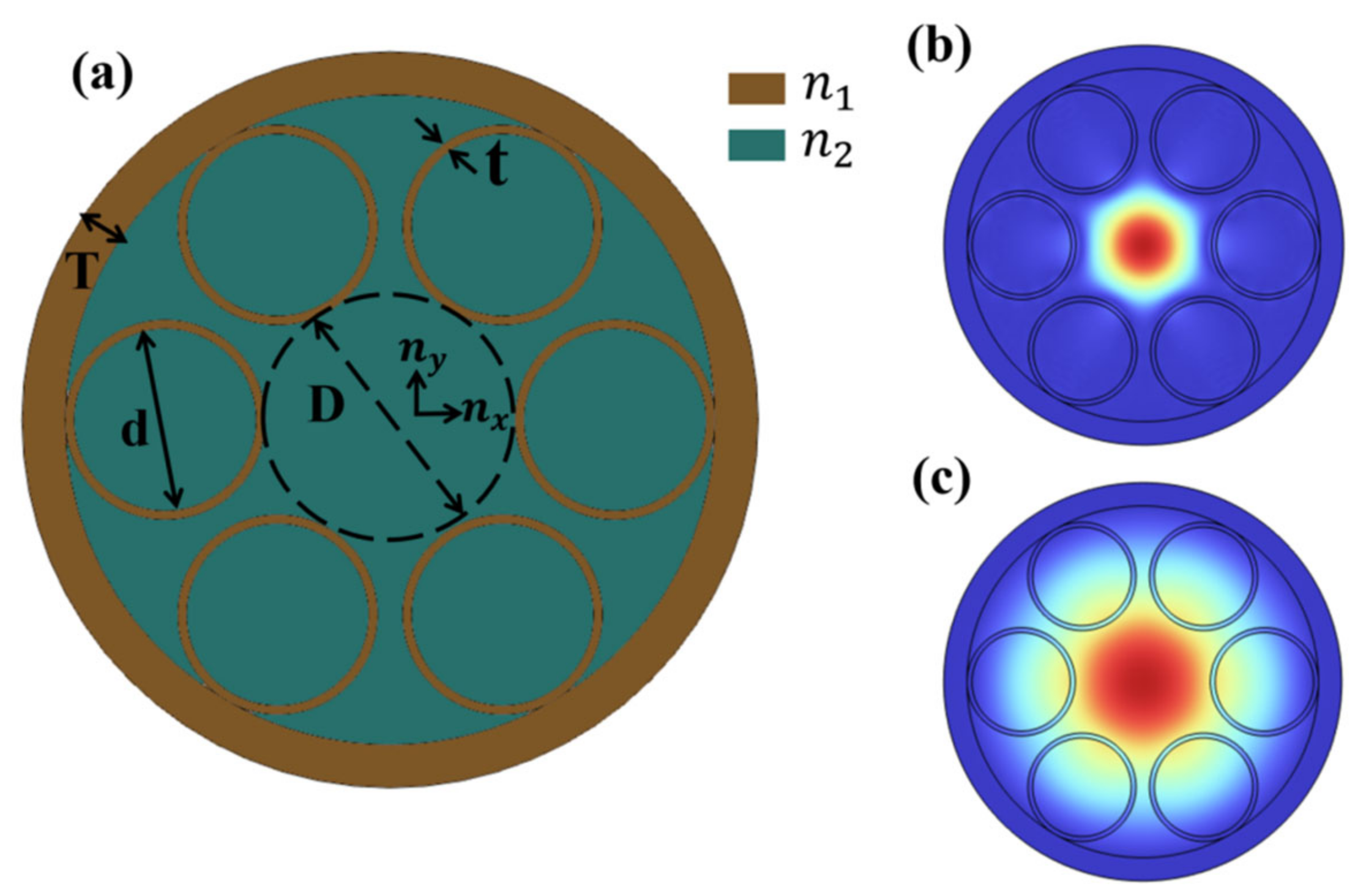
2. Fiber Structure and Performance
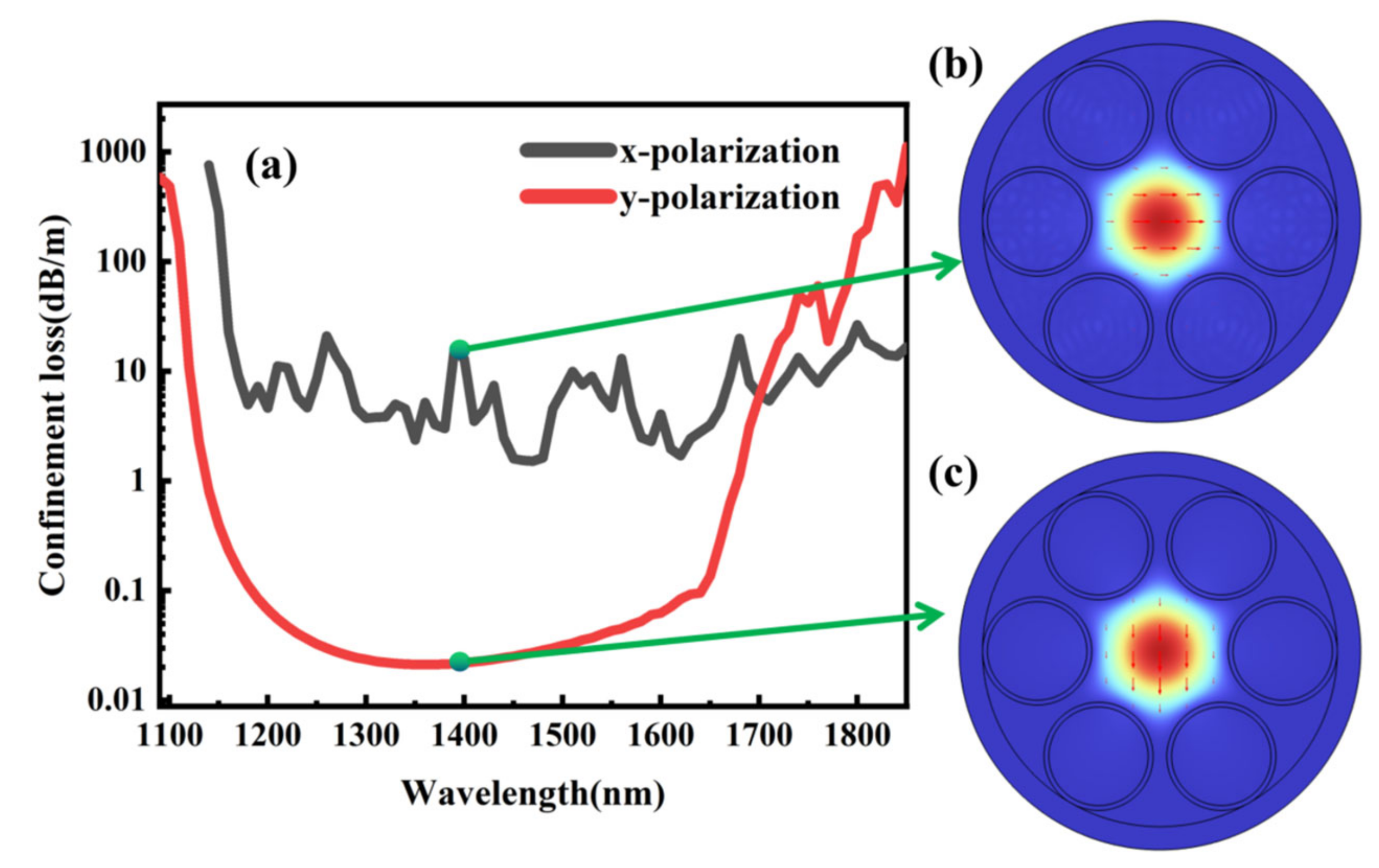
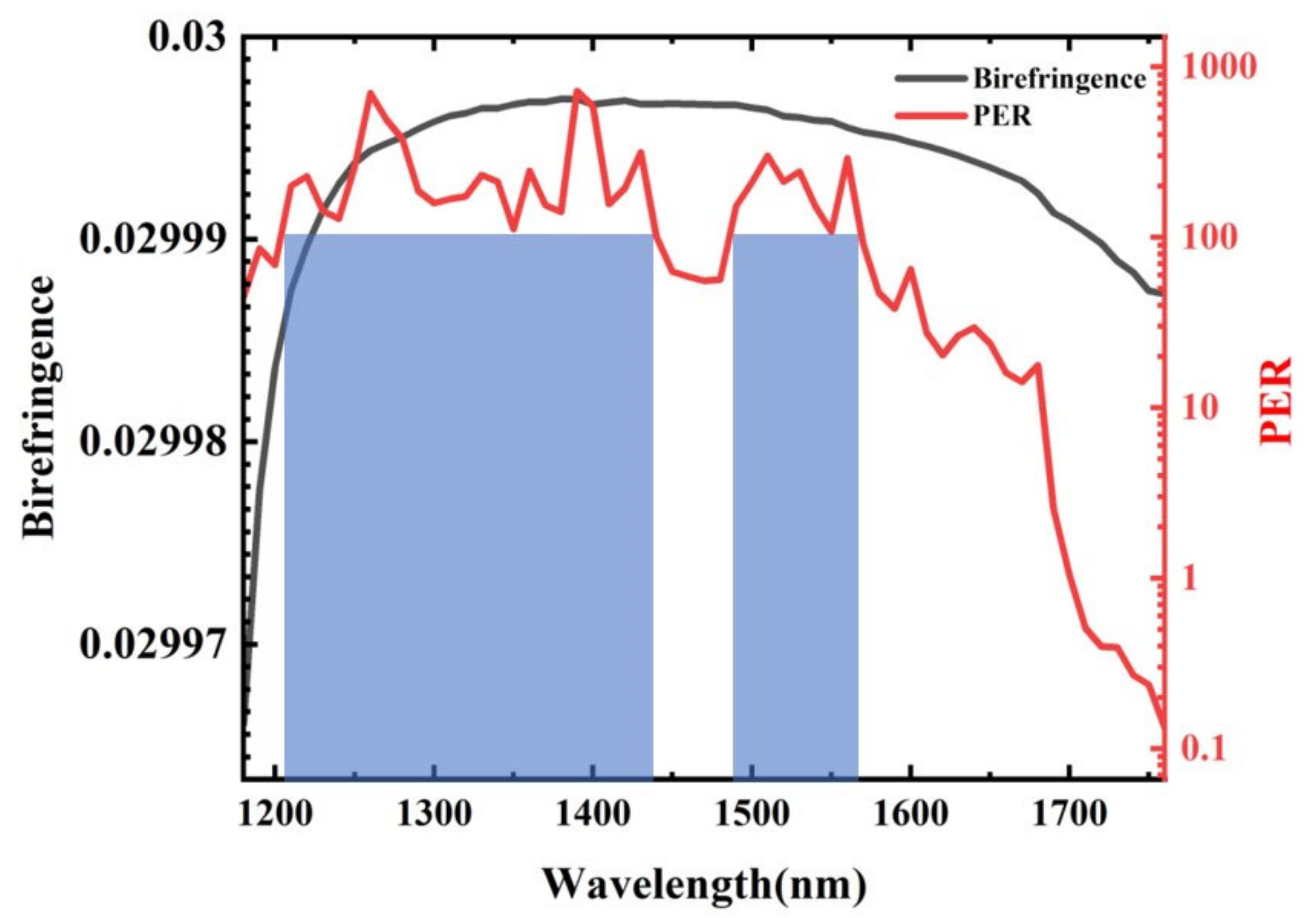
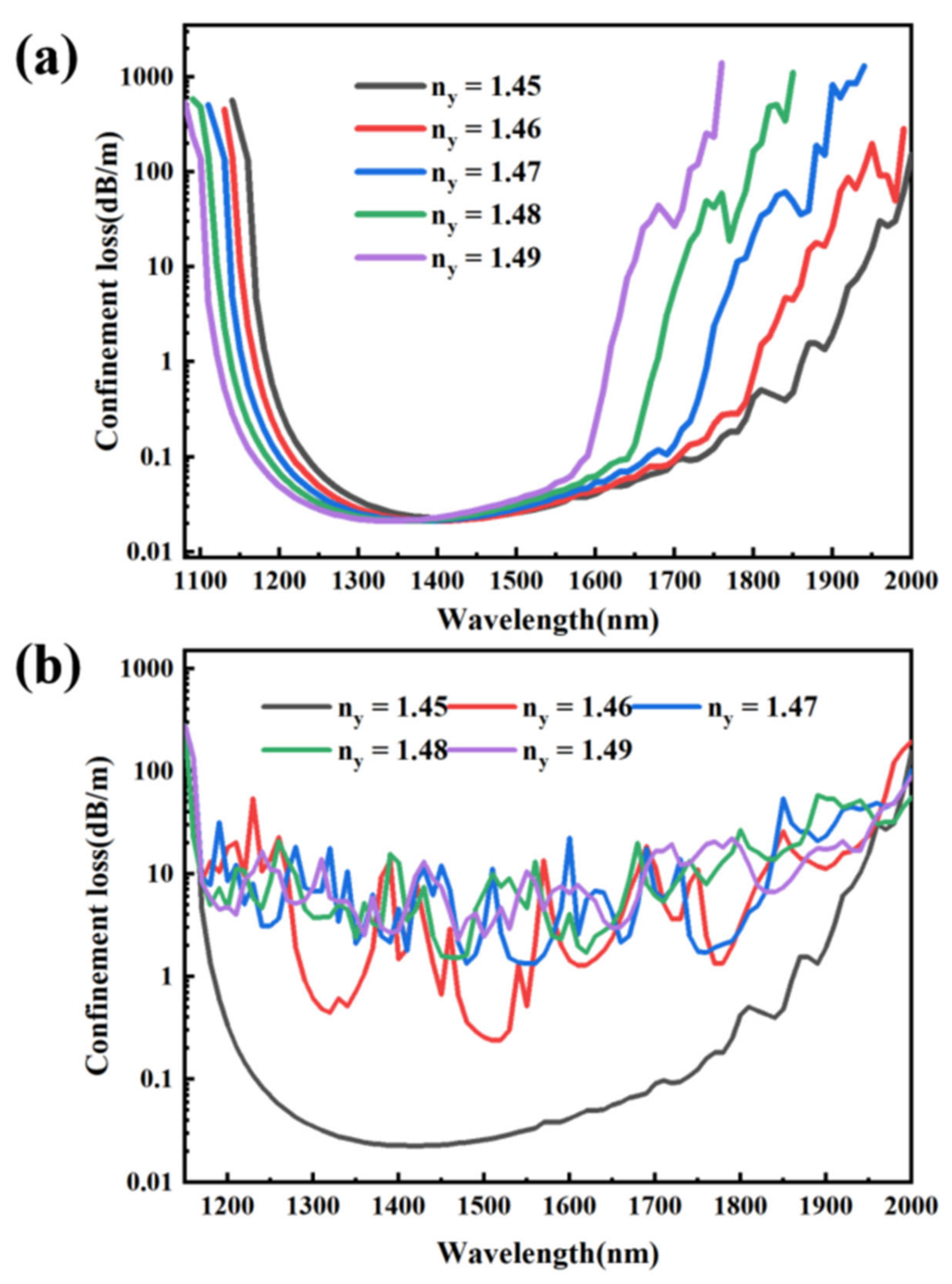
3. Fiber Properties
4. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shaw, L.B.; Kong, F.; Gu, G.; Hawkins, T.W.; Parsons, J.; Jones, M.; Dunn, C.; Kalichevsky-Dong, M.T.; Pulford, B.; Dajani, I.; et al. Polarizing 50 μm core Yb-doped photonic bandgap fiber. Proc. SPIE 2015, 9344, 934403. [Google Scholar] [CrossRef]
- Zhu, Y.; Song, N.; Gao, F.; Xu, X. Single-polarization single-mode hollow-core photonic-bandgap fiber with thin slab waveguide. Opt. Express 2021, 29, 30371–30383. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Lou, S.; Zhang, W.; Lian, Z. Single-polarization single-mode double-ring hollow-core anti-resonant fiber. Opt. Express 2018, 26, 31160–31171. [Google Scholar] [CrossRef] [PubMed]
- Ding, W.; Wang, Y. Analytic model for light guidance in single-wall hollow-core anti-resonant fibers. Opt. Express 2014, 22, 27242–27256. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Xu, M.; Knight, J.C. Experimental study of low-loss single-mode performance in anti-resonant hollow-core fibers. Opt. Express 2016, 24, 12969–12975. [Google Scholar] [CrossRef]
- Habib, M.S.; Bang, O.; Bache, M. Low-loss single-mode hollow-core fiber with anisotropic anti-resonant elements. Opt. Express 2016, 24, 8429–8436. [Google Scholar] [CrossRef]
- Chen, Y.; Saleh, M.F.; Joly, N.Y.; Biancalana, F. Low-loss single-mode negatively curved square-core hollow fibers. Opt. Lett. 2017, 42, 1285–1288. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, S.; Wang, X.; Yan, S.; Tang, Z.; Xing, Z. A broadband single mode single polarization metal wires-embedded hollow core anti-resonant fiber for polarization filter. Opt. Fiber Technol. 2019, 53, 102011. [Google Scholar] [CrossRef]
- Yerolatsitis, S.; Shurvinton, R.; Song, P.; Zhang, Y.; Francis-Jones, R.J.A.; Rusimova, K.R. Birefringent Anti-Resonant Hollow-Core Fiber. J. Lightwave Technol. 2020, 38, 5157–5162. [Google Scholar] [CrossRef]
- Yu, F.; Cann, M.; Brunton, A.; Wadsworth, W.; Knight, J. Single-mode solarization-free hollow-core fiber for ultraviolet pulse delivery. Opt. Express 2018, 26, 10879–10887. [Google Scholar] [CrossRef]
- Alam, M.Z.; Tahmid, M.I.; Mouna, S.T.; Islam, M.A.; Alam, M.S. Design of a novel star type photonic crystal fiber for mid-infrared supercontinuum generation. Opt. Commun. 2021, 500, 127322. [Google Scholar] [CrossRef]
- Ghanbari, A.; Olyaee, S. Highly Nonlinear Composite-Photonic Crystal Fibers with Simplified Manufacturing Process and Efficient Mid-IR Applications. Crystals 2023, 13, 226. [Google Scholar] [CrossRef]
- Ahmad, R.; Komanec, M.; Zvanovec, S. Circular lattice photonic crystal fiber for mid-IR supercontinuum generation. IEEE Photonics Technol. Lett. 2016, 28, 2736–2739. [Google Scholar] [CrossRef]
- Hao, L.; Wang, X.; Jia, K.; Zhao, G.; Xie, Z.; Zhu, S. Narrow-linewidth. single-polarization fiber laser using non-polarization optics. Opt. Lett. 2021, 46, 3769–3772. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Song, N.; Song, J.; Jin, J.; Wang, X. Transverse magneto-optic error of a miniature solid-core photonic-crystal fiber optic gyroscope. IEEE Access 2019, 7, 20106–20112. [Google Scholar] [CrossRef]
- Chen, X.; Antonelli, C.; Chandrasekhar, S.; Raybon, G.; Sinsky, J.; Mecozzi, A.; Winzer, P. 218-Gb/s single-wavelength, single-polarization, single-photodiode transmission over 125-km of standard singlemode fiber using Kramers-Kronig detection. In Proceedings of the Optical Fiber Communications Conference, Los Angeles, CA, USA, 19–23 March 2017. [Google Scholar] [CrossRef]
- Yan, S.; Lian, Z.; Lou, S.; Wang, X.; Zhang, W.; Tang, Z. Single-polarization single-mode hollow-core negative-curvature fiber with silicon-coated cladding. Opt. Quantum Electron. 2020, 52, 269. [Google Scholar] [CrossRef]
- Zhao, X.; Xiang, J.; Wu, X.; Li, Z. High birefringence, single-polarization, low loss hollow-core anti-resonant fibers. Opt. Express 2021, 29, 36273–36286. [Google Scholar] [CrossRef]
- Shang, L.; Feng, S.; Liu, G. Hole-Assisted Solid Core Bragg Fibers with a High-Index-Contrast Cladding for Broadband Single-Polarization Operation. J. Lightwave Technol. 2020, 38, 6104–6113. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, S.; Sheng, Q.; Shi, W.; Yan, Z.; Yao, J. Low-loss polarization-maintaining solid-core anti-resonant fiber in mid-infrared region. Results Phys. 2021, 26, 104439. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, S.; Sheng, Q.; Shi, W.; Yan, Z.; Tian, H.; Yao, J. Polarization-Maintaining Performance of Solid-Core Anti-Resonant Fiber with Nested Circular Tubes in 3 μm Wavelength. J. Lightwave Technol. 2022, 40, 1137–1143. [Google Scholar] [CrossRef]
- Payne, D.N.; Barlow, A.J.; Hansen, J.R. Development of low-and high-birefringence optical fibers. IEEE Trans. Microw. Theory Tech. 1982, 30, 323–334. [Google Scholar] [CrossRef]
- Urbanczyk, W.; Martynkien, T.; Bock, W.J. Dispersion effects in elliptical-core highly birefringent fibers. Appl. Opt. 2001, 40, 1911–1920. [Google Scholar] [CrossRef]
- Sihvola, A.H. Electromagnetic Mixing Formulas and Applications; The Institution of Electrical Engineers: Stevenage, UK, 1999. [Google Scholar]
- Wang, A.; George, A.K.; Liu, J.F.; Knight, J.C. Highly birefringent lamellar core fiber. Opt. Express 2005, 13, 5988–5993. [Google Scholar] [CrossRef]
- Waddie, A.J.; Buczynski, R.; Hudelist, F.; Nowosielski, J.; Pysz, D.; Stepien, R.; Taghizadeh, M.R. Form birefringence in nanostructured micro-optical devices. Opt. Mater. Express 2011, 1, 1251–1261. [Google Scholar] [CrossRef]
- Hsu, K.Y.; Yang, M.H.; Jheng, D.Y.; Huang, S.L.; Mennemann, K.; Dietrich, V.; Dubinskii, M. Single crystalline YAG-core fiber with a lanthanum dense flint glass cladding. In Proceedings of the 2013 Conference on Lasers and Electro-Optics Pacific Rim, CLEOPR 2013, Kyoto, Japan, 30 June–4 July 2013; pp. 1–2. [Google Scholar] [CrossRef]
- Michalik, D.; Anuszkiewicz, A.; Buczynski, R.; Kasztelanic, R. Toward highly birefringent silica Large Mode Area optical fibers with anisotropic core. Opt. Express 2021, 29, 22883–22899. [Google Scholar] [CrossRef] [PubMed]
- Anuszkiewicz, A.; Bouet, M.; Michalik, D.; Stepniewski, G.; Kasztelanic, R.; Filipkowski, A.; Pysz, D.; Cassez, A.; Klimczak, M.; Bouwmans, G.; et al. All-solid polarization-maintaining silica fiber with birefringence induced by anisotropic metaglass. Opt. Lett. 2022, 47, 401–404. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Huang, X.; Han, Y.; Chen, E.; Guo, P.; Zhang, W.; An, M.; Pan, Z.; Xu, Q.; Guo, X.; et al. High-performance γ-MnO2 Dual-Core, Pair-Hole Fiber for Ultrafast Photonics. Ultrafast Sci. 2023, 3, 0006. [Google Scholar] [CrossRef]
- Li, X.; Xu, W.; Wang, Y.; Zhang, X.; Hui, Z.; Zhang, H.; Wageh, S.; Al-Hartomy, O.A.; Al-Sehemi, A.G. Optical-intensity modulators with PbTe thermoelectric nanopowders for ultrafast photonics. Appl. Mater. Today 2022, 28, 101546. [Google Scholar] [CrossRef]
- Li, X.; An, M.; Li, G.; Han, Y.; Guo, P.; Chen, E.; Hu, J.; Song, Z.; Lu, H.; Lu, J. MOF-Derived Porous Dodecahedron rGO-Co3O4 for Robust Pulse Generation. Adv. Mater. Interfaces 2022, 9, 2101933. [Google Scholar] [CrossRef]
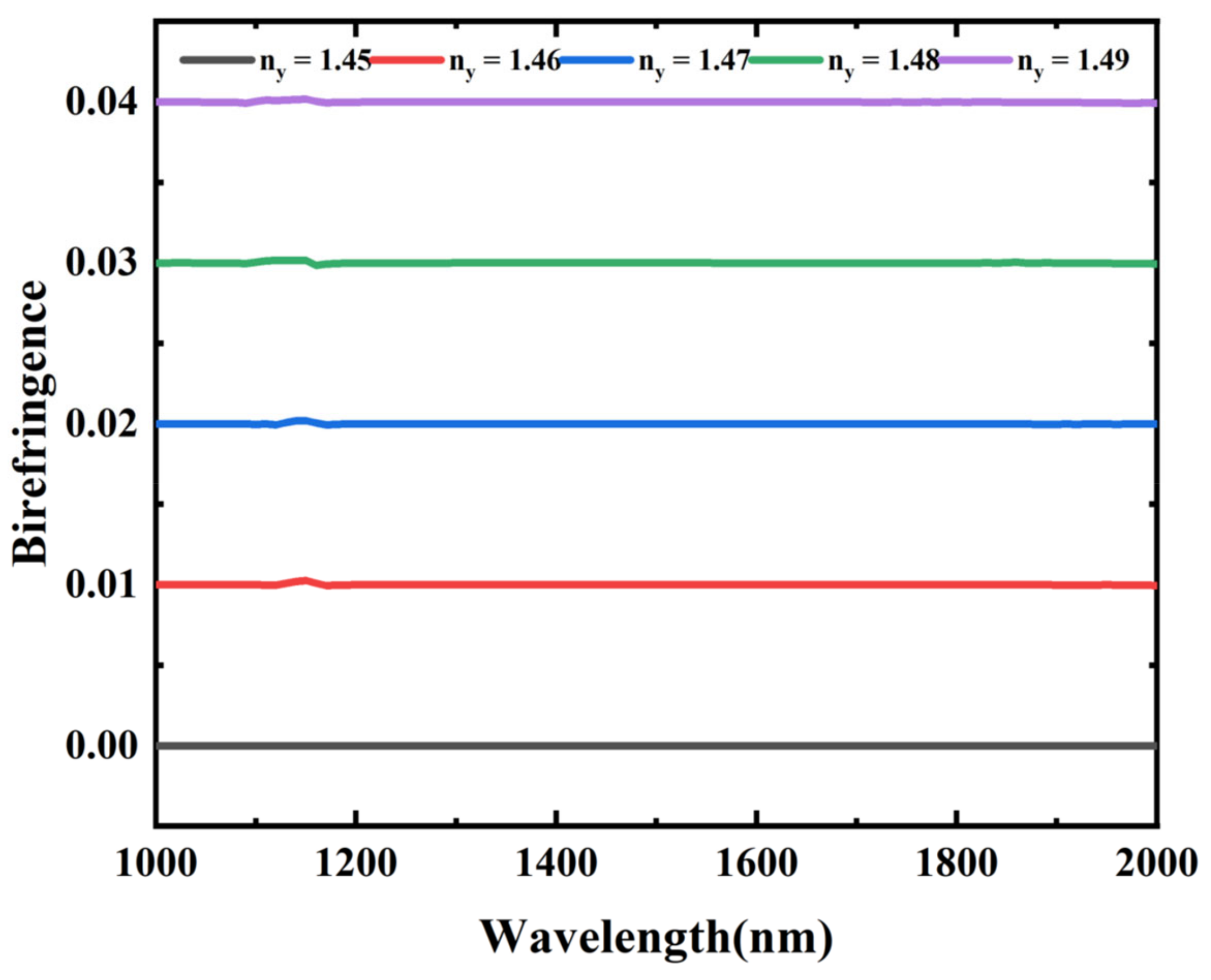


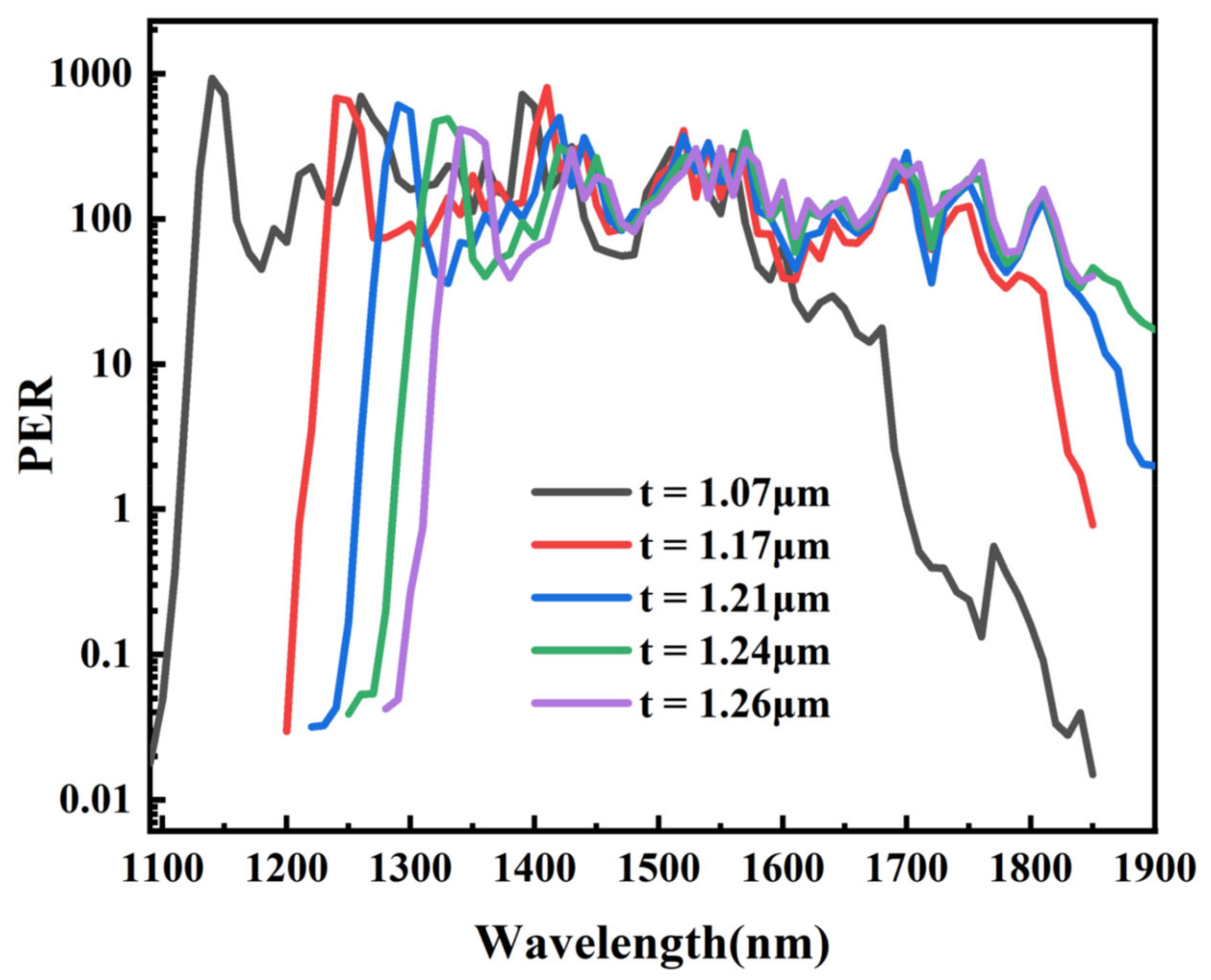
| Fiber Type | Method | Birefringence/PER | Bandwidth | Ref. |
|---|---|---|---|---|
| HC-PBGF | Add thick TSW structure | 2.40 × 10−4/15 dB | 120 nm | [2] |
| HC-ARF | Silicon-coated double-ring cladding structure | -/14,232 | 15 nm; 10 nm; 30 nm | [17] |
| HC-ARF | Non-touching nested structure | 3.07 × 10−4/4432 | 12 nm | [18] |
| SC-PBGF | Fill circular air holed | 10−3/15.7 | 277 nm | [19] |
| SC-ARF | Fill different materials | 1.56 × 10−5/- | - | [20] |
| SC-ARF | Fill different materials | 3.07 × 10−5/- | - | [21] |
| SC-ARF | Fiber-ore base on material anisotropy | 10−2/722 | 230 nm; 70 nm | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, W.; Zhang, B.; Xiao, A.; Duan, Z.; Ling, Q.; Zhang, Y.; Yu, Z.; Guan, Z.; Chen, D. All-Solid Single-Polarization Anti-Resonant Fiber Base on Anisotropic Glass. Photonics 2023, 10, 412. https://doi.org/10.3390/photonics10040412
Luo W, Zhang B, Xiao A, Duan Z, Ling Q, Zhang Y, Yu Z, Guan Z, Chen D. All-Solid Single-Polarization Anti-Resonant Fiber Base on Anisotropic Glass. Photonics. 2023; 10(4):412. https://doi.org/10.3390/photonics10040412
Chicago/Turabian StyleLuo, Weixuan, Bin Zhang, Anping Xiao, Zhiwei Duan, Qiang Ling, Yusheng Zhang, Zhangwei Yu, Zuguang Guan, and Daru Chen. 2023. "All-Solid Single-Polarization Anti-Resonant Fiber Base on Anisotropic Glass" Photonics 10, no. 4: 412. https://doi.org/10.3390/photonics10040412
APA StyleLuo, W., Zhang, B., Xiao, A., Duan, Z., Ling, Q., Zhang, Y., Yu, Z., Guan, Z., & Chen, D. (2023). All-Solid Single-Polarization Anti-Resonant Fiber Base on Anisotropic Glass. Photonics, 10(4), 412. https://doi.org/10.3390/photonics10040412







