Prospects for the Implementation of an Intense Source of Ultraviolet Radiation Based on a Gas-Discharge Plasma in a Quasi-Optical Cavity Excited by a Pulse of Terahertz Radiation
Abstract
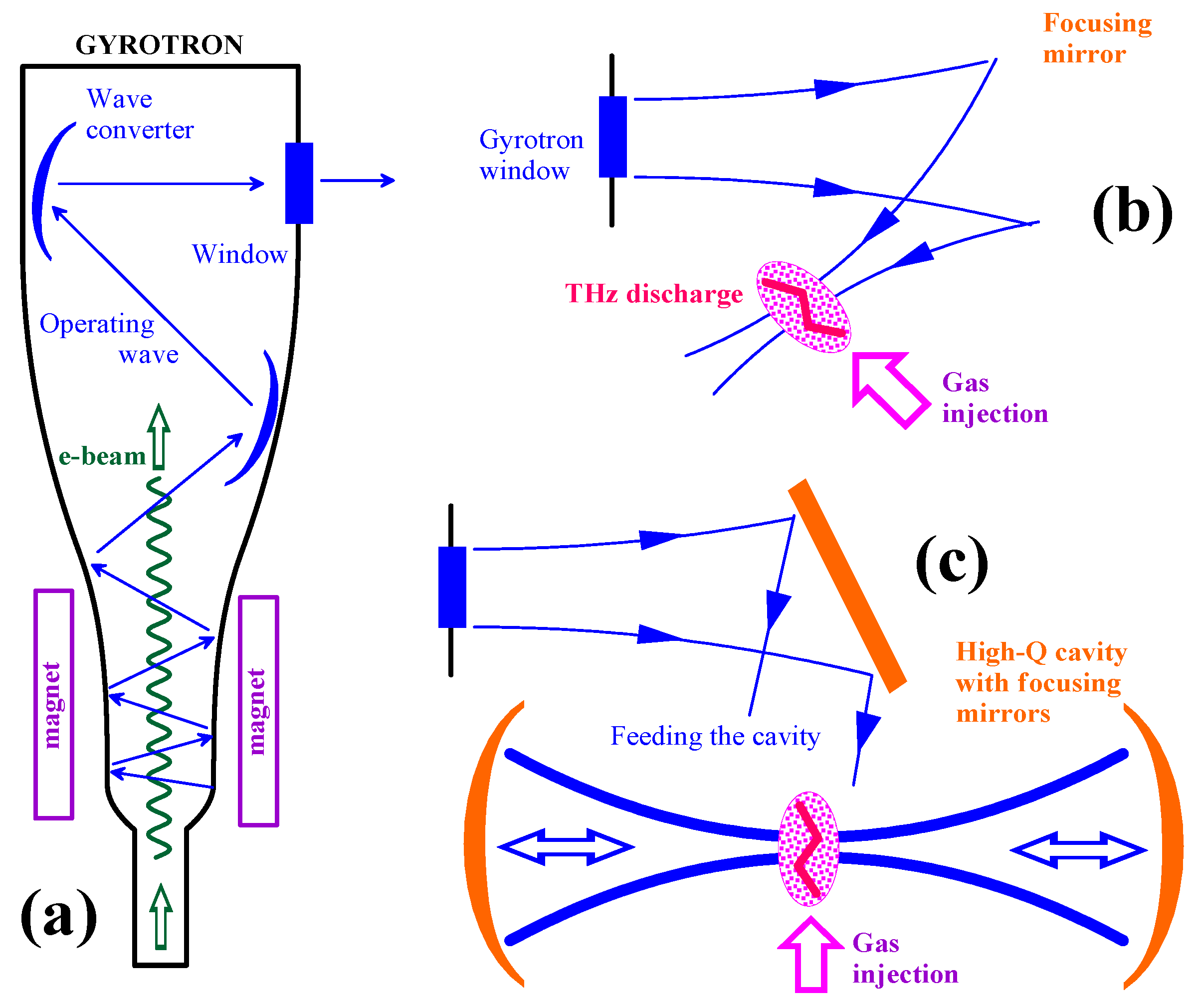
:1. Introduction
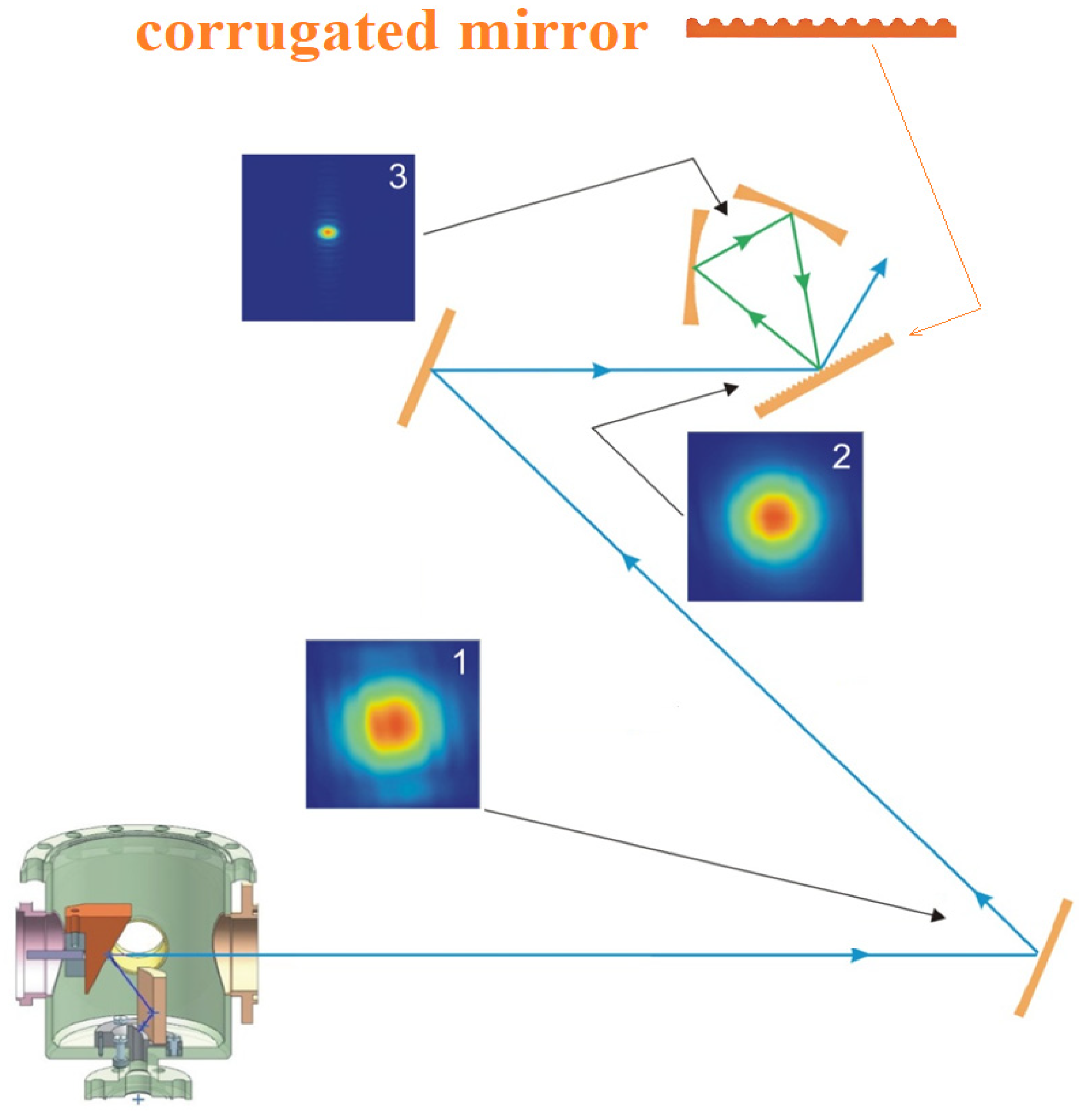
2. Calculations of a Quasi-Optical Cavity with a Traveling Wave
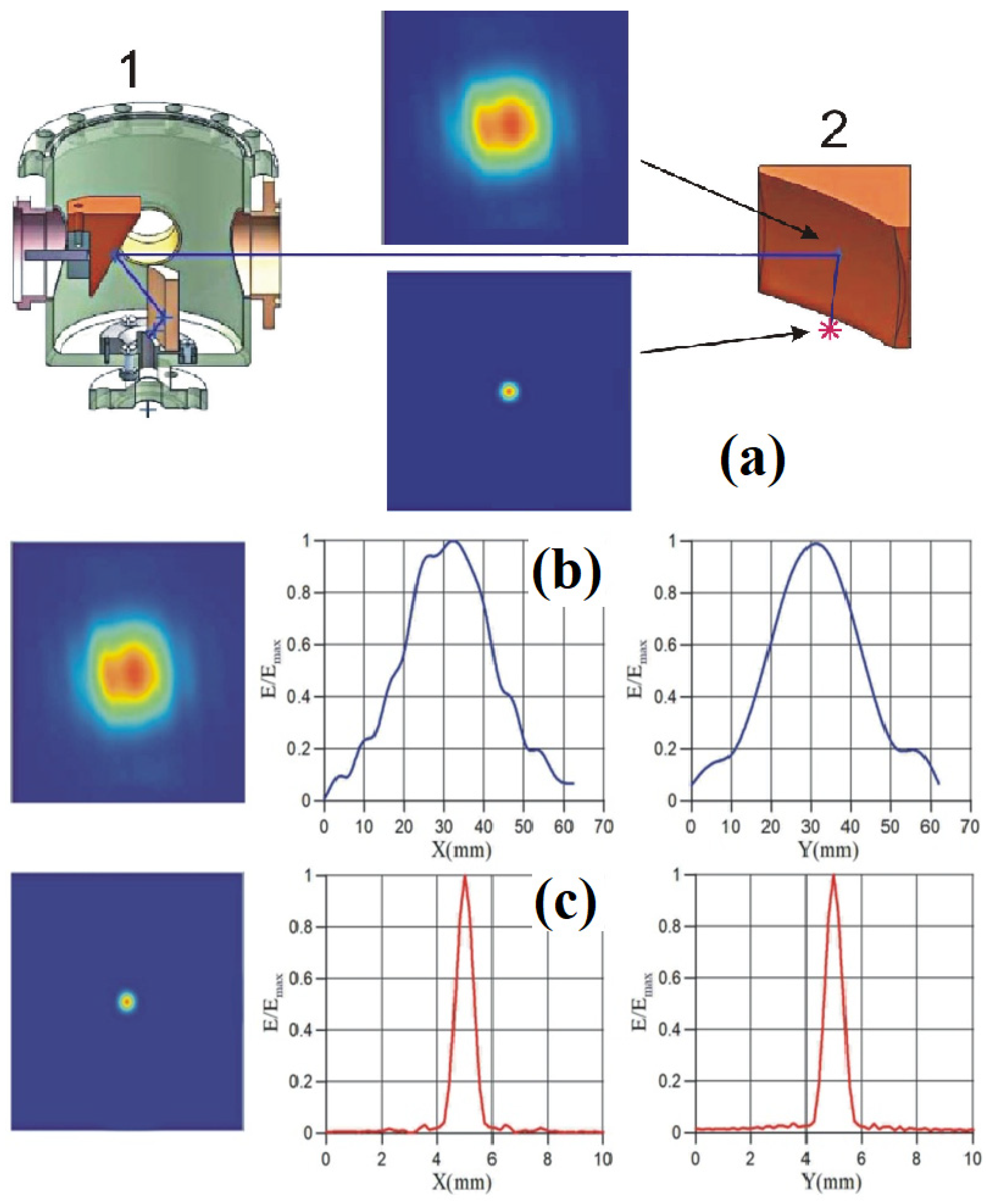
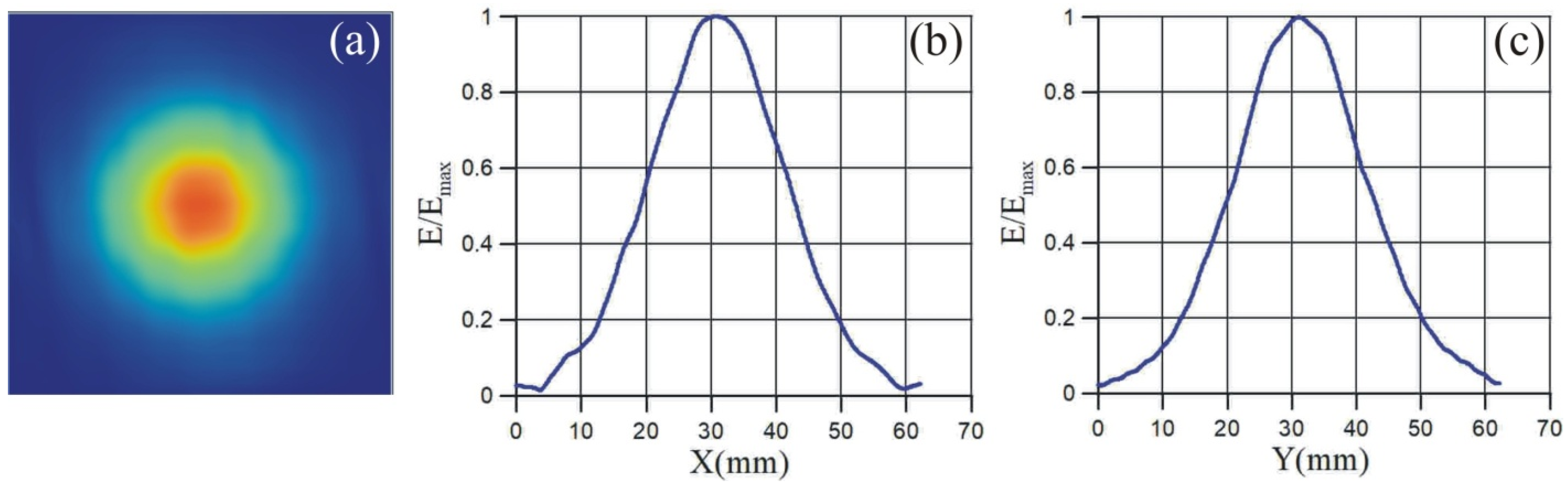
3. Focusing a Wave Beam in The Cavity
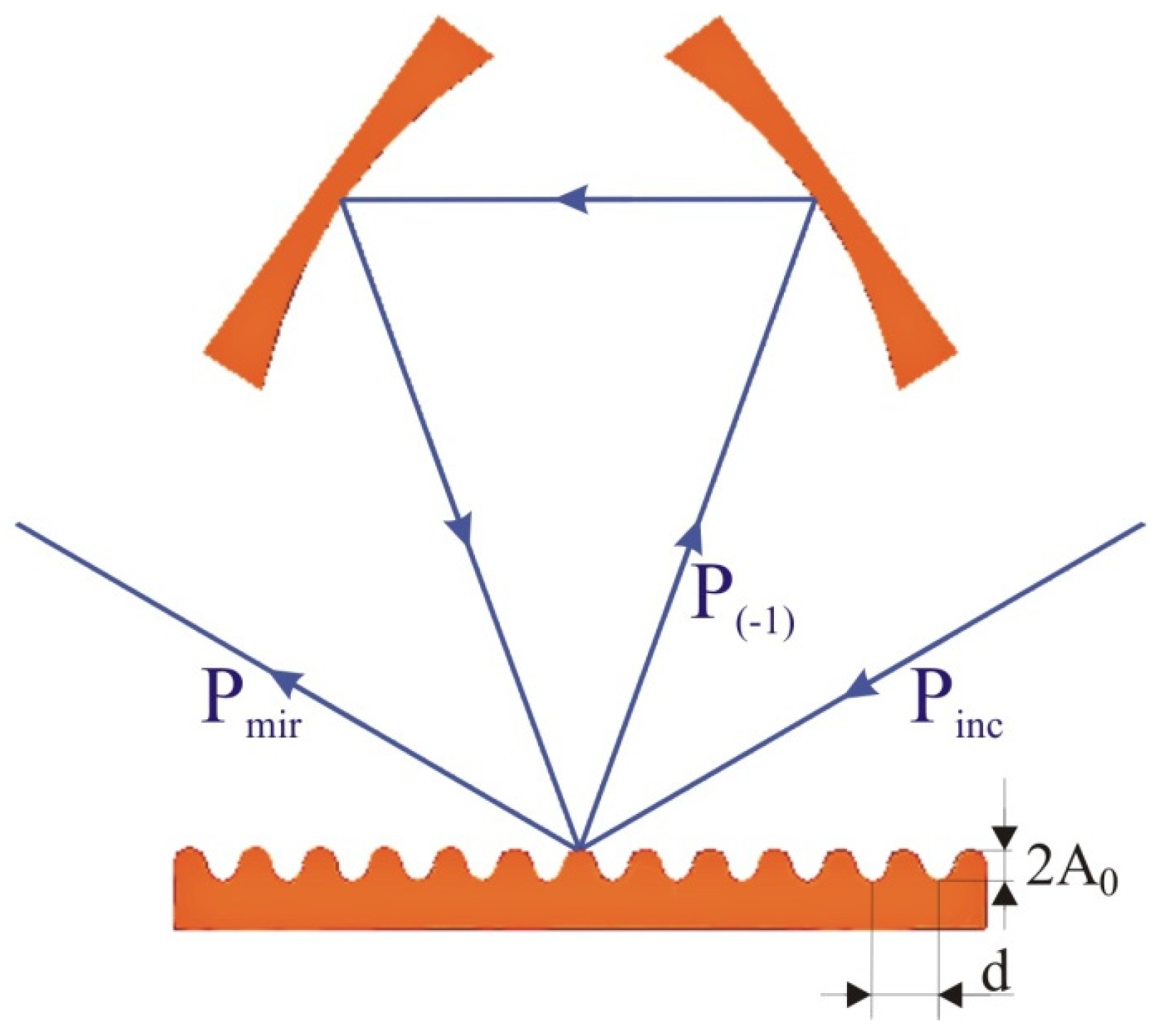
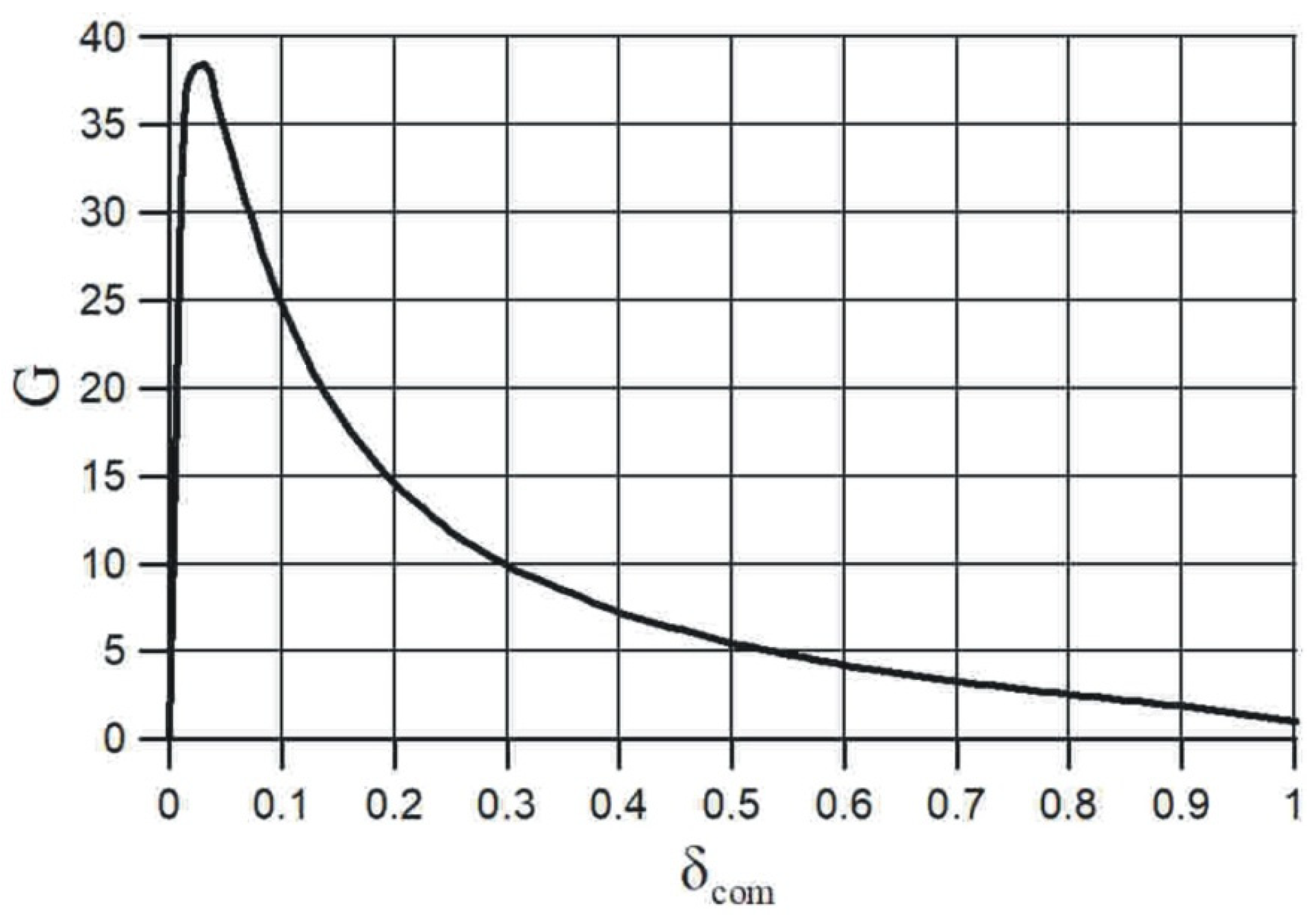
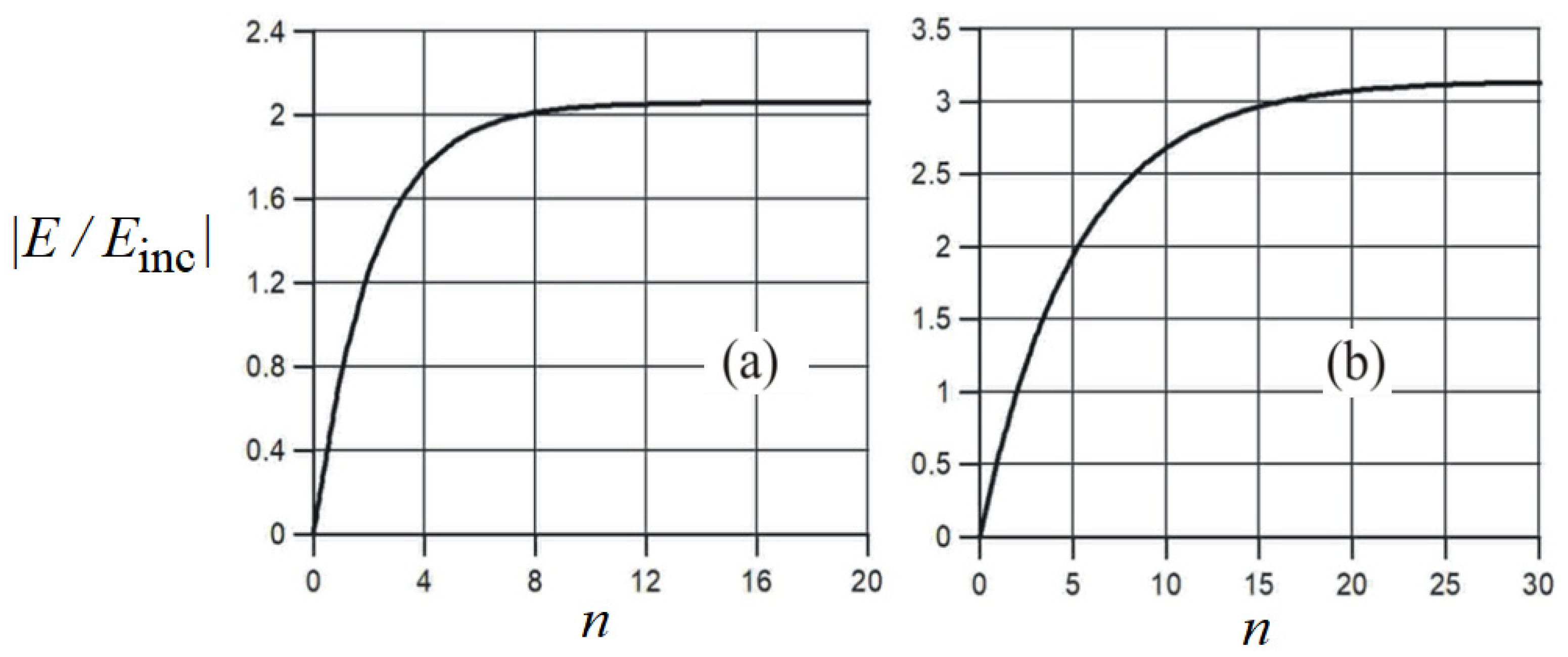
4. Increasing the Electric Field Strength
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, M.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.; Keiser, G.R.; Sternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.; et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 2012, 487, 345. [Google Scholar] [CrossRef] [PubMed]
- Feorst, M.; Manzoni, C.; Kaiser, S.; Tomioka, Y.; Tokura, Y.; Merlin, R.; Cavalleri, A. Nonlinear phononics as an ultrafast route to lattice control. Nat. Phys. 2011, 7, 854–856. [Google Scholar]
- Schubert, O.; Hohenleutner, M.; Langer, F.; Urbanek, B.; Lange, C.; Huttner, U.; Golde, D.; Meier, T.; Kira, M.; Koch, S.W.; et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nat. Photonics 2014, 8, 119–123. [Google Scholar] [CrossRef]
- Zhang, W.; Maldonado, P.; Jin, Z.; Seifert, T.S.; Arabski, J.; Schmerber, G.; Beaurepaire, E.; Bonn, M.; Kampfrath, T.; Oppeneer, P.M.; et al. Ultrafast terahertz magnetometry. Nat. Commun. 2020, 11, 4247. [Google Scholar]
- Kubacka, T.; Johnson, J.A.; Hoffmann, M.C.; Vicario, C.; De Jong, S.; Beaud, P.; Gr€ubel, S.; Huang, S.-W.; Huber, L.; Patthey, L.; et al. Large amplitude spin dynamics driven by a THz pulse in resonance with an electromagnon. Science 2014, 343, 1333. [Google Scholar]
- Piccirillo, B.; Paparo, D.; Rubano, A.; Andreone, A.; Rossetti Conti, M.; Giove, D.; Vicuña-Hernández, V.; Koral, C.; Masullo, M.R.; Mettivier, G.; et al. Liquid Crystal-Based Geometric Phase-Enhanced Platform for Polarization and Wavefront Analysis Techniques with the Short-TeraHertz FEL Oscillator TerRa@BriXSinO. Symmetry 2023, 15, 103. [Google Scholar]
- Zhu, X.; Bacon, D.R.; Madéo, J.; Dani, K.M. High Field Single- to Few-Cycle THz Generation with Lithium Niobate. Photonics 2021, 8, 183. [Google Scholar] [CrossRef]
- Novelli, F.; Ma, C.Y.; Adhlakha, N.; Adams, E.M.; Ockelmann, T.; Das Mahanta, D.; Di Pietro, P.; Perucchi, A.; Havenith, M. Nonlinear TeraHertz Transmission by Liquid Water at 1 THz. Appl. Sci. 2020, 10, 5290. [Google Scholar]
- Li, G.; Tan, J.; Xu, Y.; Cui, H.; Tang, B.; Jiao, Z.; Zhou, W.; Zeng, J.; Xia, N. High-Performance Dual-Channel Photonic Crystal Terahertz Wave Modulator Based on the Defect Mode Disappearance of a Combined Microcavity. Photonics 2023, 10, 298. [Google Scholar] [CrossRef]
- Mølvig, B.H.; Bæk, T.; Ji, J.; Bøggild, P.; Lange, S.J.; Jepsen, P.U. Terahertz Cross-Correlation Spectroscopy and Imaging of Large-Area Graphene. Sensors 2023, 23, 3297. [Google Scholar] [CrossRef]
- Bratman, V.L.; Zorin, V.G.; Kalynov, Y.K.; Koldanov, V.A.; Litvak, A.G.; Razin, S.V.; Sidorov, A.V.; Skalyga, V.A. Plasma creation by terahertz electromagnetic radiation. Phys. Plasmas 2011, 18, 083507. [Google Scholar]
- Bratman, V.L.; Izotov, I.V.; Kalynov, Y.K.; Koldanov, V.A.; Litvak, A.G.; Razin, S.V.; Sidorov, A.V.; Skalyga, V.A.; Zorin, V.G. Features of the plasma glow in the low pressure terahertz gas discharge. Phys. Plasmas 2013, 20, 123512. [Google Scholar]
- Glyavin, M.Y.; Golubev, S.V.; Izotov, I.V.; Litvak, A.G.; Luchinin, A.G.; Razin, S.V.; Sidorov, A.V.; Skalyga, V.A.; Vodopyanov, A.V. A point-like source of extreme ultraviolet radiation based on a discharge in a non-uniform gas flow, sustained by powerful gyrotron radiation of terahertz frequency band. Appl. Phys. Lett. 2014, 105, 174101. [Google Scholar]
- Sidorov, A.V.; Razin, S.V.; Golubev, S.V.; Safronova, M.I.; Fokin, A.P.; Luchinin, A.G.; Vodopyanov, A.V.; Glyavin, M.Y. Measurement of plasma density in the discharge maintained in a nonuniform gas flow by a high-power terahertz-wave gyrotron. Phys. Plasmas 2016, 23, 043511. [Google Scholar]
- Shalashov, A.G.; Vodopyanov, A.V.; Abramov, I.S.; Sidorov, A.V.; Gospodchikov, E.D.; Razin, S.V.; Chkhalo, N.I.; Salashchenko, N.N.; Glyavin, M.Y.; Golubev, S.V. Observation of extreme-ultraviolet light emission from an expanding plasma jet with multiply-charged argon or xenon ions. Appl. Phys. Lett. 2018, 113, 153502. [Google Scholar]
- Shalashov, A.G.; Gospodchikov, E.D. Simple Approach to Electromagnetic Scattering by Small Radially Inhomogeneous Spheres. IEEE Transac. Antennas Propag. 2016, 64, 3960. [Google Scholar]
- Abramov, I.S.; Shalashov, A.G.; Gospodchikov, E.D. Extreme-ultraviolet light source for lithography based on an expanding jet of dense xenon plasma supported by microwaves. Phys. Rev. Appl. 2018, 10, 034065. [Google Scholar]
- Glyavin, M.Y.; Luchinin, A.G.; Golubiatnikov, G.Y. Generation of 1.5-kW, 1-THz coherent radiation from a gyrotron with a pulsed magnetic field. Phys. Rev. Lett. 2008, 100, 015101. [Google Scholar] [PubMed]
- Bratman, V.L.; Kalynov, Y.K.; Manuilov, V.N. Large-Orbit Gyrotron Operation in the Terahertz Frequency Range. Phys. Rev. Lett. 2009, 102, 245101. [Google Scholar]
- Thumm, M. State-of-the-art of high-power gyro-devices and free electron masers. J. Infrared Millim. Terahertz Waves 2020, 41, 140. [Google Scholar]
- Urbanus, W.H.; Bongers, W.A.; Van Der Geer, C.A.J.; Manintveld, P.; Plomp, J.; Pluygers, J.; Poelman, A.J.; Smeets, P.H.M.; Verhoeven, A.G.A.; Bratman, V.L.; et al. High-power electrostatic free-electron maser as a future source for fusion plasma heating: Experiments in the short-pulse regime. Phys. Rev. E 1999, 59, 6058. [Google Scholar] [CrossRef]
- Vinokurov, N.A. Free electron lasers as a high-power terahertz sources. J. Infrared Millim. THz Waves 2011, 32, 1123. [Google Scholar] [CrossRef]
- Green, B.; Kovalev, S.; Asgekar, V.; Geloni, G.; Lehnert, U.; Golz, T.; Kuntzsch, M.; Bauer, C.; Hauser, J.; Voigtlaender, J.J.S.R.; et al. High-field High-repetition-rate Sources for the Coherent THz Control of Matter. Sci. Rep. 2016, 6, 22256. [Google Scholar]
- Snively, E.C.; Xiong, J.; Musumeci, P.; Gover, A. Broadband THz amplification and superradiant spontaneous emission in a guided FEL. Opt. Express 2019, 27, 20221. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.-W.; Eduardo Granados, E.; Huang, W.R.; Hong, K.-H.; Zapata, L.E.; Kärtner, F.X. High conversion efficiency, high energy terahertz pulses by optical rectification in cryogenically cooled lithium niobate. Opt. Lett. 2013, 38, 796. [Google Scholar] [CrossRef] [PubMed]
- Ovchinnikov, A.V.; Chefonov, O.V.; Agranat, M.B.; Grishunin, K.A.; Il’in, N.A.; Pisarev, R.V.; Kimel, A.V.; Kalashnikova, A.M. Optical Second Harmonic Generation Induced by Picosecond Terahertz Pulses in Centrosymmetric Antiferromagnet NiO1. JETP Lett. 2016, 104, 441. [Google Scholar] [CrossRef]
- Kalynov, Y.K.; Bandurkin, I.V.; Zavolskiy, N.A.; Manuilov, V.N.; Movshevich, B.Z.; Osharin, I.V. High-Power Pulsed Terahertz-Wave Large-Orbit Gyrotron for a Promising Source of Extreme Ultraviolet Radiation. Radiophys. Quantum Electron. 2020, 63, 354. [Google Scholar]
- Kalynov, Y.K.; Razin, S.V.; Sidorov, A.V.; Vodopyanov, A.V.; Veselov, A.P. Prospects of the gas-discharge EUV source based on the plasma creation by powerful pulsed terahertz gyrotrons. In Proceedings of the SPIE 11582, Fourth International Conference on Terahertz and Microwave Radiation, Generation, Detection and Applications 115820P, Tomsk, Russia, 24–26 August 2020. [Google Scholar]
- Denisov, G.G.; Shmelev, M.Y. Effective power input into quasi-optical cavity with travelling wave. Int. J. Infrared Millim. Waves 1991, 12, 1187. [Google Scholar]
- Electromagnetic Theory of Grating; Petit, R. (Ed.) Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1980. [Google Scholar]
- ANSYS HFSS as a part of the ANSYS Electromagnetics Suite 2022R1, license of the Institute of Applied Physics of the Russian Academy of Sciences, customer #280108.
- Koposova, E.V. Ohmic Losses During Scattering of a Plane Electromagnetic Wave by a Metal Corrugated Surface. Radiophys. Quantum Electron. 2015, 85, 350. [Google Scholar] [CrossRef]



| σ (S/m) | |||
|---|---|---|---|
| 0.007 | 0.012 | 0.026 |
| Material | Cooper | |
|---|---|---|
| δcom | 0.3 | 0.6 |
| A0 | 0.17 λ | 0.33 λ |
| G | 9.9 | 4.2 |
| Q | 14600 | 7600 |
| Δf (MHz) | 68 | 131 |
| ΔL (mm) | 0.016 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalynova, G.; Kalynov, Y.; Savilov, A. Prospects for the Implementation of an Intense Source of Ultraviolet Radiation Based on a Gas-Discharge Plasma in a Quasi-Optical Cavity Excited by a Pulse of Terahertz Radiation. Photonics 2023, 10, 440. https://doi.org/10.3390/photonics10040440
Kalynova G, Kalynov Y, Savilov A. Prospects for the Implementation of an Intense Source of Ultraviolet Radiation Based on a Gas-Discharge Plasma in a Quasi-Optical Cavity Excited by a Pulse of Terahertz Radiation. Photonics. 2023; 10(4):440. https://doi.org/10.3390/photonics10040440
Chicago/Turabian StyleKalynova, Galina, Yuriy Kalynov, and Andrei Savilov. 2023. "Prospects for the Implementation of an Intense Source of Ultraviolet Radiation Based on a Gas-Discharge Plasma in a Quasi-Optical Cavity Excited by a Pulse of Terahertz Radiation" Photonics 10, no. 4: 440. https://doi.org/10.3390/photonics10040440
APA StyleKalynova, G., Kalynov, Y., & Savilov, A. (2023). Prospects for the Implementation of an Intense Source of Ultraviolet Radiation Based on a Gas-Discharge Plasma in a Quasi-Optical Cavity Excited by a Pulse of Terahertz Radiation. Photonics, 10(4), 440. https://doi.org/10.3390/photonics10040440





