An Ultra-Low-Loss Waveguide Based on BIC Used for an On-Chip Integrated Optical Gyroscope
Abstract
1. Introduction
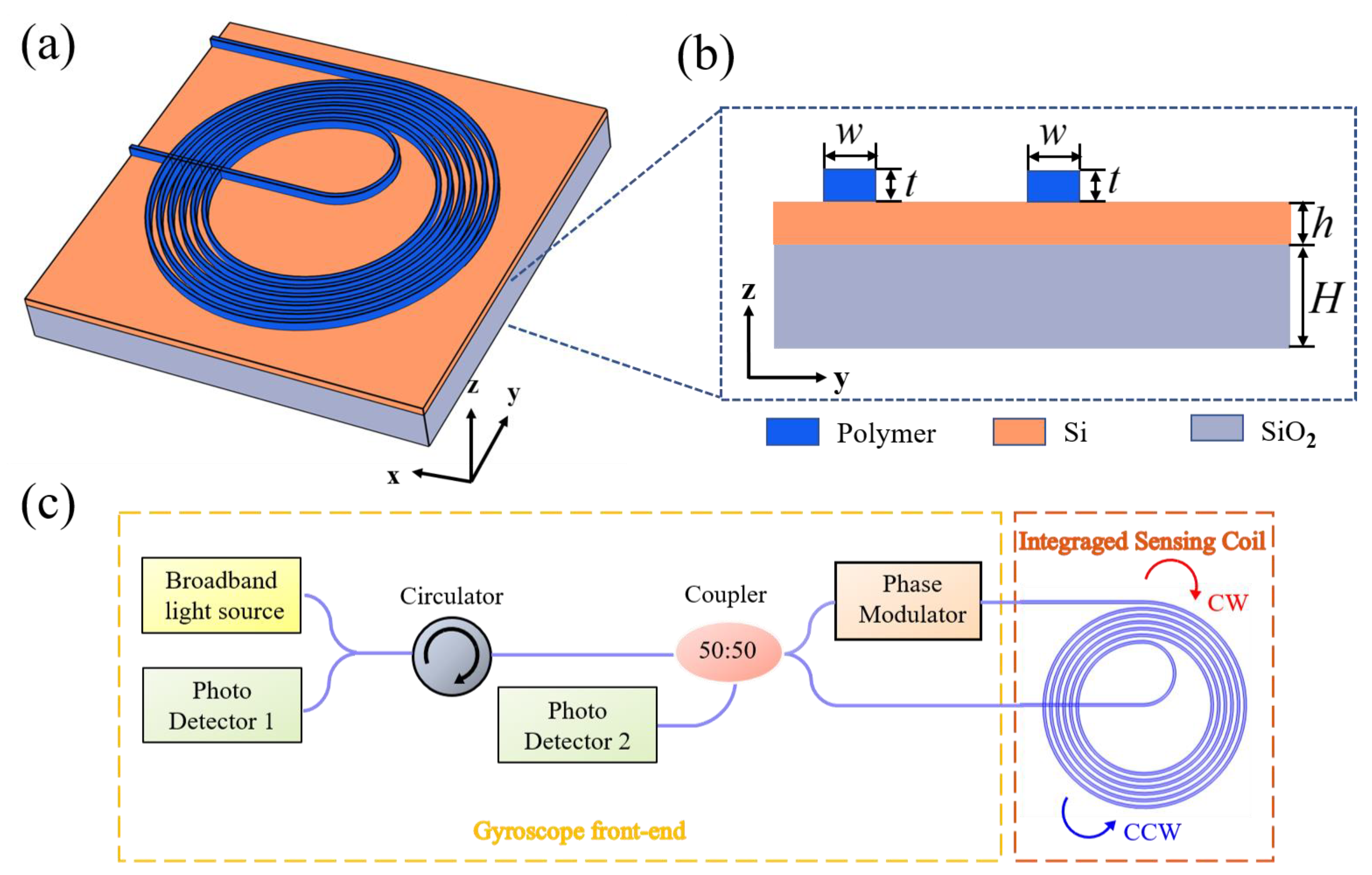
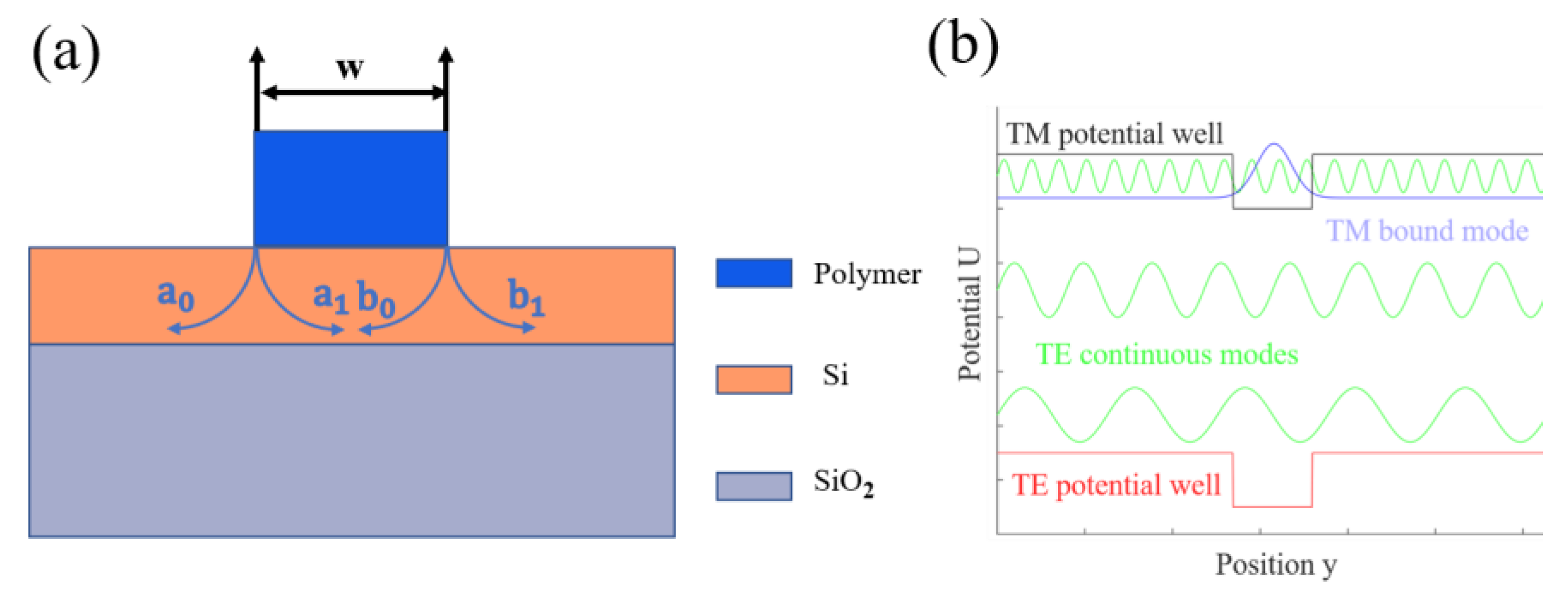
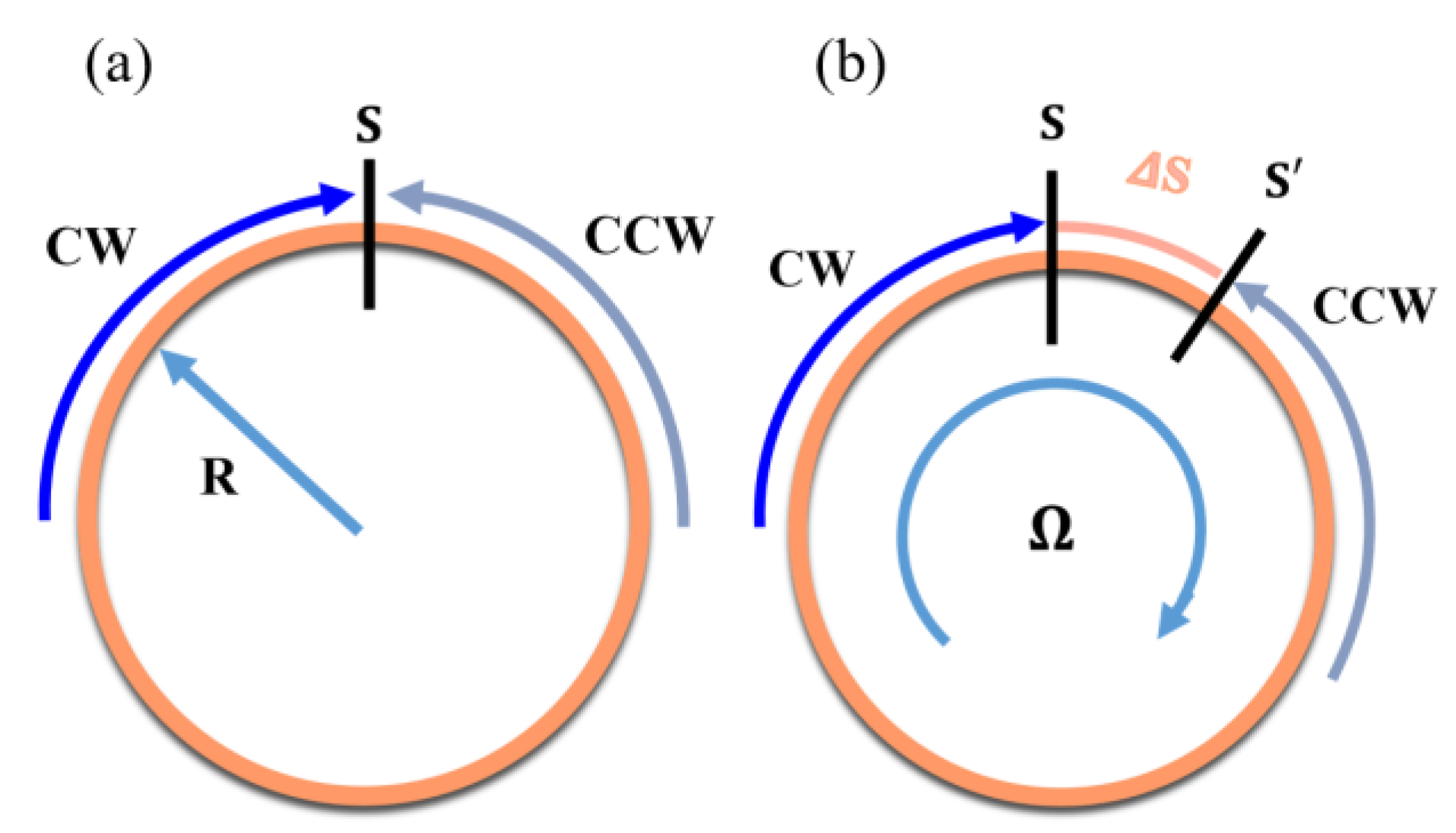
2. Model and Theory
3. Simulations and Analysis
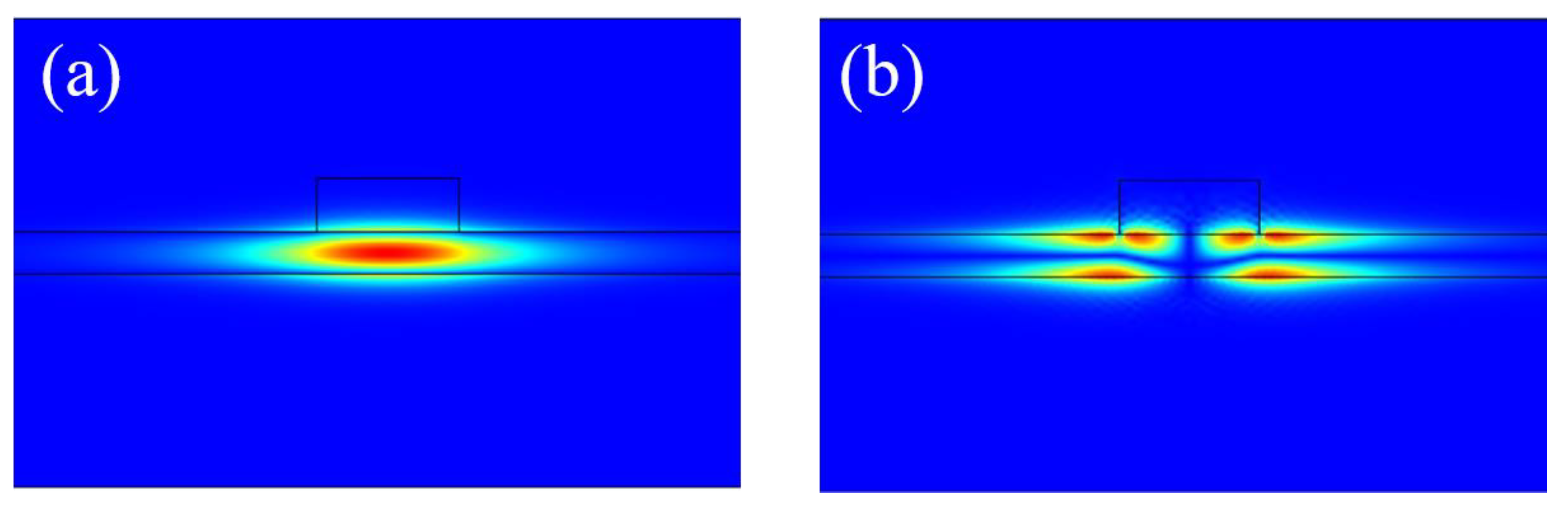
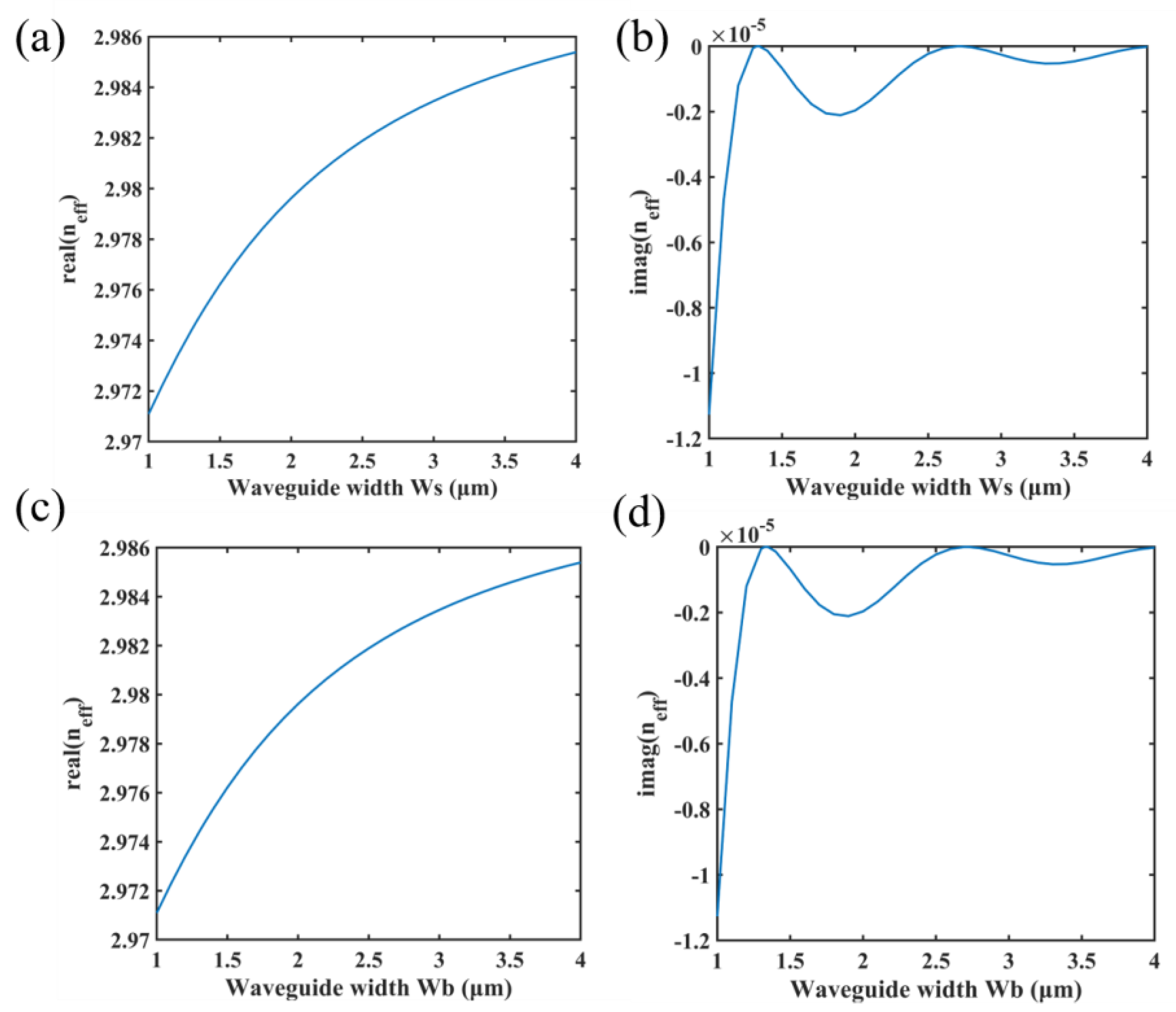
3.1. BIC in a Straight Waveguide
3.2. BIC in a Bent Waveguide
3.3. Dispersion Effects at a Single Wavelength
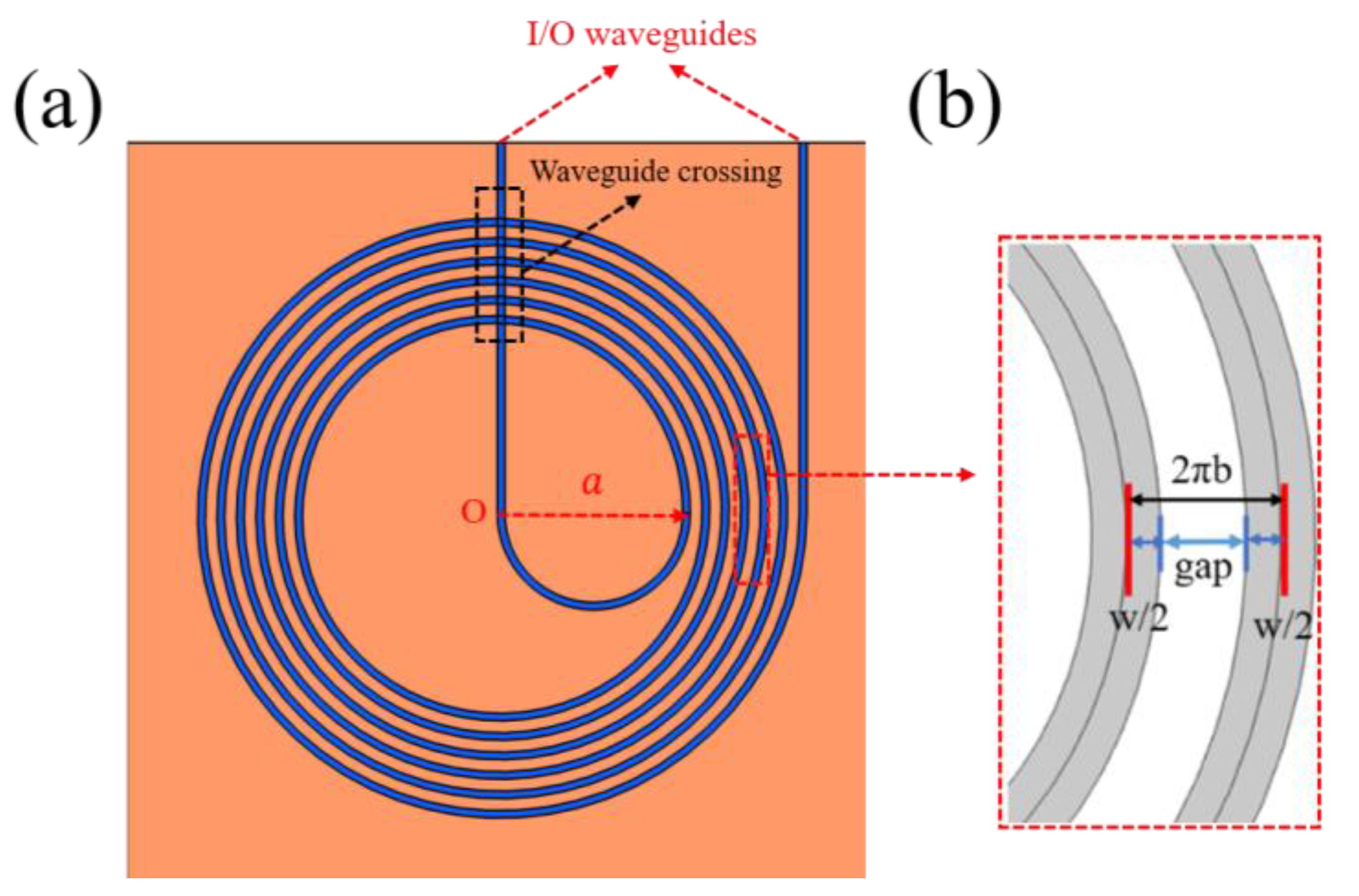
3.4. Design of Archimedes Spiral Waveguide Coil
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ezekiel, S.; Balsamo, S. Passive ring resonator laser gyroscope. Appl. Phys. Lett. 1977, 30, 478–480. [Google Scholar] [CrossRef]
- Venediktov, V.Y.; Filatov, Y.V.; Shalymov, E.V. Passive ring resonator micro-optical gyroscopes. Quantum Electron. 2016, 46, 437. [Google Scholar] [CrossRef]
- Chow, W.; Gea-Banacloche, J.; Pedrotti, L.; Sanders, V.; Schleich, W.; Scully, M. The ring laser gyro. Rev. Mod. Phys. 1985, 57, 61. [Google Scholar] [CrossRef]
- Culshaw, B.; Giles, I. Fibre optic gyroscopes. J. Phys. E Sci. Instrum. 1983, 16, 5. [Google Scholar] [CrossRef]
- Khial, P.P.; White, A.D.; Hajimiri, A. Nanophotonic optical gyroscope with reciprocal sensitivity enhancement. Nat. Photonics 2018, 12, 671–675. [Google Scholar] [CrossRef]
- Xue, X.-M.; Tang, J.; Zhou, H.-L.; Qin, Y.-Y.; Song, Y.; Li, R.-Z.; Zhang, X.-Y.; Zhang, T. All-polymer monolithic resonant integrated optical gyroscope. Opt. Express 2022, 30, 42728–42737. [Google Scholar] [CrossRef]
- Suzuki, K.; Takiguchi, K.; Hotate, K. Monolithically integrated resonator microoptic gyro on silica planar lightwave circuit. J. Light. Technol. 2000, 18, 66–72. [Google Scholar] [CrossRef]
- Gundavarapu, S.; Huffman, T.; Moreira, R.; Belt, M.; Bowers, J.E.; Blumenthal, D.J. Integrated ultra-low-loss silicon nitride waveguide coil for optical gyroscopes. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 20–24 March 2016; p. W4E. 5. [Google Scholar]
- Horikawa, T.; Shimura, D.; Mogami, T. Low-loss silicon wire waveguides for optical integrated circuits. MRS Commun. 2016, 6, 9–15. [Google Scholar] [CrossRef]
- Ciminelli, C.; Dell’Olio, F.; Armenise, M.N.; Soares, F.M.; Passenberg, W. High performance InP ring resonator for new generation monolithically integrated optical gyroscopes. Opt. Express 2013, 21, 556–564. [Google Scholar] [CrossRef]
- Ciminelli, C.; D’Agostino, D.; Carnicella, G.; Dell’Olio, F.; Conteduca, D.; Ambrosius, H.P.; Smit, M.K.; Armenise, M.N. A high-Q InP resonant angular velocity sensor for a monolithically integrated optical gyroscope. IEEE Photonics J. 2015, 8, 6800418. [Google Scholar] [CrossRef]
- He, Y.; Lu, Z.; Kuai, X.; Feng, Z.; Han, W.; Li, Z.; Yan, W.; Yang, F. Heterogeneous integration of InP and Si3N4 waveguides based on interlayer coupling for an integrated optical gyroscope. Appl. Opt. 2021, 60, 662–669. [Google Scholar] [CrossRef]
- Wu, B.; Yu, Y.; Xiong, J.; Zhang, X. Silicon integrated interferometric optical gyroscope. Sci. Rep. 2018, 8, 8766. [Google Scholar] [CrossRef]
- Wu, B.; Yu, Y.; Zhang, X. Mode-assisted Silicon integrated interferometric optical Gyroscope. Sci. Rep. 2019, 9, 12946. [Google Scholar] [CrossRef] [PubMed]
- Lim, A.E.-J.; Song, J.; Fang, Q.; Li, C.; Tu, X.; Duan, N.; Chen, K.K.; Tern, R.P.-C.; Liow, T.-Y. Review of silicon photonics foundry efforts. IEEE J. Sel. Top. Quantum Electron. 2013, 20, 405–416. [Google Scholar] [CrossRef]
- Tien, M.-C.; Bauters, J.F.; Heck, M.J.; Spencer, D.T.; Blumenthal, D.J.; Bowers, J.E. Ultra-high quality factor planar Si3N4 ring resonators on Si substrates. Opt. Express 2011, 19, 13551–13556. [Google Scholar] [CrossRef]
- Gundavarapu, S.; Belt, M.; Huffman, T.A.; Tran, M.A.; Komljenovic, T.; Bowers, J.E.; Blumenthal, D.J. Interferometric optical gyroscope based on an integrated Si3N4 low-loss waveguide coil. J. Light. Technol. 2017, 36, 1185–1191. [Google Scholar] [CrossRef]
- El Dirani, H.; Youssef, L.; Petit-Etienne, C.; Kerdiles, S.; Grosse, P.; Monat, C.; Pargon, E.; Sciancalepore, C. Ultralow-loss tightly confining Si3N4 waveguides and high-Q microresonators. Opt. Express 2019, 27, 30726–30740. [Google Scholar] [CrossRef]
- Huffman, T.; Davenport, M.; Belt, M.; Bowers, J.E.; Blumenthal, D.J. Ultra-low loss large area waveguide coils for integrated optical gyroscopes. IEEE Photonics Technol. Lett. 2016, 29, 185–188. [Google Scholar] [CrossRef]
- Bauters, J.F.; Heck, M.J.; John, D.; Dai, D.; Tien, M.-C.; Barton, J.S.; Leinse, A.; Heideman, R.G.; Blumenthal, D.J.; Bowers, J.E. Ultra-low-loss high-aspect-ratio Si3N4 waveguides. Opt. Express 2011, 19, 3163–3174. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Li, H.; Wang, X.; Liu, H.; Ni, P.; Liu, N.; Feng, L. Interferometric optical gyroscope based on an integrated silica waveguide coil with low loss. Opt. Express 2020, 28, 15718–15730. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ma, H.; Li, H.; Jin, Z. Single-polarization fiber-pigtailed high-finesse silica waveguide ring resonator for a resonant micro-optic gyroscope. Opt. Lett. 2017, 42, 3658–3661. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Suh, M.-G.; Vahala, K. Microresonator brillouin gyroscope. Optica 2017, 4, 346–348. [Google Scholar] [CrossRef]
- Feng, L.; Wang, J.; Zhi, Y.; Tang, Y.; Wang, Q.; Li, H.; Wang, W. Transmissive resonator optic gyro based on silica waveguide ring resonator. Opt. Express 2014, 22, 27565–27575. [Google Scholar] [CrossRef] [PubMed]
- Qian, G.; Zhang, T.; Zhang, L.-J.; Tang, J.; Zhang, X.-Y.; Lu, Y.; Wan, F.-H. Demonstrations of centimeter-scale polymer resonator for resonant integrated optical gyroscope. Sens. Actuators A Phys. 2016, 237, 29–34. [Google Scholar] [CrossRef]
- Liu, J.; Yu, L.; Wu, J. Optical Gyroscope Based on Multi-gap Surface Plasmon Optical Waveguide. J. Appl. Sci. Eng. 2019, 22, 299–306. [Google Scholar]
- Zhang, M.; Wang, C.; Cheng, R.; Shams-Ansari, A.; Lončar, M. Monolithic ultra-high-Q lithium niobate microring resonator. Optica 2017, 4, 1536–1537. [Google Scholar] [CrossRef]
- Vannahme, C.; Suche, H.; Reza, S.; Ricken, R.; Quiring, V.; Sohler, W. Integrated optical Ti: LiNbO3 ring resonator for rotation rate sensing. In Proceedings of the 13th ECIO 2007, Copenhagen, Denmark, 25–27 April 2007. [Google Scholar]
- Savchenkov, A.A.; Matsko, A.B.; Ilchenko, V.S.; Maleki, L. Optical resonators with ten million finesse. Opt. Express 2007, 15, 6768–6773. [Google Scholar] [CrossRef]
- Savchenkov, A.A.; Liang, W.; Ilchenko, V.; Matsko, A.; Maleki, L. Crystalline waveguides for optical gyroscopes. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–11. [Google Scholar] [CrossRef]
- Brunetti, G.; Dell’Olio, F.; Conteduca, D.; Armenise, M.N.; Ciminelli, C. Comprehensive mathematical modelling of ultra-high Q grating-assisted ring resonators. J. Opt. 2020, 22, 035802. [Google Scholar] [CrossRef]
- Liu, K.; Jin, N.; Cheng, H.; Chauhan, N.; Puckett, M.W.; Nelson, K.D.; Behunin, R.O.; Rakich, P.T.; Blumenthal, D.J. Ultralow 0.034 dB/m loss wafer-scale integrated photonics realizing 720 million Q and 380 μW threshold Brillouin lasing. Opt. Lett. 2022, 47, 1855–1858. [Google Scholar] [CrossRef]
- Yu, Z.; Xi, X.; Ma, J.; Tsang, H.K.; Zou, C.-L.; Sun, X. Photonic integrated circuits with bound states in the continuum. Optica 2019, 6, 1342–1348. [Google Scholar] [CrossRef]
- Yu, Z.; Sun, X. Acousto-optic modulation of photonic bound state in the continuum. Light Sci. Appl. 2020, 9, 1. [Google Scholar] [CrossRef] [PubMed]
- Zou, C.L.; Cui, J.M.; Sun, F.W.; Xiong, X.; Zou, X.B.; Han, Z.F.; Guo, G.C. Guiding light through optical bound states in the continuum for ultrahigh-Q microresonators. Laser Photonics Rev. 2015, 9, 114–119. [Google Scholar] [CrossRef]
- Qin, H.; Shi, X.; Ou, H. Exceptional points at bound states in the continuum in photonic integrated circuits. Nanophotonics 2022, 11, 4909–4917. [Google Scholar] [CrossRef]
- Post, E.J. Sagnac effect. Rev. Mod. Phys. 1967, 39, 475. [Google Scholar] [CrossRef]
- Feng, Z.; He, Y.; Yan, W.; Yang, F.; Han, W.; Li, Z. Progress of waveguide ring resonators used in micro-optical gyroscopes. In Proceedings of the Photonics, 2020, Online, 29 September–1 October 2020; p. 96. [Google Scholar]
- Liu, Y.; Shainline, J.M.; Zeng, X.; Popović, M.A. Ultra-low-loss CMOS-compatible waveguide crossing arrays based on multimode Bloch waves and imaginary coupling. Opt. Lett. 2014, 39, 335–338. [Google Scholar] [CrossRef]
- White, T.; Kuhlmey, B.; McPhedran, R.; Maystre, D.; Renversez, G.; De Sterke, C.M.; Botten, L. Multipole method for microstructured optical fibers. I. Formulation. JOSA B 2002, 19, 2322–2330. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Ciminelli, C.; Passaro, V.M.; Dell’Olio, F.; Armenise, M.N. Three-dimensional modelling of scattering loss in InGaAsP/InP and silica-on-silicon bent waveguides. J. Eur. Opt. Soc.-Rapid Publ. 2009, 4, 09015. [Google Scholar] [CrossRef]
- Thyagarajan, K.; Shenoy, M.; Ghatak, A.K. Accurate numerical method for the calculation of bending loss in optical waveguides using a matrix approach. Opt. Lett. 1987, 12, 296–298. [Google Scholar] [CrossRef]
- Ciminelli, C.; Dell’Olio, F.; Campanella, C.E.; Armenise, M.N. Photonic technologies for angular velocity sensing. Adv. Opt. Photonics 2010, 2, 370–404. [Google Scholar] [CrossRef]

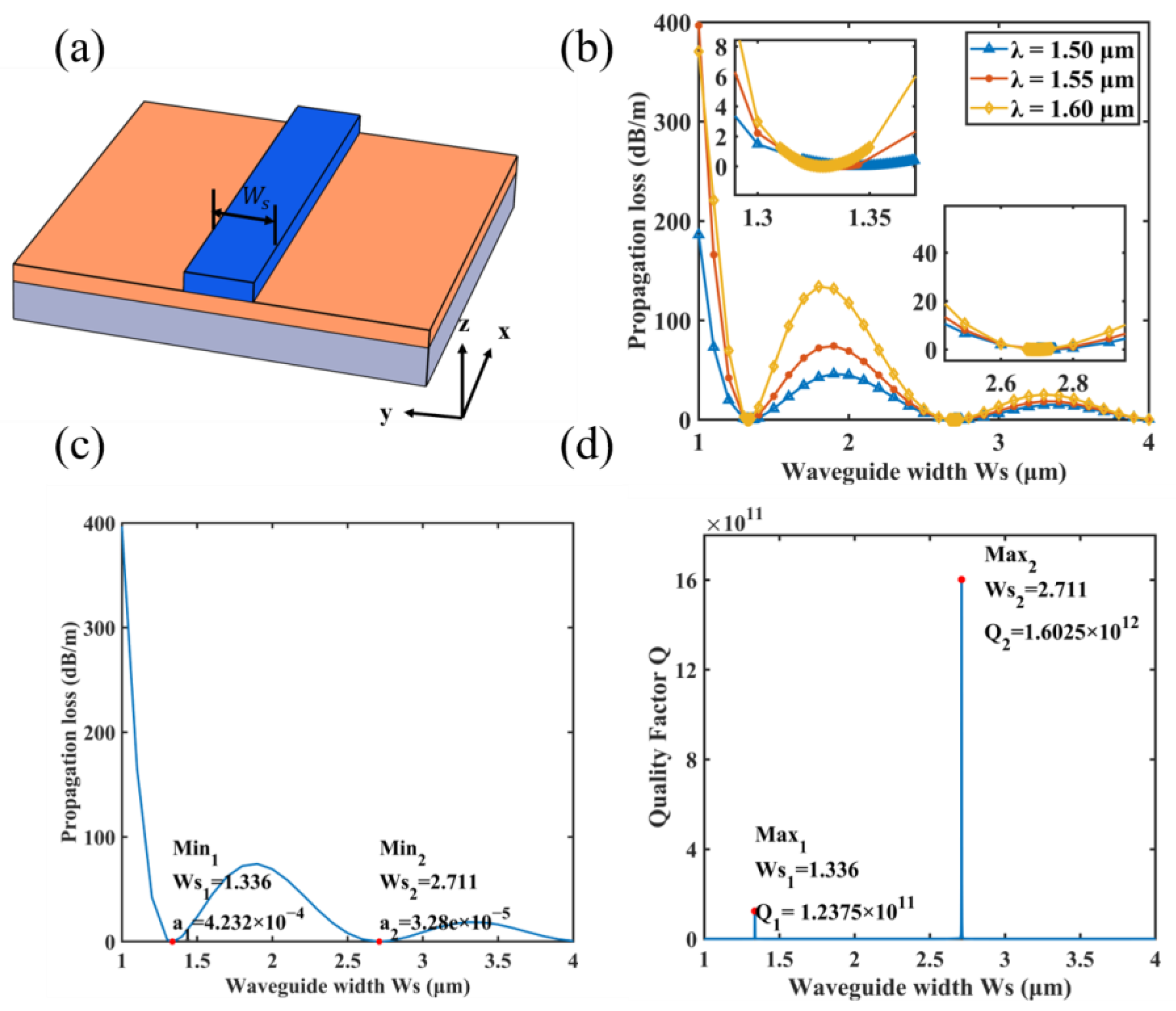
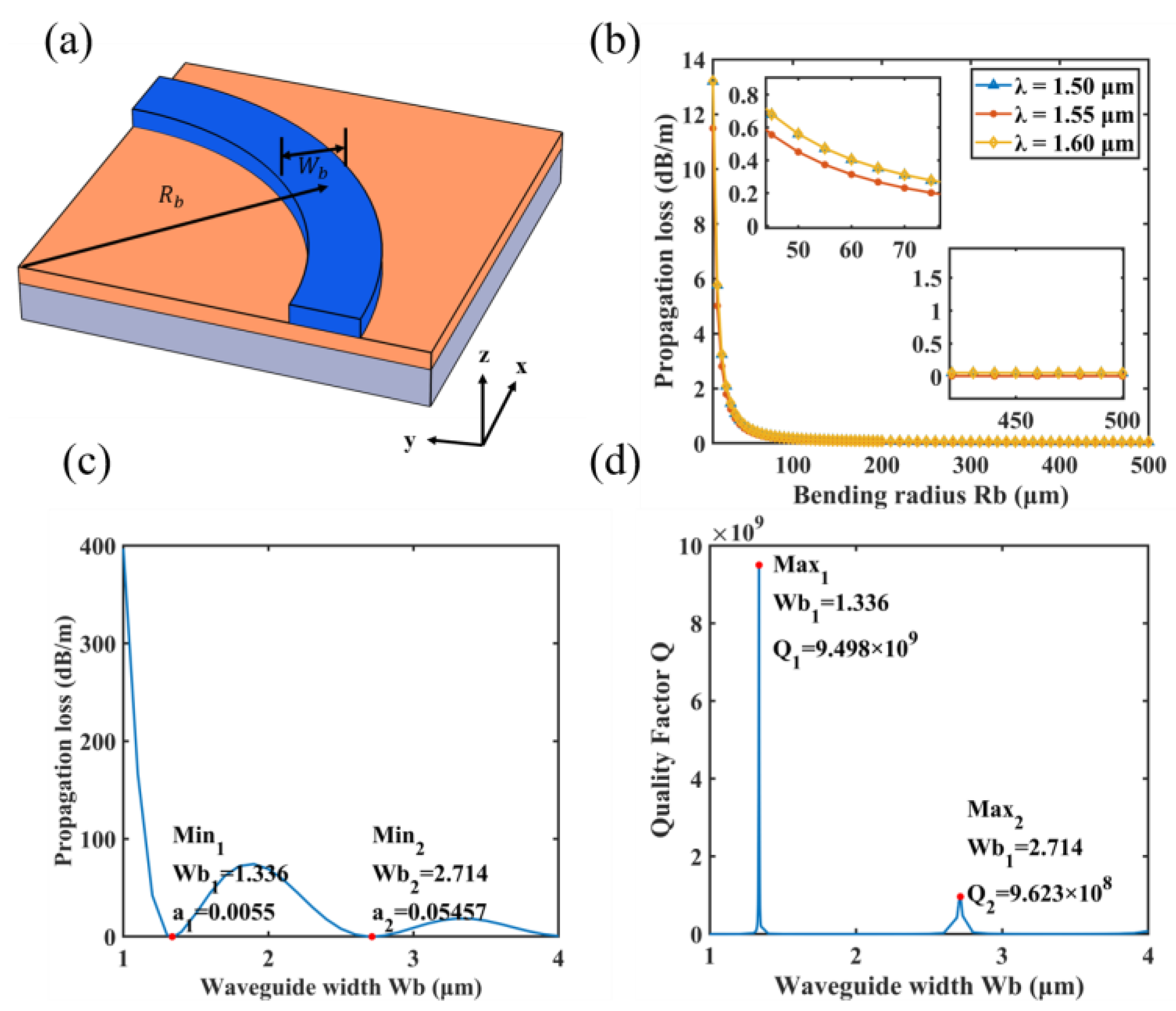
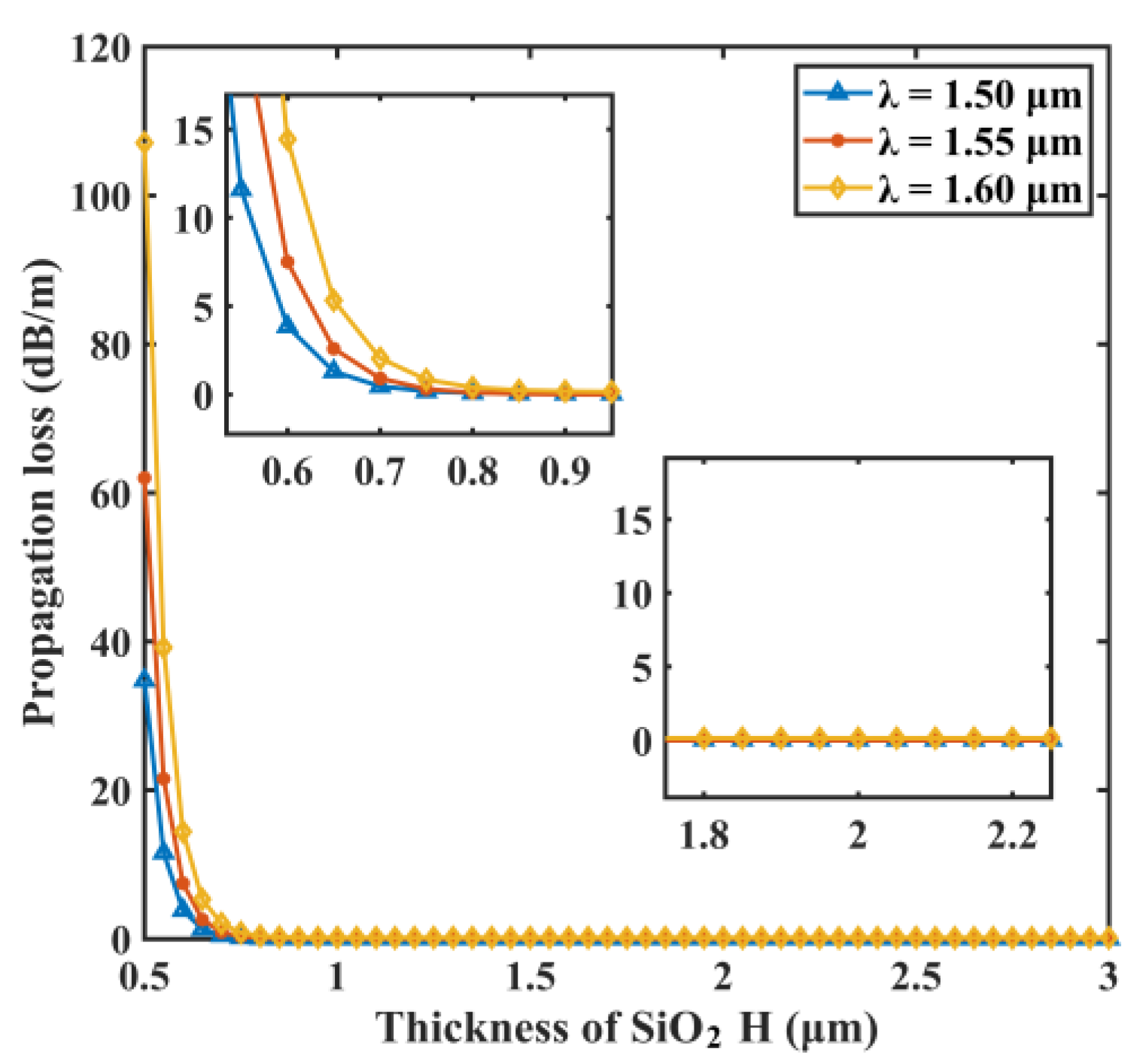
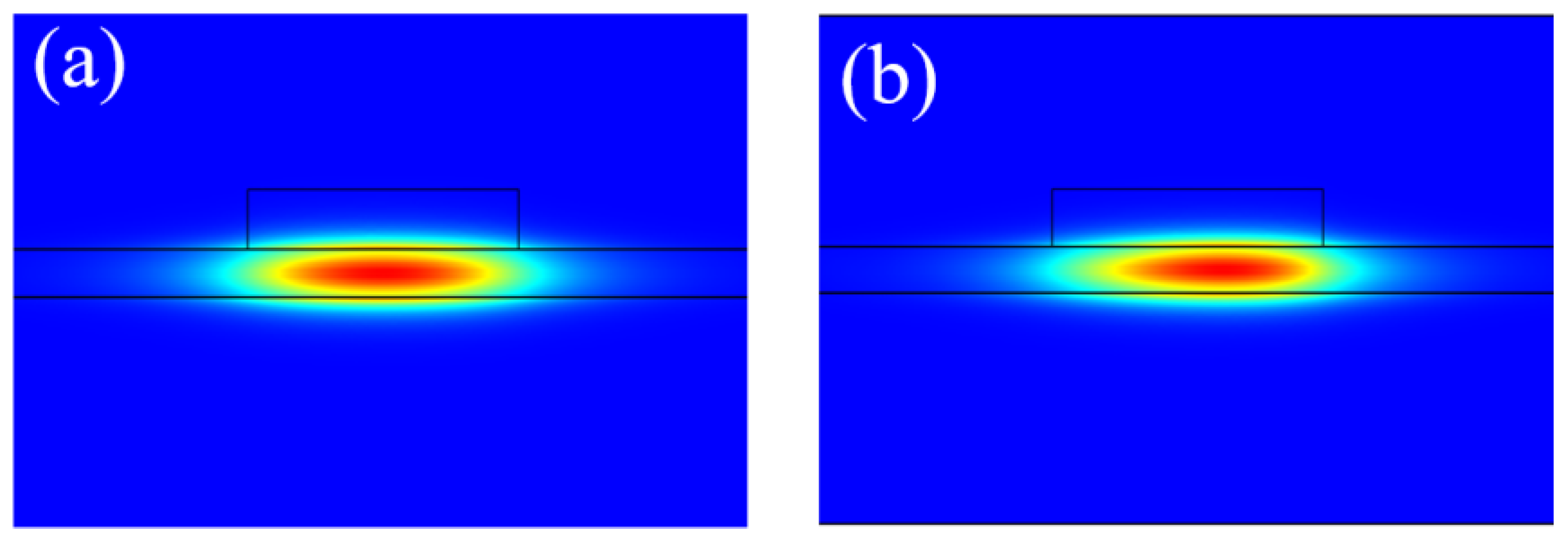

| Reference | Material | Propagation Loss | Q Factor |
|---|---|---|---|
| [10] | InP | 0.45 dB/cm | 106 |
| [13] | SOI | 1.328 dB/cm | \ |
| [17] | Si3N4 | 7.8 × 10−3 dB/cm | 108 |
| [21] | SiO2 | 5.0 × 10−3 dB/cm | 109 |
| [25] | Polymer | 0.5 dB/cm | 105 |
| [27] | LiNbO3 | 2.7 × 10−2 dB/cm | 107 |
| [29] | GaF2 | 1 × 10−4 dB/cm | 1010 |
| This Work | BIC | 4.232 × 10−6 dB/cm | 1011 |
| Symbol | Parameter | Value |
|---|---|---|
| Operating wavelength | 1.55 μm | |
| Speed of light in vacuum | 3 × 108 m/s | |
| Detection bandwidth | 20 Hz | |
| Planck constant | 6.626 × 10−34 J·s | |
| Photodetector efficiency | 0.9 | |
| Input optical power | 10 mW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Z.; Chen, J.; Chen, D.; Zhu, S.; Yang, J.; Zhang, Z. An Ultra-Low-Loss Waveguide Based on BIC Used for an On-Chip Integrated Optical Gyroscope. Photonics 2023, 10, 453. https://doi.org/10.3390/photonics10040453
Yuan Z, Chen J, Chen D, Zhu S, Yang J, Zhang Z. An Ultra-Low-Loss Waveguide Based on BIC Used for an On-Chip Integrated Optical Gyroscope. Photonics. 2023; 10(4):453. https://doi.org/10.3390/photonics10040453
Chicago/Turabian StyleYuan, Zhenkun, Jian Chen, Dingbo Chen, Shuolong Zhu, Junbo Yang, and Zhenrong Zhang. 2023. "An Ultra-Low-Loss Waveguide Based on BIC Used for an On-Chip Integrated Optical Gyroscope" Photonics 10, no. 4: 453. https://doi.org/10.3390/photonics10040453
APA StyleYuan, Z., Chen, J., Chen, D., Zhu, S., Yang, J., & Zhang, Z. (2023). An Ultra-Low-Loss Waveguide Based on BIC Used for an On-Chip Integrated Optical Gyroscope. Photonics, 10(4), 453. https://doi.org/10.3390/photonics10040453







