Research on Very-Low-Frequency Hydroacoustic Acoustic Velocity Sensor Based on DFB Fiber Laser
Abstract
1. Introduction
2. Structure and Principle
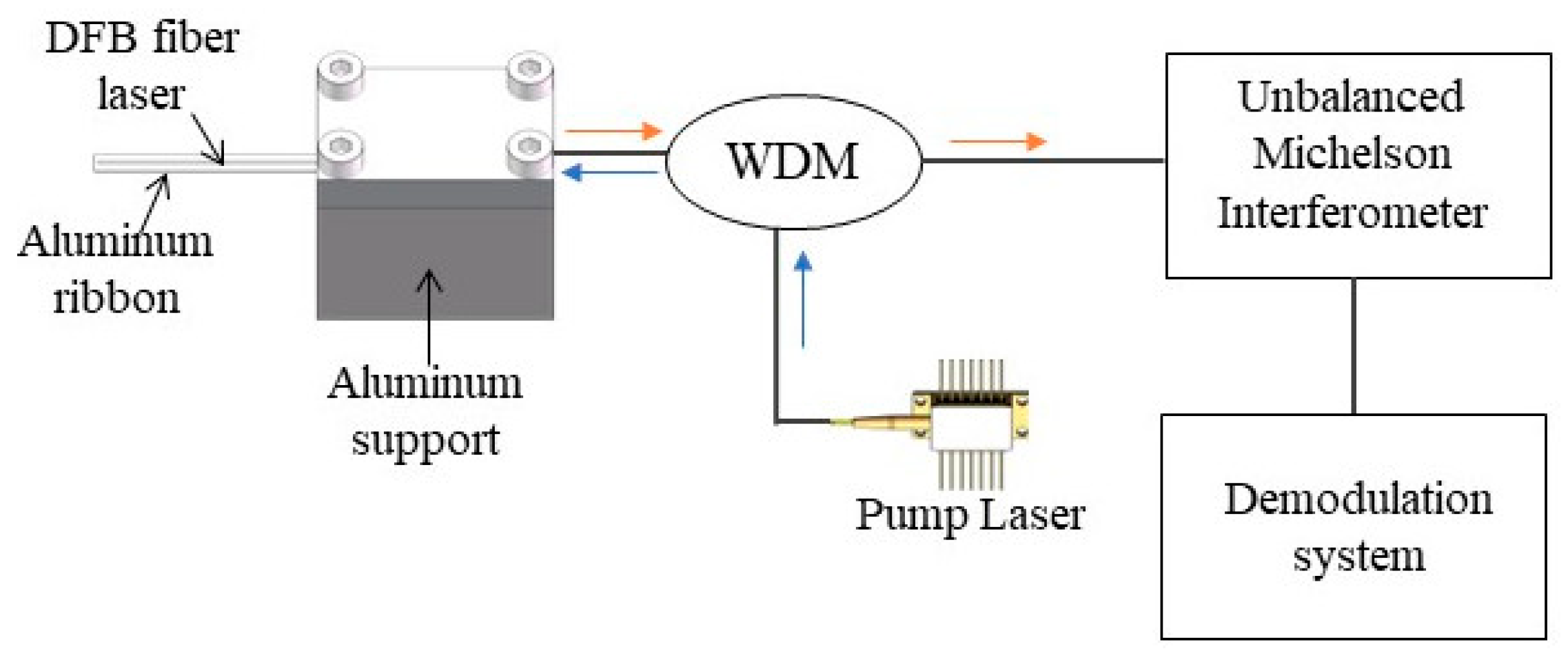
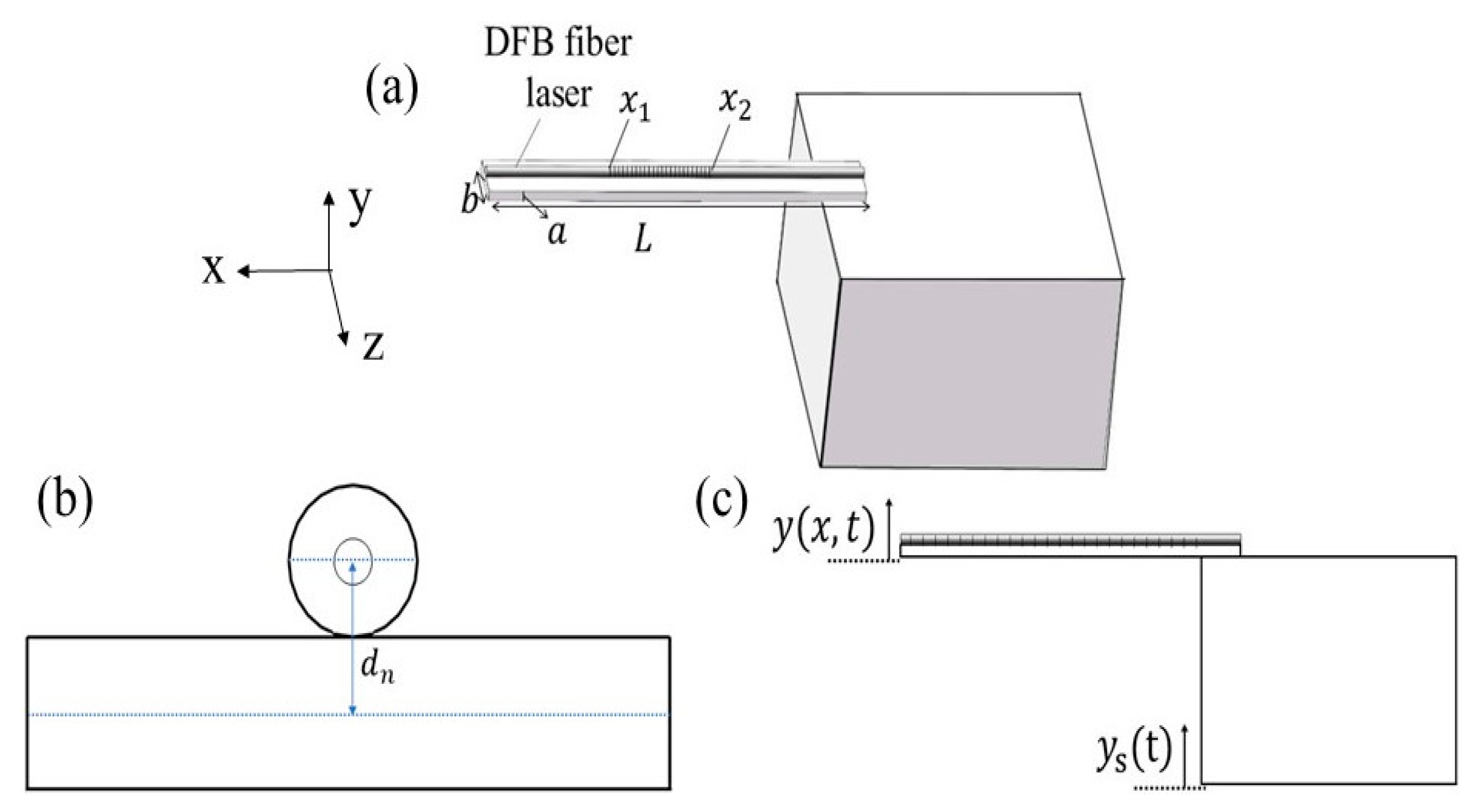
2.1. Sensor Structure
2.2. Demodulation Algorithm
2.3. Theoretical Model of the Velocity Sensor
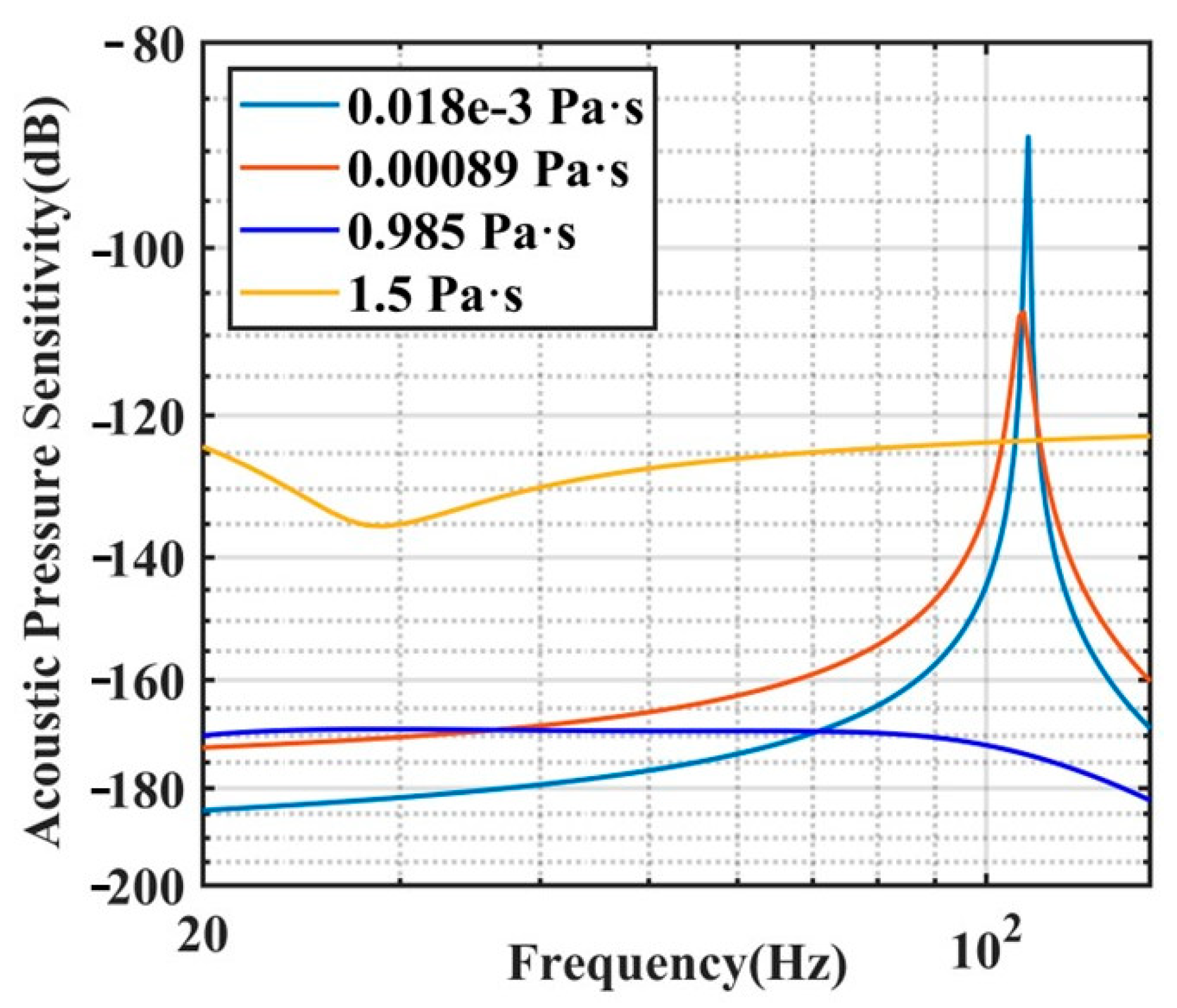
2.4. Simulations
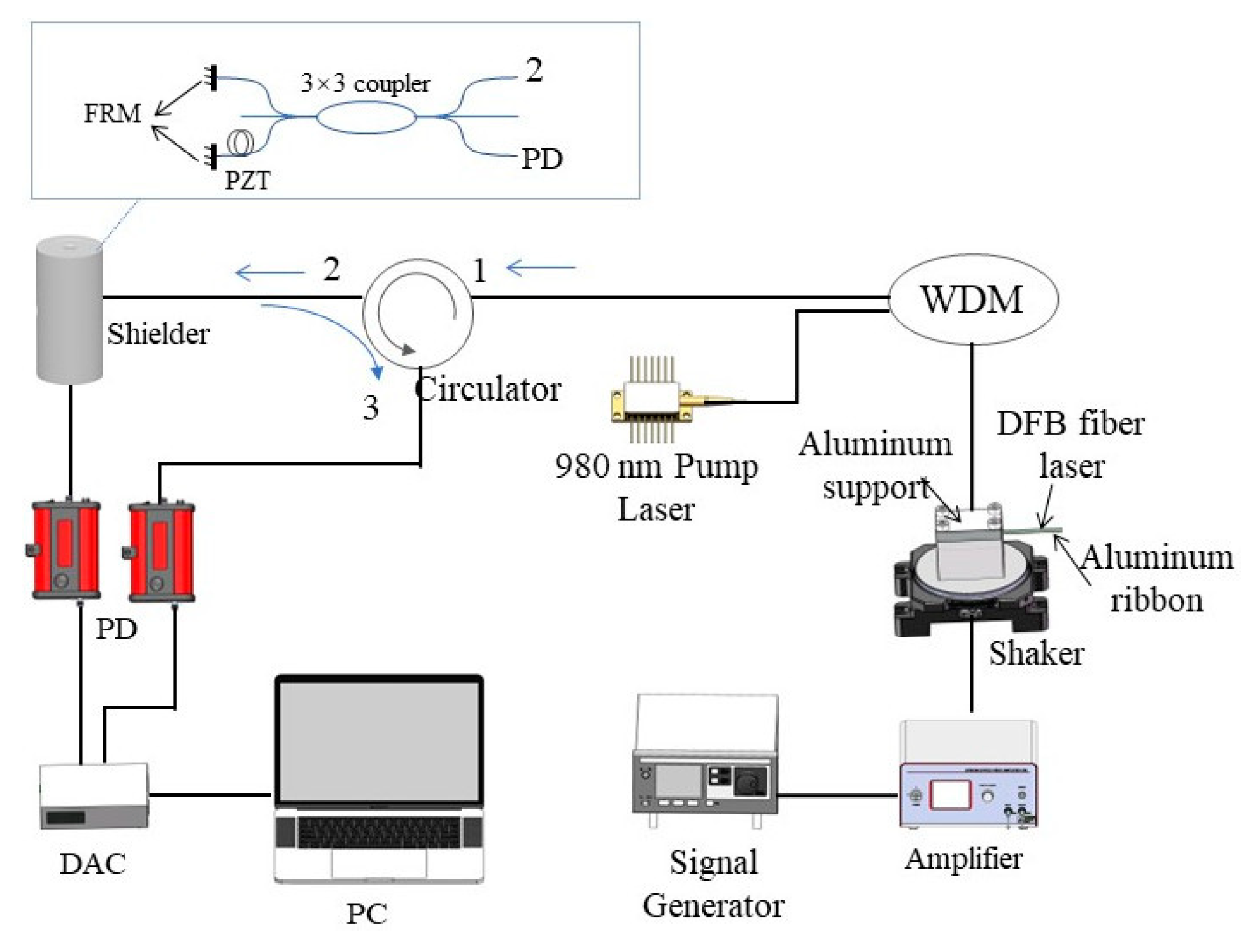
3. Experimental Results and Discussions
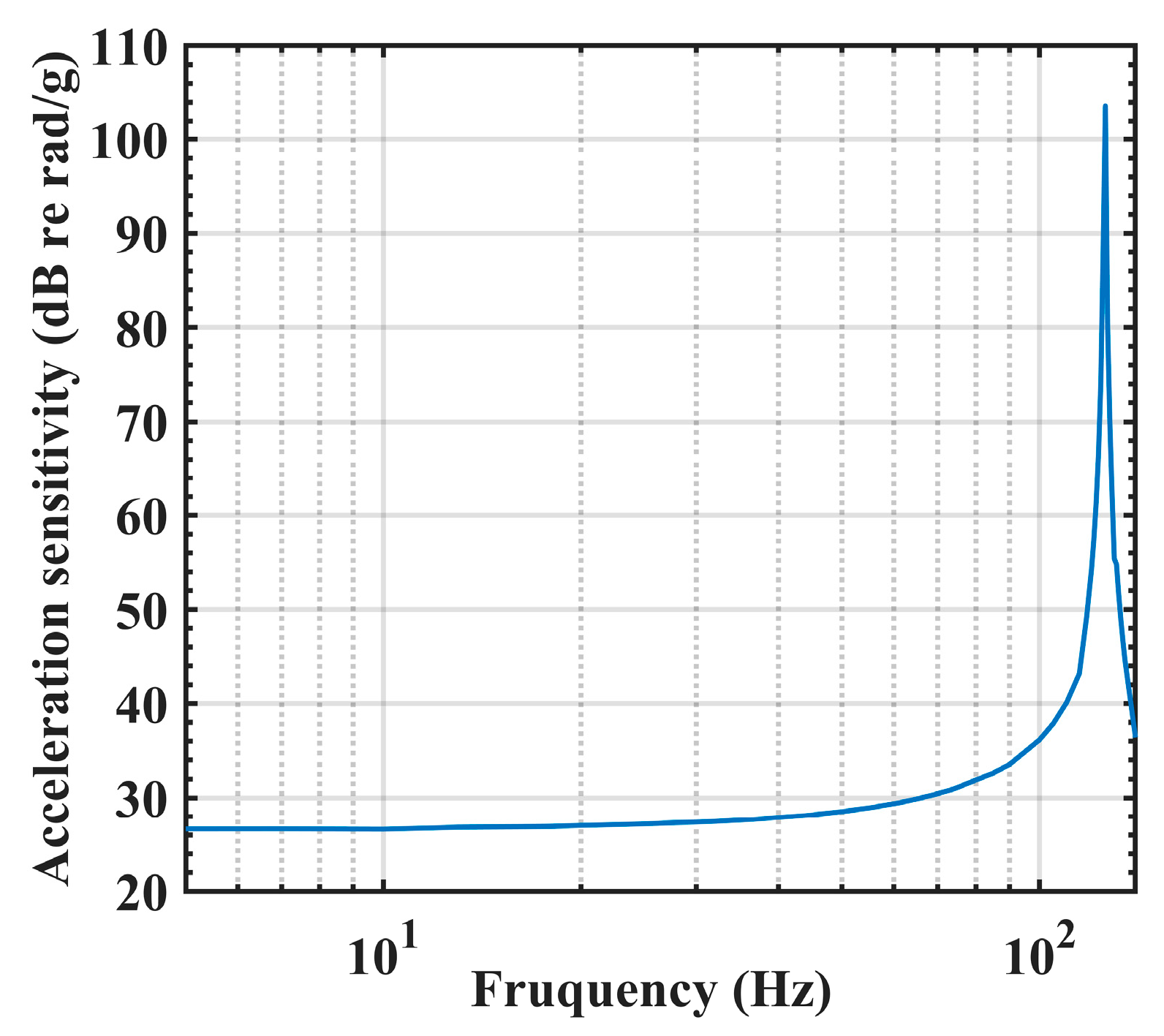
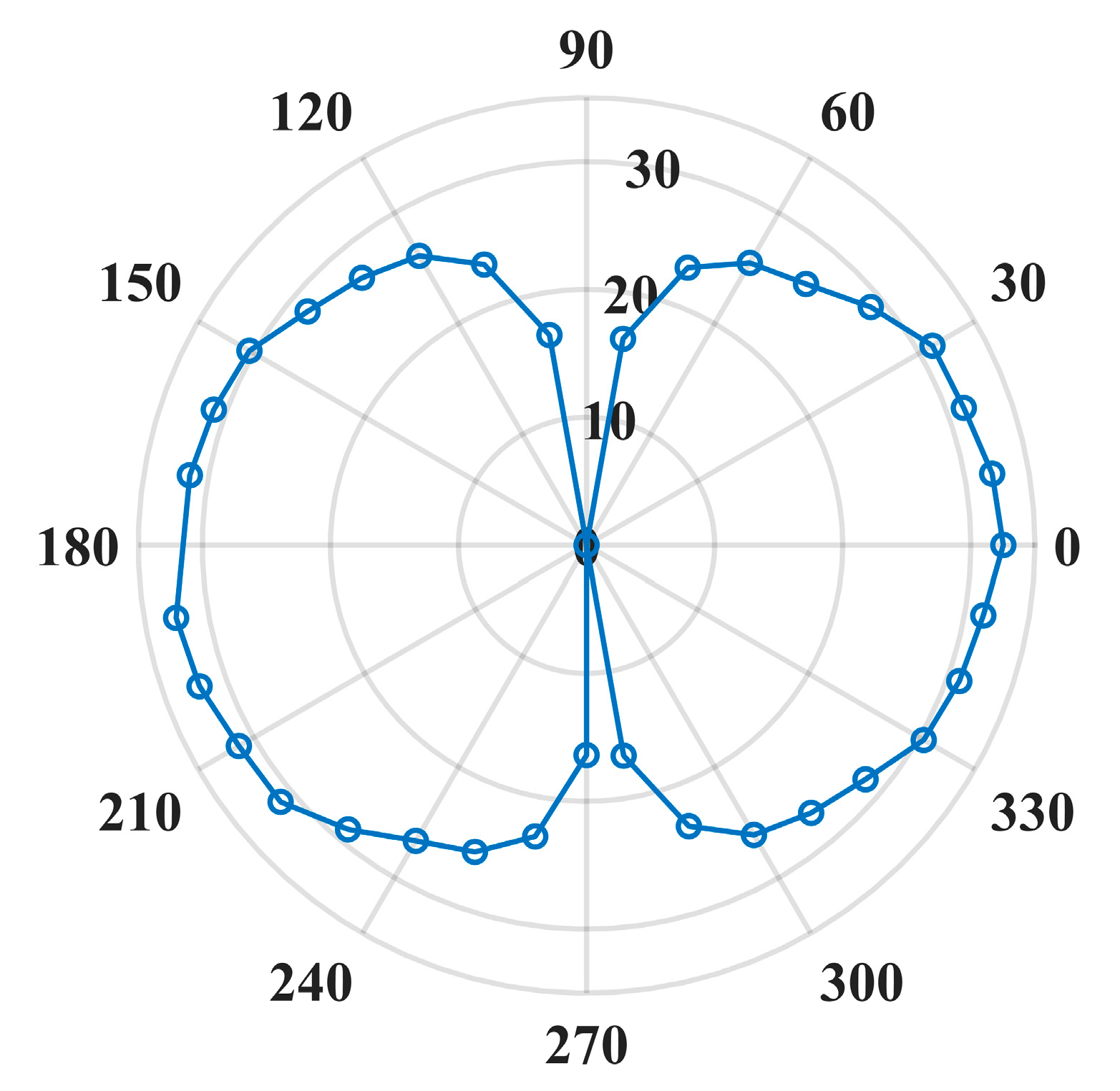
3.1. Response of the Cantilever
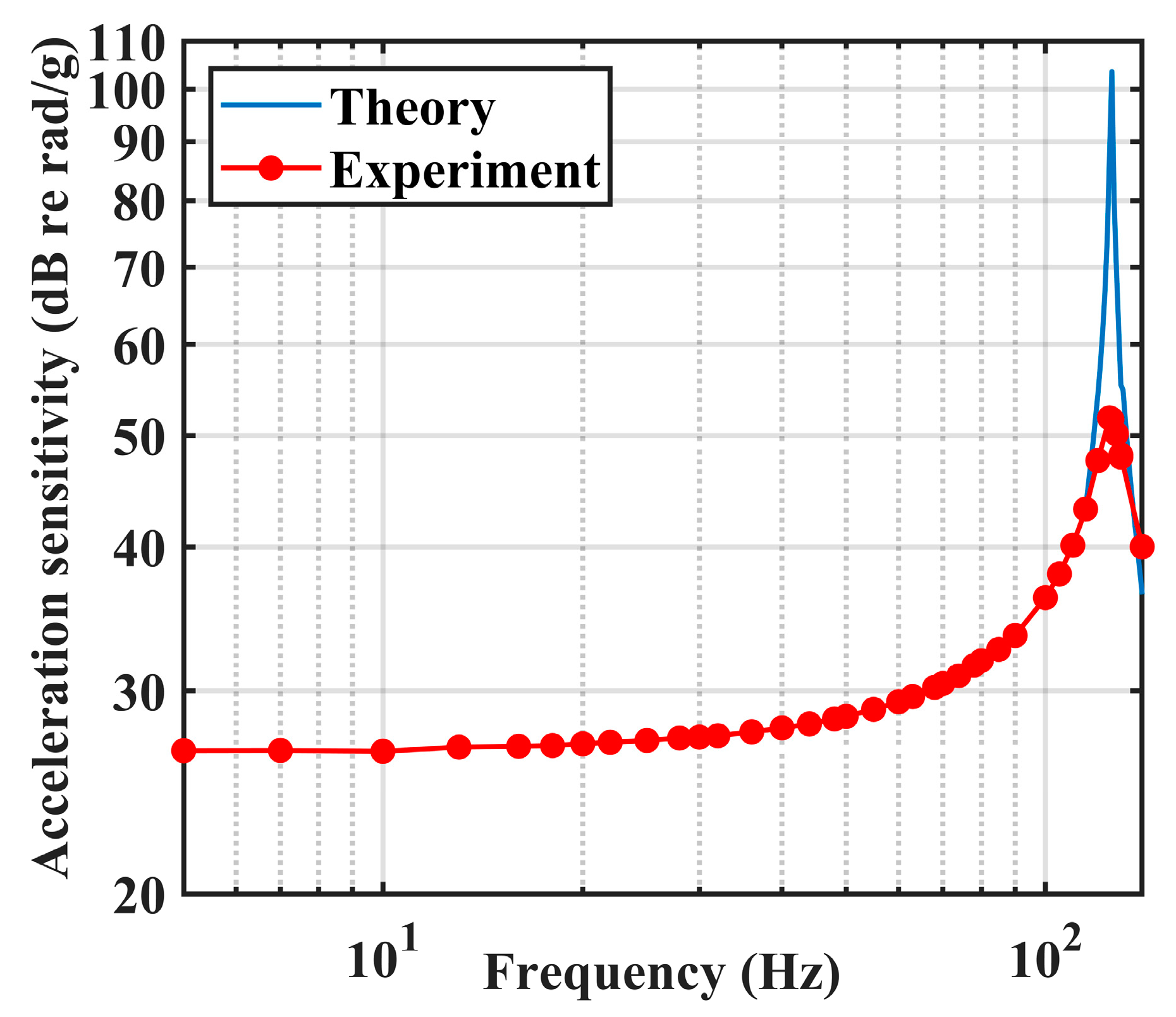
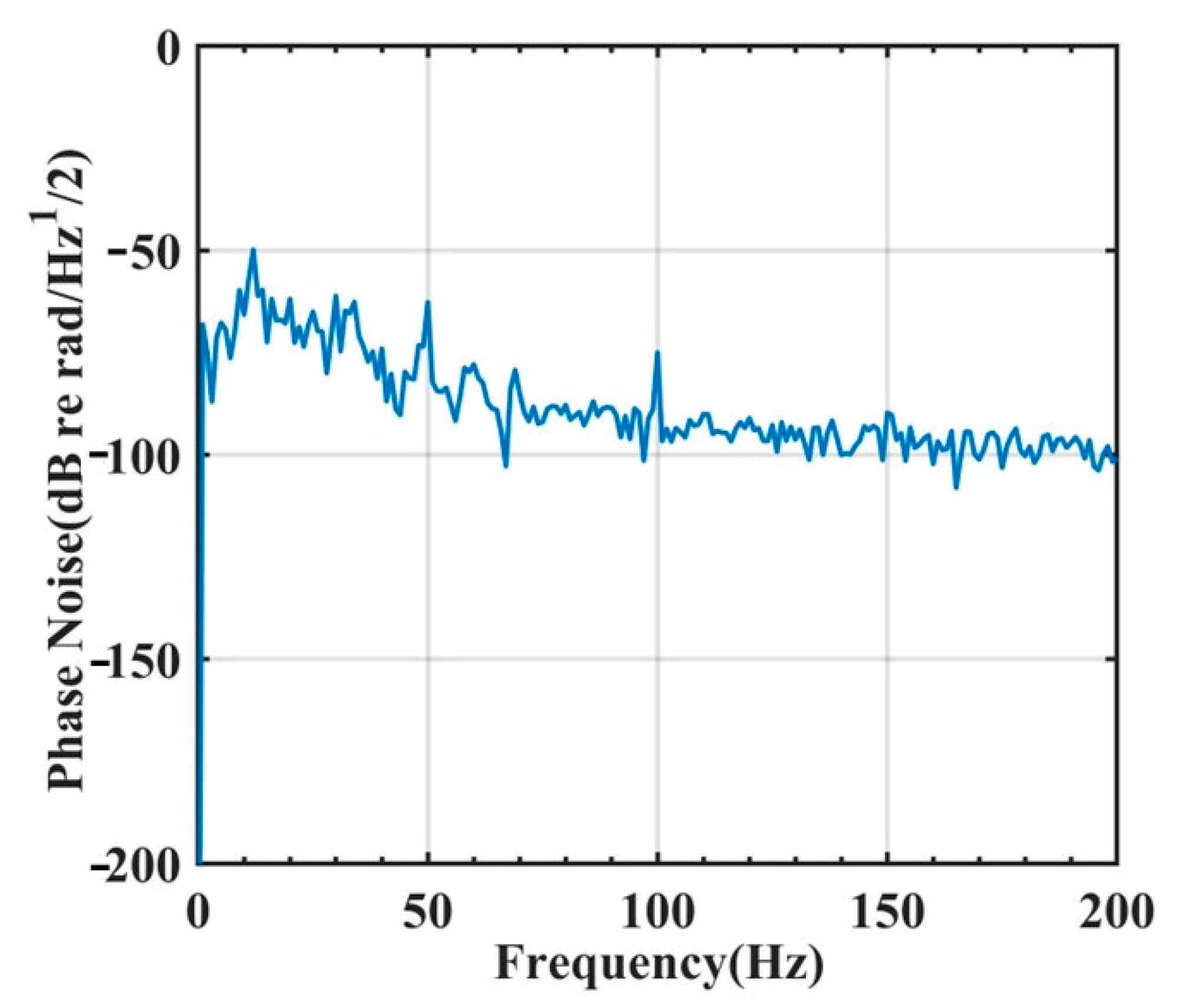
3.2. Performance of the Sensor
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiong, S.; Wang, F.; Yao, Q.; Chen, H.; Hou, Q.; Xia, L. Recent progress in optical fiber pressure gradient sensors. Adv. Sens. Syst. Appl. X 2020, 11554, 94–106. [Google Scholar]
- Zhang, W.; Zhang, F.; Li, F.; Liu, Y. Pressure-gradient fiber laser hydrophone. SPIE 2009, 7503, 550–553. [Google Scholar]
- Li, Y.; Hong, L. Research of eddy current sensors applied to displacement-based vector hydrophones. Sens. Actuators A Phys. 2021, 331, 112968. [Google Scholar] [CrossRef]
- Wang, H.; Ju, B.; Li, W.; Feng, Z. Ultrastable eddy current displacement sensor working in harsh temperature environments with comprehensive self-temperature compensation. Sens. Actuators A Phys. 2014, 211, 98–104. [Google Scholar] [CrossRef]
- Zhao, G.; Ying, J.; Wu, L.; Feng, Z. Eddy current displacement sensor with ultrahigh-resolution obtained through the noise suppression of excitation voltage. Sens. Actuators A Phys. 2019, 299, 111622. [Google Scholar] [CrossRef]
- Todd, M.D.; Johnson, G.A.; Althouse, B.A.; Vohra, S.T. Flexural beam-based fiber Bragg grating accelerometers. IEEE Photonics Technol. Lett. 1998, 10, 1605–1607. [Google Scholar] [CrossRef]
- Mita, A.; Yokoi, I. Fiber Bragg grating accelerometer for structural health monitoring. In Proceedings of the Fifth International Conference on Motion and Vibration Control, Sydney, Australia, 4–8 December 2000. [Google Scholar]
- Liu, Q.; Qiao, X.; Zhao, J. Novel Fiber Bragg Grating Accelerometer Based on Diaphragm. IEEE Sens. J. 2012, 12, 3000–3004. [Google Scholar] [CrossRef]
- Ames, G.H.; Maguire, J.M. Erbium Fiber Laser Accelerometer. IEEE Sens. J. 2007, 4, 557–561. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, F.; Jiang, S.; Min, L.; Li, M.; Peng, G.; Ni, J.; Wang, C. Short cavity DFB fiber laser-based vector hydrophone for low-frequency signal detection. Photonic Sens. 2017, 7, 325–328. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, J.; Ma, L.; Wu, Y.; Xu, P.; Hu, Z. Experimental Research of a Separate Type Fiber Optic Vector Hydrophone based on FBG Accelerometers. In Proceedings of the Optical Fiber Sensors, Lausanne, Switzerland, 24–28 September 2018. [Google Scholar]
- Jin, M.; Ge, H.; Li, D.; Ni, C. Three-component homovibrational vector hydrophone based on fiber Bragg grating FP interferometry. Appl. Opt. 2018, 57, 9195–9202. [Google Scholar] [CrossRef]
- Jia, Z.; Zhang, X.; Li, K.; Fan, Q. Research on a Cantilever Fiber Bragg Grating Vibration Sensor. Piezoelectric Acousto-Opt. 2019, 41, 21–24. [Google Scholar]
- Zhou, X.; Meng, Z.; Wang, J.; Liang, Y.; Wang, M.; Chen, M. Fiber-laser-based cantilever-type vector sensor for acoustic motion measurement. SPIE 2020, 11554, 232–238. [Google Scholar]
- Jin, M.; Ge, H.; Zhang, Z. The optimal design of a 3D column type fiber-optic vector hydrophone. In Proceedings of the IEEE/OES China Ocean Acoustics (COA), Harbin, China, 14–17 July 2021; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Wang, J.; Luo, H.; Meng, Z.; Hu, Y. Experimental research of an all-polarization-maintaining optical fiber vector hydrophone. J. Light. Technol. 2011, 30, 1178–1184. [Google Scholar] [CrossRef]
- Cranch, G.A.; Lane, J.E.; Miller, G.A.; Lou, J.W. Low frequency driven oscillations of cantilevers in viscous fluids at very low Reynolds number. J. Appl. Phys. 2013, 113, 194904. [Google Scholar] [CrossRef]
- Cranch, G.A.; Miller, G.A.; Kirkendall, C.K. Fiber-optic, cantilever-type acoustic motion velocity hydrophone. J. Acoust. Soc. Am. 2012, 132, 103. [Google Scholar] [CrossRef] [PubMed]
- Gabrielson, T.B.; Gardner, D.L.; Garrett, S.L. A simple neutrally buoyant sensor for direct measurement of particle velocity and intensity in water. J. Acoust. Soc. Am. 1996, 97, 2227–2237. [Google Scholar] [CrossRef]
- Abraham, B. Low-cost dipole hydrophone for use in towed arrays. AIP Conf. Proc. 1996, 368, 189–201. [Google Scholar]
- Shipps, J.C.; Deng, K.A. A miniature vector sensor for line array applications. Oceans 2003. In Proceedings of the Celebrating the Past… Teaming Toward the Future (IEEE Cat. No. 03CH37492), 22–26 September 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 5, pp. 367–2369. [Google Scholar]
- Butler, J.; Butler, D.M.S.C.; Cavanagh, G. Metallic glass velocity sensor. AIP Conf. Proc. 1996, 368, 101–133. [Google Scholar]
- Cranch, G.; Flockhart, G.; Kirkendall, C. Distributed feedback fiber laser strain sensors. IEEE Sens. J. 2008, 8, 1161–1172. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, X.; Dong, F.; Li, Z.; Hu, Y. Experimental research on all polarization maintaining fibre magnetostrictive sensor. J. Opt. A Pure Appl. Opt. 2005, 7, S352. [Google Scholar] [CrossRef]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Bruneau, M. Fundamentals of Acoustics; John Wiley & Sons: New York, NY, USA, 2013; pp. 112–116. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Saunders, J.V. Fundamentals of Acoustics; Wiley: New York, NY, USA, 1982; pp. 97–99. [Google Scholar]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics. Am. J. Phys. 1954, 22, 410–413. [Google Scholar] [CrossRef]
- Foster, S. Spatial mode structure of the distributed feedback fiber laser. IEEE J. Quantum Electron. 2004, 40, 884–892. [Google Scholar] [CrossRef]
- Zhang, Y.; Meng, Z.; Wang, J.; Chen, M.; Liang, Y.; Hu, X. The Two-Stage Suspension System of the Fiber Optic Vector Hydrophone for Isolating the Vibration from the Mooring Rope. Sensors 2022, 22, 9261. [Google Scholar] [CrossRef] [PubMed]






| Parameter | Definition | Value |
|---|---|---|
| Fluid properties | ||
| Density | 997 kg/m3 (Castor oil) 1.29 kg/m3 (Air) | |
| Sound speed | 340 m/s (Air) 1540 m/s (Castor oil) | |
| Fluid viscosity | 1.8 × 10−5 Pa·s (Air) 0.985 Pa·s (Castor oil) | |
| Fiber properties | ||
| Density | 2200 kg/m3 | |
| Youngs modulus | 70 GPa | |
| Coating radius | 62.5 × 10−6 m | |
| Grating coupling coefficient | 180 m−1 | |
| Speed of light | 3 × 108 m/s | |
| Wavelength | 1550 nm | |
| Core index of refraction | 1.47 | |
| Ribbon properties | ||
| Youngs modulus | 70 GPa | |
| Poisson’s ratio | 0.33 | |
| Density | 2700 kg/m3 | |
| Length | 32 mm | |
| Width | 3 mm | |
| Thickness | 80 μm |
| Liquid | Viscosity (Pa·s) | Density (Kg/m3) |
|---|---|---|
| air | 1.8 × 10−5 | 1.4 |
| water | 8.9 × 10−4 | 998 |
| castor oil | 0.985 | 961 |
| glycerin | 1.5 | 1261 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, C.; Chen, M.; Yu, Y.; Zhang, Y.; Wang, J.; Zhang, Z.; Yang, J.; Zhu, S.; Qu, B. Research on Very-Low-Frequency Hydroacoustic Acoustic Velocity Sensor Based on DFB Fiber Laser. Photonics 2023, 10, 463. https://doi.org/10.3390/photonics10040463
Ruan C, Chen M, Yu Y, Zhang Y, Wang J, Zhang Z, Yang J, Zhu S, Qu B. Research on Very-Low-Frequency Hydroacoustic Acoustic Velocity Sensor Based on DFB Fiber Laser. Photonics. 2023; 10(4):463. https://doi.org/10.3390/photonics10040463
Chicago/Turabian StyleRuan, Chenxia, Mo Chen, Yang Yu, Yichi Zhang, Jianfei Wang, Zhenrong Zhang, Junbo Yang, Shuolong Zhu, and Boyuan Qu. 2023. "Research on Very-Low-Frequency Hydroacoustic Acoustic Velocity Sensor Based on DFB Fiber Laser" Photonics 10, no. 4: 463. https://doi.org/10.3390/photonics10040463
APA StyleRuan, C., Chen, M., Yu, Y., Zhang, Y., Wang, J., Zhang, Z., Yang, J., Zhu, S., & Qu, B. (2023). Research on Very-Low-Frequency Hydroacoustic Acoustic Velocity Sensor Based on DFB Fiber Laser. Photonics, 10(4), 463. https://doi.org/10.3390/photonics10040463








