Scintillation Increase Induced by Focusing (Invited)

Abstract

We show that the focusing of a random electromagnetic beam by a lens gives rise to a scintillation index at the geometrical focus that generally differs from that of the incident beam. In the examples we present, focusing produces a significant increase of the index. This observation is of particular relevance for optical communication systems in which scintillation is a major cause of signal degradation.

1. Introduction

Scintillation is the fluctuation over time of the intensity of an optical signal. Two common causes of scintillation are a certain randomness in the source [1,2] and propagation through atmospheric turbulence [3,4]. For a stochastic beam-like field, the intensity fluctuations are trivially seen to be identical to those of the first Stokes parameter, denoted $S_0$. In [5], the fluctuations of all four Stokes parameters were examined. It was shown, under the assumption of Gaussian statistics, that their normalized variances, dubbed ”Stokes scintillations”, are not independent, but rather obey a sum rule. More precisely, the sum of the four Stokes scintillations always equals two. Their interplay in the far zone of a beam-generating source was analyzed in [6].

It is well known that the focusing action of a lens changes a monochromatic scalar field in the front focal plane into its Fourier transform in the back focal plane [7]. Recently it was described that the correlation functions that characterize a random beam undergo a similar effect when the beam is focused. This discovery paved the way to the concept of Fourier processing of correlation functions with a $4f$ system [8,9]. The formalism was also employed to analyze the complicated spatial distribution of the four Stokes scintillations in the focal plane [10]. Here, we further study the classical scintillation index (i.e., the normalized scintillation of $S_0$) at the geometrical focus in its dependence on the different parameters that characterize the incident field. We take the field to be a member of the wide class of Gaussian Schell-model beams [11,12]. In general, the scintillation index is found to be increased by the focusing process. In fact, it is only in special cases that the scintillation is not affected by the lens.

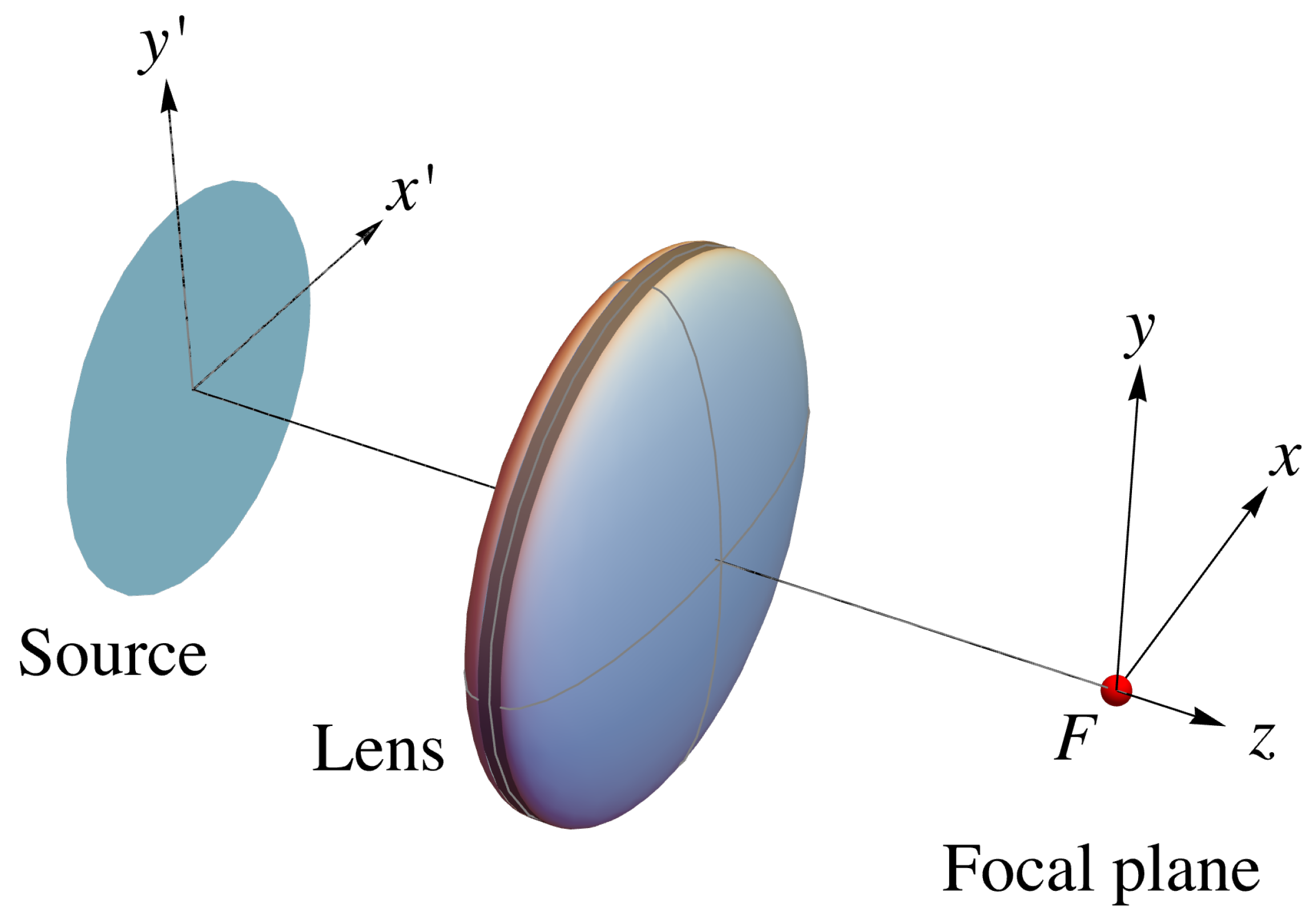
2. Focusing

The scalar field $U^{\left(f\right)}(\rho ,\omega )$ in the focal plane of a thin paraxial lens with focal length f, is proportional to the two-dimensional Fourier transform of the beam-like field $U^{\left(\mathrm{i}\right)}\left({\rho }^{\prime },\omega \right)$ in its front focal plane (Section 5.2, [7]), i.e.,

$$\begin{array}{c}\hfill U^{\left(f\right)}(\rho ,\omega )=\frac{1}{j\lambda f}{\int }_{-\infty }^{\infty }{U}^{\left(\mathrm{i}\right)}\left({\rho }^{\prime },\omega \right)P\left({\rho }^{\prime }\right)exp\left(-jk\rho ·{\rho }^{\prime }/f\right){\mathrm{d}}^2{\rho }^{\prime }.\end{array}$$

(1)

Here, the transverse vectors $\rho =(x,y)$ and ${\rho }^{\prime }=(x^{\prime },y^{\prime })$ denote positions in the back and front focal plane, respectively. The wavenumber $k=2\pi /\lambda =\omega /c$, with wavelength $\lambda$ and speed of light c. The finite extent of the lens is accounted for by associating with it a pupil function $P\left({\rho }^{\prime }\right)$, defined by $P\left({\rho }^{\prime }\right)=1$ for points inside the lens aperture, and otherwise $P\left({\rho }^{\prime }\right)=0$. When the physical extent of the input beam is smaller than the lens aperture, as we henceforth assume, the factor $P\left({\rho }^{\prime }\right)$ may be neglected.

Consider next the case where the incident field is a random electromagnetic beam generated by a planar source in the front focal plane, as sketched in Figure 1. Such a source may be described by a cross-spectral density (CSD) matrix [2]

$$\mathrm{W}({\rho }_1,{\rho }_2,\omega )=\left(\begin{array}{cc}{W}_{xx}({\rho }_1,{\rho }_2,\omega )\hfill & W_{xy}({\rho }_1,{\rho }_2,\omega )\hfill \\ W_{yx}({\rho }_1,{\rho }_2,\omega )\hfill & W_{yy}({\rho }_1,{\rho }_2,\omega )\hfill \end{array}\right).$$

(2)

Its four elements are

$$W_{ij}\left({\rho }_1,{\rho }_2,\omega \right)=〈E_i^{*}\left({\rho }_1,\omega \right)E_j\left({\rho }_2,\omega \right)〉,i,j\in \{x,y\},$$

(3)

where $E_i$ represents a Cartesian component of the electric field vector and the angular brackets and the asterisk indicate ensemble averaging and conjugating, respectively. After substituting from Equation (1) into (3) and interchanging the order of integration and ensemble averaging, the transformation of the CSD matrix by the lens is seen to be given by the expression [8]

$$\begin{array}{cc}\hfill W_{ij}^{\left(f\right)}\left({\rho }_1,{\rho }_2\right)=& \frac{1}{{\lambda }^2{f}^2}{\int \int }_{-\infty }^{\infty }{W}_{ij}^{\left(\mathrm{i}\right)}\left({\rho }_1^{\prime },{\rho }_2^{\prime }\right)\hfill \\ \hfill & \times exp\left[-jk\left({\rho }_2·{\rho }_2^{\prime }-{\rho }_1·{\rho }_1^{\prime }\right)/f\right]{\mathrm{d}}^2{\rho }_1^{\prime }{\mathrm{d}}^2{\rho }_2^{\prime }.\hfill \end{array}$$

(4)

Here, the superscripts $\mathrm{i}$ and f indicate the front focal plane and the back focal plane, respectively, and the $\omega$ dependence is no longer shown. Equation (4) states that the CSD matrix elements in the focal plane are the four-dimensional spatial Fourier transform of the corresponding elements in the front focal plane. This derivation is under the assumption of weak focusing, meaning that no significant longitudinal field component is created. For our purpose, the study of the scintillation behavior at the geometrical focus F, we need the matrix elements evaluated at ${\rho }_1={\rho }_2=(0,0)$. For that particular choice of observation point, the dependence on the focal length f drops out, and Equation (4) reduces to the DC term of a 4D-Fourier transform.

3. The Scintillation Index

Because the incident beam is stochastic, its spectral density, or intensity at frequency $\omega$, will be a random quantity. The fluctuation around its average value is

$$\Delta I\left(\rho \right)=I\left(\rho \right)-〈I\left(\rho \right)〉,$$

(5)

where $I\left(\rho \right)$ is the random intensity of a single realization and $〈I\left(\rho \right)〉$ is its ensemble average. On making use of Equation (5) it follows that the Hanbury Brown–Twiss (HBT) correlation [5], the correlation of intensity fluctuations at two points, ${\rho }_1$ and ${\rho }_2$, equals

$$\begin{array}{c}\hfill \langle \Delta I\left({\rho }_1\right)\Delta I\left({\rho }_2\right)\rangle =\langle I\left({\rho }_1\right)I\left({\rho }_2\right)\rangle -\langle I\left({\rho }_1\right)\rangle \langle I\left({\rho }_2\right)\rangle .\end{array}$$

(6)

The first term on the right-hand side involves a fourth-order correlation. Under the assumption that the source is governed by Gaussian statistics, this can be expressed in terms of second-order correlations (CSD matrix elements) by using the Gaussian moment theorem (Section 1.6.2, [1]). The result is

$$\langle \Delta I\left({\rho }_1\right)\Delta I\left({\rho }_2\right)\rangle =\sum _{i,j}{\left|W_{ij}({\rho }_1,{\rho }_2)\right|}^2.$$

(7)

The scintillation index ${\sigma }^2\left(\rho \right)$ is defined as the normalized version of the HBT correlation at two coincident points [4], i.e.,

$${\sigma }^2\left(\rho \right)\equiv \frac{\langle {[\Delta I\left(\rho \right)]}^2\rangle }{{\langle I\left(\rho \right)\rangle }^2}=\frac{{\sum }_{i,j}{\left|W_{ij}(\rho ,\rho )\right|}^2}{{\left[{\sum }_i{W}_{ii}(\rho ,\rho )\right]}^2}.$$

(8)

Clearly, because the lens modifies the elements of the CSD matrix, it is to be expected that the lens also changes the scintillation index. The degree of polarization of the field is given by the expression [2]

$$\begin{array}{c}\hfill P\left(\rho \right)=\sqrt{1-\frac{4\mathrm{Det}\mathrm{W}(\rho ,\rho )}{{\left[\mathrm{Tr}\mathrm{W}(\rho ,\rho )\right]}^2}}.\end{array}$$

(9)

From the previous two equations it can be derived that the scintillation index is related to the degree of polarization through the formula (see Section 8.4, [1]) and [13,14])

$${\sigma }^2\left(\rho \right)=\frac{1}{2}\left[1+P^2\left(\rho \right)\right].$$

(10)

Since $0\le P\left(\rho \right)\le 1$, it then follows that the scintillation index is bounded, i.e., $1/2\le {\sigma }^2\left(\rho \right)\le 1$.

4. Gaussian Schell-Model Sources

We take the field in the front focal plane to be that of a source of the Gaussian Shell-model (GSM) type. Such a source has CSD matrix elements of the form [2]

$$\begin{array}{c}{W}_{xx}^{\left(\mathrm{i}\right)}({\rho }_1^{\prime },{\rho }_2^{\prime })=A_x^{2}exp\left[-({\rho }_1^{\prime 2}+{\rho }_2^{\prime 2})/\left(4{\sigma }_{\mathrm{S}}^2\right)\right]exp[-{({\rho }_2^{\prime }-{\rho }_1^{\prime })}^2/\left(2{\delta }_{xx}^2\right)],\hfill \\ W_{yy}^{\left(\mathrm{i}\right)}({\rho }_1^{\prime },{\rho }_2^{\prime })=A_y^{2}exp\left[-({\rho }_1^{\prime 2}+{\rho }_2^{\prime 2})/\left(4{\sigma }_{\mathrm{S}}^2\right)\right]exp\left[-{({\rho }_2^{\prime }-{\rho }_1^{\prime })}^2/\left(2{\delta }_{yy}^2\right)\right],\hfill \\ W_{xy}^{\left(\mathrm{i}\right)}({\rho }_1^{\prime },{\rho }_2^{\prime })=A_x{A}_y{B}_{xy}\left[-({\rho }_1^{\prime 2}+{\rho }_2^{\prime 2})/\left(4{\sigma }_{\mathrm{S}}^2\right)\right]exp\left[-{({\rho }_2^{\prime }-{\rho }_1^{\prime })}^2/\left(2{\delta }_{xy}^2\right)\right],\hfill \\ W_{yx}^{\left(\mathrm{i}\right)}({\rho }_1^{\prime },{\rho }_2^{\prime })=W_{xy}^{\left(\mathrm{i}\right)*}({\rho }_1^{\prime },{\rho }_2^{\prime }).\hfill \end{array}$$

(11)

Here, $A_x$ and $A_y$ are the roots of the spectral densities of the two Cartesian components of the electric field, ${\sigma }_{\mathrm{S}}$ is the effective beamwidth, and $B_{xy}$ describes the correlation between $E_x$ and $E_y$, with $|B_{xy}|\le 1$. The coherence radii ${\delta }_{ij}$, with ${\delta }_{yx}={\delta }_{xy}$, must satisfy so-called realizability constraints [15], namely

$$\sqrt{\frac{{\delta }_{xx}^2+{\delta }_{yy}^2}{2}}\le {\delta }_{xy}\le \sqrt{\frac{{\delta }_{xx}{\delta }_{yy}}{\left|B_{xy}\right|}},$$

(12)

from which it follows that

$$\begin{array}{c}\hfill |B_{xy}|\le \frac{2}{{\delta }_{xx}/{\delta }_{yy}+{\delta }_{yy}/{\delta }_{xx}}.\end{array}$$

(13)

On making use of Equation (9) the degree of polarization across the front focal plane is found to be homogeneous, i.e.,

$$\begin{array}{c}\hfill P\left(\rho \right)=\frac{{(A_x^2-A_y^2)}^2+4A_x^2{A}_y^2{\left|B_{xy}\right|}^2}{{(A_x^2+A_y^2)}^2}.\end{array}$$

(14)

On substituting from Equations (11) into Equation (4), it is found that the four elements of the CSD matrix at the geometrical focus F (i.e., ${\rho }_1={\rho }_2=(0,0)$) are given by the expressions

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill W_{xx}^{\left(F\right)}& =\frac{4{\pi }^2{\sigma }_{\mathrm{S}}^2}{{\lambda }^2{f}^2}{A}_x^2{\mathsf{\Omega }}_{xx}^2,\hfill \\ \hfill W_{xy}^{\left(F\right)}& =\frac{4{\pi }^2{\sigma }_{\mathrm{S}}^2}{{\lambda }^2{f}^2}{A}_x{A}_y{B}_{xy}{\mathsf{\Omega }}_{xy}^2,\hfill \\ \hfill W_{yx}^{\left(F\right)}& =\frac{4{\pi }^2{\sigma }_{\mathrm{S}}^2}{{\lambda }^2{f}^2}{A}_x{A}_y{B}_{xy}^{*}{\mathsf{\Omega }}_{xy}^2,\hfill \\ \hfill W_{yy}^{\left(F\right)}& =\frac{4{\pi }^2{\sigma }_{\mathrm{S}}^2}{{\lambda }^2{f}^2}{A}_y^2{\mathsf{\Omega }}_{yy}^2,\hfill \end{array}\end{array}$$

(15)

where we have introduced

$$\begin{array}{c}\hfill \frac{1}{{\mathsf{\Omega }}_{ij}^2}=\frac{1}{4{\sigma }_S^2}+\frac{1}{{\delta }_{ij}^2},i,j\in \{x,y\}.\end{array}$$

(16)

On using Equations (11) in Equation (8) it readily follows that the scintillation index is uniform across the source plane, namely

$${\sigma }_{\mathrm{i}}^2=\frac{A_x^4+2{\left(A_x{A}_y\left|B_{xy}\right|\right)}^2+A_y^4}{{\left(A_x^2+A_y^2\right)}^2}.$$

(17)

The scintillation index at the geometrical focus is found by substituting from Equations (15) into Equation (8), with the result

$${\sigma }_F^2=\frac{{\left(A_x{\mathsf{\Omega }}_{xx}\right)}^4+2A_x^2{A}_y^2{\left|B_{xy}\right|}^2{\mathsf{\Omega }}_{xy}^4+{\left(A_y{\mathsf{\Omega }}_{yy}\right)}^4}{{\left(A_x^2{\mathsf{\Omega }}_{xx}^2+A_y^2{\mathsf{\Omega }}_{yy}^2\right)}^2}.$$

(18)

On comparing Equations (17) and (18) it is seen that the scintillation index at the geometrical focus generally differs from its counterpart in the front focal plane. This is because the three coherence radii ${\delta }_{ij}$ are absent in the expression for ${\sigma }_{\mathrm{i}}^2$, but they do occur in the expression for ${\sigma }_F^2$ via ${\mathsf{\Omega }}_{ij}$. In the special case that the three radii are all equal, i.e., when

$$\begin{array}{c}\hfill {\delta }_{xx}={\delta }_{yy}={\delta }_{xy},\end{array}$$

(19)

will the beam’s scintillation not be affected by the lens, irrespective of the value of the correlation coefficient $B_{xy}$.

As a side remark, we note that taking different effective widths for the matrix elements in Equations (11) would have led to a non-uniform scintillation index of the incident field. Similarly, in general, the index in the focal plane will not be homogeneous.

The expressions (11) for the incident beam’s CSD matrix have seven independent parameters. To illustrate the effects of the focusing process on the scintillation index, we must therefore limit ourselves to some selected cases.

(1).

For an unpolarized source, $A_x=A_y$ and $B_{xy}=0$. The index of the source then attains its minimum value $({\sigma }_{\mathrm{i}}^2=1/2)$, and, according to Equation (18), the scintillation index at focus equals

$$\begin{array}{c}\hfill {\sigma }_F^2=\frac{{\mathsf{\Omega }}_{xx}^4+{\mathsf{\Omega }}_{yy}^4}{{({\mathsf{\Omega }}_{xx}^2+{\mathsf{\Omega }}_{yy}^2)}^2}.\end{array}$$

(20)

The dependence of ${\sigma }_F^2$ on the coherence radius ${\delta }_{yy}$ is illustrated in Figure 2. It is seen that if ${\delta }_{yy}$ is equal to ${\delta }_{xx}=1\mathrm{mm}$, then ${\sigma }_F^2={\sigma }_{\mathrm{i}}^2=1/2$. In all other cases the lens significantly increases the scintillation.

(2).

For a fully polarized source $|B_{xy}|=1$, and the scintillation index across the source takes on its maximum value $({\sigma }_{\mathrm{i}}^2=1)$. The constraint given by expression (12) implies that now ${\delta }_{xx}={\delta }_{yy}=\delta$. On using this in (13) it follows that ${\delta }_{xy}=\delta$, meaning that all coherence radii, and hence also all factors ${\mathsf{\Omega }}_{ij}$, are equal. In this case, the scintillation index at the geometrical focus also takes on its maximum value, i.e.,

$${\sigma }_F^2={\sigma }_{\mathrm{i}}^2=1.$$

(21)

It is worth noting that any partially coherent, linearly polarized beam always produces a maximum scintillation index at focus $({\sigma }_F^2=1)$, even when its spatial coherence is not Gaussian as is assumed in Equation (11). This can be seen as follows. Without loss of generality, we can take the direction of linear polarization to be along the x-axis. Then, $W_{xx}^{\left(\mathrm{i}\right)}({\rho }_1^{\prime },{\rho }_2^{\prime })$ is the only non-zero CSD matrix element of the field in the front focal plane. Consequently, $W_{xx}^{\left(F\right)}$ is the only non-zero element at the geometrical focus. The application of Equation (8) then immediately yields that ${\sigma }_F^2=1$.

(3).

For a partially polarized source with equal spectral densities of the two Cartesian field components $(A_x=A_y)$, we find from Equations (17) and (18) that

$$\begin{array}{cc}\hfill {\sigma }_{\mathrm{i}}^2& =\frac{1}{2}+\frac{1}{2}{\left|B_{xy}\right|}^2,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\sigma }_F^2& =\frac{{\mathsf{\Omega }}_{xx}^4+2{\left|B_{xy}\right|}^2{\mathsf{\Omega }}_{xy}^4+{\mathsf{\Omega }}_{yy}^4}{{\left({\mathsf{\Omega }}_{xx}^2+{\mathsf{\Omega }}_{yy}^2\right)}^2}.\hfill \end{array}$$

(23)

As an example, we set ${\delta }_{xx}=1.2{\delta }_{yy}$ and let ${\delta }_{xy}$ vary between its bounds given by (12), for three selected values of $|B_{xy}|$. The resulting scintillation index at focus is shown in Figure 3. In all three cases the scintillation index at focus is significantly larger than its counterpart in the front focal plane (dashed line). Furthermore, in all three cases, the index attains its maximum value of unity when ${\delta }_{xy}$ reaches its upper bound.

(4).

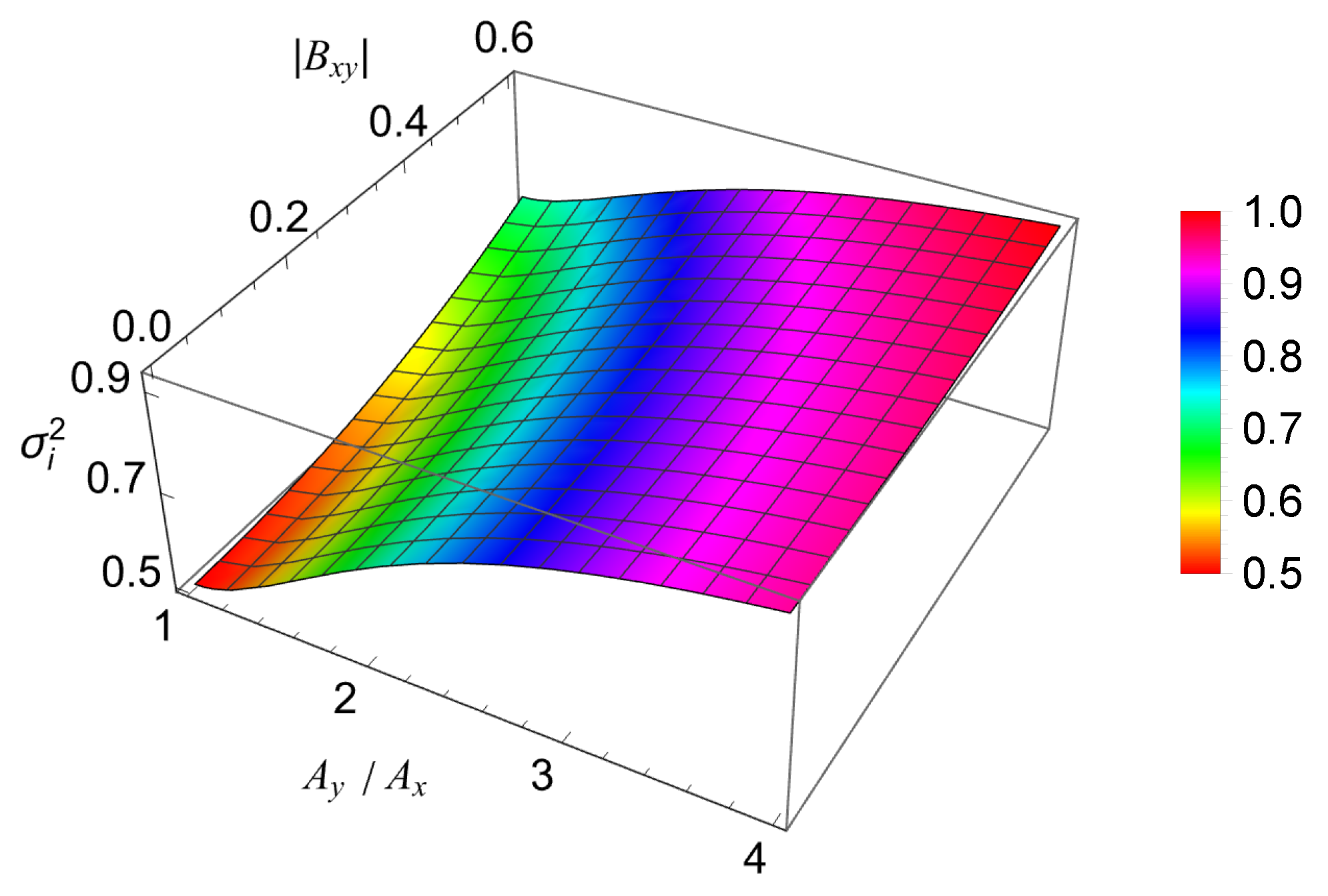
When the amplitudes of the two field components are not equal $(A_x\ne A_y)$, Equations (17) and (18) cannot be further simplified. The behavior of the uniform scintillation index in the front focal plane is illustrated in Figure 4. The three independent coherence radii are fixed, and $|B_{xy}|$ is varied over its range given by the realizability conditions. It is seen that the index in the front focal plane grows with increasing ratio $A_y/A_x$ as well as with increasing $|B_{xy}|$. Clearly, the scintillation at focus also depends on these quantities. The difference between the two indices, $\Delta ={\sigma }_F^2-{\sigma }_{\mathrm{i}}^2$, is plotted in Figure 5, and reaches its maximum when $A_y/A_x=1$. In all cases, the scintillation at focus is larger than the scintillation in the front focal plane. The increase due to focusing can be as high as 0.25, which in that case is an increase of $37\%$.

5. Conclusions

The scintillation index of a partially coherent and partially polarized electromagnetic beam can be derived, for the case of Gaussian statistics, from the cross-spectral density matrix. Upon focusing by a thin paraxial lens, the CSD matrix elements undergo a four-dimensional Fourier transform. This implies that such a lens may alter the scintillation index.

We have demonstrated, for incident beams of the wide class of Gaussian Schell types, that the scintillation index at focus is typically significantly larger than the scintillation index of the incident beam.

We have used the Gaussian Schell-model source as an illustration because it represents a broad class of fields that are often encountered in practice. However, taking Equation (4) as a starting point, the effect of focusing of any random beam on the scintillation index can be analyzed.

Because beam scintillation is undesirable for optical communication, our results may be relevant for any detection scheme of signal-carrying beams in which lenses are being deployed.