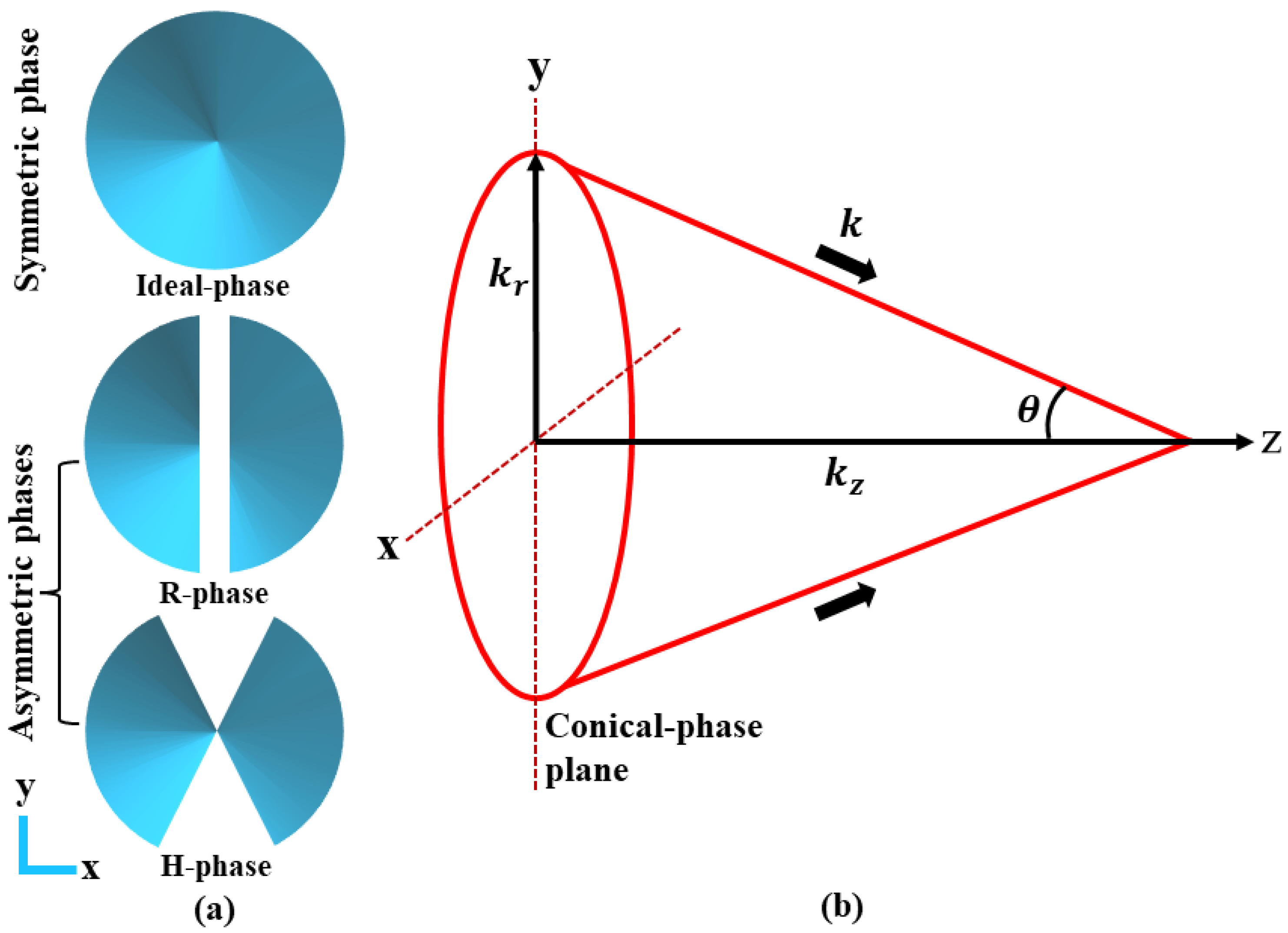
1. Introduction
In the last few decades, the implementation of the ultrafast Bessel–Gauss (BG) beam has had a significant impact on the field of laser-material processing. With an extended depth of focus, the non-diffractive central core of the focused micro-BG beam facilitates highly stable non-linear ionization with axial energy confinement [
1,
2,
3,
4]. All these characteristics enable the fabrication of high-aspect-ratio nanostructures, ultra-precision laser machining, drilling, and cutting applications [
5,
6,
7,
8,
9]. An axicon (conical lens or phase) is the most convenient means to realize a BG beam and has been employed in various applications [
10,
11,
12,
13,
14,
15]. Recent studies suggest that the non-ideal axicon phase can result in peculiar intensity patterns [
16,
17,
18], including the elliptical BG beam, which has potential in a wide range of applications [
19,
20].
In laser processing applications, the elliptical BG beam has recently become a topic of interest. The elliptical central core of this asymmetric beam accompanied by side multichannels makes it an attractive tool in the fabrication of ultra-high-aspect-ratio multi-nano-channels and material cleaving with sub-micron precision [
21,
22], and also facilitates intra-volume material modification [
19]. Such elliptical beams have also previously shown their ability to determine asymmetric stress field with preferential crack orientation, guiding cleavage and fracture planes to facilitate cutting of transparent materials [
23,
24]. In this context, maintaining the central core ellipticity of these asymmetric beams is a challenging task and plays an important role in achieving uniform modifications and crack orientations.
The realization of an elliptical BG beam requires beam-shaping solutions. Several beam-shaping techniques are noted for the generation of such asymmetric beams, which are mostly dedicated to either using the tilted axicon [
17,
22,
25,
26] or the amplitude masks [
21,
24]. Another technique to produce useful asymmetric beam patterns is implementing the generalized axicon, the combination of a radially symmetric axicon phase and an azimuthally dependent arbitrary phase, retrieved by optimizing with respect to the desired optical beam profile [
23]. In the case of a tilted axicon, the oblique incident plane of the axicon introduced asymmetry to the conical phase and hence generates the elliptical BG beam. The main limitation of this technique is the presence of astigmatic aberration and the misaligned optic axis where the axicon has to be laterally shifted precisely to maintain the generated beam profiles [
27]. The amplitude filers, such as a rectangular-shaped filter [
21] and an hourglass-shaped filter (H-amp) [
24], can generate an elliptical BG beam by partially blocking the Bessel ring at the back focal plane (also known as Fourier plane) of the lens in the axicon-lens assembly without disturbing the optic axis of the beam. The dimensions of the amplitude filters define the ellipticity of the generated beam. However, amplitude filtering is inherently a loss of energy.
Recently, there has been a quest to attain the most convenient technique for the controlled generation of elliptical BG beams with non-diffractive central core. The phase-only solution including asymmetric elements represents a promising path to conserve energy. A particularly robust solution conserving ellipticity over a long distance was implemented in Chen et al. [
28], corresponding to an hourglass (H) phase designed to compensate diffraction along the axial lobe. From a general point of view, it is then of interest to investigate the propagation of asymmetric phase elements superposed on the conical phase pattern, starting with the simplest rectangular elements and their influence on the stability, asymmetry, and energy content of the beam. In this paper, we perform an in-depth study of the controlled generation of non-diffractive elliptical BG-like beams by computing different asymmetric phase-only computer-generated holograms (CGHs), displayed on a reflective-type phase-only LCOS-SLM (liquid crystal on silicon-based spatial light modulator) device for having precise control over phase parameters. We equally discuss the stability of different phase-modulated solutions and highlight the propagation dynamics of phase anisotropies. LCOS-SLM works in the principle of phase modulation, which spatially shapes the input laser beam to produce the desired output beam based on the gray-scale image of the CGH displayed on its screen [
29]. We implement the blazed grating phase on the initially generated CGHs (for R- and H-phase, as discussed later) that can efficiently eliminate any optical noises at the Fourier plane and can produce uniform micro-elliptical BG-like beams (without partially blocking the Bessel ring). Subsequently, we analyze and present the performances of those modified CGHs in terms of the non-diffractive properties of the generated asymmetric beams. Furthermore, a numerical model based on the Fresnel transfer function method (FTFM) is developed to compare the experimentally obtained beam profiles. The excellent agreement of experimental results with simulation confirms the accuracy and reliability of the beam-shaping technique. This study will help to increase the efficiency and controllability of laser processing applications.
3. Numerical Modeling and Validation
This section emphasizes the generation of demagnified symmetric and asymmetric BG beams (in air) by numerical simulation. An algorithm based on FTFM method in scalar diffraction theory is developed, which is the theoretical basis for this simulation [
32].
The schematic of the algorithm is depicted in
Figure 3, representing the propagation of the Bessel beams (initially generated by the conical phases) through a telescopic 4f system. The 4f system is modelled in such a way that the initially generated BG beam behind the axicon phase is demagnified by a factor (
;
= 1 m and
= 50 mm are the focal lengths associated to the 4f-system) of 20 after the 4f propagation. Thus, a subsequent reduction of Bessel length is expected by a factor of
. The calculating area of the object plane (at
) is sampled with 1000 × 1000 pixel-grids with a pixel dimension of 10
m × 10
m throughout the simulation.
To solely realize the non-diffractive nature of the generated beam, the resulting final beam is reconstructed as a stack of slices parallel to the transverse (x–y) plane, and hence extended along the propagation direction (z). The simulation is carried out completely in the spatial domain; therefore, there is no temporal influence of the input laser beam on the generated Bessel beams.
3.1. Reconstruction Method
To generate a symmetric BG beam, a thin axicon phase with
= 0.4
is considered on the object plane, which is illuminated with a collimated laser beam of beam-waist
= 0.93 mm (at 1/
) at a given wavelength (
) of 800 nm. The complex amplitude distribution just after the object plane can be obtained by
Here, is the amplitude of the input beam, = being the amplitude transmission function of a thin axicon with the axicon phase: .
Under the Fresnel approximation, the complex amplitude distribution of the output beam at a distance
z from the axicon phase can be expressed by [
32,
33]
where
, being the Fresnel’s impulse response function. Now, by taking Fourier transform on both side of the Equation (
5) and then applying the inverse Fourier transform, we obtain the expression for computing the diffracted field (Bessel distribution) as the following:
where
{} and
{} denote the inverse fast Fourier transform and the fast Fourier transform operators respectively;
is referred to as the Fresnel transfer function associated to
;
and
are the spatial coordinates in the frequency domain.
Now, we numerically model a 4f optical system by considering thin lens approximation (i.e., far-field Fraunhofer approximation) by simply taking the Fourier transforms of the Equation (
6) twice in order to solely realize the demagnified version of the diffracted field (i.e.,
) corresponds to the initially obtained diffracted field (i.e.,
), as depicted in
Figure 3:
The first
operation in the above expression gives the angular spectrum distribution at the FP, while the second
operation calculates the demagnified field after the 4f system. It is essential to mention that the sampling interval does not remain the same in the far-field diffraction calculations. Thus, the sampling interval after performing the 4f propagation becomes [
33]:
where
and
are the spatial dimensions of the sampling window, and
and
are the sampling interval associated to the FP in the orthogonal directions, respectively. Similarly,
and
are the spatial dimensions of the sampling window associated with the object plane, and
and
are the corresponding sampling intervals. The terms
and
denote the pixel densities along the
x and
y axes, respectively.
3.2. Reconstruction of Symmetric BG Beams
The implication of our numerical model results in the formation of a symmetric BG beam. Interestingly, the on-axis intensity profile of the resulting BG beam (after 4f propagation) with the non-diffractive Bessel length
0.59 mm (calculated at FWHM) profoundly matches the theoretical profile, as shown in
Figure 4b.
Furthermore, the reconstructed longitudinal evolution of the resulting beam in the
x–
z and
y–
z planes (see
Figure 4a) and its invariant central core sizes at different propagation distances (see
Figure 4c) clearly indicates the non-diffractive ideal nature of the BG beam, and hence validates our numerical model.
3.3. Reconstruction of Asymmetric BG Beams
This section mainly focuses on the implementation of our developed numerical model to simulate the elliptical BG beams using different asymmetric phases (R- and H-phase). In the simulation, the ellipticity of the beam profiles is defined by the parameter
e, which is calculated as the ratio of FWHM of the central core intensity along
x and
y axes (i.e.,
e =
; where
). Therefore, a smaller value of
e corresponds to the higher ellipticity of a beam profile. Note that for simplicity, we use an annular filter in simulation to block the central noise in the FP (a beam-shaping technique to eliminate such optical noises is discussed later in the
Section 4).
3.3.1. Numerical Analysis for R-Phase
Simulation is carried out for different in-phase filter dimensions (
) of the R-phase (orientated along
y axis).
Figure 5a shows a notable change in the on-axis profile in comparison to the ideal-phase. Firstly, a successive decrease in the Bessel length (
0.74 mm, 0.66 mm and 0.54 mm, respectively) along with a longitudinal shift of the on-axis profile is observed as the parameter
increases. Secondly, an increased Bessel length (
= 0.74 mm) is noted for
= 0.31 mm as compared to the ideal case (see
Figure 4), which is surely the consequence of the modulated Bessel ring introduced by R-phase as discussed before.
Figure 5b shows the longitudinal intensity maps (in
x–
z and
y–
z planes) which verify the existence of an elliptical central core surrounded by the evolution (along
x) of side multichannels.
Figure 5c shows the images of the beam profiles for different
values and the corresponding transverse intensity distributions (along
x and
y) at different peak on-axis intensity positions. It is observed that the ellipticity of the central core increases with
(for
= 0.31 mm, 0.81 mm, and 1.41 mm, the obtained value of
e = 0.82, 0.65, and 0.50, respectively).
3.3.2. Numerical Analysis for H-Phase
Simulation is carried out for different in-phase filter dimensions (
) of the H-phase. A maintained Bessel length of
0.58 mm is observed (see
Figure 6a) for different values of
(oriented along
y axis). Interestingly, in contrast to the R-phase, the H-phase shows no longitudinal shift of the on-axis profile as
increases.
Figure 6b shows the longitudinal intensity maps (in
x–
z and
y–
z planes), which indicates an elliptical central core surrounded by the evolution (along
x) of side multichannels.
Figure 6c shows the images of the beam profiles for different
values and the corresponding transverse intensity distributions (along
x and
y) at the peak on-axis intensity position (at
z = 0.45 mm, same for all
). An increase in ellipticity is observed with
(for
= 28.07
, 61.93
, and 90
, the obtained value of
e = 0.83, 0.62, and 0.46, respectively).
Finally, our numerical analyses reveal the influences of the asymmetric R- and H-phase in the formation of elliptical BG beams and systematically support the mathematical interpretations as shown in Equation (
3), which validates our approach. In principle, if the rectangular (R) phase modulation produces along propagation a propagation variant effect, the H-phase compensates this, as the radial variability of the phase pattern compensates the evolution along the axis.
4. Experimental Setup and Methods for Beam-Shaping
The experimental setup for the generation of the elliptical BG beams is shown in
Figure 7. The laser pulse (pulse duration ∼ 110 fs, repetition rate ∼ 50 MHz) originated from a femtosecond laser oscillator (IMRA/femtolite, FX-10-STD) at 800 nm wavelength is expanded and perfectly collimated using a beam expander setup containing a concave lens and a plano-convex lens (PCL) of focal lengths −25 mm and 75 mm, respectively. The energy of the laser beam is adjusted using a set of calibrated neutral density (ND) filters and hence directed (using the dielectric mirrors
and
) to the active area (screen) of the reflective type phase-only LCOS-SLM device (X10468 series, Hamamatsu Photonics, Shizuoka, Japan) at a low angle of incidence (∼8
) for obtaining the maximum efficiency. The experimental setup is configured in such a way that one can directly implement it during the laser processing application. Therefore, to avoid any damages and non-linear effects during the intense beam propagation through the optical elements, the CGHs are created (see
Figure 8) for a thin axicon of
=
with
n = 1.45. For characterization purposes, the energy of the input beam is kept far below the damage threshold of the LCOS-SLM device. LCOS-SLM modulates the phase of the incident collimated laser beam according to the CGH displayed on its screen and thus spatially shapes the input beam to produce the elliptical BG beam upon reflection. The incident beam size (
2.5 mm at 1/
) is kept smaller than the window size of the LCOS-SLM screen (792 × 600 pixels, pixel-pitch = 20
m) to avoid any undesired aperture effect in the generated beam.
The illumination on the pixelated LCOS-SLM screen diffracts light mainly into three components (0-th order undiffracted, and +1, −1 order diffracted beams). The superposition of this 0-th order component (basically noise) with the other diffracted orders strongly modulates the intensity profile of the generated beam along the propagation direction after the LCOS-SLM, as shown in the inset-A (typical image obtained in simulation) of
Figure 7. Therefore, it is essential to spatially separate and block the undesired diffraction orders to make the beam oscillation free, and it is accomplished by adding a blazed grating phase to the initially calculated CGH using the mathematical expression given by [
29,
34]:
Here,
is the phase expression of the in-phase filters imposed on the axicon phase
, and
9 lines/mm and
= 0 are the spatial frequencies of the blazed grating along
x and
y axes, respectively. The calculated CGHs are wrapped over [0–2
] using the function ‘
mod’, and hence converted into the gray-scale before displaying on the LCOS-SLM screen, as shown in
Figure 8.
The modified CGHs spatially separate the diffracted components at the FP of a PCL (
:
= 1 m), where we place an aperture mounted on a
-transnational stage only to allow the +1 order (containing relatively higher energy) to pass through the second PCL (
:
= 50 mm) of the 4f system. Note that a properly designed blazed grating can achieve above 90% diffraction efficiency in the +1 order [
34,
35], and with the damage threshold of around 1 mJ, the used LCOS-SLM can deliver enough energy to the sample plane to make laser-induced damage. This efficient and highly controllable beam-shaping technique produces a uniform and demagnified (by a factor of 20) version of the elliptical BG beam after the 4f system, which is hence ready for the laser-material processing, as shown in the inset-B (typical image obtained in simulation) of
Figure 7. The generated elliptical micro-BG beam is finally characterized using a high-resolution 4f imaging system mounted on a micro-precision
-transnational stage by recording several transverse images along the optical axis. The imaging system consists of a long working distance microscope objective with a high numerical aperture (50X/NA 0.42, Mitutoyo), a tube lens (
:
= 40 mm), and a calibrated CCD camera having linear response.
5. Results and Discussions
Experimental investigations and characterization of the ultrafast micro-elliptical BG beams are carried out (see
Figure 9) using the computed CGHs of different types and the optical scheme (
Figure 7) as discussed before. The experimentally obtained beam profiles are compared with the simulation to verify the performance of our beam-shaping technique using the developed numerical model (see
Section 3.1) based on the FTFM method [
32,
33]. Several spatial filtering techniques are noted for making uniform on-axis Bessel intensity profiles [
24,
36,
37], which are limited by energy loss and uncontrolled beam parameters. To solely realize a uniform axial intensity distribution, we implement a beam-shaping technique by displaying the modified CGHs on the LCOS-SLM screen, as shown in
Figure 8. It efficiently eliminates any undesired optical noises at the FP based on the controlled phase-grating parameters and thus makes the resulting demagnified beams completely uniform which would otherwise have oscillatory behavior [
19].
Figure 9a shows the uniform on-axis intensity distributions of the symmetric and elliptical BG beams generated by the modified CGHs of ideal-phase, R-phase (with
= 1.41 mm) and H-phase (with
= 90
), respectively. The experimentally measured on-axis profiles are fitted with the simulated profiles which show the closest match and clearly indicate the high uniformity of the generated beams. The on-axis profile with ideal-phase shows a non-diffractive Bessel length of
= 1.58 mm (according to fit). However, a relative reduction of Bessel length (
= 1.27 mm) is observed in the case of R-phase, while the H-phase maintains the Bessel length of
= 1.53 mm very close to that of ideal-phase irrespective of the in-phase filter dimensions. Furthermore, a significant shift of the on-axis profile is observed along the propagation direction (
z) in the case of R-phase, whereas the position and shape of the on-axis profile remain conserved for H-phase while comparing with the ideal-phase. This observation surely highlights the advantage of using the H-phase in terms of maintaining the ideal nature of the on-axis profile.
Figure 9b–d shows images of the measured beam profiles (in
x–
y plane) of the generated beams at different propagation distances. Interestingly, the experimentally measured beam profiles are observed to be in excellent agreement with the simulation. This definitively confirms the accuracy and high controllability of the LCOS-SLM-based beam-shaping technique for the generation of elliptical BG beams. The above-mentioned figures confirm that both R-phase and H-phase (oriented along
y axis) produce elliptical BG beams. It is observed that the generated beams contain elliptical central cores surrounded by the evolution of multi-channel elliptical cores (along
x axis), the asymmetry of which is entirely defined by the spatial dimensions of the in-phase filters (oriented along
y axis) as also numerically analyzed in
Figure 5 and
Figure 6, respectively, (evolution of multi-channel cores also increases with filter dimensions).
Figure 10a shows the transverse intensity profiles at the corresponding peak on-axis intensity positions (see
Figure 9a) for ideal-, R- and H-phase, respectively. The profiles are normalized with respect to the peak intensity value as obtained with the ideal-phase for intensity comparison. It is observed that the implementation of different asymmetric phases lowers the peak intensity level by a factor of ∼0.55 for R-phase and ∼0.75 for H-phase as compared to the ideal-phase. This intensity reduction is analogous to the distributed intensity from the central core to the side cores of the generated asymmetric beams for the in-phase filters of specific dimensions (in this case,
= 1.41 mm for R-phase and
= 90
for H-phase). Now, it is interesting to point out that the R-phase exhibits higher intensity contrast (∼0.21) between the central and ±1 order cores as compared to the H-phase. The relatively low intensity contrast (∼0.03) would make H-phase advantageous to use in particular application such as high-aspect-ratio multi-nano-channels, with the access of enough supplied energy (below the damage threshold of LCOS-SLM).
Figure 10b shows the variation of central core ellipticity of the generated asymmetric beams as a function of
z for different conical phases. It is observed that the ellipticity values as estimated in the simulation is fitting well with the experimentally obtained values. The ellipticity (
e) is calculated as a ratio of FWHM of the central core along
x and
y axes. We obtain the
e values (at the peak on-axis positions) of ∼0.96, 0.82, and 0.40 (in experiment), which is in good agreement with simulation (
e = 1, 0.84, and 0.46) for the ideal-, R-, and H-phase, respectively. Interestingly, the H-phase profoundly exhibits the desired non-diffractive behavior (maintained ellipticity along propagation), which is consistent with the ideal-phase. However, for the R-phase, an abrupt increase of
e value (i.e., corresponding to the decrease in overall beam ellipticity) is observed with propagation, which makes the beam pseudo-non-diffractive. This squeezing effect is mainly attributed to the modulated Bessel ring (see
Section 2.1) that remains even after applying the modified CGH. A direct influence of this instability is also noted in the on-axis profile. Specifically, the leading part of the R-phase generated on-axis profile (see
Figure 10a) becomes slowly varying. This behavior is in contrast to that of H-phase, which maintains its non-diffractive characteristic. The above observations clearly highlight the limitation of the R-phase and emphasize the effectiveness of using the H-phase for elliptical BG beam generation.
Furthermore, in order to solely realize the asymmetric characteristics of the elliptical BG beams generated by R- and H-phase, we numerically calculate the unwrapped phase profiles at different
z values, and compare the results with the ideal-phase, as represented in
Figure 11a–c.
In the case of R-phase, the effect on the phase asymmetry is clearly visible at the beginning (at
z = 0.62 mm), whereas this effect smears (loss of asymmetry) with propagation due to the strong diffraction (stronger along
x axis) caused by the rectangular-shaped filter of the R-phase. However, the diffraction effect caused by the triangular-shaped filter of the H-phase is compensated (phase asymmetry is maintained) along propagation by the radial wave-vector components kicking out in different directions. It clearly explains the origin of instability in the case of R-phase and also confirms the robustness of H-phase for the generation of high-quality nearly non-diffractive elliptical BG beams. The phase asymmetry (
) is calculated in terms of the ellipticity of the central lobe of the phase images and represented as a function of
z for different conical phases, as shown in
Figure 11d. The curves (indicated by dotted lines) show similar nature (i.e., unstable and maintained phase asymmetry for R- and H-phase, respectively) as we also previously obtained in
Figure 10b, which supports the above discussions.
The above results indicate that the R-phase is less efficient in maintaining the ellipticity but preserves a high-intensity peak (relative intensity of ∼0.45), while H-phase has a propagation-invariant ellipticity at the expense of shifting energy on the localized side lobes. This originates from the conical interaction of waveforms where radially different phase elements correspond to axially different propagation points, indicating the need to control diffraction at different distances from the conical element.
Finally, our study based on the advanced spatial beam-shaping technique (see
Figure 8) uses the highly controlled asymmetric CGHs which provide a uniform micro-elliptical BG generation (avoids unwanted energy loss in terms of not blocking the Fourier Bessel ring) with precise controllability. The obtained highly elliptical and nearly non-diffractive central core along with the side multichannels of the generated asymmetric beams ensure their applicability in the ultrafast laser-material processing applications, and particularly would be an efficient choice of interest in high-speed laser-glass cutting [
24,
25,
26], high-aspect-ratio multi-nano-channels [
21], and scientific study of non-linear optics, e.g., super-continuum generation [
38,
39]. Nevertheless, situations may appear where the high contrast of the side lobes may be detrimental. We note that this appears to be inherently related to the tradeoff between ellipticity and central lobe intensity, being related to the reconstruction capacity of the beam.