SNR Model of Optical Fiber Acoustic Sensing System Based on F-P Structure
Abstract
:1. Introduction
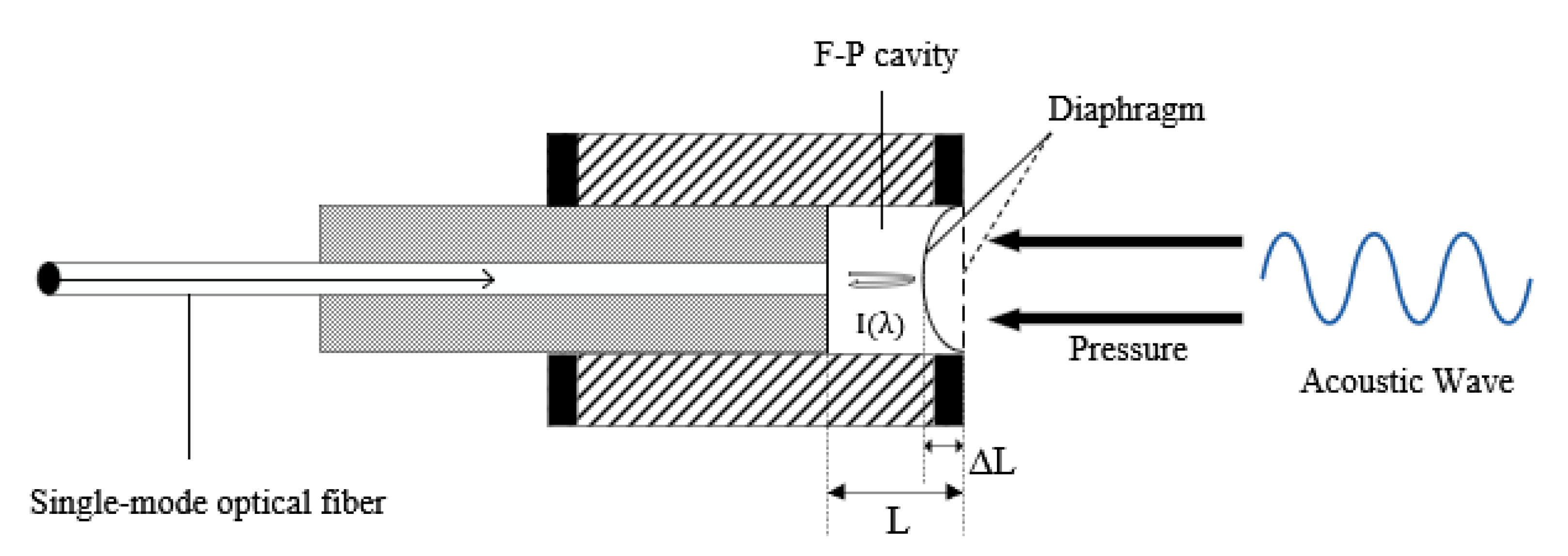
2. Theoretical Analysis
3. Signal-to-Noise Ratio Model
4. Experimental Results and Discussion
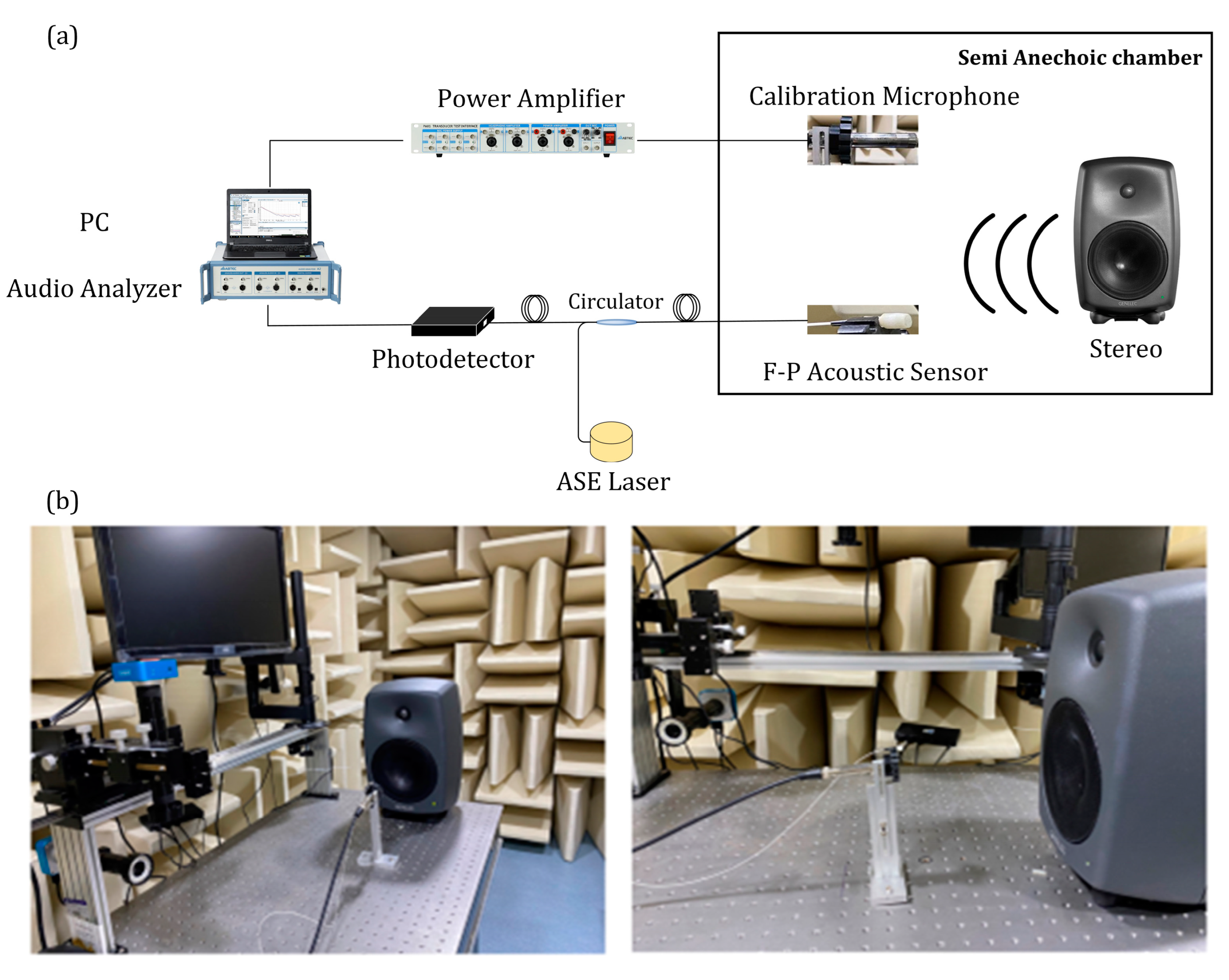
4.1. Experiments Setup
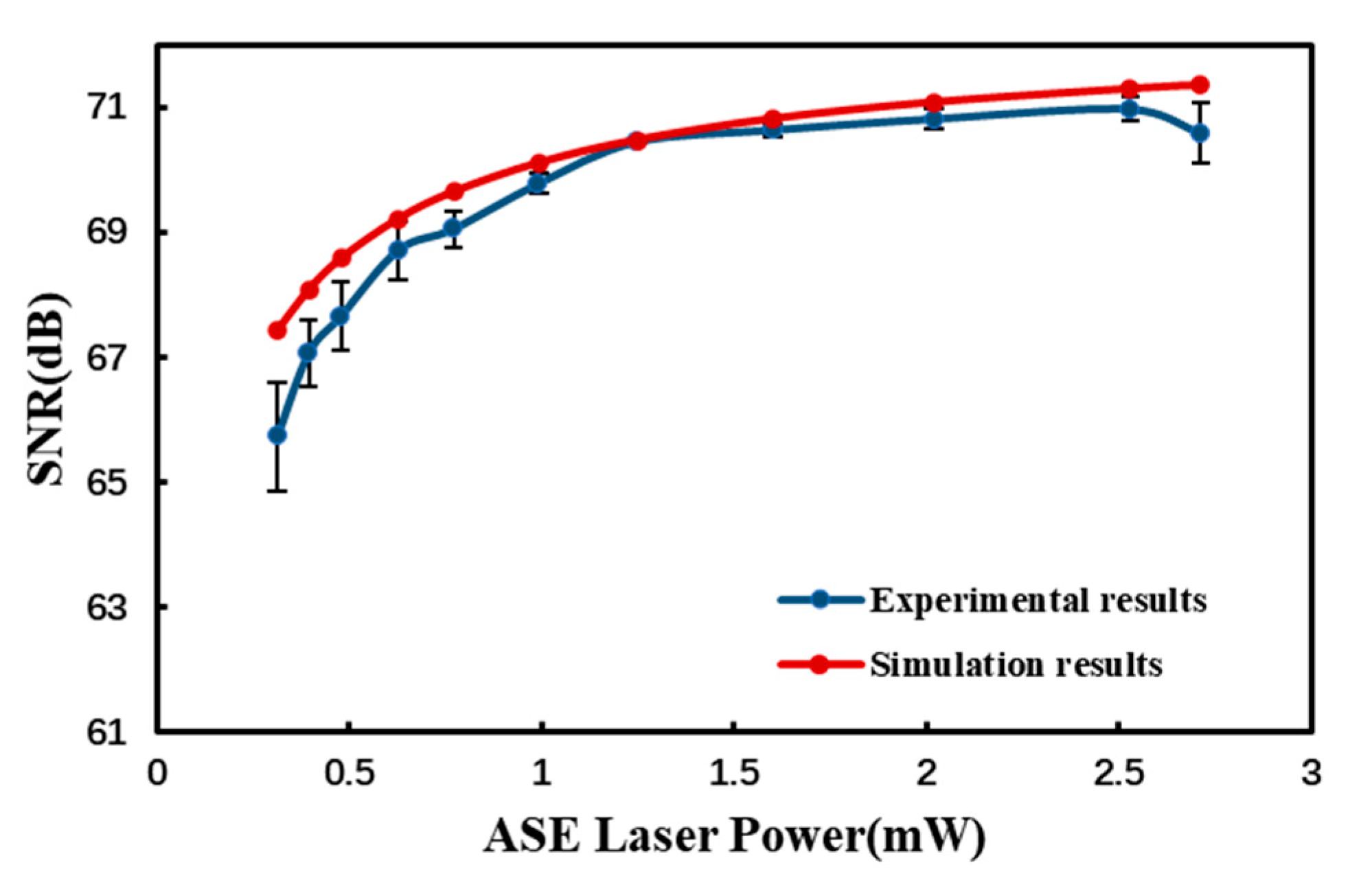
4.2. Comparison of SNR Model to Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- He, Z.; Liu, Q. Optical fiber distributed acoustic sensors: A review. J. Light. Technol. 2021, 39, 3671–3686. [Google Scholar] [CrossRef]
- Chunming, G.; Feng, N.; Ping, Z.; Binxing, Z.; Jing, W.; Bincheng, L. Optical fiber acoustic sensors. Opto-Electron. Eng. 2018, 45, 180050-1–180050-10. [Google Scholar]
- Deng, J.; Xiao, H.; Huo, W.; Luo, M.; May, R.; Wang, A.; Liu, Y. Optical fiber sensor-based detection of partial discharges in power transformers. Opt. Laser Technol. 2001, 33, 305–311. [Google Scholar] [CrossRef]
- Yu, B.; Kim, D.W.; Deng, J.; Xiao, H.; Wang, A. Fiber Fabry-Perot sensors for detection of partial discharges in power transformers. Appl. Opt. 2003, 42, 3241–3250. [Google Scholar] [CrossRef] [PubMed]
- Akkaya, O.C.; Akkaya, O.; Digonnet, M.J.F.; Kino, G.S.; Solgaard, O. Modeling and demonstration of thermally stable high-sensitivity reproducible acoustic sensors. J. Microelectromech. Syst. 2012, 21, 1347–1356. [Google Scholar] [CrossRef]
- Jo, W.; Akkaya, O.C.; Solgaard, O.; Digonnet, M.J.F. Miniature fiber acoustic sensors using a photonic-crystal membrane. Opt. Fiber Technol. 2013, 19, 785–792. [Google Scholar] [CrossRef]
- Zhang, W.; Lu, P.; Qu, Z.; Zhang, J.; Liu, D. Four-wavelength quadrature phase demodulation technique for extrinsic Fabry–Perot interferometric sensors. Opt. Lett. 2022, 47, 2406–2709. [Google Scholar] [CrossRef] [PubMed]
- Downie, J.D.; Liang, X.; Ivanov, V.; Sterlingov, P.; Kaliteevskiy, N. SNR model for generalized droop with constant output power amplifier systems and experimental measurements. J. Light. Technol. 2020, 38, 3214–3220. [Google Scholar] [CrossRef]
- Guo, M.; Chen, K.; Yang, B.; Li, C.; Zhang, B.; Yang, Y.; Wang, Y.; Li, C.; Gong, Z.; Ma, F.; et al. Ultrahigh sensitivity fiber-optic Fabry–Perot interferometric acoustic sensor based on silicon cantilever. IEEE Trans. Instrum. Meas. 2021, 70, 1–8. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, C.; Wu, F.; Li, C.; Zhou, J.; Gong, Y.; Rao, Y.; Chen, Y. A highly sensitive fiber-optic microphone based on graphene oxide membrane. J. Light. Technol. 2017, 35, 4344–4349. [Google Scholar] [CrossRef]
- Dehé, A.; Wurzer, M.; Füldner, M.; Krumbein, U. Design of a poly silicon MEMS microphone for high signal-to-noise ratio. In Proceedings of the 2013 European Solid-State Device Research Conference (ESSDERC), Bucharest, Romania, 16–20 September 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 292–295. [Google Scholar]
- Karim, A.; Devenport, J. Noise figure reduction in externally modulated analog fiber-optic links. IEEE Photonics Technol. Lett. 2007, 19, 312–314. [Google Scholar] [CrossRef]
- Xiang, Z.; Dai, W.; Rao, W.; Cai, X.; Fu, H. A Gold Diaphragm-Based Fabry-Perot Interferometer with a Fiber-Optic Collimator for Acoustic Sensing. IEEE Sens. J. 2021, 21, 17882–17888. [Google Scholar] [CrossRef]
- Ma, J.; Xuan, H.; Ho, H.L.; Jin, W.; Yang, Y.; Fan, S. Fiber-optic Fabry–Pérot acoustic sensor with multilayer graphene diaphragm. IEEE Photonics Technol. Lett. 2013, 25, 932–935. [Google Scholar] [CrossRef]
- Macedo, L.; Pedruzzi, E.; Avellar, L.; Castellani, C.E.S.; Segatto, M.E.V.; Frizera, A.; Marques, C.; Leal-Junior, A. High-Resolution Sensors for Mass Deposition and Low-Frequency Vibration Based on Phase-Shifted Bragg Gratings. IEEE Sens. J. 2022, 23, 2228–2235. [Google Scholar] [CrossRef]

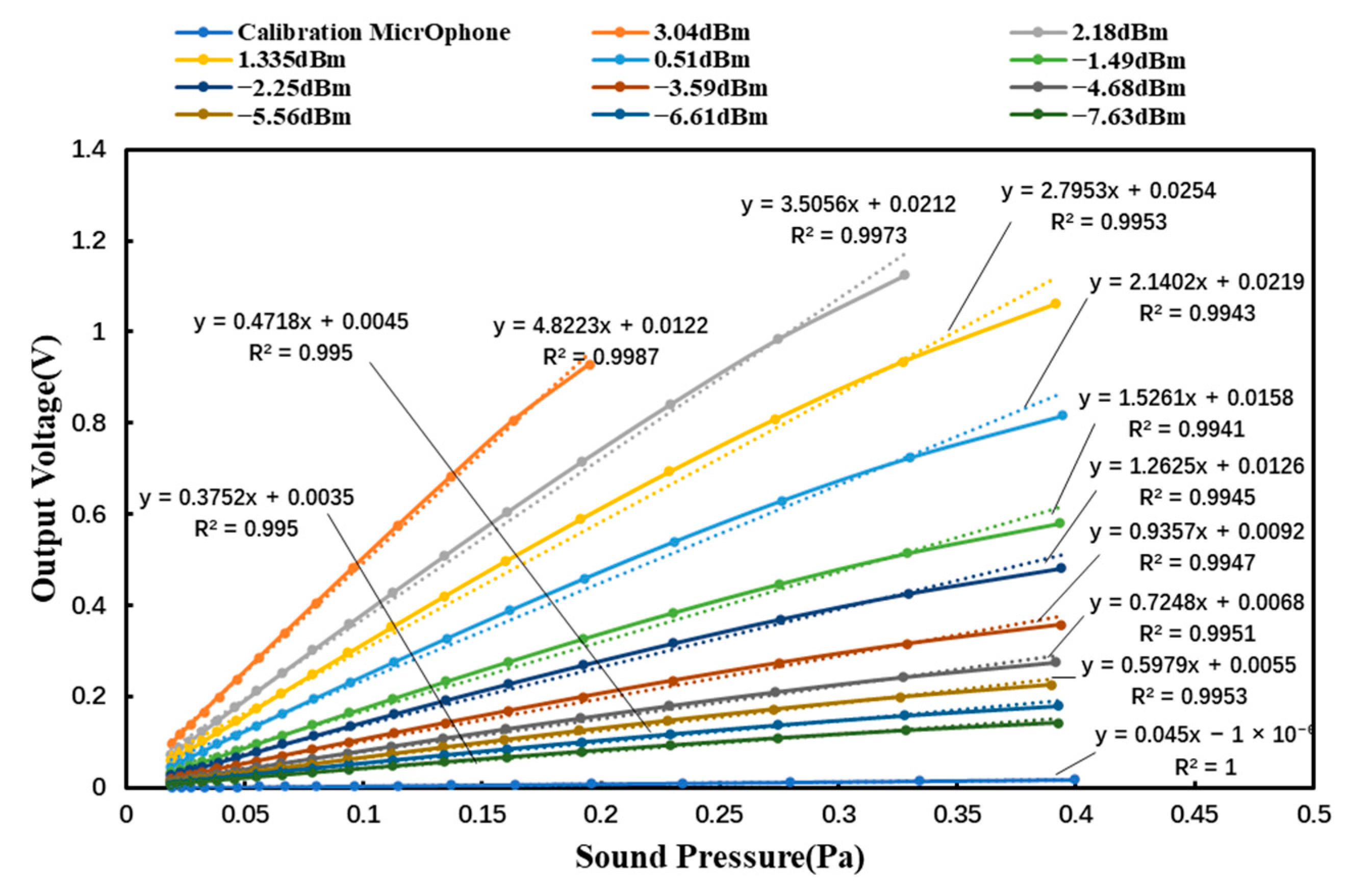

| P (dBm) | (V/Pa) | (nm/Pa) |
|---|---|---|
| 3.04 | 4.8223 | 250.3405 |
| 2.18 | 3.5056 | 236.6855 |
| 1.335 | 2.7953 | 237.4239 |
| 0.51 | 2.1402 | 245.7801 |
| −1.49 | 1.5261 | 251.2925 |
| −2.25 | 1.2625 | 246.6651 |
| −3.59 | 0.9357 | 248.5624 |
| −4.68 | 0.7248 | 246.2618 |
| −5.56 | 0.5979 | 248.3989 |
| −6.61 | 0.4718 | 250.2916 |
| −7.627 | 0.3752 | 251.5058 |
| Parameter | Symbol | Value |
|---|---|---|
| Wavelength | ||
| Relative Intensity Noise | ||
| Membrane Sensitivity | ||
| Detector Sensitivity | ||
| Bandwidth | ||
| Elementary Charge | ||
| Loss |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Guan, C.; Tong, Y.; Chu, W.; Zhou, R.; Zhou, Y. SNR Model of Optical Fiber Acoustic Sensing System Based on F-P Structure. Photonics 2023, 10, 676. https://doi.org/10.3390/photonics10060676
Liu Y, Guan C, Tong Y, Chu W, Zhou R, Zhou Y. SNR Model of Optical Fiber Acoustic Sensing System Based on F-P Structure. Photonics. 2023; 10(6):676. https://doi.org/10.3390/photonics10060676
Chicago/Turabian StyleLiu, Yingjie, Chenggang Guan, Yala Tong, Wenxiu Chu, Ruling Zhou, and Yikai Zhou. 2023. "SNR Model of Optical Fiber Acoustic Sensing System Based on F-P Structure" Photonics 10, no. 6: 676. https://doi.org/10.3390/photonics10060676
APA StyleLiu, Y., Guan, C., Tong, Y., Chu, W., Zhou, R., & Zhou, Y. (2023). SNR Model of Optical Fiber Acoustic Sensing System Based on F-P Structure. Photonics, 10(6), 676. https://doi.org/10.3390/photonics10060676




