A Novel PMDI Fiber Optic Hydrophone Incorporating IOC-Based Phase Modulator
Abstract
1. Introduction
2. System Design and Principle
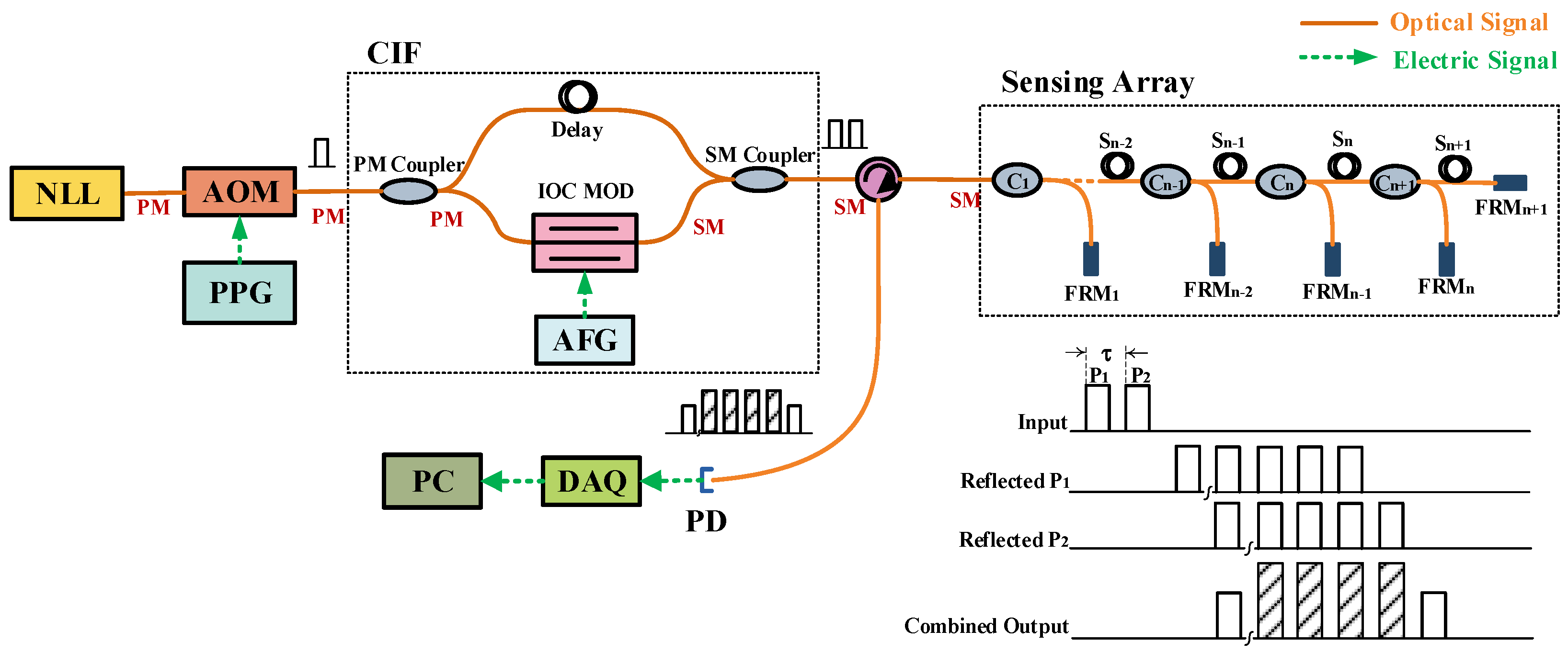
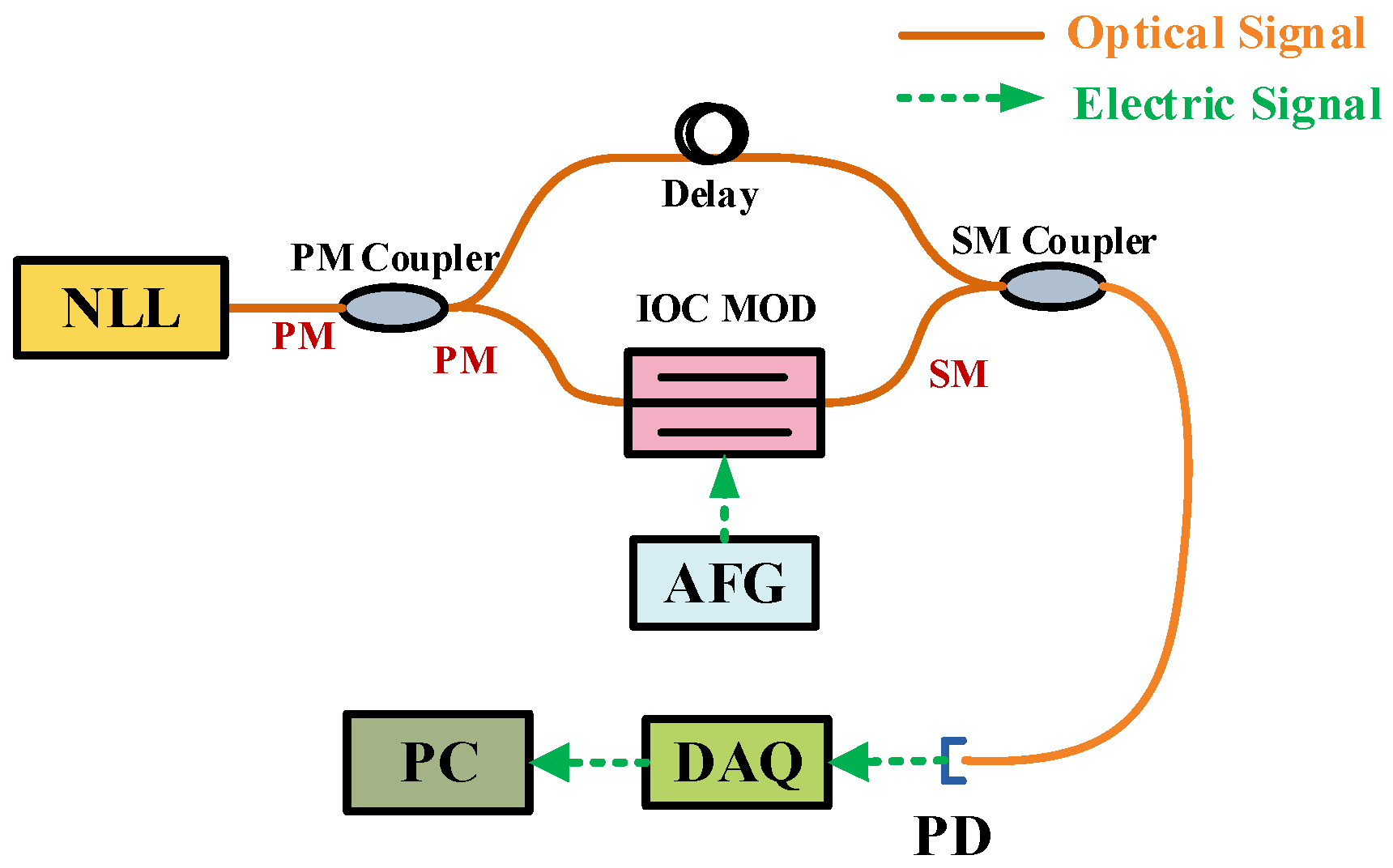
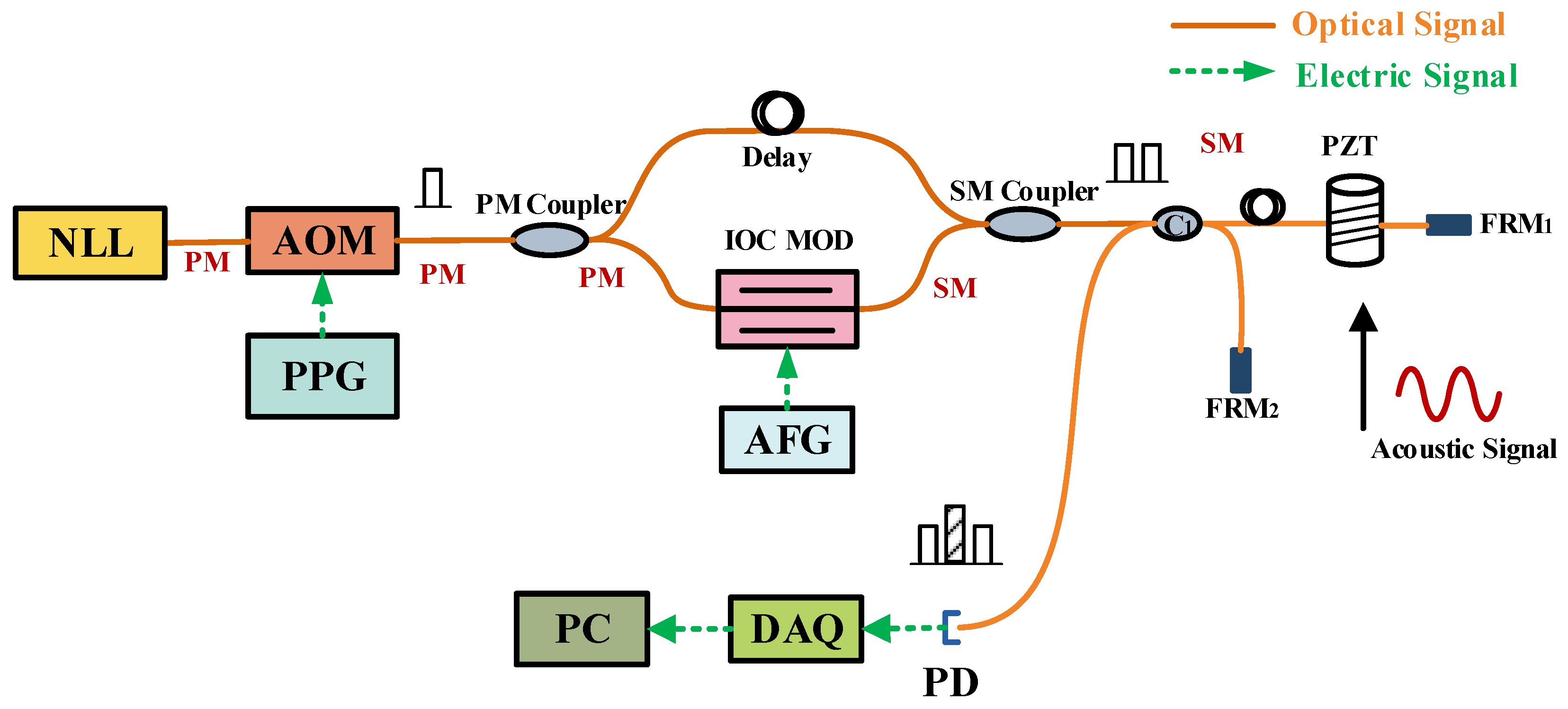
2.1. PMDI-FOH System Design
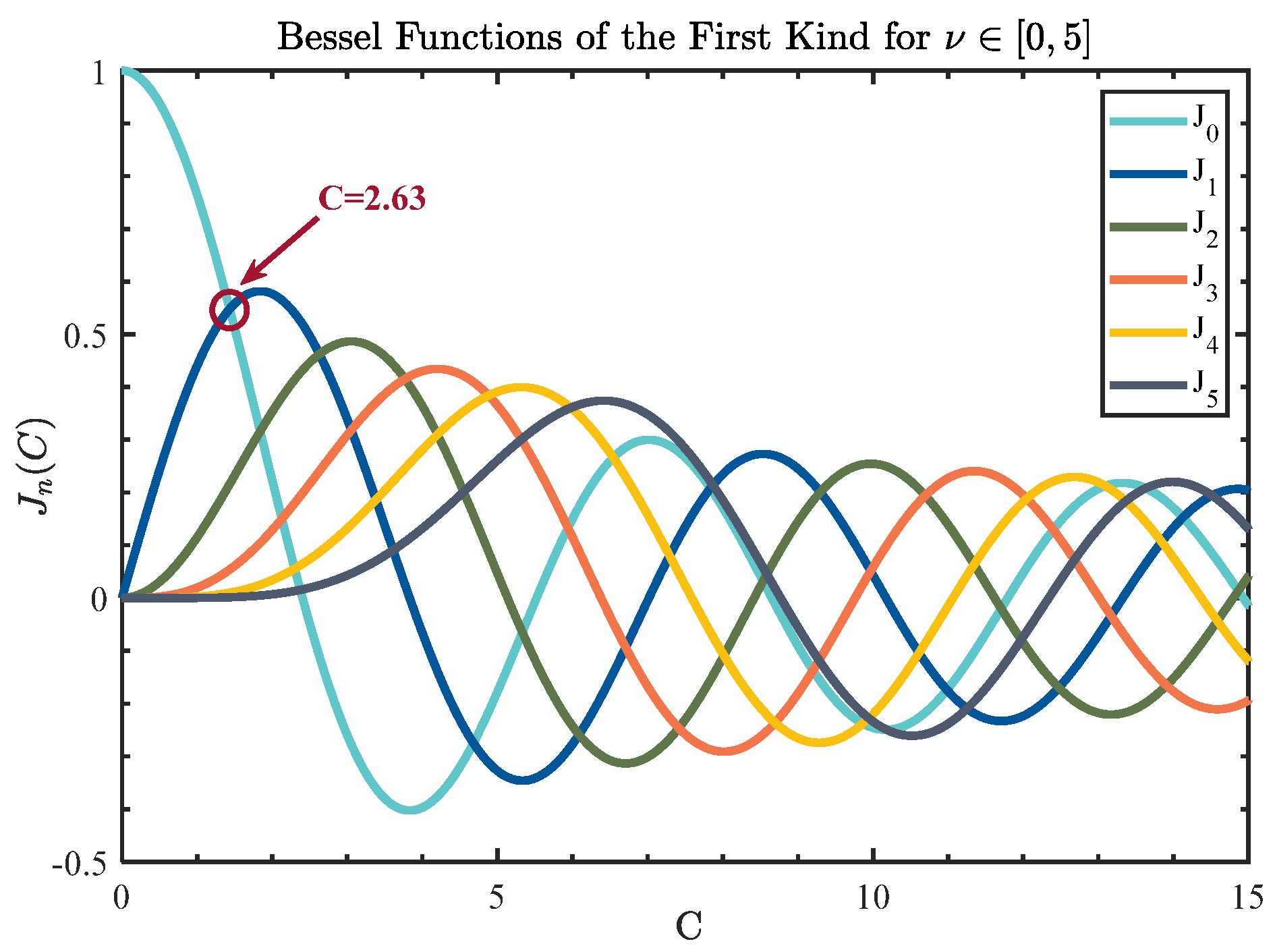
2.2. IOC-Based Phase Modulator
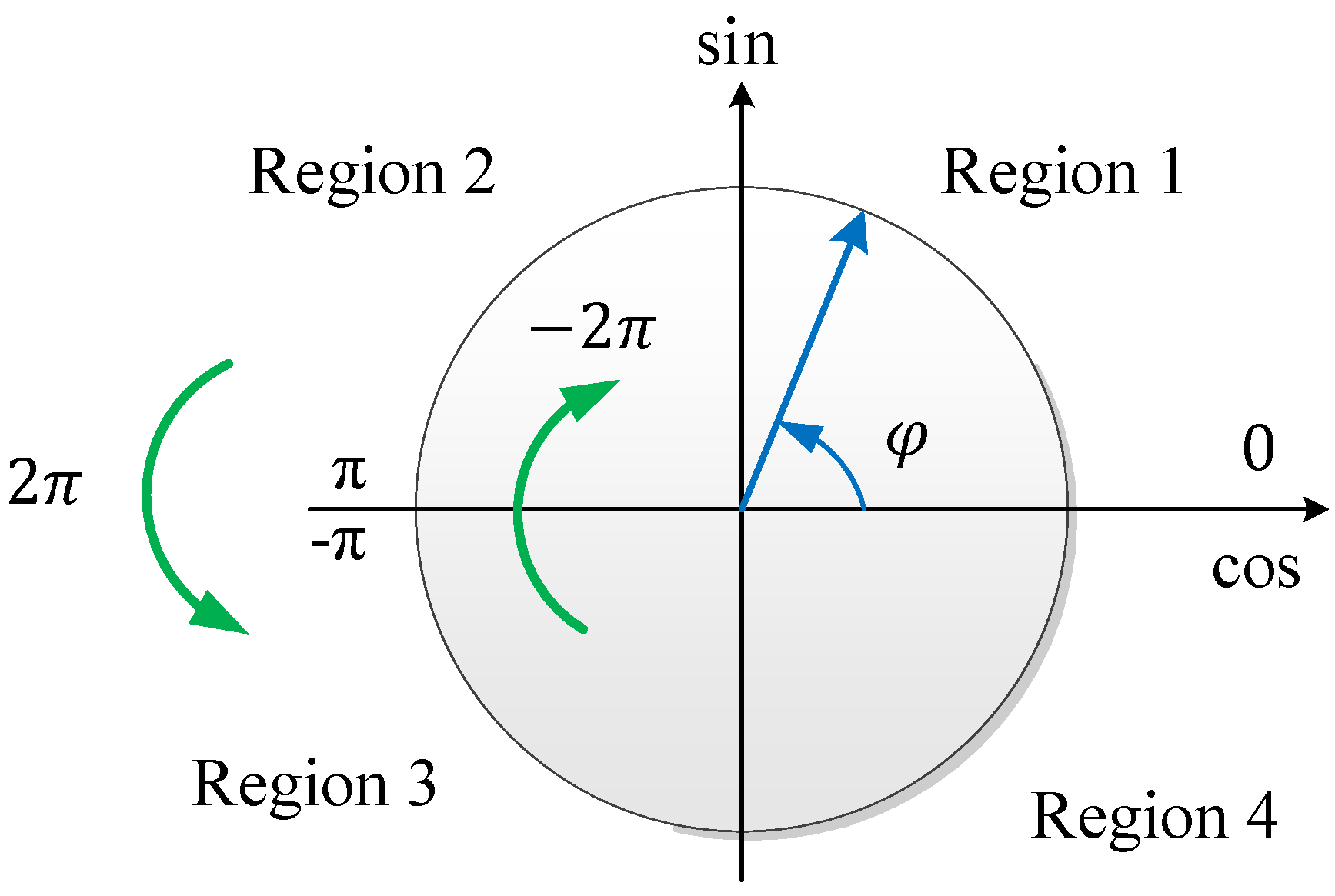
2.3. PGC-Based Demodulation Method
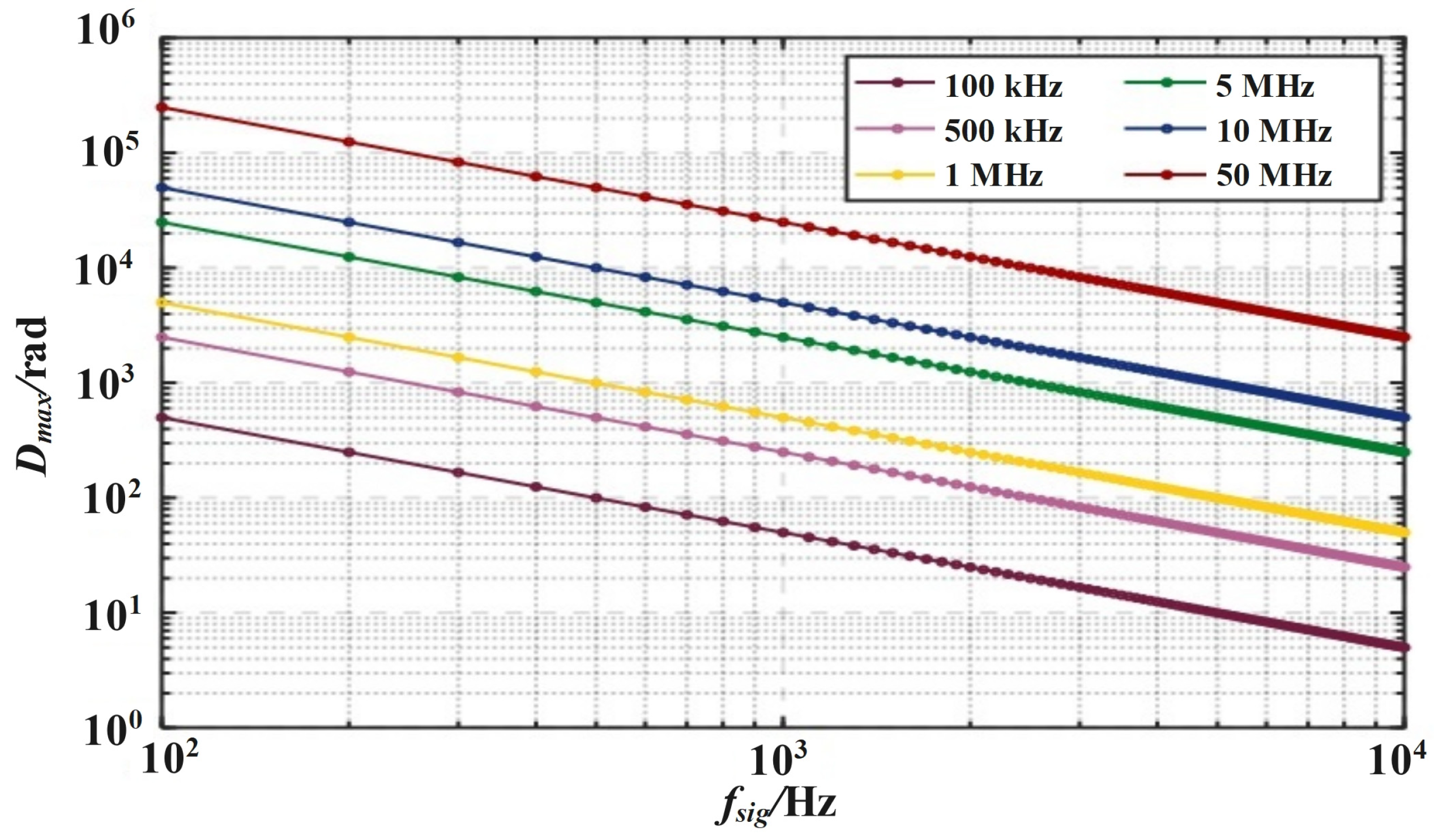
3. Experimental Methods and Results
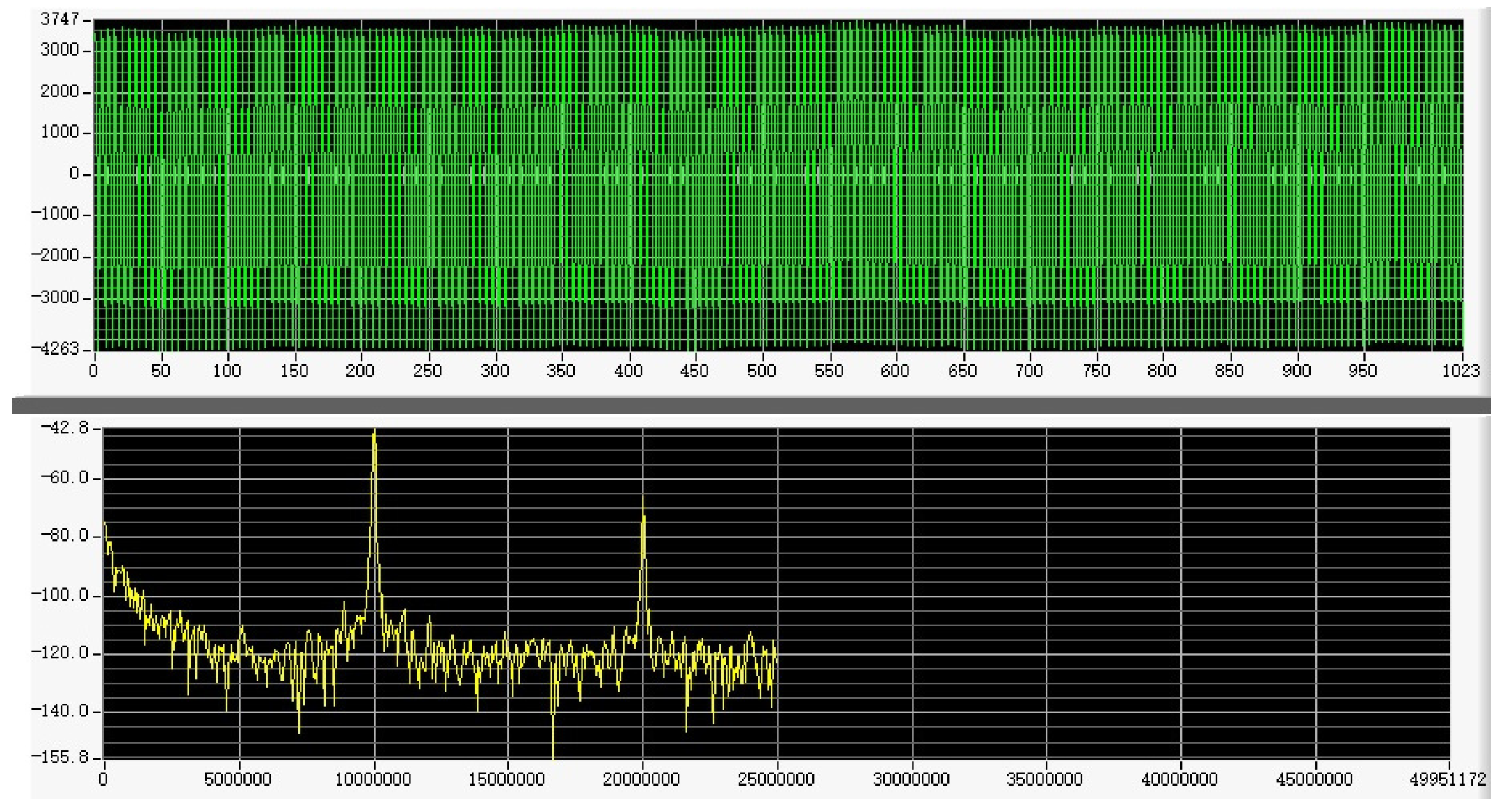
3.1. Phase-Generated Carrier Measurement Experiment
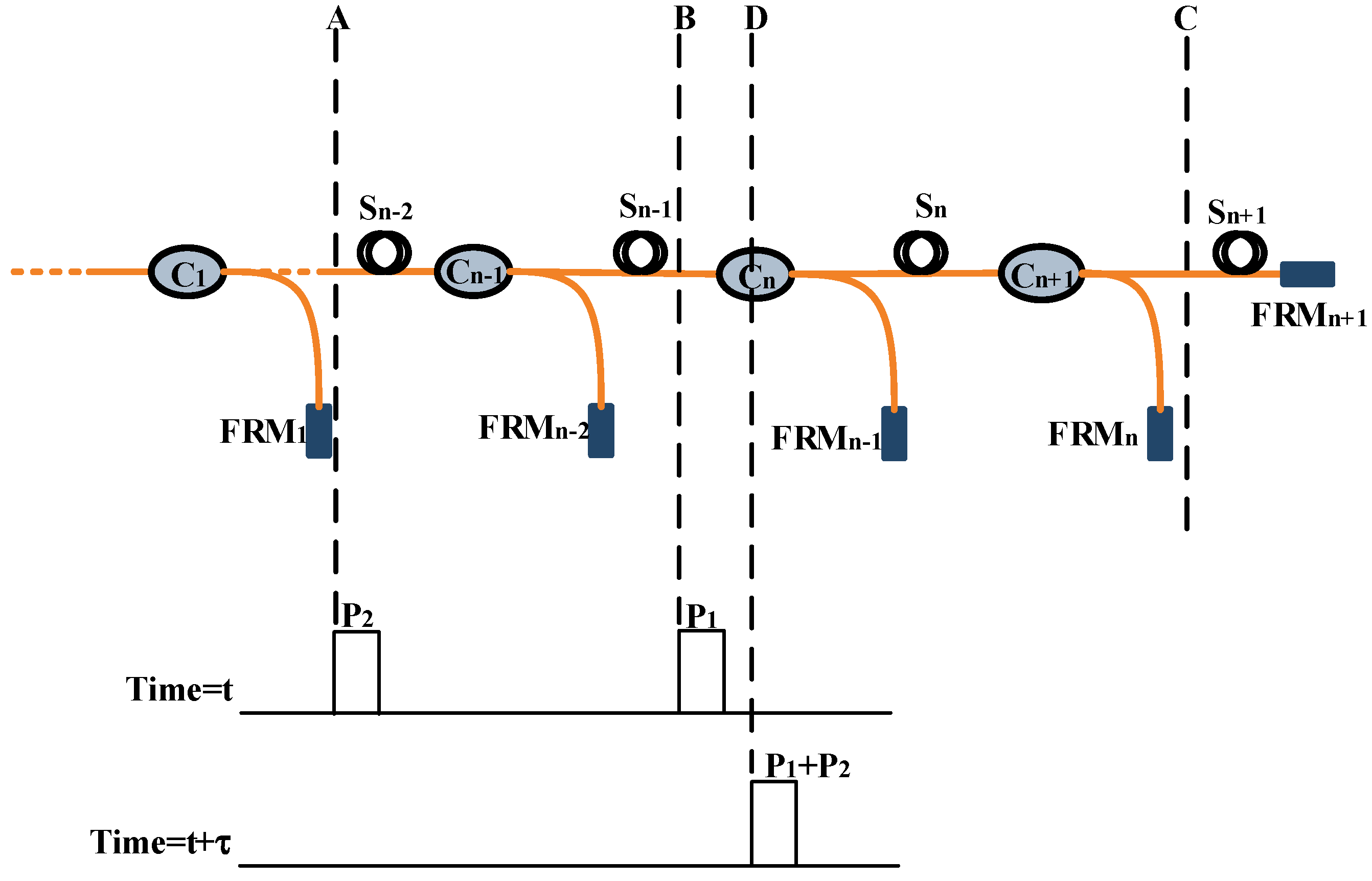
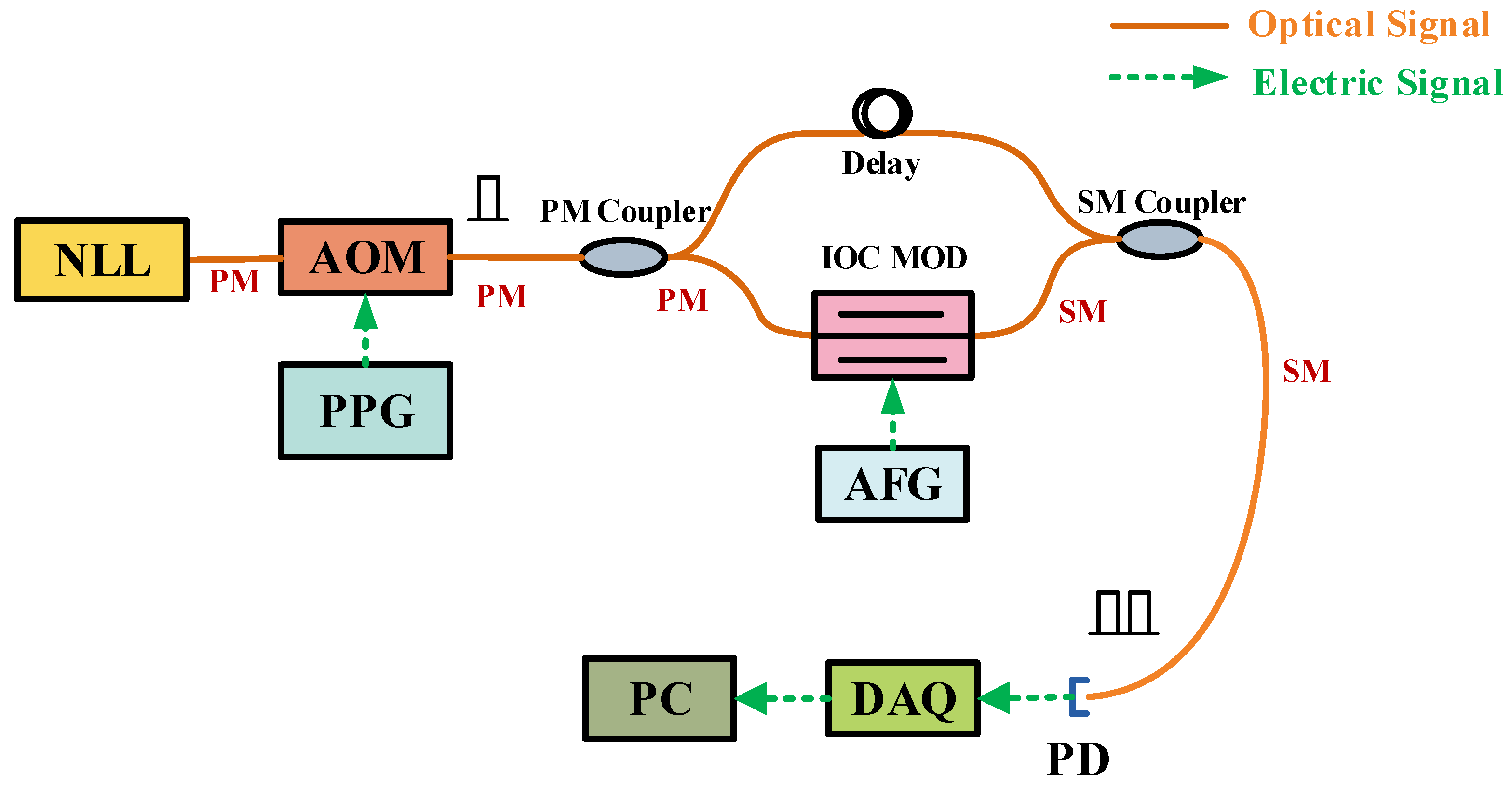
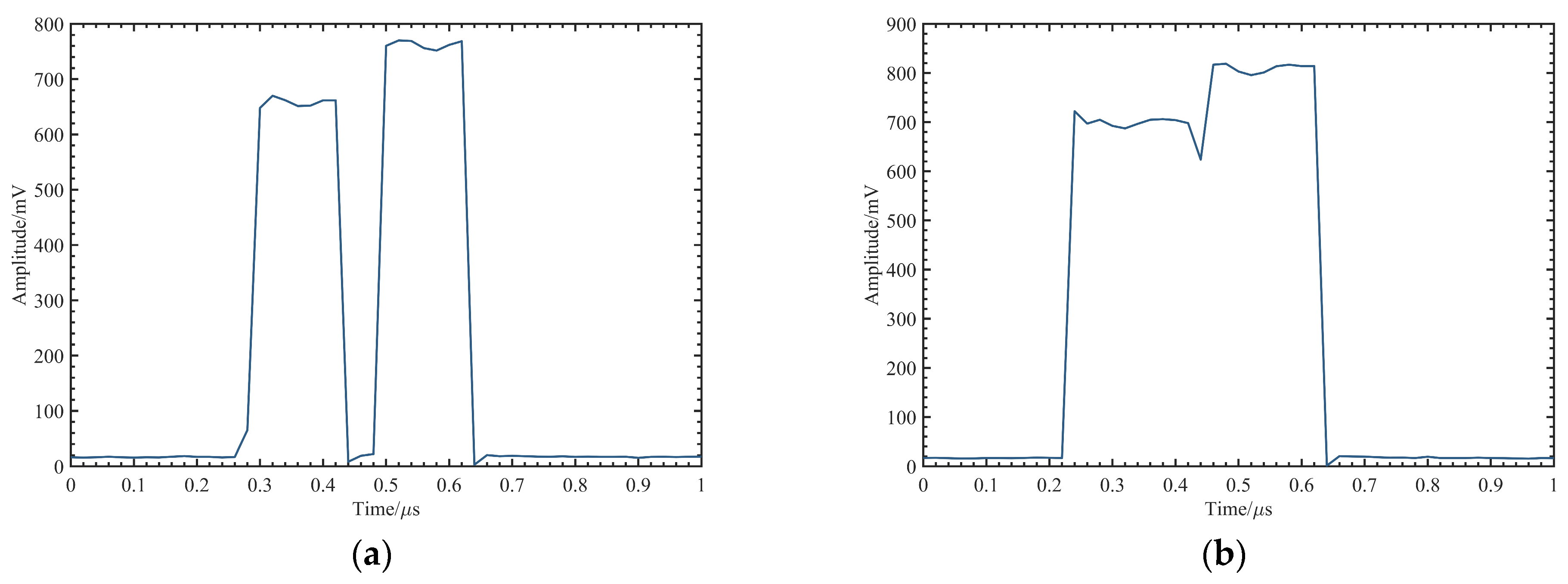
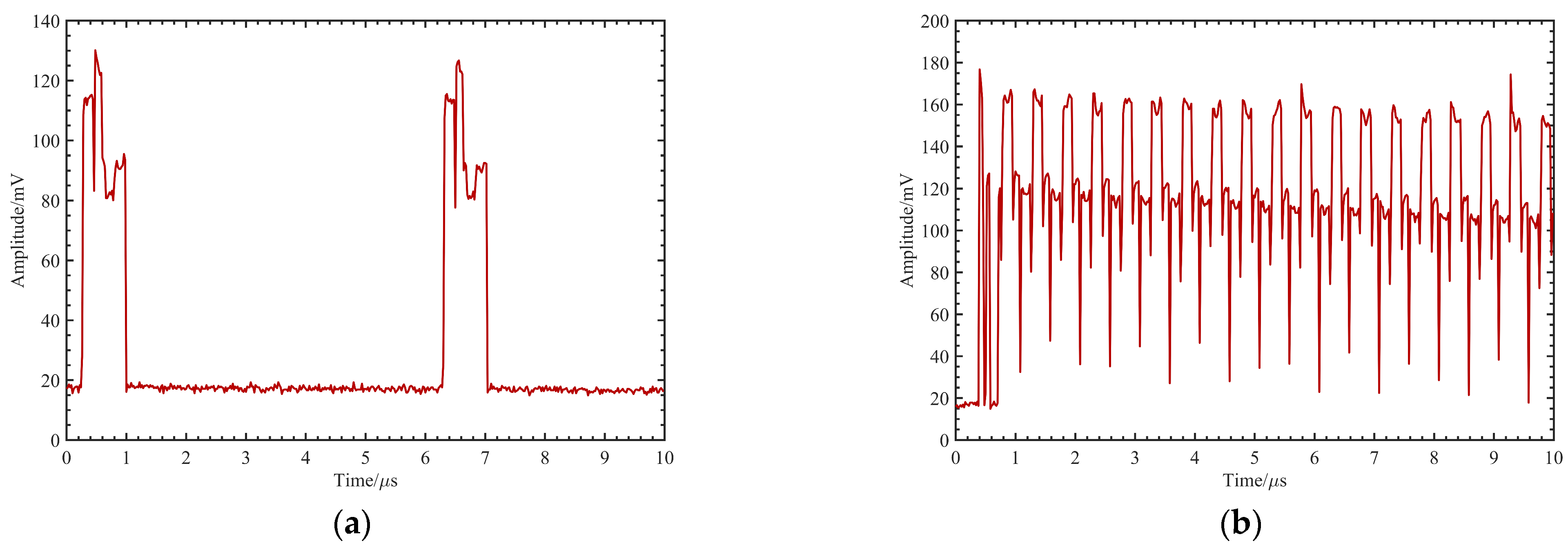
3.2. Dual Pulses Measurement Experiments
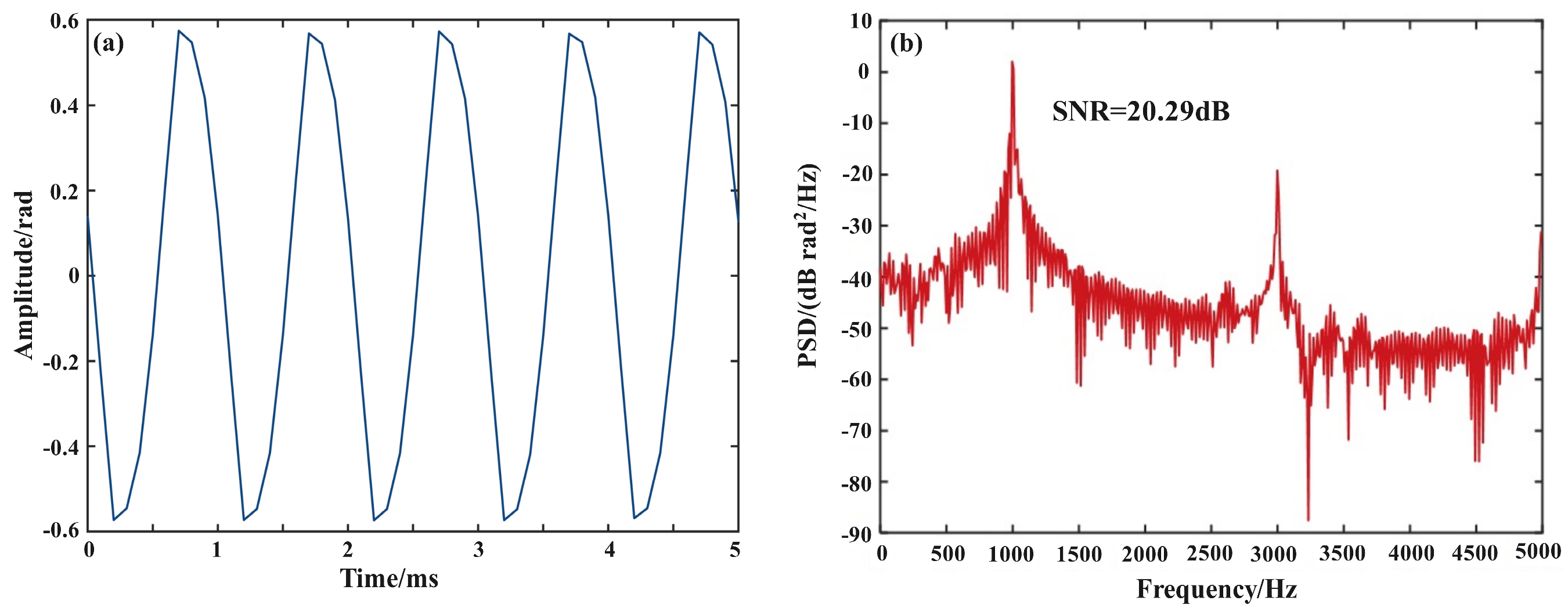
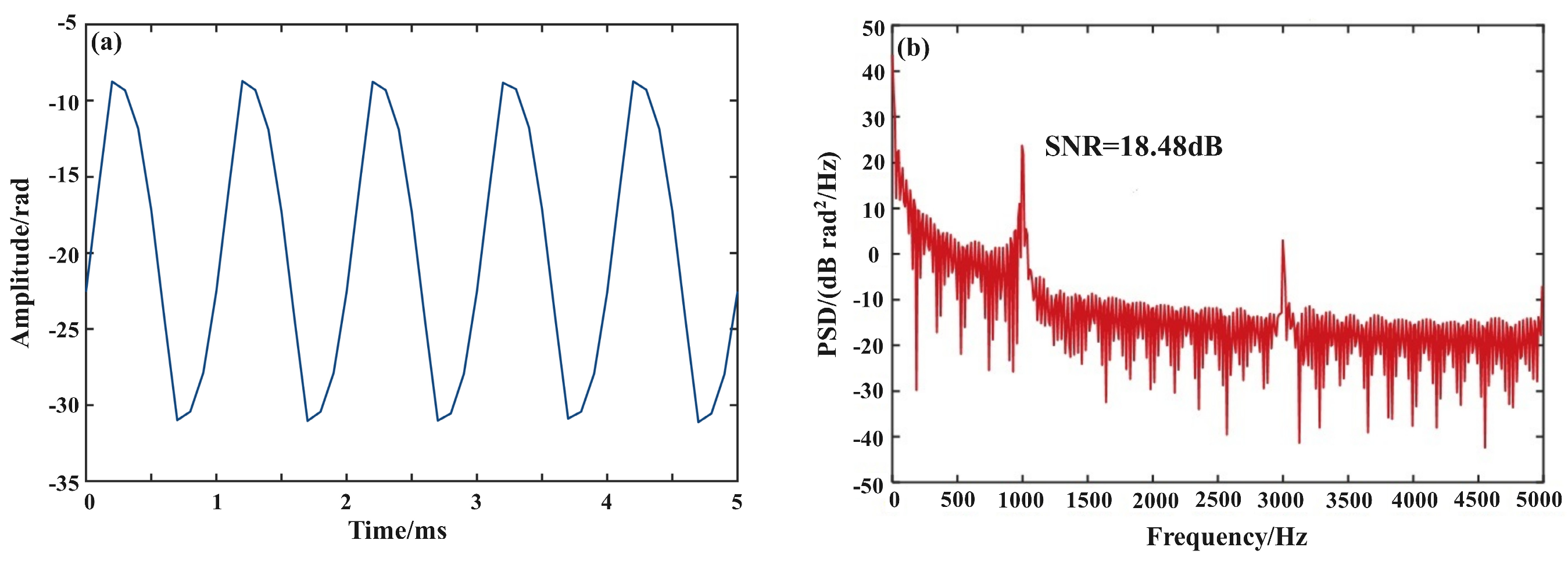
3.3. Acoustic Sensing Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cranch, G.A.; Nash, P.J.; Kirkendall, C.K. Large-scale remotely interrogated arrays of fiber-optic interferometric sensors for underwater acoustic applications. IEEE Sens. J. 2003, 3, 19–30. [Google Scholar] [CrossRef]
- Kringlebotn, J.T.; Nakstad, H.; Eriksrud, M. Fibre optic ocean bottom seismic cable system: From innovation to commercial success. Proc. SPIE Int. Soc. Opt. Eng. 2009, 7503, 75037U. [Google Scholar]
- De Freitas, J.M. Recent developments in seismic seabed oil reservoir monitoring applications using fibre-optic sensing networks. Meas. Sci. Technol. 2011, 22, 052001. [Google Scholar] [CrossRef]
- Zuberi, H.H.; Liu, S.; Sohail, M.Z.; Pan, C. Multi-user underwater acoustic communication using binary phase-coded hyperbolic frequency-modulated signals. IET Commun. 2022, 16, 1415–1427. [Google Scholar] [CrossRef]
- Portmann, C.; Renner, R. Security in quantum cryptography. Rev. Mod. Phys. 2022, 94, 025008. [Google Scholar] [CrossRef]
- Dandridge, A. Fiber Optic Interferometric Sensors at Sea. Opt. Photonics News 2019, 30, 34–41. [Google Scholar] [CrossRef]
- Bruno, F.A.; Janneh, M.; Gunda, A.; Kyselica, R.; Stajanca, P.; Werzinger, S.; Gruca, G.; Rijnveld, N.; Persiano, G.V.; Cutolo, A.; et al. Fiber Optic Hydrophones for towed array applications. Opt. Lasers Eng. 2023, 160, 107269. [Google Scholar] [CrossRef]
- Li, M.; Yu, Y.; Lu, Y.; Hu, X.; Wang, Y.; Qin, S.; Lu, J.; Yang, J.; Zhang, Z. Optical microfiber all-optical phase modulator for fiber optic hydrophone. Nanomaterials 2021, 11, 2215. [Google Scholar] [CrossRef]
- Kirkendall, C.K.; Dandridge, A. Overview of high performance fibre-optic sensing. J. Phys. D Appl. Phys. 2004, 37, R197–R216. [Google Scholar] [CrossRef]
- Yin, S.; Ruffin, P.B.; Francis, T. Fiber Optic Sensors; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Albor, N.; Herr, J.; Mastrogiovanni, S.; Mulderrig, F.; Nucci, L.; Price, A.; Remner, D.; DiTaranto, J.R. Comparison of Fiber Optic and Conventional Sensors for Naval Applications. Nav. Eng. J. 1996, 108, 29–42. [Google Scholar] [CrossRef]
- Dandridge, A.; Tveten, A.; Giallorenzi, T. Homodyne demodulation scheme for fiber optic sensors using phase generated carrier. IEEE J. Quantum Electron. 1982, 18, 1647–1653. [Google Scholar] [CrossRef]
- Dandridge, A.; Tveten, A.; Kersey, A.; Yurek, A. Multiplexing of interferometric sensors using phase carrier techniques. J. Light. Technol. 1987, 5, 947–952. [Google Scholar] [CrossRef]
- Nikitenko, A.N.; Plotnikov, M.Y.; Volkov, A.V.; Mekhrengin, M.V.; Kireenkov, A.Y. PGC-Atan Demodulation Scheme With the Carrier Phase Delay Compensation for Fiber-Optic Interferometric Sensors. IEEE Sens. J. 2018, 18, 1985–1992. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, M.Z.; Wang, H. Dynamic Range of PGC Demodulation Technology in Fiber-Optic Hydrophone System. In Proceedings of the International Conference on Applications and Techniques in Cyber Intelligence, Fuyang, China, 20–22 June 2020. [Google Scholar]
- Zhang, Z.; Cheng, J.; Kong, Y.; Zhang, D.; Zhuang, S. An Improved Phase Generated Carrier Demodulation Algorithm with High Stability and Low Harmonic Distortion. SSRN Electron. J. 2022, 524, 128800. [Google Scholar]
- Green, E.L.; Cable, P.G. Passive demodulation of optical interferometric sensors. IEEE Trans. Microw. Theory Tech. 1982, 30, 1627–1632. [Google Scholar] [CrossRef]
- Zhang, N.; Rao, W.; Meng, Z.; Xiong, S. Investigation on the maximum signal handling capability of fiber optic interferometric sensor based on the digital heterodyne demodulation scheme. Optik 2014, 125, 5771–5775. [Google Scholar] [CrossRef]
- Zhang, C.; Yang, S.; Wang, X. Dual pulse heterodyne distributed acoustic sensor system employing SOA-based fiber ring laser. Front. Phys. 2023, 11, 400. [Google Scholar] [CrossRef]
- Sheem, S.K.; Giallorenzi, T.G.; Koo, K. Optical techniques to solve the signal fading problem in fiber interferometers. Appl. Opt. 1982, 21, 689–693. [Google Scholar] [CrossRef]
- Huang, S.-C.; Lin, W.-W.; Chen, M.-H. Cross-talk analysis of time-division multiplexing of polarization-insensitive fiber-optic Michelson interferometric sensors with a 3 × 3 directional coupler. Appl. Opt. 1997, 36, 921–933. [Google Scholar] [CrossRef]
- Kumar, S.S.; Khansa, C.A.; Praveen, T.V.; Sreehari, C.V.; Santhanakrishnan, T.; Rajesh, R. Assessment of Dynamic Range in Interferometric Fiber Optic Hydrophones Based on Homodyne PGC Interrogator. IEEE Sens. J. 2020, 20, 13418–13425. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, Y.; Meng, Z.; Ni, M. Working-point control method for readout of dynamic phase changes in interferometric fiber-optic sensors by tuning the laser frequency. Appl. Opt. 2008, 47, 3524–3529. [Google Scholar] [CrossRef]
- Xu, W.; Yu, C.; Dong, B.; Wang, Y.; Zhao, W. Thin Piezoelectric Sheet Assisted PGC Demodulation of Fiber-Optic Integrated MZI and its Application in Under Mattress Vital Signs Monitoring. IEEE Sens. J. 2022, 22, 2151–2159. [Google Scholar] [CrossRef]
- Chen, X.; Chandrasekhar, S.; Randel, S.; Raybon, G.; Adamiecki, A.; Pupalaikis, P.; Winzer, P.J. All-electronic 100-GHz bandwidth digital-to-analog converter generating PAM signals up to 190 GBaud. J. Light. Technol. 2017, 35, 411–417. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, M.; Chen, X.; Bertrand, M.; Shams-Ansari, A.; Chandrasekhar, S.; Winzer, P.; Loncar, M. Integrated lithium niobate electro-optic modulators operating at CMOS-compatible voltages. Nature 2018, 562, 101–104. [Google Scholar] [CrossRef]
- He, M.; Xu, M.; Ren, Y.; Jian, J.; Ruan, Z.; Xu, Y.; Gao, S.; Sun, S.; Wen, X.; Zhou, L. High-performance hybrid silicon and lithium niobate Mach–Zehnder modulators for 100 Gbit s−1 and beyond. Nat. Photonics 2019, 13, 359–364. [Google Scholar] [CrossRef]
- Miliou, A. In-Fiber Interferometric-Based Sensors: Overview and Recent Advances. Photonics 2021, 8, 265. [Google Scholar] [CrossRef]
- Li, W.; Chen, Y.; Zhang, J. Phase-shifted Sensitivity Calibration of Fiber Optic Vector Hydrophone Based on Heterodyne Method. In Proceedings of the 2021 OES China Ocean Acoustics (COA), Harbin, China, 14–17 July 2021; pp. 261–266. [Google Scholar]
- Vlasov, A.A.; Plotnikov, M.Y.; Aleinik, A.S.; Volkov, A.V. Environmental Noise Cancellation Technique for the Compensation Interferometer in Fiber-Optic PMDI-Based Sensor Arrays. IEEE Sens. J. 2020, 20, 14202–14208. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, K.; Huang, W.; Zhang, W.; Li, F. Demodulation Scheme with Low Harmonic Distortion for PMDI-TDM Based Fiber-Optic Sensor Array. In Proceedings of the 27th International Conference on Optical Fiber Sensors, Alexandria, VA, USA, 29 August–2 September 2022. [Google Scholar]
- Ames, G.H.; Maguire, J.M. Miniaturized mandrel-based fiber optic hydrophone. J. Acoust. Soc. Am. 2007, 121, 1392–1395. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Xie, J.; Wang, F.; Pan, Y.; Hu, Z.; Hu, Y. Optical fiber acoustic sensing multiplexing system based on TDM/SFDM. Chin. Opt. Lett. 2015, 13, 010401. [Google Scholar]
- Kirkendall, C.K.; Davis, A.; Dandridge, A.D. High Extinction-Ratio Optical Switch and Bias Control. In Optical Fiber Sensors; Optica Publishing Group: Washington, DC, USA, 1997. [Google Scholar]
- Fukuma, M.; Noda, J.; Iwasaki, H. Optical properties in titanium-diffused LiNbO3 strip waveguides. J. Appl. Phys. 1978, 49, 3693–3698. [Google Scholar] [CrossRef]
- Ogawa, O.; Sowa, T.; Ichizono, S. A guided-wave optical electric field sensor with improved temperature stability. J. Light. Technol. 1999, 17, 823–830. [Google Scholar] [CrossRef]
- Takizawa, K.; Yonekura, K.; Jin, L. Temperature characteristics of a Y-cut Z-propagation LiNbO3 light modulator for application to polarimeters. Opt. Rev. 2010, 17, 30–40. [Google Scholar] [CrossRef]
- Bazzan, M.; Sada, C. Optical waveguides in lithium niobate: Recent developments and applications. Appl. Phys. Rev. 2015, 2, 040603. [Google Scholar] [CrossRef]
- Varlamov, A.V.; Plotnikov, M.Y.; Aleinik, A.S.; Agrusov, P.M.; Il’ichev, I.V.; Shamray, A.V.; Vlasov, A.A. Acoustic vibrations in integrated electro-optic modulators on substrates of lithium niobate. Tech. Phys. Lett. 2017, 43, 994–997. [Google Scholar] [CrossRef]
- Niedziela, J. Bessel Functions and Their Applications; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Wang, L.; Zhang, M.; Mao, X.; Liao, Y. The arctangent approach of digital PGC demodulation for optic interferometric sensors. In Proceedings of the SPIE Optics + Photonics, San Diego, CA, USA, 14 August 2006. [Google Scholar]
- Heydemann, P.L. Determination and correction of quadrature fringe measurement errors in interferometers. Appl. Opt. 1981, 20, 3382–3384. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, M.; Liao, Y. Introduction of a Four-Step Modulation Used in PGC Method; SPIE: Bellingham, WA, USA, 2007; Volume 6595. [Google Scholar]
- Yin, H.L.; Fu, Y.; Li, C.L.; Weng, C.X.; Li, B.H.; Gu, J.; Lu, Y.S.; Huang, S.; Chen, Z.B. Experimental quantum secure network with digital signatures and encryption. Natl. Sci. Rev. 2023, 10, nwac228. [Google Scholar] [CrossRef] [PubMed]


| Region | |||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
| Parameters | Measured Data | Unit |
|---|---|---|
| average insertion loss | 3.44 | dB |
| polarization dependent loss | 0.54 | dB |
| output polarized crosstalk | −31.0 | dB |
| half-wave voltage (TE) | 3.75 | V |
| bandwidth | MHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Yang, S.; Wang, X. A Novel PMDI Fiber Optic Hydrophone Incorporating IOC-Based Phase Modulator. Photonics 2023, 10, 911. https://doi.org/10.3390/photonics10080911
Zhang C, Yang S, Wang X. A Novel PMDI Fiber Optic Hydrophone Incorporating IOC-Based Phase Modulator. Photonics. 2023; 10(8):911. https://doi.org/10.3390/photonics10080911
Chicago/Turabian StyleZhang, Chunxi, Sufan Yang, and Xiaxiao Wang. 2023. "A Novel PMDI Fiber Optic Hydrophone Incorporating IOC-Based Phase Modulator" Photonics 10, no. 8: 911. https://doi.org/10.3390/photonics10080911
APA StyleZhang, C., Yang, S., & Wang, X. (2023). A Novel PMDI Fiber Optic Hydrophone Incorporating IOC-Based Phase Modulator. Photonics, 10(8), 911. https://doi.org/10.3390/photonics10080911